Vaderlandsche letteroefeningen. Jaargang 1834

[p. 732]

Kort geschiedkundig verslag van de quadratuur des cirkels. Door H. van Blanken.

Door quadratuur van den cirkel verstaat men eene juiste bepaling van den inhoud, wanneer de middellijn bekend is. Daar deze inhoud gelijk is aan dien van eenen driehoek, welke den omtrek des cirkels tot basis en den straal tot hoogte heeft, zoo wordt door quadratuur ook wel verstaan het vinden van den omtrek, wanneer de middellijn voor bekend wordt aangenomen.

Men onderscheidt deze quadratuur in bepaalde en onbepaalde.

Door bepaalde quadratuur verstaat men het vinden van den geheelen omtrek, of een bepaald gedeelte van denzelven; terwijl men door onbepaalde quadratuur verstaat het vinden van den boog, die tot eenigen gegeven sinus of tangens behoort.

Het zoeken naar de quadratuur, het zij volstrekt of bij benadering, heeft sedert vele eeuwen een verbazend aantal lieden bezig gehouden. Men moet hierbij echter die grondige denkers, welke met zeer veel oordeel de grenzen aangaven, waar binnen deze quadratuur moet gelegen zijn, wél onderscheiden van de zoogenaamde quadrateurs, die met eene zeer oppervlakkige kennis de volstrekte quadratuur meenden gevonden te hebben, en telkens, zoo als ligt te begrijpen is, zich vonden te leur gesteld.

Het volgende korte verslag van hetgeen gedurende meer dan 2000 jaren ter vinding van den inhoud en omtrek eens cirkels is in het werk gesteld, zal zekerlijk aan vele lezers van dit Tijdschrift niet onaangenaam zijn.

De oudste opgave van de betrekking tusschen de middellijn en den omtrek eens cirkels vindt men in I Kon. VII:23, alwaar, bij eene middellijn van 10 ellen, de omtrek op 30 ellen wordt gesteld. Men kan zich evenwel verzekerd houden, dat men toen alreeds lang wist, dat deze betrekking niet naauwkeurig was. Het is echter niet bekend, wanneer en waar men het eerst is begonnen, de betrekking tusschen de middellijn en den omtrek naauwkeurig te vinden. Ten tijde van pericles had het vraagstuk al eenige beroemd-

[p. 733]

heid gekregen. Plutarchus verhaalt ten minste van anaxagoras, dat hij zich in de gevangenis bezig hield met het zoeken naar de quadratuur van den cirkel.

Korten tijd daarna was het zoeken naar de quadratuur in Athene reeds eene zoo bekende zaak, dat aristophanes, ten einde den beroemden meton belagchelijk voor te stellen, in het tooneelspel de Vogelen een' tooneelspeler voor den dag laat komen, die, na gezegd te hebben, dat hij de alom bekende meton is, bij vele belagchelijke redenen over de Meet- en Sterrekunde, zegt: Ik zal u den cirkel quadrateren.

Weinig tijds hierna leerde hippocrates van Chio, naar de quadratuur des cirkels zoekende, den inhoud van eene halve maan bepalen. Hij dwaalde echter, toen hij deze ontdekking op de quadratuur van den geheelen cirkel toepaste.

Bryso, een tijdgenoot van plato, gaf voor, dat de cirkel middenevenredig was tusschen het om- en ingeschreven vierkant.

De meetkundige antiphon was de eerste, van wien ons berigt wordt, dat hij den cirkel als eenen veelhoek van een oneindig aantal zijden beschouwde. Zijne onderzoekingen schijnen echter niet veel merkwaardigs opgeleverd te hebben. Zoodat tot aan den tijd van archimedes, die bij de inneming van Syracusen door marcellus het leven verloor, de inhoud des cirkels nog niet met eenige naauwkeurigheid bepaald was.

Deze voortreffelijke meetkundige koos, zonder zich met het zoeken naar de volstrekte quadratuur in te laten, welke hij misschien reeds voor onmogelijk hield, den weg van benadering, en bepaalde, door het berekenen van de omtrekken der om- en ingeschrevene 96 hoeken, dat de middellijn ten naastenbij tot den omtrek staat als 7 tot 22. Deze betrekking, de naauwkeurigste, welke men in getallen van twee cijfers kan geven, wordt tegenwoordig nog veel gebruikt.

De benadering van archimedes werd door zijnen tijdgenoot apollonius pergaeus nog verder voortgezet, en door philo gaditanus, wiens leeftijd onzeker is, tot tienduizendste deelen naauwkeurig bepaald.^(*)

(*) Dinostratus vond eene kromme lijn, welke de oplossing van het vraagstuk geven zou, indien men dezelve konde beschrijvin: zij behoort tot het getal dier kromme lijnen, welke men tot heden alleen werktuigelijk kan trekken. - Red.

[p. 734]

Waarschijnlijk zal in de middeleeuwen, terwijl de zuivere meetkundige kennis meer en meer verloren ging, het aantal ongelukkige quadrateurs wel zeer groot geweest zijn; van welke de volgende twee vooral in hunnen tijd zeer vermaard zijn geweest, te weten: zekere franco, die een werkje over de quadratuur van den cirkel in het jaar 1047 aan hermannus II, Aartsbisschop van Keulen, zond, en wilhelmus grisauntus, die zich onder de regering van eduard III, omstreeks het jaar 1350, in Engeland beroemd maakte door eene verhandeling over de quadratuur van den cirkel.

Na de herstelling der wetenschappen treffen wij het eerst als quadrateur aan den Kardinaal nic. de cusa, die de volgende stelling bekend maakte: maak eenen cirkel, wiens middellijn gelijk is aan den straal van den gegeven cirkel plus de zijde van het ingeschreven vierkant, en beschrijf in den tweeden cirkel eenen gelijkzijdigen driehoek, dan zal de omtrek van dezen driehoek gelijk zijn aan den omtrek van den gegeven cirkel.

Deze stelling werd wederlegd door den beroemden regiomontanus.

Omstreeks 1530 meende orontius fineus de quadratuur van den cirkel gevonden te hebben; doch hij werd door den vermaarden nonius grondig wederlegd.

Belangrijker waren de dwalingen van den quadrateur simon van eyk, daar zij aan onzen landgenoot pieter metius de aanleiding gaven tot het ontdekken en bekend maken van de betrekking tusschen de middellijn en den omtrek als 113 tot 355, zijnde dit de naauwkeurigste, welke men in getallen van drie cijfers kan hebben, en daarom nog algemeen in gebruik.

Op het einde der zestiende eeuw meende jos. scaliger de quadratuur des cirkels gevonden te hebben, en maakte zijne vermeende ontdekking bekend in een werk, getiteld: nova cyclometria. Doch ch. clavius, Hoogleeraar te Rome, toonde aan, dat, volgens deze quadratuur, de omtrek van den ingeschreven twaalfhoek grooter was dan de omtrek des cirkels.

[p. 735]

Scaliger werd ook wederlegd door fr. vieta, die het eerst den omtrek in eene reeks uitdrukte, en voorts bevond, dat, de middellijn voor eenheid nemende, de omtrek gelijk was aan 3,1415926535, zijnde deze breuk nog in de laatste decimaal naauwkeurig.

Scaliger werd mede wederlegd door adrianus romanus, van Leuven, die met een buitengewoon geduld de zijde eens ingeschreven veelhoeks van 107374824 zijden berekende, en daardoor den omtrek des cirkels tot 15 decimalen naauwkeurig bepaalde.

Hoe verbazend echter het werk van romanus ook reeds ware, hij werd nog zeer ver overtroffen door onzen landgenoot ludolph van ceulen, die, in 1598, in een werk, getiteld: van den ronden cirkel, zijne berekening mededeelde van de zijde eens veelhoeks van 367488907637391105242 zijden, en daardoor den omtrek tot aan 35 decimalen naauwkeurig bepaalde.

Na zijn overlijden in 1610, werd het door hem gevonden getal, dat naar hem den naam van Ludolphiaansch getal draagt, op zijne grafzerk in de St. Pieterskerk te Leyden uitgehouwen.

De berekening van de ingeschrevene veelhoeken door van ceulen was zeer langwijlig. Onze landgenoot wil. snellius, Hoogleeraar te Leyden, dacht daarom, in het begin der zeventiende eeuw, eene kortere wijze van berekenen uit. Snellius vond ook onderscheidene voorstellen, waardoor men met minder moeite, dan van ceulen had aangewend, den omtrek veel nader kan bepalen.

Vele voorstellen van snellius werden bewezen en met nieuwe vermeerderd door onzen grooten landgenoot ch. huigens, die onder anderen het volgende voorstel gaf: viermaal den omtrek eens ingeschreven veelhoeks, verminderd met den omtrek eens veelhoeks, die half zoo veel zijden heeft, is zeer nabij gelijk aan driemaal den omtrek des cirkels.

Huigens berigt ons, dat de beroemde sterrekundige longomontanus, in het begin der zeventiende eeuw, de quadratuur des cirkels meende gevonden te hebben, zoodanig dat, de middellijn 100000 zijnde, de omtrek juist gelijk zou zijn aan 314185.

In het midden der zeventiende eeuw gaf gregorius a s. vincento, een Nederlander, zich zeer veel moeite,

[p. 736]

om de volstrekte quadratuur des cirkels te vinden. Na te vergeefs getracht te hebben om de spiraal van archimedes of de quadratrix van dinostratus daartoe dienstbaar te maken, meende hij eindelijk dezelve gevonden te hebben op eene wijze, welke, ofschoon hij dwaalde, hem evenwel den naam van een aanzienlijk meetkundige waardig maakte. Hij werd wederlegd door cartesius, huigens en vele anderen, en verdedigd door verscheidene van zijne discipelen.

Weinig jaren later bewees de schrandere j. gregori, uit de natuur der convergerende reeksen, in een werk, getiteld: Vera circuli et hyp. quadr., dat de quadratuur des cirkels onmogelijk was.

Omstreeks dezen tijd gaf zekere hobbes voor, de quadratuur des cirkels gevonden te hebben. Hij werd wederlegd door den beroemden wallis, die, nevens vele andere, ook de volgende merkwaardige reeks ontdekte: wanneer de middellijn voor eenheid wordt genomen, dan is de omtrek des cirkels gelijk aan 2/3 × 16/15 × 36/35 × 64/63 × enz. of ook gelijk aan 8/9 × 24/25 × 48/49 × 80/81 × enz.

De voortreffelijke wiskundige j. newton maakte in het laatst der zeventiende eeuw, nevens vele andere reeksen, ook de volgende merkwaardige bekend: indien de straal voor eenheid wordt genomen, dan is de boog, die tot den sinus x behoort, gelijk aan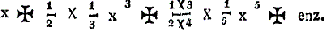

Bijna gelijktijdig maakte zijn landgenoot gregori de volgende reeks bekend: indien de straal voor eenheid wordt genomen, dan is de boog, die tot den tangens x behoort, gelijk aan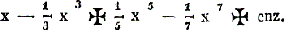

Stelt men in deze reeks x gelijk 1, dan verkrijgt men dezelfde, welke de beroemde leibnitz in 1672 bekend maakte, namelijk 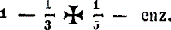welke een achtste deel van den cirkel voorstelt.

[p. 737]

Terwijl de grootste wiskundigen als om strijd de meest geschikte reeksen uitvonden, om den omtrek des cirkels of een gedeelte van denzelven bij benadering te vinden, was er geen kleiner getal quadrateurs onvermoeid werkzaam, om den volstrekten inhoud van den cirkel te bepalen. Wij zullen, alleen om de zonderlingheid, eenige van dezelve hier opnoemen.

In het begin der achttiende eeuw beweerde zekere d. waeywel, dat de middellijn naauwkeurig tot den omtrek stond als 1683 tot 5288. Hieruit zoude volgen, dat de omtrek des cirkels nog grooter was, dan die van den omgeschreven 192 hoek.

Zekere de serres bewees, omstreeks denzelfden tijd, op eene bijzondere wijze, dat de inhoud des cirkels gelijk was aan het dubbel van den ingeschreven driehoek. Volgens hem zou dus de cirkel gelijk zijn aan den ingeschreven zeshoek.

Hierbij verdient de Heer de causans genoemd te worden, die onder anderen aantoonde, dat de cirkel gelijk was aan het ingeschreven vierkant.

Niet minder vreemd was het voorgeven van zekeren j. ward. Deze meetkundige vond, volgens eene hem alleen eigene methode, dat de cirkel een veelhoek was van een bepaald getal zijden.

Ook gaf de Heer basselin, in een werkje, getiteld: Traité démonstratif de la quadrature du cercle, zich bloot aan de regtmatige bespotting der wiskundigen.

De geleerde leibnitz meende ook de onbepaalde quadratuur van den cirkel gevonden te hebben, en gaf voor de grootte van den boog, waarvan x de cosinus was, de straal gelijk aan de eenheid zijnde, de volgende uitdrukking √ (6 - √ (24 × ✠ 12)). Het was echter niet moeijelijk hem van zijne doling te overtuigen, en hierin verschilde hij wezenlijk van de andere quadrateurs.

Vóór dat wij de lijst van ongelukkige quadrateurs vervolgen, behooren wij vooraf melding te maken van eenige werkzame lieden, die met een groot geduld den omtrek des cirkels tot eene meer dan genoegzame naauwkeurigheid berekenden. De eerste, die na van ceulen deze moeijelijke taak op zich nam, was sharp, een Engelsch meetkundige. Hij berekende het getal 3,141 enz. tot 73 tien-

[p. 738]

deeligen, doch werd weldra nog ver overtroffen door machin, die deze benadering tot 100 decimalen voortzette.

Machin werd nog wederom ver overtroffen door den Heer de lagni, die in 1719 deze benadering tot 127 decimalen bekend maakte.

In het eind der zeventiende eeuw gaf brouncker, een Engelsche Lord, de volgende merkwaardige uitdrukking voor den omtrek, wanneer de middellijn voor eenheid wordt genomen: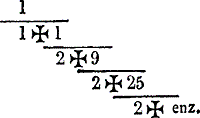

Deze uitdrukking behoort tot eene soort van breuken, welke onder den naam van gedurige breuken bekend zijn. De groote euler heeft ons het eerst zeer vele merkwaardige eigenschappen van deze breuken doen kennen. Door middel van dezelve kan men thans gemakkelijk de groote tiendeelige breuken, waardoor de omtrek wordt uitgedrukt, tot bijna gelijkwaardige kleinere gewone breuken herleiden.

Euler heeft ook voornamelijk aan de reeds bestaande reeksen, ter berekening van den omtrek des cirkels en van de sinustafels, eenen meer geschikten vorm gegeven, en dezelve met vele nieuwe vermeerderd.

Met deze hulpmiddelen heeft het von vega dan ook mogen gelukken, het getal 3,141 enz. tot 143 decimalen te berekenen; eene naauwkeurigheid, waarvan men zich naauwelijks een denkbeeld kan vormen.

Niettegenstaande de vorderingen, welke men in de twee voorgaande eeuwen in de kennis van den cirkel gemaakt heeft, is de tegenwoordige nog al rijk aan quadrateurs, die in zonderlingheid voor niemand van de vorige eeuwen behoeven te wijken. De volgende Italiaan is vooral zeer zeldzaam in zijne soort. Alle wiskundigen hielden de diagonaal van een vierkant ten opzigte van de zijde voor onmeetbaar; de geleerde gaetano rossi vond echter in het begin der negentiende eeuw, dat de zijde van een vierkant tot zijn diagonaal staat als 5 tot 7. Men had reeds lang den omtrek des cirkels ten opzigte van de middellijn als on-

[p. 739]

meetbaar beschouwd; doch de schrandere gaetano rossi vond, dat de middellijn tot den omtrek staat als 5 tot 16. Vreezende, dat iemand hem de eer van deze gewigtige ontdekkingen mogt ontrooven, plaatste hij, bij zijn vertrek van Parijs naar Londen, een kort verslag van dezelve in de Bibliothèque nationale, en liet zich daarvoor een reçu ter hand stellen. Eindelijk had hij de goedheid, zijne ontdekkingen in 1804 te Londen bekend te maken, en ook van dezelve verslag te geven in een werkje, opgedragen aan zijne Excell. r.j. schimmelpenninck, welk werkje op de volgende zonderlinge wijze eindigt: j'ose espérer que les droits que j'ai à la récompense de 600000 francs, qui, comme un prix d'émulation, ont été destinés, par l'immortel charles V, au Géomètre, qui aurait le bonheur de résoudre le problême de la Quadrature du Cercle, ne me seront point contestés.

In 1828 meende de Heer m.i.s. bevel gevonden te hebben, dat een vierde van den omtrek des cirkels juist gelijk was aan den straal plus de tangens van 30 graden, en bijgevolg de halve omtrek gelijk aan de middellijn plus de zijde van den omgeschreven zeshoek. Eene eenvoudige berekening toont echter aan, dat die som nog wel een honderdste deel van den omtrek verschilt. De constructie van den omtrek, welke de Heer bevel op zijne gemeende quadratuur grondt, geeft bijgevolg den omtrek nog minder naauwkeurig, dan die, welke men uit de betrekking van archimedes kan afleiden.

Daar zijn echter door vele voorname meetkundigen onderscheidene constructiën aangewezen, door welke men den omtrek tot eene zeer groote naauwkeurigheid kan bepalen.

Zoo vond vieta, dat de middellijn en de zijde van den tienhoek zeer nabij vijf twaalfde van den omtrek uitmaken.

Huigens toonde aan, dat de omtrek ten naastenbij gelijk is aan zesmaal den straal, plus een vijfde van de zijde des ingeschreven vierkants.

Kolhanski gaf de volgende zeer naauwkeurige constructie: trek op de beide uiteinden eener middellijn loodlijnen; maak de eene loodlijn gelijk aan 3 maal den straal en de andere aan de tangens van 30 graden, dan zal de lijn, welke de uiteinden dezer loodlijnen vereenigt, geen honderdduizendste deel van den halven omtrek des cirkels verschillen.

[p. 740]

Ofschoon de onmeetbaarheid van den omtrek tot de middellijn reeds lang is bewezen, bestaat er geene reden, waarom de quadratuur in geenen meetkundigen zin zoude kunnen gevonden worden. De groote euler heeft, in het 22 Cap. van het 2de Boek zijner Analysis des Unendlichen, eenen weg aangewezen, langs welken deze quadratuur nog wel eens bij toeval kon gevonden worden. Wij kunnen echter niemand aanraden, zijnen tijd aan het zoeken naar zoodanig eene quadratuur te besteden, wijl het vooreerst zeer onwaarschijnlijk is, dat hij ooit in zijn onderzoek zou slagen, en ten andere, zoo dit al eens mogte gelukken, der wetenschappen hiermede nog geene wezenlijke dienst zou doen.^(*)

Zwolle, den 29 Aug. 1834.

(*) Indien men de geschiedenis van de quadratuur des cirkels uitvoeriger begeert te lezen, kan men nazien het werk van montucla, uitgegeven in 1754 onder den titel van: Histoire des recherches sur la quadrature du cercle. - Red.