Tijdschrift voor Taalbeheersing. Jaargang 28

[p. 323]

Bert Meuffels en Huub van den Bergh
De ene tekst is de andere niet
The language-as-a-fixed-effect fallacy revisited: Statistische implicaties.

Samenvatting

In dit artikel wordt in praktische zin ingegaan op de statistische implicaties van de door Clark geïntroduceerde language as a fixed-effect fallacy. Getracht wordt de statistische implicaties van deze fallacy (alpha-inflatie) in niet-technische termen uit te leggen. Gedemonstreerd wordt dat de toetsingsgrootheid (F-ratio) afhankelijk is van het specifiek onderzoeksontwerp. In dat kader wordt aan de hand van vier multiple message designs (twee binnen-proefpersoon ontwerpen, twee tussen-proefpersoon ontwerpen) geïllustreerd hoe de voor die specifieke designs geëigende F-ratio geconstrueerd moet worden. Tevens wordt gedemonstreerd hoe de betreffende F-ratio's via SPSS achterhaald kunnen worden.

1. De fixed-effect fallacy gedissocieerd

In een vorige aflevering van dit tijdschrift zijn methodologische implicaties van de door Clark geïntroduceerde fixed-effect fallacy besproken (Meuffels & Van den Bergh 2005).¹ Clark zelf beschouwde deze fout (waaraan vrijwel de gehele gemeenschap van toenmalige kwantitatiefempirisch georiënteerde taalonderzoekers zich volgens hem in de jaren zestig en zeventig schuldig maakte) als een puur statistische fout. De door Clark geïntroduceerde drogreden is echter in de vorige bijdrage door ons gedissocieerd in twee typen fouten:

1. Een fallacy van methodologische aard; deze design-fout manifesteert zich wanneer in taalwetenschappelijk onderzoek de niveaus van de categoriale, gefixeerde variabele (de ‘explanatory’ variabele) waarnaar de theoretisch-inhoudelijke interesse van de taalwetenschappelijke onderzoeker uitgaat, in instrumenteel-operationele zin slechts gerepresenteerd wordt door één instantiatie: één tekst (of één zin, één woord, letter, kortom één talig element). In een dergelijk design, een single message design genoemd, kan niet gediscrimineerd worden tussen de effecten op specifiek-instrumenteel niveau en de effecten op generiek, categoriaal-abstract niveau. Omdat beide soorten effecten in een single message design verstrengeld (‘confounded’) zijn, wordt zowel de interne als de externe validiteit van zulk soort taalwetenschappelijk onderzoek aangetast. Wat de interne validiteit van een dergelijk single message design betreft: een ondubbelzinnig onderscheid tussen (pseudo-) confirmatie en (pseudo-) falsificatie van de onderzoekshypothese is als gevolg van de verstrengeling niet goed mogelijk. Wat de externe validiteit van een dergelijk design betreft: een generalisatie van de steekproefgegevens naar een populatie van gelijksoortige proefpersonen én naar een populatie van gelijksoortig talig materiaal, is - op grond van de omstandigheid dat slechts één talig element werd onderzocht - dubieus.

1 In deze bijdrage wordt voortgebouwd op een eerder in dit tijdschrift gepubliceerd artikel (Meuffels & Van den Bergh 2005) waarin met name op de methodologische implicaties van de fixed-effect fallacy werd ingegaan. Het is, gegeven het kort bestek van dit artikel, niet doenlijk de daar behandelde begrippen als fixed-effect fallacy, ‘explanatory’ variabele, ‘confounding’, interne en externe validiteit, het onderscheid tussen random en gefixeerde factoren en tussen single en multiple message designs hier opnieuw toe te lichten - in de behandeling van de statistische implicaties van de fixed-effect fallacy in dit artikel wordt er daarom vanuit gegaan dat de genoemde begrippen en onderscheidingen bekend zijn en geen verdere toelichting meer behoeven.

[p. 324]

2. Een fallacy van inductief-statistische aard; deze statistische fout treedt op in een multiple message design waarbij er in de statistische analyse ten onrechte vanuit gegaan wordt dat de random factor ‘talige/tekstuele instantiatie’ (die in taalwetenschappelijk onderzoek vaak genest is binnen de categoriale, gefixeerde ‘explanatory’ variabele) een gefixeerde factor, en niet een random factor, zou zijn. Het gevolg van deze misclassificatie is dat de - op basis van een F-ratio - geschatte alpha-fout (type I-fout) geflatteerd is, dat wil zeggen een ‘positieve bias’ vertoont². Dat heeft weer tot gevolg dat de kans dat ten onrechte de bevindingen vanuit de steekproef naar de populatie gegeneraliseerd worden, groter is dan het door de betreffende empirisch onderzoeker gerapporteerde nominale niveau van 5%. Hoeveel groter is doorgaans onbekend - soms echter kan die grootte vrij nauwkeurig geschat worden, onder andere met behulp van simulatie-studies. Uit studies als deze blijkt dat onder extreme condities de positieve bias die optreedt wanneer random factoren ten onrechte in de data-analyse als gefixeerde factoren worden behandeld, soms de grootte van een factor 10 aanneemt (Forster & Dickinson 1976). In de praktijk komt dit laatste op het volgende neer: de taalwetenschappelijke onderzoeker rapporteert een p-waarde (een alpha-fout) van p < 0.05, denkt dan op grond van het conventioneel bepaalde significantieniveau van 5% de nulhypothese: ‘geen verschil tussen gemiddelden van de niveaus van een treatment in de populatie’ te kunnen verwerpen en dus de resultaten te kunnen generaliseren naar de populatie (zowel naar de populatie ‘proefpersonen’ als naar de populatie ‘taal’), terwijl in feite het significantieniveau minstens. 50 bedraagt.

2 Als een statistische toets een positieve bias vertoont, impliceert dit dat de nulhypothese ten onrechte te snel verworpen wordt - men spreekt in dit verband ook wel van een ‘liberale’ toets. Ook het omgekeerde is uiteraard mogelijk: bij een toets die een negatieve bias vertoont (ook wel een ‘conservatieve’ toets genaamd) wordt de nulhypothese ten onrechte ‘te langzaam’, dus vaak niet verworpen terwijl dat in feite wel het geval zou moeten zijn. Zou men tussen deze twee kwaden moeten kiezen, dan zou de keuze van de wetenschappelijk-statistische gemeenschap ongetwijfeld op de conservatieve toets (met negatieve bias) vallen: liever een ‘miss’ dan een ‘false alarm’.

2. Doel

In deze bijdrage waarin kennis van statistische nulhypothese-toetsing en van variantie-analyse wordt voorondersteld, gaan we in eerste instantie in algemene, niet-technische zin in op de onder punt 2 genoemde statistische fout (technisch commentaar van statistische aard wordt in de voetnoten opgenomen). Wat houdt deze statistische fout waarvoor Clark de in retorisch opzicht³ zo toepasselijke naam ‘fixed-effect fallacy’ introduceerde, nu in feite in? Inzicht in het antwoord op deze vraag is niet zonder enig praktisch belang: in het Tijdschrift voor Taalbeheersing treft men de fixed-effect fallacy immers regelmatig aan, zo bleek uit een door ons uitgevoerde meta-analyse van experimentele artikelen die de afgelopen 23 jaargangen in dit tijdschrift verschenen zijn. In 32 van de 34 mogelijke gevallen werd de door Clark gewraakte drogreden aangetroffen (Meuffels & Van den Berg 2005: 121-122) - alle reden dus om er aandacht aan te besteden.

De fixed-effect fallacy vooronderstelt het gebruik van een multiple message design. Na een niet-technische uitleg van de fixed-effect fallacy gaan we in op de statistische verwerking van data die zijn verkregen aan de hand van zulk soort multiple message designs. Met behulp van dit type designs (designs dus waarin de categoriale, gefixeerde ‘explanatory’ variabele in instrumentele zin gerepresenteerd is door niet één, maar door verschillende talige instantiaties) is de taalwetenschappelijke onderzoeker in beginsel in staat om de verstrengeling (de ‘confounding’) van effecten op abstract-categoriaal niveau en op specifiek-instrumenteel niveau te ontrafelen. Daardoor is de interne validiteit - op dit punt althans - gewaarborgd; en het spreekt voor zich dat de externe validiteit van dergelijke designs vele malen groter is dan die van de daarmee concurrerende single message designs.

In dezelfde, door ons uitgevoerde meta-analyse van experimentele artikelen in de eerste

3 Over retorische gaven beschikte Clark onmiskenbaar: het statistische probleem immers dat hij in 1973 in zijn geruchtmakende artikel voor het auditorium van taalonderzoekers in het algemeen en van psycholinguïsten in het bijzonder behandelde, was al zo'n kleine tien jaar daarvoor door Coleman (1964) uitvoerig aan de orde gesteld, maar diens artikel dat gericht was op een breed publiek van psychologen bleek bij lange na niet de enormeinvloed te krijgen die, getuige onder andere de vele citaties, aan Clarks publicatie kan worden toegedicht.

[p. 325]

23 jaargangen van het Tijdschrift voor Taalbeheersing bleek dat in iets meer dan de helft van het gerapporteerde experimenteel-taalwetenschappelijk onderzoek (namelijk in 51 van de in totaal 94 gevallen) een, vanuit methodologisch perspectief beschouwd, inadequaat design gehanteerd werd, namelijk een single message design. En ‘inadequaat’ moet hier nadrukkelijk niet in absolute zin geïnterpreteerd worden, als wel in relatieve zin: inadequaat namelijk in het licht van de door de empirisch-taalwetenschappelijke onderzoeker zélf naar voren gebrachte claim (i.c. de in het betreffende empirisch taalwetenschappelijk onderzoek te toetsen hypothese) die, gezien de generieke aard ervan, niet zozeer betrekking heeft op één specifiek talig element (één min of meer toevallige instantiatie), maar veeleer op een meer abstracte, bovenliggende categorie die een klasse van talige verschijnselen bestrijkt waarvan het onderzochte talige specimen slechts een min of meer toevallige verbijzondering betreft.

Multiple message designs mogen dan wel voor empirisch-taalwetenschappelijk onderzoek op grond van methodologische overwegingen betreffende interne en externe validiteit superieur zijn aan single message designs, dat neemt niet weg dat zulke multiple message designs nogal gecompliceerd zijn. Dat zijn ze niet alleen qua opzet en praktische uitvoering, maar vooral ook wat betreft de statistische analyse via bestaande computerprogramma's. Anders dan voor single message designs bestaan er voor vele multiple message designs (bijvoorbeeld het specifieke design aan de hand waarvan Clark de fixed-effect fallacy bespreekt) tot op heden geen kanten-klare, computer-gegenereerde oplossingen die probleemloos de gewenste toetsingsgrootheid (F-ratio) opleveren. De onderzoeker zal in zulke specifieke gevallen zelf via een aantal computerruns en - uiteindelijk - via een zakrekenmachine de gewenste F-ratio moeten berekenen. Hierbij moet hij uitgaan van het statistisch model dat aan het gehanteerde multiple message design ten grondslag ligt; het genereren van zo'n statistische model (via algoritmische procedures) is echter bepaald geen sinecure.⁴

Om de praktische bruikbaarheid van deze bijdrage te vergroten, presenteren we een viertal multiple message designs inclusief de daarbij behorende statistische analyse. Voor elk design wordt het daaraan ten grondslag liggende statistische model geëxpliciteerd, wordt de vorm en structuur van de relevante F-ratio (ter toetsing van treatment-effecten) vermeld, en bij elk design geven we aan de hand van gefingeerde datasets steeds aan hoe de betreffende data in SPSS verwerkt worden.

De vier te bespreken multiple message designs (hierna te noemen: design I, design II, III en IV) zijn overigens niet willekeurig gekozen uit het grote potentieel aan mogelijke designs: anders dan design I en II die een binnen-proefpersonen ontwerp betreffen, vormen design III en IV tussen-proefpersonen ontwerpen. Design I is het ontwerp waar Clark in zijn bespreking van de fixed-effect fallacy van uitgaat - uit de aard der zaak kan dit ontwerp in dit artikel niet onbesproken blijven. Bovendien behelst dit design een ontwerp dat aanleiding geeft tot de constructie van een geheel afwijkend type F-ratio (namelijk een quasi F). Design II is wat complexer en betreft in feite een generalisatie van design I: is er in design I sprake van slechts één treatment, in II spelen twee onafhankelijke variabelen en hun eventuele interactie een rol. Overigens, net als design I treft men ook dit design in het Tijdschrift voor Taalbeheersing aan. Design III en IV (de tussen-proefpersonen ontwerpen) zijn als illustratieve voorbeelden van multiple message designs gekozen omdat in de praktijk van alledag vaak gekozen zal moeten worden tussen één van beide configuraties die als het ware elkaars spiegelbeeld vormen: III komt met name in aanmerking wanneer de beschikbaarheid van grote aantallen proefpersonen geen al te groot probleem vormt terwijl de constructie of ‘sampling’

4 Welk soort F-ratio als adequate toetsingsgrootheid van effecten in een bepaald design kan fungeren, is afhankelijk van het statistisch model dat ten grondslag ligt aan het gespecificeerde design. In een statistisch model zijn (1) alle variantie-bronnen die in het design aanwezig zijn, geëxpliciteerd (inclusief geneste effecten en interacties), en (2) alle variantie-bronnen herschreven (‘uiteengerafeld’, ‘gedecomponeerd’) als de som van variantiecomponenten. Een statistisch model leidt tot de verwachtingswaarden van de MS-termen (‘Mean Squares’, gemiddelde kwadratensommen) die op hun beurt de basis vormen voor de constructie van een adequate F-ratio. In de bekende handboeken (bijvoorbeeld Kirk 1968; Winer 1971; Keppel 1982; 1991) hebben statistici een scala aan statistische modellen gespecificeerd inclusief de daarbij behorende F-ratio's en vrijheidsgraden, althans voor de in de empirische wetenschappen meest frequente designs. Voor die gevallen waarin de handboeken niet voorzien - en dat geldt met name voor multiple message designs - zal men algoritmische procedures moeten toepassen (zie bijvoorbeeld Kirk 1968, 50-58; 208-212; Bennett & Franklin (1954: 413); Cornfield & Tukey (1956); Winer (o.c.371-374). Het aantal algoritmische regels verschilt enigszins per auteur (zo formuleert Kirk 6 regels, terwijl Winer er 10 nodig blijkt te hebben) en ook de precieze uitwerking van het voorgestelde algoritme verschilt soms radicaal, maar in feite komen die regels toch allemaal op dezelfde basisprincipes neer (i.c. het lineaire model) en leiden ze, mits adequaat toegepast, gegarandeerd tot het gewenste resultaat (‘these rules lead to an end product which has been proved to be statistically correct when the assumptions underlying the general lineair model are met’ (Keppel o.c. 371). De praktische toepassing van deze algoritmische procedures - die merkwaardigerwijze onder volstrekt verschillende benamingen bekend staan, bijvoorbeeld als het Cornfield-Tukey algoritme (of in IT-kringen, als de regels van Henderson) - is, ook in de ogen van de auteurs zelf, nogal ‘laborious’. Hoe dat ook zij, ter wille van de praktische bruikbaarheid van dit artikel ontwikkelen we statistische modellen voor enkele multiple message designs (en dus voor de afleiding van adequate F-ratio's), waarbij we gebruik maken van een algoritmische procedure die een (gesimplificeerde) versie van het Cornfield-Tukey algoritme betreft (dit nogal ingewikkelde algoritme is in praktische zin uitgewerkt door Glass & Stanley 1970 en verder vereenvoudigd door Keppel 1982; zie ook Jackson & Brachers 1994: 17-22).

[p. 326]

van grote aantallen talige instantiaties nogal lastig is (bijvoorbeeld wanneer met advertenties met en zonder woordspelingen op persuasieve kracht met elkaar wil vergelijken, dan zal de eerste categorie - met woordspelingen - moeizaam te implementeren zijn). IV daarentegen komt juist in de omgekeerde situatie in aanmerking: grote aantallen instantiaties kunnen gemakkelijk uit een gespecificeerd domein gegenereerd worden (bijvoorbeeld wanneer men dialoogjes wil construeren waarin al dan niet ad verecundiam drogredenen optreden) terwijl het samenstellen van steekproeven met grote aantallen proefpersonen tot de praktische onmogelijkheden behoort.

3. De fixed-effect fallacy

In empirisch-taalwetenschappelijk onderzoek wordt vaak gebruik gemaakt van de inductiefstatistische techniek die bekend staat onder de naam: variantie-analyse. Toepassing van deze statistische analyse resulteert in een toetsingsgrootheid: de zogenaamde F-ratio, met behulp waarvan nagegaan kan worden of het verschil tussen twee of meer ‘treatment’-gemiddelden dat in een steekproef is aangetroffen, geen toevalstreffer is maar een ‘echt’, substantieel verschil dat met vertrouwen - dat wil zeggen binnen de grenzen van conventioneel bepaalde waarschijnlijkheidsmarges - naar de populatie gegeneraliseerd mag worden. Het is deze toetsingsgrootheid F, oorspronkelijk in de jaren dertig door de Engelse mathematisch-statisticus en geneticus Fisher ontwikkeld (vandaar de naam: F-toets) waarop Clark zijn pijlen afvuurde - althans, op het naar zijn oordeel drogredelijk (‘fallacious’) gebruik van deze F. De onderstaande niet-technische beschouwingen over de fixed-effect fallacy zijn dus gecentreerd rond deze F-toets.

De toetsingsgrootheid F is vanuit structureel oogpunt bekeken in feite een getalsmatige uitdrukking van de verhouding van de grootte van een signaal ten opzichte van de grootte van de ruis: hoe sterker het signaal ten opzichte van de ruis, hoe groter (in absolute waarde) F en - als regel - hoe makkelijker de bevindingen in de steekproef gegeneraliseerd kunnen worden naar de populatie:

F = signaal/ruis

Is F gelijk aan of kleiner dan 1, dan kan de nulhypothese (‘er is geen verschil tussen de treatment-gemiddelden in de populatie’) nooit verworpen worden ten gunste van de door de onderzoeker geliefkoosde alternatieve hypothese (‘er is wel een verschil tussen de treatmentgemiddelden in de populatie’). In dat geval immers is de ruis (de ‘error’) minstens zo groot is als het signaal. In het algemeen geldt: hoe groter de numerieke waarde van F, hoe groter de kans dat de nulhypothese verworpen en de alternatieve hypothese geaccepteerd kan worden, dus hoe groter ook de kans dat de bevindingen in de steekproef met vertrouwen naar de populatie gegeneraliseerd kunnen worden. De teller van de F-ratio bestaat dus uit het signaal, anders uitgedrukt: uit het effect dat de onderzoeker wil aantonen (i.c. het verschil tussen gemiddelden), de noemer van de F-ratio bestaat uit een ruis-of errorterm.

In het meest eenvoudige design, het één-factor experiment, bestaat de toetsingsgrootheid F uit de ratio van variantie tussen de groepen en (‘gepoolde’) variantie binnen de groepen (ofwel: de ratio van variantie tussen de treatments en van variantie binnen de treatments).⁵

5 De specifieke opbouw en samenstelling van een F-ratio verandert onder andere al naar gelang het specifieke design, en afhankelijk van de vraag of de aldaar in opgenomen factoren als random of als gefixeerd worden beschouwd. Anders uitgedrukt: F-ratio's zijn geen onveranderlijke, op willekeurig welk design toepasbare grootheden, maar F-ratio's moeten qua opbouw en structuur juist worden toegesneden op het specifieke design waarop ze geacht worden van toepassing te zijn (zie ook noot 4).

[p. 327]

De aldus opgebouwde F-ratio heeft als rationale dat naarmate de variantie van de steekproefgemiddelden groter is ten opzichte van de in de steekproef aangetroffen ruis (de error-term, i.c. de gepoolde variantie binnen de groepen) de nulhypothese dat alle gemiddelden in de populatie aan elkaar gelijk zijn, sneller verworpen wordt.

Verschillen tussen de proefpersonen binnen de treatments worden in de variantie-analyse van het één-factor experiment dus opgevat als error, te wijten aan steekproeffouten (‘sampling error’). Het punt waar het nu bij de fixed-effect fallacy in feite om draait, is dat in een multiple message design waarin de taalwetenschappelijke variabele (de treatment) is vertegenwoordigd door een random factor ‘talige instantiaties’, de error-term van de betreffende F-ratio niet uit slechts één component bestaat (namelijk uit de error die te wijten is aan steekproeffouten bij het trekken van personen uit de populatie) maar uit twee: namelijk óók uit een component die error representeert die het gevolg is van steekproeffouten bij het trekken van de talige instantiaties (de ‘messages’) uit een gespecificeerd domein:

Vat men nu - ten onrechte overigens - de talige instantiaties op als een gefixeerde, en niet als een random factor, dan wordt de noemer van de F-ratio kunstmatig verkleind (men abstraheert dan immers van de sampling error die aan de messages kan worden toegeschreven). Een aldus kunstmatig verkleinde noemer leidt - bij gelijkblijvend teller, dus bij gelijkblijvend effect - tot een kunstmatig vergrote F-ratio. Dit is, in niet-technische termen uitgedrukt, de fixed-effect fallacy.

Wat is nu het gevolg van dit kunstmatig vergroten van de F-ratio? Als een F-ratio kunstmatig vergroot wordt, dan wordt de kans op het ten onrechte verwerpen van de nulhypothese (de alpha-fout) kunstmatig vergroot en gaat dus het nominale alpha-niveau afwijken van het werkelijke alpha-niveau. De toetsingsgrootheid F vertoont onder deze omstandigheden een ‘positieve bias’: de onderzoeker concludeert dat het aangetroffen verschil in treatmentgemiddelden, gelet op de met de toetsingsgrootheid F geassocieerde p-waarde die kleiner is dan 5%, met vertrouwen gegeneraliseerd mag worden. De feitelijke p-waarde echter (die p-waarde die verkregen zou zijn indien de random talige factor niet als gefixeerde, maar juist als random factor in de analyse verdisconteerd zou zijn) is vele malen groter is en zou juist tot een tegengestelde conclusie moeten leiden: geen verschil in treatment-gemiddelden in de populatie.

Volgens Clark bleef de language-as-fixed-effect fallacy niet beperkt tot een incidentele taalwetenschappelijke onderzoeker. In antwoord op de door hemzelf gestelde vraag hoeveel taalwetenschappers in de jaren vijftig en zestig zich dan wel schuldig zouden maken aan deze fixed-effect fallacy stelde Clark even kort als krachtig: ‘The answer, sad to say, is almost everyone.’ (Clark 1973: 355). Gelet op de frequentie van voorkomen van de (statistische) fixed-effect fallacy in het Tijdschrift voor Taalbeheersing lijkt Clark's antwoord drie decennia na dato nog even actueel.

[p. 328]

4. Design I: woorden genest binnen treatment, respondenten gekruist met woorden en treatment

Het multiple message design dat in deze paragraaf besproken wordt, betreft het design aan de hand waarvan Clark de fixed-effect fallacy bespreekt. In dit multiple message design is er sprake van een gefixeerde treatment T, waarvan de niveaus worden gerepresenteerd door (een random steekproef aan) verschillende woorden w, die op hun beurt genest zijn binnen elk niveau van de treatment (w(T)). De respondenten (r) krijgen elk woord in elke treatment conditie aangeboden waarop zij moeten reageren.

Een concreet voorbeeld van een dergelijk design (besproken door Clark in diens artikel, en aldaar Study 5 genoemd (Clark 1973: 337-338)) betreft het volgende: in het kader van een reeks psycholinguïstische experimenten (uitgevoerd in de jaren zeventig) waarin wordt nagegaan hoe snel proefpersonen beslissen of een reeks letters een woord dan wel een nietwoord vormt, werden homofonen vergeleken met niet-homofonen. In het betreffende experiment werden 25 homofonen vergeleken met 24 niet-homofonen (een voorbeeld van een (Engels) homofoon is het woord bear, een woord dat net zo wordt uitgesproken als bare, maar dat verschillend wordt gespeld en dat qua betekenis niet-identiek is). De homofonen en niet-homofonen werden één-voor-één aangeboden (overigens lukraak afgewisseld met ‘nonword filler items’); van elk woord werd de herkenningstijd (wel woord/geen woord) in milliseconden gemeten. Alle proefpersonen reageren op alle 49 aangeboden woorden.

Dit design kent dus drie factoren: (1) Homofonie, een gefixeerde factor met 2 niveaus; (2) Woorden genest binnen Homofonie, bestaande uit een random steekproef uit de populatie: alle mogelijke homofonen en niet-homofonen; en (3) Respondenten, bestaande uit een random steekproef uit alle mogelijke respondenten. Dit specifieke design betreft dus een repeated measurement design (een binnen-proefpersonen design) waarin de random factor ‘proefpersoon’ (r) gekruist is met zowel de gefixeerde treatment factor T als met de random factor ‘woorden binnen treatment’ (w(T)).

Vanuit methodologisch oogpunt beschouwd is dit design (ook wel een gemengd hiërarchisch drie-factor design genoemd) een bijzonder sterk design: aangetroffen effecten van de treatment kunnen niet worden toegeschreven aan verschillen tussen proefpersonen (zoals soms in een tussen-proefpersonen design): elke proefpersoon wordt immers geobserveerd onder alle treatment-condities en fungeert derhalve als zijn ‘eigen controle’. Bovendien - maar dit geldt in feite voor álle multiple message designs - is een uiteenrafeling van effecten van de treatment op categoriaal niveau en op instrumenteel niveau mogelijk. De keerzijde van de medaille is echter dat het statistisch model voor dit design en de constructie van een adequate F-ratio verre van eenvoudig is (zie tabel 1). Immers, de F-ratio die voor de toetsing van deze treatment geconstrueerd moet worden, is geen reguliere F-ratio maar een zogenaamde quasi F-ratio (symbolisch weergegeven als F’).⁶

6 De algemene, generieke opbouw van een F-ratio is, ongeacht de aard van het design, telkens dezelfde: tracht een F-ratio te vormen van twee MS-termen (één voor de teller, de ander voor de noemer die als error-term functioneert) waarvan de verwachtingswaarden enkel en alleen verschillen in de aanwezigheid of afwezigheid van de nulhypothesecomponent, i.c. de variantie-term die correspondeert met het te toetsen effect. In concrete termen uitgedrukt: de teller bestaat uit de verwachtingswaarde van de MS-term van het te toetsen effect (i.c. E(MS-effect)), terwijl de noemer van de F-ratio uit de verwachtingswaarde van een andere MS-term bestaat die als error-term functioneert. Het punt waar het nu om draait, is dat een MS-term in een gespecificeerd statistisch model slechts dan als error-term kan functioneren indien zijn verwachtingswaarde in alle opzichten overeenkomtmet de verwachtingswaarde van de MS-effect term, met uitzondering van de nulhypothesecomponent.

[p. 329]

Tabel 1: Verwachtingswaarden van MS-termen in design I: woorden genest binnen treatment, respondenten gekruist met woorden en treatment (N.B. t is het aantal treatment-niveaus, w is het aantal replicaties per treatment-niveau, en r is het totale aantal respondenten).

Bron	Verwachtingswaarden van MS-termen^7
Treatment [T]	σε^2 + wrθ^2T + rσ^2w(T) + wσ^2r x T + σ^2 r x w(T)
Woorden [w(T)]	σε^2 + rσ^2 w(T) + σ^2 r x w(T)
Respondent [r]	σε^2 + twσ^2 r + σ^2 r x w(T)
r x T	σε^2 + wσ^2r x T + σ^2 r x w(T)
r x w(T)	σε^2 + σ^2 r x w (T)

Zijn de verschillende variantiebronnen gedefinieerd, dan kan de quasi F geconstrueerd worden en wel zo dat bij toetsing van het effect van Treatment het verschil tussen de teller en de noemer van de F-ratio alleen de variantie van Treatment bevat, én dat in de noemer (ook) de verschillen tussen woorden binnen Treatment (w(T)) tot uitdrukking komen. Voor design I voldoet de volgende quasi F-ratio aan deze eisen:

F=MS(T) + MS(r * w(T))/ MS(r * T) + MS(w(T))

Niet alleen moet deze F-ratio handmatig berekend worden (zij het dat men via een aantal computer-runs over de benodigde MS-termen kan beschikken), dat geldt evenzeer voor de bijbehorende vrijheidsgraden:

df1=(MS(T)+MS(r* w(T))^2/MS(T)^2/df1 + MS(r* w(T))^2/df2

Een van de karakteristieke aspecten van een quasi F-ratio betreft het feit dat de daarbij behorende vrijheidsgraden niet meer exact zijn, maar moeten worden benaderd.⁸ Een andere problematische eigenschap van quasi F-ratio's is dat deze, anders dan reguliere F-ratio's, niet uniek zijn: voor hetzelfde design kunnen andere quasi F-ratio's geconstrueerd worden die tot andere toetsingsuitkomsten aanleiding kunnen geven.⁹ Uit simulatie-onderzoek is overigens gebleken dat quasi F-ratio's in het algemeen redelijke toetsingsgrootheden vormen waarop men staat kan maken (Forster & Dickinson 1976; Santa, Miller & Shaw 1979; Maxwell & Bray 1986); ze zijn echter licht conservatief.

Tot slot: in lang niet alle gevallen is het hier besproken ‘ideale’ design ook in praktische zin toepasbaar. Veronderstelt een onderzoeker bijvoorbeeld oefen-effecten (‘practice’-effecten die maken dat een proefpersoon door de herhaalde blootstelling aan de afhankelijke variabele tijdens de duur van het experiment beter gaat presteren - of juist slechter ten gevolge van vermoeidheid), dan kan het gebruik van dit design bezwaarlijk zijn. Zou hij de treatment-condities, inclusief de instantiaties, allemaal in precies dezelfde volgorde aan de proefpersonen aanbieden, dan is hij niet meer in staat de treatment- van de oefeneffecten te onderscheiden: beide effecten zijn dan immers met elkaar verstrengeld (‘confounded’). De standaardoplossing voor dit probleem bestaat eruit de messages in verschillende volgordes aan verschillende proefpersonen aan te bieden, wat meestal in de praktijk bewerkstelligd wordt door het zogenaamde ‘counterbalancing’.

7 Bij het weergeven van de verwachtingswaarden voor de kwadratensommen van de in een statistisch model optredende variantiebronnen worden de volgende conventies gehanteerd: met behulp van hoofdletters worden de gefixeerde factoren aangeduid, met behulp van de daarmee corresponderende kleine letter de niveaus van deze factor. Random factoren worden met kleine letters aangeduid; geneste factoren worden met kleine letter aangeduid, met daarachter tussen haakjes de factor waarbinnen genest is. Tot slot: variantiecomponenten voor random factoren worden met σ² aangegeven, die voor gefixeerde factoren met θ² Zoals uit de verwachtingswaarden in dit statistisch model kan worden afgeleid, is er geen simpele error-term aanwezig om het treatment-effect T te toetsen: geen enkele variantie-bron, noch Woorden, noch Respondent, noch de interactie van Respondent met treatment T (r x T) en evenmin de interactie van Respondent met de geneste factor ‘Woorden binnen treatment T’ (r x w (T)) bevat immers de vier termen die in de verwachtingswaarde van MS(T), het treatment-effect, gespecificeerd zijn. Door echter MS-termen te combineren is hetmogelijk een zogeheten quasi F te construeren waarbij de teller uitsluitend verschilt van de noemer in de aanwezigheid van de nulhypothesecomponent (de quasi F ontleent zijn specifieke naam aan de omstandigheid dat deze niet, zoals gebruikelijk bij een ‘echte’ F, gebaseerd is op de berekening van onafhankelijke kwadratensommen). Clark stelt in dit verband, in navolging van onder anderen Winer (1971), de volgende quasi F-ratio voor (zie ook Kirk 1968: 212-214): F'= MS (T) + MS (r x w (T)) / MS (r x T) + MS (w (T)). Schrijven we de verwachtingswaarden voor de betreffende MS-termen helemaal uit en worden deze gesubstitueerd in de betreffende vergelijking voor deze quasi F, dan wordt duidelijk dat F' de structuur heeft van een reguliere F, in die zin dat de teller gelijk is aan de noemer plus een extra term die correspondeert met de nulhypothesecomponent.

8 Een quasi F volgt, anders dan een reguliere F, slechts bij benadering de reguliere F-verdeling - vrijheidsgraden voor een quasi F zijn dan ook niet exact, maar moeten benaderd worden, bijvoorbeeld met een formule die oorspronkelijk ontwikkeld is door Satterthwaite (1946). Aangenomen dat de quasi F uit de volgende composieten bestaat: F'= (MS1 + MS2) / (MS3 + MS4), dan is het aantal vrijhheidsgraden voor teller respectievelijk noemer gelijk aan Df (teller) = (MS1 + MS2)² / ((MS1²/df₁) + MS2²/df₂) Df (noemer) = (MS3 + MS4)² / ((MS3²/df₃) + MS4²/df₄) Quasi F's vormen dus een benadering, en zijn in statistische zin niet exact. Gegeven het feit echter dat er geen ‘echte’ F-ratio voor het beschreven design beschikbaar is, is het wel de beste benadering die onder de gegeven omstandigheden mogelijk is.

9 Naast de gerapporteerde quasi F-ratio voor dit specifieke design is het mogelijk het treatment-effect te toetsen via: F' = MS (T) / (MS (w(T)) + MS (r x T) - MS (r x w(T)). Het nadeel van deze quasi F is dat deze tot een negatieve uitkomst kan leiden - reden waarom in de regel de voorkeur wordt gegeven aan de eerder geformuleerde F'. De non-uniciteit van quasi F's voor hetzelfde design heeft dus tot gevolg dat er verschillende toetsingsuitkomsten mogelijk zijn, afhankelijk van de gekozen quasi F - uit zowel wetenschappelijk als statistisch oogpunt bepaald geen ideale situatie.

[p. 330]

Een tweede moeilijkheid met dit design betreft de mogelijkheid van differentiële ‘carryover’-effecten. Anders dan ‘practice’-effecten die algemeen van aard zijn en alle treatment-condities gelijkelijk beïnvloeden, zijn ‘carryover’-effecten onveranderlijk specifiek. Stel dat een experiment drie treatment-condities bevat (a1, a2 en a3) die qua moeilijkheid sterk verschillen (a1 het makkelijkst, a3 het moeilijkst). De drie condities worden in twee verschillende volgorden aangeboden: a1, a2 en a3 en a3, a2 en a1: zullen nu proefpersonen die aan de moeilijkste conditie als eerste worden blootgesteld (dus aan a3), op precies dezelfde wijze reageren op de treatment-conditie waarvan verondersteld wordt dat deze middelmatig moeilijk is (dus op a2), als de proefpersonen die eerst de gemakkelijkste treatment-conditie (dus a1) moesten doorlopen? Indien het antwoord op de gestelde vraag nee is, dan hebben we te maken met een voorbeeld van differentiële carryover-effecten.

Weer een ander potentieel bezwaar tegen dit design betreft de mogelijkheid dat proefpersonen, juist door de herhaalde blootstelling aan eenzelfde type stimuli, achter het eigenlijke doel van het experiment komen waardoor de ecologische validiteit aangetast kan worden - vooral in het sociaal-psychologisch georiënteerde persuasie-onderzoek kan deze factor een sterk contaminerende invloed uitoefenen. En het in deze paragraaf besproken design is al helemáál uitgesloten indien de talige instantiaties, de ‘woorden’ (de messages) in fysieke zin niet uit ‘levensechte’ woorden bestaan die slechts een korte verwerkingstijd vergen (bijvoorbeeld woorden in een dictee), maar uit bijvoorbeeld volledige teksten die elk een aantal pagina's of zelfs hele boekwerken beslaan (zoals voorlichtingsfolders of computerhandleidingen). In louter praktische zin zou dan een repeated measurement design zoals hier besproken, uitgesloten zijn.

4.1 De verwerking van data in design I

Laten we aan de hand van onderstaande (fictieve) dataset de berekening van de quasi F in design I illustreren. We gaan uit van een gefixeerde factor T (met twee niveaus: T1 en T2), waarbinnen een random factor ‘woorden’ (w, met vier niveaus) genest is. Verder nemen we aan dat er 8 proefpersonen (r) aan het experiment deelnemen; deze proefpersonen vormen eveneens een random factor die volledig gekruist is met de random factor ‘woorden’ en de gefixeerde factor T.

Tabel 2: Fictieve dataset voor design I (woorden genest binnen treatment, respondenten gekruist met woorden en treatment).

	Treatment T1 Woorden				Treatment T2 Woorden
Respondenten	1	2	3	4	1	2	3	4
1	6	7	4	2	5	6	3	8
2	6	8	5	5	6	7	5	4
3	9	3	7	4	9	6	3	7
4	8	6	3	6	4	4	8	5
5	6	5	5	1	7	4	8	4
6	2	6	3	1	9	8	7	5
7	2	2	4	2	8	8	5	7
8	2	1	3	1	4	5	3	6

Met behulp van onderstaande SPSS-setup kunnen de vijf variantie-bronnen (i.c. MS-termen) in het statistisch model van design I achterhaald worden. Dan is men er overigens nog niet: de betreffende MS-termen dienen in de formule voor de quasi F ingevuld te worden, zodat deze F' (handmatig) berekend kan worden.

[p. 331]

De setup voor de analyse van de gegevens in Tabel 2 bestaat uit drie delen. In het eerste deel worden de data gedefinieerd, in het tweede en derde deel worden twee aparte analyses gespecificeerd.¹⁰

Tabel 3: SPSS-setup voor de analyse van de gegevens uit tabel 2.

DATA LIST FILE=’c:\data\vb1.txt’ free/w1 to w8.

MANOVA

w1 to w8

/WSFACTOR = treat (2) woord (4)

/CONTRAST (woord) = difference

/PRINT = cellinfo (means)

/WSDESIGN = treat woord treat*woord.

MANOVA

w1 to w8

/WSFACTOR = treat (2) woord (4)

/CONTRAST (woord)=difference

/PRINT = cellinfo (means)

/WSDESIGN = woord within treat.

De eerste run met manova levert drie van de in totaal vijf benodigde MS-termen voor design I op: (1) de MS-term voor Treatment (die 43.89 bedraagt, bij 1 vrijheidsgraad), (2) de MS-term voor Respondent (ter grootte van 6.18, bij 7 vrijheidsgraden) en (3) de MS-term voor de interactie van Respondent en Treatment (7.85 bij 7 vrijheidsgraden).¹¹

Tabel 4: Resultaten van de eerste MANOVA voor design I.

Test of between-subjects effects
Source	Sum of Squares	df	Mean Square	F	Sig.
Constant	1630.14	1	1630.14	263.93	.000
Within + residual (error)	43.23	7	6.18
Test of within-subjects effects
Treatment	43.89	1	43.89	5.59	.050
Error(treatment)	54.98	7	7.85
Woord	22.67	3	7.56	2.54.	.084
Error (woord)	62.45	21	2.97
Treatment * woord	9.92	3	3.31	92	.449
Error(treat*woord)	75.70	21	3.60

De tweede run met MANOVA waarin de variantie van woorden binnen Treatment geschat wordt (w(T)) en waarin wordt aangegeven dat ‘woorden’ genest zijn binnen Treatment, levert de twee resterende MS-termen voor het statistisch model van design I: de MS-term voor woorden binnen Treatment (i.c. w(T), die bij 6 vrijheidsgraden 5.43 bedraagt, en de MS-term voor de interactie tussen Respondent en ‘woorden’ binnen Treatment (groot: 3.29 bij 42 vrijheidsgraden).

10 In de setup wordt gebruik gemaakt van de zogenaamde ‘syntax-editor’ van SPSS (de manova-procedure die wij telkens zullen inschakelen, wordt immers niet ondersteund via de wat meer gebruikelijke interface). manova wordt aangeroepen, waarbij aangegeven wordt dat de variabelen w1 tot en met w8 in de analyse gebruikt gaan worden. Vervolgens wordt gespecificeerd dat het te analyseren design een binnen-proefpersonen design behelst (wsfactor) met twee variabelen: (1) treat (ment) met twee niveaus, en (2) woord met vier niveaus. De volgorde van de beide statements ‘treat (ment)’ en ‘woord’ is niet willekeurig: deze volgorde wordt immers strikt bepaald door de wijze waarop de gegevens ingevoerd zijn. In de setup is gedefinieerd dat eerst de vier woorden voor treatment T1 ingevoerd zijn (w1 t/m w4), en daarna de vier woorden (w5 t/m w8) voor treatment T2.

11 De totale variantie wordt opgesplitst in twee delen: een deel dat te maken heeft met de verschillen tussen respondenten en een deel dat zich binnen respondenten bevindt. De variantie tussen Respondenten bedraagt 43.23, bij 7 vrijheidsgraden (de hiermee geassocieerde MS-term ter grootte van 6.18 definieert dus de derde component in het in tabel 1 gedefinieerde model: de MS-term voor Respondent). Binnen respondenten ligt de zaak echter wat complexer omdat er liefst drie verschillende variantie-componenten onderscheiden moeten worden: (1) een deel dat toe te schrijven is aan de Treatment (43.89 met 1 vrijheidsgraad; de hiermee geassocieerde MS-term ter grootte van 43.89 definieert de eerste component in het in tabel 1 gedefinieerde model), (2) een deel dat toe te schrijven is aan ‘woorden’ (22.67 met 3 vrijheidsgraden), en (3) een deel dat toe te schrijven is aan de combinatie van Treatment en Woord (9.92 met 3 vrijheidsgraden). Het effect van Treatment geeft aan dat er een verschil is tussen de niveaus van de Treatment - ten minste, als er géén rekening wordt gehouden met de variantie tussen woorden! Bij elk van de drie gespecificeerde variantie-componenten hoort een ‘eigen’ error-term: voor Treatment is dat de interactie tussen Respondent en Treatment (de hiermee verbonden MS-term ter grootte van 7.85 levert dus de vierde component op in het in tabel 1 gedefinieerde model); voor Woord is dat de interactie tussen Woord en Respondent, en voor de interactie tussen Treatment en Woord kan de interactie tussen Respondent, Treatment en Woord als error-component opgevat worden.

[p. 332]

Tabel 5: Resultaten van de tweede manova voor Design I.

Test of within-subjects effects items nested within treatment
Source	Sum of Squares	df	Mean Square	F	Sig.
woord within treatment	32.59	6	5.43	1.65	.157
Within + residual (error)	138.16	42	3.29

Met behulp van 4 van deze 5 MS-termen kan vervolgens de quasi F voor de toetsing van het Treatment-effect berekend worden: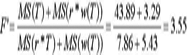

Vervolgens moeten de aantallen bij deze quasi F behorende (niet-exacte) vrijheidsgraden berekend worden. Dat leidt tot: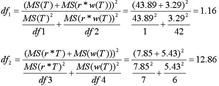

De vrijheidsgraden moeten worden afgerond op het dichtstbijzijnde gehele getal, met als resultaat: F' = 3.55; df1 = 1; df2 = 13. Dit levert een overschrijdingskans op van 0.08. Naar conventionele maatstaven gemeten (alpha <5%) kan het verschil tussen de beide condities niet gegeneraliseerd worden naar de geïntendeerde populatie van subjecten en van woorden. Zou men echter, ten onrechte overigens, uitgegaan zijn van een statistische analyse waarbij de variatie tussen woorden buiten beschouwing gelaten wordt - dus zou men zich schuldig maken aan de door Clark verguisde fixed-effect fallacy - dan zouden de toetsingsuitkomsten wél significant zijn geweest en zou men wél tot generalisatie van steekproefuitkomsten naar populatie zijn overgegaan.¹² De fixed-effect fallacy geeft dus een te optimistisch beeld.

12 In het geval van de fixed-effect fallacy zou de toetsingsgrootheid F1 bestaan uit MS(T) / MS(r x T); zou nu het treatment-effect getoetst worden tegen de error (zie tabel 4), dan zou dat een F-ratio opleveren van 5.59 bij 1 en 7 vrijheidsgraden, significant op .050 nivean.

5. Design II: woorden genest binnen de interactie van de twee gefixeerde treatments, respondenten gekruist met woorden en treatments

Dit design, dat net zoals design I een repeated measurement design is, betreft in feite een generalisatie van design I: anders dan in design I figureert in dit design niet slechts één onafhankelijke variabele, maar twee. Dit design kent twee gefixeerde, volledig met elkaar gekruiste factoren (treatments) en twee random factoren: woorden/messages en respondenten. De woorden/messages zijn genest binnen de interactie van de twee factoren, de respondenten zijn volledig gekruist met alle overige (random en gefixeerde) factoren.

Ter illustratie van dit design een concreet voorbeeld, ontleend aan een van de experimentele artikelen in het Tijdschrift voor Taalbeheersing. In het betreffende artikel werd de invloed van

[p. 333]

twee factoren (namelijk van woordfrequentie en van zinscontext) op het spellingsgedrag van intuïtieve spellers bij zwakke prefixwerkwoorden (zoals: verandert/veranderd) nagegaan. Er werden drie zinscontexten gemanipuleerd: (1) neutraal (d.w.z. context biedt geen aanknopingspunten voor de juiste spelling voor spellers die geen regels tot hun beschikking hebben); (2) context werkt mee (d.w.z. context biedt optimale aanknopingspunten om tot juiste spelling te komen); (3) context werkt tegen. Daarnaast werden drie typen woordfrequenties gemanipuleerd die, zo luidde althans de veronderstelling, (1) een correcte spelling tegenwerkten (bijvoorbeeld: ‘geloofd’, een relatief weinig frequent voorkomende woordvorm die de intuïtieve speller die op het woordbeeld vertrouwt, op het verkeerde been zal zetten); (2) een correcte spelling juist ondersteunden (bijvoorbeeld: ‘gelooft’); en (3) een neutrale uitwerking op het spellingsgedrag hadden (bijvoorbeeld: ‘gebeurd’, een woordvorm die qua frequentie min of meer overeenkomt met ‘gebeurt’). In totaal werden er aan 253 proefpersonen 72 zinnetjes in de vorm van een dictee voorgelegd (zoals: ‘Ik weet dat hij bepaal_heeft, dat niemand zijn auto mag gebruiken’ en ‘Weet je, dat ik jarenlang Jan geloof_heb?’). Aan de proefpersonen de taak de ontbrekende letter bij de 72 prefixwerkwoorden correct in te vullen.

Dit multiple message design kent vier factoren: (1) Zinscontext, een gefixeerde factor met 3 niveaus; (2) Woordfrequentie, eveneens een gefixeerde factor met drie niveaus; (3) Woorden genest binnen de interactie van Zinscontext en Woordfrequentie, bestaande uit een random steekproef van 8 te spellen prefixwerkwoorden uit de betreffende populatie; (4) Respondenten, bestaande uit een random steekproef uit alle mogelijke respondenten.

Dit specifieke design betreft, zoals gezegd, een repeated measurement design (een binnenproefpersonen design) waarin de random factor ‘proefpersoon’ (r) gekruist is met zowel de gefixeerde treatment factor Zinscontext als de gefixeerde factor Woordfrequentie en tevens gekruist is met de random factor ‘woorden genest binnen de interactie van de treatments Zinscontext en Woordfrequentie’ (w(Z x WF)). Het statistisch model voor dit design staat in onderstaande tabel (waarbij we de twee gefixeerde treatment-factoren met A en B aanduiden, de random factor ‘woorden’ met w(AB) en de random factor ‘proefpersoon’ met r).

Tabel 6: Verwachtingswaarden van MS-termen in design II: woorden genest binnen de interactie van treatment A en B, respondenten gekruist met woorden en treatments (N.B. a is het aantal niveaus van treatment A, b het aantal niveaus vantreatment B, w is het aantal replicaties per A × B interactie, en r is het totale aantal respondenten).

Bron	Verwachtingswaarden van MS-termen
Treatment [A]	σε^2 + bwrθ^2A + rσ^2w(AB) + bwσ^2A x r + σ^2 w(AB) x r
Treatment [B]	σε^2 + awrθ^2B + rσ^2w(AB) + awσ^2B x r + σ^2 w(AB) x r
Woorden [w(AB)]	σε^2 + rσ^2 w(AB) + σ^2 w(AB) x r
Respondent [r]	σε^2 + abwrσ^2r +σ^2 w(AB) x r
A x B	σε^2 + wrθ^2 A x B + wσ^2 A x B x r +σ^2 w(AB) x r + rσ^2 w(AB)
A x r	σε^2 + bwσ^2A x r + σ^2 w(AB) x r
B x r	σε^2 + awσ^2B x r + σ^2 w(AB) x r
w(AB) x r	σε^2 + σ^2 w(AB) x r
A x B x r	σε^2 + wσ^2A x B x r

Uit bovenstaande verwachtingswaarden voor de 9 variantiebronnen in dit statistisch model valt af te leiden dat een reguliere F-ratio voor toetsing van A, B of de interactie van A en B niet voorhanden is. Net zoals bij design I zal ook hier een quasi F-ratio berekend moeten worden. De drie quasi F's voor de toetsing van A, B respectievelijk de interactie tussen A en B zijn successievelijk:

[p. 334]

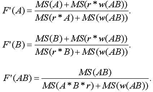De bij deze drie quasi F-ratio's behorende vrijheidsgraden moeten - alweer - benaderd worden via de daartoe geëigende formules (zie paragraaf 4).

5.1 De verwerking van data in design II

De berekening van de drie quasi F's in design II lichten we weer toe aan de hand van een concreet (getallen) voorbeeld. We gaan uit van twee gefixeerde factoren A en B (elk met twee niveaus); de random factor ‘woorden’ (w, met twee niveaus) is genest binnen de interactie van A en B. Verder nemen we aan dat er 8 proefpersonen (r) aan het experiment deelnemen; deze proefpersonen vormen eveneens een random factor die volledig gekruist is met de random factor ‘woorden’ en de twee gefixeerde factoren A en B.

Tabel 7: Fictieve dataset voor design II: woorden genest binnen de interactie van treatment A en B, respondenten gekruist met woorden en treatments.

	Treatment combinatie
	T_A1+T_B1 Woorden		T_A1+T_B2 Woorden		T_A2+T_B1 Woorden		T_A2+T_B2 Woorden
Respondent	1	2	1	2	1	2	1	2
1	6	7	4	2	5	6	3	8
2	6	8	5	5	6	7	5	4
3	9	3	7	4	9	6	3	7
4	8	6	3	6	4	4	8	5
5	6	5	5	1	7	4	8	4
6	2	6	3	1	9	8	7	5
7	2	2	4	2	8	8	5	7
8	2	1	3	1	4	5	3	6

Ook voor dit design zijn weer twee SPSS-runs nodig.¹³

Tabel 8: SPSS-setup voor de analyse van design II (zie ook tabel 7).

DATA LIST FILE=’c:\data\vb1.txt’ free/w1 to w8.

MANOVA

w to w8

/WSFACTOR = treat_A (2) treat_B (2) woord (2)

/CONTRAST (woord) = difference

/PRINT = cellinfo (means)

/WSDESIGN = woord treat_A treat_B treat_A*treat_B woord*treat_A woord*treat_B woord*treat_A*treat_B.

MANOVA

w1 to w8

/WSFACTOR = treat_A (2) treat_B (2) item (2)

/CONTRAST (woord)=difference

/PRINT = cellinfo (means)

/WSDESIGN = woord within treat_A*treat_B.

13 Merk op dat de volgorde van de items in de dataset van belang is. Eerst de twee items bij treatment_A niveau 1 en treatment_B niveau 1, dan de twee items bij treatment_A niveau 1 en treatment_B niveau 2, etc. De volgorde waarin de items genoemd zijn in het aanroepen van de manova -procedure bepaalt de volgorde waarin de factoren benoemd moeten worden.

[p. 335]

Tabel 9: Resultaten van de eerste MANAVO voor Design II.

Test of between-subjects effects
Source	Sum of Squares	df	Mean Square	F	Sig.
Constant	1630.14	1	1630.14	263.93	.000
Within + residual (error)	43.23	7	6.18
Test of within-subjects effects
Treatment_A	43.89	1	43.89	5.59	.050
Error(treatment)A)	54.98	7	7.85
Treatment_B	19.14	1	19.14	10.95	.013
Error (treatment_B)	12.23	7	1.75
Woord	3.52	1	3.52	0.92	.370
Error (woord)	26.86	7	3.84
Treatment_A * woord	3.52	1	3.52	0.84	.390
Error(Treat_A * woord)	29.36	7	4.19
Treatment_B * woord	.02	1	.02	.00	.947
Error(Treat_B * woord)	23.36	7	3.34
Treat_A * Treat_B	1.89	1	1.89	0.47	.514
Error (Treat_A * Treat_B	27.98	7	4.00
Woord * Treat_A * Treat_B	4.52	1	4.52	1.72	.231
Error(woord * Treat_A * Treat_B)	18.36	7	2.62

De eerste run van manova levert 6 van de in totaal 8 MS-termen op die nodig zijn bij de berekening van de drie quasi F's in design II: MS(A) ter grootte van 43.89 bij 1 vrijheidsgraad, MS(B) ter grootte van 19.14 bij 1 vrijheidsgraad en MS(AB): deze bedraagt 1.89 bij 1 vrijheidsgraad. De drie daarbij behorende error-termen MS(r x A), MS(r x B) en MS(r x A x B) bedragen respectievelijk 7.85, 1.75 en 4.00, elk met 7 vrijheidsgraden.¹⁴

In de tweede MANOVA-run wordt gespecificeerd dat de items/woorden/messages genest zijn binnen de interactie van beide treatments (wsdesign). Deze run levert de twee andere MS-schattingen op die nodig zijn voor de berekening van de drie quasi F's: MS(w(AB)) bedraagt 2.89 bij 4 vrijheidsgraden, MS(r x w(AB)) wordt geschat op 3.50 bij 28 vrijheidsgraden (zie uitkomsten Tabel 10).

Tabel 10: Resultaten van de tweede MANOVA voor Design II.

Test of within-subjects effects items nested within treatments
Source	Sum of Squares	df	Mean Square	F	Sig.
Item within treatment	11.56	4	2.89	0.83	.52
Within + residual (error)	97.94	28	3.50

14 Als geen rekening gehouden wordt met de variantie tussen woorden en dus de zogenaamde F1 (i.c. de fixedeffect fallacy) berekend wordt, dan blijkt er zowel een significant verschil tussen beide niveaus van treatment A (F (1,7)= 43.89; p = 0.050) als tussen de niveaus van treatment B (F(1,7) = 10.95; p = 0.013). Het interactie-effect is volgens deze fixed-effect analyse niet significant (F(1,7) = 0.47; p = 0.514). Omdat we ook willen generaliseren over woorden, moeten we een schatting van de variantie binnen de combinatie van treatments hebben. Daarvoor wordt de tweede manova-run uitgevoerd; daarin wordt gespecificeerd dat items genest zijn binnen de interactie van beide treatments (wsdesign). Deze run levert de schattingen die in Tabel 10 zijn weergegeven.

[p. 336]

De twee runs hebben de ingrediënten opgeleverd met behulp waarvan de drie quasi-F's berekend kunnen worden: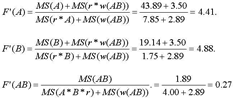

De vrijheidsgraden (voor F'(A)) bedragen: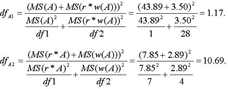

Voor het effect van treatment A geldt: F' = 4.41 (bij df_A1 = 1, df_A2 = 11; p = 0.06). We moeten derhalve concluderen dat - strikt genomen - de verschillen tengevolge van treatment A niet gegeneraliseerd kunnen worden.

Voor treatment B en het interactie-effect krijgen we na enig rekenwerk respectievelijk: F'(B) = 4.88 (df_B1 = 1, df_B2 = 9; p = 0.054), en F'(AB) = 0.27 (df_AB1 = 1, df_AB2 = 11; p = 0.61). Dus noch het effect van treatment A, noch dat van B, noch het interactie-effect kan met vertrouwen gegeneraliseerd worden. Zouden we daarentegen uitgaan van een fixedeffect analyse (vgl noot 14), dan blijken de effecten van treatment A en B - ten onrechte overigens - wél gegeneraliseerd te kunnen worden.

6. Design III: woorden genest binnen treatment, respondenten genest binnen woorden

In dit design, een tussen-proefpersonen ontwerp, figureert één onafhankelijke variabele (een gefixeerde factor) en twee random replicatiefactoren (woorden en respondenten) die hiërarchisch ten opzichte van elkaar geordend zijn: de woorden zijn genest binnen elk niveau van de treatment, de respondenten zijn genest binnen elk woord - met dien verstande dat elke persoon slechts één woord/message binnen een niveau van de treatment krijgt aangeboden.

Een hypothetisch voorbeeld van een dergelijk design betreft het volgende: stel dat een persuasie-onderzoeker de overtuigingskracht van advertenties met en zonder woordspelingen wil onderzoeken (=gefixeerde factor). In de dagbladen en media treft hij slechts 5 advertenties met woordspelingen aan; deze contrasteert hij met 5 (door hemzelf gemanipuleerde) niet-woordspelige advertenties. Aan onafhankelijke, grote groepen proefpersonen vraagt hij

[p. 337]

nu telkens één advertentie te beoordelen op een aantal relevante beoordelingsschalen (overtuigend? prikkelend? aardig? enzovoort).

Dit design, een recht-toe-recht-aan ‘single-factor independent-group’ design, is in het bijzonder geschikt voor die situaties waarin een onderzoeker gemakkelijk over grote aantallen proefpersonen kan beschikken, terwijl de voorraad messages waaruit geput kan worden, beperkt is.

Nog een voorbeeld van dit type design, nu uit een geheel andere discipline dan die van het taalwetenschappelijk bedrijf: de onderwijsresearch (het betreffende voorbeeld is eerder door ons uitvoerig toegelicht aan de hand van het two-group, experimental-control group design (o.c. 2005: 111-112). Stel dat een onderwijsresearcher de effectiviteit van een nieuw ontwikkelde didactiek wil toetsen, en deze contrasteert met een conventionele. Om een ‘confounding’ van de effecten van de (aard van de) didactiek met de onderwijskwaliteiten van de twee docenten die de experimentele respectievelijk de controle-didactiek implementeren te vermijden, introduceert de onderwijsonderzoeker in dit design een random variabele ‘docent’ die genest is binnen de aard van de didactiek - de leerlingen zijn verder genest binnen elke docent. De ‘woorden’ zijn in dit design dus vervangen door ‘docenten’, de respondenten door ‘leerlingen’.

In ons eerste voorbeeld van dit design is sprake van drie variantiebronnen: 1. een gefixeerde variabele ‘Advertentietype’, met twee niveaus: 1. met woordspelingen 2. zonder woordspelingen; 2. een replicatiefactor ‘woorden/messages’ (in dit geval de 5 advertenties); 3. een replicatiefactor ‘proefpersoon’. Beide replicatiefactoren worden verondersteld random factoren te zijn. Het statistisch model voor dit design is als volgt:

Tabel 11. Verwachtingswaarden van MS-termen in design III: woorden genest binnen treatment, respondenten genest binnen woorden. (N.B. w is het aantal replicaties per treatment-niveau; r is het aantal respondenten per woord).

Bron	Verwachtingswaarden van MS-termen
Treatment [T]	σε^2 + wrθ^2T + rσ^2w(T)
Woorden [w(T)]	σε^2 + rθ^2w(T)
Respondent [r(w)]	σε^2

Met behulp van de volgende (reguliere) F-ratio kan het effect van de treatment getoetst worden:

waarbij t het aantal niveaus van de treatment-variabele en w het aantal message-replicaties per niveau van de treatmentvariabele betreft

6.1 De verwerking van data in design III

Ter illustratie van de berekening van de F-ratio voor design III gebruiken we dezelfde numerieke gegevens als die in de vorige analyses; alleen worden in dit design alle woorden aan andere steekproeven respondenten zijn voorgelegd. Er wordt gebruik gemaakt van acht steekproeven van acht respondenten, zodat de totale steekproef uit 64 respondenten bestaat. In tabel 12 is dit design III schematisch weergegeven voor het geval er vier woorden (of vier advertenties of docenten) per conditie aanwezig zijn.

[p. 338]

Tabel 12: Schematische weergave van Design III (n=aantal observaties per woord).

Subject	Conditie	Woord	Score
1	1	1	6
2	1	2	7
3	1	3	4
4	1	4	2
5	2	5	5
...	...
9	1	1	6
...	...
63	2	7	3
64	2	8	6

In dit voorbeeld wordt uitgegaan van 4 woorden/messages per conditie. De getallen aan de hand waarvan de berekening van de F-ratio geïllustreerd wordt, zijn overigens dezelfde als die uit tabel 2, met dien verstande dat de eerste vier items (woorden) in conditie 1 geobserveerd zijn en de tweede vier in conditie 2.

De SPSS-setup voor design III is in principe simpel¹⁵, hoewel er wel (weer) enig handmatig rekenwerk verricht moet worden. In de eerste run wordt naast de gemiddelden en de standaarddeviatie per conditie ook de variantie tussen condities uitgerekend; in de tweede en derde run wordt per conditie de (teller van de) variantie geschat. Tezamen geven deze de variantie tussen woorden binnen condities.

Tabel 13: SPSS-setup voor de analyse van Design III.

data list file='c:\data\vb3.txt' free/subj cond woord score.

MEANS

TABLES = woord BY cond

/CELLS MEAN STDDEV

/STATISTICS ANOVA.

SORT CASES BY cond.

SPLIT FILE

SEPARATE BY cond.

MEANS

TABLES= score BY woord

/CELLS MEAN

/STATISTICS ANOVA.

In de tweede en derde run wordt de variantie tussen woorden per conditie uitgerekend.

15 In SPSS is het echter wel belangrijk dat in elke cel exact evenveel waarnemingen gedaan zijn (kortom: n per cel behoort gelijk te zijn). Verschillen de aantallen waarnemingen per cel, dan moeten er at random proefpersonen uit het bestand verwijderd worden totdat elke cel precies evenveel waarnemingen bevat - een uit methodisch oogpunt geen fraaie procedure.

[p. 339]

Deze runs leveren de volgende resultaten.

Tabel 14: Resultaten van de runs voor design III.

Univariate Anaysis of Variance
Source	Sum of Squares	df	Mean Square	F	Sig.
Between groups	43.89	1	43.89	10.12	.002
Within groups	268.97	62	4.34
Totaal	312.86	63
	Conditie 1
Between groups	26.094	3	8.698	1.747	.180
Within groups	139.375	28	4.978
	Conditie 2
Between groups	4.618	3	1.539	.436	.729
Within groups	98.882	28	3.531

De teller van de variantie tussen items binnen condities kan uitgerekend worden als de som van de betreffende kwadratensommen (26.094 + 4.618), hetgeen de waarde 5.12 (30.712/6) oplevert als schatting van de variantie tussen items binnen condities. Rekening houdend met de toevalsverschillen tussen items door deze als een random factor te conceptualiseren krijgt men:

F' = MS(Conditie) / MS(woord within conditie) = 13.14 / 5.12 = 2.57

Met 1 vrijheidsgraad voor de teller en [2* (4-1) =] 6 vrijheidsgraden voor de noemer, levert dit een overschrijdingskans van 0.16 op.Vat men - ten onrechte overigens - de verschillen tussen items/woorden/messages op als een gefixeerd effect, dan blijkt het verschil tussen de beide condities - precies zoals bij de vorige analyses - wél significant (p = .002).

7. Design IV: woorden genest binnen respondenten, respondenten genest binnen treatment

De keuze voor design III versus design IV (beide tussen-proefpersonen ontwerpen) is onder meer afhankelijk van de vraag of de onderzoeker makkelijker aan messages dan aan proefpersonen kan komen; is het eerste het geval, dan ligt design IV voor de hand, is het laatste het geval, dan zal de keuze op III vallen. Precies zoals design III is ook design IV een hiërarchisch design waarbij de ene replicatiefactor genest is in de andere, zij het dat nu - anders dan in design III waar de proefpersonen genest zijn binnen de messages - de messages juist genest

[p. 340]

zijn binnen de proefpersonen. Elke persoon in dit design wordt blootgesteld aan zijn eigen, ‘unieke’ message-set. Uiteraard heeft deze configuratie consequenties voor het statistisch model en de daaruit af te leiden F-ratio:

Tabel 15: Verwachtingswaarden van MS-termen in design IV: woorden genest binnen respondenten, respondenten genest binnen treatment (N.B. r is het aantal proefpersonen per treatment-niveau, w is het aantal replicaties/woorden per proefpersoon)

Bron	Verwachtingswaarden van MS-termen
Treatment [T]	σε^2 + wrθ^2T + wσ^2r(T) +σ^2 w(rT)
Repondent [r(T)]	σε^2 + wσ^2 r(T) + σ^2 w(rT)
Woorden [w(rT)]	σε^2 + σ^2w(rT)

De (reguliere) F-ratio ter toetsing van het treatment-effect heeft de volgende vorm:

F = MS(T)/MS(r(T))

df₁ = t - 1, df₂ = t (r-1), waarbij t het aantal niveaus van de treatment-variabele en r het aantal respondenten per treatment-niveau betreft

7.1 De verwerking van data in design IV

De gegevens waarop we ons baseren, zijn weer dezelfde als die in de eerdere voorbeelden, met dien verstande dat alle respondenten nu andere ‘woorden’ voorgelegd krijgen (in feite wordt dus tabel 2 in SPSS gebruikt). Hoewel de setup ook voor dit voorbeeld redelijk eenvoudig is, moet er naderhand toch weer het één en ander met de hand berekend worden.

Tabel 16: SPSS-setup voor de analyse van design IV

data list file='c:\data\vb1.txt' free/w1 to w8.

MANAVO

w1 to w8

/WSFACTOR = treat (2) woord (4)

/CONTRAST (woord) = difference

/PRINT = cellinfo (means)

/WSDESIGN = treat woord treat*woord.

compute gemc1=(w1+w2+w3+w4)/4.

compute gemc2=(w1+w2+w3+w4)/4.

DESCRIPTIVES

VARIABLES=gemc1 gemc2

/STATISTICS=VARIANCE.

[p. 341]

Dit levert (o.a.) de volgende output:

Tabel 17: Resultaten voor design IV

Test of between- subjects effects
Source	Sum of Squares	df	Mean Square	F	Sig.
Treatment	43.89	1	43.89	5.59	.050
Error(treatment)	54.98	7	7.85
Varianties tussen subjecten
Gemc1	2.669
Gemc2	0.839

Nu de variantie per conditie bekend is, kan de ‘gepoolde’ kwadratensom uitgerekend worden:¹⁶ deze bedraagt 24.56 (nl.: 2.669*7+0.839*7). De gemiddelde kwadratensom is dan 1.75 (nl.: 24.56/(2*(8-1)). Nu kan de toetsingsgrootheid F berekend worden volgens:

F = MS(T)/MS(r(T)) = 43.89/1.75 = 25.08

met df_teller = 2-1 en df_noemer = 14. De hierbij behorende overschrijdingskans is 0.001, zodat de nulhypothese verworpen kan worden.

16 Merk op dat deze ‘gepoolde’ kwadratensom ook berekend kan worden door de gemiddelden per persoon alsmede indicatoren voor de beide condities opnieuw in SPSS in te voeren, als twee aparte variabelen. Vervolgens voert men een one-way ANOVA uit, met conditie als onafhankelijke variabele en gemiddelde score als afhankelijke variabele.

8 Conclusies

In deze bijdrage is geïllustreerd dat voor multiple message designs de constructie van een correcte F-ratio (en dus een correcte toetsing van het treatment-effect) bepaald géén eenvoudige zaak is. Het is verstandig om hiermee rekening te houden voordat een experiment opgezet wordt; dit kan veel problemen en frustraties voorkomen.

Wellicht bieden de in dit artikel besproken designs, die redelijk frequent voorkomen, afdoende aanknopingspunten voor de berekening van een correcte toetsingsgrootheid. De gegeven design-voorbeelden zijn echter geenszins in generaliserende zin toe te passen op soortgelijke, op het oog verwante onderzoeksontwerpen: de onderzoeker zal zich er telkens van moeten vergewissen dat het door hem gekozen specifieke onderzoeksontwerp de facto identiek is aan dan wel een verbijzondering betreft van de in dit artikel gegeven voorbeelden. Immers, marginale verschillen in onderzoeksontwerp kunnen leiden tot grote verschillen in de te berekenen toetsingsgrootheden.

Tot slot: het verdient aanbeveling om voor de feitelijke uitvoering van een experiment het betreffende design door te rekenen met behulp van gefingeerde data-sets. Deze procedure kent twee grote voordelen: (1) de wijze van data-analyse is al bekend vóórdat de gegevens verzameld zijn - statistische ad hoc-oplossingen worden daardoor voorkomen; (2) er wordt informatie verkregen over de power van de toets, hetgeen aanleiding kan zijn om meer dan wel minder gegevens te verzamelen.

[p. 345]

Bibliografie

Clark, H.H. (1973). The language-as-fixed-effect fallacy. Journal of Verbal Learning and Verbal Behavior, 12, 335-359.

Coleman, E.B.(1964). Generalizing to a language population. Psychological Reports, 14, 219-226.

Cornfield, J. & Tukey, J.W. (1956). Average values of mean squares for factorials. Annals of Mathematical Statistics, 27, 907-948.

Davenport, J.M. & Webster, J.T. (1973). A comparison of some approximate F-tests. Technometrics, 15, 779-789.

Forster, K.I. & Dickinson, R.G. (1976). More on the Language-as-Fixed-Effect Fallacy: Monte Carlo Estimates of Error Rates for F1, F2, F', and min F'. Journal of Verbal Learning and Verbal Behavior, 15, 135-142.

Glass, G.V. & Stanley, J.C. (1970). Statistical Methods in Education and Psychology. Englewood Cliffs, NJ: Prentice Hall.

Jackson, S.(1992). Message Effects Research: Principles of Design and Analysis. New York: Guilford.

Jackson, S. & Brachers, D.E. (1994). Random Factors in ANOVA. Sage University Paper series on Quantitative Applications in the Social Sciences, 07-098. Thousand Oaks, CA: Sage.

Katz, A.N. (1989). On choosing the vehicles of metaphors: Referential concreteness, semantic distances, and individual differences. Journal of Memory and Language, 28, 486-499.

Keppel, G. (1982). Design and Analysis: A Researcher's Handbook (2nd ed.). Englewood Cliffs, NJ: Prentice Hall.

Keppel, G. (1991). Design and Analysis: A Researcher's Handbook (3rd ed.). Englewood Cliffs, NJ: Prentice Hall.

Kirk, R.E. (1968). Experimental design: procedures for the behavioral sciences. Pacific Grove: Brooks/Cole.

Raaijmakers J.G.W., Schrijnemakers, J.M.C. & F. Gremmen (1999). How to Deal with ‘The Language-as-Fixed-Effect Fallacy’: Common Misconceptions and Alternative Solutions. Journal of Memory and Language, 41, 416-426.

Satterthwaite, F.E. (1946). An approximate distribution of estimates of variance components. Biometrics Bulletin, 2, 110-114.

Shavelson, R.J. & Webb, N.M. (1991). Generalizability Theory: A Primer. Newbury Park, CA: Sage.

Smith, J.E.K. (1976). The assuming-will-make-it-so fallacy. Journal of Verbal Learning and Verbal Behavior, 15, 262-263.

Wike, E.L., & Church, J.D. (1976). Comments on Clark's ‘The language-as-fixed-effect fallacy. Journal of Verbal Learning and Verbal Behavior, 15, 249-255.

Winer, B.J. (1971). Statistical Principles in Experimental Design. New York: McGraw-Hill.