De Tijdspiegel. Jaargang 24

Leerboeken voor het middelbaar onderwijs.

Beginselen der Meetkunde, door W. Kreling, Leeraar aan de Rijks hoogere burgerschool te Groningen. Groningen, J.B. Wolters, 1865.

De wet tot regeling van het middelbaar onderwijs had nauwelijks de koninklijke sanctie ontvangen, of zij werd door het bestuur ten uitvoer gelegd met eene voortvarendheid, met eene soort van koortsachtige gejaagdheid schier, die velen in den lande onwillekeurig deed vragen, of zooveel overhaasting wel ooit tot een goed resultaat zou kunnen leiden.

In verscheidene gemeenten zag men Rijks hoogere burgerscholen verrijzen; gemeentescholen voor uitgebreid lager onderwijs werden gesupprimeerd en door middelbare vervangen. Was er dan een voldoend personeel leeraren voorhanden? Verre van daar. Hoofdonderwijzers, voorzien van toelatingen tot het geven van onderwijs in ééne of meer talen of in de wiskunde, door de opheffing hunner scholen buiten betrekking geraakt, werden overgeplaatst als leeraren aan rijks- en gemeente-burgerscholen; doctoren en advocaten verlieten het hooger onderwijs en de pleitzaal; zelfs dominé's zag men bef en toga aan de wilgen hangen en als leeraars bij 't middelbaar onderwijs optreden. Slechts een zeer klein getal leeraren verwierven hun diploma volgens de wet van 2 Mei '63; 't is alsof het hooger bestuur uitging van 't principe, dat een amalgama van hooger en lager onderwijs een goed middelbaar op moest leveren.

Of eene zoodanige handelwijze de gewenschte vruchten op zal leveren? De tijd zal zulks moeten leeren. Tot nog toe ontbreken de gegevens om daarover te kunnen oordeelen; maar later, wanneer de tegenwoordige leerlingen der burgerscholen het maatschappelijk leven

[p. 186]

zijn ingetreden, dan zal 't blijken of ‘de middelbare scholen ons land een China hebben gemaakt in miniatuur, onzen burgerstand eene klasse van onverdragelijke wijsneuzen, reeds geknakt en verstompt op het oogenblik, dat zij het practisch leven ingaan; dan of zij ons zullen brengen, wat wij meer behoeven dan goud, die algemeene kennis namelijk, waarin ons volk onbetwistbaar bij andere volken achter staat’ (Prof. J.T. Buys).

Maar den tijd afwachtende, dat men behalve de jaarlijksche verslagen, behalve rapporten der Inspecteurs ook nog de resultaten van het onderwijs tot gegevens zal hebben, om over de werking der wet te oordeelen, blijft ons nog een middel om voorloopig kennis te maken met de hoogere burgerschool: n.l. dat men zich voortdurend op de hoogte houde van de werken, die door leeraren van 't Middelbaar onderwijs ten behoeve van dat onderwijs geschreven worden. Daaruit toch zullen wij zien of de leeraar, gedachtig aan de woorden:

‘Ce que l'on conçoit bien s'énonce clairement,

de zaak, die hij onderwijst, zelf meester is; wij zullen bekend worden met zijne methode; wij zullen kunnen beoordeelen of die methode geschikt is voor knapen van den leeftijd van 12 tot 18 jaren.

Het onderwijzend personeel schijnt in den tegenwoordigen tijd aangegrepen te zijn door eene manie om te schrijven. De markt van 't lager onderwijs begint overvoerd te worden; waarom zou men er zich niet op toeleggen om ook het middelbaar van alle zijden te voorzien? Oorspronkelijke werken: zeldzaam; - vertalingen: legio. - Navolgingen en compilatiën; werken, vele zonder, weinig met een raison d'être. Uitgevers vindt men altijd; de ijdelheid, om zijn' naam gedrukt te zien, baart nog altijd schrijvers.

Maar zoo voortgaande, geachte lezers, zoude ik onwillekeurig afdwalen van den weg, dien ik mij voorgesteld heb met u te bewandelen. Laten wij ons, naar aanleiding van het werkje van den heer Kreling, eenige oogenblikken bewegen op het gebied der Meetkunde.

Het doel van een leerboek voor de Meetkunde mag geenszins daarin bestaan, dat het tracht zijn onderwerp uit te putten; het geeft slechts zooveel, dat de leerling een flink afgerond geheel in 't hoofd krijgt; later, wanneer hij aan het einde zijner reize, de differentiaal- en intregraalrekening, gekomen is, staat het hem vrij de zijpaadjes te bewandelen.

‘Je weitere gebiete,’ zegt Dr. Baltzer in de Vorrede zijner Elemente: ‘je weitere Gebiete die mathematische Forschung sich unterwirft, desto dringlicher wird die Pflicht der Lehrer, den wissenschaftlichen Bestand in seinen Grundlagen zu untersuchen, in seinen Zusammenhang darzulegen, damit die Lernenden baldigst befähigt werden, die Erbschaft früherer Meister anzutreten und zu vermehren.’

Geene meetkunde dus zooals die van den heer Badon Ghyben, die,

[p. 187]

voor het groot aantal der gevolgen, in plaats van op den vindingsgeest des leerlings te vertrouwen, alle moeilijkheden uit den weg ruimt en het zelfzoeken bijna tegenwerkt; geene theorie voor eerstbeginnenden, die den jeugdigen beoefenaar gewent aan eene wijze van behandeling, die hij later geheel of ten deele zal moeten wijzigen; van het begin tot aan de uiterste grens moet het geheel een harmonisch geheel zijn.

Zoodanig werk had ik van een leeraar aan eene middelbare school verwacht; een werk, waarin de nieuwere meetkunde, zooals zij ons door Möbius, Chasles, Witzschel en anderen geleerd wordt, niet langer geïgnoreerd, maar op het voetspoor van Baltzer met de gewone meetkunde tot een goed geordend geheel samengesmolten ware. Een zoodanig werk ontbreekt nog in onze taal. De nieuwere meetkunde en hare vele toepassingen zijn door bijna alle Nederlandsche schrijvers onopgemerkt voorbijgegaan. [De poging van Dr. Bierens de Haan, om haar in den 5^den druk van Lacroix eenigszins meer bekend te maken, kan wegens hare oppervlakkige en scheeve voorstelling hierbij volstrekt niet in aanmerking komen]. Moet dan de erfenis van Euclides altijd ongeschonden in haar geheel bewaard blijven? Is de wetenschap in 20 eeuwen niet verder vooruit gegaan, dan dat men het leesboek wat grooter van omvang maakt door het bijvoegen van corollaria, die eigenlijk den leerling hadden moeten dienen tot toepassing van het geleerde?

In 't jaar 1710 verscheen de derde druk van Abraham de Graaf's. De geheele mathesis of wiskonst, herstelt in zyn natuurlyke gedaante. Na dien tijd verschenen in onze taal de werken van Warius, Simpson, Steenstra, van Swinden, de Gelder, Badon Ghyben en van zoovele anderen van minder beteekenis; en toch is tusschen de Graaf's methode en die van den heer Kreling nog geen ander verschil, dan dat eenige gevolgen gepromoveerd werden tot stellingen, en eenige stellingen wat meer ruimschoots voorzien werden van gevolgen. Onder de behandeling van de Graaf schijnt de zieke zoo volkomen genezen te zijn, misschien wel door middel van het levenswater, dat zij na dien tijd niet alleen niet meer is ingestort, maar dat zij zelfs met telkens verjeugdigde kracht voortleefde, zonder schijnbaar te verouderen.

Ik aarzel dan ook niet te verklaren, dat ik in mijne verwachting omtrent de methode van den Heer Kreling zeer teleurgesteld geworden ben. Wel heeft deze Heer volgens zijne verklaring in het voorbericht Schlömilch's Grundzüge der Geometrie des Maasses hoofdzakelijk geraadpleegd bij de samenstelling van zijn werkje, maar ik moet ronduit bekennen, dat ik, zoo zulks in het voorbericht niet uitdrukkelijk anders gezegd was, het geheele werkje zou gehouden hebben voor eene omwerking van Badon Ghyben's planimetrie.

In mijn oog hebben Kreling's Beginselen hoegenaamd geen recht

[p. 188]

van bestaan, omdat ze noch in methode, noch in nauwkeurigheid van uitdrukking, noch in volledigheid uitmunten boven de meeste werkjes van dien aard in onze taal uitgegeven; in vele opzichten zelfs daarbij ver ten achter staan. Wie toch zal, indien hij daartoe als onderwijzer geroepen is, de aanschouwelijke wijze om de leerlingen met de inhouden der vlakke figuren bekend te maken, zooals wij die bij Schlömilch vinden, niet verkiezen boven de behandeling van hetzelfde onderwerp, zooals die voorkomt bij Badon, Kempees en nu ook weder bij Kreling? Daarenboven vind ik de volgorde der hoofdstukken bij Kreling geheel verkeerd, omdat hij, eene soort cursus schrijvende voor de eerste drie jaren op de hoogere burgerschool, de gelijk- en gelijkvormigheid der polygonen had behooren te doen volgen door het hoofdstuk over het berekenen der inhouden van rechtlijnige figuren in plaats dit laatste vooraf te doen gaan door de leer der gelijkvormigheid. Zelfs de eenvoudigste eigenschappen van den cirkel, door Kreling eerst na de inhoudsvinding opgegeven, behooren vóór de evenredigheden der lijnen behandeld te worden. Mijne ondervinding toch heeft mij herhaaldelijk geleerd, dat de leer der evenredigheden, als stennende meer op redeneering dan op aanschouwing, voor de jongere leerlingen hare eigenaardige bezwaren heeft, die gemakkelijker uit den weg geruimd worden, naarmate hunne reeds verkregene kennis van de eigenschappen der figuren grooter is.

Bovendien betwijfel ik het nog ten sterkste dat eerstbeginnenden veel nut trekken uit een leerboek over de meetkunde; van alles, wat zij daarin lezen, een enkele uitgezonderd, begrijpen zij geen jota en zelden vindt men ambitie genoeg om die moeilijkheden door te worstelen. Juist, omdat men den leerling te vroeg kwelt met een boek; juist omdat men hem te veel van buiten laat leeren van stellingen en gevolgen, die hem in 't geheel geen belang inboezemen; juist daarom is de wiskunde zóó in discrediet geraakt, dat niemand zich schaamt te verklaren, dat hij er niets van kent, want dat hij geen hoofd had om wiskunde te leeren. De wetenschap en de leerling, beiden zijn slachtoffers van de methodus docendi.

Evenmin als ik mij kan vereenigen met de methode en met de indeeling in hoofdstukken, evenmin kan ik de behandeling der afzonderlijke deelen goedkeuren. Eenige aanmerkingen mogen hier volgen.

Bl. 3. ‘De gebrokene lijn is eene lengte-uitgebreidheid, die bestaat uit de samenvoeging van eenige rechte lijnen, en niet in dezelfde richting voortgaat.’

Deze definitie bestaat uit twee halve.

Essentieele bepaling. De gebrokene lijn is eene lengte-uitgebreidheid, die niet in dezelfde richting voortgaat.

Genetische bepaling. Zij bestaat (beter: ontstaat) uit de (lees hierbij nog: niet rechte) samenvoeging van eenige rechte lijnen.

Beter ware ééne goede, dan twee halve, die onjuist zijn.

[p. 189]

Id. § 4. ‘De vlakken worden verdeeld in platte en gebogene.’

Lees: De vlakken worden verdeeld in platte, gebogene en kromme.

Tot de gebogene vlakken behoort ook het rechtlijnig vlak enz.

Id. § 7. ‘Elke opgave van de eene of andere eigenschap eener figuur noemt men eene meetkundige stelling. Daar nu de juistheid van zulk eene meetkundige waarheid of eigenschap eener figuur niet altijd dadelijk in het oog valt, heeft men daarvoor (waarvoor? Voor het oog, voor de figuur, voor de eigenschap of voor de juistheid?) Eene redeneering noodig, die de waarheid der eigenschap buiten allen twijfel stelt.’

Wanneer nu de S. in § 72 zegt: ‘Een vierhoek wordt een parallelogram genoemd, wanneer de zijden twee aan twee evenwijdig loopen;’ of in § 67: ‘Eene platte-vlakteuitgebreidheid, aan alle zijden begrensd door rechte lijnen, wordt veelhoek genoemd;’ zijn dan deze opgaven theorema's of definities? Zijn het theorema's, dan ontbreekt het bewijs; zijn het definities, dan deugt de bepaling van § 7 niet.

Bl. 4 § 7. ‘Er zijn twee soorten van bewijzen: rechtstreeksche bewijzen en bewijzen uit het ongerijmde.’

En dan het bewijs per enumerationem simplicem. Zoo de Schrijver het onder de rechtstreeksche bewijzen rekent, had het toch, op zijn minst genomen, wel eene afzonderlijke vermelding verdiend.

Bl. 5 § 9. ‘2^e Axioma. De rechte lijn is de kortste weg tusschen twee punten.’

Van dit axioma komt een deugdelijk bewijs voor in het Weekblad voor het L.M. en G. Onderwijs. Ik meende, dat men eenaxioma niet bewijzen kon.

Bladz. 7. § 12 noot. ‘Door eene vlakke kromme lijn verstaat men eene kromme lijn, waarvan alle punten in hetzelfde vlak liggen.’

Is dan de schroeflijn ook eene vlakke kromme lijn? Zij ligt toch in 't zelfde cilindervlak.

id. id. ‘Gevolgen. 1^e. Alle stralen en middellijnen van denzelfden cirkel zijn onderling gelijk.

2^e. ‘Een punt ligt op den cirkelomtrek, wanneer zijn afstand van het middelpunt gelijk is aan den straal.’

3^e. ‘Een punt ligt buiten den cirkelomtrek, wanneer zijn afstand van het middelpunt grooter is dan de straal.’

4^e. ‘Een punt ligt binnen den cirkelomtrek, wanneer zijn afstand van het middelpunt kleiner is dan de straal.’

Ik haal hier deze reeks gevolgen aan, om in het oog te laten vallen, waartoe dat stelsel om alle bepalingen en theorema's van gevolgen te voorzien, leiden moet. Alle zelfwerkzaamheid wordt den leerling ontzegd. Het onderwijs in de meetkunde wordt een onophoudelijk voorzeggen, de leerling wordt verlaagd tot papegaai.

Bladz. 8. § 13. ‘Axioma. Lijnen van verschillende richting in een vlak getrokken, moeten, behoorlijk verlengd, in één punt te zamen komen, zij hebben dan een, maar ook slecht séén punt met elkaâr gemeen.’

[p. 190]

Bladz. 22. § 36. ‘Axioma. De som van twee zijden van een driehoek is altijd grooter dan de derde zijde.’

Twee axioma's, die wel degelijk als theorema's moeten bewezen worden. De heer Kreling schijnt zich niet te kunnen vereenigen met de uitspraak van Baltzer: ‘Die gerühmte Richtigkeit der mathematischen Wissenschaften beruht darauf, dass die Anzahl ihrer Axiome äusserst gering ist, und dass ihre Theoreme sich logisch beweisen und empirisch prüfen lassen.’

Bladz. 12. § 21. ‘Wanneer men het been van een hoek door het hoekpunt heen verlengt, ontstaat er een nieuwe hoek; dezen hoek noemt men den aanliggenden hoek van den eersten.

Gevolgen. 1^e. Twee aanliggende hoeken maken een gestrekten hoek.’

Bladz. 13. § 24. ‘Aanliggende hoeken, die te zamen gelijk zijn aan twee rechte hoeken, noemt men gewoonlijk supplementshoeken.’

Zijn er dan, ondanks het gevolg van § 21, nog aanliggende hoeken, die niet gelijk zijn aan twee rechte hoeken?

Bladz. 13. § 25. ‘Twee lijnen staan loodrecht op elkaâr, enz.’

De benaming loodrecht is in de planimetrie ongepast. Zij drukt meer uit, dan er mede bedoeld wordt. Normaal ware te verkiezen.

Bladz. 14 § 26. ‘Wanneer eene lijn schuin op een andere staat, zijn de hoeken, die de eene lijn met de wederzijdsche deelen der andere maakt, elkaârs supplementen.’

Deze eigenschap wordt bewezen en zal dus wel een theorema zijn. Na het aangehaalde van § 21 beschouw ik dit bewijs als geheel overtollig.

Bladz. 17. § 31. ‘Wanneer twee evenwijdige lijnen door eene derde lijn gesneden worden, ontstaan er acht hoeken....... Overeenkomstige hoeken zijn elk paar hoeken, die aan denzelfden kant der snijlijn liggen, en de opening naar denzelfden kant gekeerd hebben.’

Zou 't ook mogelijk zijn, n.l. onder dezelfde gegevens, hoeken te vinden, die de opening naar denzelfden kant gekeerd hebben en niet aan dezelfde zijde van de snijlijn liggen? Zoo neen, dan vindt men in de bepaling iets overtolligs.

Nog een aantal aanmerkingen zoude ik kunnen neêrschrijven, maar waartoe zoude zulks dienen? Men zou mij kunnen verwijten, dat ik slechts aan mijne vitzucht bot wilde vieren, terwijl bovendien de lezer uit het aangehaalde reeds genoegzaam zien kan, hoe het werkje van den heer Kreling wemelt van onnauwkeurigheden, die door velen misschien zullen beschouwd worden als kleinigheden, maar in mijn oog groote gebreken zijn. De wiskunde in 't algemeen, de meetkunde in 't bijzonder, wordt aangeleerd om 't verstand op te scherpen, het oordeel te ontwikkelen, logisch te denken en zich juist te leeren uitdrukken. Wanneer nu het leerboek telkens vervalt in herhalingen, de stellingen in eene verkeerde volgorde plaatst en zich allerlei vrijheden veroorlooft in 't geven van bepalingen, het zal de leerling dan daarin

[p. 191]

den weg vinden om logisch te denken en zich zuiver uit te drukken?

In elementaire werken kent men geene kleinigheden; terwijl bovendien in de wiskunde slechts twee wijzen bestaan om iets te behandelen de goede of de slechte. Een midden is onmogelijk.

Nog eens herhaal ik, dat het mij spijt dat de heer Kreling in zijn werkje wederom den ouden weg bewandeld heeft, en van de ontdekkingen der laatste jaren hoegenaamd geen gebruik maakte. Zoo als het daar ligt moet mijn oordeel daarover ongunstig zijn. De werken van Badon Ghijben en van Schlömilch vertaald door Eger; het reeds tamelijk verouderde werk van J.H. van Swinden en de vertaling van Lacroix, zonder de bijvoeging van B.d.H., zijn volgens mijn gevoelen oneindig veel beter. Ik kan niet zien waarom dit boek bestaan moest.

Mocht er na tijdsverloop een tweede druk noodig zijn, dan geloof ik, dat het werk veel in waarde zou winnen door de nieuwere met de oudere meetkunst te vereenigen, het geheel naauwkeurig na te zien en in eene betere volgorde voor eerstbeginnenden te rangschikken; tot zoolang kan men zich veilig bedienen van de thans gebruikelijke leerboeken.

Aardenburg.

G.A. Vorsterman van Oyen.

W.M. Logeman, Natuurkundige stellingen. Eerste aflevering. Te Haarlem, bij de Erven F. Bohn, 1866.

Het voorzien in lang of minder lang gevoelde behoeften blijft nog steeds aan de orde van den dag, en waarlijk, in de laatste tientallen van jaren is zooveel veranderd en wordt nog dagelijks zooveel gewijzigd, dat voortdurend nieuwe behoeften ontstaan, en naarmate aan eenige voldaan wordt, worden weder nieuwe geboren.

De geschiedenis van de invoering van het middelbaar onderwijs in de tegenwoordige vormen hier te lande, levert daarvan een duidelijk voorbeeld. Pas was de nieuwe wet in werking getreden en daardoor aan de te lang miskende natuurwetenschappen recht wedervaren, of van alle zijden gingen klachten op over het gemis van veel, waaraan men vroeger nauwelijks gedacht had, en hieronder werd vooral ook de behoefte ondervonden aan geschikte handleidingen en leerboeken over de verschillende vakken van onderricht, die plotseling eene zoo gewichtige plaats in het onderwijs aan het opkomende geslacht hadden ingenomen.

Ook de natuurkunde verkeerde in dat moeilijke geval, en daar de bestaande handboeken zelden met het oog op een onderwijs als dat der middelbare scholen geschreven waren, is het niet te verwonderen dat

[p. 192]

velen, met het onderwijs in de physica belast, in de keuze van éen leerboek bemoeielijkt werden door de omstandigheid, dat ze geen enkel konden vinden, waarmede ze ex imo pectore voldaan waren.

De schrijver van het hierboven aangekondigd werkje, waarvan de eerste aflevering voor ons ligt, brengt in zijn voorbericht hieromtrent eenige gevoelens te berde, waarmede ik volkomen instem.

‘Kon het geschieden,’ zegt hij, ‘ik zou liefst mijne leerlingen in het geheel geen boek in handen geven en ze trachten te gewennen, om alleen, als hulpmiddel voor hun geheugen, te vertrouwen op korte nota's, die zij maken gedurende de les.’ Dit is echter zonder dicteeren onmogelijk, en daar dit veel tijd wegneemt, heeft schrijver, wat hij vroeger dicteerde, hier en daar aangevuld en verbeterd, en in dit boekje doen drukken.

Het denkbeeld verdient mijns inziens toejuiching, en met vreugde heb ik dan ook de natuurkundige stellingen begroet; tot mijn leedwezen moet ik er bijvoegen, dat die vreugde bij meer aandachtige beschouwing wel eenigszins is afgenomen.

In het voorbericht worden wij gewaarschuwd voor den stijl en de spelling, die we in het werkje zullen aantreffen; de eerste waarschuwing is recht op hare plaats! - Wat de spelling betreft, ik geloof niet, dat daaraan in een boekje over natuurkunde veel zal gehecht worden; dat er overigens verwarring van denkbeelden zou kunnen ontstaan, door geen onderscheid te maken in de schrijfwijze van ligt en licht, van verdigting en verdichting, van wigtje en wichtje is zeer onwaarschijnlijk; vooral de twee laatste woorden - - maar deze staan er vast alleen voor de aardigheid bij.

Belangrijker echter dan stijl en spelling is de vraag naar het gehalte van den inhoud; - beantwoordt het werkje aan het doel, waarmede het in de wereld gezonden is, is het bruikbaar als handboekje bij het onderwijs in de physica aan hoogere burgerscholen?

Die vraag durf ik noch geheel ontkennend, noch ook bevestigend te beantwoorden; het boekje kan als middel tot herinnering voor de leerlingen in vele opzichten nuttig zijn, doch het is onmogelijk de bepalingen, voorbeelden en verklaringen onaangetast te laten: vele daarvan zijn onduidelijk, sommige niet ten volle nauwkeurig, enkele geheel onjuist. Tot staving van dit mijn gevoelen zal ik eenige voorbeelden aanvoeren.

De voorstelling in St. 12, dat men krachten door rechte lijnen kan voorstellen, omdat bij de laatste ‘nagenoeg’ hetzelfde als bij de krachten plaats vindt, is niet juist; nimmer zou de graphische methode eene zoo uitgestrekte toepassing op allerlei takken van wetenschap en industrie hebben kunnen verkrijgen, als men krachten alleen daarom door rechte lijnen kon voorstellen^(*).

(*) Ook koppels worden voorgesteld door rechte lijnen; is hier ook ‘nagenoeg hetzelfde het geval’?

[p. 193]

In St. 26 wordt gezegd, dat het zwaartepunt van eenen driehoek op ⅓ der hoogte, van eene piramide op ¼ der hoogte gelegen is; ofschoon zich dit nu wel laat verdedigen, is de bedoeling voor den beginner niet te verstaan, en bij eigene ondervinding kan ik getuigen, dat het steeds wordt opgevat, alsof het zwaartepunt bij elken driehoek (resp. piramide, kegel) op ⅓ (resp. ¼) van de loodlijn zou gelegen zijn, uit den top op de basis neêrgelaten.

Bij St. 29 had behooren vermeld te worden, dat een lichaam ten opzichte van verschillende richtingen in een verschillend soort van evenwicht kan zijn. (Een liggende cilinder is zoowel in indifferent als in stabiel evenwicht.)

In St. 33 had de formule r = vt zeer gevoegelijk eene plaats kunnen vinden, terwijl dan tevens de beteekenis van v als snelheid helder had kunnen aangeduid worden. Eene definitie van snelheid ware overigens ook zonder dat noodig geweest.

De redeneering in St. 37 tot staving der formule h = ½ gt² is geen bewijs.

Aan het einde van St. 40 leest men:

‘Men houde wel in het oog, dat hieruit niet volgt: eene kracht moet n-maal grooter zijn, om hetzelfde ligchaam dezelfde ruimte te doen doorloopen in n-maal kleineren tijd. Uit het bovenstaande volgt namelijk, dat eene kracht, die twee, drie n-maal grooter is dan eene andere, hetzelfde ligchaam bij eene eenparig versnelde beweging dezelfde ruimte zal doen doorloopen in vier, negen, n² maal korteren tijd.’

Noemt men de versnelling door de eene kracht teweeggebracht g en die door de andere n g, dan heeft men:

r = ½ g t ² = ½ n g t₁ ²

en dus:

t ² = n t₁ ²

of: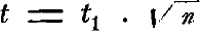

Bovenstaande redeneering is dus valsch.

Dat de formule van den slinger

in de mechanica streng bewezen wordt (St. 62) is onwaar, daar het slechts eene benaderende formule is.

In St. 69 moet men zich iets denken, wat zich niet denken laat. Wij lezen daar:

‘Wanneer een ligchaam om een vast punt als middenpunt in eenen cirkel wordt rondbewogen, dan moet het daarbij onophoudelijk van rigting veranderen. Voor elk klein deel zijner baan nu, zoo klein dat men het als regtlijnig kan beschouwen, kan men zich zijne snelheid in twee zamenstellende ontbonden denken, die loodregt op elkander gerigt zijn, en waarvan de eene het verlengde is der lijn, welke eenig punt van het ligchaam met het middenpunt verbindt, of van den straal des cirkels, welke dit punt beschrijft.’ Een leerling, naar dit voorschrift eene uitdrukking voor de centrifugaal-kracht trachtende te vin-

[p. 194]

den, zal óf het spoor bijster raken, óf logisch tot de gevolgtrekking komen, dat die kracht bij eene cirkelvormige beweging gelijk nul is!

In St. 75 had ik bij de hefboomen liever de verdeeling in drie soorten gezien, dan die in een- en tweearmige.

Volgens St. 89 verstaat men door de woorden ‘cohaesie’ en ‘adhaesie’ volkomen hetzelfde, en wel ‘de aantrekkingskracht van zamenhang.’ De schrijver, die zoo gaarne zelfs het uiterlijke onderscheid van ligt en licht wil bewaard zien, mocht waarlijk het in de spreeken schrijftaal zoo nuttige onderscheid tusschen deze beide wijzen van uiting der molecutaire krachten niet zoo lichtvaardig wegwerpen.

Uit St. 104 zou men lichtelijk tot de conclusie geraken, dat, als bij eene vloeistof de cohaesie gelijk is aan de adhaesie aan eenen wand, de vloeistof horizontaal zal blijven staan, hetgeen onjuist is; de adhaesie toch behoort op gronden, die hier niet vermeld kunnen worden, verdubbeld te worden, eer we haar met de cohaesie hier vergelijken.

In het begin van St. 108 komt men tot de overtuiging, dat hier alleen van homogene lichamen sprake is, hetgeen echter verderop blijkt niet het geval te zijn: overigens heb ik nergens eene bepaling of verklaring omtrent het al of niet homogeen zijn van een lichaam aangetroffen, ofschoon hier en daar het begrip stilzwijgend als bekend ondersteld wordt.

De letters in de formule van St. 110

s G = G/G-g

zijn ongelukkig gekozen; wanneer ik althans goed begrijp dat s G is: ‘specifiek gewicht.’

In St. 114 wordt minder juist gezegd, dat bij de gassen, van de aantrekking, die de deeltjes op elkander uitoefenen niets meer te bespeuren is; ‘de kracht, die ze van elkander drijft, heeft onbeperkt de overhand.’

De daar aangehaalde St. 90 handelt over iets anders (drukfout?).

St. 118 leert ons het onderscheid tusschen gassen en dampen.

‘Dampen zijn afkomstig van drupvormige vloeistoffen, bij verkoeling of zamendrukking nemen zij voor een deel den drupvorm weder aan.’

Deze onderscheidende kenmerken der dampen zijn al zeer vaag; zou het niet beter zijn de dampen met de gassen te identificeeren, met de aanmerking, dat de eerste zonder kunstmatige afkoeling of samendrukdrukking vloeistoffen kunnen worden? - In dezelfde stelling wordt verder gezegd, dat geen der enkelvoudige gassen of mengsels daarvan drupvormig zijn kunnen gemaakt worden; een aantal samengestelde gassen echter wel.

Elk weet dat chloorgas bij ongerveer 4 athmospheeren drukking, of ook bij afkoeling tot 40^o C. eene vloeistof wordt; of acht de schrijver bewezen, dat chloor eene verbinding van murium-oxyde en zuurstof is?

In de daaropvolgende stelling zou ik gaarne eene aanduiding gevon-

[p. 195]

den hebben betrekkelijk de hooge belangrijkheid der kennis van de dichtheden der gassen en dampen, uitgedrukt ten opzichte van waterstof, als eenheid, wegens het verband met de atoomgewichten; scheikunde en natuurkunde zijn nog steeds al te zeer van elkander gescheiden; laten wij toch de gemeenschappelijke grensdistricten (Lothar Meyer) niet langer onbebouwd laten.

In stelling 121 - - - doch ik heb genoeg gezegd, om mijn gevoelen te staven.

Omtrent de volgorde van behandeling kan ik ook niet in alle opzichten met den schrijver overeenstemmen; ook heb ik eenige zaken in het boekje gemist, die ik gaarne met een enkel woord had vermeld gezien, terwijl daarentegen o.a. St. 145 naar mijn oordeel korter had kunnen zijn.

Zoo b.v. zouden de proeven met olie van Plateau ná de grondstelling van Archimedes behooren vermeld te worden; de verklaring van den dompelaar (St. 141) heeft de leeraar reeds bij de behandeling der hydraulische pers (St. 98) moeten geven; de osmose der vloeistoffen had ik liever achter de capillariteit geplaatst, - St. 151 staat nu wel wat vreemd tusschen de overige in.

Bij St. 11 had ik gaarne den dynamometer vermeld gezien. - Het algemeene beginsel der gelijkheid van actie en reactie heb ik nergens gevonden; vooral bij St. 23 ware de mededeeling dat een willekeurig lichaam en de aarde elkander en wel met dezelfde kracht aantrekken nuttig geweest. - De proeven van Plateau met draadfiguren en glycerinehoudend zeepwater zouden bij de co- en adhaesie vermeld hebben kunnen worden, enz.

Bovendien zou ik gaarne gezien hebben, dat hier en daar de namen dergenen, die zich in physische wetenschappen, door uitvindingen, ontdekkingen of uitgebreide onderzoekingen beroemd hebben gemaakt, vermeld waren; dit kan echter ieder leeraar naar eigen goedvinden aanvullen.

En nu nog een enkel woord tot slot. Na al hetgeen door mij gezegd en opgemerkt is, zou het kunnen schijnen, dat ik, consequent handelende, het boekje ten eenenmale moest afkeuren; toch doe ik dit niet en, wat meer zegt, het wordt door mijne leerlingen (nevens een meer omvattend handboek) gebruikt.

De oorzaak hiervan ligt in de omstandigheid, dat ik, even als de heer Logeman van oordeel ben, dat bij het onderwijs in de natuurkunde de mondelinge voordracht, hier en daar door zoo eenvoudig mogelijk ingerichte proefnemingen toegelicht, nagenoeg alles moet doen, en dit in het oog houdende, en met omzichtigheid gebruikt, geloof ik, dat het boekje wel nut kan stichten; het onmogelijk te dulden dicteeren kan door het gebruik van dit werkje veranderd worden in het aangeven van die wijzigingen en aanvullingen, als de leeraar wenschelijk acht.

Dr. Sibru.