Tabu. Jaargang 24

(1994)– [tijdschrift] Tabu– rechtenstatus

Komparatief, komparatiever, komparatiefst
Peter I. Blok & Jaap Hoepelman

0 Inleiding

In dit artikel willen wij de aandacht vestigen op constructies als de volgende:

(1)	a	Jan is meer (een) schaker dan Piet
	b	Jan is meer (een) schaker dan (een) dammer
	c	Als bridger is Jan meer (een) schaker dan Piet
	d	Als bridger is Jan meer (een) schaker dan (een) dammer

In de traditionele Montagoviaanse modeltheoretische semantiek (als b.v. in Montague 1973, van nu af aan te noemen PTQ) lijkt er geen plaats te zijn voor zinnen als in (1); immers, iemand is een schaker of zij is dat niet en iemand is dammer of is dat niet. De betekenis van (1)a zou hier dan ook zijn dat Jan een schaker is en Piet niet en van (1)b dat Jan een schaker is en geen dammer. Dit is echter niet in overeenstemming met de intuïtieve betekenis van (1)a en (1)b. Iets dergelijks geldt voor (1)c en d: in een naïeve semantiek zou Jan in (1)c een schakende bridger zijn, en Piet wel bridger en geen schaker; in (1)d is Jan dan een schakende bridger zijn en geen dammende bridger (en dus geen dammer). Het is evenwel goed mogelijk dat Jan nauwelijks kan bridgen en zelfs de spelregels van het schaakspel niet beheerst, hij wereldkampioen dammen is, terwijl (1)c toch de stand der dingen correct beschrijft.

Het moge duidelijk zijn dat de zinnen in (1) een interpretatie van nomina behoeven die principieel afwijkt van de tot nu toe gangbare. In sectie 1 zullen wij een theorie beschrijven die als eerste de mogelijkheid biedt om nomina in comparatieve constructies te gebruiken. In sectie 2 bespreken we twee problemen waarop men stuit als de theorie uit sectie 1 aangewend wordt om de zinnen in (1) te interpreteren. In sectie 3 presenteren we een uitgebreidere theorie die voor deze problemen een oplossing biedt. Sectie 4 geeft een grammatica voor de theorie van sectie 3 in de stijl van Montague's PTQ.

1 Het nomen als adjectief

Hoepelman (1986) observeert dat vanuit een semantisch perspectief nomina zich in het algemeen als adjectieven gedragen. Een adjectief als groot deelt de denotatie van een nomen, zeg man, op in twee deelverzamelingen, nl. de grote mannen en de niet-grote mannen. Het nomen man doet eigenlijk hetzelfde, maar dan met betrekking tot het universum U: het deelt U op in de verzameling mannen en de verzameling niet-mannen. Voor adjectieven geldt dat ze meerdere malen toegepast kunnen worden op hetzelfde nomen, als in grote

grote man. De denotatie van deze uitdrukking is de verzameling mannen die groot zijn met betrekking tot de verzameling grote mannen. Voor nomina hebben we deze syntactische constructie niet, maar het lijkt erop dat we dezelfde soort interpretatiestrategie toepassen in uitdrukkingen als echte man. De verzameling echte mannen is die verzameling die onstaat als men de mannen opdeelt in de mannen onder de mannen en de minder mannen onder de mannen. Dat we zo een constructie goed kunnen gebruiken mag blijken uit de ongeldigheid van de volgende afleiding:

(2)		Alle en slechts alle schakers zijn bridgers
	∴	Alle en slechts alle bedreven schakers zijn bedreven bridgers

De intensionaliteit van het adjectief bedreven kan direct uitgedrukt worden in termen van de set waar het adjectief betrekking op heeft: hoewel de verzamelingen schakers en bridgers samenvallen, hoeven de verzameling schakers onder de schakers en bridgers onder de bridgers nog niet samen te vallen. In een model met domein U en toekenningsfunctie F is de situatie dan F(schaker,U) = F(bridger,U) en F(schaker,F(schaker,U)) ≠ F(bridger,F(bridger,U)).

De interpretatie van nomina als keuzefuncties op ieder willekeurig domein maakt het ook mogelijk om zinnen als

(3)	Papagaaien zijn de linguisten onder de dieren

te interpreteren. Ook al is F(linguist,U) een verzameling mensen, disjunct van dieren, dan wil dat nog niet zeggen dat F(linguist,F(dieren,U)) leeg is.

Om de lezer een indruk te geven hoe deze grammatica functioneert geven we enkele voorbeelden van vertalingen en interpretaties. Voor details verwijzen we naar Hoepelman (1986).

Een grammatica die nomina als functies van verzamelingen naar verzamelingen behandelt vertaalt nomina natuurlijk naar objecten van type <<e,t>,- <e,t>>. Als adjectieven gezien worden als modificators van nomina krijgen ze het type <<<e,t>, <e,t>>, <<e,t>, <e,t>>>. De combinatie van adjectief en nomen is dus weer van type <<e,t>,<e,t>>.

Aangezien de verzameling met betrekking waartoe een nomen geïnterpreerd wordt niet altijd expliciet gemaakt wordt als in (3), en met name niet als deze verzameling het universum is, introduceren we een dummy symbool voor U, te weten T. Aangezien adjectieven schijnbaar zonder nomen voor kunnen komen (als in Jan is groot), introduceren we ook een dummy nomen, I, dat te interpreteren is als ‘ding’. Jan is groot wordt dan gelezen als Jan is een groot ding (met betrekking tot U). Comparatieven worden vertaald m.b.v. de operatoren more en less. Jan is groter dan Piet wordt dus geïnterpreteerd als Jan is MORE een groot ding ten opzichte van U dan Piet. Op dezelfde manier worden superlatieven behandeld: Jan is de grootste man wordt vertaald in Jan is MOST een grote man. Zonder op de bijzonderheden van de syntax in te gaan geven we de volgende interpretaties:

(4)
a	Jan is een man ↪ man'_{<<e,t>,<e,t>>}(T_<e,t>)(j_e) iff Jan ∈ [man'](U)
b	Jan is groter dan Piet ↪ more(groot' _{<<<e,t>,<e,t>>,<<e,t>,<e,t>>>} (I_{<<e,t>,<e,t>>})(j_e,p_e)) iff [groot'](ding){Jan,Piet} = {Jan}
c	Piet is een grotere sukkel dan Jan ↪ more(groot' _{<<<e,t>,<e,t>>,<<e,t>, <e,t>>>} (sukkel'_{<<e,t>,<e,t>>})(j_e,p_e)) iff [groot']([sukkel']{Jan,Piet} = {Piet}
d	Piet is de domste man ↪ most(dom' _{<<<e,t>,<e,t>>,<<e,t>,<e,t>>>} (man'_{<<e,t>,<e,t>>})(p_e,x_e)) iff voor alle g, [dom']([man']){Piet,g(x)} = {Piet}

(4)a laat zien hoe de semantiek zich verhoudt tot standaard interpretaties. In de interpretatie van 4(b) neemt het adjectief groot eerst de dummy I (die elke set op zichzelf afbeeldt) en de zo gevormde nominale uitdrukking vergelijkt Jan en Piet.

In (4)c neemt groot eerst het nomen sukkel, wat de functie oplevert die uit elke verzameling de grote sukkels kiest. Voor de verzameling {Jan,Piet} blijkt dat Piet te wezen. Indien een object in elk paar waar het in zit gekozen wordt door een nominale uitdrukking AN, is dat object het AN-ste object, hetgeen in 4(d) het geval is voor Piet onder de domme mannen.

Om deze semantiek volledig te laten werken moeten we ten minste de volgende regels aannemen: Zij Z de betekenis van een willekeurige nominale uitdrukking, en K een verzameling dan

(5)
a	∀v (v ∈ Z(K) → v ∈ K)
b	∀v (Z({v}) = ∅ → ∀K (v ∉ Z(K))
c	(Z(K)) = K ⇔ ∀v∀w ((v ∈ K & w ∈ k) → Z({v,w}) = {v,w})
d	(Z(K)) = ∅ ⇔ ∀v∀w ((v ∈ K & w ∈ k) → Z({v,w}) = ∅)

en in de meeste gevallen de volgendeGa naar eind1.:

e	∀v∀w((v ∈ K & w ∈ K & v ∈ Z(K) & w ∉ Z(K)) → Z({v,w} = {v})
f	∀v∀w ((Z({v,w} = {v} & v ∈ K & w ∈ K) → (w ∈ Z(K) → v ∈ Z(K))

(5)a zegt dat als Jan een aap onder de jongens is, Jan ook een jongen is. In 5(b) wordt toepasbaarheid uitgedrukt: in principe kiest de keuzefunctie Z uit een verzameling de elementen die het meest Z zijn. Heeft die verzameling maar één lid, dan kiest Z dat lid of ∅. Als ∅ gekozen wordt is het Z totaal niet van toepassing, als bijvoorbeeld in man({17}). (5)b drukt uit dat als een nomen totaal niet van toepassing is op een (uniset van een) object, dat object geen lid zal zijn van dat nomen toegepast op een set, als bv. man(mathematische objecten). (5)c en d drukken uit dat als een verzameling objecten ononderscheidbaar is met betrekking tot een nomen, elk paar (en, als eenvoudig te bewijzen, elke deelverzameling) ononderscheidbaar is met betrekking tot dat nomen. (5)e en f zijn eveneens een soort monotonie postulaten: als v en w zich verschillend gedragen met betrekking tot een nomen en een set waar ze

in zitten, gedragen ze zich ook verschillend ten opzichte van dat nomen met betrekking tot de set bestaande uit v en w (waaruit volgt dat v en w onderscheidbaar zijn in elke subset van Z waar ze beide in zitten). Andersom, als v meer Z is dan w, dan is v in elke set waar v en w in zitten ten minste zo Z als w.

De lezer wordt uitgenodigd om de regels (5)a-f toe te passen op de interpretaties in (4) en de intuïtive geldigheid van de gevolgtrekkingen na te gaan.

De voorgestelde semantiek voor nomina en comparatieven stelt ons in staat enkele in de natuurlijke taal gangbare, maar voor de traditionele semantiek moeilijk behandelbare uitdrukkingen te interpreteren. Benevens (3) kan ook aan zinnen als het eerder genoemde

Jan is een echte man

Jan is een echtere man dan Piet

een op zijn minst plausible interpretatie gegeven worden. Ons inziens heeft het adjectief echt (in deze context) de functie van het herhalen van het nomen dat er op volgt. Jan is een man in U als Jan ∈ man(U). Jan is een echte man op U als Jan ∈ man(man(U)) (merk op dat echt, en dus man, hier niet als adjectief maar als nomen geïnterpreteerd wordt: het tweede man modificeert niet het eerste, maar neemt het totaal van man(U) als argument). En Jan is een echtere man dan Piet als er een n is zodat Jan ∈ man_n(man_n-1 (...(man₁(U)) en Piet niet.

Combinaties van adjectieven en nomina gedragen zich niet totaal hetzelfde als ‘kale’ nomina. De bron hiervan is het scalaire karakter van adjectieven. Groot staat op een schaal met klein, en intelligent met dom. In principe is natuurlijk de verzameling grote dingen het complement van de kleine dingen en vice versa. Echter, als Jan een even grote man is als Piet, wil dat nog niet zeggen dat Jan groot is, maar als Jan een even kleine man is als Piet, dan is hij wel degelijk klein. En voor intelligentie geldt hetzelfde: Als Piet een even intelligente man is als Jan, kan hun IQ nog steeds onder de 90 liggen, maar als Piet een even domme man is als Jan zijn ze geen van beide briljant. De kant van de schaal die altijd toepasbaar is (groot, intelligent) is altijd tevens de naam van de schaal (grootte, intelligentie). Als de naam niet toepasbaar is op een nomen en een set, is de andere kant van de schaal ook niet toepasbaar (als er geen grote dingen zijn zijn er ook geen kleine), maar niet vice versa. Om deze inzichten in de grammatica te verwerken moeten we in principe twee dingen doen: we moeten de schalen in de syntax opnemen, en we moeten de afleidingen als betekenispostulaten aan de schalen opleggen. We doen dit als volgtGa naar eind2.: de elementen van de verzameling adjectieven BE_ADJ (ADJ) dragen indices zodat:

-	voor elke index i er precies 2 elementen van ADJ zijn die index i dragen.

-	Als A_i en B_i ∈ ADJ, dan is er dan wel een A ∈ BE_CN zodat A de nominalisering van A_i is dan wel een B ∈ BE_CN zodat B de nominalisering van B_i is, maar niet beide.
-	<A_i,B_i> dan wel <B_i,A_i> een schaal is, waarbij een schaal aan de volgende betekenispostulaten voldoet:

Laat <A_i,B_i> een willekeurige schaal zijn. Dan noemen we [A_i] A¹ en [B_i] A⁰. Laat N een willekeurige nominale betekenis zijn en P een verzameling. We krijgen nu de volgende betekenispostulaten:

(5)
g	Voor alle x, x ∈ (A¹(N))(P) → x ∉ (A⁰(N))(P)
h	(A¹(N))(P) = ∅ → (A⁰(N))(P) = ∅
i	(A¹(N))(P) = P → (A⁰(N))(P) = ∅
j	(A⁰(N))(P) ≠ P

(5)g drukt uit dat een object niet tegelijk groot en klein kan zijn. (5)h zegt dat als de top van een schaal niet toepasbaar is op een nomen en een set, de hele schaal niet toepasbaar is. (5)i en j drukken uit dat bijvoorbeeld alle mannen in een verzameling even groot kunnen zijn, maar niet even klein.

De kern van Hoepelman (1986) is dat komparatieven en superlatieven uitgedrukt kunnen worden in termen van de adjectieven doordat nomina reeds een komparatieve semantiek hebben. Deze theorie is in principe geen verandering van de klassieke, maar een uitbreiding. Klassieke denotaten van nomina (subsets van U) zijn een speciaal geval van de algemenere keuzefuncties die een subset van een willekeurige set geven.

2 Twee problemen

Het moge duidelijk zijn dat de semantiek van Hoepelman (1986) zich uitstekend leent voor de interpretatie van zinnen als (1)a; de zin betekent gewoon schaker({j,p}) = {j}. En uit (5) volgt dan ook dat als Piet onverhoopt een schaker onder de bestuurders is, en Jan een bestuurder, dat Jan dan ook een schaker onder de bestuurders is. Wat niet volgt is dat Jan een schaker in het algemeen (dat is, ten opzichte van U) is. De lichte variatie op (1)a (1c) zou als volgt kunnen worden geïnterpreteerd: Jan en Piet zijn beide bridgers, en als we het nomen schaker loslaten op de verzameling bridgers, zit Jan wel in schaker van {x|bridger(x)}Ga naar eind3. en Piet niet. Oftewel: Jan ∈ {x|bridger(x)} & Piet ∈ {x|bridger(x)} & Jan ∈ [schaker']({x|bridger(x)}) & Piet ∉ [schaker']({x|bridger(x)}). Een gevolg is echter dat [schaker']({Jan,Piet}) = {Jan} door (5)e, hoewel het is niet zo zeker of de gevolgtrekking hier wel juist is: mogelijkerwijs is ook (6) het geval:

(6)	Als dammer is Piet meer een schaker dan Jan

Uit (6) volgt analoog aan bovenstaand argument dat [schaker']({Jan,Piet}) = {Piet}, wat in tegenspraak is met de gevolgtrekking uit (1)c. Merk op dat we (5)e voor schaker niet zomaar weg kunnen latenGa naar eind4.: als Jan een schaker is met betrekking tot U en Piet niet, dan is Jan de schaker van de twee.

Dit probleem is nauw verwant aan het volgende: laat in een bepaald model [bridger'] gelijk zijn aan [dammer']. Dan zouden de volgende zinnen contradictoir moeten zijn:

(7)	a	Als bridger is Jan een schaker
	b	Als dammer is Jan geen schaker

Immers, [schaker']({x|bridger(x)}) = [schaker']({x|dammer(x)}), omdat {x|bridger(x)} = {x|dammer(x)}. Intuïtief is de situatie (7) echter zeer goed mogelijk: als Jan bridged gedraagt hij zich als een schaker en als hij damt niet. Laten we dit het intensionaliteitsprobleem noemen.

De bron van het probleem is natuurlijk de volledige extensionaliteit van de theorie; in een intensionele semantiek kan er een onderscheid tussen de eigenschappen bridger en dammer gemaakt worden terwijl hun extensies gelijk zijn. In de volgende paragraaf zullen wij een theorie ontwikkelen die recht doet aan het intensionele karakter van de modificeerdes als N in (1), (6) en (7), zonder buiten de ontologie van paragraaf 1 te treden.

Voorbeeld (1)b, en daarmee (1)d, lijkt als volgt binnen de theorie van paragraaf 1 te behandelen te zijn: als een nomen een keuzefunctie is die een domein van individuen opdeelt, kan een subject gezien worden als een keuzefunctie op een domein van eigenschappen. Laat de JAN de keuzefunctie van Jan zijn. Dan is (1)b waar d.e.s.d.a.

JAN({schaker,dammer}) = schaker

Over het algemeen zal het niet zo zijn dat als JAN({P,Q,R...} = {P} dan ook Jan ∈ P(U). Immers, als Jan meer een schaker is dan een dammer, dan wil dat nog niet zeggen dat Jan een schaker is m.b.t. U.

In traditionele quantorentheorie is Jan is een schaker waar d.e.s.d.a.

[schaker] ∈ JAN

waarbij [schaker] = {x|schaker(x)} en JAN een verzameling eigenschappen (verzamelingen). Hier hebben we natuurlijk wel dat als P ∈ JAN, dan Jan ∈ P. Aangezien het systeem van sectie 1 totaal klassiek wordt als we als referentieset U kiezen moet het volgende gelden:

P ∈ JAN(U_{<<e,t>,<e,t>>}) ⇔ Jan ∈ P(U)

De interpretatie van JAN voor minder omvattende gevallen is minder duidelijk: als JAN({schaker,dammer}) = schaker wil dat waarschijnlijk wel zeggen dat er een verzameling V is zodat Jan ∈ schaker(V), maar het is ons inziens

niet uitgesloten dat er een verzameling V' is zodat Jan ∈ dammer(V'), en ook de relatie tussen V en V' is niet eenvoudig uit te drukken met behoud van de intuïtieve betekenis van (1)b.

De quantoraanpak van (1)b stuit op nog een, wellicht ernstiger, bezwaar. Beschouw de zinnen in (8):

(8)	a	Sommige jongens zijn meer schaker dan dammer
	b	Sommige jongens zijn meer dammer dan schaker

In de voorgestelde semantiek betekenen 8(a) en 8(b) respectievelijk:

(9)	a	SOMMIGE JONGENS({schaker,dammer}) = {schaker}
	b	SOMMIGE JONGENS({schaker,dammer}) = {dammer}

(8)a en (8)b kunnen tegelijkertijd waar zijn maar (9)a en (9)b niet (al was het maar omdat de interpretatierelatie dan geen functie zou zijn). Dit betekent dat er iets fundamenteel mis is met het idee van de quantor als keuzefunctie over objecten van type <<e,t>,<e,t>>. Laten we dit het ophogingsprobleem noemen.

In de volgende paragraaf zullen we een theorie presenteren die, uitgaande van de basisideeen van paragraaf 1, een oplossing biedt voor zowel het intensionaliteitsprobleem als het ophogingsprobleem.

3 Een fijne semantiek

In de grammatica van paragraaf 1 is de denotatie van een nomen een functie van verzamelingen naar verzamelingen. Gegeven een verzameling A levert een nomen N dus de verzameling Nnen in A op. De betekenis van ¬N in A is natuurlijk het complement van N(A) op A, dat is, A - N(A). Noem dit N⁰A, en wat N(A) was in paragraaf 1 N¹A. N¹A en N⁰A vormen nu samen een partitie van A (want N¹A ∪ N⁰A = A en N¹A ∩ N⁰A = ∅). In ons nieuwe voorstel laten we de betekenis van N op A deze hele partitie zijn. N(A) is dus in principe een partitie op A, dat is, een verzameling verzamelingen. Merk echter op dat N(A) nu gelijk is aan ¬N(A). Om bij te houden welke cel in de partitie het ‘positieve’ deel is en welk het ‘negatieve’, geven we cellen labels: N¹A krijgt label 1 en N⁰A label 0. N(A) is nu dus een functie f van labels naar verzamelingen zodat

f(0)	=	N⁰A
f(1)	=	N¹A

Op elk van deze functiewaarden kunnen we N weer toepassen, wat weer gelabelde cellen oplevert. N¹A valt dan uiteen in N¹N¹A en N⁰N¹A en N⁰A in N¹N⁰A en N⁰N⁰A. In principe kunnen we deze procedure oneindig voortzetten.

Als notatie stellen we voor de rij N-waarden als een binaire macht van N te schrijven die van links naar rechts de waarde van de keuzefunctie weergeeft. Dus N¹N¹A = N¹¹A, N⁰N¹A = N¹⁰A, N¹N⁰A = N⁰¹A en N⁰N⁰A = N⁰⁰A.

Het hieronder gegeven plaatje toont hoe N geïnterpreteerd wordt op A. Wat boven de dubbele lijn zit zijn de elementen die in een klassieke sematiek in de denotatie van het nomen zitten, en er onder die er niet in zitten. N^aA(x) is dus klassiek het geval als a met een 1 begint.

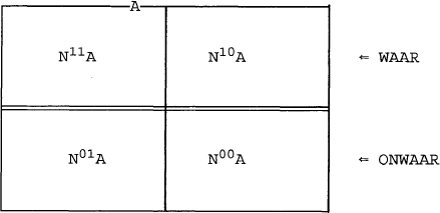
Omdat de waarde van de de interpretatie van een nomen op een domein een (gelabelde) partitie is, en we elke cel van de partitie weer als mogelijk input voor het nomen willen zien, is het technisch handig om als input reeds partities te nemen. De interpretatie van een nomen is dan dus een functie van partities naar gelabelde partities. Bovendien kunnen we de labels als binaire getallen zien, zodat we de cellen met recht kunnen nummeren. De waarde van een nummer is natuurlijk afhankelijk van het aantal keren dat het nomen toegepast is. In het bovenstaande plaatje is cel nummer 3 (N¹¹A) de hoogste; als we N tien keer toegepast zouden hebben is cel 3 relatief klein (en N klassiek onwaar voor zijn elementen!). Het aantal keren dat een nomen toegepast is, de fijnheid van de partitie, geven we aan met een subschrift op N. N_nA zal dus 2ⁿ cellen hebben.

Tot nu toe begonnen we met een verzameling en kregen een gelabelde partitie. De verzameling wordt nu de partitie van die verzameling met die verzameling als enig lid. In ons voorbeeld is dat {A}. We krijgen aldusGa naar eind5.:

N₁({A})	=	{(1,N¹A),(0,N⁰A)}
N₂({A})	=	{(3,N¹¹A),(2,N¹⁰A),(1,N⁰¹A),(0,N⁰⁰A)}

Neem nu de zin (1)a

(1)a	Jan is meer een schaker dan Piet

Uit (1)a volgt noch dat Piet noch dat Jan een schaker is ten opzichte van het domein. Kies in ons plaatje voor A het domein U, en neem N₂ = schaker₂. (1)a is nu waar als Jan in een cel zit met een hoger nummer dan de cel waarin Piet zit. Zit Jan in cel 1 (schaker⁰¹({U})) en Piet in cel 0 (schaker⁰⁰({U}), dan zijn Jan noch Piet schaker, maar is Jan meer schaker dan Piet. Uiteraard laat het model ook toe dat alleen Jan of beide schaker zijn.

We definiëren de functie f:

f(N_n({A}),x) is de functie die voor elke x ∈ A het nummer geeft van de cel waartoe x behoort.

We krijgen dan

1(a) d.e.s.d.a. f(schaker_n({U}),Jan) > f(schaker_n({U}),Piet)

en voor

(1)b	Jan is meer (een) schaker dan (een) dammer
(1)b	d.e.s.d.a. er een n is zodat f(schaker_n({U}),Jan) > f(dammer_n({U}),Jan)Ga naar eind6.

Bezie nu de zin

(10)	Als bridger is Jan een schaker

Uit (10) volgt dat Jan een bridger is m.b.t. U. We hebben dus een absolute maat nodig die vaststelt of een propositie ‘waar’ dan wel ‘onwaar’ is. We hadden al vastgesteld dat de klassieke denotatie van een nomen de vereniging van de cellen die met een 1 beginnen is. Als in een model een nomen met fijnheid n geëvalueerd wordt is de hoogste waarde die een cel kan aannemen 2ⁿ-1. De verzameling cellen die met een 1 beginnen zijn die van waarde 2^n-1 en groter. Dus de verzameling cellen waar het klassiek waar is dat Jan een bridger is, zijn

{P|∃m P = bridger({U})(m) & m ≥ 2^n-1}

waar n gegeven is door het model. Noem deze verzameling {bridger({U})(1)}. Voor (10) wordt schaker nu geëvalueerd voor deze partitie van de klassieke verzameling schakers. (10) is waar als Jan een element is van een van de ‘ware’ cellen van schaker({bridger({U})(1)}):

(10)	d.e.s.d.a. ∃P Jan ∈ P & P ∈ {schaker({bridger({U})(1)}(1)}

Merk op dat inderdaad volgt dat

-	Jan ∈ U
-	∃P Jan ∈ P ∈ {bridger({U})(1)} (Jan is een bridger) en dat niet volgt dat
-	∃P Jan ∈ P ∈ {schaker({U})(1)} (Jan is een schaker m.b.t. U)

Dit resultaat hadden we echter ook al in sectie 1. We zullen nu laten zien dat het intensionaliteitsprobleem daadwerkelijk opgelost is. De cruciale zin was

(11)	Als bridger is Jan een schaker, maar als dammer is Jan geen schaker

In een min of meer klassieke semantiek betekent de aanname dat de verzameling bridgers hetzelfe is als de verzameling dammers dat [bridger]_M = [dammer]_M. Daardoor impliceert die aanname dan ook dat [schaker (bridger)]_M = [schaker(dammer)]_M, wat in strijd is met (11).

In ons voorstel betekent de aanname dat de bridgers en de dammers samenvallen echter niet dat [bridger]_M = [dammer]_M (dat is, {bridger ({U})(1)} = {dammer({U})(1)}), maar slechts dat ∪{bridger({U})(1)} = ∪{dammer({U})(1)}. Ergo, al vallen de bridgers en de dammers samen, het hoeft nog niet het geval te zijn dat [schaker(bridger)]_M = [schaker (dammer)]_M. Dit betekent dat de aanname dat de dammers en de bridgers samenvallen niet in strijd is met (11).

Er blijft natuurlijk wel een residu van het intensionaliteitsprobleem over. Indien

∃P Jan ∈ P ∈ {bridger({U})(1)} &
∃Q Jan ∈ Q ∈ {dammer({U})(1)} &
P = Q

dus als de cel waar Jan als bridger in zit precies dezelfde cel is als waar hij als dammer in zit, dan treedt het intensionaliteitsprobleem weer op. Dit hoeft echter onder de aanname dat de bridgers en de dammers samenvallen helemaal niet het geval te zijn. Immers, dan geldt slechts ∪{bridger({D})(1)} = ∪{dammer({D})(1)}.

In de volgende paragraaf zullen we een schets van een formele uitwerking van deze semantiek geven. Aan de hand daarvan wordt vervolgens het ophogingsprobleem opgelost.

4 Maatwerk voor de komparatieve nomina

In deze paragraaf zullen we een eenvoudige grammatica voor de zinnen in (1) formuleren. Aangezien onze aandacht op dit moment zich meer op de semantiek dan op de syntaxis richt, kan het zijn dat de laatste een beetje

‘brute force’ overkomt. In tegenstelling tot Montague's PTQ voeren we een aparte klasse van koppelwerkwoorden in, omvattende is (een) <nomen>, is meer (een) <nomen> dan (een) <nomen>, is meer (een) <nomen> dan <eigennaam>. Om al te grote complicaties te voorkomen interpreteren we de constructies met deze koppelwerkwoorden syncategorematisch. Ook dienen we Als <nomen> syntactisch in te voeren. We gaan er vanuit dat elke zin met Als nomen begint; in het bijzonder, IVs beginnen met als ding, hoewel dat normalerwijze fonetisch niet gerealiseerd is.

4.1 Syntax

Uitgaande van een PTQ-achtige syntax (categorieën, constructie regels etc.) geven we de volgende basisexpressies aan de taal Nieuwerlands (NL):

B_T:	{Jan, Piet,.....}
B_CN:	{schaker, bridger, dammer, jongen,.....}
B_IV/IV:	{als⁀ding}

en een verzameling syncategorematische uitdrukkingen syn

syn: {is⁀een,is⁀meer⁀een⁀...⁀dan...,is⁀meer⁀een⁀...⁀dan⁀een..., als, ...}

We hebben de volgende (speciale) regels:

S₁₀₀:	als α,β ∈ P_CN, γ ∈ P_T, dan F₁₀₀(α), F₁₀₁(α,β), F₁₀₂(α,γ) ∈ P_IV
	waar	F₁₀₀(α)	= is⁀een α
		F₁₀₁(α,β)	= is⁀meer⁀een⁀α⁀dan⁀een β
		F₁₀₂(α,γ)	= is⁀meer⁀een⁀α⁀dan γ

S₁₀₁:	als α ∈ P_CN, dan F₁₀₃(α) ∈ P_{(IV/IV)/(IV/IV)}
	waar F₁₀₃(α) = als α

S₁₀₁ werkt als volgt: we nemen aan dat elke IV met als ding begintGa naar eind7.. Dus Jan is een schaker wordt gelezen als Als ding is Jan een schaker. Als bridger is Jan een schaker wordt nu gelezen als Als bridger als ding is Jan een schaker. De enig mogelijke syntactische analyse voor deze zin is:

(((als bridger_{(IV/IV)/(IV/IV)}(als ding_IV/IV))_IV/IV(is een schaker_IV))_IV(Jan_T))_t

Merk op dat ook in Als bridger, als diepzeeduiker, als ding, is Jan een schaker ‘als ding’ eerst met ‘als diepzeeduiker’ combineert, en dat geheel met ‘als bridger’, om dan een IV/IV te vormen die met ‘is een schaker’ combineert tot een IV.

In deze regels is de mogelijkheid van een IV zonder als ding ervoor opengelaten, om de aansluiting met de terminologie van PTQ niet totaal te verliezen. De prijs die we ervoor betalen is de merkwaardige omstandigheid

dat de lege string in pre-VP positie een interpretatie krijgt. Gelukkig is dit in de syntaxis over het algemeen niet geheel ongewoon.

4.2 Komparatieve logica

We volgen de PTQ strategie van een vertaalprocedure van NL in een geïnterpreteerde logische taal. Die taal zullen we KL noemen. KL heeft drie basistypen, te weten e, t en n. De recursieve definitie voor de verzameling betekenisvolle uitdrukkingen van type a (ME_a) is als in PTQ met de volgende uitbreiding:

Als α,β ∈ ME_{<<<e,t>,t>,<n,<e,t>>>}, dan more₁(α,β) ∈ ME_{<<<e,t>,t>,<e,t>>}
Als α ∈ ME_{<<<e,t>,t>,<n,<e,t>>>}, γ ∈ ME_e, dan more₂(α,γ) ∈ ME_{<<<e,t>,t>,<e,t>>}
Als α ∈ ME_{<<<e,t>,t>,<n,<e,t>>>}, dan is as(α) ∈ ME_{<<<e,t>,t>,<n,<e,t>>>} I ∈ ME_<<e,t>,t>

Mogelijke betekenissen worden gedefiniëerd met betrekking tot twee niet-lege verzamelingen U en ℕ:

D_e,U,ℕ	= U
D_t,U,ℕ	= {0,1}
D_<a,b>,U,ℕ	= D_b,U,ℕ^Da,U,ℕ
D_<n,a>,U,ℕ	= D_a,U,ℕ^ℕ

De interpretatie (of model) is als volgt. Laat M het volgende quintuppel zijn: <U,ℕ,≤,n,F>, zodat U,ℕ niet-lege verzamelingen zijn, ≤ een stricte ordening is op ℕ, n ∈ ℕ, en F een functie van constanten van type a naar D_a,U,ℕ. Bovendien is er een verzameling assignments G, waarbij elke g ∈ G een functie is van variablen van type a naar D_a,U,ℕ. De betekenis van een uitdrukking α is α^M,g, de denotatie α^M,m,g, m ∈ ℕ en m ≤ n. De betekenis van een constante α wordt gegeven door het model en is F(α). Intuitief geeft, in het geval van nomina, de betekenis α^M,g de hele opdeling van het domein. De denotatie α^M,m,g is dat gedeelte van het domein (bepaald door m) waar we α(x) waar willen noemen. Zo krijgen we als denotatie een (partitie van) een deelverzameling van het domein waardoor de semantiek zelf weer tweewaardig wordt: een object zit erin of niet. Doordat de ‘grens’ m model-onafhankelijk is blijft het mogelijk verschillende graden van waarheid binnen het model met elkaar te vergelijken. De relatie tussen betekenis en denotatie is als volgt:

Definitie 4.2
1	Als α ∈ ME_<a,<n,b>> (a en b zuivere e,t typen), dan is α^M,m,g ∈ D_{<a,<b,t>>,U,ℕ} zodat voor iedere a ∈ D_a,U,ℕ, α^M,m,g(a) = {P\| ∃ n_i, m≤n_i≤n, P = α^M,g(a)(n_i)}

2	Als α ∈ ME_<a>, a een zuiver e,t type, dan α^M,m,g = α^M,g
3	α^M,m,g is ongedefinieerd in alle andere gevallen.

Het idee is dat n de fijnheid van het model uitdrukt; intuïtief twee tot de macht het aantal keren dat een nomen toegepast wordt min één. De maat m is de waarde waarboven we de uitdrukking ‘waar’ noemenGa naar eind8.. Als de betekenis van een nomen een functie is van partities naar functies van getallen naar verzamelingen, dan is de denotatie onder maat m de functie van partities naar de verzamelingen die toegekend worden door de getallen tussen m en n. In het klassieke geval van bijvoorbeeld PTQ geldt dat m=n=1.

In sectie 3 lieten we nomina een bepaald aantal keren op zichzelf los om zo een grotere fijnheid in de denotaties te verkrijgen. Deze iteratie wordt nu direct in het model gegeven, door de waarde van n en de overeenkomstige genummerde partities. De relatie tussen de twee zienswijzen kunnen we als volgt uitdrukken: daar waar iedere keer een nomen op zichzelf losgelaten wordt in sectie 3, gaan we hier naar een overeenkomstig, maar fijner model. Overeenkomstige modellen met een verschillende fijnheid verhouden zich als volgt: zij M₁ <U,ℕ,≤,n,F> en M₂ <U',ℕ',≤',n+p,F'>. M₂ is een uitbreiding van M₁ d.e.s.d.a.

U'	=	U
ℕ'	=	ℕ
≤'	=	≤
F	=	F' voor wat betreft de constanten anders dan de nomina

Voor elk nomen α, alle m ≤ n, alle partities van U A: ∪[α^M1,m,g(A)] = ∪[α^M2,m',g(A)], waar m' = 1/2 p + m. Een q-voudige iteratie in sectie 3 komt nu overeen met een modeluitbreiding van n tot 2^qn. Merk op dat er voor een iteratie van sectie 3 altijd een modeluitbreiding is, maar niet andersom: als p oneven is (bv door van n=5 naar n = 20 te gaan), zitten we mooi met de brokken.

Laat is a een afkorting zijn voor λQ_<<e,t>,t> λx_e∃P_<e,t> [α'(Q)(P) ⋀ P(x)]

We hebben nu de denotaties:Ga naar eind9.

1	Als α een constante is, dan α^M,g is F(α)Ga naar eind10.
2	Als α een variabele is, dan α^M,m,g is g(α)
3	Als α ∈ ME_<a,b> en β ∈ ME_a, dan [α(β)]^M,m,g = α^M,m,g(β^M,m,g)
4	Als α,β ∈ ME_{<<<e,t>,t>,<n,<e,t>>>}, dan is [more₁(α,β)]^M,m,g een functie f van objecten in D_<<e,t>,t> zodat voor elke Q ∈ D_<<e,t>,t>, f(Q) = {x ∈ U\|∃m'[x ∈ [is a (α)(Q)]^M,m',g & x ∉ [is a (β)(Q)]^M,m',g] & ¬∃m'' [x ∈ [is a (β)(Q)]^M,m'',g & x ∉ [is a (α)(Q)]^M,m'',g]}
5	Als α ∈ ME_{<<<e,t>,t>,<n,<e,t>>>}, γ ∈ ME_e, dan is [more₂(α,γ)]^M,m,g een functie f van objecten in D_<<e,t>,t> zodat voor elke Q ∈ D_<<e,t>,t>, f(Q) = {x ∈ U\|∃m'∃m'' (x ∈ [is a (α)(Q)]^M,m',g & γ^M,m,g ∈ [is a (α)(Q)]^M,m'',g & m' > m'') & ¬(∃m'∃m'' (x ∈ [is a (α)(Q)]^M,m'',g & γ^M,m,g ∈ [is a (α)(Q)]^M,m',g & m' > m''))}
6	Als α ∈ ME_{<<<e,t>,t>,<n,<e,t>>>} dan [as(α)]^M,m,g = α^M,m,g

7	I^M,m,g = {U}, voor alle m
8	De regels voor logische connectieven van PTQ

4.3 Vertalingen van NL in KL

We zullen hier alleen de vertaalregels geven die betrekking hebben op onze voorbeelden. Elke niet-gegeven vertaling is als in een extensionele variant van PTQGa naar eind11..

T₉₉:	als α ∈ P_CN, dan wordt α vertaald in α'_{<<<e,t>,t>,<n,<e,t>>>}
T₁₀₀:	als α,β ∈ P_CN, γ ∈ P_T, en α,β,γ worden respectievelijk als α',β',γ' vertaald, dan wordt
	is⁀een α vertaald in λQ_<<e,t>,t> λx_e∃P_<e,t> [α'(Q)(P) ⋀ P(x)],
	is⁀meer⁀een⁀α⁀dan⁀een β als more₁(α',β'),
	is⁀meer⁀een⁀α⁀dan γ als more₂(α',γ')

T₁₀₁:	als α ∈ P_CN, en α wordt als α' vertaald, dan wordt als α als as(α') en als ding als I vertaald

Merk op dat more₁ en more₂ geïnterpreteerd worden onder gebruikmaking van de interpretatie van de vertaling van is⁀een. Dit bewijst dat de komparatief hier inderdaad in termen van de normale predicatie wordt uitgedrukt.

4.4 Voorbeelden

We zullen nu laten zien dat ons fragment de juiste interpretatie van de voorbeelden oplevert.

(12)	Jan is een schaker = Als ding is Jan een schaker
	Als ding ↝ I
	Jan ↝ j
	schaker ↝ schaker'
	is een schaker ↝ λQ_<<e,t>,t> λx_e∃P_<e,t> [schaker'(Q)(P) ⋀ P(x)]
	is een schaker (als ding) (Jan) ↝ ∃P[schaker'(I)(P) ⋀ P(j)]

	[∃P[schaker'(I)(P) ⋀ P(j)]]^M,m,g = 1 d.e.s.d.a.
	er een assignment g' is die ten hoogste m.b.t P van g verschilt zodat [schaker']^M,m,g({U})(g'(P)) en g'(P)(Jan)

[schaker']^M,m,g is, door de definitie van denotatie, een functie van partities naar verzamelingen verzamelingen waar de maat groter of gelijk aan m is. Als er een g' is zodat g'(P) tot de functiewaarde behoort, en Jan zit in g'(P), dan is (12) dus waar.

(13)	Jan is meer een schaker dan een dammer = Als ding is Jan meer een schaker dan een dammer

	Als ding ↝ I
	Jan ↝ j
	schaker ↝ schaker'
	dammer ↝ dammer'
	is meer een schaker dan een dammer ↝ more₁(schaker',dammer')
	is meer een schaker dan een dammer (als ding) (Jan) ↝ more₁(schaker',dammer')(I)(j)

	[more₁(schaker',dammer')(I)(j)]^M,m,g = 1 d.e.s.d.a. Jan ∈ {x ∈ U\|∃m'[x ∈ [is a (schaker')(I)]^M,m',g & x ∉ [is a (dammer')(I)]^M,m',g] & ¬∃m'' [x ∈ [is a (dammer')(I)]^M,m'',g & x ∉ [is a (schaker')(I)]^M,m'',g]}

Merk wederom op dat [is a(schaker')(I)]^M,m',g precies die mensen zijn waartoe Jan in (12) behoort, zij het daar voor maat m. (13) zegt dus dat Jan tot die mensen behoort die tot een eventueel zwakkere maat m' dan m schaken m.b.t. {U}, maar niet tot die maat m' dammen, en niet andersom.

(14)	Jan is meer een schaker dan Piet = Als ding is Jan meer een schaker dan Piet

	als ding ↝ I
	Jan ↝ j
	Piet ↝ p
	schaker ↝ schaker'
	is meer een schaker dan Piet ↝ more₂(schaker',p)
	is meer een schaker dan Piet (als ding) (Jan) ↝
	more₂(schaker',p)(I)(j)

	[more₂(schaker',p)(I)(j)]^M,m,g = 1 d.e.s.d.a. Jan ∈ {x ∈ U\|∃m'∃m'' (x ∈ [is a (schaker')(I)]^M,m',g & Piet ∈ [is a (schaker')(I)]^M,m'',g & m' > m'') & ¬(∃m'∃m'' (x ∈ [is a (schaker')(I)]^M,m'',g & Piet ∈ [is a (schaker')(I)]^M,m',g & m' > m'')}

Ook in de komparatief (14) blijkt uit de semantiek dat de komparativiteit reeds verborgen ligt in de relativiteit van het nomen. Tot slot van deze sectie geven we de afleiding voor als α zinnen, in het simpelste geval. De lezer wordt uitgenodigd met behulp van (13), (14) en (15) de voorbeelden (1)c, en d uit te werken.

(15)	Als bridger is Jan een schaker = Als bridger, als ding, is Jan een schaker.

	bridger ↝ bridger'

als bridger ↝ as bridger'

als ding ↝ I

Jan ↝ j

is een schaker ↝ λQ_<<e,t>,t> λx_e∃P_<e,t> [schaker'(Q)(P) ⋀ P(x)]

is een schaker (als bridger(als ding)) (Jan) ↝ ∃P[schaker'(as bridger'(I))(P) ⋀ P(j)]

[∃P[schaker'(as bridger'(I))(P) ⋀ P(j)]]^M,m,g = 1 d.e.s.d.a.

er een assignment g' is die ten hoogste m.b.t P van g verschilt zodat [schaker']^M,m,g([bridger']^M,m,g({U})(g'(P)) en g'(P)(Jan)

Het enige verschil met (12) ligt hem natuurlijk in als bridger. De denotatie (dat is de betekenis m.b.t. maat m) is een functie van partities naar verzamelingen verzamelingen. [bridger']^M,m,g({U}) is dus een verzameling verzamelingen, en wel die verzamelingen waar de maat voor bridger m.b.t. U m of hoger is. Op deze partitie wordt [schaker']^M,m,g losgelaten, wat weer een partitie oplevert. De rest is als in (12).

Doordat de uikomsten in deze sectie gelijk zijn aan die van sectie 3, hebben we bewezen dat het intensionaliteitsprobleem ook hier opgelost is. Er rest ons nu nog het zogenaamde ophogingsprobleem. Hoe quantoren functioneren in KL bespreken we in 4.5.

4.5 Gequantificeerde uitdrukkingen

Het ophogingsprobleem was dat

(16)	a	Sommige jongens zijn meer schaker dan dammer
	b	Sommige jongens zijn meer dammer dan schaker

beide tegelijkertijd waar kunnen zijn. In het hierboven geschetste PTQ-achtige kader is de oplossing eenvoudig: sommige jongens α wordt geïnterpreteerd als ‘er is een x, x is een jongen en x α. Jongen en α worden niet geïnterpreteerd m.b.t. dezelfde partitie, dus als sommige jongens schaker zijn als bridger, dan is dat niet hetzelfde als zij die jongen zijn onder de bridgers zijn schaker onder de bridgers. Doordat de relativiteit m.b.t. een partitie betrekking heeft op de IV, kunnen we de quantor als een verzameling IV denotaten zien, zoals gewoonlijk. Voor de restrictor kunnen we terugvallen op de vertaling van is een.

We breiden syn in NL uit met sommige en S₁₀₂: als α ∈ P_CN dan is F₁₀₄(α) ∈ P_T, waar F₁₀₄(α) = sommige α.

We vertalen sommige α als volgt:

T₁₀₂: als α ∈ P_CN wordt vertaald als α' dan wordt sommige α vertaald als λQ_<<e,t>,t> λβ_<e,t> ∃y_e∃P_<e,t> [α'(Q)(P) ⋀ P(y) ⋀ β(y)]

We krijgen nu voor

(17)	Sommige jongens zijn schakers = Als ding zijn sommige jongens als ding schakers

	Als ding ↝ I
	jongen ↝ jongen'
	sommige jongens ↝ λQλβ∃y∃P[jongen'(Q)(P) ⋀ P(y) ⋀ β(y)]
	sommige jongens als ding ↝ λβ∃y∃P[jongen'(I)(P) ⋀ P(y) ⋀ β(y)]
	schaker ↝ schaker'
	is een schaker ↝ λQλx_e∃P'[schaker'(Q)(P') ⋀ P'(x)]
	is een schaker als ding ↝ λx∃P'[schaker'(I)(P') ⋀ P'(x)]
	((sommige jongens) (als ding)) (zijn schakers (als ding)) ↝
	∃y∃P∃P'[jongen'(I)(P) ⋀ P(y) ⋀ [schaker'(I)(P') ⋀ P'(y)]

wat inderdaad betekent dat er objecten zijn die jongen zijn m.b.t. maat m en schaker zijn m.b.t. maat m.

Het cruciale voorbeeld (16)a gaat als volgt:

(18)	Sommige jongens zijn meer schaker dan dammer = Als ding zijn sommige jongens als ding meer schaker dan dammer

	Als ding ↝ I
	jongen ↝ jongen'
	sommige jongens ↝ λQλβ∃y∃P[jongen'(Q)(P) ⋀ P(y) ⋀ β(y)]
	sommige jongens als ding ↝ λβ∃y∃P[jongen'(I)(P) ⋀ P(y) ⋀ β(y)]
	schaker ↝ schaker'
	dammer ↝ dammer'
	is meer een schaker dan een dammer ↝ more₁(schaker',dammer')
	is meer een schaker dan een dammer (als ding) ↝ more₁(schaker',dammer')(I)
	(sommige jongens (als ding)) (zijn meer schaker dan dammer (als ding)) ↝ ∃y∃P[jongen'(I)(P) ⋀ P(y) ⋀ more₁(schaker',dammer')(I)(y)]

Als we naar de interpretatie van more₁(α,β) kijken is het direct duidelijk dat het zeer wel mogelijk is dat er enerzijds personen zijn die met maat m jongen zijn m.b.t. U en met een (mogelijkerwijze andere) maat schaker zijn die groter is de maat waarmee ze dammer zijn, en anderzijds dat er personen zijn die met dezelfde maat m jongen zijn maar meer dammer dan schaker (als in 16b). Tevens volgt dat dit niet dezelfden kunnen zijn.

De introductie van andere quantoren gaat natuurlijk analoog.

Bibliografie

Hoepelman, J. (1986), Action, Comparison and Change, Tübingen

Montague, R. (1973), ‘The Proper Treatment of Quantification in Ordinary English’ in: J. Hintikka, J. Moravcsik and P. Suppes (eds.) Approaches to Natural Language, Dordrecht

IBM Scientific Centre

Vangerowstraße 18 69115 Heidelberg Duitsland

e-mail: pblok@heidelbg.ibm.com

hoepel@mazvm01.vnet.ibm.com

eind1.: Om redenen van eenvoud hebben we (5) geheel in termen van denotaten gegeven. Er zijn echter betekenissen die niet aan (5) e en f voldoen, zoals de denotaten van constructies met onecht. Voor een uitgebreide bespreking van de noodzakelijke betekenispostulaten voor de verschillende klassen van adjectieven verwijzen wij naar Hoepelman (1986).

eind2.: De hieronder gegeven definities en betekenispostulaten wijken licht af van Hoepelman (1986) 116-7. We hebben er hier overigens voor gekozen om de intuïtie van polaire adjectieven uit te drukken in termen van de betekenispostulaten, en dus de syntax (het vormen van schalen) aan de hand van de semantiek te vormen. Een meer canonieke manier zou zijn om de polaire adjectieven als lijst in de syntax op te nemen, en de modellen overeenkomstig te beperken.

eind3.: Om verwarring tussen de denotaties van nomina en predicaten te voorkomen worden de predicaten expliciet als verzamelingen (in tegenstelling tot functies van verzameleingen naar verzamelingen) genoteerd.

eind4.: Zie noot 1.

eind5.: Merk op dat het niet zo is dat N₂({A}) = N(N₁({A}); N neemt partities als argument en geen gelabelde partities. Wel geldt:
N₂({A}) = {(x,y)| ∃(u,v) ∈ N₁({A}) & ∃(p,q) ∈ N₁({v}): (x,y) = (2u+p,q)}
en algemeen:
N_n({A}) = {(x,y)| ∃(u,v) ∈ N_n-1({A}) & ∃(p,q) ∈ N₁({v}): (x,y) = (2u+p,q)}
N_n({A}) wordt dus berekend uit N_n-1({A}) door op elke cel v van N_n-1({A}) N₁({v}) toe te passen. Stel het nummer van v was u. N¹v krijgt nu nummer 2u+1 en N⁰v nummer 2u. Zoals al uit het type van de nomina blijkt is het niet onze bedoeling om deze relatie een onderdeel van de grammatica te laten zijn. In sectie 4 zal de iteratie van nominale functie applicatie gedefinieerd worden als verhoging van de fijnheidsgraad van interpreterende modellen.

eind6.: Het is eenvoudig te bewijzen dat als dit geldt voor een n, dan ook voor alle m > n; bovendien is er geen p zodat f(schaak_p({U}),Jan) < f(dam_p({U}),Jan)

eind7.: In het Nederlands verschijnt een als α frase meestal voor het subject: Als bridger is Jan een schaker, maar het kan ook elders opduiken: Jan is, als bridger, een schaker of Jan, als bridger, is een schaker. De lezer kan naar behoefte constructieregels opstellen.

eind8.: In sectie 3 was n het aantal keren dat een nomen toegepast werd. Het nummer van de hoogste cel was dan ook 2ⁿ - 1. In de hier gegeven semantiek laten we de relatie tussen het aantal keren toepassen van een nomen en de nummers in principe los: de hoogste cel kan ieder nummer hebben (en dus niet per se een nummer waarvoor er een n is zodat dat nummer gelijk is aan 2ⁿ - 1). Daarom gaan we over op het aangeven van het hoogste nummer n (en de ‘waarheidsmaat’ m) in absolute zin, i.t.t. een macht.

eind9.: Het is mogelijk is meer een... dan een apart te interpreteren en niet syncategorematisch zoals hier. Dit vereist echter een operatie gelijkend op Montague's ‘⌃’; het probleem is dat de interpretatie van een nomen alleen de cellen met waarde groter dan m oplevert, waardoor de onderste helft verloren gaat. We zouden dus is meer een... dan een als argumenten dingen moeten meegeven die onder M,m,g nog steeds de hele functies van partities naar functies van getallen naar verzamelingen opleveren, dat is, een soort intensies. We hebben de bijkomende complicaties hier willen vermijden.

eind10.: Zoals een anonieme reviewer aangaf is deze definitie niet helemaal correct: α^M,g is geen denotatie, maar een betekenis. De bedoeling moge echter duidelijk zijn: α^M,m,g wordt uit α^M,g (in dit geval dus F(α)) berekend volgens definitie 4.2.
Het is natuurlijk mogelijk met definitie 4.2 een functie Ψ te associeren die uit α^M,g en m de waarde α^M,m,g berekent. Denotatieregel (1) wordt dan:
Als α een constante is, dan α^M,m,g = Ψ(F(α),m)

eind11.: De recursieve transitie van categorieën naar typen is werk in voortgang.

Vorige Volgende

Tabu. Jaargang 24

Komparatief, komparatiever, komparatiefst
Peter I. Blok & Jaap Hoepelman

0 Inleiding

1 Het nomen als adjectief

2 Twee problemen

3 Een fijne semantiek

4 Maatwerk voor de komparatieve nomina

4.1 Syntax

4.2 Komparatieve logica

4.3 Vertalingen van NL in KL

4.4 Voorbeelden

4.5 Gequantificeerde uitdrukkingen

Bibliografie

Over dit hoofdstuk/artikel

auteurs

taalkunde

Komparatief, komparatiever, komparatiefst Peter I. Blok & Jaap Hoepelman

0 Inleiding

1 Het nomen als adjectief

2 Twee problemen

3 Een fijne semantiek

4 Maatwerk voor de komparatieve nomina

4.1 Syntax

4.2 Komparatieve logica

4.3 Vertalingen van NL in KL

4.4 Voorbeelden

4.5 Gequantificeerde uitdrukkingen

Bibliografie

Over dit hoofdstuk/artikel

auteurs

taalkunde

Komparatief, komparatiever, komparatiefst
Peter I. Blok & Jaap Hoepelman