Tabu. Jaargang 24

[p. 127]

Een algebraische semantiek voor lokatieve PP's^1.
Joost Zwarts

1 Inleiding

Het onderwerp van dit paper is de lexicale semantiek van de lokatieve preposities in (1):^2.

(1)	voor, achter, boven, onder, naast, tussen, binnen, buiten, bij, in, op

Traditioneel worden deze preposities opgevat als relaties tussen objecten. Zin (2a) wordt dan bijvoorbeeld geïnterpreteerd als (2b):

(2)	a	Jan is achter het huis
	b	achter(jan, het huis)
	b'	loc(jan, achter(het huis))

Jan en het huis worden in deze relatie respectievelijk thema en referentieobject genoemd.^3. In veel recente analyses wordt de relatie tussen thema en referentieobject echter ontleed in twee componenten: (i) een voor elke prepositie specifieke functie die het referentieobject afbeeldt op een ruimtelijke sector, een bepaald deel van de ruimte, en (ii) een algemene lokatierelatie die het thema in die sector plaatst. Zin (2a) krijgt dan analyse (2b'), waarin achter het huis afbeeldt op de ‘achter-sector’ van het huis en loc aangeeft dat Jan zich in die sector bevindt.^4. Als de loc-relatie buiten beschouwing wordt gelaten, kan de semantiek van locatieve PPs uitsluitend worden bestudeerd in termen van sectoren. Daarbij moeten onder andere de volgende vragen beantwoord worden: (i) wat zijn de algemene formele eigenschappen van sectoren? (ii) op welke wijze definieert een prepositie een sector op basis van een gegeven referentieobject?

In dit paper stel ik voor om een sector op te vatten als een verzameling plaatsvectoren, dat wil zeggen gerichte ruimtelijke lijnstukken met een vast beginpunt. Elke prepositie beeldt zijn referentieobject dus af op een verzameling vectoren die vertrekken uit dat referentieobject. De PP bij het huis kan worden geïnterpreteerd als de verzameling vectoren die hun beginpunt in het huis hebben en waarvan de lengte kleiner is dan een contextueel bepaalde waarde; de PP boven het huis denoteert de verzameling vectoren die vanuit het huis in opwaartse richting wijzen; de PP tussen het huis en de schuur correspondeert met de vectoren die vanuit het huis in de richting van de schuur wijzen; enzovoort.

Sectie 2 laat zien dat zo'n vector-semantiek van lokatieve PPs gemotiveerd kan worden door het soort modificeerders dat we bij deze PPs vinden. Maar wat een vector-benadering vooral zo interessant maakt is dat de verzameling vectoren uit één punt een rijke en grondig bestudeerde algebra vormt, een

1. Ik ben Henk Verkuyl en Ton van der Wouden en de luisteraars op de TABU-dag erkentelijk voor commentaar en discussie. Het onderzoek voor dit paper is mogelijk gemaakt door de Stichting voor Taal, Spraak en Logica, die wordt gesubsidieerd door de Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO).

2. Allerlei (potentieel) lokatieve preposities blijven in dit paper buiten beschouwing zoals aan, tegenover, langs in Hij woont langs het water, uit in Wij zijn uit de haven. Ook over de relatie tussen het directionele en het lokatieve gebruik van in en op heb ik hier niets te zeggen.

3. Ook wel figure en ground (Talmy 1978) of trajector en landmark (Langacker 1987).

4. Zie Jackendoff (1983) en Wunderlich (1991) voor argumenten voor en uitwerkingen van deze benadering. In de Engelstalige literatuur worden de termen place, region of location gebruikt. Ik gebruik hier de neutrale term sector om hinderlijke connotaties van andere termen te vermijden.

[p. 128]

vectorruimte met operaties van vectoroptelling, scalaire vermenigvuldiging en rotatie. Het begrippenapparaat van de vectoralgebra, dat wordt uitgelegd in sectie 3, vormt de basis voor de semantische definities van preposities in sectie 4. Vervolgens kunnen in sectie 5 empirisch relevante klassen van preposities worden onderscheiden op basis van afsluitingseigenschappen van de sectoren die ze denoteren. Sectie 6 bevat tenslotte voorstellen voor mogelijke semantische universalia van lokatieve preposities die cruciaal gebruik maken van de vectoroperaties.

2 Modificatie van preposities

PPs kunnen op verschillende manieren gemodificeerd worden. Voor dit paper is modificatie door middel van adjectieven (3a), adverbia (3b) en maatbepalingen (3c) van belang:

(3)	a	ver achter het huis
	b	schuin boven de deur
	c	twee meter buiten het veld

Deze modificeerders vallen op grond van hun betekenis in twee klassen uiteen. Adverbia als ver, hoog, dicht, vlak en maatbepalingen als twee meter zeggen allemaal iets over de afstand tussen thema en referentieobject, een notie die precies correspondeert met de lengte van de vector die van referentieobject naar thema wijst. Modificeerders als recht en schuin geven een precisering van de richting waarin het thema ten opzichte van het referentieobject gezocht moet worden, hetgeen correspondeert met de oriëntatie van de vector ten opzichte van een referentieas. Een op vectoren gebaseerde denotatie van PPs leidt dan tot een eenvoudige interpretatie van de modificatiestructuren in (4):^5.

(4)	a	{v | v ∈ achter(het huis) & ver(v)}
	b	{v | v ∈ boven(de deur) & schuin(v)}
	c	{v | v ∈ buiten(het veld) & twee meter(v)}

Merk op dat de interpretatie van PPs hier niet één enkele vector is, maar een verzameling vectoren. Het is dus niet zo dat de PP achter het huis een vector aanduidt waarvan de lengte ongespecificeerd is, terwijl de PPs twee meter achter het huis of ver achter het huis juist vectoren aanduiden waarvan de lengte wèl gespecificeerd is. Een vector heeft altijd een bepaalde lengte en richting en PPs verschillen in de algebraïsche eigenschappen van de vectorverzameling die ze denoteren, zoals sectie 5 en 6 duidelijk zullen maken.

In een semantiek van lokatieve PPs die gebaseerd is op punten of op een domein van mereologisch gestructureerde lokaties (zoals bijvoorbeeld in Wunderlich 1991) is de semantiek veel gecompliceerder:^6.

5. Vectoren zullen worden aangeduid met de vetgedrukte kleine letters u, v en w.

6. In (4) als (5) is niet verantwoord dat ver en schuin relatieve begrippen zijn. ver vereist een impliciet vergelijkingspunt als extra argument en schuin een referentieas. In (4) zouden ver en schuin dus tweeplaatsig moeten zijn.

[p. 129]

(5)	a	{p | p ∈ achter(het huis) & ver(p, het huis)}
	b	{p | p ∈ boven(de deur) & schuin(lijn(p, de deur))}
	c	{p | p ∈ buiten(het veld) & afstand(p, het veld) = twee meter}

In (5a) drukt ver(p,het huis) uit dat ver altijd betrekking heeft op de afstand van een punt met het referentieobject en schuin(lijn(p,de deur)) in (5b) geeft aan dat schuin iets zegt over de lijn die de positie met het referentieobject verbindt. De p in deze definities is een eerste-orde variabele voor ruimtelijke punten of primitieve lokaties. Het voornaamste probleem van de interpretaties in (5) is dat ze gegeven de syntactische structuren van de PPs in (3) niet compositioneel tot stand kunnen komen. De interpretatie van de gehele PP moet een functie zijn van de interpretaties van modificeerder en de PP die gemodificeerd wordt, maar om tot de interpretaties in (5) te komen moet gebruik worden gemaakt van het normaal gesproken niet toegankelijke referentieobject. Dit probleem doet zich bij de vector-semantiek in (4) niet voor omdat daar de positie van het referentieobject als het ware mee naar boven wordt genomen in het beginpunt van de vectoren.

3 Rekenen met vectoren

Om een op vectoren gebaseerde semantiek te kunnen formuleren breiden we het domein van individuen E uit met een verzameling S van plaatsvectoren. Voor elk tweetal punten P en Q in de ruimte is er een vector van P naar Q en een vector van Q naar P. De lokatierelatie loc is een relatie in E ∪ S. loc(x,v) betekent dat object x zich bevindt op het eindpunt van vector v en loc(v,x) betekent dat het beginpunt van v zich bevindt in object x. In dit paper wordt de idealisatie gemaakt dat objecten puntvormig zijn, dat wil zeggen: geen ruimtelijke extensie hebben. Als gevolg hiervan kan geen verschil worden gemaakt tussen de lokatieve preposities die juist veronderstellen dat er wel een extensie is (in, op en binnen). Deze preposities krijgen in sectie 4 allemaal dezelfde definitie, maar kunnen worden onderscheiden zodra we de punt-idealisatie opheffen.

De verzameling vectoren die in hetzelfde punt beginnen, vormen tezamen een vectorruimte. Een vectorruimte V over een verzameling reële getallen R is een verzameling die gesloten is onder twee operaties:

(6)	a	vectoroptelling: voor elk paar v, w ∈ V is er precies één v + w ∈ V, de vectorsom van v en w
	b	scalaire vermenigvuldiging: voor elke v ∈ V en s ∈ R is er precies één sv ∈ V, het scalair product van v met scalar s

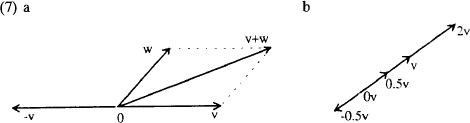
Vectoroptelling is commutatief (u + v = v + u) en associatief ((u + v) + w = u + (v + w)). De nulvector 0 ∈ V is identiteitselement (v + 0 = 0 + v = v) en elke vector heeft een inverse -v (v + (-v) = 0). Hoe vectoroptelling

[p. 130]

werkt en welke rol de nulvector en inverse vector spelen illustreert (7a). Een vectorsom kan worden gevonden door gebruik te maken van de de parallellogramregel: als de vectoren v en w opgevat worden als de zijden van een parallellogram, dan is v + w de vector die diagonaal het parallellogram doorsnijdt. Scalaire vermenigvuldiging kan geometrisch worden geïnterpreteerd als een operatie op de lengte en/of oriëntatie van de vector, zoals (7b) laat zien. Als de scalar groter is dan 1 wordt de vector uitgerekt in dezelfde richting, als hij tussen 0 en 1 ligt, wordt de vector ingekrompen, 0v levert de nulvector 0 op en een negatieve scalar keert de richting om.^7.

De interpretatie van een lokatieve PP is altijd een deelverzameling van een beperkt ruimtelijk universum dat bepaald wordt door het referentieobject. Ik zal dat hier aanduiden als space(x), gedefinieerd als {v ∈ S | loc(v,x)}.^8. Het referentieobject fungeert als de oorsprong van het vectoruniversum van een PP en elke positie in de ruimte kan alleen ten opzichte van het referentieobject gespecificeerd worden. Merk op dat bovengenoemde vectoroperaties geen expliciete rol spelen in de semantiek van PPs. Het is dus in de semantiek die hier wordt voorgesteld niet zo dat in schuin boven de deur vectoroptelling plaats vindt van de vectoren van schuin en boven de deur of dat ver een soort scalaire vermenigvuldiging uitvoert op de vectoren van achter het huis met als resultaat ver achter het huis. De vectoroperaties zijn nodig om de ruimte en daarmee ook de PP-denotaties een algebraïsche structuur te geven. Vectoroptelling en scalaire vermenigvuldiging vinden dus plaats in de sector van elke lokatieve PP, hoewel niet elke sector gesloten zal zijn onder die operaties, zoals we later zullen zien.

De interpretatie van een PP heeft in het algemeen de schematische vorm in (8a) en zinnen van het type Jan is achter het huis krijgen de waarheidsconditie in (8b):

(8)	a	|| [PP P NP] ||M = {v ∈ space(|| NP ||M) | ... v ...}
	b	|| [S NP is PP] ||M = 1 desda ∃v ∈ || PP ||M zodanig dat loc
		(|| NP ||M, v)

De zin Jan is achter het huis is dus waar als Jan zich op het eindpunt van een vector bevindt in de ‘achter’-sector van het huis.

7. Merk op dat 0 een scalar is en 0 een vector.

8. Onder de punt-idealisatie is space(x) voor elke x een vectorruimte. Als die idealisatie wordt losgelaten is space(x) de vereniging van een verzameling vectorruimtes.

[p. 131]

4 Definities van lokatieve preposities

Net als bij de modificeerders in sectie 2, zien we ook bij de lokatieve preposities zelf een onderscheid tussen preposities die gedefinieerd zijn in termen van afstand (in, op, buiten, binnen, bij) en preposities die gedefinieerd zijn in termen van richting (voor, achter, boven, onder, naast, tussen). Dit onderscheid correspondeert met het onderscheid tussen topologische en projectieve preposities dat vaak gemaakt wordt in de literatuur (zie bijvoorbeeld Herskovits 1986). Ik zal die twee termen ook hier gebruiken.

De topologische preposities kunnen als volgt geïnterpreteerd worden (waarin |v| de lengte van vector v aangeeft):

(9)	a	|| op NP || = || in NP || = || binnen NP || =	{v ∈ space(||NP||)| |v| = 0}
	b	|| buiten NP || =	{v ∈ space(||NP||)| |v| > 0}
	c	|| bij NP || =	{v ∈ space(||NP||)| |v| < r}

Omdat de interne structuur van objecten in dit paper buiten beschouwing blijft kan geen verschil worden gemaakt tussen op, in en binnen.^9. PPs met deze preposities denoteren de verzameling van alle vectoren met lengte 0. Er is maar één vector met lengte 0 in space(||NP||), namelijk de nulvector 0, en daarom denoteren deze PPs in elk model een singleton met de unieke nulvector die begint en eindigt in het referentieobject. Omdat zo'n nulvector eigenlijk gezien kan worden als een gewoon punt in de ruimte, denoteren deze PPs de positie van het referentieobject, het gewenste resultaat.^10. PPs met buiten denoteren juist het complement hiervan: de verzameling van alle vectoren met een lengte groter dan 0. PPs met bij denoteren een ‘omgeving’ van het referentieobject, gedefinieerd door alle vectoren te nemen die een lengte hebben kleiner dan een pragmatisch gegeven radius r. De sectoren van deze PPs kunnen als volgt in diagrammen worden weergegeven:^11.

9. Merk in dit verband op dat er talen zijn die geen onderscheid maken tussen op en in, zoals bijvoorbeeld het Spaans (en).

10. Gevallen als midden in, diep in, hoog op duiden erop dat voor een adequate analyse van gemodificeerde preposities ook vectoren verondersteld moeten worden in het referentieobject zelf.

11. In deze en volgende diagrammen correspondeert het kleine vierkantje met het referentieobject en het gearceerde gebied met de eindpunten van de vectoren van de sector. De stippellijn rond een sector geeft aan dat de sector topologisch open is (d.w.z. de begrenzing hoort er niet bij). De diagrammen geven natuurlijk slechts tweedimensionale doorsnedes weer van driedimensionale sectoren.

[p. 132]

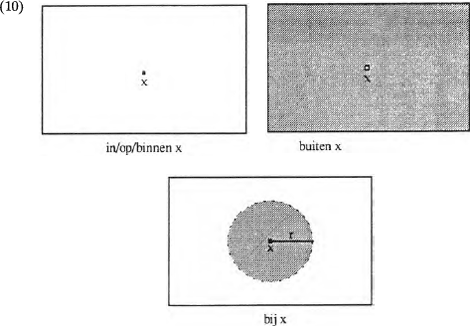
Deze diagrammen en vergelijkbare diagrammen voor andere preposities verderop in dit paper doen misschien denken aan het soort plaatjes dat een belangrijke rol speelt in de Cognitive Grammar of Space Grammar (Langacker 1987 en vooral Hawkins 1984). De hier gegeven diagrammen hebben echter - anders dan in de Cognitieve Grammatica - geen theoretische status; het zijn slechts hulpmiddelen om een beeld te krijgen van de denotaties van PPs. De werkelijke semantische analyse van een PP is als een deelverzameling van een algebraïsch gestructureerd model van interpretatie.

De projectieve preposities hebben met elkaar gemeen dat ze gedefinieerd worden in termen van projecties op een as. Een as wordt hier gedefinieerd als een verzameling vectoren die dezelfde richting of dezelfde oriëntatie hebben. Onderdeel van het model zijn twee functies die twee onderling loodrechte assen toekennen aan referentieobjecten: vert kent aan elk object x de as toe die bestaat uit alle vectoren die vanuit x recht omhoog wijzen (de verticale as) en front kent aan elk object x de as toe van die vectoren die vanuit x recht naar voren wijzen (de frontale as). Hoe die assen worden toegekend aan referentieobjecten blijft hier buiten beschouwing, voornamelijk omdat daaraan in de bestaande literatuur al veel aandacht wordt besteed.^12. Merk op dat vert(x) en front(x) halfassen zijn, dus alleen de gedeelten die met boven en voor corresponderen. De complementaire halfassen worden gegeven door de verzameling van alle inverse vectoren te nemen: -A = {v | -v ∈ A}. En dus is -vert(x) de as die omlaag wijst en -front(x) de ‘achterwaartse’ as. De as die voor naast relevant is, de laterale as lat(x), is een symmetrische as loodrecht op het vlak waarin vert(x) en front(x) liggen. Technisch gesproken is deze laterale as het orthogonale complement van dit vlak. Als A een

12. Zie bijvoorbeeld Leech (1969), Fillmore (1971), Clark (1973) en Herskovits (1986).

[p. 133]

(half)as of vlak is, dan is de verzameling van alle vectoren loodrecht op A, genoteerd als ˔A, het orthogonale complement van A. Dankzij de assen wordt aan de ruimte space(x) van x de structuur van een assenstelsel toegekend.^13.

Een vector v kan ten opzichte van een as A worden ontleed in twee componenten: één component in A (de projectie van v op A, v_A) en één component loodrecht daarop (de projectie van v op ˔A, v_˔A.^14. In het volgende diagram is v_vert(x) de projectie van v op de verticale as van x en v_˔vert(x) de projectie van v op het grondvlak:

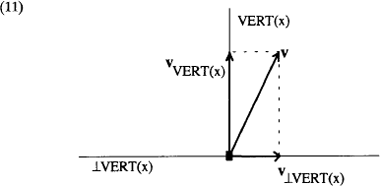
We kunnen aan dit plaatje ook zien wanneer een vector naar boven wijst: als een vector meer naar omhoog wijst dan naar opzij, oftewel: als de opwaartse component (v_vert(x)) langer is dan de zijwaartse component (v_˔vert(x)). De preposities boven, onder, voor, achter, naast en tussen krijgen de volgende definities:

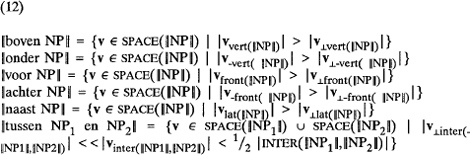
De sectoren kunnen als volgt worden weergegeven:

13. Een derde functie dext(x) zou nodig zijn om aan het object x een rechteras toe te kennen (loodrecht op vert(x) en front(x) en dus in lat(x)) om de uitdrukkingen rechts van en links van te interpreteren.

14. De definitie van de projectie van vector v op een as of vlak X is als volgt: v_X is die vector v_i ∈ X waarvoor een vector v_j te vinden is, zodat v_i ˔ v_j en v_i + v_j = v. In tegenstelling tot de in de lineaire algebra vaak gebruikte definitie van projectie van een vector op een andere vector spelen hier de sinus of cosinus van een hoek hier geen rol.

[p. 134]

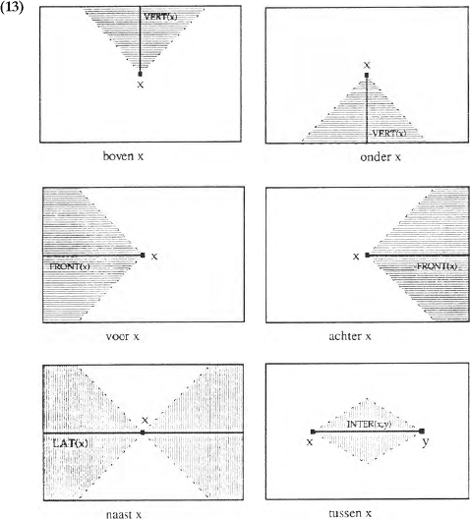
Het gaat hier natuurlijk om idealisaties van het werkelijke gebruik van deze preposities. De ‘uitwaaiering’ van de sector boven of onder het referentieobject lijkt bijvoorbeeld afhankelijk te zijn van de aard van het object. Als een vliegtuig op enige kilometers hoogte de Nederlandse kust nadert, is het pas boven Nederland als het de kustlijn werkelijk gepasseerd is en niet al een paar kilometers uit de kust.^15. Dit soort effecten kunnen verklaard worden zodra referentieobjecten niet langer alleen maar als punten worden gezien, maar ook als vlakken of volumes.

De sector en definitie van tussen is afwijkend. Er is wel sprake van projectie van de vector op een as, maar de aard van de as is anders. Tussen heeft twee referentieobjecten en de as hiertussen, inter(x,y) kan gedefinieerd worden als de verzameling vectoren die van het ene naar het andere referentieobject wijzen. In dit paper neem ik aan dat de sector bestaat uit die

15. Ton van der Wouden bracht dit voorbeeld onder mijn aandacht.

[p. 135]

vectoren waarvan de component langs de as (veel) groter is dan de orthogonale component, maar kleiner dan de helft van de lengte van de as zelf. Alleen de duidelijkste voorbeelden met tussen kunnen hiermee verantwoord worden. Habel (1989) geeft een aardig idee van de complexiteit van tussen, die een echt adequate definitie van tussen zou moeten vangen.

5 Twee sluitingseigenschappen en twee soorten modificeerders

We hebben eerder gezien dat de twee kenmerkende eigenschappen van de vector, lengte en richting, herkenbaar zijn in klassificaties van preposities en hun modificeerders. In een vectorruimte kunnen twee unaire operaties worden onderscheiden die steeds één van deze twee eigenschappen manipuleren en de andere constant houden. Scalaire vermenigvuldiging verandert de lengte van de vector maar houdt de oriëntatie constant en rotatie verandert de oriëntatie van een vector terwijl de lengte constant blijft. Met behulp van deze operaties kunnen we de afsluitingseigenschappen van sectoren onderzoeken, dat wil zeggen, we kunnen de lengte of oriëntatie van een vector in een bepaalde sector veranderen en vervolgens kijken of het resultaat zich al dan niet in de sector bevindt. Ik zal laten zien dat op deze manier empirisch relevante klassen van preposities kunnen worden onderscheiden.

De eerste eigenschap is sluiting onder verlenging:

(14)	Een PP is gesloten onder verlenging desda als in elk model M: voor elke v ∈ ||PP||M als w een verlenging is van v dan w ∈ ||PP||M.

In een vectorruimte is w een verlenging van v desda v en w geen nulvectoren zijn en er een scalar s is groter dan 1 zodat w = sv. Deze eigenschap kan in bepaalde opzichten vergeleken worden met monotone stijging in de gegeneraliseerde kwantoren-semantiek van de NPs. Op basis van deze eigenschap kunnen we binnen de klasse van simpele (dat is ongemodificeerde) preposities de volgende twee klassen onderscheiden:^16.

(15)	Gesloten onder verlenging	Niet gesloten onder verlenging
	voor - achter	in, op, binnen
	boven - onder	bij
	naast, buiten	tussen

Ook gemodificeerde preposities laten zich door deze eigenschap in twee groepen delen: hoog boven, meer dan twee meter voor en ver naast zijn gesloten onder verlenging, maar laag boven, minder dan twee meter voor, dicht naast en precies twee meter voor zijn niet gesloten onder verlenging. Wat is de empirische relevantie van sluiting onder verlenging? Sluiting onder verlenging blijkt verband te houden met de mogelijkheid maatbepalingen te gebruiken. Alleen als een simpele prepositie gesloten is onder verlenging kunnen maatbepalingen gebruikt worden:

16. De algebraïsche term gesloten werkt hier in combinatie met de diagrammen misschien verwarrend. De sector van buiten is in algebraïsch opzicht gesloten, maar grafisch juist niet terwijl de sector van bij algebraïsch niet gesloten is, maar grafisch wel.

[p. 136]

(16)	twee meter...	twee meter...
	... voor/achter de auto	*... in/op de berg
	... boven/onder ons	*... binnen de stad
	... naast het raam	*... bij de auto
	... buiten de stad	*... tussen het raam en de deur

Wat hiervan verder ook de verklaring moge zijn, vast staat in ieder geval dat sluiting onder verlenging geen arbitraire formele eigenschap is, maar een significante generalisatie die alleen mogelijk is door het gebruik van een vector-algebraïsche semantiek voor lokatieve PPs.^17.

Een tweede eigenschap is sluiting onder rotatie:

(17)	Een PP is gesloten onder rotatie desda in elk model M: voor elke v ∈ ||NP||M als w een rotatie is van v dan w ∈ ||PP||M.

Ook hier krijgen we weer twee soorten simpele preposities:

(18)	Gesloten onder rotatie	Niet gesloten onder rotatie
	bij	voor - achter
	in, binnen, op	boven - onder
	buiten	naast, tussen

Deze eigenschap blijkt te corresponderen met de mogelijkheid om directionele modificeerders te gebruiken zoals recht en schuin:

(19)	recht/schuin...	recht/schuin...
	*... binnen/buiten het huis	... voor/achter de auto
	*... bij de auto	... boven/onder de auto
	*... in/op het huis	... naast de auto
		... tussen de auto en het huis

De bijdrage van recht en schuin aan de interpretaties van de PPs in de rechterkolom is als volgt:

(20)	recht:	|v˔A| = 0
	schuin:	|v˔A| > 0

a is hierin de as van de sector (gedefinieerd door front, vert, lat of inter).

17. Er zijn voorbeelden te bedenken waarbij binnen wel maatbepalingen heeft zoals 10 kilometer binnen de Nederlandse territoriale wateren, één stap binnen de bebouwde kom. Mijn vermoeden is dat in deze gevallen geen sprake is van een afgesloten gebied (zoals bij binnen de stad) maar dat ‘ingezoomd’ wordt op een gedeelte van de grens van dit gebied. De tegenoverliggende grens raakt dan uit het zicht en de binnen-sector kan zich dan - net als de buiten-sector - onbeperkt uitstrekken.

6 Universele eigenschappen van lokatieve PPs

In sectie 5 hebben we al de eigenschap van sluiting onder verlenging geïntroduceerd, waarvan sluiting onder verkorting de tegenhanger is:

[p. 137]

(21)	Een PP is gesloten onder verkorting desda in elk model M: voor elke v ∈ ||PP||M als w een verkorting van v dan is w ∈ ||PP||M.

In een vectorruimte is w een verkorting van v desda v en w beide niet 0 zijn en er een s > 1 is zodat v = sw.^18. We krijgen weer twee klassen. Voorbeelden van preposities die gesloten zijn onder verkorting zijn bij, boven, in, dicht bij, vlak naast. Voorbeelden van preposities die niet gesloten zijn onder verkorting zijn niet bij, ver boven, minstens twee meter naast, midden tussen.^19. Het blijkt nu dat de simpele preposities allemaal gesloten zijn onder verkorting en dat de preposities die niet gesloten zijn onder verkorting allemaal gemodificeerd zijn. Dit suggereert een universale die als volgt geformuleerd kan worden:

(22)	Universale 1: Elke simpele PP is gesloten onder verkorting.

Intuïtief betekent dit dat simpele PPs alleen sectoren kunnen denoteren die raken aan het referentiepunt of het referentiepunt bevatten. Anders gezegd: er mag geen kloof zijn tussen sector en referentieobject. Universale 1 leidt tot een belangrijke voorspelling: er is geen simpele prepositie voor de sector ver van het referentieobject, dus een prepositioneel ver als tegenhanger van bij. Zo'n prepositie is er in het Nederlands en de mij bekende talen inderdaad niet, maar alleen een verkenning van een groot aantal talen zal kunnen uitwijzen of het hier werkelijk om een universale gaat.^20.

Een andere universale heeft betrekking op de continuïteit van sectoren: in een normale sector bevinden zich geen gaten of breuken. Met andere woorden: als twee vectoren zich in de sector bevinden, dan ook elke vector ertussenin. Een vector kan zich op twee manieren tussen twee andere vectoren in bevinden. Een vector v bevindt zich lineair tussen u en w als w een verlenging is van u ‘over v heen’. Een vector v bevindt zich radiaal tussen u en w als w een scherpe rotatie is van u die over v gaat. Een sector R kan dan ook lineair en radiaal continu zijn. Deze begrippen maken het mogelijk om de volgende universale te formuleren:

(23)	Universale 2: Simpele PPs denoteren sectoren die lineair en radiaal continu zijn.

Ook de meeste gemodificeerde PPs zijn in deze tweeledige zin continu, maar er zijn wel gemodificeerde PPs te bedenken die niet aan deze universale voldoen. De PP een even aantal meters buiten de stad is niet lineair continu, omdat hij een sector denoteert die bestaat uit een oneindig aantal discontinue concentrische ‘schillen’ rond het referentieobject met een onderlinge afstand van twee meter. De PP schuin boven de stad denoteert een sector waarin ten opzichte van de sector van boven de stad een smalle kegel in het centrum ontbreekt waardoor een radiale discontinuïteit ontstaat. Continuïteit is dus een eigenschap van alle simpele en de meeste gemodificeerde PPs.

18. Sluiting onder verkorting uit zich in de diagrammen doordat de sector verbonden is met het referentieobject.

19. PPs met midden tussen en precies twee meter naast zijn niet gesloten onder verlenging en niet gesloten onder verkorting. Ze zijn te vergelijken met de niet-monotone kwantoren in de gegeneraliseerde kwantoren theorie, wat gezien de aanwezigheid van een element als precies ook niet verwonderlijk is.

20. Merk op dat het Nederlands als tegenhanger van bij wel een constructie heeft van de vorm ver van, die ik echter niet opvat als prepositie. Hier is ofwel sprake van een gemodificeerd van (en dus geen simpele prepositie) ofwel van het adjectief ver met een van-PP als complement (en dus geen prepositie).

[p. 138]

7 Conclusie

De interpretatie van lokatieve PPs in termen van vectoren maakt een algebraische benadering van deze categorie mogelijk, met alle voordelen van dien. De betekenissen van preposities kunnen precies gedefinieerd worden en allerlei algebraïsche eigenschappen, universele en klassificerende kunnen worden afgeleid. Daardoor kan ook een begin worden gemaakt met de verantwoording van de distributie en interpretatie van modificeerders in PPs. In dit paper kwam het gedrag van maatbepalingen en de adverbia recht en schuin aan de orde, verder onderzoek zal moeten uitwijzen of het gedrag van de dimensieadjectieven hoog, laag, diep, ver en dicht en adverbia als vlak en pal zich ook in termen van vectoren laat vangen. Het vectorbegrip lijkt ook voor deze gevallen een gunstige invalshoek te bieden.

[p. 139]

Bibliografie

Clark, H.H (1973) ‘Space, Time, Semantics, and the Child’. In T.E. Moore, (ed.) Cognitive Development and the Acquisition of Language. New York: Academic Press, 27-64.

Fillmore, C.J. (1971) Santa Cruz Lectures on Deixis. Bloomington, Indiana: Indiana University Linguistics Club.

Habel, C. (1989) ‘Zwischen-Bericht’. In C. Habel, M. Herweg & K. Rehkämper, eds.) Raumkonzepte in Verstehensprozessen. Interdisziplinäre Beiträge zu Sprache und Raum. Tübingen: Niemeyer. 37-69.

Hawkins, B. (1984) The Semantics of English Spatial Prepositions. Ph.D. University of California at San Diego.

[p. 140]

Herskovits, A. (1986) Language and Spatial Cognition: An Interdisciplinary Study of the Prepositions in English. Cambridge: Cambridge University Press.

Jackendoff, R. (1983) Semantics and Cognition. Cambridge, Massachusetts: MIT Press.

Langacker, R. (1987) Foundations of Cognitive Grammar. Stanford, California: Stanford University Press.

Leech, G.N. (1969) Towards a Semantic Description of English. London: Longman.

Talmy, L. (1978) ‘Figure and ground in complex sentences’. In J.H. Greenberg et al., eds., Universals of Human Language 4. Stanford, California: Stanford University Press.

Wunderlich, D. (1991) ‘How do prepositional phrases fit into compositional syntax and semantics’. Linguistics 29, 591-621.