Tabu. Jaargang 19
(1989)– [tijdschrift] Tabu–
[pagina 76]
| |||||||||||||||||||||||||
Over een lineaire kategoriale ontleder
| |||||||||||||||||||||||||
2 SyntaxisDe syntaktische komponent kan worden omschreven als een tweezijdige lineaire monotone kategorieënrekening. De onderliggende algebra K wordt naar het volgende rekursieve schema voortgebracht door een verzameling van primitieve (ongelede) kategorieën B.
Kategorieën α/β zijn aan te duiden als rechts zoekende of rechts gerichte | |||||||||||||||||||||||||
[pagina 77]
| |||||||||||||||||||||||||
funktoren of rechtse delingen van β op α, kategorieën β\α daarentegen als links zoekende of links gerichte funktoren of linkse delingen van β op α. Kategorieën α*β heten produkten of verketeningen. Noch de deling noch het produkt is kommutatief. De kategorieënrekening kent naast identiteit slechts twee regelschema's, te weten toepassing en samenstelling van ongelijk gerichte funktoren (Samson):
Bij de ontleding van een ingevoerde reeks worden termen paarsgewijs aan de rekening onderworpen met behulp van de generalizatie
Elk regelschema van de vorm T * U » V kan derhalve uit syntaktisch oogpunt als volgt worden gelezen: indien een instantie t van de kategorie T gevolgd wordt door een instantie u van de kategorie U, is de keten tu een instantie van de kategorie V. De lineariteit van de Kompong-syntaxis is gelegen in de beperking dat het oplosbare element Y in (c1) - (d2) primitief is, i.e. Y B. Deze beperking is alleen dan zinvol als de eindige verzameling B van primitieven syntaktisch relevant gekozen is. De syntaktische algebra in Kompong wordt voortgebracht door een verzameling die goeddeels is afgeleid van het corpus van kategorieën dat in de transformationele grammatika wordt gehanteerd. De monotonie van de syntaxis vloeit voort uit het ontbreken van regelschema's die de orde (komplexiteit) van kategorieën verhogen. De notie orde van x is hierbij als volgt rekursief gedefinieerd:
Regels die de orde van kategorieën wijzigen, zijn van de vorm
Dergelijke monadische regels, waarbij het eerste lid produktvrij is, hanteert Kompong alleen in het lexikon. Aangezien het lexikon bij definitie eindige reeksen informatie bevat, wordt de monadische regelvorm in het lexikon niet gebruikt als regelschema, maar slechts geïnstantieerd in termen van kategoriale konstanten. De syntaktische rekening is zelfs monotoon dalend in die zin dat de orde van de resultaat-kategorie altijd lager is dan de som van de ordes van de operanda. Vanwege de lineaire beperking is deze daling konstant; voor elke (lineaire) regel van de vorm (h) geldt (i):
| |||||||||||||||||||||||||
[pagina 78]
| |||||||||||||||||||||||||
Dit lineaire monotone kategoriale kader mag in verhouding tot de rekeningen van de Lambek-hiërarchie bijzonder arm heten. In strikte zin is de rekening zelfs niet kompatibel met de Lambek-systemen omdat de regel Samson niet afleidbaar is onder de axiomatiek van deze systemen. Taalkundig belichaamt de ontleder niettemin de pretentie dat de lineair en monotoon beperkte rekening (c1) - (d2) voldoende is om de hoofdkonfiguraties van het nederlands genoegzaam te struktureren; de ontleder is met name gericht op de struktuur van de werkwoordelijke en naamwoordelijke groepen. De weerbarstige vormen van meervoudige en elliptische nevenschikking waar het nederlands in grossiert, vallen evenwel buiten de macht van Kompong. Deze eigenaardigheden, kategoriaal te lijf gegaan in bijvoorbeeld Houtman (1988), vergen een hardere hand dan de automaat in z'n huidige vorm kan bieden. Gelet op de symptomatische aanwezigheid van konjunkties in dergelijke strukturen en hun lokaal karakter, moet het mogelijk zijn ze met een apart, gespecializeerd syntaktisch apparaat te behandelen. In deze zin is Kompong te zien als een bijdrage tot een grammatisch modulaire benadering van automatische taalverwerking. Tot de belangrijkste taalkundige implikaties van Kompong behoort dat de ontleder diskontinuïteiten van de types (j) wél maar diskontinuïteiten van de types (k) niet kan herkennen:
Voor de verwerking van diskontinuïteiten heeft Kompong slechts de Samsonregels (d1) en (d2) ter beschikking. Bijgevolg kan Kompong alleen diskontinuïteit verwerken tussen een funktorkategorie en een passend argument indien de twee slechts gescheiden worden door een ‘brug’ van kategorieën met een richting tegengesteld aan die van de funktor in kwestie. De hier geschetste kategorieën-rekening is derhalve te beschouwen als een eigenzinnige ‘Move-α-theorie. Komputationeel buit de automaat de beperkingen van het systeem uit om explosieve rekentijden te vermijden. Dat wordt in de paragrafen 4 en 5 verder beschreven. | |||||||||||||||||||||||||
2* Lineariteit en SamsonDat in Kompong Samson samengaat met een lineair regiem op de toepassing van regels, is niet willekeurig. Bezie de ‘normale’ samenstelling van gelijk gerichte funktoren
| |||||||||||||||||||||||||
[pagina 79]
| |||||||||||||||||||||||||
onder de lineaire beperking dat Y B. Zij nu G de lineair beperkte grammatika <K, T, Toepas> en G+ de lineair beperkte grammatika <K, T, Toepas, Samstel>, met steeds T B. Nu geldt voor elke reeks A over K de stelling:
De stelling zegt dus dat twee lineaire grammatika's, de een met Toepas en de ander met Toepas en Samstel, zwak ekwivalent zijn met betrekking tot een gespecificeerde primitieve kategorie, bijvoorbeeld een sententiële kategorie. Dit betekent dat Samstel niets toevoegt aan het herkennend vermogen van een minimale lineaire grammatika G. Het is niet moeilijk in te zien dat dit ook daadwerkelijk het geval is. Uiteraard is het zo dat een bewijs A »» T in G ook een bewijs in G+ is. Derhalve zijn slechts die gevallen van belang waarbij een bewijs in G+ verloopt via Samstel. Stel dat A de deelreeks <U/b b/c c> omvat. Onder G wordt deze reeks herleid op A door toepassing van b/c op c en toepassing van U/b op het resultaat b. G+ biedt behalve deze analyse ook nog de samenstelling van U/b en b/c en de toepassing daarvan op c. Nu stel dat U ∊ B en niet U = T. Dan is een bewijs A »» T slechts voorhanden indien A een kategorie U\X of X/U bevat, maar de toepassing van deze kategorie op U is zowel onder G als G+ mogelijk. Nu stel dat U ∉ B en U = P/q, q ∊ B. Dan is een bewijs A »» T slechts voorhanden indien A een kategorie q of een kategorie q/r bevat. De toepassing van U op q is opnieuw zowel onder G als G+ mogelijk. Als A niet q maar wel q/r bevat, levert G+ in ieder geval de samenstelling van U en p/r. Dan geldt evenwel dat A »» T slechts te konstrueren valt als A ook r bevat. Maar dan biedt G uiteraard een analyse waarin eerst p/r op r wordt toegepast en vervolgens U op het resultaat q. Nu stel dat U = p/Q, Q ∉ B. Dan kan onder G+ deze kategorie nog wel een samenstelling met X/p ten deel vallen, maar daarna houdt 't op: de resulterende kategorie X/Q is niet meer naar T te brengen, omdat Q onder lineariteit onoplosbaar is. Bijgevolg geldt dan dat noch in G noch in G+ een bewijs A »» T te leveren valt. Oftewel: als A »» T in G+, dan ook A »» T in G en als A »» T niet in G+, dan ook niet A »» T in G; hetgeen bewezen moest worden. Uit het bovenstaande volgt dat bij lineariteit gewone samenstelling (d1*)-(d2*) geen voor de hand liggende optie is: toevoeging van deze regel vergroot niet het bereik van een lineair beperkte kategoriale grammatika. Er kan evenwel geen twijfel over bestaan dat Samson het bereik van een dergelijke grammatika wezenlijk vergroot. Een deelreeks <a/b a\c b> is onder G en G+ nooit herleidbaar op c, maar G verrijkt met Samson levert een éénduidige analyse. Overigens is ook in te zien dat toevoeging van allerlei ordeverhogende regels aan een lineaire grammatika zinloos is indien deze regels niet-primitieve argumentkategorieën introduceren. De Geach-regel A/B »(A/C)/(B/C) -bijvoorbeeld- levert een lineair onoplosbare grootheid (B/C) in argumentpositie, en voegt dus in het geheel niets toe aan het vermogen van een lineaire grammatika. Iets vergelijkbaars geldt ook voor een regel als associatie: (A/B)/C » A/(B/C). Indien de rechter kategorie niet gelijkwaardig is met A/B/c, c primitief, is ze lineair onoplosbaar. Bijgevolg kan de syntaxis van Kompong wellicht opgevat worden als een maximaal lineair kategoriaal systeem. | |||||||||||||||||||||||||
[pagina 80]
| |||||||||||||||||||||||||
3 LexikonDe konkrete analyse van nederlandse zinnen in het hierboven omschreven kategoriale kader krijgt z'n beslag in de toewijzing van kategorieën uit de algebra K aan elementen van het lexikon. Deze toewijzing belichaamt in feite de taalkundige grondslag van het systeem. Een wezenlijk aspekt van deze toewijzing is dat de finiete vormen de sententiële kategorieën introduceren en dus als hoofdfunktor in elke zinskonstruktie optreden. Daarnaast is kenmerkend voor Kompong dat naamwoordelijke voorwerpen en voorzetsel-voorwerpen in beginsel worden aangemerkt als linkse argumenten van het werkwoord waardoor ze geregeerd worden, en werkwoordelijke en sententiële voorwerpen als rechtse argumenten. Het lexikon wordt grotendeels voortgebracht door redundantieregels, gemarkeerde instanties van het schema (g). Deze regels kennen bijvoorbeeld aan elke finiete vorm van een werkwoord een aantal kategorieën toe die afgeleid zijn van de toewijzing(en) aan de infiniete vorm. Het is met name komputationeel van belang dat in het lexikon geen kategoriale variabelen voorkomen. Alle toewijzingen, de basistoewijzingen zowel als de afgeleide, geschieden in termen van K. | |||||||||||||||||||||||||
4 SturingGegeven een invoerreeks A, selekteert de besturingskomponent voor elk element ai van A de verzameling van lexikale kategorieën. Het cartesisch produkt over deze selektie is een verzameling van reeksen geordende paren << a1, k1>... <ai, ki... <an, kn>> waar ai het i-de lexikale element van A is en ki een willekeurig lid van de verzameling kategorieën die het lexikon aan het betreffende lexikale element heeft toegewezen. In beginsel kan elk lid van het cartesisch produkt aan de kategorieënrekening worden onderworpen. Indien dit daadwerkelijk zou gebeuren en zelfs indien alleen maar het cartesisch produkt zou worden gevormd, zou de automaat vervallen tot bruut rekengeweld onder een tijdsbeslag dat exponentioneel afhankelijk zou zijn van de lengte van de ingevoerde reeks. De besturingskomponent van Kompong omzeilt evenwel het cartesisch produkt door bij de konstruktie van elementen ervan voortdurend lokaal te toetsen of tot dan gevormde delen van leden van het produkt kompatibel zijn met de lineariteit van de syntaxis. De monotonie van de syntaxis garandeert dat (deel)reeksen die niet aan deze lokale toetsen voldoen, zonder verlies verder buiten beschouwing kunnen blijven. Die fraktie van het cartesisch produkt die daadwerkelijk wordt gevormd, ondergaat opnieuw enkele toetsen. Ook deze toetsen zijn ontleend aan de karakteristieke eigenschappen van de kategorieënrekening. Slechts die (volledige) reeksen die ook deze batterij doorstaan, wordt aangeboden aan de syntaktische komponent. Deze beslist vervolgens welke van deze benoemde reeksen tot een geslaagde analyse van de invoerreeks A leiden en levert de (volledige of partiële) ontledingen van alle aangeboden reeksen. | |||||||||||||||||||||||||
[pagina 81]
| |||||||||||||||||||||||||
4* Ontleding en toetsingEen ontleding van een benoemde reeks R0 = <<a1, k1>...<an, kn>> slaagt onder Kompong dan en slechts dan als er een n-tallige reeks <RO, Rn-1> gekonstrueerd kan worden waarbij Rj = << a'1, k'1>... <a'm, k'm >>, met 1 j (n - 1) en m = (n - j), gevormd wordt uit Rj-1 door precies één paar >> ai, ki>, <ai+1, ki+1>> in Rj-1 krachtens één van de schema's (c1) - (d2) te herleiden op een term <a', k'> waar a' de juxtapositie van ai en ai+1 voorstelt en k' het resultaat van de toepassing van het schema op het produkt ki*ki+1, en Rj in de overige termen gelijk is aan Rj-1 Dan is in elke Rj het aantal termen gelijk aan (n - j) en bevat Rn-1 dus één term waarvan het eerste lid gelijk is aan de juxtapositie a1...an en het tweede lid de kategorie van de totale reeks representeert. De monotonie van de syntaxis staat borg voor de beslisbaarheid van de konstruktie <R0, Rn-1>. De pre-syntaktische toetsen waaraan de toewijzing van lexikale kategorieën aan zinnen onderworpen worden, zijn vier in getal, te splitsen in twee ‘vliegende’ en twee ‘staande’. De vliegende toetsen zijn, als gezegd, werkzaam gedurende de vorming van het cartesisch produkt. De eenvoudigste is die welke per mogelijke lexikale kategorie beziet of het aantal linker- en/of rechterargumenten van de kategorie in overeenstemming is met de positie van het betreffende element in de reeks. Indien bijvoorbeeld het tweede element een kategorie c\b\a heeft, is deze kategorie op voorhand in die tweede positie lineair niet te bevredigen en kan ze dus als toewijzing buiten beschouwing blijven. Deze toets is weliswaar slechts bij randelementen zinvol maar uiterst effektief omdat in het nederlands zich juist aan het begin en einde van zinnen komplexe operatoren plegen op te houden. In het voorbeeld dat in de volgende paragraaf wordt besproken, is deze toets verantwoordelijk voor een reduktie van de invoer in de syntaktische komponent met ca. 75%. De tweede vliegende toets beziet per lexikale kategorie van het i-de element of te bevredigen rechter argumenten van deze kategorie nog ‘vrij’ voorkomen in al gevormde toewijzingen over de elementen i+1 t/m n. Dat hier slechts de rechter argumenten in het geding zijn, hangt samen met de vanachter-naar-voor-waartse richting van de opbouw van het cartesisch produkt. Deze richting is gekozen als tribuut aan het rechts-vertakkend karakter van de nederlandse zinsbouw. De werking van de toets laat zich als volgt verhelderen. Stel dat over een reeks met n elementen onder meer al de toewijzing <b\a/cc/d d> aan de laatste drie elementen is opgebouwd. Stel voorts dat het n-4de element de lexikale kategorieën e/a en e/d kent. De kategorie e/d heeft een rechter argument d nodig, maar de enige kandidaat in de staart-toewijzing is al ‘bezet’ door de voorlaatste kategorie. De kategorie e/d is derhalve niet te bevredigen en hoeft niet aan deze staartreeks te worden toegevoegd. De kategorie e/a daarentegen is in de onderhavige staartreeks in beginsel te bevredigen en blijft als enige kandidaat over. Deze toets impliceert geen ontleding maar slechts kontrole van een met de staartreeks geassocieerde, haast ongestruktureerde opslag van ‘vrije’ doelkategorieën. Alhoewel éénzijdig van aard, is deze toets eveneens bijzonder effektief; in het nog te bespreken voorbeeld is de toets goed voor een reduktie van het aanbod met een faktor 4000. De twee ‘staande’ toetsen werken op volledige toewijzingen, i.e. die leden van het cartesisch produkt die de vliegende toetsing hebben overleefd. De ene | |||||||||||||||||||||||||
[pagina 82]
| |||||||||||||||||||||||||
toets kontroleert of de linker-argumenten van toegewezen kategorieën in beginsel bevredigbaar zijn, eveneens door inspektie van een ongestruktureerde opslag van doelkategorieën. De andere staande toets gaat na of de som van de ordes van een reeks toewijzingen gelijk is het aantal elementen van de reeks min één; alleen als dit zo is, kan de toewijzing slagen onder de gegeven lineaire beperkingen. Deze beide toetsen reduceren in het volgende voorbeeld de selektie uit het cartesisch produkt met een faktor 95. | |||||||||||||||||||||||||
5 WerkingDe procedure die in de vorige paragraaf is geschetst, laat zich illustreren aan de hand van de verwerking van de invoerreeks
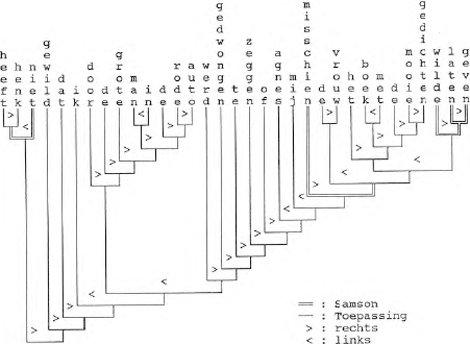 | |||||||||||||||||||||||||
[pagina 83]
| |||||||||||||||||||||||||
van de nieuwe toevoer uit het lexikon. Op geen moment zijn méér dan 394 (deel)reeksen in behandeling, bij een gemiddelde van 66,25. Van de 192 reeksen die de vliegende toetsing doorstaan, worden er slechts 2 aan de syntaktische komponent voorgelegd. Deze voert hiervan één tot een geslaagde analyse van de zin onder toekenning van de struktuur op p.82 (met weglating van kategoriale etiketten). Voor deze hele procedure - van inlezen tot en met ontleding - heeft het prototype van Kompong op een rekenapparaat met 80386-processor circa acht sekonden nodig. | |||||||||||||||||||||||||
5* RekentijdDe rekentijd van Kompong is slechts in een te verwaarlozen mate afhankelijk van de omvang van het lexikon. De tijd die de automaat nodig heeft om te beslissen of een zin grammaticaal en te struktureren is, wordt in hoofdzaak bepaald door een vrij ingewikkelde samenhang tussen de mate van lexikale polykategorialiteit van elementen in de reeks en de aard van deze polykategorialiteit. Deze interaktie bepaalt het aantal te behandelen (deel)reeksen en dit aantal bepaalt haast lineair de rekentijd. Een sterk polykategoriaal element als wilde kan in bepaalde omgevingen het aantal kansrijke reeksen sterk verminderen, in andere omgevingen kan het (tijdelijk) een ware uitzaaiing van opties te weeg brengen. Heldere verbanden tussen rekentijd en lengte van de aangeboden reeks zijn bijgevolg moeilijk aan te geven. Voor ongrammatikale, aselect gekozen reeksen over het lexikon tot een lengte van honderdnegentig elementen heeft Kompong vrijwel konstant twee à drie sekonden nodig: de dynamische toetsing reduceert hier het aantal opties al snel tot nul. Bij een verzameling van grammatikale reeksen werden diffuse waarnemingen gedaan. Automatische ‘curve-fitting’ over de rekentijden (gemeten op een 80286-machine) bij een veertigtal willekeurige zinnen, in lengte variërend van 5 tot 34 elementen, leverde op dat de gemeten tijden relatief het best korreleerden met een lineair verband in de orde van (L - 4) sekonden rekentijd bij zinslengte L. Iets minder scoorde een polynoom in L met koëfficiënten > 10-3 en wisselende tekens. Het slechts korreleerden verbanden met L positief in de exponent, zelfs als de konstanten zeer klein gekozen werden. De korrelatie was overigens in geen geval indrukwekkend. | |||||||||||||||||||||||||
6 SemantiekHet prototype van de ontleder is niet voorzien van een semantische komponent. De kategorialiteit van het systeem garandeert evenwel dat de syntaxis puntsgewijs afbeeldbaar is op een semantische algebra. In 6* wordt een door Van Benthem uitgewerkte omzetting geparafrazeerd. Sprekender is de vraag of een syntaxis als de hier gehanteerde, die min of meer traditionele strukturen toekent, voldoende grondslag biedt om alle interpretaties van een gegeven zin voort te brengen. De kategoriale systemen die momenteel in zwang zijn, leveren beduidend rijker gestoffeerde analyses, juist met het oog op de semantische substraten. Schrijver dezes is echter niet overtuigd van de noodzaak om het verband tussen vorm en betekenis als één-op-één of zelfs veel-op-één gestalte te geven. Laten we eens aannemen dat | |||||||||||||||||||||||||
[pagina 84]
| |||||||||||||||||||||||||
met elke syntaktische analyse een veld van onderling samenhangende, partieel geordende interpretaties geassocieerd kan worden. De syntaktische analyse markeert dan één of meerdere van deze interpretaties. Uit de ordening in het veld worden vervolgens de overige kompatibele interpretaties afgeleid. Een dergelijke benadering vertoont overeenkomsten met de logische-vorm-ideologie van regeer-en-bind-theorieën, en met het meetkundige inzicht dat ruimtes door een gering aantal punten volledig bepaald zijn. De vraag of de klasse van interpretaties van een zin zich daadwerkelijk zo laat beschrijven, waag ik overigens niet te beantwoorden. | |||||||||||||||||||||||||
6* Lambda-interpretatieDe volgende omzettingen van de regels (c1) - (d2) in een getypte substitutie-rekening met lambda-operator (‘£’) bieden een stramien voor de interpretatie van een (lineaire) kategoriale syntaxis. Zij @ een afbeelding van (syntaktische) kategorieën op (semantische) typen waarvoor geldt:
Het type van een samengestelde kategorie Y/X of X\Y is dus een klasse van funkties van het type van X naar het type van Y. Zij voorts, voor elke X ∊ K, #x een vertaling van uitdrukkingen van de kategorie X in uitdrukkingen van het type @X en #X(a) = a. De afbeelding σ van benoemde reeksen op elementen van de typenrekening verloopt dan volgens het patroon
Vervolgens zijn kategoriale toepassing (c1) en (c2) en kategoriale samenstelling (d1) en (d2) te vertalen als respektievelijk funktionele toepassing en funktionele samenstelling:
Een - bijvoorbeeld - modeltheoretische interpretatie voor de lambda-rekening is dan te beschouwen als een interpretatie voor kategoriaal ontlede reeksen.
Prof. H.C. van Hall Instituut Postbus 17, 9700 AA Groningen | |||||||||||||||||||||||||
[pagina 85]
| |||||||||||||||||||||||||
Bibliografie
|

