Tabu. Jaargang 16

[p. 69]

Vendler-klassen moeten worden genegeerd
H.J. Verkuyl^*

1. Inleiding.

In 1957 publiceerde de taalfilosoof Zeno Vendler een beroemd geworden artikel ‘Verbs and Times’. Voor taalkundigen werkend op het terrein van de aspecten (Aktionsarten), vervult Vendler een functie vergelijkbaar met die van Reichenbach met betrekking tot het tempus: een obligaat vertrekpunt voor de theorievorming.

Ook in Groningen heeft Vendler gezag (cf. Vet 1980, De Vuyst 1983, Ter Meulen 1983; 1984 en Hoeksema 1984). De laatste twee gieten zijn voorstellen in formalismes van de zogeheten theorie der gegeneraliseerde kwantoren (Zwarts 1981;1983; Van Benthem 1983). Mijn bedoeling is de voorstellen van Ter Meulen en Hoeksema kritisch te bekijken¹. Hiermee voldoe ik wat Hoeksema betreft alsnog aan een in 1984 helaas niet gerealiseerde verplichting aan de vertrekkende ordinarius om te opponeren tegen een van zijn promovendi.

Ik zal heel kort uiteenzetten wat Vendler-klassen zijn. Dan zal ik schetsen waarom ik ze in Verkuyl (1972) in tweeën opbrak. Zo verklaar ik mijn verbazing over de hardnekkigheid waarmee men ze telkens weer uit de kast haalt. Naar mijn overtuiging dient het bestaan ervan voor de structurele semantiek ontkend te worden. Dit is blijkbaar niet de mening van Ter Meulen en Hoeksema. Ter Meulen doet een poging om de vier klassen hiërarchisch ten opzichte van elkaar te ordenen in termen van gegeneraliseerde kwantoren. Hoeksema probeert de vier klassen kruisclassificerend te ordenen. Beide voorstellen worden verworpen ten gunste van een soortgelijke analyse die een precisering inhoudt van mijn tweedeling uit 1972. Bij de verwerping van beide voorstellen is een belangrijk argument dat zinsnegatie de verschillen tussen de vier klassen elimineert. De titel van dit artikel is derhalve met opzet dubbelzinnig.

* Ik dank hierbij Johan van Benthem, Els Blokland, Franciska de Jong, Harriët Kwekkeboom, Johan Lock, Alice ter Meulen, Henk Rhebergen, Harry Sitters en Frans Zwarts voor commentaar op een eerdere versie.

1 De Vuyst geeft geen formele karakterisering, maar zijn omschrijvingen brengen hem dicht in de buurt van Ter Meulen.

2. Vendlers classificatie.

Ik beperk me tot een uiterst beknopte weergave van Vendlers voorstel. Hij onderscheidt vier handelingscategorieën: Toestanden(States), Activiteiten (Activities), Eindpuntgebeurens (Accomplishments) en Puntgebeurens (Achievements). Hij verbindt daarmee vier zogeheten tijdschema's (1967:106):

(1)	a	Toestand: ‘A hield van B van t1 tot t2’ betekent dat A op elk tijdstip tussen t1 en t2 van B hield.
	b	Activiteit: ‘A liep op t’ betekent dat t op een interval ligt gedurende hetwelk A liep.
	c	Eindpuntgebeuren: ‘A at een boterham op t’ betekent dat t op het interval ligt tijdens hetwelk A die boterham at.
	d	Puntgebeuren: ‘A won de race tussen t1 en t2’ betekent dat het tijdstip waarop A de race won tussen t1 en t2 ligt.

Dit schema kan in twee oppositieparen worden vertaald. De eerste is de oppositie [+Interval] vs. [-Interval]: in (1b) en (1c) loopt t over een interval, in (1a) en (1d) wordt gesproken over ogenblik en tijdstip. De tweede tegenstelling is die tussen [+Bepaald] vs. [-Bepaald]; in (1c) en (1d) wordt gesproken over het interval en het tijdstip, in (1a) en (1b) over elk ogenblik en een interval. Een redelijke interpretatie van [-Bepaald] lijkt: ‘er is niet sprake van een uniek punt of interval’². Beide opposities samen genomen leveren het volgende schema op:

2 De hier gegeven interpretatie wordt gesteund door het op (1) volgende commentaar van Vendler zelf: ‘This shows that the concept of activities calls for periods of time that are not unique or definite. Accomplishments, on the other hand, imply the notion of unique and definite time periods. In an analogous way, while achievements involve unique and definite time instants, states involve time instants in an indefinite and nonunique sense’ (1967: 106/107).

[p. 70]

(2)		A -Interval	B +Interval
	α: -Bepaald	Toestand	Activiteit
	β: +Bepaald	Puntgebeuren	Eindpuntgebeuren

In het Nederlands zijn criteria voorhanden die het onafhankelijk bestaan van elk der vier klassen zouden motiveren^3.. Ik bespreek er enkele van.

Het voortgangscriterium vooronderstelt [+Interval]. Het idee is dat men het gebeuren als het ware van binnen uit kan presenteren, wat niet kan bij [-Interval], omdat de ‘ruimte daarvoor’ ontbreekt:

(3)	a	??Myra was aan het sterfelijk zijn (Aα)
	b	Judith was aan het wandelen (Bα)
	c	Jessica was bezig een boterham te eten (Bβ)
	d	?Patty was bezig te winnen (Aβ)

Een vervelende complicatie voor het criterium is dat (3d) eigenlijk heel goed is. Het is niet in te zien waarom men het criterium zou moeten verdedigen met de opmerking dat (3d) naar de toekomst verwijst en de andere niet; ook (3c) verwijst naar een situatie waarin men gerekend vanaf een waarnemingspunt ‘op weg is naar’ een eindpunt in de toekomst ervan. Hiertegenover staat dat (3a) wel degelijk problematisch is, al zijn er gevallen van De acrobaat is nu aan het hangen (=doet hangoefeningen) tegenover ??De klok is nu aan het hangen. In elk geval behandelt het criterium ten onrechte (a) en (d) beide als A-gevallen.

Het uitwisselbaarheidscriterium moet Puntgebeurens scheiden van de andere klassen. Het zegt dat Puntgebeurens gekenmerkt worden door het feit dat als men op een bepaald ogenblik in het Praesens zegt Nu wint Patty, men ook had kunnen zeggen Nu heeft Patty gewonnen, en andersom. Bij de andere klassen is dat niet zo:

(4)	a	Myra haat wanorde ↮ Myra heeft wanorde gehaat
	b	Judith wandelt ↮ Judith heeft gewandeld
	c	Jessica at een boterham ↮ Jessica heeft een boterham gegeten
	d	Patty wint ↔ Patty heeft gewonnen

Het is geen sterk criterium, getuige:

(4)	a′	Myra haat tot nu toe elke vorm van wanorde ↔ Myra heeft tot nu toe elke vorm van wanorde gehaat
	b′	Judith wandelt nu al een uur met Lisa ↔ Judith heeft nu al een uur met Lisa gewandeld
	d′	Myra wint vandaag ↮ Myra heeft vandaag gewonnen

Als (4d) uitwisselbaarheid garandeert, dan zeker (4b′) en ook wel (4a′). Bovendien gaat veel van de aantrekkelijkheid van het criterium verloren doordat het niet van toepassing is in gevallen als (4d′).

Het iteratiecriterium is het meest bekend. Het ligt ten grondslag aan het aloude verschil tussen imperfectief, duratief of atelisch aspect enerzijds en het perfectief, nonduratief of telisch aspect anderzijds. Het levert de tweedeling α vs. β in (2) op (x indiceert blokkering van de enkelvoudige lezing).

(5)	a	Myra houdt al jarenlang van hockey.
	b	Judith wandelde urenlang met haar hondje.
	c	xJessica at de hele dag door een boterham.

3. Voor het Engels o.a. Dowty (1979), Mourelatos (1981), Carlson (1981).

[p. 71]

d	xPatty won de hele dag.

De zinnen (5c) en (5d) kunnen niet worden geïnterpreteerd als betrekking hebbend op een enkelvoudig gebeuren: er is een zekere dwang om ze te interpreteren als iteratief: de handeling ‘een boterham eten’ resp. ‘winnen’ wordt op een nogal mechanische wijze herhaald.

Het conjunctiecriterium houdt in dat nevengeschikte tijdsbepalingen hun eigen domeinwaarde blijven behouden als ze voorkomen met zinnen die betrekking hebben op Aβ en Bβ. Het brengt dezelfde scheiding aan tussen α en β in (2) als het iteratiecriterium, maar op iets andere wijze:

(6)	a	Myra was gisteren en eergisteren ziek.
	b	Judith wandelde gisteren en eergisteren.
	c	xJessica at gisteren en eergisteren drie boterhammen.
	d	xPatty won gisteren en eergisteren.

Het criterium onderscheidt Eindpuntgebeurens en Puntgebeurens doordat er in (6c) en (6d) sprake is van respectievelijk zes boterhammen die gegeten zijn en van twee overwinningen, gedistribueerd over twee intervallen die aaneensluitend zijn. In (6a) en (6b) kan het ziek zijn en het wandelen continu voor de somtotaal van gisteren en eergisteren gelden.

Er zijn nog andere criteria die een tweedeling α vs. β tot stand brengen, maar ik volsta met de hierboven genoemde. Het bestaan van een Vendler-categorie Puntgebeurens lijkt primair te zijn gemotiveerd door kennis van de wereld. Als ontploffingen, tikken, botsingen Puntgebeurens zijn, dan zijn ze dat omdat we ze ‘normaal’ als zodanig ervaren. Maar sprekend over ontploffingen, botsingen, etc. kan men ze representeren als duurhebbend, zodat ze als Eindpuntgebeurens worden voorgesteld. Bij een vertraagde filmopname van de lancering van de Challenger kan men heel goed zeggen: Kijk, nu is-ie bezig te ontploffen. En andersom, Eindpuntgebeurens kunnen worden gecomprimeerd: een reus die een boterham eet, verricht een Puntgebeuren^4.. De relevante vraag is dan ook of er linguïstisch gezien mogelijkheden zijn om Puntgebeurens en Eindpuntgebeurens van elkaar te onderscheiden. Het uitwisselbaarheidscriterium en het voortgangscriterium lijken me niet voldoende om een categorie, Momentaan, te rechtvaardigen^5..

Samenvattend constateer ik dat het voortgangscriterium ten onrechte Puntgebeurens uitsluit van een dynamische presentatie ervan, en dat het uitwisselbaarheidscriterium nogal dubieus is. De andere twee zijn wel redelijk bruikbaar te noemen gezien het feit dat het onderscheid tussen duratief aspect en terminatief aspect dat ze oproepen, linguïstisch gezien een vaste grond heeft. Opgemerkt zij dat Vendler een lexicale classificatie op het oog had en dat het derhalve aan degenen die de Vendler-klassen in de linguïstische theorie hanteren, is om aan te tonen dat de classificatie vanuit een structureel oogpunt van belang is.

Mij bewust zijnde van het feit dat de Vendler-klassen ontologische categorieën zijn en dat Vendler als lexicaal semanticus (dus als filosoof) opereerde, heb ik in Verkuyl (1972) zijn classificatie op structureel niveau vorm gegeven. Dat kon door een specifieke interpretatie te geven aan de door Vendler gehanteerde parameters. Het kenmerk [+Interval] heb ik geïnterpreteerd in termen van een kenmerk [+ADD TO], dat lexicaal aan bepaalde werkwoorden toekomt, nl. aan die welke een dynamiek, een voortgang in de tijd uitdrukken^6.. De intuïtieve karakterisering van dit kenmerk is dat het de produktie van intervallen aangeeft. Het werkwoord haten is [-ADD TO], omdat het geen voortgang in de tijd uitdrukt, in tegenstelling tot wandelen, eten, spelen, etc., die als [+ADD TO] worden gekenmerkt^7.. Met andere woorden, Vendlers [+Interval] wordt geïnterpreteerd als het toevoegen van nieuwe delen tijd aan een reeds afgelegd interval (1972:88-97). Daarmee wordt aan de analyse van het aspect een constructieve (zo men wil, combinatorische) benaderingswijze ten grondslag gelegd, een benaderingswijze die past binnen de intervalsemantiek (cf. Dowty 1979; Bennett and Partee 1978). De tegenstelling [±ADD

4. Van belang is in te zien dat het eindpunt van gebeurens vaak conventioneel is vastgelegd, maar dat het gebeuren ‘er om heen’ ook meetelt. Promoveren bijvoorbeeld is typisch een puntgebeuren: van het ene moment op het andere wordt men doctor, maar toch zal men promoveren vaak ervaren als een eindpuntgebeuren binnen hetwelk het ‘omslagpunt’ wordt gelokaliseerd. Theoretisch is een grensovergang een puntgebeuren, maar er zijn ook goede argumenten om te spreken over een eindpuntgebeuren.

5. Dit in tegenstelling tot Verkuyl (1972) waar momentaan wordt onderscheiden van terminatief, zij het binnen een categorie die voor aspecten van belang is, nl. de nonduratieve. Door het laten vallen van het onderscheid kan ik nu de wat onhandige (want negatiebevattende) term ‘nonduratief’ vervangen door ‘terminatief’.

6. Naar mijn mening is er voor wat betreft de analyse van aspecten niet een wezenlijk onderscheid tussen een kenmerk [+ADD TO] en een Gruberiaanse categorie ADD TO, of een kenmerk [-Specified Quantity of X] en een categorie UNSPECIFIED QUANTITY OF X. Beide soorten specificaties zijn afkortingen en vereisen een precieze interpretatie (cf. Verkuyl 1985a).

7. Dit onderscheid lijkt sterk op dat tussen ‘dynamicity’ en ‘stativity’ in Timberlake (1982) en is ook terug te vinden in Carlson (1981), zij het bij beiden in formeel niet precies uitgewerkte vorm.

[p. 72]

TO] scheidt Activiteiten en (Eind)puntgebeurens van Toestanden.

De tegenstelling α vs. β krijgt in Verkuyl (1972) vorm door de tegenstelling [±SQA]. Als en NP [+SQA] is, dan heeft de NP betrekking op een eindige hoeveelheid van A en is dus (in principe) bepaald^8.. Het terminatieve aspect (β) wordt geconstrueerd door de combinatie van een semantisch element [+ADD TO] dat lexicaal geassocieerd is met werkwoorden die een voortgang in de tijd uitdrukken, en van het semantische element [+SQA]. Afwezigheid van een NP houdt [-SQA] in, terwijl sommige NPs ook [-SQA] zijn doordat ze door de aard van de determinator of door negatie geen eindigheidsinformatie kunnen uitdrukken zoals zichtbaar wordt in :

(7)	a	Zij verkocht jarenlang veters.
	b	Zij leent al jaren geld van haar vader.
(8)	a	Jessica at de hele dag geen boterham.
	b	Patty won maandenlang niet.

In paragraaf 6 ga ik nader in op de werking van het constructiemechanisme dat β van α scheidt. Daarbij is van belang op te merken dat (8a) en (8b) bijzondere gevallen zijn, die niet goed door (2) worden bestreken: negatie maakt van β-constructies α-constructies.

8. Preciezer: Als NP = Det + N en ∥N∥ = A, dan is NP gekenmerkt door [+SQA] dan en slecht dan als | A | > 0 en als het universum U (A ⊆ U) eindig is. (∥N∥ is te lezen als ‘de interpretatie van N’(in U) en | | als ‘de cardinaliteit van’).

3.Gegeneraliseerde kwantoren

In de afgelopen jaren is de modeltheoretische semantiek in toenemende mate gemeengoed geworden in de taalkunde. In de laatste jaren is daardoor betekenistoekenning in termen van structurering van een interpretatiedomein voorwerp van veel studie. De algebraïsering die dit heeft opgeleverd, is zichtbaar in de benadering van kwantificatie: NPs worden gezien als collecties deelverzamelingen met een bepaalde structuur die bepaald wordt door de wijze waarop aanwezige deelverzamelingen zich tot elkaar verhouden. Ik veronderstel Zwarts (1981) bekend, maar terwille van de leesbaarheid geef ik een concreet model met enkele kwantoren, zodat de karakterisering van de Vendler-klassen in Ter Meulen (1983;1984) en Hoeksema (1984) daarmee kan worden vergeleken.

We nemen aan dat er een model M₄ = <E, ∥ ∥ > is, waarbij het interpretatiedomein E = {a,b,c,d} en waarbij ∥ ∥ de interpretatiefunctie is die aan uitdrukkingen uit het Nederlands entiteiten uit E toevoegt. We maken nu de volgende afspraken (|α| = cardinaliteit van α):

(9)		∥fietsen∥ = {a,b,c,}; ∥gestolen worden ∥ = {b,c,d}; ∥auto∥ = {d}
(10)	a	∥enkele N∥ = {X ⊆ E| |X ∩ ∥N∥ | ≥ 2}
	b	∥geen N∥ = {X ⊆ E| X ∩ ∥N∥ = ø}
	c	∥de N (plur)∥ = {X ⊆ E| X ∩ ∥N∥ = ∥N∥ & | ∥N∥ | ≥ 2}
	d	∥de N(sg)∥ = {X ⊆ E| X ∩ ∥N∥ = ∥N∥ & | ∥N∥ | = 1}
	e	∥precies n N∥ = {X ⊆ E| |X ∩ ∥N∥ | = n}

In M₄ krijgen de kwantoren, in (10) gedefinieerd voor alle mogelijke modellen, de volgende interpretatie:

(11)	a	∥enkele fietsen∥= {{a,b}, {a,c}, {b,c}, {a,b,c,}, {a,c,d}, {a,b,d}, {b,c,d}, {a,b,c,d}}
	b	∥geen auto∥ = {ø, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}}
	c	∥de fietsen∥ = {{a,b,c}, {a,b,c,d}}
	d	∥de auto∥ = {{d}, {a,d}, {b,d}, {c,d}, {a,b,d}, {a,c,d}, {b,c,d}, {a,b,c,d}}
	e	∥precies één fiets∥ = {{a}, {b}, {c}, {a,d}, {b,d}, {c,d}}

[p. 73]

De kwantoren in (11) vertonen verschillende soorten structuur. Zo zijn (11a), (11c) en (11d) monotone stijgers. De door de definities in (10) toegelaten deel-verzamelingen van E in een monotoon stijgende kwantor voldoen aan de volgende twee equivalente condities, die voor elk model gelden:

(12)	a	∀X,Y ⊆ E, X ∩ Y ε Q → (X Q & Y ε Q)
	b	∀X,Y ⊆ E, (X ε Q & X ⊆ Y) → Y ε Q

De kwantor in (11b) daarentegen is een monotone daler:

(13)	a	∀X,Y ⊆ E, X ∩ Y ε Q →(X µ Q & Y ε Q)
	b	∀X,Y ⊆ E, X ε Q & Y ⊆ X → Y ε Q

Andere monotone dalers zijn: niet alle N, weinig N, geen van de N, etc.

Als een kwantor monotoon dalend is, dan heeft hij ook de volgende eigenschap (Zwarts 1981:63):

(14)	∀X,Y ⊆ E, (X ε Q & Y ε Q) → X ∩ Y ε Q

Deze eigenschap geldt dus wel voor (11b) maar niet voor (11a). Maar zij geldt ook voor (11c), terwijl deze een monotone stijger is. Dat is gemakkelijk te verklaren. De kwantor in (11c) is een filter, die wordt gekarakteriseerd doordat hij zowel eigenschap (12a) als (14) heeft, hetgeen resulteert in (15):

(15)	∀X,Y ⊆ E, (X ε Q & Y ε Q) ↔ X ∩ Y ε Q^9.

De kwantor in (11d) is ook een filter. Naast (15) heeft hij een eigenschap die hem tot ultrafilter maakt nl. voor alle X ε Q geldt dat het complement van X binnen E niet ook lid van de kwantor mag zijn. De kwantor in (11a) is geen filter, en dus ook geen ultrafilter.

Tenslotte, hoewel (11e) niet de structuur vertoont van monotone stijgers, zijn er modellen denkbaar waarin dit wel het geval is. Stel dat E = {a, d}. Dan is (11e) monotoon stijgend, omdat (11e′) zou gelden:

(11)e′

∥precies één fiets∥ = {{a}, {a,d}}

Dit maakt ∥precies één N∥ echter niet tot een monotone kwantor: de structuur van de kwantor verschilt in modellen, terwijl de eigenschap van monotone stijging, modelonafhankelijk dient te zijn (cf. Zwarts 1981: 65).

Het doet er weinig toe welke ontologische status de elementen van de verzamelingen in de kwantor hebben: a, b, c, en d zijn hier concrete entiteiten, maar als men processen of intervallen op het oog heeft, gelden alle structurerende principes die ik hier heb geïllustreerd (zie echter Van Benthem 1986). Van belang is dat de eigenschappen van tal van kwantorstructuren in talrijke linguïstische verschijnselen zichtbaar zijn te maken, zoals Zwarts (1981) duidelijk maakt (cf. Barwise and Cooper 1981; De Jong en Verkuyl 1985).

9. In Zwarts (1986: 302) worden structuren die voldoen aan (15) quasi-filters genoemd. Filter zijn quasi-filters met de additionele eigenschap X ∪ X∃ ε Q, d.w.z. de som van X en zijn complement moet ook lid zijn van de kwantor (1986: 325). Dat is bijvoorbeeld het geval in (11c) waar X={a,b,c}, X∃={d); {a,b,c}∪{d} = {a,b,c,d] en deze verzameling is lid van Q. Voor mijn betoog maakt deze definitieverandering geen enkel verschil.

4. Een Vendler-hiërarchie.

De karakterisering van de Vendler-klassen in Ter Meulen (1983;1984) moet in termen van de theorie van gegeneraliseerde kwantoren worden begrepen, zij het dat haar karakterisering van VPs niet zo direct van de huid van de taal kan worden afgelezen als bij NP-kwantificatie. Gezegd moet worden dat het idee van een hiërarchie nogal verrassend is: immmers, het is niet eenvoudig de tijdschemata in (1) zo te interpreteren dat ze in een inclusierelatie tot elkaar staan.

Ter Meulens basiselementen zijn processen P. Een proces wordt door haar opgevat als een verzameling. Een P maakt deel uit van P, een nietlege verzameling van

[p. 74]

processen, die dus een verzameling van verzamelingen is. Uiteraard wordt de structurering van deelverzamelingen van P uitgedrukt in temporele relaties, zoals strikt voorafgaan (≤) en overlap, maar beknoptheidshalve zal ik Ter Meulens definities weergeven met behulp van de temporeel neutrale Boolese relaties (∩, ∪, ⊆). Om de vergelijking met (12) - (15) te vergemakkelijken vervang ik haar variabele X (X ⊆ P) door de variabele Q.

De Vendler-hiërarchie wordt als volgt opgezet: Toestanden zijn te karakteriseren met conditie (16a), Activiteiten met condities (16a)+(16b), Eindpuntgebeurens met (16a)+(16b)+(16c), en Puntgebeurens met de condities (16a) - (16d). Het zijn condities op Q. Voor alle X,Y ε P en voor alle collecties Q ≤ P geldt:

(16)	a	(X ε Q & X ⊆ Y) → Y ε Q
	b	(X ε Q & X ε Q) → ∃ Z ε Q (Z ⊆ X & Z ⊆ Y)
	c	X = X1 ∪ X2 → (X1 ε Q ∨ X2 ε Q)
	d	∃X ε Q (Y ⊆ X → Y ε Q)

Conditie (16a) is identiek met (12b) en derhalve equivalent met (12a); (16b) zegt dat voor elke twee deelverzamelingen van E die lid van Q zijn er een Z uit Q is die zowel deel uitmaakt van X als van Y. Dit is niet equivalent met de eigenschap (14), zoals ik zal laten zien. In (16c) moet ‘∨’ exclusief worden genomen (d.w.z. als òf-òf); bij de decompositie van X in X₁ en X₂ wordt gestipuleerd dat de drie klassen ongelijk zijn. Conditie (16d) is een existentiële instantiatie van (13b). Ik zal nu kort enkele bezwaren aanvoeren tegen het voorstel van Ter Meulen.

Ter Meulen karakteriseert Toestanden in termen van monotone stijging omdat toestanden volgens haar worden gekarakteriseerd door het volgende: ‘if some state holds in a part of the temporal domain P₁, it continues to hold in P₂ that has P₁ as part’ (1983: 180). Dus als ik ziek ben op woensdag, dan ben ik in de week waarin die woensdag valt ziek. Maar als ik op woensdag ziek ben, ben ik dan de hele week waarin die woensdag valt ziek? Nee. Toch bevat die week de woensdag als deel^10.. Merk ook op dat uit Marie was op woensdag niet ziek niet volgt Marie was in die week niet ziek, terwijl hier toch sprake is van twee toestanden. Toestanden geven volgens Ter Meulen geen informatie over delen van processen in Q ‘and hence do not express any changes in the world’ (1984:263). Een eenvoudig tegenargument is dat als dit zo is, dit natuurlijk ook zou moeten gelden voor monotone daling zoals gedefinieerd in (13b)^11..

Ten aanzien van Activiteiten geldt de volgende motivering: ‘the semantically relevant property of activities like eating or reading is that part of them are also an activity of eating or reading respectively’ (1983:181); (16a) en (16b) sluiten gaten uit tussen processen X en garanderen een continue interne structuur door de eis dat ‘any divisible event must contain the process that is a common part for each two processes in the event’ (1983:182;1984:264).

Het is niet goed in te zien waarom aan Activiteiten de structuur moet worden toegegekend die in M₄ toekomt aan kwantoren zoals ∥enkele N∥. Neem in M₄ een structuur Q_A = {{b},{a,b},{a,b,c},{a,b,c,d}}. Deze is monotoon stijgend, zodat voldaan wordt aan (16a), d.w.z. aan (12b). Q_A voldoet ook aan (16b) want voor elk van de tweetallen X en Y uit Q_A geldt dat er een Z ε Q_A is die zowel deelverzameling van X als van Y is, nl. {b}. Merk op dat de zgn. eigenschap van geslotenheid onder (eindige) doorsnede, d.w.z.(14), niet opgaat voor Q_A, d.w.z. Q_A is niet gekarakteriseerd door de conjunctie van (12b) en (14) die van Q_A een filter zouden maken. In dat geval zou {b,c} een element moeten zijn van Q_A. Met andere woorden, Activiteiten hebben bij Ter Meulen geen filterstructuur gedefinieerd door (15), maar een ‘slappere’ structuur ongeveer overeenkomend met die van zwakke stijgers (cf. Zwarts 1981:84). Maar waarom neemt Ter Meulen deze ‘slappe’ vorm van homogeniteit? Noch ontologisch noch linguïstisch wordt dit gemotiveerd^12..

De Eindpuntgebeurens worden uit de Activiteiten gevormd door toevoegingen van

10. Ter Meulen (1984: 267) zegt dat John was ill last week = John was ill on Wednesday last week een geldige inferentie is. Maar in dat geval moet last week een duurbepaling zijn, want als het wordt geïnterpreteerd als een tijdens-bepaling dan kan John was ill last week heel goed betekenen dat hij ziek was op vrijdag en dan geldt de inferentie niet. Maar wil de inferentie uit de geciteerde passage (1983: 80) geldig zijn, dan moet de tijdsbepaling P₁ een tijdens-bepaling zijn.

11. Het is opmerkelijk dat als Galton (1984: 24) Toestanden karakteriseert, hij dat doet in termen van monotone daling (ook al formaliseert hij zijn definitie niet): ‘A State is dissective in the sense that any stretch of time in which a particular state obtains can be broken down into substretches in each of which that state obtains’.

12. Ter Meulen (1984: 269) probeert met enkele inferenties aannemelijk te maken dat (16a) en (16b) in het geding zijn bij Activiteiten: uit de hele nacht schaakspelen volgt enige tijd spelen en uit een kar door de stad duwen volgt een kar door een deel van de stad duwen, maar deze inferenties zeggen mij als vorm van linguïstische evidentie niets. Integendeel, bij monotone stijging zou men eerder een andere inferentierichting verwachten.

[p. 75]

(16c). Deze eis zorgt er, met (16a) en (16b), voor gegeven zeg {a,b,c,d} ε Q, dat als {a,b} ε Q, {c,d} ∉ Q, en omgekeerd als {c,d} ε Q, {a,b} ∉ Q. Vervelend is nu dat Q_A ook door (16c) wordt toegelaten. Daarentegen valt (11a) af. Conditie (16c) houdt dus wel een verscherping in, maar het resultaat is nog niet (15). Naast Q_A worden kwantoren als ∥de (plur) N∥, ∥alle N∥ etc. door(16a) - (16c) bestreken. Ter Meulen vindt deze ‘ruwe’ structuur een deugd. Een VP gedefinieerd door (16a) - (16c) is ‘coarse-grained’: ‘the accomplishment of writing a book may be divided into a finer-grained event of writing a chapter, a page, etc’ (1983:184), dit tegenover Puntgebeurens. Linguïstisch is er naar mijn mening echter geen enkel verschil tussen een boek schrijven, een essay schrijven, een brief schrijven en een zin schrijven en een voord schrijven, en een punt schrijven, al hebben we enige moeite om een situatie te bedenken waarin dat laatste het geval is (maar denk aan een Chinese schrijfschool).

Conditie (16d) zorgt dat Puntgebeurens worden opgevat als echte ultrafilters door de toevoeging van een existentiële uitgave van de eigenschap van monotone daling (12a). Ter Meulen zegt: ‘The set generated by such a process can be considered a semantic atom in the model based on the process structure’ (1984:264).

Tenslotte, een ernstig probleem lijkt mij dat, zoals gezegd, negatie een toestand uitdrukt in alle Vendler-klassen, d.w.z. het verschil tussen de Vendiler-klassen opheft. De zinnen Myra houdt niet van limonade, Judith heeft niet gewandeld, Jessica at geen enkel chocolaatje en Patty heeft geen enkele keer gewonnen geven alle een toestand aan, maar de eerste is de negatie van een Toestand, de tweede van een Activiteit, de derde van een Eindpuntgebeuren, en de vierde van een Puntgebeuren. Men zou dus mogen verwachten dat negatie bij Ter Meulen toevoert naar Toestanden, m.a.w. dat de negatie opererend op (16a) + (16c) toevoert naar (16a), de negatie opererend op (16a) - (16c) ook, en de negatie die opereert op (16a) - (16d) ook. Maar dat gebeurt niet. Het lijkt mij een serieus bezwaar tegen de hiërarchische opzet.

Mijn conclusie ten aanzien van Ter Meulens hiërarchie is: (i) dat de gekozen formaliseringen in (16) op zijn minst implausibel zijn als uitwerkingen van verbale karakteriseringen van de Vendler-klassen zoals die in de literatuur bestaan, bijvoorbeeld in (1); (ii) dat de gekozen karakteriseringen linguïstisch niet of niet goed worden gemotiveerd; (iii) dat negatie roet in het eten gooit.

5. Kruisclassificatie

Hoeksema definieert de Vendler-klassen met behulp van kenmerken die hij preciseert in termen van gegeneraliseerde kwantoren. Hij vertaalt de tegenstelling [±Interval] als [+Duration] en [-Duration], en de tegenstelling [±Bepaald] als [-Count] en [+Count]. Deze kenmerken krijgen de volgende interpretatie^13.:

(17)	a	-Count: ∀ X,Y ⊆ W, X ε Q & Y ε Q → X ∪ Y ε Q
	b	+Count: ∀ X,Y ⊆ W, X ε Q & Y ε Q → X ∪ Y ∉ Q
	c	-Duration: ∀ X,Y ⊆ W, X ε Q & Y ⊆ X → Y ε Q
	d	+Duration: ∀X ⊆ W, X ε Q → ∼∀ Y (Y ⊆ X → X ⊆ Y)^14.

In (17a) figureert de eigenschap van geslotenheid onder eindige vereniging. Zij is een noodzakelijke maar niet voldoende voorwaarde voor monotone stijging. Sommige monotone dalers hebben deze eigenschap ook, bijvoorbeeld ∥geen auto∥ in (11b).

De eigenschap (17b) is logisch equivalent met (17b′):

(17)b′

∼((X ε Q & Y ε Q) & X ∪ Y ε Q)

Deze eigenschap zegt dat als Z ε Q, Z nooit is op te splitsen in deelverzamelin-

13. Hoeksema ziet gebeurens als een verzameling mogelijkheden W. Zijn definities zijn vertaald in (18) - (20), waarbij Q ⊆ W.

14. In feite geeft Hoeksema de definitie (opnieuw enigszins aangepast): X ε Q → ˜INST(X), met INST(X) gedefinieerd als ∀Y(Y ⊆ X → X ⊆ Y). Ik heb de ontkenning ervan weergegeven als ˜∀ Y(Y ⊆ X → X ⊆ Y), hetgeen neerkomt op ∃Y(Y⊆X & X ⊈ Y). Het idee van (17d) moet zijn dat X niet atomair is.

[p. 76]

gen die ook lid van Q zijn en dat als X en Y element van Q zijn, hun vereniging niet lid is van Q. Geen van de kwantoren in (16) voldoet aan eis (17b′): monotone dalers triviaal niet, want ø ε Q en elke vereniging van ø met X ε Q levert X op. Sterke monotone stijgers niet omdat als E ε Q en Y ε Q hun vereniging altijd E is. Ook zwakke stijgers die E bevatten in sommige van de modellen, voldoen niet aan (17b′). Kortom, (17b′) lijkt ons te brengen bij niet-monotone structuren, zoals (11e).

Het kenmerk [-Duration] wordt in (17c) geïnterpreteerd als monotone daling, terwijl [+Duration] in (17d) wordt gekarakteriseerd als de eigenschap dat X geen moment is. In de theorie van gegeneraliseerde kwantoren zijn beide evenwel geen negatie van elkaar. Datzelfde geldt voor (17a) en (17b)/(17b′).

Hoeksema karakteriseert nu de Vendler-klassen met behulp van telkens twee kenmerken.

-18	Toestanden:	X ε Q & Y ε Q → X ∪ Y ε Q	(=17a)
		X ε Q & Y ⊆ X → Y ε Q	(=17c)
-19	Activiteiten:	X ε Q & Y ε Q → X ∪ Y ε Q	(=17a)
		X ε Q → ∼∀ Y (Y ⊆ X → X ⊆)	(=17d)
-20	Eindpuntgebeurens:	X ε Q & Y ε Q → X ∪ Y ∉ Q	(=17b)
		X ε Q → ∼∀ Y (Y ⊆ X → X ⊆ Y)	(=17d)
-21	Puntgebeurens:	X ε Q & Y ε Q → X ∪ Y ∉ Q	(=17b)
		X ε Q & Y ⊆ X → Y ε Q	(=17c)

Toestanden worden bij Hoeksema dus gekenmerkt door monotone daling (=17c) en door de zogeheten eigenschap van geslotenheid onder eindige vereniging (=17a). Vergeleken met Ter Meulen lijkt de keuze voor (17c) me een verbetering, zeker in het licht van de karakterisering die Galton (1984) geeft van toestanden (zie voetnoot 11). Combinatie van (17a) en (17c) leidt tot een type kwantor waartoe ook ∥geen N∥, ∥alleen N ∥ en ∥ geen van beide N ∥ en ∥geen van de N∥ behoren. Positief is ook dat beide voorwaarden beperkend werken ten opzichte van elkaar.

Zo niet bij Activiteiten: (17d) legt nauwelijks enige beperking op aan de klasse die door (17a) wordt gekarakteriseerd. Neem bijvoorbeeld aan dat (17a) geldt. Wat voegt (17d) dan toe? Deze conditie zegt dat er echte deelverzamelingen Y van X zijn. Maar dat wordt ook al uitgedrukt door (17a). Stel dat Y ⊆ X, dan is X ∪ Y ε Q, want in dat geval geldt X ∪ Y = X. Dus (17d) zou alleen relevant kunnen zijn voor die Y ⊂ X die zelf niet element van Q zijn. Maar (17a) staat ook toe dat elke X een deelverzameling heeft. Triviaal is dat altijd het geval met de lege verzameling ø, die immers deelverzameling van elke X ε Q is. In feite karakteriseert Hoeksema Activiteiten dus simpelweg in termen van (17a)^15..

Eindpuntgebeurens worden door (17b) gedefinieerd als niet-monotoon, maar zonder de mogelijkheid om, zoals (11e), in sommige modellen wel monotoon te zijn^16.. Maar eigenschap (17d) veronderstelt nu juist monotonie om zinnig te kunnen functioneren. Wat doet (17d) eigenlijk? Deze conditie is relevant voor de situatie Y ⊂ X. Dat geval wordt echter door (17b) uitgesloten, want als X ε Q en Y ⊂ X, en ook Y ε Q, dan geldt ook X ∪ Y ε Q. Maar dat mag niet van (17b). Met andere woorden, (17d) werkt leeg in dat geval. Stel dat X ε Q en Y ⊂ X en Y ∉ Q. Dan werkt (17d) wel samen met (17b), maar triviaal, want stel dat |X| = 1. Dan nog geldt (17d) omdat de lege verzameling voldoet aan (17d) en de lege verzameling is in elk geval een deelverzameling van de singleton X. Voor de gevallen waarin de cardinaliteit van X en Y hoger is dan 1, is (17d) niet nodig.

Voor Puntgebeurens geldt in feite hetzelfde bezwaar: (17b) is op zich wel plausibel, maar de eigenschap (17c) werkt doodeenvoudig triviaal op kwantoren van het type (11e′). Want stel dat (17b) geldt, dan wordt een klasse van structuren toegelaten waarvoor geldt dat Y ⊈ X. Het antecedens van (17c) wordt daardoor een

15. Johan van Benthem (pers. comm.) wees er op dat {ø} voldoet aan (17a); maar niet aan (17d), maar in dat geval geldt X = Y = ø, hetgeen linguïstisch niet bijster beperkend mag worden genoemd.

16. Johan van Benthem wees me op een extra-moeilijkheid met (17b): in het geval X = Y geldt: X ε Q → X ∉ Q, hetgeen inhoudt dat voor alle X geldt dat X niet tot Q behoort. Deze complicatie vereist op zich al een herziening van (17b).

[p. 77]

nogal loze aangelegenheid want het werkt nooit op (17b), tenzij triviaal.

Samenvattend constateer ik dat de eigenschappen (17) weinig onderlinge samenhang vertonen. Bij Toestanden gaat het nog wel goed: men kan (17a) opvatten als een inperking op de structuren die door (17c) worden toegelaten. Bij Activiteiten gaat het al mis: de twee karakteristieken beperken elkaar niet, waardoor een nogal heterogene structurering ontstaat. En bij de twee andere gaat het ook echt mis: (17b) haakt niet in op (17d) en (17c) en kan dus niet beperken of beperkt worden. Dit maakt Hoeksema's voorstel om louter technische redenen nogal onaantrekkelijk.

Ook de toetsing van (18) - (21) aan de negatietest levert voor Hoeksema problemen op. Immers, geen van de complementen van de klasse van structuren die door (19), (20) en (21) worden gedefinieerd levert (18) op. Dat wil zeggen, de negatie van de vier kenmerken in (17) levert geen monotone daling op. Ook Hoeksema verantwoordt dus niet een linguïstisch relevant verschijnsel, nl. dat negatie verschillen tussen Vendler-klassen neutraliseert.

Hoeksema probeert zijn kenmerkencombinaties overigens wel linguïstisch te onderbouwen. Zo wordt de blokkering van (5c) en (5d) verantwoord door de hele dag te zien als een predikaat over Q met de eis dat subintervallen van ∥de hele dag∥ correleren met elementen van Q, maar omdat Q in dit geval geen ‘proper parts’ heeft, gaat er iets mis. Hoeksema verantwoordt echter niet de geforceerde iteratie (Cf. Oversteegen en Verkuyl 1985 voor een poging daartoe).

Hoeksema's poging om de Progressive-operator in is aan het/bezig zijn te te definiëren in samenhang met (17), lijkt me ook niet overtuigend. Hij definieert deze operator als incompatibel met monotone daling, hetgeen inderdaad door (17c) Toestanden en Puntgebeurens uitsluit van de Progressive Form, maar we zagen al in (3) dat Puntgebeurens zich weinig aantrekken van het voortgangscriterium, althans een ander soort afwijkend gedrag vertonen dan de Toestanden.

Tenslotte moet Hoeksema's belangrijkste motivering voor een classificatie in (18) - (21), nl. een op zichzelf interessant onderscheid tussen morfologische bouwsels met het prefix ge- en/of met het suffix -ing in termen van toestand en toestandsveranderingen, nader worden bekeken. Voor de ge- gevallen wordt een beroep gedaan op ‘activity’. Helaas zegt Hoeksema niet of (17a) of (17d) of beide worden aangeroepen.

Voor de -ing gevallen is een generalisatie nodig over (19), (20) en (21), maar deze bevatten strijdige kenmerken. Zonder precies aan te geven op welke kenmerken hij een beroep doet, zegt hij dat de interpretaties van -ing, ∥ -ing ∥, een functie is die zo gedefinieerd is dat X ε Q nooit is ingebed in een grotere verzameling X′ zodanig dat X′ ε Q het geval zou zijn. Met andere woorden, het lijkt er op dat (17b) wordt aangesproken, want die sluit dat uit (als X ε Q & X ⊆ X′ & X′ ε Q, dan X ∪ X′ ε Q). Maar hoe werkt ∥-ing ∥ op (19)? Simpelweg door ∥-ing∥ als een identiteitsfunctie te nemen in het geval van Activiteiten die geen ‘definite endpoints’ hebben. Immers, men kan dan niet de maximale X te pakken krijgen met ∥-ing∥. Maar wat zijn Activiviteiten met ‘definite endpoints’? Hoeksema zegt dat ∥-ing∥ ‘turns activities with definite endpoints into accomplishments’ (1984: 221), maar (17) - (21) laat een dergelijke overgang niet toe. Hoe men het ook keert of wendt, Hoeksema heeft twee verschillende functies nodig: een ∥-ing∥ werkend op Eindpuntgebeurens en Puntgebeurens en een ∥-ing∥ werkend op Activiteiten. Zijn analyse in termen van kenmerken leidt dus in het geheel niet tot generalisatie en zeker niet tot een linguïstische onderbouwing van (17) - (21).

Samenvattend constateer ik dat ook de kruisclassificatie van de Vendler-klassen, althans die wordt voorgesteld door Hoeksema, niet echt goed werkt. Wel vind ik dat Hoeksema met zijn interpretatie van Vendlers tijdschema's in (1) de juiste factoren te pakken heeft, nl. [± telbaar] en [± Duration], zij het dat deze factoren niet kruisclassificerend moeten worden behandeld. Ik zal in paragraaf 6 laten zien hoe naar mijn mening de Vendler-klassen linguïstisch moeten worden teruggebracht tot een tweedeling.

[p. 78]

6. Een compositionele tweedeling

In deze paragraaf zal ik iets preciezer het combinatorische mechanisme beschrijven waarmee het terminatieve VP-aspect wordt gevormd. Mijn bedoeling is te laten zien dat de [+ADD TO]-operator waarover ik al sprak, kan worden opgevat als een intervalproducerende functie met als output een collectie intervallen met een filterstructuur. Activiteiten zijn dankzij de aanwezigheid van [+ADD TO] op te vatten als entiteiten met een filterstructuur. (Eind)puntgebeurens zijn eindige filters waarvan de eindigheid bepaald wordt door [+SQA], terwijl Toestanden gekenmerkt worden door [-ADD TO]^17.. Ik zal deze schets hieronder iets nader uitwerken.

Ik zal eerst zeer beknopt en schematisch aangeven wat het combinatorisch aspectmechanisme voorgesteld in Verkuyl (1972) inhoudt. Ik ontdoe me daarbij van tijdgebonden generatieve formalismen en werk met kenmerken waarbij ik opmerk dat deze thans een precieze modeltheoretische interpretatie hebben (Verkuyl 1985a). t staat voor terminatief (telisch, perfectief, etc). Gegeven deze niet essentiële aanpassingen ziet de verantwoording van de opbouw van het VP-aspect er als volgt uit:

(22)		NP V
	[+SQA] + [-ADD TO] → [-T]	Den Uyl bewonderen
	[-SQA] + [-ADD TO] → [-T]	politici bewonderen; haten
	[-SQA] + [+ADD TO] → [-T]	kilometers wandelen; wandelen boterhammen eten; eten
	[+SQA] + [+ADD TO] → [+T]	een boterham eten, enkele happen eten; drie boterhammen eten

Het oppositiepaar Onbepaald-Bepaald uit (1) heb ik geïnterpreteerd als resp. [UNSPECIFIED QUANTITY OF A] vs. [SPECIFIED QUANTITY OF A], hetgeen synoniem is met de kenmerken [-Telbaar] vs. [+Telbaar], zoals uiteengezet in Verkuyl (1972: 59), waarbij opgemerkt moet worden dat telbaarheid een eigenschap is van de NP, waarbij A de referent is van het naamwoord van de NP. In Verkuyl (1985a) is de tegenstelling gepreciseerd in termen van de theorie van gegeneraliseerde kwantoren. Ik kom daar in paragraaf 6 op terug, maar kort de oppositie af als [-SQA] vs. [+SQA].

Bij de opbouw van het Prop-S aspect werken soortgelijke mechanismes nu als combinaties van [±SQA] met [±T]^18.. Ik wijs op zinnen als Patiënten stierven hier maandenlang bij bosjes als een voorbeeld van [-SQA]+[+T], terwijl de Prop-S van (6c) en (6d) voorbeelden zijn van [+SQA]+[+T].

In Verkuyl (1985a) heb ik voorgesteld om aan werkwoorden met een [+ADD TO]- karakterisering de interpretatie (23) toe te kennen, gegeven een model M waarin T de oneindige verzameling tijdspunten is, I de oneindige verzameling tijdsintervallen, en < een strikt partiële ordening.

(23)	∥[+ADD TO]∥ = die functie s: I → I zodanig dat als I = (a,b), dan ∃c[s(I) = (b,c)] en als a,b,c ε T, dan a < b < c

Dat wil zeggen, s is een periodiseringsfunctie en zorgt zo voor de verantwoording van voortgang in de tijd, uitgedrukt door een klasse van werkwoorden waartoe lopen, eten, zien, bellen, veroveren, etc. wèl, maar werkwoorden zoals haten, ziek zijn, sterfelijk zijn, etc. niet behoren. Inmiddels ben ik tot de conclusie gekomen dat (23) enkele problemen oplevert (zoals dat van de ‘gaten’ tussen I_j en I_i+1) die vermeden worden door (24). En niet alleen dat, (24) heeft als bereik

17. Hiermee zit ik op dezelfde lijn als Mourelatos (1981) die Toestanden fundamenteel onderscheidt van niet-Toestanden (cf. Verkuyl (1985b)).

18. In zinnen als (5) is Prop-S de S minus de adverbiale duurbepaling.

[p. 79]

een verzameling intervallen waarvan de structuur die van een filter is:

(24)	∥[+ADD TO] ∥ = die functie s: I → I` zodanig dat als I = (a,b) dan ∃c≥b [s(I) = (a,c)], waar a≤b en I` ⊆ I.

Dat wil zeggen een [+ADD TO]-werkwoord produceert een collectie intervallen waarvan de som een interval is. De filterstructuur van intervallen geproduceerd door (24) beantwoordt aan (14). Naar mijn mening vermijdt (24) allerlei problemen die door o.a. De Vuyst (1983:162) en Ter Meulen (1983:188f) aan de intervalsemantiek worden toegeschreven.

Activiteiten hebben met Terminatieven gemeen dat ze een [+ADD TO] karakterisering hebben, die gegeven de oneindigheid van I er voor zorg draagt dat er geen begrenzing nodig is. Bij Terminatieven wordt s echter beperkt doordat ze gekoppeld wordt aan een eindig domein. Ik zal dat hier demonstreren met behulp van een voorbeeldzin:

(25)	Ze veroverden drie steden.

Een transitief werkwoord kan worden gezien als een constituent die samen met het direct object een VP vormt. Meestal wordt de V gezien als functor met als input het direct object. In elk geval is in de compositionele interpretatie van de ‘losse constituenten’ veroveren en drie steden tot een structurele eenheid drie steden veroveren minstens een element van het betrokken worden van drie steden in de veroveringshandeling: er zijn drie steden die veroverd werden. Maar dit kan op verschillende manieren zijn gebeurd: alle drie tegelijk, twee tegelijk en een later of eerder, en een voor een. Zin (25) zegt daar niets over. Linguïstisch dient dit gegeven te worden verantwoord.

De tijdsbetrokkenheid van drie steden kan vrij natuurlijk worden verantwoord omdat met elke finiete verzameling een canonieke afbeelding k is te associëren die de zogeheten quotiëntverzameling genereert. Anders gezegd, met elke eindige verzameling is een verzameling van equivalentieklassen te verbinden als men over een daartoe geschikte equivalentierelatie beschikt. Stel A = {a,b,c}. Dan zijn van A op verschillende wijzen partities te maken, bijvoorbeeld:

(26)	a	{{a}, {b, c}}
	b	{{a}, {b}, {c}}
	c	{{a, b, c}}

In (26a) bevat de partitie twee leden; (26b) bevat drie leden en representeert daarmee de één-voor-één lezing, terwijl (26c) één lid bevat en daarmee de zogeheten collectieve lezing representeert. Als |A| = n, dan is het aantal partities eindig en de partitie met het hoogste aantal leden bevat dan n leden.

De passende equivalentierelatie P (de P van Participant) is te preciseren als ‘gezamenlijk betrokken op een tijdsinterval’. Om ruimte uit te sparen teken ik mijn bedoelingen bij een situatie dat twee steden tegelijk werden veroverd en één stad ervoor of er na:

(27)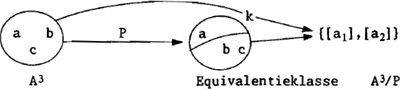

De equivalentierelatie P verdeelt A³ in twee deelverzamelingen en deze worden lid

[p. 80]

van de quotiëntverzameling A³/P waarvan leden in de relatie P tot elkaar staan. Men kan zich gemakkelijk voorstellen dat bepalingen als één voor één en achtereenvolgens P zodanig bepalen dat toevoeging aan zin (25) zou leiden tot drie leden van A³/P met elk één element.

Van belang is op te merken dat men het canonieke afbeeldingsmechanisme k ‘gratis meekrijgt’: zodra zich een geschikte equivalentierelatie voordoet, geldt datgene waarvan (27) een voorbeeld is. Men kan dit gegeven dankbaar benutten, zeker binnen de Gruberiaanse thematische rollenanalyse waarbij P bepaalt hoeveel entiteiten betrokken zijn in de predikatie. Technisch wordt het voorstel om gebruik te maken van k aantrekkelijker als men A³/P neemt als het domein van een participantenfunctie p. Met andere woorden, gegeven de cardinaliteit n van een verzameling die betrokken is in de VP-predikatie, wordt er ‘gratis’ een Aⁿ/P aangereikt waarvan de precieze samenstelling niet bekend is, tenzij P gemodificeerd is door bepalingen als achtereenvolgens, in groepjes, stuk voor stuk, etc.

Het ligt nu voor de hand om Aⁿ/P te verbinden met intervallen en wel zodanig dat de samenstelling van Aⁿ/P bepalend is voor de produktie van intervallen door de ADD TO-functie s. Met andere woorden, we kunnen s beperken door het domein van s, te weten I, te zien als de output van p:

(28)	∥[+SQA] ∥ = die functie p: A^n/P → I gedefinieerd door p ([ai]) = Ii

De functie p is injectief, m.a.w. p is één-éénduidig. De functie s is surjectief: Ran(s) = I∃. In beeld:

(29)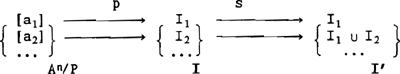

Het is nu gemakkelijk in te zien dat het terminatieve aspect kan worden geanalyseerd als een produktfunctie sop. Dat wil zeggen:

(30)	∥[+T]∥ is de produktfunctie t: A^n/P → I∃ gedefinieerd als: t([ai]) = s(p([ai])).

Het is nu duidelijk te merken dat Puntgebeurens beter kunnen worden aangepakt: op lexicaal niveau kan de instructie worden meegegeven dat [+ADD TO] zodanig is beperkt dat s slechts één keer werkt. Eventueel kan men s nog zo inperken dat a=b=c. Dergelijke beperkingen zijn waarschijnlijk afhankelijk van kennis van het domein waarover gesproken wordt^19..

19. De hier voorgestelde analyse moet, zoals opgemerkt door Johan Lock, aparte voorzieningen treffen voor de analyse van constituenten als de kar duwen, die duratief zijn. Naar het zich laat aanzien moet de thematische structuur van de zin betrokken worden bij de werking van p en s.

7. Samenvatting

Met de bovenstaande analyse kan verklaard worden waarom (25) Zij veroverden drie steden terminatief is, d.w.z. eindige informatie bevat en uitdrukt. Tevens wordt duidelijk dat structureel gezien niet elke Vendler-klasse ‘een eigen gezicht heeft’: de aspectivische hoofdafdeling is die tussen [+T] en [-T].

Samenvattend kan het volgende over de Vendler-klassen worden vastgesteld. Het is wel degelijk mogelijk de theorie van gegeneraliseerde kwantoren toe te passen op de analyse van aspect. Echter, Eindpuntgebeurens zijn door [+ADD TO] wezenlijk verbonden met de klasse der Activiteiten en Puntgebeurens zijn slechts speciale gevallen van Eindpuntgebeurens. Dit blijkt goed uit het volgende schema (2∃) waarin nu ook negatie is verwerkt:

[p. 81]

(2')		+Beperkt	-Beperkt
	+Filter	Eindpuntgebeurens Puntgebeurens	Activiteiten Termnegatie
	-Filter		Toestanden Zinsnegatie

Zou men de Vendler-klassen koste wat het kost willen handhaven op ontologisch vlak door ze niet langer als lexicale klassen te zien maar als die structureel gevormde klassen die een linguïstisch correlaat hebben, dan zou de volgende classificatie denkbaar zijn:

(31)

De ‘hoofdindeling’ is die tusen (a)+(b) enerzijds en (c)+(d) anderzijds, d.w.z. tussen [+Beperkt] en [-Beperkt], d.w.z. tussen terminatief en duratief. Dit is de tegenstelling tussen α en β in (2). De andere tweedeling is die tussen nietfilterstructuur (a) enerzijds en de filterstructuren (b)+(c)+(d) anderzijds. Deze wordt gevormd door de aan-of afwezigheid van een kenmerk [+ADD TO] dat lexicaal wordt aangereikt tenzij er sprake is van negatie. In dat geval wordt [+ADD TO] veranderd in [-ADD TO]. Maar nogmaals, ik heb enige moeite met (31) omdat het de suggestie van het bestaan van de Vendler-klassen blijft geven.

Voor (31a) heb ik niet veel directe argumenten of het zou moeten zijn dat de negatie van (31b), (31c) en (31d) steeds tot monotone daling leidt. Immers, de negatie van filters is monotoon dalend. Schema (31) is derhalve in overeenstemming met de taalfeiten. Ik heb me bij de behandeling van zinnen uit (5) en (6) beperkt tot zinsnegatie. Bij termnegatie wordt een Eindpuntgebeuren tot Activiteit. In termen van (29) zou zinsnegatie werken op s o p, waardoor een Toestand ontstaat, terwijl bij termnegatie de p geen domein heeft en dus niet werkt, zodat de s wel kan werken. Daarmee verantwoordt men dat een zin als (32) als niet-terminatief maar toch als een Activiteit beschouwd kan worden: ze at wel zij het niet drie boterhammen.

(32)	Jessica heeft niet die drie boterhammen gegeten.

Het feit dat (a) zo keurig de negatie is van de stijgers in de andere categorieën, en dat daarmee zo'n principiële breuk wordt gemaakt tussen Toestanden en niet-Toestanden is in overeenstemming met de analyses van Mourelatos (1981) en Galton (1984). Bezwarend voor (31) is wel dat de negatie van Toestanden ook naar Toestanden moet voeren, hetgeen naar het zich laat aanzien twee soorten Toestanden met zich mee zou brengen^20.. Dit is echter geen bezwaar tegen mijn analyse in paragraaf 6.

Tenslotte, het verschil tussen de semantiek van -ing en die van ge- kan met behulp van (31) heel goed worden verantwoord. Voor ge- deed Hoeksema een beroep op ‘Activiteit’, met alle onduidelijkheid ervan. Met (31) kan men een beroep doen op niet-eindige filterstructuur. Voor de -ing-gevallen moest Hoeksema een beroep doen op ‘definite endpoint’. Met (31) gaat het eenvoudiger: een beroep op eindige filterstructuur is voldoende. Merk op dat (31b) ongespecificeerd is ten aanzien

20. Een voor mij intuïtief veel aantrekkelijker wijze om Toestanden te karakteriseren zou zijn het principieel in het midden laten of er sprake is van daling of stijging. Dus iets als:

(i)	(X ε Q & X ⊆ Y → Y ε Q) ∨ (X ε Q & Y ⊆ X → Y ε Q)

Hiermee zou het bezwaar tegen (32) wellicht kunnen worden vermeden. Een voordeel van (i) is de nietszeggendheid ervan en de afwezigheid van enige structuur. Maar ik heb vooralsnog geen argumenten voor (i).

[p. 82]

van de oneindigheid of eindigheid: er zijn ook eindige Activiteiten. In She walked is de Activiteit kennelijk eindig, maar dat wordt niet direct uitgedrukt door walk zelf.

[p. 83]

Literatuur

Barwise, J. and R. Cooper (1981) Generalized Quantifiers and Natural Language. In: Linguistics and Philosophy 4, 159-219.

Bennett, M. and B. Partee (1978) Toward the logic of tense and aspect in English. IULC. Bloomington, Indiana.

Benthem, J. van (1983) Determiners and Logic. In: Linguistics and Philosophy 6, 447-478.

Benthem, J. van (1986) Het categoriale wereldbeeld. In deze bundel.

Carlson, L. (1981) Aspect and quantification. In: P.J. Tedeschi and A. Zaenen, Tense and aspect. New York, 31-64.

Dowty, D.R. (1979) Word meaning and Montague grammar. The Semantics of Verbs and times in generative semantics and in Montague's PTQ. Dordrecht/London.

Galton, J. (1984) The Logic of Aspect. Oxford.

Hoeksema, J. (1984) Categorial Morphology. Diss. RUG Groningen.

Jong, F.M.G. de and H.J. Verkuyl (1985) Generalized Quantifiers: the Properness of their strength. In: J. van Benthem and A. ter Meulen (eds.), Generalized Quantifiers: Theory and Applications. GRASS 4. Dordrecht, 21-43.

Meulen, Alice ter (1983) The Representation of Time in Natural Language. In: Alice ter Meulen (ed.), Studies in Modeltheoretic Semantics. GRASS 1. Dordrecht, 177-191.

[p. 84]

Meulen, Alice ter (1984) Events, Quantities and Individuals. In: F. Landman and F. Veltman (eds.), Varieties of Formal Semantics. Proceedings of the 4th Amsterdam Colloquium September 1982. Dordrecht, 259-279.

Mourelatos, A.P.D. (1981) Events, Processes and States. In: P.J. Tedeschi and A. Zeanen, Tense and Aspect. New York, 191-211.

Oversteegen, E. en H.J. Verkuyl (1985) De temporele zinsstructuur van het Nederlands: twee tijdsbanden. In: GlOT 7, 257-297.

Timberlake, A. (1984) Invariance and the Syntax of Russian Aspect. In: P.J. Hopper (ed.), Tense-Aspect: Between Semantics & Pragmatics. Containing the Contributions to a Symposium on Tense and Aspect, held at UCLA, May 1979. Amsterdam/Philadelphia, 305-331.

Vendler, Z. (1957) Verbs and Times In: The Philosophical Review 66, 143-160. Geciteerd uit: Z. Vendler (1967), 197-221.

Vendler, Z. (1967) Linguistics in Philosophy. Ithaca, New York.

Verkuyl, H.J. (1972) On the Compositional Nature of the Aspects. Foundations of Language Supplementary Series 15. Dordrecht.

Verkuyl, H.J. (1985)a Nondurative Closure of Events. In: J.A.G. Groenendijk, D. de Jongh and M.J.B. Stokhof (eds.), Information, Interpretation and Inference. Proceedings of the 5th Amsterdam Colloquim on Formal Semantics. (te ver schijnen).

Verkuyl, H.J. (1985)b Temporal Insulation: On the Construction of Events. In: Dutch Crossing 27, 22-45.

Vet, J.P. (1980) Temps, aspects et adverbes de temps en français contemporain. Genève.

Vuyst, J. de (1983) A Semantic Analysis of Temporal Elements in Dutch and English. Diss. RUG. Groningen.

Vuyst, J. de (1983) Situation-descriptions: temporal and aspectual semantics. In: Alice ter Meulen (ed.), Studies in Modeltheoretic Semantics. GRASS 1. Dordrecht, 161-176.

Zwarts, F. (1981) Negatief polaire uitdrukkingen I. In: Glot 4, 35-132.

Zwarts, F. (1983) Determiners: A Relational Perspective. In: A.G.B. ter Meulen (ed.), Studies in Modeltheoretic Semantics. GRASS 1. Dordrecht, 37-62.

Zwarts, F. (1986) Categoriale grammatica en algebraïsche semantiek. Een onderzoek naar negatie en polariteit in het Nederlands. Dissertatie R.U. Groningen.