Tabu. Jaargang 16

[p. 19]

Onvolledige constituenten
Gosse Bouma

0. Introductie

Eén van de leerstellingen van Gazdar (1981), en meer in het algemeen van de theorie die bekend staat als ‘Generalized Phrase Structure Grammar’ (GPSG), is dat de zinnen in (1) op een elegante en generaliserende wijze gegenereerd kunnen worden zonder dat van transformaties gebruik hoeft te worden gemaakt.

(l)	a	Welk boek kreeg Marijke op haar verjaardag?
	b	Dit boek kreeg Marijke op haar verjaardag.
	c	...het boek dat Marijke op haar verjaardag kreeg.

Dit is een verrassende stelling, aangezien de constructies in (1) (zogenaamde ‘unbounded dependency constructions’, of UDCs) binnen de Standaard Theorie (Chomsky 1965), en ook binnen daarop geënte theorieën, als een argument voor het invoeren van transformaties worden gehanteerd.

Gazdars oplossing is geformuleerd in termen van een (abstracte) herschrijf-grammatica. Deze grammatica wordt verrijkt met complexe categorieën (‘slashed categories’) van de vorm X/Y, die aanduiden dat aan een constituent van categorie X, een element van categorie Y ontbreekt. Verder wordt gebruik gemaakt van metaregels, regels die op basis van een verzameling herschrijfregels een nieuwe verzameling herschrijfregels kunnen creëren. Het aldus ontstane systeem vertoont enige oppervlakkige overeenkomsten met de regels en categorieën die worden gehanteerd binnen de categoriale grammatica, met name voor wat betreft het gebruik van complexe categorieën. Een opvallend verschil is evenwel dat een uitdrukking met categorie X/Y in GPSG expliciet wordt geïnterpreteerd als een uitdrukking van categorie X, waaraan een element van categorie Y ontbreekt. In de categoriale grammatica is het gebruik van complexe categorieën veel algemener. Een uitdrukking met categorie X/Y is in de eerste plaats een uitdrukking die gecombineerd met een element van categorie Y een uitdrukking van categorie X oplevert. In categoriale systemen die zijn verrijkt met compositie, lijkt voor complexe categorieën ook de interpretatie ‘uitdrukking van categorie X, met een gat van categorie Y’ beschikbaar. Deze verrijkte systemen bieden evenwel geen bevredigende analyse waar het UDCs betreft.

In dit artikel wordt beargumenteerd dat desalniettemin binnen de categoriale grammatica een analyse van UDCs mogelijk is. Om dit te bereiken is het in de eerste plaats nodig zowel de ‘Gazdariaanse’ als de standaard categoriale interpretatie van complexe categorieën toe te staan (paragraaf 1). Bovendien moet tussen beide interpretaties een strikte scheiding worden aangebracht. Dit maakt het mogelijk een aantal specifieke regels voor het afleiden van UDCs te introduceren (paragraaf 2). Verder leidt deze scheiding ertoe dat restricties op vooropplaatsing op een eenvoudige wijze geformuleerd kunnen worden (paragraaf 3).

1. De interpretatie van complexe categorieën

Een eenvoudig categoriaal systeem wordt verkregen wanneer slechts gebruik wordt gemaakt van regels in (2).

(2)	a	Rechtse Applicatie (RA):	a/b b ⇢ a
	b	Linkse Applicatie (LA):	b b\a ⇢ a

[p. 20]

In (2) noemt men a/b en b\a ‘functor’, b is steeds het ‘argument’. Met behulp van deze regels kunnen de zinnen in (3) worden afgeleid:

(3)	a	Marijke		lacht
	b	Marijke	krijgt		een zoen

De afleidingen in (3) tonen aan dat constituenten met categorie a/b of b\a opgevat moeten worden als uitdrukkingen die samen met een constituent van categorie b een constituent van categorie a kunnen vormen. Het onrechtvaardige aspect aan deze uitleg is dat met evenveel recht kan worden gezegd dat een VP (= NP\S in de bovenstaande voorbeelden) een NP nodig heeft om een S te vormen, als andersom. (Dit zou betekenen dat NP gelezen moet worden als S/VP of S/(NP\S)). Verder blijkt uit (3b) dat een transitief werkwoord een NP nodig heeft om een VP te vormen, maar het omgekeerde geldt natuurlijk ook (een NP heeft een transitief werkwoord nodig om een VP te vormen). Deze onevenwichtigheid wordt opgeheven, wanneer de volgende regel wordt toegevoegd:

(4)

Categorie Ophoging (CO):

a ⇢ b/(a⋓,(b/a)▽

Categorie-ophoging heeft tot gevolg dat er geen vaste functor-argument-verhoudingen meer bestaan. In (5) wordt aangetoond dat nu ook de hierboven voorgestelde interpretaties van NP-categorieën mogelijk zijn.

(5)	Marijke	krijgt	een zoen

Categorieën doen dus min of meer dienst als herschrijfregels. Het verschil tussen ‘lachen’ en ‘krijgen’ is dat alleen de laatste een direct object nodig heeft; dit wordt tot uitdrukking gebracht in de categorie voor ‘krijgen’ ( = (NP\S)/NP). Evenzo zijn preposities gecategoriseerd als PP/NP, determinatoren als NP/N, adjectieven als N/N, enz. Dit alles komt overeen met de volgende NP/N, herschrijf regels:

(6)	a	S ⇢ NP VP
	b	VP ⇢ V(intr.)
	c	VP ⇢ V(trans.) NP
	d	NP ⇢ DET N
	e	N ⇢ ADJ N
	f	PP ⇢ P NP

Dit type categoriale grammatica zal vooral dienst kunnen doen als beschrijvingsmiddel voor constituent-structuur (zie bijvoorbeeld Flynn 1983 voor een interessante toepassing). De overeenkomst tussen deze eenvoudige categoriale grammatica en herschrijfgrammatica's is (formeel) uitgewerkt in Bar-Hillel et al. (1960).

Willen we komen tot een behandeling van UDCs, dan is een uitbreiding nodig van

[p. 21]

de door (2) en (4) gedefinieerde grammatica. Zulke uitbreidingen kunnen verschillende vormen aannemen. Zo kan men aan de grammatica transformaties, of andere operaties die woordvolgorde beïnvloeden, toevoegen.

Uitbreidingen waarbij slechts de syntactische operatie concatenatie (het samenvoegen van twee constituenten tot een nieuwe constituent zonder daarbij woordvolgorde te veranderen) gebruikt wordt, zijn te vinden in Lambek (1958), Cohen (1967), Bach (1981) en Ades and Steedman (1982). Deze voorstellen hebben gemeen dat ze de volgende regels bevatten:

(7)	a	Rechtse Compositie (RC):	a/b b/c ⇢ a/c
	b	Linkse Compositie (LC):	c\b b\a ⇢ c\a

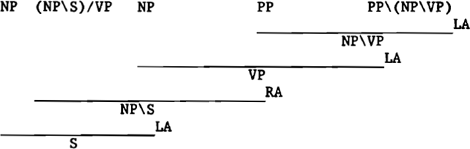
Een onmiddellijk gevolg van compositie is dat er geen sprake meer kan zijn van een eenduidige constituent-structuur:

(8)	Marijke	wil	een boek	op haar verjaardag	hebben
(9)	Marijke	wil	een boek	op haar verjaardag	hebben

In (8) wordt een links-vertakkende afleiding van een zin gepresenteerd, (9) toont aan dat met enige inventiviteit van dezelfde zin ook een rechts-vertakkende afleiding te geven valt. De situatie in (8) en (9) brengt mee, dat niet meer goed valt vol te houden dat bijvoorbeeld ‘wil’ een VP nodig heeft, om een NP\S te vormen. Blijkbaar kan ‘wil’ ook met een subject samengaan om een categorie S/VP te vormen. Deze ambivalentie in het gedrag van complexe categorieën heeft ertoe geleid dat men elementen met een categorie van de vorm a/b of b\a ook wel opvat als elementen van de categorie a, met daarin een gat van categorie b. Zo stelt Zwarts (1986: 73) dat ‘elk categoriaal reductiesysteem feitelijk een precieze definitie behelst van twee begrippen die naar aanleiding van het werk van Gazdar (1981) reeds ter sprake zijn gebracht, namelijk dat van een volledige en dat van een onvolledige uitdrukking’. Deze zienswijze verklaart de ambivalentie van ‘willen’. ‘Willen’ is een NP\S waaraan een VP ontbreekt. Een categorie NP\S kan samen met een NP een S vormen; dit gebeurt dan ook in (9). Logisch gevolg is evenwel dat de aanwezigheid van een gat van categorie VP behouden blijft, en dus dat een categorie S/VP resulteert.

Een belangrijk verschil tussen deze interpretatie van complexe categorieën, en de interpretatie die eerder werd gegeven, is dat een constituent met categorie

[p. 22]

a/b nu wordt beschouwd als zijnde van de categorie a (zij het dat er een b ontbreekt). Volgens de eerder gegeven interpretatie kan een element van categorie a/b alleen door toevoeging van een b overgaan tot een constituent van categorie a.

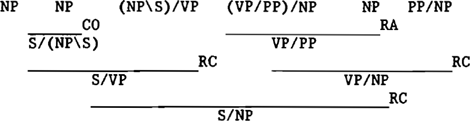
Een gevolg van de aldus ontstane ruimere interpretatiemogelijkheden voor complexe categorieën is dat ook de analyse van UDCs binnen het bereik van de grammatica lijkt te komen. Een UDC bestaat uit drie delen. Ten eerste, de introductie van een ‘gat’ of onvolledige constituent. Ten tweede, het doorgeven van de informatie (tot het zinsniveau) dat er een ‘gat’ aanwezig is, en ten derde, het combineren van een vooropgeplaatst element met de onvolledige zin (cf. Gazdar et al. 1985: 137). De eerste twee aspecten van een UDC lijken verantwoord te worden door een categoriaal systeem met compositie. Neem bijvoorbeeld zin (10)(Gazdar et al. 1985: 147):

(10)	Sandy	Kim	wants	to give	a book	to

Vatten we ‘to’ op als een PP waaraan een NP ontbreekt, dan is aan het criterium dat er een ‘gat’ geïntroduceerd moet worden, voldaan. Door gebruik te maken van compositie slagen we erin deze informatie door te geven tot het zinsniveau (met andere woorden, er onstaat een categorie S/NP). Het enige wat nu nog nodig lijkt te zijn, is een regel om NP en S/NP (in die volgorde) samen te voegen.

Dat dit een al te optimistische veronderstelling is, blijkt uit (11)^1..

(11)	Welk boek	wil	Marijke op haar verjaardag	hebben

In (11) worden we geconfronteerd met het probleem dat een rechts-directionele en een links-directionele categorie zich niet laten combineren. Geen van de eerder gememoreerde uitbreidingsvoorstellen voor de categoriale grammatica, biedt een pasklare oplossing voor dit probleem.

De oorzaak van deze onverwachte hindernis lijkt te liggen in het ambivalente karakter van een categorie als NP\VP. Passen we een combinatie met een NP toe, dan heeft het zin te eisen dat deze NP zich links van de categorie NP\VP bevindt. Interpreteren we NP\VP echter als een VP, met een gat van categorie NP, dan is de positie van dit gat ineens onbelangrijk. Dit wordt eens te meer duidelijk, wanneer we de constituent ‘wil Marijke op haar verjaardag hebben’ in ogenschouw nemen. Deze constituent omvat een gat van categorie NP, zodat noch de categorie NP\S, noch de categorie S/NP op zijn plaats lijkt. (Het Engelse voorbeeld loopt zo soepel, omdat het gat zich daar aan het eind van de zin bevindt.)

In de volgende paragraaf wordt daarom voorgesteld het onderscheid tussen ‘gewone’ complexe categorieën, en categorieën die als een onvolledige constituent moeten worden beschouwd, expliciet te maken. Dit leidt tot een systeem, waarin onvolledige constituenten dezelfde (gemarkeerde) status hebben, ongeacht of ze aan hun linker- of rechter-grens een gat bevatten, of zelfs een gat omvatten.

1. De relatie tussen de volgorde subject-finiet werkwoord in hoofdzinnen, en de geïnverteerde volgorde, als in (11), wordt vastgelegd in de volgende regel: geïnverteerde volgorde, als in (11), wordt vastgelegd in de volgende regel:

(i)	(NP\S)/X ⇢ (Si/X)/NP,

waarbij X de eventuele complementen van het werkwoord aanduidt, en [i] een kenmerk is dat aangeeft dat er sprake is van inversie tussen werkwoord en subject.

2. De introductie van onvolledige constituenten

Het is gebruikelijk om een uiteenzetting over categoriale grammatica te begin-

[p. 23]

nen met een definitie van de te hanteren categorieën. De standaard definitie, die uitgaat van de e,t-notatie, is gegeven in (12).

(12)	a	e, t ɛ BC	(BC = basis-categorieën)
	b	BC ⊆ CC	(CC = complexe categorieën)
	c	a/b, b\a ɛ CC	dan en slechts dan als a,b ɛ CC

In dit geval is de verzameling der categorieën (C) gelijk aan de verzameling CC. Dat in de bovenstaande definitie BC slechts bestaat uit e (= entity) en t (= truth-value), is vooral een gevolg van overwegingen betreffende de relatie syntaxis-semantiek. Een nadeel van deze notatie is dat een aantal syntactisch gebruikelijke categorieën alleen onderscheiden kunnen worden na het toepassen van een aantal kunstgrepen (voor de categorieën N, VP en AP zijn bijvoorbeeld in eerste instantie slechts de categorieën t/e en e\t beschikbaar). Een aanmerkelijk hanteerbaarder systeem ontstaat, wanneer we als basis-categorieën een iets grotere verzameling nemen, waarin bovendien plaats is voor het toekennen van kenmerk-specificaties.

(13)	a	NP, VP, AP, N, S, PP ɛ BC
	b	X[F] ɛ BC	dan en slechts dan als X ɛ BC
	c	BC ⊆ CC
	d	a/b, b\a ɛ CC	dan en slechts dan als a,b ɛ CC

De verzameling BC bestaat nu uit een zestal categorieën, die eventueel voorzien kunnen zijn van een aantal kenmerk-specificaties. Merk echter op, dat de verzameling BC eindig is, zolang het aantal mogelijke kenmerk-specificaties eindig wordt gehouden (we nemen aan dat iedere categorie ten hoogste één specificatie voor een bepaald kenmerk kan hebben).

Voor categorieën van de vorm a/b of b\a zal de interpretatie worden aangehouden dat het een constituent betreft, die slechts door combinatie met een b tot de categorie a kan gaan behoren. De opvatting waarbij een complexe categorie wordt beschouwd als een onvolledige constituent, is voorbehouden aan een speciale klasse van ‘afgeleide’ categorieën.

(14)	a	NP, VP, AP, N, S, PP ɛ BC
	b	X[F] ɛ BC	dan en slechts dan als X ɛ BC
	c	BC ⊆ CC
	d	a/b, b\a ɛ CC	dan en slechts dan als a,b ɛ CC
	e	a//b ɛ AC (= afgeleide categorie) dan en slechts dan als a,b ɛ CC
	f	C = CC ⋃ AC

Een categorie a//b wordt opgevat als een categorie a, met (ergens) een gat van categorie b. Merk op dat de verzameling AC niet recursief gedefinieerd is, zodat categorieën van de vorm (a//b)//c uitgesloten zijn. Dit heeft tot gevolg dat er hoogstens één gat per constituent aanwezig kan zijn.

Dat in de analyse van UDCs drie delen kunnen worden onderscheiden, komt ook in de nu volgende regels naar voren. Als basis voor het categoriale systeem nemen we de regels Applicatie en Ophoging, zoals gedefinieerd in (2) en (4). De introductie van gaten en onvolledige constituenten betekent dat de volgende regel is toegepast:

(15)		Onvolledige Constituent Introductie (OCI)
	a	a/b ⇢ a//b
	b	b\a ⇢ a//b

[p. 24]

Met behulp van (15) kunnen categorieën van de vorm VP//NP of PP//NP afgeleid worden van categorieën van de vorm NP\VP of PP/NP. De a//b notatie geeft dus op geen enkele manier richting aan. Dit verklaart ook waarom links- en rechts-directionele functoren kunnen worden omgezet in dezelfde onvolledige constituent.

Het doorgeven van de informatie dat er een onvolledige constituent aanwezig is, geschiedt door het toepassen van (16):

(16)		Onvolledige Constituent Percolatie (OCP)
	a	a/b b//c ⇢ a//c
	b	b//c b\a ⇢ a//c

In eerste instantie lijkt (16) slecht een notationele variant van compositie (zie (7)) te zijn. Het verschil tussen (16) en compositie ligt in het feit dat OCP de mogelijkheid biedt om constituenten af te leiden die een gat omvatten. In (17) wordt dit gedemonstreerd (waarbij 0 de positie van het gat aangeeft):

(17)a

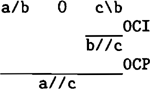(17)b

Tenslotte zijn er regels nodig om een vooropgeplaatst element met een onvolledige zin te combineren, teneinde tot een relatieve zin, een vraagzin of een topicalisatie-constructie te komen. Voor het afleiden van de laatste twee constructies is de volgende regel nodig:

(18)	WH, TOPIC-regel (WTR)
	a Si//a ⇢ Si

Omdat topicalisatie en het vooropplaatsen van WH-woorden in het Nederlands gepaard gaan met inversie, moet worden geëist dat S het kenmerk [i] heeft (vgl. voetnoot 1).

De regels in (15), (16) en (18) maken het mogelijk het eerdere probleemgeval (11) af te leiden:

(11)	Welk boek	wil	Marijke op haar verjaardag	hebben

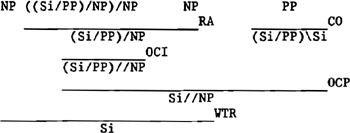
De regels die betrekking hebben op onvolledige constituenten, zijn algemeen van aard. Zo volgt bijvoorbeeld uit (15) en (16) dat er geen enkele restrictie is op de aard van de vooropgeplaatste constituent. Op het eerste gezicht lijkt zo'n restrictie wel aanwezig te zijn, aangezien (15) en (16) steeds betrekking hebben op complexe categorieën. De aanwezigheid van Categorie-Ophoging brengt evenwel met zich mee dat iedere argument-categorie kan worden omgezet in een functiecategorie, en daarmee iedere basis-categorie in een complexe categorie. Deze flexibiliteit is in sommige gevallen noodzakelijk (zoals is geïllustreerd in

[p. 25]

(19)), in andere gevallen lijkt ze tot nodeloze overgeneralisatie te leiden (zoals in (20)).

(19)		Wat	gaf		Marijke		aan Nynke
(20)	*	Aan		gaf		Marijke	het boek	Nynke

De regels in (15), (16) en (18) geven het algemene mechanisme veer, dat nodig is voor de analyse van UDCs. Om overgeneralisaties als in (20) uit te sluiten, is het evenwel nodig nog een aantal aanvullende restricties te formuleren.

3. Restricties

Voor het formuleren van restricties op UDCs zijn er binnen het categoriale kader twee mogelijkheden. Men kan restricties op één of meer regels in (15), (16) en (18) formuleren, of men kan restricties formuleren op AC, de verzameling afgeleide categorieën. Van een keuze voor de eerste of de tweede benadering lijkt niet veel af te hangen. In het navolgende is slechts gekozen voor de tweede benadering, omdat een keuze voor de eerste benadering zou betekenen dat een aantal restricties voor iedere regel opnieuw geformuleerd moet worden.

Beperkingen op het formeren van UDCs zijn nodig om twee redenen:

(21)	*	Op	haar	verjaardag	hebben	wil	Marijke	het	boek

[p. 26]

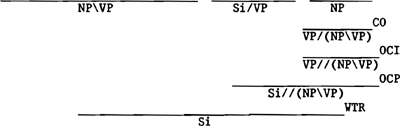(22)	a	*Dat	Mathilde	ziek	is	bevestigt	Henk	het	feit
		_____
			S'					NP/N	N/S'
	b	*Appel	at	Nynke	een
		N			NP/N

De ongrammaticaliteit van (21) en (22) zou kunnen worden toegeschreven aan de aard van de vooropgeplaatste constituent, of aan de aard van de constituent waarin zich het corresponderende gat bevindt. Voor (21) lijkt de eerste verklaring op zijn plaats. Er is geen enkele constructie te bedenken, waarin een constituent van de categorie NP\VP vooropgeplaatst is, en dus lijkt het verstandig, gaten van de categorie NP\VP uit te sluiten. Voor (22) is de tweede benadering geschikter. (23) toont aan dat er situaties zijn, waarin een S′ vooropgeplaatst is.

(23)	Dat Mathilda ziek is, gelooft Henk niet.

Dit betekent dat de ongrammaticaliteit van de zinnen in (22) moet worden toegeschreven aan het feit dat de categorie N of NP een gat bevat. Omdat verplaatsingen vanuit een NP in het algemeen onmogelijk zijn, getuige (22b), lijkt het zinvol onvolledige NPs als ongrammaticaal te bestempelen. Deze tweedeling tussen wat vooropgeplaatst mag worden, en waar een gat zich mag bevinden, wordt weerspiegeld door de restricties die geformuleerd zullen worden.

Afgeleide categorieën spelen een rol in alle UDCs. Wanneer a//b geldt als de algemene vorm van een onvolledige constituent, dan kunnen er restricties geformuleerd worden op a en op b. Restricties op a komen overeen met restricties op de categorie van onvolledige constituenten, en dus met restricties op de positie waar een gat gecreëerd mag worden. Restricties op b komen overeen met restricties op de categorie van het gat, en dus met restricties op de categorie van vooropgeplaatste elementen.

In (24) wordt een voorstel gedaan voor een herformulering van de definitie voor AC (waarbij verondersteld wordt, dat de overige verzamelingen categorieën gedefinieerd zijn als in (14)):

(24)	a//b ɛ AC dan en slechts dan als:
	(i)	b ɛ BC	en
	(ii)	a ɛ CC,	waarbij
	(iii)	a ≠ NP
	(iv)	a ≠ AP
	(v)	a ≠ PP,	met als uitzondering dat PP//NP[+R] ɛ AC.

(24i) eist dat vooropgeplaatste elementen van de categorie NP, N, PP, AP, VP of S zijn. Op deze manier wordt de afleiding van (21) bijvoorbeeld uitgesloten. (24i) lijkt nog iets te ruim, omdat het vooropplaatsen van elementen van de categorie N ongrammaticaal is. Deze constructies worden echter door (24iii) uitgesloten. Verder moet het gebruik van de categorie VP tot infinitiefconstructies beperkt blijven.

De restricties in (24iii)-(24v) kunnen worden beschouwd als eilandcondities voor respectievelijk NP, AP en PP. Het effect van deze restricties is namelijk dat de betreffende categorieën nooit een gat mogen bevatten. Dit komt overeen met het scheppen van een eiland in de transformationele aanpak. De uitzondering in (24v) is nodig om de volgende gaten te kunnen beschrijven:

(25)	a	Nynke houdt daarvan.
	b	Waarvan houdt Nynke?

[p. 27]

(26)	a	*Wie houdt Nynke van?
	b	Waar houdt Nynke van?

NPs als ‘daar’, ‘waar’ en ‘er’ onderscheiden zich o.a. van andere NPs, doordat ze aan een prepositie voorafgaan, in plaats van erop volgen. In Van Riemsdijk (1978) wordt voorgesteld om zulke NPs van een kenmerk [+R] te voorzien. In categoriale termen duiden de zinnen in (25) erop dat preposities behalve de categorie PP/NP, ook de categorie NP[+R]\PP toegekend moeten krijgen. De constructies in (26) tonen vervolgens aan dat alleen voor NP[+R] de PP-grens niet als eiland moet gelden.

De behandeling van restricties die hier is gepresenteerd, heeft natuurlijk een enigszins schetsmatig karakter. De definitie in (24) doet in grote lijnen de juiste voorspellingen, maar het is niet onmogelijk dat een gedetailleerde bestudering van de feiten de noodzaak tot enige aanpassingen aan het licht brengt. (24) is dan ook in de eerste plaats bedoeld om aan te tonen dat de algemene regels uit de vorige paragraaf op een eenvoudige wijze in hun toepassingsbereik kunnen worden beperkt. De hier voorgestelde behandeling van onvolledige constituenten leidt dus zowel tot de mogelijkheid om een aantal algemene regels voor het afleiden van UDCs te formuleren, als tot de mogelijkheid om restricties op eenvoudige wijze uit te drukken.

Literatuur

Ades, A. and M. Steedman (1982) On the Order of Words. In: Linguistics and Philosophy 4, 517-558.

Bach, E. (1981) Discontinuous Constituents in Generalized Categorial Grammar. In: NELS XI, 1-12.

Bar-Hillel, Y. et al. (1960) On Categorial and Phrase-Structure Grammars. In: Bulletin of the Research Council of Israel 9 F, 1-16.

Chomsky, N. (1965) Aspects of the Theory of Syntax. Cambridge, Mass.

Cohen, J.M. (1967) The Equivalence of Two Concepts of Categorial Grammar. In: Information and Control 10, 475-484.

Flynn, M. (1983) A Categorial Theory of Structure Building. In: G. Gazdar, E. Klein and G. Pullum (eds.) (1983), Order, Concord and Constituency. Dordrecht.

Gazdar, G. (1981) Unbounded Dependencies and Coordinate Stucture. In: Linguistic Inquiry 12, 155-184.

Gazdar, G. et al. (1985) Generalized Phrase Structure Grammar. Oxford.

Lambek, J. (1958) The Mathematics of Sentence Structure. In: American Mathematical Monthly 65, 154-169.

Riemsdijk, H.C. van (1978) A Case Study in Syntactic Markedness: The binding nature of prepositional phrases. Dordrecht.

Zwarts, F. (1986) Categoriale Grammatica en Algebraïsche Semantiek: Een onderzoek naar negatie en polariteit in het Nederlands. Dissertatie, R.U. Groningen.