Tabu. Jaargang 16

[p. 1]

Het categoriale wereldbeeld
Johan van Benthem

1. Inleiding

In het Groningse semantische milieu, onder Albert Sassens vleugels dus, valt de laatste jaren een herleving te bespeuren van de Categoriale Grammatica, een door inzichten van Frege en Husserl geïnspireerde syntactische theorie van Poolse origine. Het aantrekkelijke van deze richting ligt in haar sterke semantische motivering, vanuit een achterliggende typentheorie. Bovendien is het categoriale gezichtspunt bijzonder geschikt gebleken in de studie van algemene semantische patronen in natuurlijke taal, zoals de rol van monotonie-verschijnselen (zie Zwarts 1986), of brede analogieën tussen diverse families van grammaticale constructies (zie Keenan and Paltz 1985). Bij dit alles moet overigens niet gedacht worden aan de klassieke calculus van Ajdukiewicz/Bar-Hillel, rond 1960 definitief door Chomsky's TGG overtroefd - maar aan rijkere versies met flexibele typenovergangen. Binnen Nederland vindt men deze verdedigd in, onder meer, Hoeksema (1984), Moortgat (1986), Van Benthem (1986a), Zwarts (1986). (Twee internationale verzamelbundels zijn Bach, Oehrle and Wheeler 1986; Buszkowski, Marciszewski and Van Benthem 1986.) Er is overigens ook een confluentie met recente ontwikkelingen in een sterker syntactisch bewust geworden Montague Grammatica (vergelijk Bach 1984, Groenendijk and Stokhof 1984).

Ondanks de semantische motivering van de Categoriale Grammatica, kan deze laatste toch worden gezien als een in eerste instantie combinatorisch syntactisch kader, dat nog vele uiteenlopende semantische interpretaties toestaat. Deze bijdrage is gewijd aan twee van zulke semantische variaties, en valt daarmee uiteen in twee tamelijk losstaande delen.

In een eerste deel bespreken we uitbreidingen van de gangbare typentheorie, en wel met modale en temporele structuren. Eén speciale reden om dit nader te bekijken is het slechte geweten waarmee sommige categoriale grammatici rondlopen: ze zeggen wel dat dit soort uitbreidingen van de extensionele standaard-theorie ‘routine’ zijn, maar helemaal zeker van hun zaak zijn ze niet. Een tweede reden is dat deze uitbreiding noodzakelijk is om een voldoende ruim modelbegrip te krijgen dat ook plaats biedt aan die andere centrale component in de Groningse semantiek: de studie van temporele uitdrukkingen. Temporeel perspectief wordt ingebracht in paragraaf 4, voorafgegaan door modale structuur in paragraaf 3 - in beide gevallen met een bespreking van diverse resulterende onderzoeksthema's: over de aansluiting bij het oorspronkelijke extensionele geval, maar ook over de intrinsiek nieuwe kwesties die nu rijzen. Aan het eind wordt nog eens bezien in hoeverre deze modaal-temporele uitbreiding de standaard extensionele categoriale grammatica in haar waarde laat.

In het tweede deel worden dan juist inkrimpingen besproken van de gangbare typen-theorie, met diverse bezuinigingen en modificaties op de standaard functie-argument-structuur. De bedoeling is hier met name te laten zien hoe een categoriaal grammaticus toch nog veel semantische gewetensvrijheid kan worden gegund. Anders gezegd: de taalkundige feiten ‘onder-determineren’ de semantische theorie. Wel zullen we steeds aangeven welke rol taalkundige argumentatie toch blijkt te spelen bij het creëren of vergelijken van alternatieve modelleringen. De discussie in dit tweede deel is meer caleidoscopisch dan die in het eerste: het gaat hier veeleer om het vrijmaken van de semantische fantasie.

[p. 2]

2. Categoriale semantiek in een notedop

Categoriale Grammatica is een manier van toekennen van categorieën aan woorden en woordgroepen, zodat complexe uitdrukkingen herkend kunnen worden door (functionele) combinatie van categorieën van hun componenten. Dit mechanisme staat uitvoerig beschreven in de eerder genoemde publikaties. Voor een goed begrip van het volgende volstaat het begrijpen van de achterliggende semantische typenstructuur, die we hier kort schetsen. (Dit is geen artikel over categoriale syntaxis: en we gaan dus niet nader in op de mogelijke speelruimte in de koppeling tussen syntactische categorieën en semantische typen.)

Uitgangspunt zijn basis-typen e (‘entiteit’ of ‘individu’) en t (‘waarheidswaarde’; E: ‘truth value’). Bijvoorbeeld eigennamen duiden individuele objecten aan, en hebben dus type e, terwijl gehele zinnen typisch t zullen toegewezen krijgen (maar misschien ook enkelvoudige woorden, zoals ‘ja’). Vervolgens is er één operatie die samengestelde typen vormt, van de vorm (a,b) (staande voor functies van type-a objecten naar type-b objecten). Voorbeelden van samengestelde typen, met een corresponderende talige realisering zijn de volgende:

(e,t):

toekenning van waarheidswaarden aan individuele objecten, ofwel één-plaatsige predikaten; gerealiseerd door
-intransitieve werkwoorden (‘schreit’)
-zelfstandige naamwoorden (‘papegaai’)

(t,t):

toekenning van waarheidswaarden aan waarheidswaarden, ofwel één-plaatsige waarheidsfuncties; gerealiseerd door
-zinsoperatoren (‘niet’, ‘noodzakelijk’)

Samenstellingen zijn ook weer te herhalen:

(e,(e,t)):

functies van individuen naar één-plaatsige predikaten, ofwel twee-plaatsige predikaten; gerealiseerd door
-transitieve werkwoorden (‘kiest’)
-transitieve zelfstandige naamwoorden (‘vijand’)

(t,(t,t)):

-binaire zinsoperatoren (‘en’, ‘als’)

We kunnen nu over welgevormde zinnen denken als die uitdrukkingen waarvan de (met hun syntactische categorieën gekoppelde semantische) typen ‘passen’ tot een eindtype t, via de ene regel

(a,b) + a ⇒ b
a + (a,b) ⇒ b	(Applicatie)
VOORBEELD ‘Sonja schreit’:	e(e,t)/t

Er is overigens niets geprivilegieerds aan de zinscategorie: we kunnen bijvoorbeeld ook samengestelde intransitieve werkwoorden herkennen.

VOORBEELD ‘kiest Teresa’:

(e,(e,t)) e/(e,t)

En dit combinatieproces suggereert zelf weer verdere typentoekenningen, getuige de volgende gevallen.

[p. 3]

VOORBEELD ‘[Een papegaai]NP schreit’:

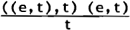
Het algemene NP-type is hier ((e,t),t) (niet: e) - om de bekende Fregeaanse redenen: NP's duiden in het algemeen geen individuele objecten aan, maar eigenschappen van hun VP-predikaten. Gezien dit resultaat volgt dan het determinatortype vanzelf:

‘[een]Det papegaai’:

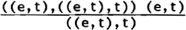
Anders gezegd, een determinator heeft twee predikaten nodig om een zin te vormen. We beschouwen nog enkele categorieën.

VOORBEELD ‘een [[oude]Adj papegaai]’:

Een bijvoeglijk naamwoord als ‘oude’ modificeert een éénplaatsig predikaat tot een (complex) één-plaatsig predikaat: type ((e,t), (e,t)). Eenzelfde type gaat op voor bijwoorden (‘schreit [hartverscheurend]_Adv’). Een laatste voorbeeld: voorzetsels combineren met NP's tot zulke predikaatmodificatoren (‘[met]_Prep een papegaai’), en hebben derhalve type (((e,t),t),((e,t),(e,t))). Dit laatste is zowat het meest ingewikkelde type dat we in de praktijk tegenkomen.

Nogmaals, we kunnen ons dus het proces van herkenning van een uitdrukking meteen voorstellen als de opbouw van een mogelijke semantische interpretatie via, combinatie van zijn typen. Daarbij kunnen nog wel alternatieve ‘lezingen’ optreden, weerspiegeld in verschillende constituentenstructuren.

VOORBEELD ‘Vaak schreit Sonja niet’:
lezing 1:	(‘vaak niet’)
lezing 2:	(‘niet vaak’)

Dit is de standaard categoriale grammatica, met de volgende modellen op de achtergrond. Voor elk type a is er een domein D_a waar D_e een of ander ‘discussieuniversum’ is van de relevante individuen, D_t bestaat uit de conventionele waarheidswaarden {0,1} - en D_{(a b)} de verzameling is van alle functies f : D_a → D_b, met domein D_a en beeld bevat in D_b. (Dit is ook de kern van de extensionele modeltheorie in de Montague Semantiek. Zie Gamut 1982.)

We kunnen in deze modellen natuurlijk meerdere genres talen interpreteren. Bijvoorbeeld, een handige logische taal ‘op maat’ heeft variabelen van elk type (x_a,y_a,...), en evenzo constanten (c_a,d_a,...) - met de volgende syntactische operaties:

-	als t1 een term is van type (a,b) en t2 één van type a, dan is t1(t2) een term van type b. (Applicatie)
-	als t een term is van type b en x een variabele van type a, dan is λ x.t een term van type (a,b). (Lambda-Abstractie)
-	als t1, t2 termen van eenzelfde type zijn, dan is t1 ≡ t2 een term van type t. (Identiteit)

[p. 4]

Deze taal zal geschikt blijken als logisch steno voor natuurlijke taai-betekenissen.

Gaandeweg is gebleken dat doorvoeren van een Categoriale Grammatica een extra idee vereist, te weten de introductie van type-veranderingsregels. Zo willen we graag ‘schreit niet’ op zich als één-plaatsig predikaat beschouwen; waarbij dan ‘niet’ niet als zinsnegatie, maar als werkwoordsnegatie moet optreden:

‘schreit niet’:

De overgang hier is de zgn. Geach Regel:

Type (a,b) kan verspringen naar ((c,a),(c,b)), voor elk type c.

Een andere toepassing hiervan beregelt NP's in direct-object-positie:

‘kiest een papegaai’:

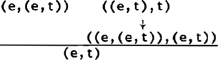
Er zijn ook andere type-veranderingen voorgesteld, zoals de Montague Regel, die coördinaties toestaat als in ‘Sonja en een papegaai’: waar ‘Sonja’ van type e naar het NP-type ((e,t),t) moet worden verheven. Algemeen:

Type a kan verspringen naar ((a,b),b), voor elke b.

Dergelijke regels zijn niet willekeurig. Ze vertonen een fraai systeem dat reeds in de jaren vijftig door J. Lambek werd ontdekt. (Voor een logische uiteenzetting, zie Van Benthem 1986c.) Dit systeem uit zich onder meer in simpele ‘recepten’, formuleerbaar in de eerder gegeven formele taal, om de betekenis van een uitdrukking na een type-sprong te herleiden tot zijn oorspronkelijke.

VOORBEELD ‘schreit niet’:

Nieuwe betekenis voor ‘niet’:

»x_(e,t). »y_e. niet (x(y));

en daarmee voor ‘schreit niet’:

»x_(e,t). »y_e. niet (x(y)) (schreit)

ofwel:

»y_e. niet (schreit (y)).

De precieze aard en kracht van het typeveranderingssysteem in natuurlijke talen staan overigens nog ter discussie.

Een categorische semantiek biedt een kader voor studies van globale semantische verschijnselen in natuurlijke talen, zoals in paragraaf 1 aangestipt. Maar ook laten zich vele detailstudies inpassen van categorieën uitdrukkingen op zich,

[p. 5]

zoals determinatoren of NP's. Bijvoorbeeld, het zgn. Gegeneraliseerde Kwantor-perspectief is niet anders dan de studie van de categorieën ((e,t),t) en ((e,t), ((e,t),t)). We zullen in het vervolg soms teruggrijpen op dit speciale gebied (zie bijvoorbeeld Barwise and Cooper 1981, Zwarts 1981, Van Benthem 1986a).

3. Situaties

De gedachte dat zinnen waarheidswaarden aanduiden is een technische abstractie, bedacht door Frege om het idee te kunnen doorvoeren dat elke talige uitdrukking naar ‘iets’ verwijst. En als zodanig is deze kunstgreep zeer nuttig gebleken. Niettemin zal duidelijk zijn (en is ieder weldenkend semanticus altijd duidelijk geweest) dat deze abstractie ver staat van de realiteit. Zinnen zijn veeleer beschrijvingen van wisselende ‘situaties’ waarover we mededelingen doen. Dit bleek reeds bij de invoering van modellen in het voorgaande, waar D_e een of ander ‘discussiedomein’ was, dat per (of zelfs tijdens een) conversatie kan veranderen. En deze speling blijkt ook in een taalkundige semantiek essentieel, zodra zich zgn. intensionele constructies voordoen, die refereren aan méér dan alleen de huidige situatie. Men kan hier denken aan de notoire filosofische voorbeelden, maar het verschijnsel is werkelijk zeer algemeen. Zelfs als de dansers in de huidige situatie de zangers zijn, dan nog hoeven de ‘langzame dansers’ niet de ‘langzame zingers’ te zijn (het bijwoord ‘langzaam’ is non-extensioneel), noch ‘dansen’ hetzelfde als ‘zingen’ (infinitief-vorming is evenmin extensioneel). Er is dus alle reden meerdere situaties tegelijk in onze modellering toe te laten.

Deze speelruimte zat ook al van meet af aan in de gangbare extensionele Tarski-semantiek. Maar veel gebruikers daarvan plegen toch eerder te denken aan één vast model voor de beschreven taal: zeg een soort fysische en conceptuele kosmos als schouwtoneel voor alles wat wij verder nog kunnen beschrijven. Aan het andere extreem vinden we dan talloze vluchtige ‘momentane beschreven situaties’. In de praktijk ligt echter voor de hand dat beide een rol spelen: kleinere beschreven situaties zwevend in een groter achtergrondmodel. (Voor verdere discussie, mede in verband met mogelijke werelden-semantiek en ‘situatie-semantiek’, zie Van Benthem 1986d.) Wij zullen ons hier niet precies vastleggen op de te hanteren situatie-structuren. We nemen alleen aan dat modellen voortaan verzamelingen situaties bevatten, eventueel geordend door bepaalde nuttige relaties, zoals inclusie of temporeel voorafgaan.

De natuurlijke denonatie voor zinnen wordt nu simpelweg deze: ze verwijzen naar verzamelingen situaties! (Alternatief: zinnen beschrijven ‘situatie-typen’: zie paragraaf 5.) Bijvoorbeeld: ‘Een papegaai zingt’ beschrijft al die situaties waarin een zingende papegaai aanwezig is. Natuurlijk kan een spreker één speciale situatie op het oog hebben waarover hij rapporteert - maar dat kunnen we dan reconstrueren als ‘de situatie die ik bedoel is van het type uitgedrukt door deze zin’. Zo gezien moeten we nu het eerder toegekende type t herinterpreteren: van ‘waarheidswaarde’ tot ‘verzameling situaties’. We kunnen dit als volgt met typen coderen. Er wordt een nieuw basistype s ingevoerd (voor situaties) met bijbehorend domein D_s en er vindt een type-verandering plaats, als volgt:

oud type t wordt nieuw type (s,t).

Hier staat rechts ‘t’ weer voor waarheidswaarde, en (s,t) voor 1-plaatsig predikaat over situaties, of Montagoviaans: voor een ‘propositie’.

Men kan deze Intensionalisering ook anders motiveren: door erop te wijzen dat zinnen proposities uitdrukken, eerder dan waarheidswaarden - en dan op te merken dat, onder minimale voorwaarden, een structuur van proposities altijd valt te herbeschrijven als een familie van deelverzamelingen van zekere abstracte collectie van ‘indices’, ‘werelden’, ‘situaties’. (Zie Van Benthem 1985, Stalnaker 1986.)

[p. 6]

Het effect van deze type-verandering valt te illustreren aan eenvoudige zinnen (vergelijk paragraaf 2).

VOORBEELD ‘Sonja schreit’:

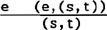
De uitgedrukte propositie is thans de klasse der situaties waarin Sonja schreit.

VOORBEELD ‘Sonja schreit niet’:

Om hier de juiste betekenis te krijgen moeten we aannemen dat ‘niet’, nu opgevat als operatie op proposities, werkt als een complement op verzamelingen situaties. Hoe dit bereikt moet worden, blijkt later.

De aldus ontstane typen vertonen een zekere gelijkenis met die welke we aantreffen in Montague Semantiek - en dit is niet toevallig (vergelijk Van Benthem 1986b voor het precieze verband). Ook de interpretatie-vragen zijn zonder meer vergelijkbaar. Bijvoorbeeld, nu elk predikaat, om zo te zeggen, een extra situatie-index s draagt, ontstaan diverse opties.

VOORBEELD ‘Elke papegaai zingt’.

‘Lokaal’ kunnen we dit laten slaan op alle situaties waarin alle papegaaien binnen die situatie zingen. Maar het is ook heel goed mogelijk dat we de papegaaien uit een andere situatie bedoelen, die in de beschreven situatie zingen. De nieuwe, rijkere typentoekenning staat dit in elk geval toe: en misschien moeten we hier ook niet verder reglementeren. (Een linguïst als M. Enç heeft zelfs beargumenteerd dat elke vorm van situationeel ‘invangen’ hier kan voorkomen.)

Het blijkt dus dat interpretatie van uitdrukkingen in een ruimere intensionele typen-structuur geen principiële problemen oplevert (al moeten wel enkele knopen worden doorgehakt). Wel rijzen in dit nieuwe perspectief meteen vragen betreffende de verhouding tot de eerdere extensionele categoriale grammatica. In hoeverre behoudt die haar waarde?

Eén van die vragen is meer syntactisch. Er is vaak door taalkundigen opgemerkt dat intensionele constructies, hoe intrigerend ook semantisch, syntactisch vrij saai zijn: ze gedragen zich als alle andere. Eén ding dat we dan zouden wensen is een zekere ‘conservativiteit’: overschakelen op de nieuwe intensionele typen hoort de oude syntactische constituentenstructuren op te leveren: niet meer, en niet minder. En inderdaad valt te bewijzen dat een rij oude e,t-typen tot een eindtype a combineert in onze vorige calculus dan en slechts dan als hun nieuwe e,t,s-versies dat doen. (Een bewijs staat in Van Benthem 1986b.) Dit was al te zien aan de eerdere voorbeelden.

Maar er zijn natuurlijk ook meer semantische vragen. Zoals we boven zagen zijn de nieuwe intensionele typen het natuurlijke leefklimaat voor meer intensionele uitdrukkingen. Bijvoorbeeld, een uitdrukking als ‘vaak’ komt qua betekenis niet tot zijn recht in het oude type (t,t): het is eigenlijk geen één-plaatsige waarheidsfunctie. Maar, als functie van proposities naar proposities kan zij zinvol zeggen dat ‘in veel situaties’ de betrokken gebeurtenis moet optreden. Aan de andere kant zijn er ook extensionele uitdrukkingen die niet echt van betekenis veranderen in het nieuwe kader. Een voorbeeld is de eerdere negatie ‘niet’, die per situatie nog steeds de oude waarheidsfunctionele negatie blijft. Is er in dit laatste geval een betekenisveranderingsregel, die extensionele betekenissen ‘kosmetisch’ intensioneel maakt?

In het geval van ‘niet’ ligt zo'n regel voor de hand: de overgang van (t,t) naar ((s, t),(s,t)) is een geval van het eerdere Geach patroon (vergelijk de stap naar ((e,t),(e,t))): en een geheel analoog veranderingsrecept werkt. Betekent dit

[p. 7]

nu dat we de stap van t naar (s,t) als een type-veranderingsregel kunnen opvatten analoog aan die van paragraaf 2? De meningen hierover lopen uiteen: ikzelf denk ‘alleen maar zeer ten dele’ (en zie Van Benthem 1986b voor nadere uitwerking). In elk geval schuilt hierachter ook een verrassende vraag. Hoe moeten we semantische ‘extensionaliteit’ eigenlijk algemeen definiëren in intensioneel gemaakte modellen? Dit blijkt niet eens vanzelf te spreken (getuige ook de vele epicycles op dit punt in Keenan and Faltz 1985) - en daarmee houdt de verhouding tussen onze eerdere extensionele aanpak en de huidige intensionele toch zo zijn geheimen.

Het is dus niet zonder meer duidelijk hoe de eerdere extensionele modelstructuren technisch ingepast moeten worden in de nieuwe intensionele. De oude extensionele denotaties zijn nog wel aanwezig als een soort ‘limiet-geval’, wanneer we de aandacht beperken tot geïsoleerde situaties - maar er resten onplezierige technicalia. Niettemin, de geest van de eerdere extensionele modeltheorie blijft zeker overdraagbaar. Voor puur intensionele noties blijken vragen en antwoorden van belang die oorspronkelijk voor extensionele ontwikkeld waren. Zo is het intensionele type der tweeplaatsige zinsoperatoren, te weten ((s,t),((s, t), (s,t))), formeel vrijwel identiek met dat der determinatoren. En inderdaad blijken eerdere definieerbaarheidstechnieken voor (monotone) gegeneraliseerde kwantoren hier evenzeer toepasbaar (zie Van Benthem 1986a, hoofdstuk 4).

Overigens kunnen dergelijke toepassingen wel leiden tot belangrijke verfijningen. Dit is te illustreren aan de belangrijke notie van monotonie zelf. Bijvoorbeeld, opwaartse monotonie voor een NP als ‘elke slang’ wordt vaak op verschillende manieren uitgelegd. Eén, de canonieke, is deze. Als elke slang P-t en het predikaat P impliceert zeker predikaat Q (ofwel: Q heeft een grotere extensie dan P), dan volgt dat elke slang Q-t. Maar ook treft men wel het meer levendige volgende verhaal. ‘Stel dat elke slang P-t, en we leren vervolgens dat de extensie van P groter is dan we dachten, dan nog blijft gelden dat elke slang P-t’. Deze stabiliteit is welbeschouwd een conglomeraat van twee wijzen van groei. Ten eerste kan P blijken op te gaan voor meer individuen in de oude situatie: en dan hebben we precies de eerdere monotonie. Ten tweede kan P echter blijken op te gaan voor nieuwe individuen in een nieuwe (of toch nog de oude?) situatie. Dit tweede soort gedrag volgt zeker niet uit het eerste. Bijvoorbeeld, ‘elke P is Q’ is monotoon met betrekking tot Q binnen één vaste situatie; maar bij uitbreiding van de situatie (met groeiende Q) hoeft deze bewering toch niet te blijven gelden. (Er kunnen immers extra P's zijn bijgekomen die Q missen). Pas in een structuur met verschillende situaties kunnen we dergelijke verschillen signaleren en verantwoorden. Zelfs vanuit een extensioneel perspectief kan het dus nuttig zijn naar meer situaties tegelijk te kijken.

4. Tijd

Een andere vorm van afwisseling in ons wereldbeeld komt voort uit temporele structuur. We kunnen zelfs de vorige situaties in eerste instantie duiden als temporele entiteiten. In een minimale opzet kunnen dan de eerdere indices D_s worden opgevat als tijdstippen, die fungeren als momentopnamen van zekere moederstructuur (‘de Geschiedenis’). De dan opkomende vraagstellingen zijn geheel analoog met die in de voorafgaande paragraaf; zij het met een duidelijke couleur locale. Bijvoorbeeld, éénplaatsige zinsoperatoren (type ((s,t),(s,t))) hebben nu een veel interessantere structuur, dankzij de aanwezigheid van een volgorde op tijdstippen. Zo geeft Van Benthem (1986a: hoofdstuk 5) een classificatie van mogelijke ‘werkwoordstijden’ in termen van monotonie en andere passende eigenschappen. Het blijkt dat juist de gangbare ‘perspectivische’ operatoren voldoen: heden, verleden, toekomst / progressive en varianten/en ‘drempeltijden’ als ‘net gezongen’, ‘net gaan zingen’. (De term ‘werkwoordstijd’ is hier eigenlijk misplaatst. Het gaat veeleer om operatoren die gebeurtenissen in temporeel perspectief plaatsen; waarna de echte tijden (OTT, OVT) dit totale beeld deictisch in de echte tijd verankeren.)

[p. 8]

Maar men kan natuurlijk ook heel goed de wending meemaken naar een interval-semantiek (zie Dowty 1979, Van Benthem 1982), en de D_s-objecten navenant opvatten, met naast een ordening van temporeel voorafgaan nu ook één van temporele inclusie. Weer rijker is nog een gebeurtenis/proces-semantiek (als in Kamp 1979). Telkens blijven hierbij de algemene conclusies van paragraaf 3 van kracht, terwijl de extra temporele structuur daarnaast zijn eigen vragen genereert. Tenslotte ligt het echter toch voor de hand de twee perspectieven te combineren: er zijn situaties, en die hebben zelf weer temporele structuur. (Dit is bijvoorbeeld de manier van Barwise and Perry 1983 - die uiteindelijk daarbij het begrip ‘situatie’ oprekken tot een zgn. ‘course of events’: een door de tijd uitgestrekt stukje geschiedenis.)

In deze paragraaf beperken we ons tot één simpele keuze, om nieuwe verschijnselen te illustreren die voortvloeien uit de eigenaardigheden van temporele situaties. We laten daartoe D_s bestaan uit intervallen, gelicht uit een of andere achtergrondgeschiedenis.

Wanneer we nu de thema's van paragraaf 3 weer langslopen, is de eerste vraag hoe de getemporaliseerde basis-uitdrukkingen te interpreteren. Met name, hoe duiden we ‘x heeft P op interval i’? Zoals bekend, kleven hieraan enkele vaagheden. Wordt nu bedoeld P over de hele i, of op minstens een deel, of nog iets anders? In de praktijk is dit niet geheel exact te beslechten - en misschien is dat ook niet nodig. We komen op deze kwestie nog terug.

In elk geval gaat nu een nieuw aspect spelen, veroorzaakt door de op intervallen aanwezige inclusierelatie (⊑). Bijvoorbeeld, sommige soorten predikaten P zijn ‘homogeen’, in die zin dat als x aan P voldoet op i, dan voldoet x ook aan P op elk interval j bevat in i. (Dit geldt bijvoorbeeld voor activiteiten als reizen of toestanden als verliefd zijn - extreem korte fysische subintervallen daargelaten). Andere zijn niet-homogeen, maar juist bijvoorbeeld ‘atomair’, in de zin: als x voldoet aan P in i, dan is er geen j echt bevat in i waar x nog P heeft. Dit is een sterke ontkenning van de eerdere homogeniteit. (Merk op dat dit alleen een relatieve ‘ondeelbaarheid’ van i geeft met betrekking tot P, en geen absolute ondeelbaarheid in een of andere sterke fysische zin.)

Daarnaast kunnen we ook indelen naar andersoortige eisen, zoals ‘termineren’ (een eigenschap die refereert aan de temporele ordening < van intervallen). Dit zijn vooralsnog niet meer dan welbekende observaties uit de semantiek van aspecten en Aktionsarte (waarover veel recente Nederlandse literatuur bestaat, in Groningen en elders).

Waar het hier om gaat is echter niet dit gebied op zich, maar alleen de juiste manier van inpassen van dit verfijnde temporele perspectief in het categoriale wereldbeeld. Globaal gezien blijven wel de bevindingen van paragraaf 3 van kracht; maar elke nieuwe structuur genereert natuurlijk zijn eigen additionele vragen, die soms ook weer terugwerken op de oude theorie.

Een voorbeeld van dit laatste vormt de notie van inclusie. Ook tussen situaties hadden we eigenlijk reeds verschillende noties van inclusie kunnen onderscheiden. Een situatie omvat diverse individuen en relaties daartussen, maar is niet noodzakelijk identiek met een loutere lijst van deze gegevens. Zo gezien, is er om te beginnen een notie van verdere specificatie van een situatie, door meer feiten erover te geven. Daarnaast kan men spreken over echt uitbreiden van kleinere tot grotere situaties, via een of ander ⊑-patroon. En wanneer we ‘modale’ en ‘temporele’ situaties gaan mengen, vermenigvuldigen zich de mogelijkheden. In alle gevallen rijzen daarbij vragen over al dan niet geldig blijven van beweringen bij het overgaan naar omvattende, of omvatte situaties, zoals we zagen bij homogene predikaten, maar ook al eerder bij monotone determinatoren.

Tot slot onderzoeken we enkele meer concrete illustraties van deze mogelijke wisselwerkingen.

De eerdere nevenschikking suggereert een parallel, die in de literatuur ook vaak

[p. 9]

wordt aangehaald, tussen temporele en ‘gewone’ monotonie. Is bijvoorbeeld ‘dansen’ niet een predikaat dat voldoet aan precies dezelfde formele eigenschappen die de theorie der gegeneraliseerde kwantoren zou toekennen aan een NP als ‘geen mens’? In beide gevallen lijkt de structuur immers die van een zgn. ideaal, met eigenschappen van ‘monotone daling’ en ‘homogeniteit’:

-	als x danst op i en j ⊑ i, dan danst x op j
-	als x danst op i en op j, dan danst x op de vereniging i ⊏ j.

(Eigenlijk is dit alleen evident als i,j temporeel overlappen.) Evenzo,

-	als ‘geen mens P’ en Q⊆P, dan ‘geen mens Q’
-	als ‘geen mens P’ en ‘geen mens Q’ dan ‘geen mens P⋃Q’.

Hoe aantrekkelijk ook, dit soort analogieën tussen de extensionele theorie van gegeneraliseerde kwantoren en die van temporele uitdrukkingen blijkt bij nadere beschouwing weinig hout te snijden. We werken dit nader uit, om te illustreren dat temporaliseren van de oude theorie de nodige zorg behoeft (met enig wantrouwen tegen wiskundige fata morgana's).

Bijvoorbeeld, categoriaal oogt de boven gesuggereerde analogie reeds verdacht. ‘Dansen’ heeft type (e,t), ‘geen mens’ het NP-type ((e,t),t). De (dalende) monotonie van deze laatste uitdrukking hangt samen met de Boolese inclusierelatie op het (e,t)-domein - en daarvoor heeft D_e geen analoog. En bovendien, de ‘daling’ bij ‘dansen’ heeft niets te maken met het e-argument (vergelijk de bovenstaande parameter x), maar eerder met het t-argument, of beter, de D_s bij het geïntensionaliseerde type (e,(s,t)). En de relevante temporele inclusie-structuur op D_s is van geheel andere aard dan de Boolese (en moet ook ‘van buiten af’ in modellen worden ingevoerd). Dit wil niet zeggen dat een algemene motivering van ‘stabiliteit’ niet in beide gevallen kan spelen, maar er is geen naadloze parallel.

Hoe vaart zo gezien een andere beweerde parallel, en wel die tussen VP's en zelfstandige naamwoorden? Onlangs verdedigde Bach (1986) bijvoorbeeld nog met klem de vele analogieën tussen VP's, opgevat als verwijzers naar ⊑-gestructureerde stukjes tijd, en niet-telbare zelfstandige naamwoorden, opgevat als verwijzers naar stukjes materie met een of andere fysische inclusie-relatie. Hier is de categoriale grammatica geheel akkoord: VP en ZNW hadden oorspronkelijk zelfs beide hetzelfde type (e,t). Nochtans valt ook hier een evidente discrepantie te bespeuren na de temporalisering tot type (e,(s,t)): immers, de inclusies spelen in het VP-geval in het s-argument, in het (niet-telbare) ZNW-geval in het e-argument! We moeten dus in elk geval omzichtig te werk gaan bij het claimen van vergaande analogieën.

Misschien urgenter dan een volmaakte isomorfie tussen temporele VP-verwijzingen en gegeneraliseerde kwantoren is hun samenleven bij zinsinterpretatie. En dat blijkt in elk geval harmonieus. Bijvoorbeeld, hoe verloopt de interactie tussen transitieve werkwoorden en direct object NP's in de opbouw van een VP, zeg, ‘zingt elk lied’? Hier werkt gewoon de standaarduitleg van paragraaf 3: voor elk individu x, duidt deze uitdrukking de intervallen aan waarop x ieder lied-in-dat-interval zingt.

Kan dit wel het hele verhaal zijn? In de literatuur wordt vaak gesproken over de ‘compositionele opbouw’ van aspect, waarbij het temporele gedrag van de complexe VP systematisch ontstaat tijdens de bouw van diens betekenis. Met name moeten daarbij verschuivingen in temporeel monotonie-gedrag mogelijk zijn. Maar dat gebeurt in het bovenstaande ook. Bijvoorbeeld, bij beschouwen van diverse genres objects-NP valt het volgende te noteren. Hoewel ‘zingen’ neerwaarts ⊑-bewaard bleef, verdwijnt deze eigenschap bij objecten als ‘de Marseillaise’, ‘een schlager’, ‘elk lied’. Bijvoorbeeld, als x op i elk lied-in-i zingt, dan maakt hij in sommige subintervallen wellicht bepaalde daar voorkomende liederen (nog) niet af. (Evenmin blijft elk lied zingen opwaarts ⊑-bewaard: iets wat een opper-

[p. 10]

vlakkige analogie met de stijgende monotonie van de NP ‘elk lied’ zou kunnen doen vermoeden). Omgekeerd creëren sommige objecten juist temporele monotonie: ‘geen taak volbrengen’ is neerwaarts ⊑-bewaard, hoewel ‘volbrengen’ op zich deze eigenschap ontbeert. Dit zijn natuurlijk slechts illustraties - en er resteren diverse vragen.

Er schuilen nog vele andere subtiliteiten in de opbouw van aspect, zoals de invloed van verdere temporele bepalingen, adverbia, en dergelijke (zie Verkuyl 1972). Maar gezien het bovenstaande mag onze verwachting luiden dat niets de incorporatie van daar verworven inzichten in een getemporaliseerde categoriale grammatica in de weg staat.

De twee voorgaande paragrafen leiden tot de volgende conclusies. Het is inderdaad mogelijk een extensionele categoriale grammatica intensioneel/temporeel te verrijken tot een passend medium voor interpretatie van non-extensionele uitdrukkingen. (Zoveel was in wezen ook wel duidelijk vanuit de Montague Semantiek.) Wel resteren enkele technische problemen bij het zo glad mogelijk inpassen van de oorspronkelijke extensionele denotaties. Maar de hoofd-ideeën uit de theorie van dat extensionele raamwerk blijken nog steeds dienstig - met dien verstande dat hun oorspronkelijke formuleringen nu soms oplossen in een familie van mogelijke varianten. Dat laatste is evenwel de prijs die we betalen voor elke rijkere modeltheorie.

Appendix

De voorafgaande discussie volgde de grote lijn van recente literatuur over tijd en aspect, in het aanhalen van ‘standaardwijsneden’ over temporele gedragingen (zoals de inclusie-monotonie van activiteitswerkwoorden). Het semantisch geweten gebiedt echter te bekennen dat deze kwesties bij nadere beschouwing toch vrij complex liggen.

Om te beginnen, er wordt altijd gewezen op standaardvoorbeelden zoals het bewaard blijven van, zeg, ‘x leest’ bij het afdalen naar temporele subintervallen. Maar in wezen is een oordeel hier al vrij lastig te geven: wat betekent deze frase op zich? We kunnen het opvatten als een progressive (‘x is aan het lezen’), en dan klopt de bewering over subintervallen - maar we kunnen het ook opvatten als elliptisch voor ‘x leest iets’. En dan wordt de vraag hoe we beweringen als ‘x leest y’ willen opvatten: met voltooid aspect, of niet. Anders dan bijvoorbeeld de Russen markeren wij dit verschil niet, en daarmee heeft zo'n basisbewering al twee verschillende gebruiksvijzen, met kennelijk verschillende vormen van temporeel monotoniegedrag.

Een verwante variatie betreft de aard van de eerder genoemde semantische clausules ‘x leest y op interval i’. Wat is de intuïtie achter zo'n constatering over i:

A	i valt precies samen met de tijdsduur van een complete ‘x,y-leesgebeurtenis’, of
B	i omvat zo'n tijdsduur, of
C	i is bevat in zo'n tijdsduur?

Veel mensen zijn geneigd hier voor A te opteren (i moet een ‘passende’ tijdspanne zijn), maar alternatieven zijn verdedigbaar. Weer zal duidelijk zijn dat oordelen over temporele monotonie sterk afhangen van de duiding van de i-formule.

Meningen over deze laatste kunnen overigens worden beïnvloed door het beschouwen van de interactie met complexe objects-NP's. Zo zou een aanhanger van visie A in eerste instantie kunnen instemmen met de eerder genoemde uitleg van ‘x leest elk boek op i’, als het in i uitlezen van elk in i aanwezig boek. Maar daarbij kan voor elk boek apart slechts een deel van i nodig zijn geweest: zodat we toch bij visie B zijn beland.

Ditzelfde kan anders belicht worden, als een kwestie van toegestane gevolg-

[p. 11]

trekkingen over een interval. Stel dat x elk boek leest op i, en ‘In Cold Blood’ figureert in i, volgt dan dat x op i dit speciale boek leest? Wel in visie B, maar niet in visie A... Dat bij bepaalde wijzen van interpretatie gangbare logische gevolgen in gevaar kunnen komen hoeft overigens niet te verbazen. Met name wanneer ‘minimaliteits-overwegingen’ een rol spelen is dit geen onbekend verschijnsel. (Bijvoorbeeld, in een denktrant van ‘niet beweerd = onwaar’ zou de onschuldige gevolgtrekking van ‘A en B’ naar ‘A’ reeds incorrect zijn: de conclusie zou gelezen worden als ‘A en niet-B’. Om zo te zeggen, de halve waarheid concluderen wordt bestraft.) Weer leidt dit tot het onderscheiden van verschillende gebruikswijzen voor i-formules: ‘minimaal’, ‘neutraal’, of wellicht nog anders.

Deze laatste zienswijze wordt bevestigd door te letten op verschillende genres vragen. ‘Wat deed je gisteren?’ ‘Ik las “In Cold Blood”.’ Er is een ‘minimale’ interpretatie van dit antwoord, met als passende reactie bijvoorbeeld ‘Dus van eerlijk werk is niets gekomen’. Maar er is ook een meer neutrale (‘En wat deed je nog meer?’). In het algemeen zal de pragmatische context hier duidelijkheid moeten verschaffen over het betreffende genre interpretatie.

Er is bij dit alles nog geen reden tot wanhoop. We kunnen immers de verschillende interpretatienormen allemaal bestuderen. Een eerste aanzet is de intervaltijdslogica in Van Benthem (1982), die een ‘neutrale’ basisnotie hanteert van ‘φ is waar op i’, maar dan verder operatoren heeft voor ‘waar in zeker subinterval’ (B-variant) en ‘waar in zeker superinterval’ (C-variant). Maar er valt ook meteen te werken met directe interpretatie van natuurlijke taal.

Dit onderscheid in temporele gebruikswijzen heeft diverse repercussies voor de eerdere extensionele theorie van natuurlijke taal. Zo zal bijvoorbeeld de bekende bewering dat transitieve werkwoorden ‘homomorfismen’ zijn, in de zin dat onder meer

V(NP₁ en NP₂) ↔ (V NP₁) en (V NP₂).

niet langer zonder kwalificatie opgaan. (Het geldt wel in de B-optiek, niet in de A-optiek). En iets soortgelijks geldt voor gevallen als ‘V(elke N)’. Er ontstaan verschillende lezingen die doen denken aan de ‘de re/de dicto’ -onderscheidingen in de gangbare intensionele logica (zij het dat de oorzaak een andere is).

Ons leven is dus wel rijker, maar niet rustiger geworden.

5. Moduleren op functies

Wellicht het centrale idee in Categoriale Grammatica is het gebruik van de functie/argument-structuur als syntactisch en semantisch bindmiddel. Deze uit zich zowel in het interpretatiemechanisme van woordgroepen als in de modelstructuur van de achterliggende functie-hiërarchieën. Tot op zekere hoogte zijn deze twee aspecten los te koppelen. Misschien kunnen we toe met minder functies, of juist met een ander gebruik van functies. Aan beide zal thans aandacht worden besteed, in een serie losse beschouwingen over diverse alternatieven voor de standaardopzet.

Functies of Relaties?

De feitelijke voorbeelden van categoriale combinaties zijn nogal gemengd. Zo is er het predikatieve patroon van ‘(Sonja) schreit’ tegenover het meer kennelijk functionele ‘(loopt) niet’, of ‘langzaam (lopen)’. Maar bijvoorbeeld voor determinatoren is weer een relationele kijk aantrekkelijk: ‘elke (slang, schreit)’ lijkt een binaire relatie uit te drukken tussen twee predikaten. Het zou wel eens zo kunnen zijn dat de natuurlijke taal hier niet uniform is: sommige combinatiewijzen berusten meer op een achterliggende relatie, andere op een functie. Zoals bekend, kunnen functies wiskundig als relaties worden opgevat, en vice versa: en

[p. 12]

dus is er geen technisch bezwaar tegen één uniforme keuze. Bijvoorbeeld, Montague (1974) neemt overal functies, en Barwise and Perry (1983) overal relaties. En de waarheid ligt uiteraard in het midden (Van Benthem 1986d): soms is het één nuttiger, soms het ander. In elk geval blijft het dan goed om in te zien dat Categoriale Grammatica eveneens zou zijn door te voeren met structuren van relaties, in plaats van functies, op de achtergrond. (Zie Muskens 1986 voor een relationele typentheorie, zijn voorgeschiedenis - en een pleidooi voor gebruik ervan in de moderne semantiek.)

Men zou kunnen denken dat linguïstische overwegingen hier nog een keuze kunnen forceren. Bijvoorbeeld, dwingen gewenste constituenten-structuren als ‘Sonja (ziet Teresa)’ of ‘(Elke slang) schreit’ ons toch niet tot het gebruiken van éénplaatsige complexe functies, die een volgorde der argumenten in de uitgedrukte semantische relaties coderen? Nee, want we zouden de typencombinatie kunnen laten werken als vroeger, en alleen de band met een uiteindelijke (relationele) evaluatie iets losser maken.

Totale of Partiële Functies?

Iets wat relaties iets gemakkelijker modelleren dan functies is partialiteit, dat wil zeggen niet-totale gedefinieerdheid van een functie in zeker domein. Zo hebben veel predikaten ‘selectie-restricties’ bij zich: ze zijn alleen zinvol toepasbaar op bepaalde soorten individuen. Dit is een linguïstisch algemeen geaccepteerd feit - en we moeten ons dus eigenlijk voorstellen dat typen-domeinen ingedeeld zijn in soorten, terwijl functies of relaties komen met indicaties binnen welke soorten hun argumenten en waarden mogen vallen. Dit lijkt een routineuze amendering; maar ze zal straks een grotere rol gaan spelen.

Overigens zijn er nog vele andere bronnen van partialiteit. Functies kunnen ongedefinieerd zijn, zelfs binnen een in principe acceptabele soort, door vaagheid, falen van presupposities, of gewoon rekenkronkels (zoals bij ‘delen door nul’).

Waar zit de Aantrekkingskracht?

Het gebruik van functies loste een oud filosofisch probleem op: wat is de conceptuele ‘lijm’ die een individu en een predikaat samenplakt tot een bewering? Men dacht hier wel aan een soort (onuitgesproken) predikatierelatie - maar raakte dan verzeild in de regressie van ‘wat plakt die relatie dan weer aan zijn argumenten?’ Frege's fameuze idee dat predikaten ‘onverzadigd’ kunnen zijn (technisch weergegeven als functies die hongeren naar argumenten) moest dit oplossen. Niettemin is ook dit maar een metafoor; en er zijn zeker filosofen die van harte opteren voor het oude alternatief: individuen en predikaten zijn allebei een soort ‘objecten’ (zie bijvoorbeeld Bealer 1982). De ‘lijm’ moet dan emergent ontstaan, als een applicatie-relatie, opgeroepen, zeg, door syntactische nevenschikking. (Of bijvoorbeeld, een werkwoordsstam zou het predikaat-als-object kunnen aanduiden, terwijl de persoonsvorm de applicatierelatie oproept.)

Voor semantiek van de natuurlijke taal is dit beeld voorgesteld in de ‘Situatie Semantiek’ van Barwise and Perry (1983) - en het leidt tot een theorie die functie-toepassing vervangt door conjunctie van eisen. Dit heeft diverse taalkundigen overtuigd, onder meer vanuit de volgende overweging. Eén van de aantrekkelijke kanten in bijvoorbeeld X̄-syntaxis is de analogie tussen zinnen, intransitieve en transitieve werkwoorden, als meer of minder volledige aanduidingen van ‘situaties’. Om die te handhaven zou het aanhechten van een direct object aan een transitief werkwoord liever begrepen worden als een toevoegen van verdere informatie over een situatie. En de situatie-semantiek doet dit, als volgt. ‘Kiest’ beschrijft een type ‘keuze’-situatie, met twee nog in te vullen ‘individual indeterminates’ x,y (‘x kiest y’). ‘Teresa’ beschrijft een indeterminate z in een situatie (gelijkgesteld aan degene die in die situatie ‘Teresa’ heet), en ‘kiest

[p. 13]

Teresa’ wordt de conjunctie van al deze eisen, onder identificatie van de twee beschreven situaties, alsmede van de indeterminates y en z. Voor complexe NP-objecten kan deze uitleg eveneens worden doorgevoerd; maar dan met behulp van zg. ‘rôle indeterminates’.

Opvallend aan de gegeven voorbeelden is overigens wel dat een sterke parallel aanwezig blijft met onze eerdere typenstructuur. De indeterminates corresponderen kennelijk met de argumenten in de betrokken typen ((e,(e,t)): twee individuen/ ((e,t),t): een rol). En inderdaad blijkt onze categoriale grammatica ook in deze trant ‘conjunctief’ interpreteerbaar te zijn (zie Van Benthem 1986d). We hebben in de situatie-semantiek alleen de functie-argument toepassing als het ware uitgesmeerd over abstracte situatietypen plus identificatie-instructies voor indeterminates.

Eén opmerkelijk punt verdient nog vermelding. Volgens Barwise en Perry moeten we bij dit alles toekunnen met slechts twee genres indeterminates: voor individuen en voor rollen. In categoriale termen vertaalt dit als volgt. We mogen ten eerste alleen typen gebruiken van de vorm (a₁ (a₂,...,t)...)): ook op te vatten als n-plaatsige relaties met argumenten van typen a₁,...a_n (respectievelijk). Bovendien mogen a₁ t/m a_n zelf slechts zijn van de vormen e of (e,t) (en misschien (e,(e,t)), (e,(e,(e,t))),...). Deze restrictie keert straks nog terug.

Opmerking

Nog een saillant punt in de situatie-semantische behandeling is dit. Wat categoriaal een functie in het domein D_(e,t) zou zijn wordt nu voorgesteld als een ‘geparametriseerde situatie’ - om zo te zeggen, een D_t-object met een gat erin. Evenzo zou een D_(e,e)-object een onvolledig individu zijn, waarin eerst nog een ander individu moet worden ingevuld om een echt individu te krijgen. Dit is curieus, maar toch ook intrigerend. Het sluit bijvoorbeeld aan bij oudere wiskundige ideeën over functies als ‘variabele waarden’ - en vormt daarmee weer een aardige conceptuele variatie voor het categoriale grammatica kader.

We stappen nu over van interpretatie-varianten naar alternatieve inrichtingen voor de categoriale modelstructuren.

Welke basisdomeinen?

Wat met enkele van de bovenstaande discussies in feite ook in het geding is, is de keuze der basisdomeinen in onze modellering. Tot nu toe waren dit een verzameling individuen D_b en een verzameling waarheidswaarden D_t (eventueel opgeblazen tot proposities). Maar, er is ook veel voor te zeggen om van meet af aan een tweede basisdomein D_p van eigenschappen of predikaten in te voeren. Dit werd reeds voorgesteld in Lewis (1972), en gebeurt evenzo weer in Keenan and Faltz (1985). Deze laatsten elimineren dan zelfs D_e (eigennamen gaan meteen naar type (p,t)); om met name twee taal-betrokken argumenten. Ten eerste zouden kinderen eerder predikaten leren hanteren dan namen van objecten - en ten tweede maakt een D_p,D_t-opzet elke categorie in het verdere systeem vatbaar voor Boolese operaties (‘niet’, ‘en’, ‘of’), een alomtegenwoordigheid die Keenan en Faltz ook inderdaad voelen.

Tot op zekere hoogte wordt deze keuze tussen D_e,D_p ondergraven door onze eerdere typeverandering-regels. Immers, in paragraaf 2 hadden we reeds de vrijheid over predikaten (e,t) te denken als verzamelingen individuen, maar evenzeer over individuen als bundels (zij het speciale) van predikaten, via de Montague omzetting van e in ((e,t),t). Indien we bovendien de filosofische controverse niet duidelijk beslecht achten ten faveure van één van deze beide concepties, dan ligt een compromis voor de hand: sta een meersoortig basisdomein toe, met (onder meer) ‘echte’ individuen, maar ook predikaten-als-objecten. Het ligt dan overigens nog steeds in de rede een dubbel perspectief te hanteren: predikaten als objecten ‘kleven’ niet, en daarnaast willen we misschien dus ook nog een ‘onver-

[p. 14]

zadigde’ D_(e,t) versie. Denk aan een predikaat in D_p als een sticker met plakstrook erop, de correponderende D_e,t-versie heeft de plakstrook verwijderd. Dit heeft ook nog een serieuze linguïstische achtergrond: aanbrengen van de plakstrook zou corresponderen met nominalisering (zie beneden).

Groeien van Typen

Na een keuze der basisdomeinen kunnen we ook de constructie van hogere typen(-domeinen) ter discussie stellen. Zo zijn extra typen-vormende operaties denkbaar, zoals toestaan van meer argumenten tegelijk (bijvoorbeeld de conjunctie ‘en’ lijkt echt binair: ‘(t - t, t)’); en daarmee de vorming van produkt-typen a × b voor domeinen van geordende paren (levend in het Cartesisch produkt D_a × D_b). Dit valt allemaal onder de noemer ‘kleine wiskundige variaties’. Serieuzer is echter de volgende kwestie. Het lijkt wel alsof het met de inhoud van typen-domeinen precies de verkeerde kant opgaat: de functionele domeinen nemen exponentieel in omvang toe, terwijl het aantal talige (basis-)uitdrukkingen in hogere typen juist steeds schaarser wordt. (Vergelijk de opmerking in paragraaf 2 dat het met de voorzetsels, in type (((e,t),t), ((e,t), (e,t))), wel is gebeurd.) In Chierchia (1985) vinden we zelfs de empirische hypothese dat in natuurlijke talen geen uitdrukkingen voorkomen met een type van orde hoger dan 3. Hierbij is de orde van een type als volgt recursief gedefinieerd: de orde van basistypen is 0; orde (a,b) = maximum (orde (a) + 1, orde (b)). (De orde van NP's is dus bijvoorbeeld 2, evenals die van determinatoren; terwijl voorzetsels orde 3 hebben.) Ordes meten de complexiteit van argumenten in een type. Bijvoorbeeld, de situatiesemantische these dat alleen e en (e,t)-‘rollen’ voorkomen als argumenten zou zelfs een restrictie inhouden tot hoogste orde 2.

Nu kan men dit op verschillende manieren verwerken. Eén is om te laten zien dat hogere typen in een of andere natuurlijke zin ‘overbodig’ zijn. Bijvoorbeeld, Zwarts (1986) wijst erop dat, door een resultaat van Gaifman, elke contextvrije taal zelfs reeds met eerste-orde typen valt te herkennen: dus om syntactisch-combinatorische redenen hoeven we niet hogerop. Een meer intrinsieke semantische verklaring zou kunnen liggen in een of ander definieerbaarheidsresultaat van denotaties in hogere-orde typen in termen van lagere: eventueel alleen eerste-orde. Op dit thema komen we later nog terug.

Een eerste-orde-restrictie sluit goed aan bij het feit dat de enige objecten die we zelfstandig kunnen bevragen in natuurlijke taal individuen lijken te zijn (‘wie’, ‘wat’). Zelfs een schijnbaar hogere-orde geval als ‘hoe’ (‘Hoe vermoordde Barry Jason?’ ‘Met een spade.’) blijkt bij nader inzien toch eerder genominaliseerde voorzetsel-bepalingen te betreffen: ‘Met een spade is hoe Barry Jason vermoordde’. Het lijkt algemeen alsof we objecten eerst moeten overhvelen naar het individuendomein om ze te kunnen bevragen. (Dit geldt evenzo voor kwantificeren. Zo is een bekende ‘hogere-orde’-zin als Russels ‘Napoleon had alle eigenschappen van een groot generaal’ juist geen kwantificatie over D_e,t maar over een ‘deelsoort’ van D_e: en wel die individuen die aan het predikaat ‘eigenschap’ voldoen.)

Bijna alle in paragraaf 2 genoemde typen zijn reeds eerste-orde in e,p,t; wanneer we p als extra basistype nemen. Er resteert slechts het tweede-orde geval der voorzetsels: ((p,t), (p,p)). Maar hier is in ieder geval een lagere inschaling verdedigbaar (vergelijk Keenan and Faltz 1985): te weten (e,(p,p)).

VOORBEELD ‘danst met Jan’:

Voor een complex NP-argument (‘danst met elk mens’) hanteren we dan een typeveranderingsregel; of eventueel een andere constituentenstructuur:

[p. 15]

De betekenis wordt daarmee het correcte ‘voor elk mens x, danst met x’.

Groeien van domeinen

Met het beheersen van de typen-constructie beheersen we tevens de groei der (relevante) functiedomeinen. Maar er zijn ook andere, onafhankelijke manieren om dit effect te bereiken. Daarbij dienen dan wel twee zaken te worden onderscheiden: de structuur der mogelijke denotaties, en daarbinnen die der in de taal gerealiseerde denotaties. Juist de spanning tussen deze twee zorgt voor enkele der aardigste resultaten in Keenan and Faltz (1985) of Van Benthem (1986a). Er worden daar semantische constraints geformuleerd waaraan natuurlijke taal categorieën voldoen, die leiden tot beperkingen op de realiseerbare denotaties. Voor wat resteert wordt dan gezocht naar definieerbaarheidsresultaten, die zeggen dat alles verder in de taal definieerbaar is.

Een andere manier van denken beperkt modellen van meet af aan tot wat expliciet in de taal definieerbaar is. (Dit is natuurlijk één extreme filosofische visie op modellen, als volledig taalgeïnduceerd. Het zou vele meer bui tentalige structuren buitensluiten.) Bijvoorbeeld, stel dat een eindig domein D_e gegeven is, van n met name bekende individuen. We kunnen dan beginnen D_(e,t) (bijvoorbeeld) met alle 2ⁿ mogelijke predikaten te vullen. Immers, voor elke deelverzameling X ⊆ D_e kunnen we het volgende predikaat definiëren: ‘is Jan of is Piet of is...’, waar de eigennamen X doorlopen. En dit predikaat geldt precies van de objecten in X. Daarmee hebben we alle mogelijke predikaten. Kan dit proces nu herhaald worden om de hele hiërarchie op te vullen? Enkele technische resultaten over deze kwestie zijn te vinden in Van Benthem (1986e). Het antwoord komt neer op: ‘in het algemeen niet’. Wellicht is echter het volgende resultaat nog vermeldenswaard. Hoewel de eerste-orde-uitdrukkingen niet alle hogere objecten definiëren, produceren ze wel bevolking in elk hoger type, in de volgende zin. Bij elk type b (van willekeurige orde) is een rij eerste-orde-typen A te vinden zodat A herschrijfbaar is tot b via de typenveranderende categoriale grammatica van paragraaf 2.

Tenslotte dient nog vermeld te worden dat in de logica reeds van oudsher een alternatieve opzet voor een typentheorie bestaat, waarin zgn. general models figureren - met slechts een selectie van alle mogelijke functies. (Zie Gallin 1975 voor achtergronden.) In het volledigheidsbewijs voor de bijbehorende deductieve calculus worden zelfs modellen in dit genre geconstrueerd waarin enkel objecten en functies voorkomen die in de taal een corresponderende uitdrukking hebben. Deze modellen zijn dus ook de moeite van het overwegen waard.

Overigens kan men desgewenst over ‘general models’ ook denken als modellen voor een meersoortige versie van een typenlogica, waar elk type a slechts ‘een’ domein D_a aanduidt, terwijl eventuele functionele of relationele verbanden gecodeerd liggen in extra soort-overschrijdende predikaten. (Vergelijk de eerdere discussie over een extra applicatiepredikaat.) Bijvoorbeeld, er zou een ternair predikaat Res kunnen zijn dat soorten ‘(a,b)’, ‘a’ en ‘b’ relateert, met Res (f,x,y) in geval y het ‘resultaat’ codeert van ‘toepassen’ van f op x. (Zulke gezichtspunten worden binnen de technische logica veel gebruikt: vergelijk Van Benthem and Doets 1983.) Dit zijn dan wel anders gemotiveerde ‘soorten’ dan de eerder voorgestelde.

[p. 16]

Nominalisering

Een meer linguïstisch aangrijpingspunt voor discussie van de groei van domeinen kunnen we vinden in de recente literatuur over nominalisering. Zo is door Turner (1983) beargumenteerd dat een adequate behandeling van dit verschijnsel de klassieke opvatting van domeinen welhaast onmogelijk maakt. Want, in zijn optiek kan elk werkwoord op zich ook in nominale positie voorkomen, en daarmee ook als individu. En aldus ontstaan klassiek onoplosbare telproblemen. Stel er zijn n individuen in D_e. Dan zijn er 2ⁿ mogelijke éénplaatsige predikaten in D_e,t - en die passen niet allemaal in D_e. De oplossing van Turner zelf is overschakelen op zgn. ‘Scott-domeinen’, met sterke restricties op de functie-ruimte constructie voor domeinen D_(a,b)(alleen ‘continue’ functies in een technische zin komen in aanmerking). Het nadeel hiervan is de geringe intuïtieve evidentie van deze techniek. Maar ook taalkundig lijkt de voorstelling bij Turner een al te ‘magische’ versie van nominalisering. Predikaten zijn geen individuen, ze worden het, door een nominaliseringsoperatie (vorming van infinitieven, en dergelijke), zelf gelegen in type ((e,t),e).

Deze tweede visie is evenmin zonder spektakel. Intuïtief creëren we door nominaliseren nieuwe individuen, waarna er weer nieuwe predikaten ontstaan, die weer genominaliseerd kunnen worden, enzovoorts,... Om dit te modelleren zouden we ketens van expanderende eindige hiërarchieën moeten opstellen (op zichzelf ook geen slechte manier van denken over de constructie van Scott-domeinen), of: een general model nemen met oneindige domeinen. Dit laatste zou dan één van de vele gevallen zijn waar een oneindige structuur een soort ‘evenwichtsmodel’ is, waar een eindig exploderende constructie tot rust is gekomen.

Met alleen deze genreschildering zijn we er overigens niet: er liggen ook enkele randvoorwaarden. Het lijkt bijvoorbeeld niet onredelijk te eisen dat de nominaliseringsoperator aan zekere semantische minimumeisen voldoet. Sommige daarvan zouden een adequate logica moeten afdwingen voor genominaliseerde predikaten; maar hier meer ter zake is simpelweg de eis dat de cruciale functie injectief zou moeten zijn: extensioneel verschillende predikaten kunnen niet dezelfde nominalisering hebben. Welnu, het is helemaal niet evident wanneer aan een dergelijke eis in een general model kan worden voldaan. (Bijvoorbeeld, indien we in zulke modellen onbeperkte Comprehensie-axioma's willen laten gelden - die zeggen dat elke complex gedefinieerde predikaat-uitdrukking weer een binnen het model aanwezig predikaat definieert -, dan kunnen we zelfs weerleggen dat de nominaliseringsfunctie injectief is. Er zal dus ergens water in de wijn moeten komen.)

Er bestaat voor dit probleem een ‘goedkopere’ oplossing: theoretisch niet zo fraai, maar linguïstisch wel gemotiveerd. Eerder zagen we reeds goede redenen voor een opdeling van domeinen in soorten. En, het lijkt evident dat genominaliseerde predikaten een zeer speciaal soort individuen vormen, zelf geschikt voor weinig verdere predikaatvormingen. Dat wil zeggen dat de nominaliseringsoperatie eventueel slechts 1-1 hoeft te zijn op een deelsoort van D_(e,t)- en dan zijn de combinatorische problemen zonder meer overkomelijk. De modellen worden op deze manier wel een lapjesdeken van veelsoortige domeinen, maar misschien is dit nu eenmaal een feit des levens over de natuurlijke taal.

Bezuinigen op situaties

De voorgaande bezuinigingsoperatie is tenslotte heel wel uit te breiden tot de intensionele modeltheorie van de paragrafen 3 en 4. Zo was bijvoorbeeld een ‘propositie’ wel te koppelen aan een deelverzameling van D_s; maar er is omgekeerd geen enkele verplichting om ook elke deelverzameling van D_s tot een mogelijke propositie te verklaren. (Dit is hoogstens de praktijk van barokke filosofen, zoals David Kaplan, die vervolgens op allerlei ‘paradoxen’ stuiten.) We zouden zelfs vrij zuinige universa van ‘situatie-typen’ kunnen aanleggen, vanuit de taal gegenereerd.

[p. 17]

Het zou met name ook nuttig kunnen blijken dit perspectief terstond aan te leggen in de voorafgaande behandeling van nominalisatie: hetgeen kennelijk een intensioneel verschijnsel is. Dan biedt zich bijvoorbeeld ook een meer Montagoviaanse route aan, en wel de nominalisatie van een predikaat simpelweg interpreteren als de intensie van dat predikaat (d.v.z.: zijn extensie door alle situaties heen.) Wat we dan echter zullen moeten oplossen zijn extra ‘spiegelingsproblemen’: ditmaal van globale intensionele functies binnen de individuen-universa van specifieke situaties.

De conclusie van deze paragraaf kan zijn dat een categoriale semantiek een overvloed aan alternatieve modelleringen toestaat voor haar centrale functie/- argument-idee. Dat is ook niet verwonderlijk. Veel van de door ons besproken kwesties betreffen het aanbrengen van een ‘conceptuele bovenbouw’ op een ‘empirische onderbouw’ in het basisdomein D_e (en wellicht D_p). En de natuurlijke taal staat ons hierbij nog diverse composities van de wereld toe.

Literatuur

Bach, E. (1984) Some Generalizations of Categorial Grammars. In: F. Landman and F. Veltman (eds.) Varieties of Formal Semantics (GRASS-serie, deel 3). Dordrecht.

Bach, E. (1986) The Algebra of Events. In: Linguistics and Philosophy 9, 5-16.

Bach, E., R. Oehrie and D. Wheeler (eds.) (1986) Categorial Grammars and Natural Language Structures (Studies in Linguistics and Philosophy, te verschijnen). Dordrecht.

Barwise, J. and R. Cooper (1981) Generalized Quantifiers and Natural Language. In: Linguistics and Philosophy 4, 159-219.

Barwise, J. and J. Perry (1983) Situations and Attitudes. Boston.

Bealer, G. (1982) Quality and Concept. Oxford.

Benthem, J. van (1982) The Logic of Time (Synthese Library, deel 156). Dordrecht.

Benthem, J. van (1985) A Manual of Intensional Logic (CSLI Lecture Notes 1, Center for the Study of Language and Information). Stanford.

Benthem, J. van (1986)a Essays in Logical Semantics (Studies in Linguistics and Philosophy, deel 29). Dordrecht.

Benthem, J. van (1986)b Strategies of Intensionalization. Te verschijnen in: L. Pólos (ed.) Filozófiai Figyelö (Festschrift for Imre Rusza).

Benthem, J. van (1986)c The Lambek Calculus. Rapport 86-06, Mathematisch Instituut, Universiteit van Amsterdam. (Te verschijnen in Bach, Oehrie and Wheeler (eds.) (1986)).

Benthem, J. van (1986)d The relational Theory of Meaning. Te verschijnen in: Logique et Analyse.

Benthem, J. van (1986)e Logical Syntax. Rapport, Mathematisch Instituut, Universiteit van Amsterdam (te verschijnen).

Benthem, J. van and K. Doets (1983) Higher-Order Logic. In: D. Gabbay and F. Guenther (eds.) Handbook of Philosophical Logic, deel I, 275-329. Dordrecht.

Buszkowski, W., W. Marciszewski and J. van Benthem (eds.) (1986) Categorial Grammar (te verschijnen). Amsterdam.

Chierchia, G. (1985) Formal Semantics and the Grammar of Predication. In: Linguistic Inquiry 16, 417-443.

Dowty, D. (1979) Word Meaning and Montague Grammar. Dordrecht.

Gallin, D. (1975) Intensional and Higher-Order Modal Logic (Mathematics Studies, deel 19). Amsterdam.

Gamut, L.T.F. (1982) Logica, Taal en Betekenis, 2 delen. Utrecht.

Groenendijk, J. and M. Stokhof (1984) On the Semantics of Questions and the Pragmatics of Answers. Proefschrift, Filosofisch Instituut, Universiteit van Amsterdam (Te verschijnen).

Hoeksema, J. (1984) Categorial Morphology. Proefschrift, Nederlands Instituut,

[p. 18]

Rijksuniversiteit, Groningen (Ook verschenen in: J. Hankamer (ed.), Outstanding Dissertations in Linguistics).

Kamp, B. (1979) Events, Instants and Temporal Reference. In: R. Bäuerle, U. Egli and A. von Stechow (eds.) Semantics from Different Points of View. Berlijn.

Keenan, E. and L. Faltz (1985) Boolean Semantics for Natural Language (Synthese Language Library, deel 23). Dordrecht.

Lewis, D. (1972) General Semantics. In: D. Davidson and G. Harman (eds.) Semantics of Natural Language (Synthese Library, deel 40). Dordrecht.

Montague, R. (1974) Formal Philosophy. (R. Thomason (ed.)). New Haven.

Moortgat, M. (1986) Compositionality and the Syntax of Words. In: J. Groenendijk, D. de Jongh en M. Stokhof (eds.) Information, Interpretation and Inference (GRASS-serie, deel 8). Dordrecht.

Muskens, R. (1986) Relational Type Theory. Manuscript, Filosofisch Instituut, Universiteit van Amsterdam.

Stalnaker, R. (1986) Possible Worlds and Situations. In: Journal of Philosophical Logic 15, 109-123.

Turner, R. (1983) Montague Semantics, Nominalization and Scott's Domains. In: Linguistics and Philosophy 6, 259-288.

Verkuyl, H. (1972) On the Compositional Nature of the Aspects. Dordrecht.

Zwarts, F. (1981) Negatief-polaire Uitdrukkingen I. In: Glot 4, 35-132.

Zwarts, F. (1986) Categoriale Grammatica en Algebraïsche Semantiek. Proefschrift, Nederlands Instituut, Rijksuniversiteit, Groningen.