Onze Taal. Jaargang 59

[p. 85]

Wetenschap over spelling

Eind vorig jaar werd de eerste prijs in de veelbesproken ECI-prijsvraag ‘Gaat het Nederlands teloor?’ uitgereikt aan de taalkundige mw. J. Wester. Westers essay spitst zich toe op de huidige spelling van het Nederlands, die volgens haar een wonder van systematiek is, veel systematischer dan velen aannemen. G. Booij, eveneens als taalkundige geïnteresseerd in uitspraak en spelling van het Nederlands, is niet overtuigd door Westers analyses. Hieronder volgt een fragment uit Westers essay over het trema, Booijs kanttekeningen daarbij, gevolgd door een nawoord van Wester.

Het tremawonder
Jet Wester - winnares eerste prijs ECI-essayprijsvraag ‘Gaat het Nederlands teloor?’

Laten we ervan uitgaan dat u bekend bent met het trema, en de volgende taalvormen als juist herkent:

(1)	a) met	b) zonder	c) zonder
	trema	trema	trema
	geïnd	geinen	Beatrijs
	geüniformeerd	beunhaas	gloria
	beërven	beer	beo
	kopiëren	pier	patio

Het systeem achter deze feiten is bij wet geregeld [1]:

(2) ‘Het deelteken (trema) wordt geschreven op de tweede van twee opeenvolgende klinkers die samen als een klinker of alseen tweeklank kunnen, maar niet moeten worden gelezen.’

Dus: het rijtje onder (1a) kent trema's om de combinatie-lezingen te blokkeren die in (1b) juist bedoeld zijn. Het rijtje onder (1c) staat apart omdat er daar geen combinaties mogelijk zijn in de zin der wet, al staan er wel steeds twee klinkers naast elkaar.

Tot zover is het allemaal precies zoals we konden verwachten: een beetje saai, beetje simpel en uitermate prescriptief. Maar stop nu niet met lezen. Het geweldige feit doet zich namelijk voor dat dit allemaal niet waar is! Ik nodig u uit mij te volgen in burgerlijke ongehoorzaamheid wanneer ik de rijtjes van (1) aanvul met de eveneens gewone en juiste vormen van (3). Let daarbij vooral op het rijtje onder (b).

(3)	a) met trema	b) zonder trema
	smeuïg	ingenieur
	theorieën	bloeien
	geëist	geuit
	kippeëi	eierdop
	hindoeïst	kopieer
	geëuropeaniseerd	koeieuier

De vraag die zich aandient is natuurlijk: waarom hebben de vormen onder (b) hier geen trema en die onder (a) wel? Koeieuier, het meest spectaculaire geval van (3b), heeft maar liefst elf mogelijkheden in zich (namelijk oei, oe, ei, ie, eu, ui, ie, e, i, o en u), samen logisch goed voor zo'n zestien verschillende lezingen. En het woord kent niet één trema. Smeuïg, met een trema, lijkt daarentegen in niets wezenlijk te verschillen van geuit of ingenieur - behalve dan in het trema zelf. En waarom kopieer zonder trema en kopiëren of geëist met?

Omdat hier iets volstrekt anders aan de hand is, namelijk dit: het Nederlands gaat in stilte gewoon zijn eigen gang, volgt zijn eigen wetten. Veel subtieler dan waar de Spellingwet ooit van droomde en tegelijkertijd zo natuurlijk of ‘gewoon’ dat problemen als in (3b) zelfs nog nooit als probleem gesignaleerd zijn.

Ik zal het u laten zien.

Wanneer we orde willen scheppen in de schijnbare grilligheid van het trema is het goed om eerst eens precies op een rijtje te zetten welke combinatielezingen voor klinkers er in (1) en (3) eigenlijk mogelijk zijn. Zo'n rijtje kan er, een tikje formeel, uitzien als in (4): een verzameling van regels die de mogelijk bij elkaar horende letters steeds onder één ‘paraplu’ plaatsen.

(4)	1) ee
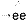
	2) oei
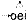
	3) oe
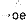
	4) ei
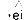
	5) ui
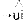
	6) eu
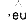
	7) au
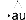
	8) ou
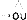
	9) ie

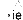
Het grote voordeel van juist deze manier van opschrijven is dat we (4) nu ook kunnen zien als een minimodel van wat een lezer doet wanneer hij leest. De lezer ziet twee of meer klinkers naast elkaar (‘links van de pijl’) en hij interpreteert ze (= de pijl zelf) als bij elkaar horend (de paraplu rechts van de pijl). En zo opgeschreven wordt ook een andere, onzichtbare werkelijkheid zichtbaar: de regels staan los van elkaar en staan dus noodzakelijkerwijs ook in een bepaalde volgorde. Deze laatste, haast triviale werkelijkheid nu, is één van de wonderen waarvan het Nederlands zich bedient.

Beschouw nogmaals het woord koeieuier. We zagen dat dit woord (behalve een e, een i, een o en een u) een oei, oe, ei, ie, eu, ui en nogmaals een ie in zich heeft, die getuige het leesmodel van (4) alle zeven even goed zijn, en samen nog eens goed voor wie weet hoeveel mogelijke lezingen voor het totale woord. Opperste verwarring dus? Nee, want ook de volgorde maakt deel uit van het leesmodel en precies deze ordening filtert ‘tussen de regels door’ alle mogelijkheden uit ten faveure van slechts één lezing, namelijk de juiste. We kunnen het narekenen. Van boven naar beneden door de regelset gaand, is eerst regel 2) aan de orde, die oei van een paraplu voorziet. Is dit gebeurd, dan kan regel 3) niet meer werken, omdat er nu geen vrije (‘parapluloze’, dat wil zeggen ongeïnterpreteerde) oe meer bestaat. Hetzelfde geldt voor de ‘ei’-regel, regel 4). De eerstvolgende

[p. 86]

regel is nu regel 5), die ui bij elkaar neemt. En dat is direct ook de laatste regel die van toepassing is. Het nettoprodukt van de regels wordt daarmee, correct, koei-e-ui-er. In (5) is de situatie voor de duidelijkheid nog eens in schema gezet.

5)		koeieuier
	regel 2):
	regel 5):
	uitkomst:

Hetzelfde principe gaat op voor de andere gevallen van (3b) (en voor alle verdere voorbeelden die we kunnen bedenken). Geuit, met een mogelijke eu of ui, wordt correct ge-uit en niet geu-it omdat ui getuige de ordening in (4) bij lezing prioriteit heeft boven eu. Kopieer levert kopi-eer en niet kopie-er omdat regel (4,1) voor regel (4,9) komt. Enzovoort. [2]

En nu we deze slag gemaakt hebben, komt ook een inzicht in het werkelijke tremasysteem binnen ons bereik: trema's zijn aan de orde in precies die gevallen waarin de standaardleesprioriteiten, de ordeningen van (4), ‘overruled’, omgekeerd moeten worden! Krijgt geuit via het principe ‘ui vóór eu’ automatisch de correcte lezing geuit; voor smeuig zou de lezing op grond van dit zelfde principe dus smeuig worden - en het trema moet in actie komen om de eu hier vóór te laten gaan. Krijgt kopieer op grond van het principe ‘ee vóór ie’ automatisch de correcte lezing kopi-eer, in kopieren is er niet zo'n dubbele ee aanwezig en het is dus aan het trema om de ‘ie’ - lezing hier te blokkeren. Theorieën zal, zo is de voorspelling, eveneens een trema moeten voeren, maar nu om de standaardlezing ‘ee vóór ie’ te blokkeren die in het tremaloze kopieer juist bedoeld was. Enzovoort, enzovoort. Samenhang, samenhang.

En de vragen dringen zich op. Wat is dit voor organisme, dit ‘Nederlands’, dat het zonder voorschrift, of liever: tegen de verdrukking van de voorschriften in, zulke wonderlijk intelligente en subtiele dingen doet die niemand bedacht heeft? En wat bent u, tremagebruiker, voor wonder dat u dit alles allang wist zonder het te weten? Waar heeft u dat geleerd?

Taalkundigen over de hele wereld zijn naarstig aan het speuren naar een dieper inzicht in dit soort kwesties - en het gaat goed met het onderzoek. De wonderen worden groter en groter.

Deze tekst verscheen eerder als paragraaf 1.1 van het winnende essay De Too van taal, of: Chanel no. 5 en het Geval Nederlands in de ECI-bundel Gaat het Nederlands teloor?

[1] De Wet is hier de Spellingwet van 1947 met de bijbehorende officiële Woordenlijst van de Nederlandse taal, samengesteld in opdracht van de Nederlandse en Belgische regering. (Den Haag 1954). Het citaat (de meest heldere formulering die ik vinden kon) is uit De spelling van de Nederlandse taal. Publikatie van de Centrale directie Voorlichting van het Ministerie van Onderwijs en Wetenschappen (Schaap en Mols, 1980).

[2] Wanneer u me wilt narekenen voor ook andere typen woorden dan die van (1) en (3), moet de eerste regel van het regelsetje van (4) even gegeneraliseerd worden over sequenties van identieke klinkers. Er kunnen ook nog wat marginale regels worden toegevoegd, zoals ‘ai wordt parapluutje -ai’ (voor mayonaise, fair, etc.). U komt hier ongetwijfeld uit.

We lezen veelal als Chinezen
Geert Booij - hoogleraar Algemene Taalwetenschap, VU Amsterdam

Het rijtje regels onder (4) is niet toereikend om alle gevallen van tremaplaatsing te voorspellen. Wellicht is dat ook niet de pretentie van mw. Wester. Zo moet voorspeld worden dat er in woorden als Aäron, Adelaïde en Bethsaïda een trema geplaatst wordt, wat regels veronderstelt die aa en ai ‘onder een parapluutje’ brengen. Ook de letterreeksen ieu en eeu (zoals die bijv. voorkomen in nieuw en eeuw) moeten een regel krijgen die ze onder zo'n paraplu brengt, net zoals regel (2) dat doet voor oei, gezien de psychologi-

[p. 87]

sche interpretatie die mw. Wester aan dit soort regels geeft: het zijn regels die aangeven welke letterreeksen de lezer interpreteert als bij elkaar horend. Daarnaast zijn er ook uitzonderingen op de tremaplaatsingsregels, in het bijzonder bij woorden die eindigen op -eum zoals museum en linoleum.

Met de psychologische interpretatie van dat regelsysteem moeten we echter wel voorzichtig zijn. Dat regelsysteem is primair de beschrijving van een stukje kennis van ons spellingsysteem, een soort kennis die zeker bij het lezen van woorden een rol kan spelen. We weten echter ook dat taalgebruikers het totale spellingbeeld van veel woorden in hun geheugen opslaan. Voor het woord geit bijvoorbeeld is er al een letterreeks g+e+i+t in ons geheugen opgeslagen, een ‘plaatje’ van het woord, waardoor we dat woord in zijn geschreven of gedrukte vorm in één keer kunnen herkennen. Kinderen van zes jaar herkennen het woord geit al sneller dan het woord gijt, zelfs als ze het maar een paar maal gezien hebben. Dat blijkt uit onderzoek van Reitsma (1983). Met andere woorden: omdat we al bekende woorden veelal lezen ‘als Chinezen’, dus op basis van een beeld van de grafische vorm van een woord, is directe herkenning vaak mogelijk zonder elke letter afzonderlijk waar te nemen. In al die gevallen spelen de hier besproken regels geen enkele rol. Die regels veronderstellen immers wel dat de woorden letter voor letter gelezen worden.

Weerwoord
J. Wester

Bij professor Booijs eerste alinea: beschouw, liefst met een glimlach, voetnoot (2) bij mijn essay. Wie puzzelt, zal voorts ontdekken dat de regels ook eenvoudiger kunnen: regels als voor eau, eu, au en ou kunnen worden samengeklapt tot één enkele regel die zegt dat klinkerreeksen met een u rechts een parapluutje boven zich krijgen. Enzovoort. Merk echter op dat de -eum in museum expres níet behandeld moet worden. Generatieve regels horen het kaf van het koren te scheiden, en door precies deze vorm fout te laten gaan, kunnen we verantwoorden dat -eum inderdaad uitzonderlijk is (zie bijv. Schaap en Mols 1980, blz. 23).

Over de psychologie van de tremaregels is veel te zeggen. Bijvoorbeeld dat ze juist hun nut bewijzen voor complexe woorden die niet in één keer ‘gezien’ worden (daarom het rare koeieuier als voorbeeld). Fundamenteel is echter dat zo'n psychologische onderbouwing van mijn (soort) regels helemaal niet cruciaal is: de analyses staan of vallen er niet mee. Dit is misschien een misverstand, ontstaan doordat niet mijn wetenschappelijke werk hier uitgangspunt voor de discussie is, maar slechts het prijskonijn van mijn essay. Voor alle duidelijkheid: mijn claim is niet dat theoretischtaalkundig, ‘systeemintern’ spelling-onderzoek goed is, of gewenst, of nodig, omdat er direct (of indirect) psychologisch of didactisch gewin in het spel zou zijn. Mijn claim is wel dat dit soort onderzoek goed is, en gewenst, en nodig (en genoemd moet worden door de Taalunie), omdat het wetenschappelijk onderzoek is. Precies zoals theoretische taalkunde goed is, en gewenst, en nodig omdat het wetenschap is, en op een heel eigen manier de ‘aard’ van taal onderzoekt. Wetenschap is belangrijk, en het spellingsysteem van het Nederlands is, qua systeem, tot op heden onvoldoende onderzocht. Ook ben ik van mening dat kennis van het systeem vooraf hoort te gaan aan verandering van dat systeem - zeker wanneer zulke kennis gewoon te vergaren is.