De Nieuwe Taalgids. Jaargang 88

[p. 22]

Rekenkundige voegwoorden: de ‘logica’ van samentrekkingen

Emmeken van der Heijden en Maarten Klein

0 Inleiding

In vrijwel alle beschrijvingen van samentrekkingsverschijnselen in het Nederlands vinden we als uitgangspunt dat deze zich uitsluitend voordoen in nevengeschikte structuren. De Algemene Nederlandse Spraakkunst (ANS; Geerts e.a. 1984) geeft ook wat dit betreft de bestaande ideeën goed weer. In de Inleiding van hoofdstuk 27 vinden we de volgende omschrijving: ‘Samentrekking is het verschijnsel dat gemeenschappelijke bestanddelen van twee of meer leden van een nevenschikking slechts één keer genoemd worden.’ (Geerts e.a. 1984: 1170). De ANS maakt een onderscheid tussen voorwaartse en achterwaartse samentrekking (1) enerzijds en zogenaamde gappingstructuren (2) anderzijds.

(1)a	Jan heeft Marie ontmoet en (-) heeft haar langdurig gesproken. (voorwaartse samentrekking)
(1)b	Jan heeft Marie (-) en Piet heeft Truus gezien. (achterwaartse samentrekking)
(2)	Jan heeft Marie gezien en Piet Truus. (gapping)

In dit artikel zullen wij laten zien, dat samentrekkingsstructuren en gappingstructuren zeker niet het voorrecht van nevengeschikte structuren zijn. De analyse die wij hier presenteren, toont naar onze mening duidelijk aan, dat een samentrekkingsstructuur als in (1) en een gappingstructuur als in (2) voor kunnen komen bij sommige nevenschikkende én bij sommige onderschikkende voegwoorden (paragraaf 1 en 2). Dat roept natuurlijk meteen de vraag op wat deze voegwoorden gemeenschappelijk hebben. Waarom is het mogelijk bij deze voegwoorden woord-, woordgroeps- of zinsdelen weg te laten en bij andere voegwoorden niet? Die vraag zullen wij beantwoorden in paragraaf 3. In paragraaf 4, 5 en 6 gaan wij vervolgens in op de vraag waarin samentrekkingsstructuren en gappingstructuren verschillen.

1 Welke voegwoorden staan gappingstructuren toe?

Zoals gezegd is het een wijdverbreide gedachte dat samentrekkingsstructuren en gappingstructuren alleen mogelijk zijn in nevengeschikte structuren. Die gedachte is zo algemeen, dat men in de meeste literatuur over deze structuren volstaat met voorbeelden waarin de nevenschikkende voegwoorden en en of een rol spelen. De ANS vormt hierop geen uitzondering. Deze beperking tot en- en of-nevenschikkingen is weliswaar aantrekkelijk - zij geeft een betrekkelijk eenvoudige beschrijving van het verschijnsel ‘samentrekking’ -, maar versterkt ook het idee dat samentrekking alleen maar in nevenschikkende zinnen kan voorkomen. Toen sommigen er oog voor begonnen te krijgen, dat gappingstructuren ook in comparatiefzinnen voor konden komen, zoals in (3), dat een volledige pendant als (4) heeft:

[p. 23]

(3)	Charlotte heeft meer boeken gekocht dan Jan cd's.
(4)	Charlotte heeft meer boeken gekocht dan (dat) Jan cd's heeft gekocht.

haastten zij zich om, ondanks de typische bijzinsplaats van persoonsvorm en werkwoordelijke rest in de dan-zin in (4), de comparatiefzin tot een nevengeschikt verbonden zin te verklaren en het voegwoord van vergelijking dan tot een nevenschikkend voegwoord (Napoli 1983; Klein 1985b, 1986, 1991; Corver 1990; Hendriks 1991). De gedachte dat gapping ook voor kan komen in zinnen die ingeleid worden door een onderschikkend voegwoord, was - en is - blijkbaar té onaantrekkelijk. De volgende voorbeelden tonen echter aan, dat gappingstructuren in zoveel samengestelde zinnen met een voor-pv én een achter-pv (Paardekooper 1976) mogelijk is, dat het onwaarschijnlijk is, dat we de traditionele voorstelling van zaken ‘Samentrekking is het verschijnsel dat gemeenschappelijke bestanddelen van twee of meer leden van een nevenschikking slechts één keer genoemd worden.’ (Geerts e.a. 1984: 1170) kunnen handhaven.

(5a)	Behalve een boek aan Jan heeft Marie een cd aan Karel gegeven. (toevoegend behalve)
(5b)	Niemand heeft zijn vrouw een cadeau gegeven, behalve Karel de zijne. (beperkend behalve)
(6)	De soldaat heeft de generaal een bevel gegeven in plaats van de generaal de soldaat.
(7)	Jan heeft jou behandeld zoals jij Jan.

Gesteld dat deze zinnen inderdaad van volledige zinnen afgeleid zouden zijn, dan zouden deze als volgt luiden:

(8a)	Behalve dat zij een boek aan Jan gegeven heeft, heeft Marie een cd aan Karel gegeven.
(8b)	Niemand heeft zijn vrouw een cadeau gegeven, behalve dat Karel de zijne een cadeau gegeven heeft.
(9)	In plaats van dat de generaal de soldaat een bevel heeft gegeven, heeft de soldaat de generaal een bevel gegeven.
(10)	Jan heeft jou behandeld zoals jij Jan behandeld hebt.

In deze zinnen (8a)-(10) gaat het, getuige de plaats van de werkwoordsgroep aan het eind van de zin, om ondergeschikte zinnen. Het lijkt ons een moeilijke opgave aan te tonen dat in deze zinnen syntactisch sprake is van nevenschikking, als men althans de gangbare betekenis van de begrippen ‘onderschikking’ en ‘nevenschikking’ geen geweld wil aandoen.¹ A fortiori geldt dit voor als... dan-zinnen, die, behalve door Paardekooper (bijv. 1976: 837), in de taalkundige literatuur nog niet eerder met samentrekkingsverschijnselen in verband zijn gebracht. Ook hier kunnen in het tweede deel ‘losse’ constituenten voorkomen:

1 De mogelijkheid om ten minste twee zinnen met hoofdzinsvolgorde te verbinden achten wij het wezenlijke kenmerk van nevenschikkende voegwoorden. En, of, noch, maar, doch en want zijn dus nevenschikkende voegwoorden. Behalve, in plaats van enz. hebben die mogelijkheid niet (zij worden altijd gevolgd door een zin met bijzinsvolorde) en zijn dus geen nevenschikkende voegwoorden.

[p. 24]

(11)	Als Josefien Rutger een kus mag geven, dan Rutger ook Josefien.
(12)	Als Marinel op hockey mag, dan Frank ook op golf!
(13)	Als een ding met een tweede equivalent is, dan ook het tweede met het eerste. (Freudenthal 1967: 21)

Voor zover wij weten, heeft niemand ooit beweerd, dat er in als...dan-zinnen syntactisch sprake is van nevenschikking. Hoe zou dat ook kunnen? Toch zijn - getuige de rechterleden van (11)-(13) - ook in dit type zinnen gappingstructuren mogelijk.²

Gesteld dat men, om welke reden dan ook, gappingstructuren tóch alleen met syntactische nevenschikking in verband zou willen brengen en voegwoorden als behalve en als...dan als nevenschikkende voegwoorden zou willen beschouwen, dan komt men onvermijdelijk voor het probleem te staan waarom deze regel dan niet mag werken op de a-zinnen van (14)-(16):

(14a)	Toen Willy Caroline kuste, kuste Adam Patricia ook.
(14b)	*Toen Willy Caroline kuste, Adam Patricia ook.
(15a)	Omdat Willy Caroline kuste, kuste Adam Patricia ook.
(15b)	*Omdat Willy Caroline kuste, Adam Patricia ook.
(16a)	Hoewel Willy Caroline kuste, kuste Adam Patricia ook.
(16b)	*Hoewel Willy Caroline wel kuste, Adam Patricia niet.^3

De b-zinnen zijn alle duidelijk ongrammaticaal. Er is voor zover wij zien, geen onafhankelijk gemotiveerd principe, geen regel of wat dan ook ten aanzien van het begrip nevenschikking, dat begrijpelijk maakt dat een gappingregel⁴ wel in behalve dat-, in plaats van dat-, dan (dat)-, zoals- en als...dan-zinnen mag werken, maar niet in zinnen die beginnen met toen, omdat of hoewel. Bovendien is er geen enkele verklaring, waarom de regel niet mag werken in zinnen met want, hoewel dit voegwoord wel twee hoofdzinnen verbindt:

(17a)	Amaril had Karel uitgescholden, want Karel had haar ook uitgescholden.
(17b)	*Amaril had Karel uitgescholden, want Karel haar ook.

Samenvattend kunnen we stellen, dat gappingstructuren voor kunnen komen in bepaalde nevengeschikte structuren en in bepaalde structuren met onderschikking. Hoe kan dat? Met andere woorden: wat hebben en, behalve, zoals enzovoort dat bijvoorbeeld toen, omdat, hoewel en want niet hebben? Op die vraag zullen we in paragraaf 3 het antwoord proberen te formuleren. Eerst zullen wij laten zien, dat deze voegwoorden ook andere eigenschappen gemeenschappelijk hebben hebben die gewoonlijk aan nevenschikkende voegwoorden worden toegeschreven.

2 Opmerkelijk is natuurlijk wel, dat de gappingstructuur in als...dan-zinnen voorkomt in het gedeelte met de voor-pv. Het gedeelte met de bijzinsvolgorde (achter-pv) blijft volledig.

3 Ook als gapping in de bijzin toegepast zou worden, zou dit een ongrammaticale zin opleveren: *Adam kuste Patricia, toen Willy Caroline.

4 Zie voor een overzicht van de verschillende voorstellen van de regel ‘gapping’ met name Neijt (1979).

[p. 25]

2 Andere gemeenschappelijke kenmerken

Afgezien van het feit dat de hierboven genoemde voegwoorden gappingstructuren toelaten, hebben zij nog enkele opvallende overeenkomsten.⁵ Zo staan de meeste, net als ‘gewone’ coördinatoren, achterwaartse samentrekking op woordniveau toe (Klein & Visscher 1992: 173):

(18)	Jan heeft behalve tulpen- ook narcissenvelden aangelegd.
(19)	Jan heeft in plaats van tulpen- narcissenvelden aangelegd.
(20)	Jan heeft meer tulpen- dan narcissenvelden aangelegd.
(21)	Jan heeft evenveel tulpen- als narcissenvelden aangelegd.
(22)	Jan heeft evenmin tulpen- als narcissenvelden aangelegd.^6

Verder is het bij al deze woorden mogelijk op zinsniveau achterwaarts samen te trekken:

(23)	...dat Jan behalve dat hij naar het meisje achter (-) ook naar het meisje voor de HEMA gekeken had.
(24)	...dat Jan in plaats van dat hij naar het meisje achter (-) ook naar het meisje voor de HEMA gekeken had.
(25)	...dat Jan vaker naar het meisje achter (-) dan dat hij naar het meisje voor de HEMA gekeken had.
(26)	...dat Jan even vaak naar het meisje achter (-) als dat hij naar het meisje voor de HEMA gekeken had.
(27)	...dat Jan evenmin naar het meisje achter (-) als dat hij naar het meisje voor de HEMA gekeken had.

We gebruiken hier voorbeeldzinnen met bijzinsvolgorde, omdat samentrekkingsstructuren, voorwaarts of achterwaarts, nooit mogelijk zijn in een samengestelde zin die bestaat uit een deel met hoofdzinsvolgorde en een deel met bijzinsvolgorde:

(28)	*Als je straks naar school toegaat en (-) komt langs de bakker, koop dan een krentebol. (voorwaartse samentrekking)^7
(29)	*Jan heeft meer grammofoonplaten (-) dan Piet cd's heeft gekocht. (achterwaartse samentrekking)

Dit is ook de reden waarom achterwaartse samentrekking onmogelijk is in als...dan-zinnen (verg. *Als Jan Marie, dan mag Marie ook Jan kussen).

Wat achterwaartse samentrekking betreft vormen de hier besproken voegwoorden dus een natuurlijke klasse. Deze vorm van samentrekking is weer niet mogelijk bij voegwoorden als toen, omdat of want:

5 Paardekooper (1966) heeft voor het eerst gewezen op de overeenkomsten tussen nevenschikkende voegwoorden als en en of, en behalve. Klein (1985b) wees erop, dat dan en in plaats van zich gedragen als behalve. In beide artikelen gaat het er in de eerste plaats om aan te tonen dat deze woorden geen voorzetsels zijn, maar voegwoorden.

6 Wij wijzen erop, dat achterwaartse samentrekkingen niet mogelijk zijn bij voorzetsels. Men kan de zin Jan heeft tulpen achter narcissenvelden aangelegd niet zo interpreteren, dat er sprake is van tulpenvelden en narcissenvelden.

7 Deze zin is wel goed als het tweede gedeelte van de als-zin de bijzinsvolgorde heeft: Als je straks naar school toegaat en (als je) langs de bakker komt, koop dan een krentebol.

[p. 26]

(30)	*...dat Jan naar het meisje achter, toen Klaas naar het meisje voor de HEMA gekeken had.
(31)	*...dat Jan naar het meisje achter, omdat Klaas naar het meisje voor de HEMA gekeken had.
(32)	*Jan had naar het meisje achter, want Klaas had naar het meisje voor de HEMA gekeken.

Een tweede gemeenschappelijke eigenschap van deze voegwoorden betreft de distributie van het woord omgekeerd (of andersom). Kraak en Klooster (1968: 255) wijzen erop, dat omgekeerd/andersom als rechterlid van een nevenschikking kan voorkomen:

(33)	Jan bewondert Marie en omgekeerd (ook).

Omgekeerd kan ook voorkomen na in plaats van (34) en voegwoorden van vergelijking ((35)-(36)):

(34)	De soldaat heeft de generaal een bevel gegeven in plaats van omgekeerd/ andersom.
(35)	Jan bewondert Marie meer dan omgekeerd/andersom.
(36)	Jan bewondert Marie evenzeer als omgekeerd/andersom.

En zelfs bij als...dan-zinnen is dit mogelijk:

(37)	Als Jan Marie mag kussen, dan omgekeerd/andersom natuurlijk ook.

Ook in het geval van omgekeerd moeten we vaststellen, dat dit woord niet kan verschijnen na toen, omdat of want:

(38)	*De soldaat had de generaal een bevel gegeven toen omgekeerd/andersom.
(39)	*Jan bewondert Marie omdat omgekeerd ook/andersom.
(40)	*Jan bewondert Marie want omgekeerd ook/andersom.

Overzien we de in de vorige en in deze paragraaf vermelde feiten, dan is er eigenlijk maar één conclusie mogelijk: zowel gappingstructuren (paragraaf 1) als samentrekkingsstructuren (deze paragraaf) zijn alleen maar mogelijk bij één bepaalde groep van voegwoorden: en, of, noch enz. maar ook behalve, in plaats van, dan, even...als enz. In als...dan-zinnen vinden we alleen gappingstructuren. De meeste leden van deze groep van voegwoorden staan omgekeerd/andersom als rechterlid van de conjunctie toe (zie (33)-(37)).

Eén vraag dringt zich nu natuurlijk in het bijzonder op. Wat hebben de leden van deze groep gemeenschappelijk? Waarom zijn juist bij deze groep van woorden gappingstructuren en samentrekkingsstructuren mogelijk? En waarom zijn deze structuren onmogelijk bij andere voegwoorden, zoals toen, omdat, want enzovoort? Op deze vragen zullen we in de volgende paragraaf een antwoord proberen te formuleren.

[p. 27]

3 Wat hebben deze voegwoorden gemeen?

Opvallend is, dat alle zinnen met een van de hierboven besproken vormen van samentrekking een voegwoord bevatten, dat gezien kan worden als een talige tegenhanger van een rekenkundig teken of een teken uit de verzamelingenleer of de formele logica. Wij willen zeker niet beweren, dat er in alle opzichten een volledige parallellie is tussen taal en rekenkunde, maar opvallende overeenkomsten zijn er zeker. In het vervolg zullen we daarom - heel algemeen - spreken over ‘talige tekens’ en ‘rekenkundige tekens’. Het volgende overzicht maakt meteen duidelijk wat wij bedoelen:

(41)	talige tekens:	rekenkundige tekens:
	en	+ (5 + 3), ∧ (p ∧ q; logica), ∩ (A ∩ B; doorsnede, verzamelingenleer)
	noch	en niet (bijvoorbeeld⌝ p ∧ ⌝ q; logica), (A* ∩ B*; verzamelingenleer)
	of	∨ (p ∨ q; logica), ∪ (A ∪ B; vereniging, verzamelingenleer)
	maar	tegenstellend en (zie Gamut 1982: 34, 247)
	behalve	- (5 - 3),/ (B/A; verschil, verzamelingenleer (Freudenthal 1967)
	in plaats van	A ∩ B* (logica)
	even...als	= (‘is gelijk aan’)
	dan	> (groter dan, ‘is niet gelijk aan’)
	als...dan	→ (p → q; logica; equivalent met ⌜ p ∨ q)

Wat op het eerste gezicht een disparate verzameling woorden lijkt, is dus in werkelijkheid helemaal niet zo onsamenhangend. Al deze woorden stellen ons in staat in taal een bepaalde relatie te leggen tussen getallen, hoeveelheden, verzamelingen of proposities, zoals de rekenkundige tekens dat in de rekenkunde⁸ doen. We noemen ze van nu af aan rekenkundige voegwoorden.⁹

We kunnen nu met (41) als basis de volgende hypothese opstellen:

(42)	Alleen rekenkundige voegwoorden staan samentrekkings- en gappingstructuren toe.

Deze hypothese geeft een goede verklaring voor het hierboven aangegeven probleem: na toen, omdat, hoewel of want kunnen geen samentrekkings- of gappingstructuren volgen, omdat deze verbindingswoorden nimmer opgevat kunnen worden als een talige tegenhanger van enig rekenkundig teken. En, behalve, dan enzovoort zijn dat wel.

Enigszins problematisch voor (42) blijven in plaats van en want. Beide woorden hebben geen duidelijke tegenhanger in de rekenkunde; niettemin is bij in plaats van samentrekking en gapping mogelijk, maar na want niet. Men zou dit misschien eerder andersom verwacht hebben, omdat want van beide woorden nog het meest

8 Nogmaals: met ‘rekenkundige elementen’ bedoelen we hier in heel algemene zin elementen uit de gewone rekenkunde (lagere school), verzamelingenleer en formele logica.

9 In de literatuur is natuurlijk op vele plaatsen een relatie gelegd tussen voegwoorden als en en of en de logische connectieven ∧ en ∨. Zie bijvoorbeeld Kraak & Klooster (1968: 241 e.v.). Veel minder aandacht is besteed aan de ‘rekenkundige waarde’ van andere voegwoorden.

[p. 28]

in de logica gebruikt wordt (het is immers het omgekeerde van dus). Dat in plaats van een groter rekenkundige belang heeft dan want, blijkt wel uit het feit dat men wel in plaats van kan gebruiken om een bepaalde relatie tussen getallen of verzamelingen te leggen (Jan kocht vijf in plaats van drie knikkers; alle meisjes mochten naar de schouwburg in plaats van alle jongens), maar want niet (*Jan zag veel want honderd meisjes, *Jan zag voertuigen want fietsen).¹⁰

Met andere woorden: in plaats van is in (41) een uitzondering omdat het geen duidelijke rekenkundige tegenhanger lijkt te hebben. Maar de essentie is voor ons, dat de woorden in (41) een rekenkundig of kwantitatief begrip uitdrukken. Daarop maakt in plaats van geen uitzondering. De voorbeelden in (41) illustreren dus het rekenkundige karakter van de daar gebruikte woorden, maar definiëren dat niet. Ook is onze lijst niet volledig; er zijn nog vele andere voegwoorden te noemen met dezelfde eigenschappen als die in (41). Zie in dit verband ook de lijst van nevenschikkende voegwoorden die in de ANS (Geerts e.a. 1984) wordt opgesomd.

Niet onbelangrijk is ook, dat de tekens in (41) alle varianten lijken te zijn van en en of, al dan niet gecombineerd met niet. Voor een deel (bijvoorbeeld bij evenals, noch, maar) is dit vanzelfsprekend en staat dit al in (41) aangegeven. Het beperkende behalve is in de verzamelingentheorie vertegenwoordigd met het teken / (Freudenthal 1967): A / B wil zeggen: de verzameling A minus de verzameling B, bijvoorbeeld: als A de verzameling is van alle volwassenen en B de verzameling van alle mannelijke mensen, dan is A / B de verzameling van alle volwassen vrouwen. De verzameling A / B is gelijk aan de verzameling A ∩ B* (het sterretje geeft het complement van B aan, ofwel alles wat niet tot B behoort). Deze gelijkheid is gemakkelijk aan te tonen: A ∩ B* is de verzameling waarvan de leden volwassen zijn én niet behoren tot alle mannelijke mensen, d.w.z. A ∩ B* is de verzameling van alle volwassen vrouwen. Ook voor getallen gaat deze wetmatigheid op: 5 - 3 = 5 + (-3).

Bij gelijkheids- en ongelijkheidsrelaties (Jan is even groot als Piet, Jan is groter dan Piet) ligt de zaak iets gecompliceerder. Als verzamelingen equivalent zijn, kunnen we dat als volgt weergeven: A ≈ B. In taal drukken we het gelijkwaardig zijn van objecten in de werkelijkheid ten aanzien van bepaalde aspecten uit door bijvoorbeeld ‘even groot als’, ‘even veel als’, ‘even mooi als’ enzovoort:

(43)	Jan is even groot als Piet.

De vergeleken ‘objecten’ zijn hier Jan en Piet en zij worden vergeleken op het aspect ‘grootte’. We kunnen de semantiek hiervan als volgt weergeven:

(44)	Wat grootte betreft, Jan ≈ Piet.

De ongelijkheidsrelatie vinden we in comparatiefzinnen als (45):

10 In geschreven Nederlands komt men wel zinnen tegen als Jan was doorgezakt want geslaagd. Naar ons gevoel gaat het hier om een zeer gekunstelde constructie, die niet als bewijs kan dienen voor de stelling dat na want samengetrokken kan worden.

[p. 29]

(45)	Jan is groter dan Piet.

Ook hier vergelijken we Jan en Piet op het aspect ‘grootte’. Het resultaat van deze vergelijking is ‘ongelijkheid tussen Jan en Piet’. Enigszins geformaliseerd:

(46)	Wat grootte betreft, Jan ≉ Piet

Door verschillende taalkundigen is gewezen op de semantische overeenkomst tussen comparatiefzinnen als (46) en gewone nevenschikkingen (Seuren 1973; Stassen 1986). Zo zou men de semantiek van (45) kunnen weergeven als (47):

(47)	Er is een maat x, Jan is groot ten opzichte van x, en Piet is niet groot ten opzichte van x.

Sommige als...dan-zinnen zijn nauw verwant aan deze vergelijkingszinnen. Beschouwen we de zin:

(48)	Als Jan boeken koopt, dan koopt hij boeken van Vestdijk.

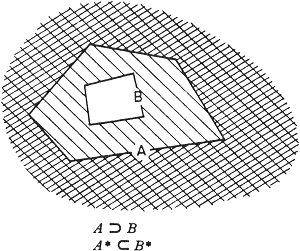
Hierin is sprake van twee verzamelingen: ‘boeken’ in de als-zin en ‘boeken van Vestdijk’ in de dan-zin. De tweede verzameling is uiteraard een deelverzameling van de veel grotere klasse ‘boeken’. In Venn-diagram (A = boeken, B = boeken van Vestdijk):

(49)	Freudenthal blz. 9

Nu is het bekend, dat logisch gezien als p, dan q equivalent is aan niet-p of q:

(50)	p → q = ⌜ | ∨ q

Van den Toorn (1972) heeft al gewezen op zinnen met of die in semantisch opzicht gelijk zijn aan (48):

[p. 30]

(51)	Jan koopt geen boeken (-p) of (hij koopt) boeken van Vestdijk (q)

(51) kunnen we ook met het voegwoord dan weergeven:

(52)	Jan koopt geen (andere) boeken dan boeken van Vestdijk^11

Al met al lijkt de conclusie gerechtvaardigd, dat de voegwoorden in (41) een natuurlijke semantische klasse vormen. Het zijn voegwoorden waarvan althans bepaalde betekenissen een tegenhanger hebben in de rekenkunde. Een vergelijking tussen talige en rekenkundige samentrekking ligt nu voor de hand.

11 In Van Calcar (1971) vinden we op blz. 194-197 een overzicht van oudere grammatica's die dan en behalve met elkaar in verband brengen.

4 Wat is samentrekking?

Nu we weten wat woorden als en, of, behalve enz. gemeenschappelijk hebben, kunnen we ons de vraag stellen wat samentrekkingsstructuren en gappingstructuren eigenlijk voor structuren zijn en waarom ze alleen bij de genoemde voegwoorden voorkomen. Gezien het rekenkundige karakter van deze voegwoorden, kunnen we verwachten dat zij eigenschappen, geheel of gedeeltelijk, gemeenschappelijk hebben met hun niet-talige tegenhangers in (41). Enkele van deze overeenkomsten zijn in grammatica's terug te vinden. Zo vermeldt de ANS (blz. 1082 e.v.) dat in woordgroepen die verbonden worden door en en of de leden omkeerbaar zijn, zoals in (53) en (54). Dit verschijnsel komt overeen met de commutativiteitswet in de rekenkunde (55)-(56):

(53)	Hendrik en Jozef hadden binnenpretjes.
(54)	Jozef en Hendrik hadden binnenpretjes.
(55)	5 + 3 = 3 + 5
(56)	A ∩ B = B ∩ A

Andere rekenkundige wetten die we in gewone taal bij en en of aantreffen, zijn de wetten van De Morgan. Deze logicus wees als eerste op de volgende equivalenties:

(57)	⌝ p en ⌝ q = ⌝ (p of q)
	⌝ p of ⌝ q = ⌝ (p en q)

Kraak & Klooster (1968: 268) behoorden tot de eersten die wezen op deze wetmatigheden in taal, overigens zonder de naam van De Morgan te noemen. Wij geven hier als voorbeeld:

(58)	Jan komt niet en Piet komt niet	=	Het is niet zo, dat Jan komt of dat Piet komt.
	Jan komt niet of Piet komt niet	=	Het is niet zo, dat Jan komt en dat Piet komt.

Is er nu ook een parallel waar te nemen tussen samentrekking in taal en

[p. 31]

samentrekking in de rekenkunde? Volgens ons is dit inderdaad het geval.¹² Beschouw daartoe voorbeeld (59) en (60):

(59)	dagbladen en weekbladen = (dag- en week)bladen
(60)	Jan heeft het meisje voor de HEMA gezien en Piet heeft het meisje achter de HEMA gezien = (Jan heeft het meisje voor (-) en Piet heeft het meisje achter) de HEMA gezien

en vergelijk deze voorbeelden met (61):

(61)	ap + bp = (a + b)p

ap + bp in (61) en dagbladen en weekbladen in (59) hebben beide een gemeenschappelijk element, respectievelijk p en bladen. In de rekenkunde kunnen we dit verkort weergeven door (a + b)p, waarin p ‘buiten haakjes’ gebracht is.¹³ Een soortgelijke afkorting, maar dan in taal, zien we in het tweede deel van (59), waar bladen ‘buiten haakjes’ staat. Hetzelfde procédé op zinsniveau zien we in (60). Samentrekkingsstructuren zijn dus te vergelijken met rekenkundige ‘afkortingen’ als (a + b)p in (61).

Laten we deze gedachte verder uitwerken. Beschouw (62):

(62)a	Jan heeft tulpen- in plaats van narcissenvelden aangelegd.
(62)b	Jan heeft in plaats van narcissen- tulpenvelden aangelegd.
(62)c	*Jan heeft tulpenvelden in plaats van narcissen- aangelegd.
(62)d	*Jan heeft in plaats van narcissenvelden tulpen- aangelegd.

(62a) en (62b) zijn correcte samentrekkingen, omdat het gemeenschappelijke element velden geheel rechts staat. Het staat dus buiten haakjes:

(63)a	Jan heeft (tulpen- in plaats van narcissen)velden aangelegd. (a in plaats van b)p
(63)b	Jan heeft (in plaats van narcissen- tulpen)velden aangelegd. (in plaats van b a)p

(62c) is geen correcte samentrekking, omdat het gemeenschappelijke element velden niet uiterst rechts staat ((ap) in plaats van b, waarin p uiteraard niet met b verbonden mag worden). (62d) is om dezelfde reden geen correcte samentrekking, met dien verstande dat p hier niet met a verbonden mag worden (in plaats van (bp) a).

Dezelfde observaties kunnen we doen ten aanzien van woordgroepen met behalve en dan:

12 Onafhankelijk van ons zijn Günther u.a. (1993: 316, 340) tot een vergelijking van samentrekkingen en ‘arithmetischen Klammerregeln’ gekomen.

13 Booij (1983) onderscheidt terecht twee soorten van conjunctie binnen gelede woorden: het type dag- en weekbladen en het type peper-en-zoutstel. In het laatste is geen sprake van samentrekking (peperstel en zoutstel is immers onmogelijk). In dit artikel laten we dit tweede type buiten beschouwing. Voor interessante observaties ten aanzien van beide types verwijzen we hier naar De Haas (1984).

[p. 32]

(64)a	Jan heeft (behalve tulpen- ook narcissen) velden aangelegd. (behalve a ook b)p
(64)b	*Jan heeft behalve tulpenvelden ook narcissen- aangelegd. (behalve (ap) ook b)
(65)a	Jan heeft (meer tulpen- dan narcissen) velden aangelegd. (a > b)p
(65)b	*Jan heeft meer tulpenvelden dan narcissen- aangelegd. (ap) > b

Bij voorwaartse samentrekking op woordniveau zien we dezelfde wetmatigheid, alleen moet hier het gemeenschappelijke element nu geheel links staan:

(66)a	Jan heeft dorps(straten en -pleinen) bestudeerd. p(a + b)
(66)b	Jan heeft meer dorps(straten dan -pleinen) bestudeerd. p(a > b)
(66)c	Jan heeft dorps(straten in plaats van -pleinen) bestudeerd. p(a in plaats van b)

Als we de woordgroep met in plaats van vooropplaatsen, wordt de zin geheel volgens verwachting ongrammaticaal:

(67)	*Jan heeft in plaats van dorpspleinen -straten bestudeerd. (in plaats van (pa) b)

Samenvattend kunnen we stellen, dat een groot aantal verschijnselen in de rekenkunde die samenhangen met de rekenkundige tekens in (41) in taal teruggevonden worden bij de rekenkundige voegwoorden. ‘Buiten haakjes plaatsen’ is, getuige de in deze paragraaf besproken voorbeelden, één zo'n verschijnsel. Het komt in hoge mate overeen met samentrekken in taal.¹⁴

14 In de literatuur (Kerstens 1980) is gewezen op de ongrammaticaliteit van zinnen als *Jan koopt cd's en Piet verkoopt - en *dat Jan cd's koopt en Piet - verkoopt. Dat deze zin onwelgevormd is, komt doordat het gemeenschappelijke element (cd's) niet ‘buiten haakjes’ staat. Dat is wel het geval bij de grammaticale zin (Jan koopt - en Piet verkoopt) cd's.

5 Wat zijn gappingstructuren niet?

Vertoont samentrekking dus overeenkomst met het buiten haakjes plaatsen in de rekenkunde, bij gappingstructuren gaat het om wezenlijk andere zaken. Voordat wij onze ideeën over ‘rekenkunde en gapping’ naar voren brengen (zie paragraaf 6), geven we hier eerst de gangbare opvatting over gappingstructuren weer en noemen we enkele problemen die nog steeds niet goed opgelost zijn.

Algemeen gaat men ervan uit, dat een zin als (69) afgeleid is van een volledige zin als (68)¹⁵:

(68)	Johan zag Marie en Peter zag Heidi.
(69)	Johan zag Marie en Peter (-) Heidi.

Streepjes, zoals in (69), of letters voor lege plaatsen (zoals t en e) visualiseren in vele artikelen over gapping de traditionele samentrekkings- of weglatingsgedachte. Die visie is echter niet zonder problemen (Klein 1985a).

Een eerste probleem betreft de tegenstelling tussen de volgende zinnen:

(70)	Johan kwam hongerig de badkamer uit en Petra kwam de slaapkamer uit.
(71)	Johan kwam hongerig de badkamer uit en Petra de slaapkamer.

15 Voor de meest uitgewerkte versie van deze opvatting verwijzen wij naar Neijt (1979).

[p. 33]

Er is een aanzienlijk verschil tussen deze twee zinnen. In (70) wordt in het linkerconjunct gezegd dat Johan hongerig was, maar in het rechterconjunct wordt niet beweerd dat Petra dat ook was; in (71), de gappingversie, is dat wel het geval. Met andere woorden: in (71) heeft hongerig bereik over Petra, maar in de volledige versie van deze zin is dat niet het geval. Kennelijk is het tweede conjunct van (71) dus geen zinsachtige constituent aanwezig.

Fiengo en Lasnik (1974) hebben als eersten gewezen op een tweede probleem voor een transformationele gappingregel. Zij wijzen erop, dat een zinsdeel als not Mary John in (72) in het Engels niet vervolledigd kan worden (73):

(72)	John has seen Mary, not Mary John.
(73)	*John has seen Mary, not Mary has seen John.

Ook dit wijst erop, dat in het tweede conjunct van (72) geen zinsachtige constituent aanwezig is.

Gappingzinnen die niet goed te vervolledigen zijn, zijn ook in het Nederlands te vinden:

(74)	Eén jongen danste steeds met één meisje, en wel Piet met Marie
(75)	*Eén jongen danste steeds met één meisje, en wel Piet danste steeds met Marie.

Een derde probleem voor de gangbare deletietheorie vormen negaties. Als in beide delen van de conjunctie een negatie voorkomt (76), dan zou men verwachten, dat deze in het tweede deel kan komen te vervallen (77). Dit is echter niet zo; alleen (78), met niet ook in het tweede deel, is correct:

(76)	Marco heeft Marie niet gezien en Piet heeft Truus niet gezien.
(77)	*Marco heeft Marie niet gezien en Piet Truus.
(78)	Marco heeft Marie niet gezien en Piet Truus niet.

Het is opvallend, dat niet wel alleen in het tweede deel kan voorkomen:

(79)	Marco heeft Marie gezien en Piet Truus niet.

Bovendien is het zo, dat de negatie wel bereik heeft over het tweede conjunct, als zij helemaal vooraan in de zin staat:

(80)	Nimmer heeft Marco Marie gezien of Piet Truus.

Op deze verschijnselen komen we hieronder nog uitgebreid terug.

Ten slotte is het voor een samentrekkings- of weglatingstheorie¹⁶ een probleem waarom er geen gappingrestanten kunnen zijn in het eerste deel van het conjunct:

(81)	*Marco Marie en Piet heeft Truus gezien.

16 Neijt noemt niet ook een uitzondering op haar gappingregel (1979: 66: ‘It is a general feature of Gapping [...] that negative particles never delete.’). Waarom dat een uitzondering zou moeten zijn, vermeldt zij niet.

[p. 34]

Al deze problemen zijn kenmerkend voor een theorie die uitgaat van volledige zinnen waar dan elementen uit weggelaten worden. Een theorie die ervan uitgaat dat het tweede conjunct niet uit restanten bestaat, kent deze problemen niet. Zo'n theorie is al aan het eind van de jaren zestig voorgesteld door Simon Dik in zijn proefschrift over Coordination (Dik 1968: 142). In de volgende paragraaf zullen wij zijn voorstel bespreken.

6 Wat zijn gappingstructuren wel?

Als gappingstructuren geen restanten zijn van volledige zinnen, wat zijn het dan wel?

Gappingstructuren bevatten altijd beklemtoonde constituenten. Dit is geen bijzonderheid van deze structuren alleen: alle constituenten die door een van de rekenkundige elementen uit (41) verbonden worden, zijn beklemtoond:

(82)	Hij en zij; *hij en ze
	Jan zag hem en wij haar; *Jan zag hem en we d'r.
(83)	Iedereen behalve zij; *Iedereen behalve ze
	Elke jongen gaf elk meisje een boek, behalve hij haar; *Elke jongen gaf elk meisje een boek, behalve hij d'r.
(84)	Meer boeken dan zij (heb ik niet); *meer boeken dan ze (heb ik niet.
(85)	Jan koos haar in plaats van hem; *Jan koos d'r in plaats van 'm.
(86)	Als Jan Marie mag kussen, dan zij hem ook; *als Jan Marie mag kussen, dan ze 'm ook.

Kortom, de rekenkundige voegwoorden verbinden altijd focusconstituenten (dus beklemtoonde constituenten), en het maakt in principe niet uit of zij combinaties van één, twee of meer focusconstituenten verbinden. In schema:

(87)

focusconstituent^n

rekenkundig voegwoord

focusconstituent^n

Wel is van belang, uiteraard, dat ter linker- en ter rechterzijde evenveel focusconstituenten staan en dat de grammatische functies van deze constituenten links en rechts gelijk zijn. Dik (1968: 142) formuleert dit als volgt:

(88)	Diks theorie
	Given a coordination &(M1, M2,... Mn),
[a]	if M1, M2, and... Mn are each single constituents, then there must be a grammatical function Fi such that Fi(M1), Fi(M2,..., Fi(Mn).
[b]	if M1, M2, and ... Mn are each combinations of constituents, then the total set of the grammatical functions of these constituents (FI, FJ, ..., Fn) must be the same for each of the members M1, M2, ... Mn.

Met [b] verantwoordt Dik de zogenaamde gappingzinnen. In Jan zag Marie en Piet Truus zijn (Jan, Marie) en (Piet, Truus) beide een combinatie van constituenten, waarvan de leden dezelfde grammaticale functies moeten hebben (subject, object). Dik voegt hier nog aan toe: ‘These functions will normally occur in the same order in each of the coordinated members, but [...] under certain circumstances this order may be different.’ Als voorbeeld van dit laatste geeft Dik I'll give you three dollars for all the books but for one of them no more than fifty cents.

[p. 35]

Op grond van wat we in paragraaf 3 besproken hebben, dienen we in (88) nu de eerste regel te vervangen door ‘Gegeven een conjunctie met een rekenkundig voegwoord uit (41)’. Met de ‘combinations of constituents’ bedoelt ook Dik ongetwijfeld ‘combinations of focusconstituents’.¹⁷

Het volgende dient als toelichting op (88). In (71), voor het gemak hier herhaald als (89), zijn (Johan, de badkamer) en (Petra, de slaapkamer) de combinaties van focusconstituenten. De verbinding tussen deze twee groepen focusconstituenten is alleen deugdelijk als de grammaticale functies van deze constituenten parallel lopen. Met andere woorden: de zin is alleen correct als Johan en Petra, en de badkamer en de slaapkamer dezelfde grammaticale functies hebben. Die grammaticale functies worden aan deze NP's toegekend door het werkwoord uitkomen en ‘doorgegeven’ door het rekenkundig voegwoord.

	F	F	F	F
(89)	Johan kwam boos de badkamer uit en Petra de slaapkamer
	subj.	obj.	subj.	obj.

(89) bevat ook een presuppositie (bekend veronderstelde informatie): boos uitkomen. Deze presuppositie heeft bereik over beide delen van de door het rekenkundig voegwoord gelegde verbinding. In termen van Diks theorie (88b) gebeurt het volgende. Er zijn twee combinaties van (focus)constituenten met dezelfde syntactische functies: (Johan, de badkamer) en (Petra, de slaapkamer). In schema:

(90)	presuppositie ((Focus^n) rekenkundig voegwoord (Focus^n))

Zo bezien is het hierboven geconstateerde verschil tussen (71) Johan kwam boos de badkamer uit en Petra kwam de slaapkamer uit en (72) (= (89)) verantwoord. Boos maakt in (89) deel uit van de presuppositie die ook betrekking heeft op het rechterdeel van de conjunctie, maar (71) heeft in het rechterdeel een eigen presuppostie (nl. alleen uitkomen).

Hieronder volgen nog een paar voorbeelden, waarin de constituenten tussen haakjes focusconstituenten zijn en de letters eronder de grammaticale relaties (Subject, Object, Indirect Object).

(91) Jan bemint	Marie	en Piet	Truus.
beminnen	((Jan,	Marie)	en (Piet,	Truus))
	S	O	S	O

(92)	Elk meisje heeft elke jongen een boek gegeven, behalve Truus Willem.
	een boek geven ((elk meisje, elke jongen) behalve (Truus, Willem))
		S	IO	S	IO

17 In Koster (1986) verwerpt de auteur een transformationele analyse van gapping-zinnen en verantwoordt de feiten op een wijze die op z'n minst doet denken aan Diks theorie. Koster beroept zich evenwel met name op Williams (1978).

[p. 36]

(93)	De soldaat gaf de generaal een bevel in plaats van de generaal de soldaat.
	een bevel geven ((de soldaat, de generaal) in plaats van (de generaal, de soldaat))
		S	IO	S	IO

(94)	Jan kust Marie vaker dan Piet Truus.
	vaker kussen ((Jan, Marie) dan (Piet, Truus))
		S	O	S	O

(95)	Als Jan Marie mag kussen, dan Piet Truus ook.
	mogen kussen ((Jan, Marie) → (Marie, Jan))
		S	O	S	O

Hoe zit het nu met negaties? We constateerden hierboven dat het voor een deletieanalyse een onbegrepen feit is dat (56) *Marco heeft Marie niet gezien en Piet Truus ongrammaticaal is. Staat dit feit op zichzelf of kan het met andere negatiefeiten in verband gebracht worden?

Bij een eenvoudige nevenschikking als Jan en Piet kunnen we de negatie op twee plaatsen invoeren:

(96)	Niet Jan en Piet
(97)	Jan en niet Piet

In (96) heeft de negatie betrekking op de nevenschikking Jan en Piet, niet op Jan alleen. Een goede zin is Niet Jan en Piet gingen naar de schouwburg, maar Peter en Willem. We kunnen (96) niet zo opvatten, dat Jan niet, maar Piet wel naar de schouwburg gaat (vergelijk *Niet Jan en Piet gaat/gaan naar de schouwburg). In (97) kunnen we de nevenschikking wel op deze wijze interpreteren: Jan en niet Piet ging naar de schouwburg. In deze zin gaat alleen Jan naar de schouwburg. We concluderen derhalve, dat de negatie de hele nevenschikking bindt als zij geheel links staat en alleen het rechterconjunct bindt als zij direct rechts van het voegwoord staat:

(98)	Niet (Jan en Piet) (= 96)
(99)	Jan en (niet Piet) (= 97)

Onmogelijk is dus de lezing (niet Jan) en Piet.

Precies hetzelfde zien we in gappingstructuren:

(100a)	Het is niet zo, dat Marco Marie heeft gezien of Piet Truus.^18
(100b)	Nimmer heeft Marco Marie gezien of Piet Truus.
(101a)	*Marco heeft Marie niet gezien of Piet Truus.
(101b)	*Marco heeft Marie nimmer gezien of Piet Truus.
(102a)	Marco heeft Marie gezien en Piet Truus niet.
(102b)	Marco heeft Marie gezien en Piet Truus nimmer.

In (100) hebben de negaties niet en nimmer bereik over (Marco, Marie) en over (Piet, Truus). De negaties staan hier links van de beide combinaties focusconsti-

18 Krachtens de wetten van De Morgan verschijnt in deze en de volgende voorbeeldzin niet en maar of.

[p. 37]

tuenten. In (101) binden de negaties alleen de focusconstituenten in het linkerconjunct. Dat is onmogelijk, net zoals dat onmogelijk is in (96) Niet Jan en Piet. In het Nederlands - en vermoedelijk in alle talen - hebben we alleen de lezingen (A en B)* en (A en B*), maar niet (A* en B). (Het sterretje geeft hier de negatie aan.)

Daarmee hebben we het negatieprobleem rond de zin (77) *Marco heeft Marie niet gezien en Piet Truus - een probleem voor de deletieanalyse - teruggebracht tot een algemeen probleem rond het voegwoord en (en of). Bij andere voegwoorden kan de negatie wel degelijk op de eerste plaats staan, zoals bij niet Jan, maar Piet gaat naar de schouwburg; Jàn heeft Màrie niet gekust, maar Piet Truus (wel).

Ook het probleem rond zin (58) *Marco Marie en Piet heeft Truus gezien kunnen we terugvoeren tot een algemener probleem. Wat we zien is, dat de zogenaamde gappingstructuur alleen mogelijk is in het rechterdeel van de conjunctie. Blijkbaar is het rekenkundig voegwoord het element dat de presuppositie (predikaat) doorgeeft aan de constituenten rechts van zich. In (58) gaat aan Marco Marie geen voegwoord vooraf dat de presuppositie kan doorgeven. Bij andere voegwoorden, zoals behalve en in plaats van kan dit wel: Behalve een boek aan Marie heeft Jan een cd aan Truus gegeven; In plaats van de generaal de soldaat, heeft de soldaat de generaal een bevel gegeven.

7 Conclusie

We hebben in dit artikel naar voren willen brengen, dat het traditionele beeld ten aanzien van zogenaamde gappingzinnen onjuist is. Een dergelijke zin is geen resultante van een deletieregel die ten minste de persoonsvorm deleert. Veeleer hebben we in het tweede conjunct te maken met een combinatie van focusconstituenten die opponeert met een combinatie van focusconstituenten in het eerste deel van de neven- of onderschikking. In principe is de regel zoals Dik die in zijn proefschrift geformuleerd heeft correct (1968). Een absolute voorwaarde voor samentrekkings- en gappingstructuren zijn de voegwoorden die een rekenkundig karakter hebben en die derhalve naar onze mening voortaan als ‘rekenkundige voegwoorden’ in grammatica's opgenomen dienen te worden. Dat de klasse van woorden veel meer leden bevat dan de bijna altijd gebruikte nevenschikkende voegwoorden en en of moge uit het bovenstaande duidelijk zijn geworden.

Bibliografie

Booij, G.E. (1983). ‘Conjunctiereductie in gelede woorden, een terreinverkenning’, in Spektator 13, 3-19

Calcar, W. van (1971). Over comparatief- en vergelijkingszinnen. Assen: Van Gorcum & Comp. N.V.

Corver, N. (1990). The Syntax of Left Branch Extractions. Diss. Tilburg.

Dik, S. (1968). Coordination. Its implications for the theory of general linguistics. Amsterdam: North-Holland Publishing Company.

Fiengo, R. & H. Lasnik (1974). ‘Complement Object Deletion’, in Linguistic Inquiry V, 535-571.

Freudenthal, H. (1967). Exacte logica. Tweede druk, Haarlem: De Erven F. Bohn N.V.

Geerts, G., W. Haeseryn, J. de Rooij & M.C. van den Toorn (1984). Algemene Nederlandse Spraakkunst. Groningen-Leuven: Wolters-Noordhoff.

U. Günther e.a. (1993). ‘Elliptische Koordination. Strukturen und Prozesse lokaler Textkohärenz’, in Linguistische Berichte 146, 312-342.

[p. 38]

Haas, W. de (1984). ‘Conjunctiereductie of nevenschikking in gelede woorden’ in Spektator 14, 216-220.

Hendriks, P. (1991). ‘The coordination-like structure of comparatives’, in F. Drijkoningen en A. van Kemenade (ed.) Linguistics in the Netherlands 1991. Amsterdam/Philadelphia: John Benjamins Publishing Company, 41-50.

Kerstens, J. (1980). ‘Over samentrekking’ in De nieuwe taalgids 73, 375-394.

Kerstens, J. (1981). ‘Bestaat Gapping eigenlijk wel?’ in Spektator 11, 61-79.

Klein, M. (1985a). ‘Koordination oder Gapping?’ in: Kürschner, W. & R. Vogt, Grammatik, Semantik, Textlinguistik. Akten des 19. Linguistischen Kolloquiums Vechta 1984. Band I. Tübingen 1985: Max Niemeyer Verlag.

Klein, M. (1985b). ‘Behalve: voorzetsel of voegwoord?’ in De nieuwe taalgids 78, 363-368.

Klein, M. (1986). ‘Coördinatieverschillen tussen Nederlands en Engels’ in Spektator 15, 396-405.

Klein, M. (1991). ‘Coördinatie in de ANS’, in Gramma 15, 227-234.

Klein, M. & M. Visscher (1992). Handboek Verzorgd Nederlands. Groningen: Martinus Nijhoff.

Koster, J. (1987). Domains and Dynasties. The Radical Autonomy of Syntax. Dordrecht: Foris Publications.

Kraak, A. & W. Klooster (1968). Syntaxis. Culemborg: H. Stam Internationaal N.V.

Kutschera, F. von, & A. Breitkopf (1972). Inleiding tot de moderne logica. Aula 482 Utrecht/ Antwerpen: Het Spectrum.

Napoli, D.J. (1983). Comparative Ellipsis: A Phrase Structure Analysis, in Linguistic Inquiry 14, 675-694.

Neijt, A. (1979). Gapping: a contribution to sentence grammar. Dordrecht: Foris Publications.

Paardekooper, P.C. (1966). ‘Behalve als zn-patroondeel’, in De nieuwe taalgids 59, 171-179.

Paardekooper, P.C. (1976). Beknopte ABN-syntaksis. Vijfde druk, Eindhoven: uitgave in eigen beheer.

Seuren, P.A.M. (1973). ‘The Comparative’, in F. Kiefer & N. Ruwet (eds.) Generative Grammar in Europe. Dordrecht: Reibel, 528-564.

Stassen, L. (1984). Comparison and Conjunction. An essay in Universal Grammar. Diss. KU Nijmegen.

Toorn, M.C. van den (1972). ‘Balansschikking en disjunctie’, in De nieuwe taalgids 65, 104-123.

Williams, E.S. (1978). ‘Across-the-Board Rule Application’, in Linguistic Inquiry 9, 31-43.