| |
(‘er is een waarde w dusdanig dat Jans grootte dichter bij 0 staat dan w, en Piets grootte niet dichter bij 0 staat dan w’) |
Voor verdere details verwijs ik naar Kloosters artikel. Wat nu opvalt is dat op blz. 540/1, waar Klooster probeert (1) af te leiden, hij niet de analyse met
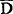
gebruikt, d.w.z. (5) (zijn (21)), maar een logisch daarvan afgeleide analyse met D, hier weergegeven als (6):
| (5) |
Ew[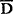 ((de i (Jan met snelheid i)), w) & niet (M( ((de i (Jan met snelheid i)), w) & niet (M(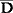 ((de i (Jan met snelheid i)), w)))] ((de i (Jan met snelheid i)), w)))] |
| (6) |
Ew[niet (D((de i (Jan met snelheid i)), w)) & niet (M(niet (D((de i (Jan met snelheid i)), w))))] |
Hij geeft daarbij de volgende lexikale regel voor M (het ‘gebiedende’
moeten/hoeven/mogen):
| (7) |
M → moet / ----- p |
| |
M → hoef / ----- nietp |
| |
M → mag /----- niet p |
| |
(waarbij p geen uitdrukking is die begint met ‘niet’) |
Uitgaande van (6) en (7), zegt Klooster nu, kan voor de konfiguratie ‘& niet M niet’ alleen
mogen gekozen worden als lexikalisatie van
M, en ‘& niet’ wordt nu, zoals steeds, -
er dan. Hij signaleert echter (noot 5) de problemen die rijzen bij deze behandeling, met name wat betreft de veelvuldig overschietende negaties. De aldus gegenereerde zin wordt dan:
| (8) |
Jan reed minder snel dan hij mocht. |
Het lijkt me echter dat, evenals een afleiding gepostuleerd werd van (4) naar (3), we een afleiding kunnen postuleren die daaraan geheel analoog verloopt, van (5) naar (1). Volgens regel (7) laat (5) de lexikalisatie
hoeven toe voor M. We kunnen (5) nu informeel lezen als: ‘er is een waarde
w dusdanig dat Jans snelheid negatief is t.o.v.
w, en Jans snelheid hoeft niet negatief t.o.v.
w te zijn’. Klooster verkrijgt (8) slechts met behulp van extra assumpties, die heel goed vermeden kunnen worden, en, als (1) inderdaad een goede zin is, ook vermeden moeten worden.
Er is echter nog iets anders aan de hand, en dit is mijn derde en laatste punt. Zin (8) is voor dubbele uitleg vatbaar, is dus ambigu. Deze ambiguïteit treedt typisch op in de struktuur:
| (9) |
X - minder - { |
adjektief |
} - Y - dan - U - mogen - W |
| |
X - minder - { |
adverbium |
} - Y - dan - U - mogen - W |
Zin (8) kan nl. betekenen dat Jans snelheid lager was dan de toegestane snelheid (lezing
a), of dat Jans snelheid lager was dan de vereiste snelheid (lezing
b). In lezing
a is Jan niet in overtreding: hij blijft beneden de maximum snelheid. In lezing
b is Jan wel in overtreding: hij blijft beneden de voorgeschreven minimum snelheid. Lezing
a houdt in dat de toegestane snelheid niet zo laag was als de snelheid waarmee Jan reed. Lezing
b houdt in dat Jan niet zo langzaam (weinig snel) mocht rijden als hij deed.