Streven. Jaargang 14

[p. 614]

James Jeans en de cosmogonie
door O. van de Vijver S.J.

Op 16 September 1946 overleed in Engeland op 69 jarigen leeftijd sir James Hopwood Jeans^1.. Door zijn populaire werken waarvan de meeste in het Nederlands werden vertaald is Jeans bij ons geen onbekende. Door zijn levende stijl en zijn concrete beelden neemt hij niet alleen onmiddellijk contact met zijn lezers maar hij slaagt erin hen te doen delen in de geestdrift die hem zelf bij zijn verrassende ontdekkingen heeft bezield. Wie aan de laatste bladzijde komt van een van Jeans' boeken heeft niet zelden het weemoedig gevoel dat hij afscheid neemt van een intieme vriend die hem met sympathie over de meest verscheidene problemen van het heelal heeft onderhouden.

Jeans heeft zijn bekendheid hoofdzakelijk te danken aan zijn cosmogonische ideeën. Het woord 'Cosmogonie' dat 'wereld-wording' betekent, kan tot verwarring leiden. Inderdaad, een wetenschappelijke Cosmogonie stelt zich niet ten doel een uitleg te geven voor het tot stand komen van de stof, maar alleen voor de transformaties en het vormkrijgen van een gegeven oorspronkelijke chaos. Zij heeft dus niets te maken met 'schepping' in de stricten zin van het woord. Om haar doel te bereiken maakt zij zoveel mogelijk gebruik van bekende dementen en natuurwetten en ze postuleert slechts onbekende krachten voor zover en in de mate alleen waarin het onvermijdelijk blijkt en dan nog met de hoop ze zodra mogelijk door bekende gegevens te kunnen vervangen.

1. Jeans werd geboren te Southport op II September 1877. Na schitterende studies aan het Trinity College te Cambridge werd hij in 1901 Fellow aan dezelfde Universiteit. Van 1905 tot 1909 was hij professor in de toegepaste Wiskunde aan de Universiteit van Princeton en werd daarna 'Stokes Lecturer' te Cambridge. Jeans was te zeer een ontdekkersnatuur om zich te houden aan de lang gebaande wegen van het professoraat en daar dit ambt te veel van zijn tijd in beslag nam, besloot hij zich voortaan hoofdzakelijk te wijden aan louter wetenschappelijk onderzoek. Vanaf 1906 was hij lid van de 'Royal Society', in 1919 kreeg hij de Royal Medal en werd tevens secretaris van de 'Royal Society', ambt dat hij waarnam tot in 1929. In 1922 werd hij vereerd met de Gold Medal van de 'Royal Astronomical Society', waarvan hij president was van 1925 tot 1927. In 1928 werd hij ridder en in 1939 kreeg hij het Order of Merit.

Abstracte wiskunde

Zijn gewone methode volgend behandelt Jeans de hele kwestie

[p. 615]

eerst op grondige wijze langs zuiver mathematische weg. Zo kan hij zonder vooroordeel het resultaat van deze abstracte wiskunde aan de concrete, physische werkelijkheid toetsen.

Jeans' meesterwerk is ontegensprekelijk zijn Problems of Cosmogony and Stellar Dynamics van 1919^1..

Welke zijn nu de resultaten van dit wiskundig onderzoek? Wel, de berekening toont aan dat alle lichamen, welke ook hun inwendige structuur weze, bij kleine omwentelingssnelheden, de vorm aannemen van een afgeplatte sfeer. Zo komt het dat ook de aarde, met haar geringe hoeksnelheid, aan de polen afgeplat is. Neemt nu de rotatiesnelheid toe, dan is de vorm van het lichaam niet alleen meer functie van die snelheid, maar eveneens van zijn inwendige samenstelling. Van zeer groot belang wordt dan de dichtheid in of nabij het middelpunt.

Een roterend lichaam kan volgens twee verschillende evolutieschema's ontwikkelen naargelang het een onsamendrukbare massa vertegenwoordigt, zoals water, of een samendrukbare zoals gas. In het eerste geval heeft het bewuste lichaam een eenvormige dichtheid, en bezit dus geen centrale verdichting: in het tweede geval neemt de dichtheid van buiten naar binnen toe, zodat de massa sterk geconcentreerd is bij het middelpunt.

Het evolutieschema van elk dezer categorieën, gerangschikt volgens toenemende omwentelingssnelheid, ziet eruit als volgt:

1. Dit boek is een antwoord op een prijsvraag uitgeschreven in 1917 door de Commissie voor de Adamsprijs. Het werd onbetwist bekroond.

[p. 616]

Concrete werkelijkheid

Dit alles is het resultaat van louter wiskundige berekening. De toepassing op de hemellichamen is niet zo eenvoudig als misschien op het eerste gezicht zou lijken. Jeans wijst er met nadruk op dat alleen min of meer waarschijnlijke veronderstellingen kunnen gemaakt worden, en hierin is hij het eens met Eddington die verklaarde: 'The time for arriving at conclusions in cosmogony has not yet come'.

Een eerste reden om op zijn hoede te zijn is de volgende. Om op wiskundig gebied niet onmiddellijk voor onoverkomelijke moeilijkheden te staan heeft Jeans een belangrijke vereenvoudiging ingevoerd. Als basis voor zijn beide evolutieschema's heeft hij twee uiterste gevallen genomen: een eenvormige niet samendrukbare massa en een samendrukbare massa die zeer sterk in haar centrum gecondenseerd is. Tussenvormen zijn mogelijk en de hemellichamen komen zich eerder tussen beide uitersten rangschikken volgens hun graad van centrale verdichting. Het gevolg is dat, wanneer de graad van verdichting verandert een hemellichaam een tijd lang het eerste evolutieschema volgt en vanaf een bepaald ogenblik het tweede.

Een tweede reden tot voorzichtigheid volgt uit de waarnemingsgegevens. Inderdaad, men kan de verschillende voorwerpen aan de hemel volgens hun grootte niet rangschikken in een continue afdalende reeks. Ze moeten ondergebracht worden in vier reeksen die totaal van elkaar gescheiden blijven. Het zijn de volgende:

1.	Spiraalnevels: grootte-orde ongeveer een milliard sterren.
2.	Sterren.
3.	Planeten: grootte-orde ongeveer 1/1000 van de zon.
4.	Satellieten: grootte-orde ongeveer 1/10.000 van de planeten.

[p. 617]

Om deze sprongsgewijze afdaling te verklaren doet Jeans beroep op wat hij noemt 'gravitational instability'. Newton vermoedde reeds dat in een eenvormige gasmassa na verloop van tijd een zeker aantal condensaties moest ontstaan waarrond zich de nevelstof helemaal zou concentreren. Jeans heeft dit probleem mathematisch uitgewerkt en het vermoeden van Newton bevestigd. Een dergelijke instabiliteit kan ofwel eenvoudig aan inwendige krachten te wijten zijn ofwel ook aan een evenwichtsverstoring van buiten uit. Van beide zullen wij voorbeelden aantreffen.

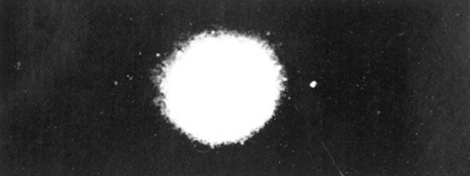
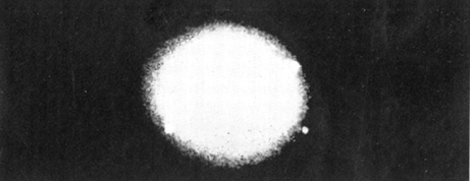
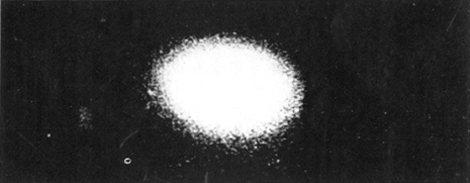
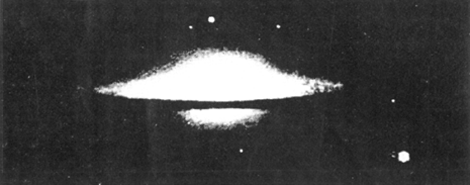
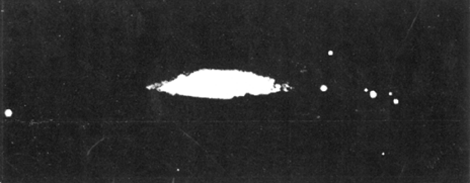
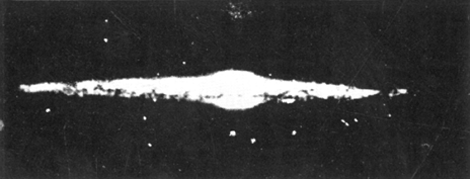
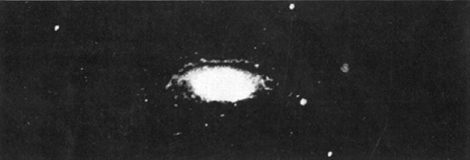
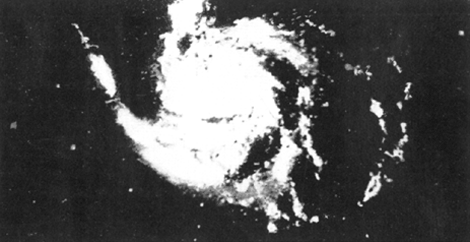
Spiraalnevels

Hoe stelt Jeans zich het ontstaan van het heelal, zoals wij het kennen, voor? Aanvankelijk was volgens hem het heelal gevuld met een uiterst ijle gasmassa. Tengevolge van kleine ongelijkheden in dichtheid ontstaan spheroïdale verdichtingen die traag om hun as wentelen. Door straling verliezen ze voortdurend energie met als gevolg dat de hele massa inkrimpt, en de hoeksnelheid of, wat hetzelfde is, de omwentelingssnelheid toeneemt. Wat te voorzien is, gebeurt: de spheroïdale vorm zet zich in het evenaarsgebied uit en wordt stilaan lensvormig. Nu komt het kritieke ogenblik. Blijft de hoeksnelheid constant dan blijft ook de gasmassa als lensvorm bestaan.

Neemt de snelheid echter nog toe dan wordt het inwendig evenwicht verbroken en de materie ontsnapt langs de scherpe zijde niet over heel de omtrek, maar tengevolge van de getijdewerking van de rest van het heelal, aan twee diametraal tegenover elkaar liggende punten. Een spiraalnevel is ontstaan. (Zie plaat 1, 2, 3.)

Ontelbare spiraalnevels bevinden zich aan de hemel. Men schat hun aantal op 30 millioen. Nauwkeurige observatie op de meest nabije heeft aangetoond dat zij een vorm hebben van wat men in de wiskunde noemt, een 'logarithmische spiraal'.

Jeans is er niet in geslaagd de spiraalvorm van de beide spiraalarmen wiskundig af te leiden. Merken wij nog even op dat de spiraalnevels ontwikkelen volgens het tweede evolutieschema; het zijn aanvankelijk enorme gasmassa's met zeer sterke centrale verdichting.

Sterren en dubbelsterren

Spiraalnevels zijn de geboorteplaats der sterren. Volgens Jeans moeten de sterren het vlugst ontstaan aan de buitenste randen, wat men nu noemt, de 'sterren-mist'. Inderdaad werden in de Andromeda-

[p. 618]

nevel, in 1925, enkele uitlopers van de spiraalarmen photographisch in afzonderlijke sterren opgelost. Twee jaar geleden is Baade, met de 100 duims telescoop van het Mt Wilson-observatorium er in geslaagd ook de kern op te lossen. Nieuwe problemen kwamen hiermede opduiken die moesten gevoegd worden bij de talrijke andere die nog op een definitieve oplossing wachten.

Evenals de spiralen kunnen ook de sterren inwendig hun stabiliteit verliezen tengevolge van hun toenemende aswenteling. Aanvankelijk spheroïdaal, gaan ze geleidelijk over naar ellipsoïden, worden sigaarvormig, vervolgens peervormig totdat de vernauwing zich zodanig ingediept heeft dat een volledige breuk ontstaat en een dubbelster gevormd wordt. Wiskundige berekeningen tonen aan dat op deze wijze alleen dubbelsterren kunnen gevormd worden wier componenten dicht bij elkander staan en wier massa's niet al te zeer verschillen. Er zijn echter talrijke binaire stelsels bekend wier componenten zeer ver van elkander verwijderd zijn. Welnu indien dubbelsterren op de boven aangehaalde wijze - het eerste evolutieschema - ontstaan zijn en indien geen invloeden van buitenuit zich laten gelden, kunnen ze in geen geval hun banen wijder maken. Om dergelijke stelsels te verklaren neemt Jeans zijn toevlucht tot een 'vang-hypothese': sterren die elkaar op korten afstand ontmoeten kunnen door de aantrekkingskracht die ze op elkaar uitoefenen wel eens gedwongen worden samen te blijven, althans indien hun snelheid niet te groot is. Een grote moeilijkheid blijft nochtans bestaan. De sterren staan zo ver uiteen dat de ontmoetingsmogelijkheden uiterst gering zijn. Volgens Jeans kunnen binnen het bereik van onze telescopen in één milliard jaar slechts tien duizend stelsels op deze wijze gevormd worden, een aantal dat zeker beneden de werkelijkheid blijft.

Onze zon is een doodgewone ster. Ook zij is een condensatie-druppel in een spiraalnevel, onze galaxis, die wij tegen de hemel afgetekend zien als de melkweg. Nog altijd is de vraag niet definitief opgelost of de melkweg een spiraal is zoals de overige ofwel een stelsel van spiraal-nevels. De moeilijkheid ligt hierin: enerzijds, dat wij er ons binnenin bevinden, anderzijds, dat de afstandsbepaling van haar verschillende onderdelen zeer wordt bemoeilijkt door de interstellaire lichtopslorping, waarvan de waarde nog niet met voldoende nauwkeurigheid bekend is.

Het zonnestelsel

Wij dalen nu een trapje lager in de reeks der hemelobjecten en komen terecht in het zonnestelsel. Zoals verder blijken zal, is zijn ontstaan niet te wijten aan een inwendige evenwichtsverstoring van

[p. 619]

de zon. Geen van de beide evolutieschema's die we boven voorstelden leidt tot iets wat ook maar van ver gelijkt op het zonnestelsel. Daarom heeft Jeans uitgekeken naar de tweede mogelijkheid van 'gravitatieinstabiliteit', een verstoring van buitenuit. Hij stelt het aldus voor. Bij de geboorte van de planeten is de zon een zeer ijle reusachtige gasbol die zich uitstrekt tot aan de huidige baan van Neptunus, dus met een straal van 4.500 millioen kilometer. Ze vervolgt rustig haar weg in het sterrestelsel, tot op zeker ogenblik, het moet ongeveer twee milliard jaar geleden zijn, een andere ster gevaarlijk dicht nadert. Het ergste wat kan gebeuren is een botsing, maar, ook al gebeurt deze niet, toch kunnen diepgaande veranderingen plaats grijpen. Zolang de ster niet binnen een bepaalde grens komt zullen door wederzijdse aantrekking in de buitenste gaslagen alleen reusachtige getijden ontstaan. De bovengenoemde grens wordt bepaald door de massa van de storende ster. Veronderstellen wij beide massa's gelijk, dan ligt ze op 2½ maal de straal van het gestoorde lichaam. In casu waren de massa's niet gelijk. Een zware ster is op een afstand van 3 zonnestralen - 13.500 millioen Km - voorbijgekomen. Dit was binnen de gevaarlijke zone. Steeds dichter nadert de ster, steeds hoger worden de vloedbergen tot plots de top wordt losgerukt. Op dat ogenblik is elk deeltje van de losgehaakte massa onderworpen aan twee verschillende krachten: de aantrekkende kracht van de zon en die van het storend lichaam. Om nu te weten welke baan het zal volgen in de ruimte moet men beroep doen op de 'crux' van de dynamica der hemellichamen, het drie-lichamen-probleem, een probleem dat totnogtoe in zijn algemene vorm zonder bepaalde oplossing is gebleven. Dit kan men in ieder geval zeggen, dat de losgerukte massa zich moet krommen en dat ze zich zal bewegen in het baanvlak van de storende ster. Tussen beide hemellichamen hangt nog binnen de aantrekkingssfeer van de zon iets als een reusachtige banaan.

Lang zal het echter niet duren: ze is inwendig niet stabiel en dus onverbiddelijk veroordeeld om in stukken te breken. Aan beide uiteinden bevinden zich de kleinste brokken en deze geven het ontstaan aan de kleine planeten, in de nabijheid van de zon Mercurius, Venus, de Aarde, Mars en aan het andere einde Uranus, Neptunus en Pluto. Het middengedeelte levert de twee grote planeten Jupiter en Saturnus. Dit wordingsproces kan verder worden bepaald. Kleine gasmassa's bezitten onvoldoende zwaartekracht om samen te ballen, zodat de kleine planeten onder vloeibare of zelfs min of meer vaste vorm ontstaan zijn, terwijl de grote gasvormig waren.

De satellieten zijn op hun beurt op dezelfde wijze uit de planeten ontstaan. Welk is dan in deze gevallen het storende lichaam geweest? Hierop antwoordt Jeans dat oorspronkelijk de planeten zeer excentrische

[p. 620]

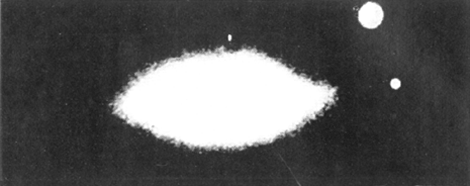
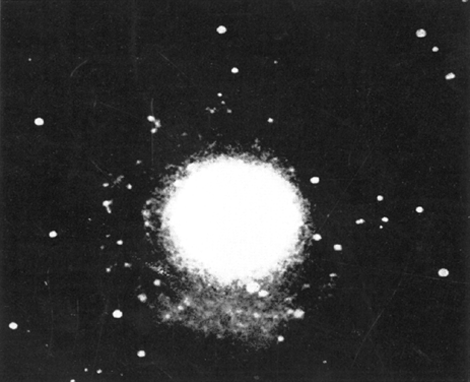
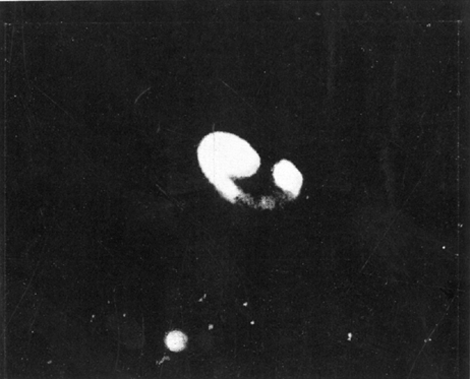
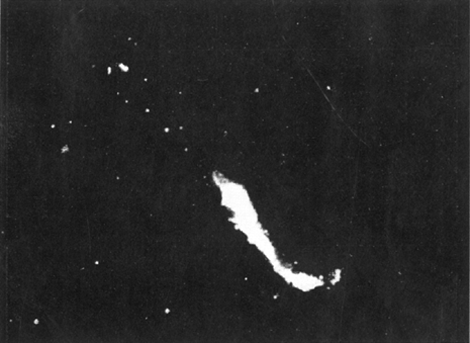
of langgerekte banen bezaten, zodat ze eens per omloop rond de zon deze op betrekkelijk korte afstand naderden en omgekeerd de zon binnen hun eigen gevaarlijke zone kwam en zo de hoogste vloedbergen wegkaapte die tot satellieten evolueerden. Tengevolge van de wrijving met de middenstof die nog rond de zon verspreid hing nam de excentriciteit geleidelijk af om te worden wat ze op dit ogenblik is. De toestand waarin de planeten tot stand kwamen geeft ook een uitleg voor het al of niet aanwezig zijn van wachters. De planeten die onder vloeibare of vaste vorm ontstaan zijn bezitten geen manen. Het zijn Mercurius en Venus. De grote planeten samen met Mars en Uranus die aanvankelijk gasvormig waren bezitten meerdere manen, Jupiter II, Saturnus 10, Uranus 4 en Mars 2. De Aarde en Neptunus zijn grensgevallen: ze zijn bij hun geboorte waarschijnlijk half-gasvormig half-vloeibaar geweest. Ze bezitten beide één Maan.

Dit is een beknopte samenvatting van Jeans' getijden-theorie. De 2 nevels van plaat 4 zijn door hem ter illustratie van zijn opvatting uitgekozen. Men kan zich wel eens afvragen of dit werkelijk een verklaring is voor het ontstaan van ons zonnestelsel en in hoever deze opvatting betrouwbaar is. De hele zaak ziet er nogal bedenkelijk uit als men alleen maar het aantal cosmogonieën nagaat die in de laatste jaren zijn voorgesteld. Om zich een min of meer juist denkbeeld te vormen omtrent de waarde van Jeans' theorie is het nodig ze even te situeren te midden van de overige cosmogonieën.

Monisme of dualisme?

De cosmogonieën van het zonnestelsel kan men in twee grote klassen onderbrengen: de monistische en de dualistische naargelang ze beroep doen op de zon alleen of op een tweede hemellichaam. Elk van beide richtingen heeft nu nog haar aanhangers.

De voornaamste vertegenwoordiger van de monistische opvatting was Laplace. Volgens hem is het zonnestelsel ontstaan uit een bolvormige nevel die zich uitstrekte tot buiten de grenzen van het huidige zonnestelsel. Deze nevel heeft een aswenteling in dezelfde richting als nu de zon en daar hij voordurend afkoelt door uitstraling krimpt hij in zodat zijn omwentelingssnelheid in evenredigheid toeneemt. In de equatorstreek wint de centrifugaalkracht het tenslotte van de zwaartekracht: een ring nevelstof Scheidt zich af die weldra zijn stabiliteit verliest, breekt en tot één massa samentrekt. Evenveel ringen als er nu planeten zijn scheiden zich af en ondergaan hetzelfde lot. Met de planeten herhaalt zich hetzelfde proces waaruit dan de satellieten ontstaan; slechts één ring is blijven bestaan, die van Saturnus.

[p. 621]

Deze hypothese, ofschoon ze heel wat gelijkenis vertoont met Jeans' evolutieschema voor samendrukbare massa's, kan het ontstaan van het zonnestelsel niet verklaren, en dit om verschillende redenen. Een omwentelingssnelheid, die groot genoeg is om nevelringen af te scheiden op de afstanden waar zich nu de planeten bevinden zou de kern - de zon - een omwentelingsmoment toekennen dat vele malen groter is dan dat van de planeten. Welnu de zon heeft een omwentelingsmoment dat vijftig maal kleiner is dan dat van de planeten. Daarbij is de massa van de ringen veel te gering om voldoende gravitatiecohaesie te bezitten, zodat ze zouden uiteenspringen door hun eigen inwendige drukking. Tenslotte de meest voor de hand liggende veroordeling is volgens Jeans de volgende: 'Indien de zon eens de vorm van een lens heeft aangenomen die nodig is om materie af te scheiden door rotatie, is het moeilijk in te zien hoe ze ooit van die vorm kan afgeraken en mooi rond worden zoals ze nu is. Het is eveneens lastig te begrijpen waarom de planeten zich op zulke verschillende afstanden van de zon bevinden'.

Andere theorieën zijn in de laatste jaren voorgesteld. Birkeland laat de planeten ontstaan uit ringen die zelf gevormd zijn door kleine positieve en negatieve deeltjes door de zon in haar equatoriale zone uitgestoten. Het magnetische veld van de zon doet deze deeltjes een spiraalvormige baan beschrijven die zich echter niet tot in het oneindige uitstrekt maar weldra in een limiet-cirkel overgaat. Op verschillende afstanden hebben zich dergelijke limiet-cirkels gevormd. Daar ontstaan dan de verschillende ringen die zich tot planeten samen trekken.

Berlage volgt voor het eerste stadium Laplace: een bolvormige nevel wordt onder invloed van zijn omwentelingssnelheid lensvormig. Op de plaats waar de planeten zullen ontstaan is dus de nodige materie aanwezig. Het komt er nu nog op aan deze zo te ordenen dat ook in werkelijkheid planeten kunnen gevormd worden. Deze ordenende werking wordt hier toegeschreven aan het electrostatische veld van de zon, dat samen met het atoomgewicht en de electrische lading van de deeltjes die in het spel zijn de plaats bepaalt waar ringen zullen tot stand komen die dan verder tot planeten kunnen samentrekken.

Samenvattend kunnen wij zeggen dat geen van deze monistische theorieën alle bijzonderheden van het zonnestelsel bevredigend verklaart.

Een andere, dualistische, mogelijkheid blijft over: de getijdentheorie met haar Varianten. Jeans is niet de eerste geweest om in deze richting te zoeken.

Maar de theorieën van zijn voorgangers kenden betrekkelijk weinig bijval. Het talent van een Jeans was nodig om een getijdentheorie op vaste grondslagen te vestigen. Ook hij echter slaagt er niet in alle

[p. 622]

eigenaardigheden van het zonnestelsel uit te leggen. Zo zijn de grote baanhelling van de Uranus-satellieten en de teruglopende manen van Jupiter, Saturnus en Neptunus onmogelijk toe te schrijven aan een getijbreuk.

Wat meer is, ook met het omwentelingsmoment is er iets niet in den haak. Berekeningen hebben uitgewezen dat dit bij het ontstaan van het zonnestelsel 35 maal groter moet geweest zijn dan het nu is, terwijl het onveranderd zou moeten gebleven zijn. Harold Jeffreys van het S. John's College te Cambridge, die aanvankelijk met Jeans een overtuigd voorstander was van de getijdentheorie, heeft deze hypothese als onverdedigbaar opgegeven en zijn toevlucht genomen tot een werkelijke botsing van de zon met een vreemde ster. Ook Gifford van Wellington (Nieuw-Zeeland) neemt een botsing aan. Een zwak punt, doch niet een onoverkomelijke moeilijkheid, waarvan Jeans zich wel bewust is en waar hij zelf op wijst, is de uiterst geringe kans voor de sterren om elkander te ontmoeten. Drie wespen verdeeld over een oppervlakte zo uitgestrekt als Europa, hebben evenveel kans elkaar te ontmoeten als de sterren om elkaar zo dicht te naderen dat een zonnestelsel kan ontstaan. Als ruwe schatting kunnen wij zeggen, aldus Jeans, dat één ster op een millioen door planeten omringd is. De kans tot een werkelijke botsing is nog veel geringer en dit is eveneens een sterk argument tegen Jeffreys en Gifford. Lyttleton, van Cambridge, is van oordeel dat de zon vroeger deel uitmaakte van een binair stelsel, toen een voorbijschietende ster het andere lid 'loshaakte' wat niet gebeurde zonder heftige beroering. Een lange sliert nevelstof raakte los en gaf het ontstaan aan het zonnestelsel.

Lyman Spitzer, van het Harvard-observatorium, heeft onlangs een nieuwe opwerping gemaakt tegen getijden- en botsingstheorieën. Zowel wiskundig als physisch heeft hij aangetoond dat geen planeten kunnen gevormd worden, door rechtstreekse condensatie van zonnestof. De zon toch, zoals de overige sterren, bestaat uit sterk overhitte gassen. Op de diepte, boven welke voldoende materiaal voorhanden is om planeten te vormen, bedraagt de temperatuur ongeveer 10 millioen graden celsius. Gelukkig heerst daar, vanwege de bovenliggende lagen, een drukking van ongeveer een millioen atmospheren, want anders zouden die lagen met geweld uitzetten en aan de gravitatiegreep van de kern ontsnappen. Wanneer nu, door getijwerking of door botsing een sliert materie uit de zon wordt losgerukt, zou deze in weinige ogenblikken als door explosie uiteenspatten. Spitzer toont zelfs aan dat de zwaartekracht van een massa die het dubbel bedraagt van die van Jupiter niet in staat zou zijn in de gegeven omstandigheden het gas bij elkaar te houden.

Dus ook de cosmogonie van Jeans heeft haar tijd gehad. Zal er

[p. 623]

iets van overblijven? Het antwoord hierop blijven wij schuldig. Poincaré, in zijn Leçons sur les hypothèses cosmogoniques (1911) bekent in alle eenvoud: 'Plus on étudie cette question sur l'origine des astres, moins on est pressé de conclure'. Professor Milne spreekt zich eveneens uit in dezelfde zin: 'It is the usual fate of cosmogonic theories not to survive'. Zoals het gewoonlijk gaat in de physica, houdt men aan een theorie vast zolang er geen betere in de plaats komt. Daarom besluit ook Russel in zijn werk: The Solar System and its Origine (1935): 'De meest aanmoedigende richting voor deze onderneming is te zoeken in de richting van een gewijzigde ontmoetingshypothese.'

De tijdschaal

Hiermede hebben wij het eenvoudigste deel van de cosmogonie behandeld. Het is de interpretatie van de waargenomen vormen der hemelobjecten.

Een tweede probleem waarvoor de cosmogonist een oplossing dient te zoeken, is bij benadering de waarde aan te geven van den tijd die nodig is voor de ontwikkeling van dergelijke cosmische processen. Jeans heeft de uitslagen van zijn onderzoek in deze richting gepubliceerd in zijn groot werk van 1928, Astronomy and Cosmogony waarin hij tevens de voornaamste resultaten van zijn Problems of Cosmogony and Stellar Dynamics recapituleert. Terwijl dit laatste werk zich uitsluitend tot wiskundigen richt, is dat van 1928 heel wat breder opgevat, zodat het, voor het grootste gedeelte, in het bereik valt van lezers die niet met de wiskunde vertrouwd zijn.

Jeans laat het bestaan van het zonnestelsel teruggaan tot voor ongeveer twee milliard jaar. Dit tijdsverloop is nodig om de planetenbanen toe te laten over te gaan van hun oorspronkelijk zeer grote excentriciteit tot de huidige waarde, en eveneens om van de gasvormige toestand door warmte-uitstraling af te koelen en vast te worden.

Het inwendige der sterren

Het kernprobleem vormen echter de sterren, hun inwendige structuur, hun stabiliteit en hun stralingsvermogen. Directe observatie is totaal uitgesloten, enerzijds omdat de sterren zo traag evolueren dat het onmogelijk is deze evolutie te constateren en anderzijds omdat de spectraalanalyse alleen inlichtingen kan verschaffen omtrent de buitenste lagen. Hier moet de natuurkunde bijspringen; en al dadelijk blijkt dat met uiterste omzichtigheid moet gehandeld worden. De

[p. 624]

natuurkunde is wel betrouwbaar voor phenomenen die aan directe experimentatie in de buitenwereld of in laboratoria kunnen onderworpen worden, doch met sterren kan men niet experimenteren. Vandaar ook de onzekerheid in de gevonden resultaten. Om deze zoveel mogelijk te reduceren vertrekt men dan ook waar het kan van uit de onmiddellijk waarneembare feiten.

De natuurkunde leert dat in een spherische gasmassa volledige Symmetrie moet heersen t.o.v. het centrum: drukking, dichtheid, zwaartekracht en temperatuur zijn functie van den afstand naar het centrum. Uitgaande nu van de oppervlakte-temperatuur kan men door toepassing van de gewone gas-wetten een idee krijgen van de inwendige temperatuur der sterren. Nemen wij als voorbeeld de zon. Haar oppervlakte temperatuur bedraagt ongeveer 5750^o C. Hieruit zou normaal voor het middelpunt volgen:

temperatuur: 455.000.000^o C.

dichtheid: 34.02 gr/cm^3

drukking: 43.000.000.000 atmospheren.

Jeans merkt op dat deze resultaten onjuist zijn. In het inwendige van de sterren moet men rekening houden met de ionisatie van de atomen. Een atoom is geïoniseerd, indien het een of meerdere electronen te veel of te weinig heeft. Het is b.v. eenmaal positief geïoniseerd indien het één electron te weinig heeft: een negatieve eenheidslading is verdwenen, het electrisch evenwicht is verbroken en het atoom, dat nu ion wordt genoemd, heeft een positieve eenheidslading. Na invoeging van deze factor valt de temperatuur terug op 31.000.000^o C, doch het aanwezig zijn van zware elementen voert dit getal op tot 40.000.000^o C. Eddington die eveneens uitgebreide studies heeft gedaan omtrent het inwendige van de sterren (The internal Constitution of the Stars - 1926) bekomt als eindwaarde 21.0000.000^o C, dus ongeveer de helft van Jeans.

Energiebronnen

Nu zijn er twee vormen van warmte, de mechanische warmte of bewegingsenergie der moleculen en de stralingswarmte of energie der ethergolvingen. Daar de stralingswarmte evenredig is met de vierde macht van de temperatuur blijkt uit het voorgaande onmiddellijk dat de sterren enorme hoeveelheden energie uitstralen. Per vierkante centimeter straalt de zon voldoende energie uit 'om een motor van 8 paardekracht zonder onderbreking in werking te houden', terwijl de heetste sterren, die een oppervlakte temperatuur bezitten tussen

[p. *45]

[p. *46]

[p. *47]

[p. *48]

[p. 625]

20-30.000^o C, eveneens per vierkante centimeter genoeg energie leveren om een express-locomotief op volle kracht te voeden. Het totale oppervlak van de zon levert jaar in jaar uit 490.000 trillioen paardekracht.

Waarvandaan halen zon en sterren die energie? Sinds de tweede helft van de vorige eeuw werden verschillende antwoorden voorgesteld die alle onvoldoende zijn gebleken. Zo Steide R. Mayer een voortdurende meteorietenregen voor, doch op de 30 millioen jaar zou de zon haar massa verdubbeld zien. Hieruit zou eveneens volgen dat de baan van de aarde ieder jaar zou verkorten en het jaar zelf zou telkens met een seconde afnemen. Dit is niet het geval. Helmholtz Steide in 1854 voor dat de zon door samentrekking of inkrimping voortdurend een deel van haar potentiële zwaartekrachtsenergie zou omzetten in kinetische energie in de vorm van moleculaire warmtebeweging. Doch de aldus verkregen energie zou onvoldoende zijn, evenals de gewone verbranding. Uitwendige energie-bronnen zijn alle ontoereikend. Men moet dus in een heel andere richting zoeken.

Hiervoor is het beter het probleem anders te stellen. Niet hoeveel energie verliest de zon per vierkante centimeter oppervlak, maar: hoeveel energie brengt ze voort per gram. Het gewicht van de zon is: 2.10³³ gram de totale uitgestraalde energie bedraagt per seconde 3,8-10³³ erg. Dit geeft dus 1,9 erg per gram en per seconde.

De ontdekking van de radioactiviteit van het uranium door H. Becquerel in 1896 opende nieuwe mogelijkheden: een eerste inwendige energiebron kwam aan het licht. In de volgende jaren werden de radioactieve elementen onder dit opzicht onderzocht doch het resultaat bleek eerder negatief te zijn. Jeans vat het onderzoek aldus samen: 'brief, uranium is to slow, radium is to rapid and all the other radioactive transformations have to little energy'.

In 1919 bracht Perrin de volgende interpretatie naar voren.

Het helium dat in de sterren aanwezig is zou kunnen gevormd zijn uit vier atomen waterstof. Op het eerste gezicht lijkt dit niet uit te komen: het atoomgewicht van helium is 4,00216, dat van waterstof 1,00778 en vier atomen waterstof wegen dus 4,03112. De berekening klopt niet 4,03112 − 4,00216=0,02896. Wanneer dus vier atomen waterstof samen één atoom helium vormen zijn 0,02896 massa-eenheden verdwenen. Waar zijn ze heen? De relativiteitstheorie van Einstein geeft hierop het antwoord in haar principe van aequivalentie tussen massa en energie. Wij kunnen dus antwoorden: de verdwenen massa is eenvoudig omgezet in energie. Indien een ster, die oorspronkelijk geheel uit waterstof bestond, zich aldus in zwaardere elementen omzet, zou per gram 6.5. 10¹⁸ erg vrij komen, een hoeveelheid energie die ruim voldoende is om het verlies door uitstraling te compenseren.

Jammer genoeg spreken de feiten deze verklaring tegen. In de

[p. 626]

veronderstelling van Perrin zouden jonge sterren veel meer waterstof moeten bevatten dan oudere en dit blijkt niet altijd het geval te wezen. Ook toont Jeans aan dat een ster uit waterstof alleen dynamisch niet stabiel zou zijn.

Massa en energie

Reeds in 1904 Steide hij zelf als oplossing voor: in de sterren wordt materie vernietigd door het op elkaar botsen van protonen en electronen. voor de quantitatieve rechtvaardiging van deze hypothese beroept hij zich eveneens op de relativiteitstheorie en het aangehaalde aequivalentieprincipe. Eén gram materie levert bij totale vernietiging 900 trillioen erg of ruim 32 millioen paardekracht. Deze energiebron is ruim voldoende om het verlies door straling te compenseren. Een onmiddellijke consequentie is echter dat de sterren stralen ten koste van hun eigen substantie. Zo verliest de zon per gram en per seconde 1,9 erg, dus per minuut 114 erg. Het gewicht van de zon bedraagt 2.10³³ gram dus een totale uitstraling van 228.10³³ erg per minuut. Om nu het equivalent hiervan te vinden hoeven wij nog slechts te delen door 9.10²⁰ (C2) en wij bekomen als verlies aan gewicht per minuut 25.10¹³ gr. of 250 millioen ton. In de veronderstelling dat de zon heel haar massa in straling zou verspillen kunnen wij besluiten dat ze nog 15 billioen jaar te leven heeft en om gedurende anderhalf milliard jaar te stralen zou ze slechts een tienduizendste deel van haar massa verliezen.

Hieruit blijkt dat de kennis van de massa en het stralingsvermogen van de ster ons een middel aan de hand kan doen om haar levensduur te bepalen. De vraag is echter of alle atomen in een ster aan dit vernietigingsproces onderhevig zijn. Hierop antwoordt Jeans ontkennend: 'Atomen die volledig ontbonden zijn in hun constituerende electronen en protonen zijn tegen vernietiging beveiligd'. Doch indien dit zo is hebben wij hier een totaal onzekere factor in de berekening van de levensduur der sterren. Wie zal immers uitmaken 'hoe lang en in welke mate hun atomen op deze wijze voor vernietiging behouden zijn?' Indien volledige ionisatie de atomen voor vernietiging behoedt, dan kan, volgens Jeans, ook gedeeltelijke ionisatie de annihilatie gedeeltelijk tegenhouden of vertragen.

Een tweede factor werkt eveneens in dezelfde richting. Vermits de straling functie is van de massa, zullen de meest massieve sterren ook het hevigst stralen en dus ook het vlugst hun massa verliezen. Hoe meer massa verloren gaat hoe minder ze bijgevolg ook gaan stralen. Als een ster dus ouder wordt verdwijnen haar beste energieproducenten het eerst, terwijl de atomen die het langst blijven bestaan

[p. 627]

tevens ook het minst stralingsernergie voortbrengen. De jongste sterren stralen dus ook het meest energie uit per eenheid van massa en zijn dus ook de zwaarste. Daaruit volgt niet noodzakelijk dat ze de hoogste of laagste inwendige temperatuur zouden bezitten noch de hoogste of laagste centrale dichtheid.

Levensduur van de sterren

Afgezien nu van de onzekerheidsfactor tengevolge van de ionisatiegraad kunnen wij de levensduur van de sterren als volgt bepalen. Wij weten dat een ster haar massa verliest evenredig met de totale uitgestraalde energie. En daar deze zelf evenredig is met de derde macht van haar massa kan men hieruit afleiden hoeveel tijd een ster nodig heeft om van een bepaalde massa door uitstraling in te krimpen tot een andere kleinere massa.

Om de totale ouderdom van een ster te kennen moeten wij weten welk haar gewicht was bij haar geboorte. Een grote moeilijkheid is dit echter niet. Een numeriek voorbeeld maakt dit duidelijk. Indien wij de tijd berekenen die verlopen is sinds de zon vier maal zwaarder was dan nu vinden wij hiervoor: 7,1.10¹² jaar. Als wij nu berekenen hoeveel tijd ze nodig zou hebben gehad om van een oneindige massa te slinken tot wat ze nu is bekomen wij: 7, 6. 10¹² jaar, een uitslag die weinig verschilt van de vorige. De werkelijkheid ligt dus zowat tussen beide in zodat we ons aan ongeveer 7 billioen jaar kunnen houden. Sterren die minder massa bezitten dan de zon op dit ogenblik zullen dus blijkbaar ouder zijn, terwijl sterren met groter massa jonger zijn.

Evolutie van de sterren

Hoe moeten wij ons volgens Jeans de evolutie van een ster voorstellen? Uit de waarnemingen blijkt dat het mogelijk is de sterren in drie grote klassen te rangschikken: reuzensterren, sterren van de middenreeks en dwergsterren. Welnu alle sterren beginnen hun bestaan als reuzen met een zeer geringe dichtheid en een grote massa met als gevolg een hoog stralingsvermogen. De temperatuur daarentegen is des te lager naarmate de massa groter is. Het massaverlies dat met de uitstraling gepaard gaat veroorzaakt een inkrimping die op haar beurt de temperatuur doet stijgen. Hieruit volgt een ionisatie in de atomen: ze beginnen dus electronen te verliezen. Wij weten dat de electronen die rond de kern lopen verdeeld worden in verschillende lagen die aangeduid worden door de letters K, L, M, N, O, P, Q in de orde van toe-

[p. 628]

nemende afstand tot het middenpunt of de kern. Een ster nu, zegt Jeans, heeft een zeer wankel evenwicht zodra een electronenlaag wordt aangetast. Het gevolg is dat, zodra dit gebeurt, een katastrophale contractie ingrijpt: de hele laag wordt als door explosie uit het atoom gestoten. Bij tussenpozen van schijnbare rusttoestand verdwijnt op die wijze de ene laag na de andere. Reuzensterren zijn nog in het beginstadium; hun atomen bezitten rond de kern nog verschillende electronenlagen. De sterren van de middenreeks bezitten nog slechts één laag rond de kern, de K-ring. Wanneer al de electronenlagen verdwenen zijn en de atomen tot hun kernen gereduceerd zijn, begint het dwerg-stadium van de ster. Daar het gewicht van de atomen bijna uitsluitend in de kern zit, verliezen totaal geïoniseerde atomen wel hun afmetingen maar niet hun gewicht. Ze kunnen dus veel dichter op elkaar gepakt worden en zo wordt het duidelijk dat het soortelijk gewicht van een massa die nog alleen uit atoomkernen bestaat, uitzonderlijk groot moet zijn. Welnu, de dwergsterren waarvan er op dit ogenblik 75 bekend zijn, onderscheiden zich alle door een zeer hoog soortelijk gewicht. Een van de meest bekende, de Van Maanenster heeft een dichtheid die 600.000 maal die van water overtreft. Een lucifersdoosje Van Maanen-stof weegt 13.500 kg.

Hoe staat het met de zon? Haar beste tijd heeft ze zeker al lang achter de rug. Ze behoort tot de middenreeks: haar atomen bezitten nog slechts de K-ring, niet meer dan twee electronen. Ze is nu in een stadium van schijnbare rust en wacht op de laatste katastrophe die haar bestaan als dwergster zal komen inluiden. Wanneer dit zal gebeuren kan niemand voorspellen; zeker zal het niet zijn in een zeer nabije toekomst.

Superradioactiviteit

Keren wij nu nog even terug tot de energiebron door Jeans voorgesteld. Wij hebben gezien dat de vernietiging van protonen en electronen enkel kan geschieden in normaal samengestelde atomen. Welke scheikundige dementen komen voor die transformatie in aanmerking? Geen enkele van de 92 ons bekende elementen. Ze bestaan dus enkel in de sterren. Om ze nader te bepalen redeneert Jeans op de volgende wijze. Opdat een ster stabiel zou zijn d.i. opdat, tengevolge van de enorme inwendige temperatuur, haar energie niet onder vorm van explosie ineens zou vrijkomen, moet er een mechanisme bestaan dat toelaat ze geleidelijk te produceren. Geen invloed van buiten uit mag enige verandering hiervan teweegbrengen en bijgevolg moeten de atomen zich spontaan ontbinden. Dergelijke atomen bestaan: het zijn de radioactieve Stoffen, doch omdat de ons bekende reeds zijn uitge-

[p. 629]

schakeld, moet de reactie geschieden in atomen wier atoomnummer in de omgeving van 95 ligt. Jeans noemt ze super-radioactieve atomen.

Hiertegen kan men de volgende opwerping maken. Volgens de quanten-theorie moet een straling veroorzaakt door de vernietiging van protonen en electronen een golflengte hebben van 0,000014 A^o, terwijl het licht van de zon en de sterren een golflengte heeft van meerdere duizenden A^o. Hierop antwoordt Jeans dat de straling in het centrum van de sterren werkelijk een zo korte golflengte bezit. Terwijl ze echter door de bovenliggende lagen van de ster-atmospheer heendringt, wordt ze daar steeds meer en meer 'verstrooid' wat een verlaging van de frequentie tengevolge heeft en dus overeenkomstig een verhoging van de golflengte.

Kernreacties

Toch blijft het een zwak punt dat Jeans moet beroep doen op totaal onbekende elementen. Ofschoon dit op zichzelf geen ernstige moeilijkheid is, verkiest men toch een theorie die een bevredigende uitleg geeft met behulp van elementen die reeds lang als verworven bezit gelden. Een opvatting die op dit ogenblik de voorkeur van de meest astrophysici geniet werd in 1939 door H. Bethe in de Physical Review gepubliceerd. Hij toonde aan dat de stellaire energie kan worden verklaard door kernreacties en wel in de vorm van een viervoudige cyclus^1..

Hierin combineren zich vier waterstofkernen tot een heliumkern, waarbij een enorme hoeveelheid stralingsernergie vrijkomt, samen met twee positronen die door twee electronen zullen vernietigd worden. Koolstof en stikstof speien slechts de rol van katalysatoren. Wij belanden dus tenslotte bij de boven besproken opvatting van Perrin, doch onder een meer bepaalde vorm.

Professor Russell berekende volgens deze methode dat de huidige samenstelling van de zon moet bestaan uit 51% waterstof en 42% helium.

De theorie van Bethe is wel stevig gegrondvest op de nog jonge kernphysica, ze is in Staat een uitleg te geven voor de energie-ontwikkeling in sommige soorten sterren, maar ze moet verder aangepast worden o.a. voor de reuzensterren. Zo geldt de koolstofcyclus niet voor de rode sterren van het spectraal type N. De kernphysica is pas

1.

C12+H1=N13+hv	N13=C13 + ε
C13+H1 = N14+hv
N14 + H1=O15	O15=N15+ε
N15+H1=C12+H4

[p. 630]

in haar beginstadium, maar de reeds bereikte resultaten laten vermoeden dat men langs deze weg de werkelijkheid heel wat dichter zal kunnen benaderen.

Er blijft nu nog één vraag te beantwoorden. Hoelang bestaat het heelal? zich baserend op dynamische principes besluit Jeans dat meer dan 60 milliard jaar nodig zijn opdat de oorspronkelijke chaos in spiraalnevels zou kunnen condenseren. Heel wat meer tijd verloopt vooraleer in de spiraalnevels, door de gravitatie-instabiliteit, sterren ontstaan. Jeans schat dit tijdsverloop op tien billioen jaar en besluit dat 'het ontstaan van de sterren bijzonder actief is geweest tussen acht en twee billioen jaar geleden en dat hun vorming sedertdien bijna volledig heeft opgehouden'.

Relativistische cosmogonie

De tijd door Jeans gepostuleerd is enorm groot, te groot en waarschijnlijk in strijd met de waarneming. 'Jeans, schrijft Prof. Lemaitre, demande cent mille milliards d'années pour cette évolution (van de sterren in de nevels), et je ne suis pas sûr qu'il ait prouvé que cela suffirait; nous ne pouvons lui accorder que le millième de ce temps.' Een van de grootste moeilijkheden in de cosmogonie van het heelal vormen de spiraalnevels. Toen men hun beweging onderzocht kwam men tot de vaststelling dat veruit de meeste onder hen zich heel snel naar alle zijden verwijderen. Hun snelheid is des te groter naarmate ze verder verwijderd zijn. Alleen de meest nabije komen naar ons toe. Snelheden van meer dan 30.000 km/sec. werden gemeten. Indien hun snelheid onveranderd is gebleven bevonden ze zich twee milliard jaar geleden is een dichte massa bij elkaar gepakt. Een herziening van de vroegere, klassieke opvatting, dringt zich onvermijdelijk op. Prof. Lemaitre heeft dan ook een cosmogonie voorgesteld die radikaal verschilf van het schema van Jeans. Dit blijkt reeds van af het vertrekpunt: een zeer ijle gasmassa voor Jeans, een sterk geconcentreerde toestand van de materie volgens Prof. Lemaitre. Ook de degradatie van de energie wijst in deze richting. Immers, deze komt ons voor als een verbrokkeling van de energie; zij wordt voortdurend verdeeld over een immer toenemend aantal quanta. En dus, hoe dieper men in het verleden doordringt hoe sterker de energie geconcentreerd is. Vandaar de vooropzetting van Prof. Lemaitre: 'Une cosmogonie vraiment complète devrait expliquer les atomes comme les soleils, et certainement les atomes ne peuvent avoir comme origine l'extrêmement diffus'.

Aanvankelijk was de materie geconcentreerd in de vorm van een

[p. 631]

atoom met reusachtige afmetingen, hoewel astronomisch gesproken nog zeer klein. Indien de materie toen de dichtheid had van water, zou de straal van het oeratoom één lichtjaar bedragen (10³⁸ cm). Dit atoom is zeer instabiel zodat het van het eerste ogenblik af in stukken breekt die op hun beurt weer breken en zo verder tot de resulterende deeltjes te klein zijn geworden om die desintegratie door te zetten. Slechts enkele, zoals uranium, zetten dit proces nu nog verder door. Gezien de enorme snelheid van het afbraakmateriaal neemt de straal van het oeratoom uiterst snel toe, terwijl de materie-verdeling voorlopig zeer homogeen blijft, ofschoon de dichtheid voortdurend afneemt.

De snelle expansie heeft als gevolg dat de relatieve snelheden van de brokstukken of atomen afnemen zodat de botsingen minder heftig zijn: terwijl ze vroeger gepaard gingen met inwendige transformaties en stralingsverschijnselen, blijven ze nu beperkt tot zuiver elastische botsingen. Zo kan hier en daar een statistisch evenwicht intreden en vormen zich wolken waarin de materie een dichtheid bezit van 10⁻²⁷ grcm³.

Nu wordt de expansiesnelheid geremd door de aantrekkingskracht die uitgaat van de plaatsen met grotere dichtheid. Toch bezitten die cosmische wolken betrekkelijk grote snelheden van de grootte-orde van 650km/sec. Ze bewegen zich kriskras door elkaar zodat nu en dan dichtere condensaties zullen ontstaan. Deze spelen de rol van een centraal aantrekkingspunt dat de meest nabije wolken naar zich toe haalt. Zo ontstaan ofwel elliptische nevels ofwel spiraalnevels naargelang het omwentelingsmoment ter plaatse helemaal onbeduidend dan wel betrekkelijk aanzienlijk was.

De cosmische wolken hebben, zoals wij gezien hebben, een dichtheid van 10⁻²⁷ - veel te gering opdat ze ook maar een tendens zouden vertonen tot contractie. Door botsing van twee wolken kan de dichtheid nu voldoende toenemen opdat de condensatie definitief zou beginnen. 'Il est clair, besluit Prof. Lemaitre, qu'une telle condensation peut donner lieu par des mécanismes connus, à un système solaire, ou une étoile simple ou multiple.'

Uit het voorgaande blijkt duidelijk dat in deze cosmogonie geen plaats is voor de evolutieschemas door Jeans vooropgezet. 'Le type spiral ou elliptique de la nébuleuse est une question de chance, il dépend de la valeur fortuite du moment angulaire dans la région de condensation. Il ne peut plus y être question d'une évolution d'un type en un autre. Il en est d'ailleurs de même pour les étoiles où le type de l'étoile est fixé par la valeur accidentelle de sa masse, c'està-dire, de la somme des masses des deux nuées dont la rencontre a produit l'étoile.'

Uit de waarneming weten wij dat de verhouding van de consti

[p. 632]

tuerende elementen dezelfde is in de zon en de sterren, op aarde en in de meteorieten. Dit was te verwachten: de afbraakprodukten moeten voorkomen in welbepaalde verhoudingen volgens de wetten van de radioactieve desintegratie. Ook geeft deze theorie een zeer aannemelijke uitleg voor de cosmische straling. Deze heeft een zo uitzonderlijke energie (meerdere milliarden electron-volts) en de straling zelf lijkt zo zeer op de stralen die het gevolg zijn van radioactieve afbraak, dat het voor de hand ligt hun een superradioactieve oorsprong toe te schrijven: ze zijn ontstaan bij de desintegratie van het oeratoom.

Samenvattend kunnen wij zeggen dat het heelal in zijn ontwikkeling drie stadia heeft doorlopen. Eerst een periode van zeer snelle expansie die ongeveer twee milliard jaar geduurd heeft. Op het einde van deze periode vormen zich cosmische wolken die het ontstaan geven aan nevels en sterren. De straal van de ruimte bedraagt dan ongeveer één milliard lichtjaren. Dan treedt een periode in van evenwicht tussen de aantrekkende- en de afstotende kracht in overeenstemming met de nieuwe gravitatiewet van Einstein. Het gevolg is een vertraging van de expansie. Dit is de tweede periode die ongeveer vijf milliard jaar geduurd heeft. Tenslotte neemt de afstotende kracht de overhand, doch nu zijn het niet meer de atomen die zich in wilde vaart van elkaar verwijderen maar wel de reeds gevormde sterrenstelsels. Deze derde periode heeft ongeveer drie milliard jaar geleden een aanvang genomen. Zo is de hele ontwikkelingsduur van het heelal teruggeleid tot amper 10 milliard jaar. Prof. Lemaitre verklaart daarbij heel optimistisch: 'Notre Univers porte les marques de la jeunesse et nous pouvons espérer reconstituer son histoire'.

Besluit

Dit is in grote trekken het beeld dat Jeans zich van het heelal heeft gevormd: het resultaat van dertig jaar onderzoek. Sommige zijner opvattingen zijn nu reeds 'verouderd', andere die nu nog worden aanvaard zullen weldra misschien hetzelfde lot delen. De cosmogonie zal nooit af zijn. Maar, zoals Jeans het zelf uitdrukt, 'the cosmogonist has finished his task when he has described to the best of his ability the inevitable sequence of changes which constitute the history of the material Universe'. Die taak heeft hij volbracht met zoveel virtuositeit dat hij terecht mag gerekend worden bij de grootste cosmogonisten van de Newtoniaanse school.