Streven. Jaargang 20

[p. 805]

Inleiding in de ruimtevaart
José De Rudder

De ruimte-experimenten horen sinds tien jaar (Spoetnik I werd gelanceerd op 4 oktober 1957) tot het dagelijkse nieuws. Wie er slechts oppervlakkig kennis van neemt, krijgt wel eens de indruk dat ze elkaar opvolgen zonder veel verband. Kunnen we de lezer niet enkele principes aan de hand doen waardoor de samenhang duidelijk wordt en een beeld gegeven van de huidige stand van zaken in zijn geheel? Een woordje voorgeschiedenis dan om te beginnen.

De eerste raketten die ons bekend zijn, werden uitgevonden door de Chinezen. In 1232 gebruikten de inwoners van Peking, in hun strijd tegen de Mongolen, de eerste bamboeraketten, eigenlijk een soort grote pijlen, die gevuld waren met buskruit, een vaste brandstof dus. Via de Indiërs kwam deze uitvinding op het eind van de 18e eeuw in Engelse handen. In 1805 vervaardigde William Congreve raketten die tegen Napoleon werden ingezet en o.m. Kopenhagen terroriseerden. Toen in 1872 het gerichte kanon werd uitgevonden, dat doeltreffender was dan de raketten, verdwenen deze op de achtergrond.

De eerste concrete ruimtevaartplannen werden gemaakt door de Rus Konstantin Eduardovitsj Tziolkowski, in het begin van deze eeuw. Vloeibare brandstof en meertrapsraketten behoorden reeds tot zijn plannen. Zelf heeft hij nooit een raket gebouwd; hij verwierf pas bekendheid in 1934, een jaar voor zijn dood, toen anderen reeds lang aan de realisatie toe waren. Eén van die anderen was de Amerikaan Goddard, die er in 1926 in slaagde, een kleine raket met vloeibare brandstof 60 m hoog te doen stijgen. In 1931 wist een raket van de Duitse Verein für Raumschiffahrt, dat gesteund werd door de mathematische studies van de Roemeen Oberth, een hoogte van 100 m te bereiken. De nazi's ontbonden de Verein en vervingen hem door het militaire raketonderzoek: Peenemünde, bij de monding van de Oder, werd het centrum waar door Werner von Braun de vernietigende V-2 - eigenlijk A-4 - werd ontworpen. Enkele kenmerken van de V-2: hij woog 14 ton, waarvan 8,75 ton brandstof; hij was 12 m lang, verbruikte 170 liter brandstof per seconde en kon een hoogte bereiken van 160 km. Maar heel nauwkeurig was de V-2 niet: slechts 25% van de raketten troffen doel.

Na de oorlog legden de Russen beslag op de basis van Peenemünde. Een deel van de ingenieurs, o.a. Werner von Braun, was met een groot aantal resterende V-2's naar Amerika gevlucht. Op het proefterrein van White Sands in New-

[p. 806]

Mexico werden in zes jaar tijd 47 V-2's afgevuurd en in 1949 werd op een V-2 een Amerikaanse Corporal-raket gemonteerd, die als tweede trap de recordhoogte van 402 km bereikte. Verdere proeven leidden tot de raketten die we nu kennen.

Het beschrijven van een baan

De zojuist genoemde V-2-Corporal-raket bereikte een hoogte van 402 km en toch kon ze nog geen satelliet lanceren. Waarom niet? Het antwoord op deze vraag wordt duidelijk als we de voorwaarden kennen voor het beschrijven van een baan om de aarde.

Veronderstellen we dat we op een berg van 400 km hoogte staan en we gooien een steen voor ons uit. De steen vliegt vooruit, laten we zeggen met een snelheid van 10 m per seconde. Maar onder invloed van de zwaartekracht is hij na de eerste seconde al 4,90 m naar de aarde toe gevallen. Hoe krachtiger we de steen gooien, hoe verder hij zal vallen, maar steeds zal hij na 1 seconde 4,90 m gedaald zijn. Welnu, de aarde is rond. Indien we een steen zo krachtig konden gooien, dat hij zich na 1 seconde boven een punt van de aarde bevindt dat zich, wegens de kromming van de aarde, ook 4,90 m lager bevindt, dan blijft de afstand tussen de steen en de aarde even groot en gaat de steen een cirkelvormige baan om de aarde beschrijven. Anders uitgedrukt: de zwaartekracht wordt tegengewerkt door een even grote middelpuntvliedende kracht. Uit de vergelijking van de twee kan men de snelheid berekenen die nodig is om een voorwerp in een baan om de aarde te brengen. Op 400 km hoogte is deze 7,9 km/sec. Hoe hoger men gaat, hoe kleiner de vereiste snelheid wordt: de zwaartekracht vermindert immers met de hoogte. Welnu, de V-2-Corporal bereikte wel een hoogte van 400 km, maar daar was zijn snelheid veel te klein, zodat hij terugviel in de atmosfeer. Wat eraan ontbrak was een derde trap.

Om het trappenprincipe te verduidelijken is een klein beetje wiskunde nodig. De grondvergelijking van de raket is: a = w. log (m/mʹ), waarbij a = de theoretisch verkregen snelheid van de raket; w = de uitstroomsnelheid van de verbrandingsgassen (afhankelijk van de gebruikte brandstof); log = de natuurlijke logaritme; (m/mʹ) = de massaverhouding (m = het totaalgewicht van de raket bij de start, mʹ = het lege gewicht, zonder brandstof, d.i. de lege brandstoftanks en de nuttige last). Nemen we het voorbeeld van de V-2 (zonder de Corporal): de massaverhouding is 3,2 en de uitstroomsnelheid 2 km/sec. De versnelling is dus: 2 × log (3,2) = 2,3 km/sec.

Om praktische redenen is het onmogelijk een grotere massaverhouding te verkrijgen dan 5. De grootst mogelijke uitstroomsnelheid is 4 km/sec. Bijgevolg is de uiterste versnelling die een ééntrapsraket kan krijgen: 4 × log 5 = 4 × 1,6 = 6,4 km/sec., dus volstrekt onvoldoende om een satelliet te lanceren. Bij een tweetrapsraket wordt de vergelijking: a = w. log(m/mʹ · M/Mʹ), waarbij m/mʹ en M/Mʹ de massaverhoudingen zijn respectievelijk van de eerste en de tweede trap. De twee massaverhoudingen worden dus vermenigvuldigd. Een voorbeeld.

[p. 807]

De massaverhouding van de Corporal is 2,58. Indien men de V-2 en de Corporal tegelijk had laten werken, dan zou de globale massaverhouding slechts 3,33 geweest zijn, dus niet veel meer dan de V-2 afzonderlijk. Doch door de Corporal als tweede trap te gebruiken, door hem namelijk te laten vetrekken wanneer de V-2 al zijn brandstof opgebruikt had, totaliseerde men een massaverhouding van 3,2 × 2,58 = 8,25. De verkregen versnelling was dus 2 × log (8,25) = 4,2 km/sec. Dit was echter nog niet genoeg om een satelliet te lanceren. Daarvoor heeft men een drietrapsraket nodig, waardoor de massaverhouding nog eens vermenigvuldigd wordt door die van de derde trap afzonderlijk.

We spreken hier van ‘theoretische versnelling’. Inderdaad, om een satelliet op 400 km hoogte te lanceren, is niet alleen de nodige snelheid vereist om in een cirkelbaan te blijven, maar ook om bij het opstijgen 1) de zwaartekracht en 2) de weerstand van de lucht in de onderste atmosfeerlagen te overwinnen. Zo zal men voor het lanceren van een satelliet toch een theoretische versnelling nodig hebben van 10 à 11 km/sec.

Voor de eigenlijke lancering zijn er twee mogelijkheden: horizontaal (zoals een vliegtuig) of verticaal. Vertrekt men horizontaal en stijgt men dus langzaam op, dan verliest men minder energie voor het overwinnen van de zwaartekracht, maar méér door de weerstand van de lucht, daar men langer in de onderste atmosfeerlagen blijft. Vertrekt men integendeel verticaal, dan verlaat men vlug de atmosfeer, maar verliest men enorm veel aan de zwaartekracht. Daarom wordt een tussenoplossing gekozen. We kunnen dit het best duidelijk maken aan de hand van de weg die Spoetnik I op 4 oktober 1957 koos.

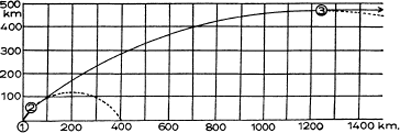
De eerste trap brengt de raket na twee minuten op een hoogte van 56 km, dus reeds buiten de dichtste atmosfeerlagen. De snelheid bedraagt reeds 2 km/sec. Op het einde begint de raket af te buigen. De tweede trap treedt in werking, maakt zich los en verplaatst zich schuin omhoog. Wanneer deze trap uitgebrand is, vliegt de raket verder in de ‘vrije’ baan, zonder aandrijving, zodat een parabool ontstaat waarvan het maximum op ongeveer 480 km ligt. De snelheid wordt ondertussen opgedreven tot 5,5 km/sec. In het maximum van de parabool, dus wanneer de raket zich een ogenblik horizontaal beweegt om daarna te vallen, start de derde trap; deze geeft de Spoetnik een snelheid van 8 km/sec., wat meer is dan de vereiste 7,9 km/sec. op deze hoogte.

Deze tussenoplossing heeft dus het voordeel dat de eerste trap een zo klein mogelijke weerstand van de lucht moet overwinnen, terwijl de tweede trap de meest voordelige baan kiest wat de zwaartekracht betreft, namelijk het langzaam schuin opstijgen.

[p. 808]

Bouw en evolutie van de raket

Om de genoemde snelheden te verwezenlijken, heeft de ruimtevaarttechniek zich gebaseerd op het reactieprincipe. Wanneer we ons in een bootje bevinden en een steen weggooien, ondergaat niet alleen de steen een bepaalde kracht, maar ook het bootje. Volgens het reactieprincipe van Newton zijn beide krachten precies even groot: K = k. Daar echter de boot zwaarder is dan de steen en de kracht gelijk is aan het produkt van massa en versnelling, zal de boot een kleinere versnelling krijgen dan de steen: .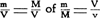

Laten we dit toepassen op de raket: de steen vervangen we door de massa verbrandingsgassen, de boot door de raket zelf. Tegen de bovenwand van de verbrandingskamer van de raket werkt dus dezelfde kracht in als die waarmee de verbrandingsgassen ontsnappen. De raket stijgt dus op. Ze duwt zich echter niet af tegen de omgevende lucht of tegen de grond; ze heeft geen steunpunt nodig. En dit is de reden waarom de raket het enige bruikbare vervoermiddel is buiten de atmosfeer. Alle klassieke vervoermiddelen vereisen immers een steunpunt: de auto de grond, het schip het water, en het schroef-vliegtuig de lucht. Naast de raket is het straalvliegtuig het enige dat geen afstootmiddel nodig heeft om zich voort te bewegen.

Hiermee komen we aan een tweede probleem. Het volstaat niet, enkel brandstof, zoals bv. keroseen, mee te nemen; we hebben ook een oxydator nodig, een stof waarmee de brandstof zich verbindt (meestal zuurstof). Nu ontbreekt deze zuurstof volledig buiten de atmosfeer. Dit maakt dan ook het onderscheid uit tussen de raketmotor en de straalmotor van een vliegtuig: het straalvliegtuig haalt zijn zuurstof uit de lucht; de raketmotor neemt ze zelf mee. De V-2 bevatte b.v. 3,75 ton ethyl-alcohol (als brandstof) en 5 ton zuurstof (als oxydator).

Om steeds grotere massa's te kunnen lanceren, moet men steeds grotere en sterkere raketten bouwen. Hoewel men nu in Amerika reeds fantastische proporties zal bereiken met de Saturn-5, heeft men de groei van de raketten toch al kunnen inperken. Herinneren we ons de formule a = w. log (m/mʹ): de twee factoren die de versnelling van een raket bepalen, zijn de uitstroomsnelheid en de logaritme van de massaverhouding. Daar de logaritme steeds veel kleiner is dan het getal zelf, heeft de massaverhouding steeds minder invloed op de

raket	brandstof	uitstroomsnelheid	massaverhouding
Atlas	keroseen	2,6 km/sec	90
Atlas-Agena	1. keroseen	2,6	70
	2. N-verbinding	2,7
Titan-2	N.-verbindingen	2,7	52
Saturn-5	1. keroseen	2,6
	2. waterstof	3,9	20
	3. waterstof	3,9

[p. 809]

versnelling dan de uitstroomsnelheid, die de versnelling recht evenredig vermeerdert. Indien men dus deze uitstroomsnelheid kan verhogen, is het zelfs mogelijk de massaverhouding aanzienlijk te verkleinen, wat op zijn beurt vermeerdering van de nuttige massa betekent. De uitstroomsnelheid tracht men te vermeerderen door de voordeligste brandstoffen te kiezen. Op ongeveer tien jaar tijd heeft men aldus de massaverhouding van 90 tot 20 kunnen terugbrengen.

Niet alleen de brandstof, maar ook de oxydator zou verbeterd kunnen worden. Fluor zou een uitstekende oxydator zijn en een uitstroomsnelheid van 5 km/sec kunnen voortbrengen, doch het tast het metaal zeer sterk aan en is daarom in zuivere vorm onbruikbaar. Doch een mengsel van zuurstof en fluor (door de Amerikanen flox genoemd) zou wèl diensten kunnen bewijzen en de ontsnappingssnelheid met 0,2 km/sec vermeerderen. Indien de Saturn-5 bijvoorbeeld uitgerust zou worden met flox, zou ze een ruimteschip van 250 ton kunnen lanceren, terwijl de gewone Saturn-5 slechts 130 ton in een baan kan brengen. Nog grotere uitstroomsnelheden zijn natuurlijk te verwachten van de atoomenergie. Een eerste toepassing hiervan zou erin bestaan, met een atoomreactor waterstof te verhitten, die dan zou ontsnappen met een snelheid van 1 km/sec. Verder hoopt men ionenmotoren te construeren, waarbij caesium-ionen door een elektrisch geladen rooster versneld worden tot 80 km/sec. Doch dit alles is nog toekomstmuziek: want om 6 gram Caesium per seconde te doen ontsnappen met een snelheid van 80 km/sec, is reeds een reactor van 215 ton nodig.

De wijzigingen van de satellietenbaan

Wat gebeurde er nu met Spoetnik I die op 480 km hoogte in een baan kwam? We constateerden dat de vereiste snelheid 7,9 km/sec was, maar dat de Spoetnik een snelheid van 8 km/sec kreeg. Het gevolg hiervan wordt direct duidelijk. De vereiste snelheid, in dit geval 7,9 km/sec., geldt alleen voor een cirkelvormige baan. Deze vereiste snelheid wordt echter kleiner bij stijgende hoogte. Met de hoogte zal dus ook de omlooptijd vergroten: de af te leggen afstand wordt immers groter en de snelheid kleiner. Zo wordt het bijvoorbeeld mogelijk dat een satelliet in 24 uur om de aarde wentelt. De juiste hoogte daarvoor is 36.000 km. Indien deze satelliet zich boven de evenaar bevindt, zal hij steeds boven hetzelfde punt blijven hangen. Dit is zeer nuttig voor een communicatiesatelliet: Early Bird en Lani Bird zijn op dit principe gebaseerd.

Spoetnik I kwam echter niet in een cirkelvormige baan terecht, omdat zijn snelheid daarvoor te groot was. Waarschijnlijk was dit ook niet bedoeld. Zijn baan werd elliptisch. Zijn apogeum (of hoogste punt) lag op 950 km. Was de snelheid nog groter geweest, dan zou de ellips nog excentrischer geweest zijn, wat betekent dat zijn apogeum nog hoger zou liggen. Indien de snelheid te klein was geweest, dan zou het een ellips geweest zijn met een perigeum (of laagste punt) van minder dan de 480 km die het nu bereikte.

[p. 810]

De snelheid kon ook zo klein zijn, dat de Spoetnik in de dampkring terecht kwam en dus geen satelliet werd.

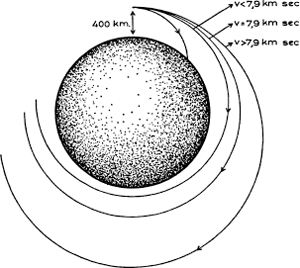
De verklaring hiervoor kunnen we opnieuw geven door de vergelijking van de zwaartekracht met de middelpuntvliedende kracht. Indien deze laatste groter is dan de zwaartekracht, dan verwijdert de satelliet zich langzaam van de aarde. Doch de zwaartekracht blijft werken en vermindert geleidelijk de snelheid van de satelliet. In het apogeum is bijgevolg de middelpuntvliedende kracht kleiner dan de zwaartekracht en valt de satelliet terug, terwijl zijn snelheid opnieuw vermeerdert.

Laten we dit op een andere manier samenvatten. Indien een satelliet zich in een cirkelvormige baan bevindt en op een bepaald punt versneld wordt, dan zal het tegenoverliggende punt van zijn baan verhoogd worden. Indien er een remming is, dan wordt het tegenoverliggende punt verlaagd. Een versnelling in het perigeum heeft dus tot gevolg een verhoging van het apogeum, terwijl het perigeum zelf gelijk blijft; een versnelling in het apogeum brengt het perigeum op een grotere hoogte.

Dit kunnen we direct toepassen op de terugkeer van een ruimteschip op aarde. Het volstaat de snelheid iets te remmen (door kleine raketstoten in de richting tegengesteld aan de beweging), om een satelliet in de dampkring te laten terechtkomen. Maar de dampkring zelf is remmende factor: beneden 200 km is het onmogelijk een baan te beschrijven, want de atmosfeer is er zo dicht, dat de satelliet na één of twee omlopen reeds terug zou keren. Doch ook boven de 200 km is er in zekere mate nog atmosfeer, wat het ruimtetuig langzaam doet dalen.

Op hetzelfde principe zijn de Gemini-rendez-vous-maneuvers gebaseerd. Deze kunnen slechts uitgevoerd worden indien bepaalde voorwaarden vervuld zijn. 1) De twee ruimteschepen moeten zich in hetzelfde vlak bewegen. Indien de twee vlakken ook maar een hoek van enkele graden vormen, heeft men méér brandstof nodig om de vlakken bij elkaar te brengen, dan de Gemini-capsule kan meevoeren. 2) Er is een bepaald faseverschil nodig. Indien b.v. de twee ruimteschepen op dezelfde hoogte vliegen, maar op een afstand van een halve omwenteling, dan is een rendez-vous praktisch onmogelijk. Inderdaad, versnelt de Gemini, dan is het gevolg niet een inhalen van de satelliet, maar het verhogen van zijn apogeum; de Gemini zal dus integendeel zijn achterstand vergroten.

[p. 811]

Nemen we als voorbeeld het eerste rendez-vous op 15 december 1965. Gemini-7 bevindt zich reeds een tiental dagen in een cirkelvormige baan op 294 km hoogte. Vooraf heeft men berekend wanneer het vlak van Gemini-7 zal samenvallen met het lanceringsvlak van Gemini-6. Dit gebeurt, vanwege de rotatie van de aarde, ongeveer eenmaal per dag. Men wacht dan tot de Gemini-7 een bepaalde plaats heeft bereikt, om Gemini-6 in een baan te brengen. De gegevens van deze baan: apogeum 261 km; perigeum 161 km. Hij bevindt zich dus onder en achter Gemini-7. De afstand is ongeveer 1900 km. Doch Gemini-6 gaat vlugger dan Gemini-7: zijn hoogte is kleiner. Hij haalt Gemini-7 dus langzaam in. Nu komt het erop aan ook de hoogte gaandeweg te vergroten, om de twee ruimteschepen bij elkaar te brengen. Na één omwenteling wordt in het perigeum een kleine raketstoot gegeven, die de gevolgen van de luchtweerstand compenseert en dus het apogeum op 261 km houdt. Bij de tweede aankomst in het apogeum, wordt de Gemini zodanig versneld, dat zijn perigeum op 214 km komt. Intussen wordt een kleine baancorrectie uitgevoerd, om beide baanvlakken nauwkeuriger te doen samenvallen. In het nieuwe perigeum wordt weer een raketstoot gegeven, zodat het apogeum op zijn beurt verhoogd wordt: 274 km. De afstand van Gemini-7 is nog slechts 309 km. Nu wordt de laatste belangrijke versnelling gegeven, die de baan ongeveer cirkelvormig maakt. Gemini-6 bevindt zich nog op 25 km onder Gemini-7. De laatste kilometers worden afgelegd tijdens een eindfase van ongeveer 30 minuten, waarbij, door herhaaldelijke oriëntatie, meting van de afstand en versnelling, de Gemini-7 wordt ingehaald.

Tijdens de volgende Gemini-vluchten werd deze achtervolging in steeds minder tijd uitgevoerd: Gemini-10 in slechts drie omwentelingen, en Gemini-11 vóór het einde van de eerste omwenteling, na slechts 94 minuten. Gemini-12 herhaalde de operatie zonder inlichtingen te krijgen vanaf de grond. De astronauten moesten dus alles zelf berekenen. Ook de verdere Gemini-maneuvers kunnen we nu begrijpen. Doordat Gemini-11 aan de Agena-raket gekoppeld werd en de motoren van deze laatste in werking stelde, kon hij zijn apogeum op een hoogte van 1370 km brengen. Om terug in de vroegere baan te geraken, was het voldoende het ruimteschip 180° te laten kantelen en dezelfde raketstoot in tegengestelde richting te geven.

Nemen we nog een ander voorbeeld: de lancering van Early Bird, op 7 april 1965. De satelliet wordt eerst in een elliptische baan gebracht met als apogeum 36.000 km en als perigeum enkele honderden kilometers. Het baanvlak valt echter nog niet samen met de evenaar, wat onontbeerlijk is om de satelliet onbeweeglijk te houden boven hetzelfde punt van de aarde. In dit geval kan men dit baanvlak veranderen, daar de satelliet slechts een 50-tal kg weegt. Wanneer dit gebeurd is, wacht men tot de Early Bird zich in zijn apogeum bevindt, en door een krachtige raketstoot brengt men ook het perigeum op 36.000 km. Dit gebeurt indien in het apogeum de snelheid van 3,07 km/sec bereikt wordt.

Wanneer echter een satelliet gelanceerd is, blijft zijn baan niet eeuwig dezelfde. Er is immers een wisselwerking van verschillende zwaartekrachten. Om van de

[p. 812]

invloed van zon en maan nog te zwijgen, willen we hier alleen de rol van de onregelmatige vorm van de aarde vermelden. De aarde is namelijk kort en dik: afgeplat aan de polen en met een buikje aan de evenaar. Al bedraagt het verschil slechts 21,5 km, toch heeft dit tot gevolg dat de aardmassa niet gelijkmatig verdeeld is. Bijgevolg is ook de zwaartekracht verschillend en wordt een satelliet versneld of vertraagd al naargelang hij over de polen of over de evenaar passeert. Dit heeft twee gevolgen voor de baan: ten eerste draait het baanvlak om de aarde, en dit des te sneller, naarmate de hoek van dit baanvlak met de evenaar (de inclinatie) kleiner is; ten tweede - en dit heeft alleen belang bij een elliptische baan - draait de baan van een satelliet in haar eigen vlak en vormt zo een rozet. Ook dit gaat sneller naarmate de inclinatie kleiner is. Doch hier is het iets ingewikkelder: indien de hoek precies 63,4° bedraagt, dan blijft de ellips onbeweeglijk in haar vlak, en indien de hoek nog groter wordt, dan beweegt de baan zich opnieuw, maar dan in tegengestelde richting. In Rusland heeft men reeds verschillende satellieten gelanceerd met een inclinatie van ongeveer 63°: indien ze een aangepaste omwentelingstijd hebben, bereiken ze hun apogeum op regelmatige tijden boven hetzelfde punt van de aarde. Indien men daarbij in acht neemt dat een satelliet trager gaat in zijn apogeum en dus de grootste tijd in zijn apogeum doorbrengt, dan begrijpt men dat een satelliet die regelmatig lange tijd boven hetzelfde punt verblijft, nuttig is als communicatie-satelliet. De breedte van 63,4° is immers meer aangepast voor Rusland dan de evenaar. Daarop zijn de Russische Molnyia-satellieten gebaseerd.

Maan- en planetensondes

Bij dit alles zijn we tot nog toe in de omgeving van onze vertrouwde aarde gebleven. Maar wat gebeurt er als men naar de maan wil?

Eerst wordt de satelliet in een baan om de aarde gebracht, een z.g. ‘parkeerbaan’. In deze baan wordt dan op het geschikte moment een aanzienlijke versnelling gegeven, zodat de maansonde in een zeer langgerekte ellips terecht komt, waarvan het apogeum in de buurt van de maan ligt. Het ruimtetuig bevindt zich echter nog steeds in het gravitatieveld van de aarde. Hoe verder het komt, hoe kleiner zijn snelheid: op 200.000 km is zijn snelheid nog slechts ongeveer 1 km/sec. Wanneer het echter zo ver komt, dat de invloed van het gravitatieveld van de maan overheerst, dan komt de maansonde, indien de richting van de baan en de snelheid juist zijn, ofwel op de maan terecht, ofwel begint ze in een baan rond de maan te cirkelen (is zijn snelheid daarvoor te groot, dan laat men de remraketten werken).

De richting van de baan moet dus zeer precies zijn. Dit hangt grotendeels af van de snelheid waarmee de satelliet vertrekt: indien deze ongeveer 0,2 km/ sec te klein is, dan mist zij de maan met een verschil van 100.000 km! Dit was het lot van Pioneer-3, die op 6 december 1958 in de V.S. werd gelanceerd. Een zeer precieze onderneming was de Russische Loenik-3 (4 oktober 1959), die éénmaal rond de maan draaide, de achterkant fotografeerde, en daarna terug in een baan om de aarde kwam.

[p. 813]

Ook het zenden van sondes naar Mars en Venus kunnen we nu verklaren. In ieder geval moet de satelliet hiervoor de vereiste snelheid bereiken om aan het gravitatieveld van de aarde te ontsnappen en om in een baan om de zon te komen. Maar, zoals men zich zal herinneren, bevindt Venus zich, in vergelijking met de aarde, dichter bij de zon, en Mars verder van de zon. Indien nu een ruimtesonde van de aarde vertrekt, dan hangt het ervan af, of zij in dezelfde richting als de beweging van de aarde wordt afgevuurd, of in tegengestelde richting. Is het in dezelfde richting, dan gaat de sonde ten opzichte van de zon sneller dan de aarde, en dit betekent dat zij haar aphelium tegemoet gaat. Ze zal dus Mars bereiken, indien tenminste 't ogenblik daarvoor geschikt is. Wordt de sonde in tegengestelde richting gelanceerd, dan werkt haar versnelling tegen de snelheid van de aarde in, en moet men ze er dus van aftrekken. Dus gaat ze, ten



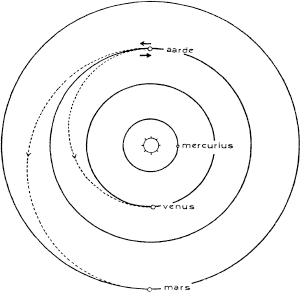
opzichte van de zon, trager dan de aarde. Ze gaat dus op weg naar haar perihelium, waar ze Venus zal bereiken.

Er bestaan zelfs plannen om op dezelfde manier Mercurius, de planeet die zich het dichtst bij de zon bevindt, met een ruimtesonde te benaderen. Op die manier zou men bepaalde afwijkingen van de baan van Mercurius nauwkeuriger kunnen berekenen en een experimenteel bewijs leveren voor de relativiteitstheorie.

Nut van de ruimtevaart

Slechts even en heel schematisch willen we de aandacht vestigen op het nut van de ruimtevaart.

De indirecte invloed van de ruimtevaart op de techniek ligt voor de hand. Door de rakettechniek werd zeer veel vooruitgang geboekt in het vervaardigen van stoffen die tegen steeds grotere hitte en druk bestand zijn. De noodzakelijkheid van kleine satellieten heeft de miniaturisatie bespoedigd.

Wetenschappelijk werden enorm veel informaties verstrekt. Geheel de aardatmosfeer werd doorzocht. Onder meer werden stralingsgordels ontdekt waarvan men vroeger niet het geringste vermoeden had. Geheel het veld van magnetische en elektrische verschijnselen, tot op honderdduizenden km van de aarde, werd verkend, en enkele kunstmatige planeten onderzochten de interplanetaire ruimte. De achterkant van de maan hebben we even goed leren kennen als de voorkant. Mars en Venus werden afgetast, al wachten hier nog veel problemen op een oplossing. Andere satellieten dienen voor geodetische

[p. 814]

doeleinden, d.w.z. voor het meten en het bepalen van de exacte vorm van de aarde. Een belangrijk experiment is de exacte meting van de afstand tussen de aarde en de zon: nl. de astronomische eenheid, die een van de fundamentele eenheden is voor de sterrenkunde. Men wil nu ook een Orbiting Astronomical Observatory (OAO) gaan lanceren, dat de sterren kan bestuderen buiten de atmosfeer; deze laatste houdt immers een groot deel van de elektro-magnetische golven tegen.

Mogelijke medische experimenten betreffen de invloed van de kosmische stralen op kankerweefsels - de kosmische stralen kunnen immers niet kunstmatig voortgebracht worden - en de gedraging van het hart in gewichtloze toestand. Ook de invloed van de gewichtloosheid op biochemische pocessen bij dieren en planten zal worden onderzocht.

De meteorologische satellieten zijn van groter belang dan men zou verwachten: Tiros-2 fotografeerde in 1960-'61 het breken van het ijs in de St.-Lawrencerivier, waardoor de scheepvaart vergemakkelijkt werd; Tiros-3 ondekte in 1961 een orkaan, twee dagen vroeger dan men het met de klassieke methodes kon doen, en dit kan belangrijk zijn om voorzorgsmaatregelen te treffen; Tiros-4 deed in 1962 aan ijsverkenning: het smelten van het ijs is immers voor een groot deel verantwoordelijk voor overstromingen. Ook kunnen sommige satellieten fungeren als bakens voor de scheepvaart: in Amerika heeft men onlangs een schip te water gelaten dat zich door middel van computers uitsluitend oriënteert op satellieten. Over de communicatiesatellieten spraken we reeds vroeger. Het geld dat daaraan besteed werd, is reeds ruim teruggewonnen door de besparing aan energie.

Welke voordelen de ruimtevaart ons nog zal brengen, is niet te voorzien. Met Werner von Braun kan men zeggen dat de ruimtevaart voor het stimuleren van de technische en wetenschappelijke vooruitgang nu dezelfde rol speelt als de oorlogen vroeger.

Het Apollo-project

We willen deze uiteenzetting niet beëindigen zonder een voorstelling van het Apollo-project, waarmede de Amerikanen de bedoeling hebben, ten laatste in 1970 twee mensen op de maan te brengen.

Eerst dan de technische middelen. De Saturn-5 raket heeft een hoogte van 110 meter. De eerste trap wordt aangedreven met keroseen. De tweede en derde trap met vloeibare waterstof, die dus op een temperatuur van -253° moet gehouden worden gedurende de gehele vlucht. De totale stuwkracht is ± 3.000 ton. Boven op de derde trap komt de LEM (Lunar Excursion Module), het eigenlijke maanlandingstoestel. Het geheel wordt bekroond door de kegelvormige Apollo-capsule, waarin drie man plaats nemen.

De eerste twee trappen brengen Apollo, LEM en derde trap in een baan om de aarde. De derde trap stuwt Apollo en LEM in de richting van de maan. Onderweg wordt de LEM uit zijn omhulsel gehaald en sturen de astronauten de neus van hun capsule in de opening van de LEM. Daartoe oefenden de

[p. 815]

Gemini-astronauten zich meermalen in hun koppelingsmaneuvres met de Agena-raket. Door de neus nu van de capsule stappen twee astronauten over in de LEM. Wanneer het geheel in een baan om de maan terechtgekomen is, maken de twee LEM-bewoners hun tuig los van de Apollo, en vertragen, zodat zij zacht op de maan terecht komen, tenminste indien de remraketten hun werk goed verrichten. De Apollo-capsule blijft ondertussen rond de maan wentelen met haar derde passagier. Beide astronauten zullen dan om beurten uitstappen om een eerste menselijke verkenning van het maanoppervlak te maken. Na volbrachte taak stappen zij terug in de LEM, waarvan het onderste gedeelte nu als lanceerplatform zal dienen. Het bovenste gedeelte verlaat de maan en bereikt volgens de bekende rendez-vous-techniek de Apollo-capsule. De twee astronauten stappen weer over; de LEM wordt vernietigd, en de Apollo begeeft zich op de terugweg.

Deze terugkeer is een zeer delicate onderneming. Het gaat erom opnieuw een ellips te beschrijven, waarvan het perigeum zo ligt dat de Apollo op de juiste manier in de dampkring terechtkomt. Het ideale perigeum bevindt zich op 60 km van het aardoppervlak. Een vergissing van enkele km is niet erg, maar indien de capsule op minder dan 50 km van de aarde terechtkomt, verbrandt ze in de atmosfeer; indien ze op meer dan 70 km van de aarde terechtkomt, vliegt ze de aarde voorbij en is er weinig kans dat de verdere vlucht nog beheerst kan worden. Het perigeum nu wordt bepaald door de remming waaraan men de capsule in het apogeum onderwerpt. Voor deze remming is een precisie van 1 m/sec vereist. De rakettechniek is er echter inmiddels reeds in geslaagd een precisie van 1 cm/sec te bereiken. De astronauten vertrekken dus van de maan naar hun apogeum. Onderweg bepalen ze hun juiste baan, door de observatie van hemellichamen, om in het apogeum de exacte remming te kunnen uitvoeren. Tijdens de lange terugkeer, die enkele dagen duurt, kunnen zij nog geringe baancorrecties aanbrengen. Hun snelheid in de atmosfeer ligt rond de 11 km/sec, terwijl de deceleratie ongeveer 8 g bedraagt. Het hitteschild van de Apollo-capsule werd speciaal bestudeerd om tegen zeer hoge temperaturen bestand te zijn.

Voorlopig kan echter niemand zeggen hoe de Amerikaanse ruimtevaartplannen verder zullen verlopen. In februari j.l. moest de eerste bemande capsule starten, maar iedereen kent daar de tragische afloop van. Een van de belangrijkste moeilijkheden is het feit dat er in de capsule een atmosfeer van zuivere zuurstof heerst, die bij de minste vonk ontvlamt. Het onderzoek, dat thans in volle gang is, zal moeten uitwijzen of het Apollo-programma met enkele secundaire wijzigingen kan voortgezet worden. Wanneer men zich integendeel verplicht zou zien, in de capsule een andere atmosfeer te scheppen, kan dit aan de Amerikaanse ruimtevaart een paar jaar vertraging kosten. In elk geval ziet het er niet naar uit, dat de Amerikanen in 1968 nog de maan zullen betreden.