|
| |
| |
| |
Wetenschappelijke kroniek
Satellieten meten de aarde
Karl-Wilhelm Schrick
ZOVER onze traditie teruggaat in het verleden, vindt men dat de mens zoekt naar het wezen en het uitzicht van de dingen die hem omgeven. Alhoewel men in de oudheid de aarde nog voor een vlakke schijf hield, omlijst door de bolschil van de hemel, toch is onze kennis van de bolvorm van de aarde ook al enkele duizenden jaren oud. Sedert de uitvinding van de verrekijker, een 350 jaar geleden, beschikt de mens over aanzienlijk nauwkeuriger meetinstrumenten en waarnemingsmogelijkheden. Vanaf dat ogenblik kon men belangrijke bijzonderheden in de vorm van de aarde aantonen. Zoals men in een sterrekijker kan zien dat de planeet Jupiter afgeplat is aan de polen, ontdekte men een zelfde afplatting aan de polen der aarde. Men vond dat de aardvorm enigszins gelijkt op een lichaam dat beschreven wordt door een ellips die rond haar kleine as, de poolas, wentelt. Daarom noemt men de aarde een omwentelingsellipsoïde die aan de polen afgeplat is. De kleine as van deze ellipsoïde stelt de omwentelingsas van de aarde voor.
Met de kunstmatige satellieten begint een nieuw tijdperk voor de geodesie, de wetenschap die de vorm van de aarde bestudeert. Het belang van de satellieten voor het meten van de aarde blijkt bijvoorbeeld al uit de bijnaam welke men aan één ervan, de ‘Anna I B’ gegeven heeft: de ‘geodetische satelliet’. Om de nieuwe mogelijkheden toe te lichten, moeten we eerst echter iets zeggen over de methoden die ons tot dusver informatie verstrekt hebben omtrent de vorm van de aarde.
| |
Hoe heeft men tot nu toe de aarde gemeten?
Het vermoeden dat het aardoppervlak gekromd is, werd een 2000 jaar geleden voor het eerst door metingen bevestigd. Op twee plaatsen in Egypte, ongeveer op de zelfde meridiaan gelegen, werd door middel van loodrecht opgestelde staven de invalshoek van de zonnestralen op het middaguur waargenomen (afb. 1). Terwijl de stralen bij staaf A loodrecht invielen, veroorzaakten ze bij staaf B een schaduw. Aan de top van staaf B werd de hoek gemeten; hij is gelijk aan het verschil in geografische breedte tussen beide plaatsen en bedroeg een vijftigste van een cirkelomtrek. Een schatting van de afstand tussen A en B, leverde derhalve, na vermenigvuldiging met 50, de lengte van de aardomtrek. Het resultaat was ongeveer 15% te groot.
Eigenlijk wordt deze methode nog steeds toegepast. Van gegeven punten op het aardoppervlak worden door astronomische waarnemingen de geografische lengte en breedte gemeten. Daardoor kent men ook de onderlinge verschillen in geografische lengte, resp. breedte. De vereiste rechtstreekse afstanden tussen deze punten kan men berekenen, door deze punten met ketens of netten van driehoeken te verbinden. Beide elementen - geografische coördinaten en driehoekssystemen - kan men tegenwoordig met grote nauwkeurigheid meten.
| |
| |
Zo is het mogelijk niet alleen de omtrek maar ook de vorm van de aarde te benaderen.
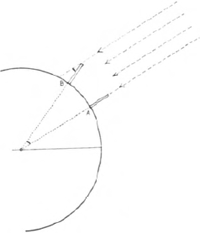
afb. 1
Even belangrijk voor het onderzoek van de vorm van de aarde zijn de metingen van de zwaartekracht. De invloed van de zwaartekracht van de aarde - afgezien van de aardrotatie - kan men als volgt aanschouwelijk maken: een gewicht, opgehangen aan een veerbalans, zal des te lichter wegen naargelang balans en gewicht zich verder verwijderen van het aardoppervlak. Aangezien bv. punten op de evenaar op een grotere afstand van het middelpunt van de aarde liggen dan de polen, moet een gewicht op de evenaar minder wegen dan op iedere andere plaats van het aardoppervlak. Het gewichtsverschil tussen de polen en de evenaar wordt nog versterkt door de middelpuntvliedende kracht, die ontstaat door de wenteling van de aarde en die het grootst is aan de evenaar. De grootte van deze middelpuntvliedende kracht is echter nauwkeurig bekend. Met zeer gevoelige meetinstrumenten kan men de zwaartekracht meten en daaruit besluiten trekken voor de vorm van de aardmassa.
| |
Een meting die de hele aarde omvat
De twee hierboven beschreven methoden kan men helaas slechts gebruiken op plaatsen van het vasteland die enigszins toegankelijk zijn, dus slechts op een betrekkelijk klein gedeelte van het aardoppervlak, waarvan men tot nog toe slechts een klein procent heeft gemeten. Onze kennis van de totale vorm van de aarde blijft daarom leemten vertonen zolang we geen meting kunnen uitvoeren die de hele aarde omvat. De kunstmatige satellieten verschaffen ons thans twee mogelijkheden tot zulke ‘globale’ opmeting. De eerste methode steunt op de beweging van de satelliet: uit de waargenomen onregelmatigheden in de banen welke de satellieten volgen kan men conclusies trekken betreffende de vorm van de aarde. In de tweede methode gebruikt men de satellieten als hooggelegen trefpunten die men vanuit verschillende plaatsen tegelijkertijd waarneemt, waardoor een geometrische studie van de aarde mogelijk wordt. Aangezien de gangbare meetmethoden reeds waardevolle resultaten opleverden, kunnen de satellieten onze voorstelling van de aarde slechts verfijnen indien alle metingen met grote nauwkeurigheid worden uitgevoerd. Daarom laten we enkele mogelijkheden hier al direct buiten beschouwing. zoals bv. het fotograferen van het aardoppervlak door middel van in satellieten ingebouwde camera's:
| |
| |
de resultaten welke dit geeft, zijn niet nauwkeurig genoeg. Het doel van opmetingen met satellieten is niet om kaarten of reliëfs te leveren: daarvoor volstaan de traditionele methoden. Bij een globale meting gaat het om de vorm van de aarde in haar geheel. Ter vereenvoudiging zou men zich een aardbol kunnen voorstellen die volkomen met water omgeven is. De rustende zeespiegel (afgezien van de golfbeweging en van ebbe en vloed) zou dan de gedaante van de aarde voorstellen, die men wil bepalen met al haar onregelmatigheden op grote schaal.
| |
Storingen van de satellietenbeweging
Iedere artificiële satelliet is, zoals de maan, een hemellichaam binnen de aantrekkingssfeer van de aarde. Indien de wederzijdse aantrekking plotseling zou uitvallen, zou de satelliet zich met de snelheid van dat ogenblik in rechte lijn van de aarde verwijderen. De aantrekkingskracht van de aarde houdt het lichaam evenwel in een gesloten baan. Aangezien elke massa een aantrekking uitoefent, werken zon, maan en planeten eveneens in op de baan van de kunstmatige satellieten. Daarbij komen nog de storingen door luchtweerstand, aanbotsende deeltjes enz. Al deze invloeden zijn van een veel kleinere orde van grootte dan de aantrekking van de aarde; daarom kunnen we ze in onze verdere uiteenzetting buiten beschouwing laten. Laten we dus doen alsof de enige kracht de aantrekking van de aarde is. Indien de totale massa van de aarde in haar zwaartepunt samengeperst of althans bolsymmetrisch eromheen verdeeld was, dan kon men het zwaartepunt van de aarde als enig uitgangspunt van de zwaartekracht beschouwen. In dit geval geldt de eerste wet van Kepler: de omloopbaan van een satelliet om de aarde is een onveranderlijke ellips (waarvan de cirkel een grensgeval is), met het zwaartepunt van de aarde in een der twee brandpunten van de ellips.
Nu bezit de aarde echter geen bolsymmetrische massaverdeling, maar ze is aan de polen afgeplat en veroorzaakt daardoor op ieder ogenblik veranderingen van de baan. De reactie van de satellietenbaan is vooral merkbaar in de beweging van de ‘knopenlijn’ en van de ‘apsidenlijn’; laten we deze verschijnselen verklaren aan de hand van afbeelding 2.
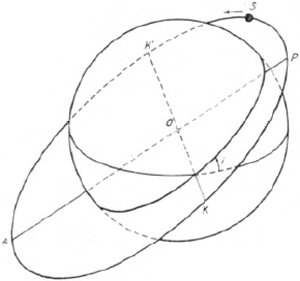
afb. 2
De tekening stelt de aarde voor met de evenaar en een satellietenbaan door de punten S, K', A, K, P. Het zwaartepunt O van de aarde ligt in een van de
| |
| |
brandpunten van de baanellips, waarvan de grote as PA ook apsidenlijn genoemd wordt. Het punt van de baan dat het dichtst bij de aarde ligt, noemen we P (perigeum), het verste punt is A (apogeum). Het baanvlak vormt met het evenaarsvlak een hoek i (helling van de baan) en de snijlijn KK' van de beide vlakken wordt knopenlijn genoemd (K = klimmende knoop, K' = dalende knoop). ‘Knopenbeweging’ noemt men het verschijnsel dat men bij een draaitol kan waarnemen als een langzame verplaatsing van het tolvlak (precessie-beweging van de tol). De helling i van de satellietenbaan, die hier als tolvlak beschouwd kan worden, blijft constant; toch draait het hele baanvlak en daarmee de knopenlijn in die zin, dat de doorgangspunten aan de evenaar uitwijken in een richting tegengesteld aan de beweging van de satelliet. De snelheid van de knopendraaiing kan bij kleine hellingen en dichtbij gelegen banen tot 9o per dag bedragen; bij meer verwijderde banen zowel als bij grotere hellingen wordt de knopenbeweging kleiner, om bij een helling van 90o (poolbaan) geheel te verdwijnen. Daar de knopenverandering in korte tijd heel hoog kan oplopen, kan men ze door waarneming van satellieten gemakkelijk meten. Zoals in al deze beschouwingen, wordt ook de knopenbeweging in een ruimtelijk vaststaand coördinatenstelsel gemeten. Om telkens de doorgangspunten aan de evenaar te vinden, moet dan ook de dagelijkse wenteling van de aarde mee verrekend worden.
Een tweede belangrijk gevolg van de afplatting der aarde is de draaiing van de grote as van de elliptische baan, de apsidenlijn. Bij een geringe helling van de baan bedraagt de dagelijkse draaiing van de grote as in het baanvlak ongeveer het dubbele van de overeenkomstige knopenbeweging en verloopt dan in dezelfde richting als de beweging van de satelliet (zie afb. 2). Het nulpunt van de draaiing ligt bij een inclinatie van ongeveer 63o; bij nog grotere inclinatie draait de apsidenlijn in tegengestelde richting. Aangezien volgens de tweede wet van Kepler een satelliet in het perigeum zijn grootste en in het apogeum zijn kleinste snelheid heeft, kunnen deze punten en bijgevolg ook hun verplaatsing door middel van reeksen waarnemingen goed bepaald worden.
Niet alleen de ligging van de knopen en van de apsidenlijn wordt door de afplatting van de aarde gewijzigd; ook andere baanelementen (de vorm van de ellips, de helling enz.) worden beïnvloed, zij het dan in veel geringere mate. Anderzijds reageren alle baanelementen ook op andere onregelmatigheden van de aarde, bv. de asymmetrie tussen noordelijk en zuidelijk halfrond, de uitrondingen van de evenaar enz. Verschillende oorzaken hebben dus min of meer gelijke gevolgen. Zo krijgt ons probleem het volgende uitzicht. In de waargenomen baanafwijkingen zitten, op zeer complexe wijze door elkaar vermengd, de resultaten van de meest uiteenlopende onregelmatigheden van de aardstructuur. Uit de waarnemingen moet men dus omgekeerd weer conclusies kunnen trekken betreffende de vorm van de aarde. Dit is mogelijk door middel van omvangrijke en langdurige mathematische berekeningen. Daarbij wordt men geholpen door de karakteristieken van onderling verschillende satellietenbanen (bv. bij poolbanen valt de knopenbeweging praktisch weg; bij een helling van 63o is er geen apsidendraaiing meer). De opgave wordt echter bemoeilijkt door de reeds vermelde bijkomende storingen (andere hemellichamen, luchtweerstand). Als een satelliet dicht bij het oppervlak van de aarde beweegt, is de nog weinig bekende invloed van de luchtweerstand een grote onzekerheidsfactor in de conclusies; als daarentegen de baan ver van de aarde ligt, dan neemt
| |
| |
de rechtstreekse inwerking van het krachtveld van de aarde meer af dan de onderzoeker lief is. Hoewel dus nooit alle gunstige omstandigheden tegelijkertijd aanwezig kunnen zijn, is men er met verloop van jaren toch in geslaagd, uit de banen van vele kunstmatige satellieten enkele essentiële eigenaardigheden van de gedaante der aarde af te leiden. Daarover handelen we in onze laatste paragraaf.
| |
Ruimtelijke triangulatie met satellieten
De tweede mogelijkheid om de vorm van de aarde door middel van kunstmatige satellieten te bepalen, steunt op geheel andere principes. Satellieten worden hier als trefpunten aangewend, met hulp waarvan een geometrische opmeting van de aarde wordt uitgevoerd. Het beginsel van deze methode berust op de volgende overwegingen.
Veronderstellen we dat een kunstmatige satelliet vanuit een observatiepost op aarde op een nauwkeurig registreerbaar tijdstip waargenomen wordt. Op dat ogenblik heeft de satelliet een bepaalde positie, die zoals de positie van de omgevende sterren gemeten kan worden. De gezichtsstraal van het station naar de satelliet legt dus een ruimtelijke richting vast. Door gelijktijdige waarneming van de satelliet vanuit meerdere waarnemingsstations, kan men dus op dat ogenblik evenveel richtingen bepalen als er stations zijn. Aangezien alle gezichtsstralen elkaar in de satelliet snijden, levert zulke gelijktijdige waarneming vanuit verscheidene stations een stralenbundel met een bepaalde oriëntatie in de ruimte. Nu kan zulke gemeenschappelijke waarneming herhaald worden op een ander ogenblik, wanneer de satelliet zich in een andere positie bevindt. Zo krijgt men meer stralenbundels, die telkens door de snijding van de overeenkomstige stralen de ligging van de waarnemingsstations ten opzichte van elkaar vastleggen. Zoals in de vlakke meetkunde afstanden bepaald worden door rechtstreekse triangulatie, zo hebben we hier te doen met een ruimtelijke onrechtstreekse triangulatie. In afb. 3 wordt dit principe vereenvoudigd voorgesteld. Op deze wijze kunnen bv. continenten meetkundig met elkaar verbonden worden.
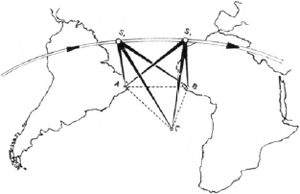
afb. 3
Het doel van deze methode is, over de hele aardbol een net van waarnemingsstations te spreiden en hun ligging ten opzichte van elkaar te bepalen. Alle stations samen vormen het geraamte dat in grote lijnen de aarde voorstelt. Op een soortgelijke manier kan dan een opmeting van een net met kleine mazen
| |
| |
tot een geometrisch nauwkeurig model van de aardvorm leiden. Daar het hier gaat om meten van driehoeken met behulp van hemellichamen, noemt men deze werkwijze ‘stertriangulatie’.
Gelijktijdige satellietenmeting vanuit verschillende ver uit elkaar liggende stations vereist over het algemeen een kostbare technische uitrusting; want de gelijktijdigheid moet tot op tenminste een duizendste van een tijdseconde gewaarborgd zijn. Een geschikt doelwit is de ballonsatelliet ‘Echo I’, die wegens zijn grote helderheid goed bruikbaar is voor de stertriangulatie, echter niet voor een dynamisch gebruik. Wegens zijn geringe massa en zijn groot volume reageert deze ballon zeer gevoelig op de stralingsdruk van de zon en op de luchtweerstand; deze kwantitatief nog weinig bekende effecten, overstemmen de baanstoringen die veroorzaakt worden door de vorm van de aarde. Een speciaal voor de stertriangulatie gebouwd object was de geodetische satelliet ‘Anna I B’, ook wel ‘flitslichtsatelliet’ genoemd. Hij bestaat nog wel, maar zendt geen signalen meer uit. Op vastgestelde tijden zond hij reeksen van telkens vijf korte, helle lichtflitsen uit en waarborgde zodoende voor alle waarnemende stations de gelijktijdigheid van de metingen. De observatoria werden door een goed werkende mededelingsdienst telkens tijdig ingelicht over de verwachte posities en zendtijden van de lichtflitsen. Een flitslichtsatelliet kan derhalve ook op het in de schaduw van de aarde gelegen deel van zijn baan lichtflitsen uitzenden, wat het gebruik over grotere afstanden mogelijk maakt. Om zeer grote afstanden (bv. van oceanen) te overbruggen, laat men de satellieten op enkele duizenden kilometers hoogte bewegen.
| |
Instrumenten en waarnemingen
Voor de kennis van de aardvorm is het van belang dat de nieuwe methoden nauwkeuriger zijn dan de oude. Satellietenmetingen maken het waarschijnlijk dat over enige jaren de vorm van de aarde tot op 10 m nauwkeurig bekend zal zijn, een orde van grootte nauwkeuriger dan vroeger. Om dit doel te bereiken, moeten aan de waarnemingstechniek zeer hoge eisen gesteld worden, zoals blijkt uit het volgende voorbeeld.
Een satelliet op 1000 km hoogte doorloopt in één seconde ongeveer 7 km. Wanneer zulk een voorwerp onder gunstige omstandigheden waargenomen wordt, zal een fout van ongeveer 1/700 seconde in de tijdmeting een fout van 10 m op de aarde veroorzaken; een fout van 2 boogseconden in de positiebepaling zou het zelfde resultaat geven. Wil men de totale fout dus reduceren tot maximaal 10 m, dan moet men er zeker van zijn dat men de tijd van de satelliet tot op ongeveer 1/1000 tijdseconde en zijn positie tot op één boogsec. kan bepalen.
Op het eerste gezicht leek alleen de fotografische techniek tegen zulke hoge eisen opgewassen. Een zichtbare satelliet kan steeds gefotografeerd worden; de meegefotografeerde omringende sterren, waarvan de posities bekend zijn, maken de positiebepaling van het satellietenbeeld op de fotografische plaat mogelijk. Voor de vereiste precisie bij het uitmeten van de plaat is een goede optiek van de camera nodig, met een voldoende lange brandpuntsafstand (sterke vergroting) en genoeg lichtsterkte. De juiste tijdmeting verkrijgt men door aan de tijdsregistratie verschillende onderbrekingen van de belichting, en bijgevolg van het satellietenspoor, te koppelen. De eigenlijke moeilijkheid bij camera's
| |
| |
met vaste opstelling en satellieten die zonlicht weerkaatsen, bestaat erin om van een snel over de fotografische plaat bewegend satellietenbeeld scherp afgetekende spoorpunten te krijgen. Er bestaan tegenwoordig verschillende camera's met ingewikkelde sluitermechanismen voor de fotografie van artificiële satellieten. Een opname van de lichtpunten van flitslichtsatellieten vereist weliswaar geen speciale sluiter, maar wel een equatoriaal opgestelde fotografische kijker. De lichtflitsen lijken in een kijker die de sterrenbeweging volgt, puntvormig zoals de sterren en kunnen zonder moeilijkheden gemeten worden. Het grootste type van deze soort toestellen is de Baker-Nunn-spiegeltelescoop, die naar keuze de beweging van de sterren of die van satellieten kan volgen. Twaalf van deze instrumenten staan op lage breedte over de hele aarde verspreid. Aan deze instrumenten danken we onze tot nog toe verzamelde kennis betreffende de satellietenbanen en hun storingen, evenals onze daaruit afgeleide verbeterde kennis van de vorm der aarde.
In de laatste tijd zijn elektronische meetmethodes zover ontwikkeld, dat zij met succes voor geodetische satellietenwaarnemingen gebruikt kunnen worden. Eén van deze werkwijzen berust op een toepassing van het ‘Dopplereffect’. Zoals men bij ervaring weet, verandert een geluidsbron die beweegt (b.v. een fluitende locomotief) voor het oor van de waarnemer van toonhoogte: de toon daalt wanneer de geluidsbron voorbij beweegt. Hoe dichter de waarnemer zich bij de baan van de geluidsbron bevindt, des te meer zal hem de toonverandering opvallen. Dit verschijnsel steunt op het feit dat de geluidsgolven in de richting van de beweging verkort en in de tegengestelde richting gerekt worden; zo verandert de golflengte en daarmee ook de frequentie. Zendt een satelliet een bepaalde frequentie uit, dan kan men op dezelfde wijze uit de aard van de frequentiewijziging tijdens haar voorbijgang enkele eigenschappen van haar baan bepalen. Deze methode van de frequentieregistratie levert op korte tijd een groot aantal metingen en geeft de mogelijkheid om uit de ligging van de satellietenbaan t.o.v. verschillende meetstations de ligging van deze stations ten opzichte van elkaar af te leiden. In de Verenigde Staten hebben zulke metingen tot plaatsbepalingen met een nauwkeurigheid van ongeveer 10 m geleid.
Met eenzelfde nauwkeurigheid kan men thans door middel van radarmetingen de afstand van kunstmatige satellieten bepalen. De grote nauwkeurigheid van zulke metingen is te danken aan het feit dat gedurende de weinige minuten van het verblijf boven de horizon automatisch duizenden radarwaarnemingen uitgevoerd worden. Wanneer met behulp van enkele stations waarvan de onderlinge ligging bekend is, uit afstanden satellietenposities berekend zijn, kan men de coördinaten bepalen van andere stations die aan de metingen deelgenomen hebben.
| |
Resultaten
De belangrijkste en tevens de best gewaarborgde conclusie uit de waarneming van de baanstoringen heeft betrekking op de afplatting van de aarde aan de polen. Het verschil tussen beide halve assen van de omwentelingsellipsoïde van de aarde wordt doorgaans uitgedrukt als een breukdeel van de grote halve as; indien de grote halve as, dus de straal van de evenaar, met a, de kleine halve as met b en de afplatting met A aangeduid worden, dan geldt voor het verschil der halve assen
a - b = A . a
| |
| |
Uit de waarnemingen van satellieten bleek de gemiddelde waarde van de afplatting te zijn
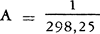
De waarde 298,25 is ongeveer voor 0,1 twijfelachtig en ligt tamelijk juist in het midden van de waarden die we kenden uit de traditionele methoden. Aangezien de straal a van de evenaar bekend is (6378 km), betekent dit resultaat dat de aardpolen gemiddeld 21,385 km (met slechts een onzekerheid van enige meters) dichter bij het middelpunt van de aarde liggen dan punten op de evenaar. - Verder ontdekte men ook, dat het zuidelijke halfrond iets sterker afgeplat is dan het noordelijke: de zuidpool ligt dus een 30-tal meters dichter bij het evenaarsvlak dan de noordpool. Daarom spreekt men nu van ‘de peervorm van de aarde’. Men moet daarbij voor ogen houden dat deze afwijking slechts ongeveer een duizendste van de aardafplatting bedraagt en op een model niet voorgesteld kan worden. (De aardafplatting zelf is zo gering, dat ze op een betrekkelijk klein model niet zou worden opgemerkt. Voorbeeld: een aardglobe met een middellijn aan de evenaar 30,0 cm, poolas 29,9 cm). De waarnemingen hebben ook reeds uitgemaakt dat de aarde zich niet in hydrostatisch evenwicht bevindt, d.w.z. haar oppervlak stemt niet overeen met dat van een vloeibaar lichaam waarvan de massaverdeling alleen van de aantrekkingskracht en de middelpuntvliedende kracht afhankelijk is. Was dat wel zo, dan zou de aarde iets meer afgeplat moeten zijn 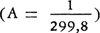 hetgeen neer zou komen op een verandering van de halve assen van ongeveer 100 m.
Over afwijkingen van de cirkelvorm aan de evenaar hebben de metingen tot nog toe geen betrouwbare informatie kunnen geven. Door verdere waarnemingen hoopt men echter deze vragen te kunnen beantwoorden, zoals men later wellicht ook plaatselijke onregelmatigheden in de massaverdeling zal kunnen ontdekken. Over enkele jaren zullen ook de resultaten van de stertriangulatie over de geometrische bepaling van de aardvorm voorhanden zijn. Een vergelijking van de geometrische vorm van de aarde met de vorm van de aardmassa zoals die thans uit de waarneming van satellieten bekend is, zal het dan mogelijk maken conclusies te trekken betreffende het inwendige van onze planeet, de aarde.
|
|