Streven. Jaargang 18
(1964-1965)– [tijdschrift] Streven [1947-1978]–
[pagina 72]
| |||||||||||||||||||
Voorrang
| |||||||||||||||||||
[pagina 73]
| |||||||||||||||||||
normale voorrangsregeling aanbrengen. Een goede voorrangsregeling immers heeft ten doel deze, waar mogelijk, overbodig te maken (vergelijk I, nr. 9). | |||||||||||||||||||
2. Benadering van het kruispuntWanneer bestuurder A, rijdend van Zuid naar Noord, in de verte een kruispunt ziet, dan is deze situatie het signaal, waarop hij aanvankelijk weliswaar mag accelereren, maar toch op het kruispunt met een zodanig afnemende snelheid moet toerijden, dat hij vóór de aansprakelijkheidszone kan stoppen. Totdat hij een tweede signaal krijgt, dat zijn stoplijn verlegt naar de as van de O-W-weg die het begin is van zijn vrije zone. De gehele straat vóór het begin van de aansprakelijkheidszone is nu een normaal remstuk, dat bij definitie lang genoeg is om zo nodig tot stilstand te komen. | |||||||||||||||||||
3. Het binnenrijden van de aansprakelijkheidszonea. Feitelijke veiligheid. Welke constellatie van factoren maakt het oversteken de facto veilig? In fig. 7a laten wij bestuurder A zover oprijden, dat hij langs de linker straathoek T het voorste deel van de wagen D ziet. (Bij RV ziet hij langs de rechter straathoek U het voorste deel van de wagen B). K is het eventuele conflictpunt voor A en D; (L dat voor A en B). Klaarblijkelijk is het oversteken de facto veilig wanneer A het conflictpunt zal verlaten hebben op het ogenblik dat voorrangsgerechtigde een gepaste veiligheidsmarge in gebruik gaat nemen (I, nr. 2). De vraag of deze veiligheidsvoorwaarde vervuld zal worden hangt af:
Wanneer nu de snelheid van voorrangsgerechtigde gelijk is aan die van voorrangsplichtige - maar zeker niet groter - mag A de wagen van D voorlangs passeren, op voorwaarde, dat de afstand DK minstens gelijk is aan de som van drie afstanden, te weten: ten eerste de afstand AK, ten tweede de bij de gegeven snelheid behorende veiligheidsmarge, en - om exact te zijn - ten derde de lengte van de wagen van A gemeten van stuur tot achterbumper. Zou echter de snelheid van D bijv. driemaal zo groot zijn als de snelheid van A, dan zou eerstgenoemde afstand uiteraard niet AK maar 3 AK moeten zijn. Tevens zou de benodigde veiligheidsmarge groter moeten zijn. De feitelijke veiligheid blijkt dus gelegen te zijn in een gunstige verhouding van de afstanden van D en A tot hun conflictpunt. Anders gezegd: A moet bij de nadering van het conflictpunt K een voorsprong hebben op D. Deze voorsprong is uit te drukken door het getal dat aangeeft hoeveel maal men AK, als lengteëenheid, kan afpassen op DK (tangens α). b. De zichtbare voorsprong van A op D is werkzaam als signaal, waarop automatisch gereageerd kan worden, zonder dat er enige theorie of berekening voor nodig is. Zoals ook een kat of eekhoorn, die een sprong wil maken, de te nemen afstand zintuigelijk taxeert in vergelijking met de afstanden die zijn ervaring hem als ‘haalbaar’ voorstelt. Zo zal ook A de afstand DK taxeren door de reeds getaxeerde afstand AK als vergelijkingsafstand (lengteëenheid) te gebruiken. In wezen - hoewel niet reflex - schat hij de grootte van zijn voorsprong (tgα) concreet. Een feit dat, als wij ons niet vergissen, door de ervaring bevestigd wordt. | |||||||||||||||||||
[pagina 74]
| |||||||||||||||||||
Samenvattend concluderen wij dat het praktisch veiligheidscriterium voor het oprijden van voorrangsplichtige A is gelegen in de zichtbare voorsprong die hij heeft op voorrangsgerechtigde D, waarvan de grootte wordt uitgedrukt in de tangens van zijn gezichtshoek (tgα). Is deze tgα in betrekking tot beider snelheden groot genoeg, dan is het natuurlijke signaal voor het binnenrijden van de aansprakelijkheidszone gegeven. | |||||||||||||||||||
4. Het dispuut over het veiligheidscriteriumIn de spaarzame literatuur die er over de voorrang bestaat, valt het op dat men zich wel eens beperkt tot gelijke straatbreedtes en een gelijke mate van Rechts Rijden (RR). Daarbij blijkt dat DK steeds groter is dan BL, zoals overigens ook de praktijk op de weg te zien geeft. Welnu, voorstanders van LV betogen dat dit op een grotere veiligheid wijst: A ziet D eerder dan B. Dit veiligheidscriterium houdt uitsluitend rekening met de afstand van voorrangsgerechtigde tot het conflictpunt (dus DK bij LV, of BL bij RV), maar verwaarloost het feit dat ook voorrangsplichtige zich naar het conflictpunt begeeft over de afstand AK (resp. AL). G. WollaertGa naar voetnoot1) daarentegen geeft aan RV de voorkeur. Hij is van mening dat men bij BL ook nog de rechthoekszijde AL en bij DK de rechthoekszijde AK moet optellen; lijnstukken die in het gezichtsveld van A liggen. Hij houdt wel - en terecht - rekening met AK of AL, maar kiest als criterium de som van de afstanden, die voorrangsgerechtigde en voor-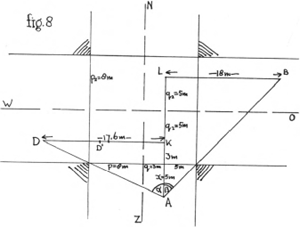 | |||||||||||||||||||
[pagina 75]
| |||||||||||||||||||
rangsplichtige moeten berijden, in plaats van het verschil, of beter, de verhouding te nemen. Ook hij verwaarloost daardoor de kapitale vraag of er een botsing zal plaats vinden of niet. Het zijn echter niet alleen de gebruikte criteria die de overtuigingskracht in de bestaande literatuur verzwakken, maar ook het feit dat men zich beperkt tot slechts enkele voorbeelden, die geen algemene bewijskracht hebben. Dit maakt het nodig, om, alvorens ons betoog voort te zetten, een eenvoudig coördinatensysteem te ontwerpen, waarmee wij tenminste alle rechthoekige kruisingen met alle situaties daarop in formule kunnen vangen. | |||||||||||||||||||
5. Oriëntatie op het kruispuntIn fig. 7b stellen wij de breedte van de Z-N-straat op 2p, en de afstand van A tot de Z-N-as op q. Deze afstand wordt in de richting WO (dus naar rechts) positief aangenomen. Voor de dwarsstraat stellen wij deze grootheden resp. op 2p2 en q2, waarbij q2 weer positief gerekend wordt naar rechts, dus naar Noord voor B en naar Zuid voor D. De gezichtshoek van A naar links noemden wij reeds α, en naar rechts β. De afstand van A tot de zuidelijke rooilijn van de OW-straat (TU) noemen wij ×. In de rechthoekige driehoeken AKD (bij LV) en ALB (bij RV) zien wij: 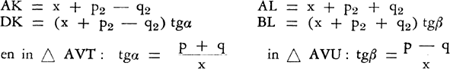 | |||||||||||||||||||
6. Toets van de besproken veiligheidscriteria (nr. 4)In de literatuur over de voorrang neemt men gewoonlijk aan dat gelijke straatbreedtes (p = p2) en een gelijke mate van Rechts Rijden (q = q2) steeds tot gevolg heeft dat DK groter is dan BL. Uit de gevonden waarden var DK, BL, tgα en tgβ uit nr. 5 vindt men inderdaad dat DK - BL = 2q. Hiermee schijnt het criterium van enige voorstanders van LV een schijn van juistheid te krijgen. Merkwaardig is intussen dat het criterium van Wollaert bij p = p2 en q = q2 geen beslissing geeft. Voor AK + DK immers vindt men dezelfde lengte als voor AL + BL, nl.: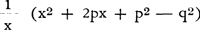 . Dit criterium is dus onbruikbaar. Alleen het criterium dat DK en BL vergelijkt dient nog getest te worden. Wij doen dit aan de hand van een situatie die volgens dit criterium gunstig zou moeten zijn voor RV, doch in feite ongunstig is. Gunstig zal het zijn voor RV als wij DK < BL kiezen, zodat × moet voldoen aan de ongelijkheden: . Dit criterium is dus onbruikbaar. Alleen het criterium dat DK en BL vergelijkt dient nog getest te worden. Wij doen dit aan de hand van een situatie die volgens dit criterium gunstig zou moeten zijn voor RV, doch in feite ongunstig is. Gunstig zal het zijn voor RV als wij DK < BL kiezen, zodat × moet voldoen aan de ongelijkheden:
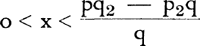 Voor p = p2 en q = q2 blijkt dit onmogelijk; (immers DK - BL = 2q). Wij moeten dus minstens één van deze twee gelijkheden laten vervallen. Een combinatie van gegevens die testcase kan zijn voor RV (tgβ = 1, d.w.z. maximaal gevaar) is de volgende: p = p2 = 8 m; × = q2 = 5 m; q = 3 m. Hiermee stellen wij samen fig. 8, waarin: | |||||||||||||||||||
[pagina 76]
| |||||||||||||||||||
Volgens bedoeld criterium is RV lichtelijk in het voordeel: BL is 40 cm langer dan DK. (Volgens het criterium van Wollaert is dit voordeel sprekender: AK + DK = 25,6 m terwijl AL = BL = 36 m. Verschil 10,4 m). Bezien wij nu voor A de mogelijkheid tot oprijden bij RV. Zijn de snelheden van A en B gelijk, dan mag A niet oprijden: wegens AL = BL (tgβ = 1) zouden zij bij L met elkaar in conflict komen. Bij LV zou A volgens het criterium, dat wij nu testen, zéker niet mogen oprijden. Is dit juist? Als immers de snelheden van A en D gelijk zijn en A het punt K reeds gaat verlaten, is D daar nog 9,6 m vandaan (D′). Ja zelfs bij gunstige omstandigheden - als de wagen van A niet lang is en beider snelheid niet te hoog - zal A zonder D te hinderen toch kunnen oversteken. Daarmee blijkt het criterium dat de afstanden van DK en BL vergelijkt ondeugdelijkGa naar voetnoot2). 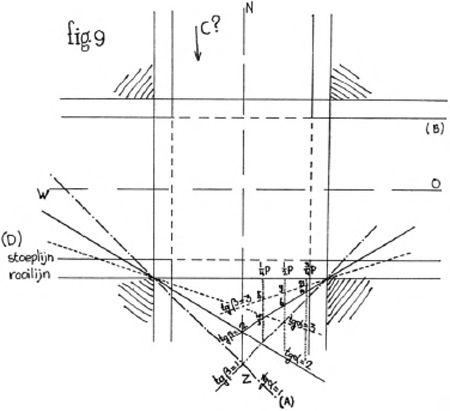 | |||||||||||||||||||
[pagina 77]
| |||||||||||||||||||
7. Veilige benedengrens voor tgαDe feitelijke grootte van tgα (fig. 7b; △ AVT) ligt vast in de formule xtgα = p + q Laten wij voor q ook negatieve waarden toe, dan betekent dit Links Rijden (LR) bij LV, dus de ‘this-side-priority’ in het spiegelbeeld van de huidige regeling RR - RV. Spiegelen wij weer terug om de Z-N-as, waarbij α overgaat in β en +q in -q, dan vinden wij de formule voor RR - RV: xtgβ = p - q die uit de figuur ook rechtstreeks is af te lezen (△ AVU).
Het zou van belang zijn te weten hoe groot tga minstens moet zijn om veilig over te kunnen steken. De formules (1) en (2) leren daaromtrent niets. Een exacte benedengrens voor tgα, die wij door de letter k zullen voorstellen, is dan ook moeilijk op te stellen. Deze hangt o.a. af van de schaal van het kruisingsvlak, het RR (q), de afmetingen van de wagens, hun snelheid, hun acceleratieen remvermogen en eventueel de conditie van de bestuurder. Boven (nr. 3) hebben wij verondersteld dat de snelheid van D zeker niet groter is dan die van A. Gelijke of kleinere snelheid van voorrangsgerechtigde vergemakkelijkt het taxeren van de nodige voorsprong (tgα). Het zou van belang zijn aan k een zodanige grootte te kunnen toekennen dat er - buiten de waarneming van A om - positionele garantie voor die veronderstelling bestaat. In fig 7b stellen wij tgα = k; dan is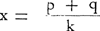 DE = k (p2 - q2) en ES = p2 + q2. De gezichtshoek van D naar links noemen wij α2. Nu is DE = k (p2 - q2) en ES = p2 + q2. De gezichtshoek van D naar links noemen wij α2. Nu is
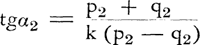 Als tgα2 <k is, heeft D nog steeds niet het signaal tot oprijden gekregen. Hij zal dan in staat moeten blijven tot stoppen vóór zijn aansprakelijkheidszone. Tot deze snelheidsvermindering zal D dus verplicht zijn als k voldoet aan: 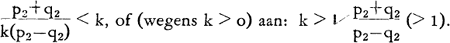 Wanneer A dus zover is opgereden, dat zijn zichtbare voorsprong op D groter is dan déze k, zal de snelheid van D minder moeten zijn dan die van A. Dit is een positionele garantie. | |||||||||||||||||||
8. Grotere doorstroming van het verkeer bij gelijke veiligheidIn fig. 9 zijn de lijnen tgα = 1, tgα = 2 en tgα = 3 opgenomen, alsmede de overeenkomstige lijnen voor tgβ. Bevindt A zich óp of ten Zuiden van de lijn tgα = 1 bij LV, resp. tgβ = 1 bij RV, dan moet hij kunnen stoppen vóór de ‘stoeplijn’ (verbindingslijn der stoepranden) wegens maximaal risico. Men ziet dat RV deze gevaarlijke zone dichter bij het kruispunt situeert en minder mogelijkheid biedt tot snelheidscorrectie. Veronderstellen wij dat de wagen van A niet te lang is, en k = 2 voldoende garantie geeft om over te steken zonder de voorrangsgerechtigde te hinderen. Bij LV mag A dan gematigd accelereren als hij de lijn tgα = 2 overschrijdt. Bij RV mag hij dat niet voor de lijn tgβ = 2 bereikt is. Het sein tot veilig | |||||||||||||||||||
[pagina 78]
| |||||||||||||||||||
oprijden wordt bij LV dus op grotere afstand van het kruispunt gegeven dan bij RV. Deze afstanden, resp. x1 en x2, zijn bij elke waarde van q af te lezen uit de figuur en te berekenen uit de formules (1) en (2). Bij q = ½p bijv. vindt men x1 = ¾ p en x2 = ¼p. Algemeen geldt:
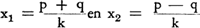 (3)
De weg tussen de punten (x1;q) en (x2q) kan bij LV door A benut worden om zijn snelheid op te voeren, zodat in het punt (x2;q) zonder veiligheidsverlies geldt: v1 > v2waarin v1 en v2 de toegestane snelheden aangeven resp. bij LV en RV. Bij deling van de formules (3): 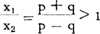 (5)
blijkt dat de grotere lengte van x1 ten gunste van LV wijst op een grotere doorstroming bij gelijke veiligheid. Dat deze doorstroming bij LV groter is blijkt dus bewijsbaar, doch de mate van deze vergroting is (nog) niet exact in een formule meetbaar. Want het verschil tussen v1 en v2 kan groot genoeg zijn voor A om bij LV veilig te profiteren van een opening tussen twee voorrangsgerechtigden, waar dit bij RV reeds niet meer mogelijk was. Dit voordeel wordt in de formules (4) en (5) niet uitgedrukt. | |||||||||||||||||||
9. Grotere veiligheid bij gelijke doorstroming van het verkeerIn nr. 8 hebben wij bij LV en RV ons steeds gehouden aan tgα = tgβ (d.w.z. gelijke veiligheid). Daaruit volgde dat x1 groter was dan x2, zodat A bij LV eerder kon oprijden. Een volgende stap is dat wij x1 en x2 gelijk stellen, zodat wij A zowel bij LV als bij RV opgesteld zien in hetzelfde, bewegelijke, punt (x; q). In deze situatie, waarin zowel LV als RV aan A toestaan om op te rijden (gelijke doorstroming), vergelijken wij tgα met tgβ (veiligheid). In fig. 9 is dit aangegeven langs de lijn tgβ = 2 bij q = ¼p, q = ½p en q = ¾p. Voor tgα vindt men daar resp. 10/3, 6 en 14. Tegenover tgβ = 2 betekenen deze cijfers voor tgα een beduidende voorsprong voor A (bij LV), en daarmee een grotere veiligheid. Het meest profiteren daarvan de fietsers, die wegens hun geringe snelheid deze grotere voorsprong nodig hebben (tgα = 10 tot 14). Daarentegen is tgβ = 2 bij RV voor hen niet veilig om over te steken. Door deling van (2) op (1) bij tgβ = k vindt men het bovenstaande als algemeen geldend samengevat in de formule: 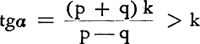 (6)
Dit nu is de wiskundige vertaling van ‘grotere veiligheid bij gelijke doorstroming van het verkeer’.
Tot hiertoe hebben wij het punt (x;q) verschoven langs de lijn tgβ = 2 (resp. tgβ = k). Wat gebeurt er wanneer wij dit punt, dat nog steeds de positie | |||||||||||||||||||
[pagina 79]
| |||||||||||||||||||
van A aangeeft, willekeurig verschuiven binnen de driehoek begrensd door de lijnen tgα = 2, tgβ = 2 en de rechter rooilijn? Aangenomen dat k = 2 nog net voldoende veilig is om op te rijden, dan blijkt dat in de gehele driehoek het oprijden bij RV gevaarlijk en bij LV veilig is. Ook dit kunnen wij met behulp van (3) algemeen geldend formuleren: In de periode dat x voldoet aan
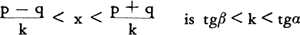 Dit wijst op veilige doorstroming bij LV, waar RV op grond van onveiligheid stagneert.
Deze verkeersanalyse ging uit van de vraag, welke voorrangsregeling een zo groot mogelijke veiligheid aan een zo groot mogelijke doorstroming kan paren. Vanuit verschillende aspecten belicht, is telkens met een natuurlijke vanzelfsprekendheid gebleken, dat alleen LV de beperkte mogelijkheden die het kruispunt aan veiligheid en doorstroming biedt (I, nr. 1), uitputtend benut en in harmonie verenigt. Waarvandaan deze vanzelfsprekendheid? Enerzijds omdat bij RR de gezichtshoek naar links (α) groter is dan naar rechts (β), en des te groter wordt naarmate men meer rechts rijdt (q), zodat de zichtbare voorsprong op verkeer van links (tgα) een grotere veiligheid waarborgt (tgα > tgβ). Anderzijds omdat bij RR het signaal tot oprijden op grotere afstand (x) gegeven wordt dan bij RV, en deze afstand des te groter wordt naarmate men meer rechts rijdt (q), zodat het eerder en daardoor sneller oprijden een grotere doorstroming waarborgt (x1 > x2). De harmonie van deze grotere veiligheid en doorstroming wordt blijkbaar gerealiseerd in het product van de zichtbare voor sprong (tgα) en de afstand tot het kruispunt (x); dit product is des te groter naarmate de halve straatbreedte (p) verruimd wordt door het RR (+ q). Symbolisch is dit neergelegd in de formule: xtgα = p + q Bij RV echter werken de halve straatbreedte en het RR elkaar tegen (- q): hoe meer men rechts rijdt, des te geringer harmonieëren veiligheid en doorstroming. Immers het product van de zichtbare voorsprong en de daarbij behorende afstand tot het kruispunt is bij RV gelijk aan het verschil van de halve straatbreedte en de mate van RR: xtgβ = p - q. Het structurele deficit van de huidige combinatie RR-RV vindt zijn wiskundige formulering hierin, dat men met een ‘-’ genoegen moet nemen waar een ‘+’ zou zijn vereist. | |||||||||||||||||||
[pagina 80]
| |||||||||||||||||||
Samenvatting in stellingenAfkortingen: RV: Voorrang aan verkeer van Rechts. RR: Rechts Rijden. SV: Voorrang voor Snelverkeer. Offside Priority is: RR-LV, of LR-RV. ‘This-side Priority’ is: RR-RV. of LR-LV. LV: Voorrang aan verkeer van Links. LR: Links Rijden.
|
|