Streven. Jaargang 2

[p. 268]

Niet-Euclidische Meetkunde
door Prof. Dr G. Verriest

WAT is de niet-Euclidische meetkunde, en welk is haar betekenis in de zuivere wiskunde en voor de studie der natuurverschijnselen? Deze vragen zullen we trachten te beantwoorden op een wijze, die voor iedere intellectueel begrijpelijk is.

De elementen van Euclides

De klassieke meetkunde is een logische wetenschap; zij gaat uit van een zeker aantal uitspraken die als evident beschouwd worden en gaat dan uitsluitend verder met behulp van de zuivere logica.

De oudste bekende systematische opbouw der meetkunde is in de 'Elementen' van Euclides (± 300 v. C.) te vinden. Euclides legt aan de grond van zijn werk tien uitspraken die men axioma's of postulaten^1. noemt, zoals bijv.: 'Door twee punten gaat steeds één rechte lijn', 'Dingen gelijk aan hetzelfde, zijn ook gelijk aan elkaar', enz.

Alhoewel de 'Elementen' voor het grootste gedeelte, nog na twee duizend jaar, een onaanvechtbare uiteenzetting der meetkunde blijven, zijn er toch, in dit groots monument van de menselijke geest, onbetwistbare leemten te vinden. Zo steunt bijv. Euclides, naast zijn tien axioma's of postulaten, stilzwijgend op een zeker aantal andere evidente uitspraken zonder ze uitdrukkelijk te vermelden, zoals bijv.: 'Als A en B twee punten van een rechte lijn zijn, dan is er op deze rechte lijn ten minste een punt C te vinden dat tussen A en B ligt', 'Van drie punten op een rechte lijn is er steeds één en ook niet meer dan één punt, dat tussen de beide andere ligt', enz. Het aantal axioma's waarop de meetkunde berust heeft men nu op een en twintig gebracht.

1. Vijf dezer uitspraken noemt Euclides 'Postulaten', de vijf andere noemt hij 'Axioma's'. Men heeft nooit kunnen uitmaken welk verschil in de geest van Euclides tussen deze twee begrippen bestond, zodat we nu de woorden 'Postulaat' en 'Axioma' als synoniemen gebruiken.

Het parallellen-postulaat

Onder de postulaten waarop de meetkunde opgebouwd wordt, is er een dat, alreeds sedert de oudheid, als minder evident dan de andere beschouwd werd; het is het beroemde parallellen-postulaat waarvan de formulering nogal ingewikkeld is maar hierop neerkomt: 'Uit een gegeven punt kan men slechts één lijn evenwijdig aan een gegeven rechte lijn trekken'.

[p. 269]

Eeuwenlang heeft men getracht dit postulaat te bewijzen met behulp van de andere postulaten ofwel van nieuwe axioma's die gemakkelijker aan te nemen waren dan het bedoelde postulaat. Zo heeft men bijv. aangetoond dat het parallellen-axioma bewijsbaar is indien men als axioma aanneemt dat de som der hoeken van een driehoek gelijk is aan twee rechte hoeken, maar niemand zal dit laatste postulaat als meer evident dan het parallellen-axioma beschouwen. De mislukking van de pogingen om het parallellen-postulaat met behulp van de andere axioma's te bewijzen gaf aanleiding tot het vermoeden dat dit postulaat van de andere axioma's onafhankelijk is en dat dus alle hoop om het te bewijzen moest opgegeven worden.

De niet-Euclidische meetkunde

Om deze vermoede onafhankelijkheid te toetsen hebben de wiskundigen, in het begin van de vorige eeuw, de volgende methode uitgedacht. Laat ons, zonder de andere axioma's te wijzigen, het parallellen-postulaat door het volgende vervangen: 'Uit een gegeven punt kan men meerdere lijnen evenwijdig aan een gegeven rechte lijn trekken' en bouwen we dan, in deze veronderstelling, een nieuwe meetkunde op, die we een niet-Euclidische meetkunde noemen. Indien het parallellen-axioma met behulp van andere axioma's bewijsbaar was, dan zouden de axioma's dezer niet-Euclidische meetkunde onverenigbaar zijn en, in de ontwikkeling dezer meetkunde, zou men dus vroeg of laat op een tegenstrijdigheid stuiten. Is daarentegen het parallellen-axioma uit de andere niet afleidbaar, dan is het nieuwe axioma met de andere niet strijdig en er zal geen tegenstrijdigheid in de niet-Euclidische meetkunde te vinden zijn.

Deze niet-Euclidische meetkunde werd uitgewerkt door Lobatschefsky (1793-1859) en wordt de meetkunde van Lobatschefsky of ook de hyperbolische meetkunde genoemd. Lobatschefsky stuitte op geen enkele tegenstrijdigheid, maar de mogelijkheid van een nog niet ontdekte tegenstrijdigheid bleef bestaan, zodat het vraagstuk steeds open bleef. De spitsvondigheid der wiskundigen heeft echter, om zo te zeggen, geen grenzen. Men slaagde er in tussen de klassieke meetkunde (die we nu de Euclidische meetkunde zullen noemen) en de meetkunde van Lobatschefsky een verwantschap te bepalen, in dier voege dat met elke stelling in de ene meetkunde een stelling in de andere meetkunde correspondeert en dat met een tegenstrijdigheid in de ene ook een tegenstrijdigheid in de andere zou te vinden zijn. Moest er dus in de meetkunde van Lobatschefsky een nog niet ontdekte tegenstrijdigheid bestaan, dan zou ook een tegenstrijdigheid in de Euclidische meetkunde te vinden zijn, en omgekeerd. Beide meetkunden zijn dus, uit logisch oogpunt, even betrouwbaar.

[p. 270]

Het eeuwenoud vraagstuk der onafhankelijkheid van het parallellen-postulaat was dus opgelost: dit postulaat is niet bewijsbaar.

De niet-Euclidische meetkunde had dus de rol vervuld waarvoor zij geschapen werd en kon nu onverstoord in de archieven der wiskunde rusten. Maar de wiskundigen zijn een rusteloos volk; zodra een vraagstuk opgeworpen is hebben ze noch rust noch duur zolang dit vraagstuk niet in al zijn bijzonderheden is doorpluisd, zonder zich te bekommeren of er ten slotte ook een practisch nut daarbij te verhopen is.

Lobatschefsky had dus een nieuwe meetkunde opgebouwd door te postuleren dat er door een gegeven punt meerdere lijnen evenwijdig aan een gegeven rechte lijn getrokken kunnen worden. Waarom zou men niet een dergelijke poging doen door te postuleren dat er door een gegeven punt geen enkele lijn evenwijdig aan een gegeven rechte lijn getrokken kan worden? Dit is immers ook een negatie van het parallellen-postulaat van Euclides, maar zij kan niet, zonder meer, het parallellen-axioma vervangen daar het gemakkelijk is te bewijzen, dat men steeds ten minste één parallelle door een gegeven punt aan een gegeven rechte lijn kan trekken. Dit nieuwe axioma zou dus tegenstrijdig zijn met de andere.

De wiskundigen hebben zich echter bij deze teleurstelling niet neergelegd; om toch een meetkunde zonder parallellen te kunnen opbouwen hebben ze onder de andere axioma's diegene laten vallen waarop het bewijs van het bestaan van ten minste één evenwijdige lijn berust. Dit bewijs steunt op verschillende axioma's; het is voldoende onder deze axioma's een enkele te laten vallen om het bewijs van het bestaan van ten minste één evenwijdige lijn onmogelijk te maken. De wiskundigen hebben dus een meetkunde opgebouwd waarin het postulaat van Euclides vervangen wordt door de volgende uitspraak: 'Door een gegeven punt kan men geen lijn evenwijdig aan een gegeven rechte lijn trekken' en waarbij bovendien een of meer andere postulaten van de Euclidische meetkunde ofwel verwijderd ofwel door andere postulaten vervangen werden. Volgens de postulaten die men laat vallen verkrijgt men verschillende meetkunden die men ook niet-Euclidische meetkunden noemt, en, meer bepaaldelijk, Riemannse meetkunden. Er bestaan dus verschillende Riemannse meetkunden die alle dit gemeenschappelijk kenmerk bezitten dat in een gegeven vlak dat een rechte lijn r en een punt P bevat, alle rechte lijnen die door het punt P gaan, de rechte lijn r snijden. Onder de Riemannse meetkunden is er een die, zoals we zullen zien, interessanter is dan de andere; men noemt ze de elliptische meetkunde.

De stellingen, die in de verschillende niet-Euclidische meetkunden bewezen worden, zijn nog al uiteenlopend; zo bewijst men bijv. in de hyperbolische meetkunde dat de som der hoeken van een driehoek kleiner

[p. 271]

is dan twee rechte hoeken; in de elliptische meetkunde daarentegen, is deze som groter dan twee rechte hoeken; men weet echter dat, in de Euclidische meetkunde deze som steeds gelijk aan twee rechte hoeken is.

Zoals we het zoëven zeiden, zal men zich wellicht afvragen waarom, nadat het hoofddoel bereikt was, de wiskundigen deze zonderlinge meetkunden verder opgebouwd hebben. Dezelfde vraag zou men kunnen stellen voor bijna alle nieuwe wiskundige theorieën: het streven naar de oplossing van een bepaald vraagstuk geeft soms aanleiding tot het scheppen van een nieuw begrip; met behulp van dit nieuw begrip wordt het gegeven vraagstuk volledig opgelost, maar de wiskundige bewerkt dit nieuw begrip verder, in diepte en in breedte, soms tot een grootse theorie waarin het eerste concept, dat aanleiding tot deze theorie gegeven heeft, nauwelijks te herkennen is. Om de bruikbaarheid van deze theorie bekommert zich de theoreticus niet, maar de ondervinding leert ons dat dit het vruchtbaarste middel is om ook aan de toegepaste wiskunde nieuwe werktuigen te bezorgen, werktuigen die men waarschijnlijk nooit gevonden had indien men alleen utilitairistische doeleinden nagestreefd had. Dit is ook het geval geweest met de niet-Euclidische meetkunde; het schijnt inderdaad dat de resultaten van zekere astronomische berekeningen dichter bij de waarnemingen aansluiten als men gebruik maakt van de elliptische meetkunde in plaats van de Euclidische meetkunde.

De oorsprong der meetkunde

Dit brengt ons tot het tweede punt van dit artikel: welk is de meetkunde van onze physische ruimte?

Wij hebben alle reden om aan te nemen dat onze meetkundige begrippen uit de ervaring ontstaan zijn; empyrische methoden om op het veld een rechte hoek te construeren, om de oppervlakken van twee akkers te vergelijken, enz., zijn, buiten twijfel, aan de logische opbouw der meetkunde voorafgegaan. De abstracte begrippen van rechte lijnen zonder breedte, van punten zonder dimensies, werden door de aanschouwing van dunne draden, van fijne korreltjes, ingegeven. De axioma's van Euclides, zoals 'Door twee punten gaat steeds één rechte lijn', zijn niet uit de lucht gegrepen, maar drukken het resultaat uit van een eeuwenoud contact met de dagelijkse ervaring.

Als men nu door middel van de logica deze axioma's bewerkt en onder elkaar combineert om er gevolgtrekkingen uit af te leiden die soms zo ver van de eerste beginselen verwijderd zijn dat er honderd of meer tussenstellingen nodig zijn om de afstand te overbruggen, dan verkrijgt men een gehele reeks resultaten die op de materiële voorwerpen toepasselijk zijn voor zoverre de materiële rechte lijnen en punten met de abstracte

[p. 272]

rechte lijnen en punten der meetkunde gelijkgesteld kunnen worden. Dit veronderstelt echter dat de eigenschappen van punt en rechte lijn, in de axioma's uitgedrukt, niet te ver afwijken van de eigenschappen der materiële punten en rechte lijnen, d.w.z. van de dunne draadjes en fijne zandkorreltjes, die we door de dagelijkse ondervinding kennen.

Zou het nu denkbaar zijn dat de mensheid zich zou vergist hebben in deze oereenvoudige waarnemingen? Een voorbeeld zal ons aantonen dat deze mogelijkheid niet a priori mag verworpen worden.

Veronderstellen we dat denkende wezens, zonder dikte, op een bol zouden leven, zo groot als de aardbol, maar dat zij zich slechts op een zeer beperkt gebied van deze bol, bijv. een vierkante kilometer, zouden verplaatsen. Op een bol is de kortste lijn tussen twee punten een boog van een grote cirkel. Indien deze denkende wezens zulk een boog een 'rechte lijn' noemen, dan zal de meetkunde die hun ervaring hen leert geheel met onze klassieke vlakke meetkunde samenvallen, want de afwijkingen tussen onze rechte en een boog van een grote cirkel, in een zeer klein gebied van de bol, zijn zo gering dat zij zonder uiterst nauwkeurige metingen niet waarneembaar zijn. Deze wezens zouden dus, zoals wij, een meetkunde opbouwen waarin twee punten een rechte lijn bepalen, waarin de afstand van twee elkaar snijdende rechte lijnen groeit naarmate men zich van het snijpunt verwijdert, waarin de som der hoeken van een driehoek gelijk is aan twee rechte hoeken. Maar indien zij, op zekeren dag, hun beperkt gebied konden verlaten en hun meetkunde voor de berekening van verre afstanden zouden willen gebruiken, dan zouden zij, tot hun verbazing, vaststellen dat deze meetkunde totaal onbruikbaar is: de afstand tussen twee hunner snijdende rechte lijnen begint nl. op een zeker ogenblik te verminderen, de som der hoeken van een grote driehoek overtreft aanzienlijk twee rechte hoeken, en er bestaan puntenparen, nl. de antipoden, waardoor oneindig veel rechte lijnen gaan.

Het schijnt dus niet zo absurd aan te nemen dat ook wij, die onze meetkunde op onze ervaring in een zeer beperkt gebied van het heelal opgebouwd hebben, slechts een approximatie-meetkunde zouden tot stand gebracht hebben van een andere meetkunde die de ware meetkunde van het heelal zou zijn en die, in grotere gebieden, zo sterk van onze meetkunde zou afwijken dat deze laatste voor astronomische doeleinden onbruikbaar zou zijn.

De meetkunde der physische wereld

Op het eerste gezicht schijnt het alsof de ruimte waarin wij ons bewegen meetkundige eigenschappen zou bezitten, onafhankelijk van de lichamen die zich daarin bevinden.

Beschouwen we een driehoek gevormd uit drie uiterst dunne lijnen die

[p. 273]

we practisch als geometrische lijnen zonder breedte kunnen beschouwen. Indien de physische meetkunde de Euclidische is, dan moet de som der hoeken van deze driehoek gelijk zijn aan twee rechte hoeken; is de physische meetkunde daarentegen de elliptische meetkunde, dan moet deze som groter dan twee rechte hoeken zijn. De waarde van de som van deze hoeken schijnt, voor iedereen, een eigenschap van de driehoek zelf te zijn, onafhankelijk van de materiële lichamen die zich in de ruimte bevinden, dus een eigenschap van de ruimte zelf. Deze mening is echter verkeerd; om ons hiervan te overtuigen, onderzoeken we nauwkeurig het vraagstuk.

Hoe zullen we de som der hoeken van de driehoek vormen? Dit schijnt zeer eenvoudig; we leggen op een eerste hoek A een graadboog en tekenen op zijn rand de zijden van deze hoek (ofwel we noteren de streepjes van de graduatie van de graadboog die met de zijden van de hoek samenvallen); wij verkrijgen aldus op de graadboog een hoek A' die de hoek A dekt en die dus aan deze hoek gelijk is. Dan verplaatsen we de graadboog naar een andere hoek B van de driehoek, zo dat de hoek A' tegen de hoek B ligt, en we tekenen op de graadboog een hoek B' die de hoek B dekt, en die dus aan de hoek B gelijk is; ten slotte verplaatsen we, op analoge wijze, de graadboog op de derde hoek C en we tekenen een hoek C' die de hoek C dekt en dus aan deze hoek gelijk is. De drie hoeken A', B', C', op de graadboog getekend, liggen naast elkaar, en de hoek gevormd uit de uiterste zijden is de som der hoeken A', B', en C'.

'Maar, zal de scepticus opwerpen, ik heb niet naar de som der hoeken A',B' en C' gevraagd, maar wel naar de som der hoeken A, B en C. De hoeken A', B' en C' hebben weliswaar achtereenvolgens eens de hoeken A, B en C gedekt, maar U hebt telkens de graadboog verplaatst en wie weet of daarbij deze hoeken A', B' en C' niet van grootte veranderd zijn. Ik zou echter dezelfde opwerping maken telkens wanneer U een willekeurige figuur verplaatst.'

Wat kunnen we op deze schijnbare naïeve opwerping antwoorden? We hadden misschien anders te werk kunnen gaan. Indien de driehoek ABC op een metalen plaatje getekend was, dan zouden we de hoeken uit de plaat kunnen zagen om ze dan naast elkaar te leggen, juist zoals de hoeken A', B', C', maar dit komt op hetzelfde neer want, om de hoeken A,B,C naast elkaar te leggen, moeten we ze verplaatsen, net als de hoeken A', B', C'.

Indien we nu ondervinden dat de aldus verkregen som gelijk is aan een gestrekte hoek, dus aan twee rechte hoeken, dan kunnen wij daaruit slechts besluiten dat de som der hoeken van een driehoek op een metalen plaatje getekend, nadat men ze zo verplaatst heeft dat ze naast elkaar liggen, gelijk is aan een gestrekte hoek.

[p. 274]

Hoe kunnen we vaststellen dat de hoeken A', B', C' gelijk gebleven zijn aan de hoeken A, B, C. Door ze weer in dekking met deze hoeken te brengen? Maar dit veronderstelt een nieuwe verplaatsing. Welke practische zin kan men echter hechten aan de gelijkheid van twee hoeken die op afstand van elkaar liggen? In de practijk postuleert men dat een hoek, op een vast lichaam getekend, bij een verplaatsing onveranderd blijft, maar dit postulaat is, in feite, veeleer een definitie van de gelijkheid: 'We noemen twee, op vaste lichamen getekende hoeken gelijk wanneer ze door een verplaatsing tot dekking kunnen gebracht worden'.

Indien dus de hoeken A', B', C' samen een gestrekte hoek vormen, dan is de som der hoeken A, B, C gelijk aan twee rechte hoeken, en de meetkunde van onze physische wereld is dus Euclidisch; maar we zien dat we hier niet met de zuivere ruimte te doen hebben, maar ook met zekere lichamen die we vaste lichamen noemen en die zich in deze ruimte verplaatsen. Zonder lengten of hoeken te vergelijken is er geen practische meetkunde mogelijk; om lengten of hoeken te vergelijken en te meten maken we gebruik van ijkeenheden op vaste lichamen getekend (internationale ijkmeter, enz.) en we beschouwen deze maateenheden als aan zichzelf gelijkblijvend in al haar verplaatsingen. Dit alles zal duidelijker worden door een voorbeeld.

Het schaduwbeeld van een spherische figuur

Beschouwen we een kristallen bol die op een horizontaal vlak α rust; in het middelpunt van de bol is een lichtbron. Elk donker vlekje A, op het onderste halfrond getekend, werpt een schaduwbeeld P op het vlak α; een vlekje A' op het bovenste halfrond werpt geen schaduw, maar indien we de stralen die door de punten van A' gaan tot aan het vlak α verlengen, dan begrenzen ze op dit vlak een beeld dat wij ook de schaduw van A' zullen noemen; m.a.w. we noemen schaduwbeeld van A' het schaduwbeeld van de overstaande vlek A. Beschouwen we nu een insect dat op deze bol rondloopt; zijn schaduwbeeld zal het vlak doorlopen, maar terwijl de afmetingen van het insect onveranderd blijven, zal het schaduwbeeld nu eens kleiner, dan weder groter zijn.

Veronderstellen we dat het schaduwbeeld van dit insect een denkend wezen is dat de veranderingen van zijn afmetingen zou willen nagaan. Te dien einde zou dit wezen zich voorzien van een meter, d.w.z. van het schaduwbeeld van een meter waarvan het insect zou voorzien zijn, want wij blijven, zoals de dichter, in de wereld der schaduwen: 'Je vis l'ombre d'un cocher, qui de l'ombre d'une brosse frottait l'ombre d'un carosse'. Daar het schaduwbeeld van het insect en het schaduwbeeld van de meter in dezelfde verhouding veranderen wanneer het insect, met zijn meter, het

[p. 275]

boloppervlak doorloopt, zal het schaduwbeeld van het insect de indruk hebben dat zijn eigen afmetingen onveranderd blijven.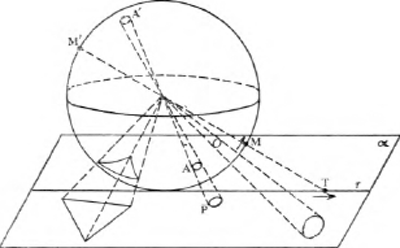

Beschouwen we nu een spherische driehoek op de bol en zijn schaduwbeeld in het vlak α. Daar de schaduwlijn van een grote cirkel een rechte lijn is, zal dit schaduwbeeld een gewone driehoek zijn. Indien we deze spherische driehoek op de bol verplaatsen, zal de driehoek die zijn schaduwbeeld is het vlak α doorlopen en zijn zijden en zijn hoeken zullen steeds van grootte veranderen. In de wereld der schaduwen echter, die het schaduwbeeld van het insect met zijn eigen schaduwinstrumenten gadeslaat, schijnt deze schaduwdriehoek onveranderd te blijven: indien nl. een zijde van de spherische driehoek twee meter lang is, d.w.z. indien een meter juist twee maal in deze zijde past, dan zal het schaduwbeeld van deze meter steeds twee maal in de schaduwlijn van deze zijde passen, en deze schaduwlijn zal dus steeds, in deze schaduwwereld, twee meter lang zijn. Hetzelfde geldt voor de hoeken; de hoeken op de bol worden nl. met een graadboog gemeten waarvan het schaduwbeeld zal dienen om de hoeken in de schaduwwereld te meten. Legt men de graadboog op een hoek van de spherische driehoek, en merkt men op deze graadboog, met twee streepjes, de zijden van deze hoek, dan zullen, in het schaduwbeeld, bij een willekeurige verplaatsing, steeds de zijden door de schaduwbeelden dezer streepjes gaan, en bijgevolg zal de schaduw van de hoek, in deze schaduwwereld gemeten, onveranderd schijnen.

Veronderstellen we nu dat een denkend schaduwwezen zou willen nagaan of de som der hoeken van een driehoek gelijk is aan twee rechte hoeken. Te dien einde zou het de drie hoeken van de driehoek naast elkaar brengen door verplaatsingen die elk dezer hoeken ten opzichte van zijn meetinstrumenten onveranderd laten. Welk zou het resultaat van dit experiment zijn?

[p. 276]

Men weet dat de som der hoeken van een spherische driehoek steeds groter is dan twee rechte hoeken. Men denke bijv. aan de driehoek gevormd uit de equator en twee op elkaar loodrechte meridianen; elk der hoeken is klaarblijkelijk recht, zodat de som der hoeken gelijk is aan drie rechte hoeken, en wanneer men, op de bol, deze hoeken naast elkaar zou leggen, zou men niet een gestrekte hoek verkrijgen maar de uiterste zijden zouden loodrecht op elkaar staan zodat de som niet 180 maar 3 × 90 graden of 270 graden zou zijn.

Wanneer men nu deze hoeken, op de bol, naast elkaar brengt, dan komen de schaduwbeelden dezer hoeken ook naast elkaar te liggen en dit na een verplaatsing waarbij deze hoeken, in de schaduwwereld, onveranderd schijnen te blijven. Daar op de bol de uiterste zijden niet een gestrekte hoek vormen, zal dit klaarblijkelijk ook in het schaduwbeeld niet het geval zijn (daar het schaduwbeeld van een gestrekte hoek op de bol een gestrekte hoek in het vlak α is, en omgekeerd), en het is gemakkelijk in te zien dat de som dezer schaduwhoeken groter zal zijn dan een gestrekte hoek. De waarnemer in de schaduwwereld zal dus besluiten: 'Wanneer men de drie hoeken van een driehoek naast elkaar legt, dan is hun som groter dan twee rechte hoeken', en, bijgevolg, zal hij zeggen: 'De som der hoeken van een driehoek is groter dan twee rechte hoeken'.

De meetkunde die deze waarnemer zal opbouwen zal dus, in veel punten van de Euclidische meetkunde afwijken; deze meetkunde zal echter volledig samenhangend zijn, want het is gemakkelijk in te zien dat elke ongerijmdheid in deze meetkunde der schaduwbeelden tot een ongerijmdheid in de meetkunde der figuren op de bol zou leiden. Deze meetkunde valt echter samen met de elliptische meetkunde waarover we hierboven gesproken hebben.

Men zal wellicht opwerpen dat deze meetkunde der schaduwbeelden een zuivere hersenschim is en dat, bijv., de som der hoeken van een driehoek groter dan twee rechte hoeken is omdat men een figuur in haar verplaatsingen als onveranderlijk beschouwt terwijl ze, in werkelijkheid, steeds van grootte verandert.

Welk is de waarde van deze opwerping? Hoe verkrijgen we het begrip der onveranderlijkheid? Keren we een ogenblik terug tot hetgeen we zoëven gezegd hebben.

De rol der vaste lichamen

In de physische wereld bestaan er lichamen die we vaste lichamen noemen. Als we zulk een lichaam verplaatst hebben, kunnen we het steeds tot zijn eerste ligging terugbrengen zo dat elk deel zijn eerste ligging nauw-

[p. 277]

keurig dekt. Daaruit zou men geneigd zijn te besluiten dat dit vast lichaam bij zijn verplaatsingen onveranderd blijft, d.w.z. dat het, bij een verplaatsing, steeds gelijk blijft aan zich zelf, maar, zoals wij het gezien hebben voor de hoeken, zou het moeilijk zijn te bepalen wat men onder deze gelijkheid verstaat. We keren dus weer de rollen om door de volgende conventie aan te gaan: 'Wij spreken af dat een figuur bij haar verplaatsingen onveranderd blijft wanneer zij zich verplaatst zoals een figuur die getekend is op een lichaam dat we, in het dagelijks leven, een vast lichaam noemen'. Deze conventie is van zuiver practischen aard en wordt ons door geen logische beschouwingen opgelegd. Het is overbodig aan te tonen dat, met deze conventie, de wiskundige studie der natuurverschijnsels veel eenvoudiger is dan bij elke andere wet van variatie der vaste lichamen die we zouden kunnen aannemen; zodra men een ijkmeter verplaatst zou men hem immers niet meer als de maateenheid mogen beschouwen; de grootte van ons eigen lichaam zou bij elke verplaatsing veranderen.

Voor het denkend wezen in de schaduwwereld daarentegen, zijn het de schaduwbeelden van de figuren op de bol die het hoofdonderwerp zijn van zijn waarnemingen. Om dezelfde reden waarom wij de vaste lichamen als onveranderlijk beschouwen, zou dit wezen de schaduwbeelden als onveranderlijk beschouwen, zodat zijn eigen lichaam, dat ook een schaduwbeeld is, en de schaduwbeelden die het omringen, bij hun verplaatsingen een onveranderlijke grootte behouden. Maar wij hebben gezien dat dit tot een geheel andere meetkunde leidt.

Met onze klassieke meetkunde kunnen we heel goed de bewegingen der schaduwbeelden nagaan en hun grootheidsveranderingen ten opzichte van onze ijkmeter berekenen. Evengoed zou het denkend wezen der schaduwwereld, met zijn elliptische meetkunde, de veranderingen in de grootte van onze vaste lichamen,^2. ten opzichte van zijn ijkmeter (schaduwbeeld van een ijkmeter op de bol) kunnen berekenen. We hebben dus daar twee verschillende meetkunden, in dezelfde ruimte, die beide dezelfde diensten kunnen bewijzen. Dit toont aan dat, bij de ruimte, niet een bepaalde meetkunde behoort. Men mag dus niet de vraag stellen of onze ruimte al of niet Euclidisch is, maar wel of de lichamen die we vaste lichamen noemen, zich op Euclidische ofwel op niet-Euclidische wijze verplaatsen, of, beter gezegd, of men de Euclidische ofwel de niet-Euclidische meetkunde verkrijgt als men de vaste lichamen bij hun verplaatsingen als onveranderlijk beschouwt.

Als nu de sterrekundigen de vaste lichamen, zoals gebruikelijk, als onveranderlijk beschouwen en gebruik maken van de Euclidische meetkunde

2. We bedoelen hier de figuren, op een vast lichaam getekend, die, bij een verplaatsing van dit lichaam, in het vlak a blijven.

[p. 278]

om zekere astronomische verschijnselen te berekenen, is het verschil tussen het berekend resultaat en het rechtstreeks waargenomen verschijnsel te groot om toegeschreven te kunnen worden aan de waarnemingsfouten die bij het gebruik van elk instrument, hoe volmaakt het ook is, onvermijdelijk zijn. Maakt de astronoom echter gebruik van de elliptische meetkunde, dan schijnt de overeenstemming beter te zijn, zodat men geneigd is aan te nemen dat de vaste lichamen zich zodanig verplaatsen dat zij aan de elliptische meetkunde voldoen, d.w.z. bijv. dat, wanneer men de hoeken van een op een plaatje getekende driehoek uitzaagt en naast elkaar legt, men een hoek verkrijgt die groter dan een gestrekte hoek is. Voor twee figuren die elkaar bij het vertrekpunt nauwkeurig dekken en die zich dan in een beperkt gebied, zoals op onze aarde, samen verplaatsen, de ene op Euclidische wijze, de andere op elliptische wijze, zou het verschil echter zo klein zijn dat zij elkaar, zelfs met onze beste instrumenten onderzocht, steeds schijnbaar nauwkeurig blijven dekken. Als men nl. met de grootste nauwkeurigheid de som der hoeken van een driehoek meet, vindt men steeds een resultaat dat zo weinig van twee rechte hoeken afwijkt dat men niet kan vaststellen of het verschil niet toe te schrijven is aan de waarnemingsfouten.

De Euclidische meetkunde zal dus, voor ons dagelijks gebruik, steeds haar eeuwenoude rol mogen vervullen.

Is de ruimte oneindig?

Om deze beschouwingen te sluiten stellen we ons nog de vraag of de oneindigheid een eigenschap der ruimte is.

Keren we terug tot het insect op de bol. Doorloopt dit insect een halve meridiaan, van M tot M', dan zal zijn schaduwbeeld de gehele rechte lijn r doorlopen van T tot het oneindige rechts om langs het oneindige links tot T terug te keren, en indien het insect de lengte van de halve meridiaan in duizend gelijke stappen aflegt, dan zal het schaduwbeeld van dit insect de gehele rechte lijn r doorlopen in duizend stappen die, voor dit schaduwbeeld, gelijk zullen schijnen; de totale lengte van de rechte r zal dus voor dit schaduwbeeld, gelijk zijn aan duizend stappen.

Hetzelfde geldt voor elke rechte lijn r die, in het vlak α door het raakpunt van de bol gaat en ook voor elke andere rechte lijn in het vlak α, want elke rechte lijn is de schaduwlijn van een halve grote cirkel van de bol. Het vlak α, dat voor de waarnemer, die de afstanden volgens de Euclidische meetkunde afmeet, oneindig is, zal dus, voor denkende schaduwbeelden, eindig zijn. Daaruit volgt dat het 'eindig zijn' of het 'oneindig zijn' niet een eigenschap van het vlak zelf is, maar dat dit afhangt van de wijze waarop de lichamen, die de waarnemer als onveran-

[p. 279]

derlijke lichamen beschouwt, zich verplaatsen. Hetzelfde geldt voor de ruimte: zij is noch eindig, noch oneindig.

Dit voorbeeld leert ons nog meer. Als het insect de meridiaan van M tot M' doorloopt, doorloopt zijn schaduwbeeld de gehele rechte r van uit T naar rechts, en tot T terug uit de linker kant, en dit in een eindig aantal stappen. De rechte r is dus een gesloten lijn van eindige lengte. Hetzelfde geldt voor elke andere rechte in het vlak α. Evenals het insect de bol in alle richtingen kan doorlopen zonder ooit op een omheining te stuiten, zo zal het schaduwbeeld het vlak α in alle richtingen kunnen doorlopen en, alhoewel dit vlak, volgens zijn begrip, eindig is, zal dit schaduwbeeld nooit tegen een grens stoten. Voor dit schaduwbeeld is de ruimte dus eindig maar grenzenloos.^3.

Zoals we gezegd hebben stroken de resultaten der berekeningen van de sterrekundigen beter met de waargenomen feiten, als men gebruik maakt van de elliptische meetkunde, d.w.z. als men veronderstelt dat de vaste lichamen, en dus ook ons eigen lichaam, zich op elliptische wijze verplaatsen. Het heelal zou dus, voor ons, eindig zijn maar zonder grenzen. Indien we ons steeds in dezelfde richting verplaatsten, zonder van de rechte lijn af te wijken, met de snelheid van het licht (nl. 300.000 kilometer per seconde), dan zouden we de gehele rechte lijn doorlopen, en dus tot ons uitgangspunt terugkomen, en dit uit de richting die we bij het vertrek de rug toe keerden, na afloop van 30 milliard jaren.

Volgens de opvatting van Lemaître zouden de afmetingen van het heelal echter niet onveranderlijk blijven. De waarnemingen tonen aan dat al de spiraalnevels zich van ons, in alle richtingen, verwijderen met een snelheid die groter is naarmate zij verder van ons af liggen. Om dit te verklaren veronderstelt Lemaître dat het heelal zich uitdijt. De snelheid dezer uitdijing zou op het huidig ogenblik zodanig zijn dat de lengte van een rechte lijn per seconde 5.000.000 kilometer toeneemt. Dit duizelingwekkend getal zal echter minder onwaarschijnlijk schijnen als men bedenkt dat dit, per kilometer, slechts een jaarlijke aanwinst van een half duizendste van een millimeter betekent.

Deze uitdijing moet echter een begin gehad hebben. Lemaître veronderstelt dat, in het begin der tijden, de gehele materie van het heelal in een enkel atoom zou geconcentreerd geweest zijn, in een ruimte waarvan de dimensies uiterst klein waren. Door splitsing van dit atoom is de uitdijing ontstaan, geremd echter door de aantrekkingskracht der materie (wet van Newton) maar anderzijds begunstigd door een repulsieve kracht der materie, die de relativiteitstheorie voorziet. De eerste kracht vermindert

3. Meer details over deze vraagstukken zijn te vinden in het vulgarisatieboekje: G. VERRIEST, Vier Voordrachten over de Wiskunde. Doornik, 1947.

[p. 280]

met de afstand, de tweede daarentegen wordt steeds groter wanneer de afstand toeneemt maar is in het begin (n.l. op afstanden gelijk aan die van de zon tot de planeten) zo gering dat ze niet waarneembaar is.

Zal de aantrekkingskracht niet op een bepaald ogenblik de bovenhand krijgen en het heelal doen terugvallen vóór dat de repulsiekracht groot genoeg zal worden? Neen, de berekeningen tonen aan dat dit gevaar sedert lang geweken is. Het kritisch ogenblik waarop deze krachten in evenwicht waren greep plaats toen de lengte van een rechte ongeveer tien maal zo klein was als nu. Sedert dien heeft de repulsiekracht de overhand en de uitdijing zet zich voort in een steeds sneller tempo. Maar op het kritisch ogenblik was het evenwicht der krachten zeer labiel, en locale storingen hebben heel goed dit evenwicht ten voordele van de aantrekkingskracht kunnen storen, zo dat, in zekere gebieden van het heelal, de algemene uitdijing met een locale inkrimping gepaard ging. Dit zou de oorsprong zijn van de sterrennevels.

Deze grootse theorie is niet een zuiver poëtische droom; zij steunt op berekeningen gebaseerd op waarnemingen.

Laat ons ten slotte opmerken dat indien het niet mogelijk is ons een ruimte voor te stellen die tegelijkertijd eindig en zonder grenzen zou zijn, het evenmin mogelijk is zich een oneindige ruimte in te beelden.