De Stijl 2 1921-1932

De beteekenis der 4e dimensie voor de nieuwe beelding¹
Henri Poincaré
Pourquoi l'espace a trois dimensions?

Les géomètres distinguent d'ordinaire deux sortes de géométries, qu'ils qualifient la première de métrique et la seconde de projective; la géométrie métrique est fondée sur la notion de distance; deux figures y sont regardées comme équivalentes, lorsqu'elles sont ‘égales’ au sens que les mathématiciens donnent à ce mot; la géométrie projective est fondée sur la notion de ligne droite. Pour que deux figures y soient considérées comme équivalentes, il n'est pas nécessaire qu'elles soient égales, il suffit qu'on puisse passer de l'une à l'autre par une transformation projective, c'est-à-dire que l'une soit la perspective de l'autre. On a souvent appelé ce second corps de doctrine, la géométrie qualitative; elle l'est en effet si on l'oppose à la première, il est clair que la mesure, que la quantité y jouent un rôle moins important. Elle ne l'est pas entièrement cependant. Le fait pour une ligne d'être droite n'est pas purement qualitatif; on ne pourrait s'assurer

1 Voor dit hoofdstuk verzamelen wij uitsluitend alle documenten die op de 4^e dimensie betrekking hebben. Als inleiding drukken wij hier, een der belangrijkste, wetenschappelijke artikelen van Henri Poincaré af.

[p. 378]

qu'une ligne est droite sans faire des mesures, ou sans faire glisser sur cette ligne un instrument appelé règle qui est une sorte d'instrument de mesure.

Mais il est une troisième géométrie d'où la quantité est complètement bannie et qui est purement qualitative; c'est l'Analysis Situs. Dans cette discipline, deux figures sont équivalentes toutes les fois qu'on peut passer de l'une à l'autre par une déformation continue, quelle que soit d'ailleurs la loi de cette déformation pourvu qu'elle respecte la continuité. Ainsi un cercle est équivalent à une ellipse ou même à une courbe fermée quelconque, mais elle n'est pas équivalente à un segment de droite parce que ce segment n'est pas fermé; une sphère est équivalente à une surface convexe quelconque; elle ne l'est pas à un tore parce que dans un tore il y a un trou et que dans une sphère il n'y en a pas. Supposons un modèle quelconque et la copie de ce même modèle exécutée par un dessinateur maladroit; les proportions sont altérées, les droites tracées d'une main tremblante ont subi de fâcheuses déviations et présentent des courbures malencontreuses. Du point de vue de la géométrie métrique, de celui même de la géométrie projective, les deux figures ne sont pas équivalentes; elles le sont au contraire du point de vue de l'Analysis Situs.

L'Analysis Situs est une science très importante pour le géomètre; elle donne lieu à une série de théorèmes, aussi bien enchaînés que ceux d'Euclide; et c'est sur cet ensemble de propositions que Riemann a construit une des théories les plus remarquables et les plus abstraites de l'analyse pure. Je citerai deux de ces théorèmes pour en faire comprendre la nature: deux courbes fermées planes se coupent en un nombre pair de points; si un polyèdre est convexe, c'est-à-dire si on ne peut tracer une courbe fermée sur sa surface sans la couper en deux, le nombre des arêtes est égal à celui des sommets, plus celui des faces, moins deux; et cela reste vrai quand les faces et les arêtes de ce polyèdre sont courbes.

Et voici ce qui fait pour nous l'intérêt de cette Analysis Situs; c'est que c'est là qu'intervient vraiment l'intuition géométrique. Quand, dans un théorème de géométrie métrique, on fait appel à cette intuition, c'est parce qu'il est impossible d'étudier les propriétés métriques d'une figure en faisant abstraction de ses propriétés qualitatives, c'est-à-dire de celles qui sont l'objet propre de l'Analysis Situs. On a dit souvent que la géométrie est l'art de bien raisonner sur des figures mal faites. Ce n'est pas là une boutade, c'est une vérité qui mérite qu'on y réfléchisse. Mais qu'est-ce qu'une figure mal faite? c'est celle que peut exécuter le dessinateur maladroit dont nous parlions tout à l'heure; il altère les proportions plus ou moins grossièrement; ses lignes droites ont des zigzags inquiétants; ses cercles présentent des bosses disgracieuses; tout cela ne fait rien, cela ne troublera nullement le géomètre, cela ne l'empêchera pas de bien raisonner.

Mais il ne faut pas que l'artiste inexpérimenté représente une courbe fermée par une courbe ouverte, trois lignes qui se coupent en un même point par trois lignes qui n'aient aucun point commun, une surface trouée par une surface sans trou. Alors on ne pourrait plus se servir de sa figure et le raisonnement deviendrait impossible. L'intuition n'aurait pas été génée par les défauts de dessin qui n'intéressaient que la géométrie métrique ou projective; elle diviendra impossible dès que ces défauts se rapporteront à l'Analysis Situs.

Cette observation très simple nous montre le véritable róle de l'intuition géométrique; c'est pour favoriser cette intuition que le géomètre a besoin de dessiner des figures, ou tout au moins de se les représenter mentalement. Or, s'il fait bon marché des propriétés métriques ou projectives de ces figures, s'il s'attache seulement à leurs propriétés purement qualitatives, c'est que c'est là seulement que l'intuition géométrique intervient véritablement. Non que je veuille dire que la géométrie métrique repose sur la logique pure, qu'il

[p. *1]

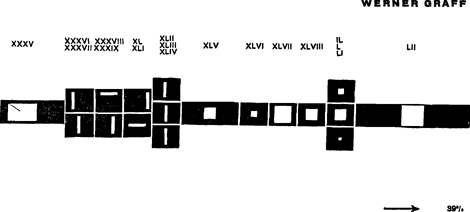WERNER GRÄFF

[p. 379]

n'y intervienne aucune vérité intuitive; mais ce sont des intuitions d'une autre nature, analogues à celles qui jouent le rôle essentiel en arithmétique et en algèbre.

La proposition fondamentale de l'Analysis Situs, c'est que l'espace est un continu à trois dimensions. Quelle est l'origine de cette proposition, c'est ce que j'ai examiné ailleurs, mais d'une façon très succincte et il ne me semble pas inutile d'y revenir avec quelques détails afin d'éclaircir certains points.

L'espace est relatif; je veux dire par là, non seulement que nous pourrions être transportés dans une autre région de l'espace sans nous en apercevoir (et c'est effectivement ce qui arrive puisque nous ne nous apercevons pas de la translation de la Terre), non seulement que toutes les dimensions des objets pourraient être augmentées dans une même proportion, sans que nous puissions le savoir, pourvu que nos instruments de mesure participent à cet agrandissement; mais je veux dire encore que l'espace pourrait être déformé suivant une loi arbitraire pourvu que nos instruments de mesure soient déformés précisément d'après la même loi.

Cette déformation pourrait être quelconque, elle devrait cependant être continue, c'est-à-dire être de celles qui transforment une figure en une autre figure équivalente au point de vue de l'Analysis Situs. L'espace, considéré indépendamment de nos instruments de mesure, n'a donc ni propriété métrique, ni propriété projective; il n'a que des propriétés topologiques (c'est-à-dire de celles qu'étudie l'Analysis Situs). Il est amorphe, c'est-à-dire qu'il ne diffère pas de celui qu'on en déduirait par une déformation continue quelconque. Je m'explique en employant le langage mathématique. Voici deux espaces E et E'; le point M de E correspond au point M' de E'; le point M a pour coordonnées rectangulaires x, y et z; le point M' a pour coordonnées rectangulaires trois fonctions continues quelconques de x, d'y et de z. Ces deux espaces ne diffèrent pas au point de vue qui nous occupe.

Comment l'intervention de nos instruments de mesure, et en particulier des corps solides donne à l'esprit l'occasion de déterminer et d'organiser plus complètement cet espace amorphe; comment elle permet à la géométrie projective d'y tracer un réseau de lignes droites, à la géométrie métrique de mesurer les distances de ces points; quel rôle essentiel joue dans ce processus la notion fondamentale de groupe, c'est ce que j'ai expliqué longuement ailleurs. Je regarde tous ces points comme acquis et je n'ai pas à y revenir.

Notre seul objet ici est l'espace amorphe qu'étudie l'Analysis Situs, le seul espace qui soit indépendant de nos instruments de mesure, et sa propriété fondamentale, j'allais dire sa seule propriété, c'est d'être un continu à trois dimensions.

(Dernière Pensées)