Spektator. Jaargang 4

[p. 347]

Gek bij Elsevier
H. Brandt Corstius

1. Inleiding

In ‘Elseviers Weekblad’ verschijnt elke week van het academisch jaar de rubriek ‘Hora est’, waar de promoties van ëën week in vermeld worden. Die rubriek is ruim opgezet. Waar in kranten een promotie hoogstens 10 cm² krijgt, is hier 30 cm² geen uitzondering. Het opvallendste van de rubriek is echter de maniakale wijze waarop aan elk promotiebericht een andere syntactische vorm wordt gegeven. Dat uit zich op vele manieren, maar wij willen in het onderstaandee alleen ingaan op de volgordes waarin de zes onderdelen van elk promotiebericht gezet zijn. Elk normaal mens (en de universiteiten die de berichten aan de samensteller(s) van de rubriek ‘Hora est’ stuurden) zou in de loop van ëën jaar twee of drie verschillende volgordes hanteren. Maar in ëën aflevering van ‘Elseviers Weekblad’ zijn soms alle volgordes verschillend. Als voorbeeld kopiëren we de eerste aflevering van de rubriek (week 1) van het jaar 1973/74 op p. 355.

Als alle mogelijke volgordes (en alle 720 volgordes van de zes hoofdbestanddelen zijn in principe mogelijk) even vaak gebruikt waren, was er verder weinig over te zeggen. Maar de samensteller (we houden verder het enkelvoud aan) heeft zich kennelijk toch door syntactische restricties laten weerhouden: sommige volgordes komen veel vaker voor dan andere. Wij willen proberen achter die restricties te komen: regels op te stellen die enigszins voorspellen hoe in het komende academische jaar de promotieberichten van ‘Hora est’ er uit zullen zien. Grondgedachte is daarbij dat een stukje generatieve grammatica niet moet letten op het al dan niet voorkomen van bepaalde syntactische patronen (dan zou voor ons materiaal een adequate grammatica niet mooi worden), maar op de frequenties van de syntactische patronen: die frequentieverdeling kan ons informatie geven over de syntactische wetten, die zich dan ook uiten in het al dan niet voorkomen van bepaalde patronen. Daarom zijn optionele transformaties met ‘gewichten’ gebruikt, getallen tussen 0 en 1 die aangeven hoe groot de kans is dat de optionele transformatie inderdaad wordt toegepast.

2. Het materiaal

In het universitaire jaar 1973/74 verschenen van 8 september 1973 (week 1) tot 6 juli 1974 (week 44) afleveringen van de rubriek ‘Hora est’ in ‘Elseviers Weekblad’. Van deze 44 weken hebben wij 22 afleveringen kunnen bemachtigen, die tezamen 313 promotieberichten bevatten (namelijk de weken 1, 2, 4, 6, 7, 14, 18, 25 t/ m 29, 32 t/ m 41). We hebben dus ongeveer de helft van de promotieberichten uit ëën jaar verzameld. Twee van de 313 bleken onbruikbaar, ëënmaal omdat (in de 2e van week 14) de promotiedatum ontbrak, en ëënmaal (in de 14e van week 41) omdat de faculteit ontbrak. Enkele van de berichten behelsden dubbelpromoties (bijvoorbeeld de 6e van week 37) die echter, door het gebruik van het woord ‘respectievelijk’ de structuur van een simpele promotie hadden, en ook als zodanig geteld werden.

[p. 348]

In het materiaal heerst een orgie van synoniemen; zo wisselen ‘proefschrift’, ‘verhandeling’ en ‘dissertatie’ elkaar af. Maar de variatie door permutatie van de informatieve bestanddelen is, zoals gezegd, het opvallendst.

De berichten zijn door een ster van elkaar gescheiden. Er is, behalve natuurlijk de met de tijd voortlopende promotiedata, geen hogere structuur aanwezig. Waar dat door het gebruik van ‘ook’ of ‘tevens’ wel zo lijkt, blijkt dat de volgorde van de promotieberichten in ëën aflevering (door een ander?) wordt gewijzigd. Zo moet het ‘tevens’ in bericht 12 van week 2 terugslaan op bericht 8 van die week, waar dezelfde promotor optreedt. Wij zien van een hogere structuur af: ons materiaal bestaat uit 311 promotieberichten. Die worden elk gereduceerd tot een permutatie van de zes elementen D, F, N, T, P en U. De keuze van deze zes hoofdbestanddelen komt nu aan de orde:

3. D, F, N, P, T, en U

In elk promotiebericht onderscheiden we zes elementen:

D	de datum van de promotie
F	de faculteit waarin de promotie plaats vond
N	de naam, leeftijd en woonplaats van de gepromoveerde
P	de promotor(es)
T	de titel van het proefschrift
U	de universiteit waar de promotie plaats vond.

Hoewel in N drie elementen zijn aan te wijzen: naam, leeftijd en woonplaats staan ze altijd in die vaste volgorde naast elkaar zodat we ze als ëën element kunnen beschouwen.

Opvallend afwezig is de persoonsvorm. Als de zes genoemde elementen in ëën zin staan is de plaats van de persoonsvorm meestal direct te bepalen (namelijk de tweede positie). Maar een promotiebericht kan best uit meer dan ëën zin bestaan. Hoewel dat in strijd is met alle taalkundige gewoontes maken wij daar geen punt van: wij zijn alleen geinteresseerd in de volgorde waarin de zes elementen in het bericht staan. In hoeveel hoofd- en bijzinnen het bericht is opgedeeld, welk element onderwerp is (meestal N natuurlijk) wordt verwaarloosd. In de persoonsvorm (‘promoveerde’, ‘ontving (de doctorsgraad)’, ‘trad (als promotor) op’) zit ook nooit enige informatie verborgen; dat wil zeggen: in een rubriek die alleen promotieberichten bevat. Het begrip ‘syntactisch’ leze men dus verder steeds als ‘grof syntactisch’ of als: ‘op de volgorde van de zes elementen betrekking hebbende’.

Als voorbeeld geven we de zes-letter-karakteristieken van de negen promotieberichten uit week 1 (zie p. 355):

1	UDFNTP	4	DNUFTP	7	TNFUDP
2	NFUDTP	5	TNDFUP	8	FUDNTP
3	FDUNTP	6	PDUNFT	9	NDUFTP

Het isoleren van de zes elementen levert nooit moeilijkheden op. D, F, T en U hebben meestal de vorm van een voorzetselbepaling, N is een zelfstandignaamwoordsgroep, en P heeft vele varianten. Met deze P wordt in de volgende paragraaf afgerekend:

[p. 349]

4. P

Wie de zes-letter-karakteristieken van de 311 promotieberichten bekijkt ziet direct dat de P er buiten staat: meestal staat hij aan het eind, een enkele keer vooraan; hoogst zelden tussen andere elementen in. Daar de P. in een aantal (Belgische) promotieberichten ontbreekt en hij syntactisch van weinig belang is, laten we hem verder buiten beschouwing. Dit heeft bovendien het voordeel dat de overblijvende vijf elementen meestal wel in ëën zin staan.

De vijf elementen kunnen in 1x2x3x4x5=120 verschillende volgordes staan. In tabel 1 zijn deze 120 volgordes in alfabetische ordening opgegeven met achter elke vijf-letterkarakteristiek het aantal keren dat een van de 311 promotieberichten die volgorde aanhield (het getal 0 is weggelaten). Het is deze tabel die als grondslag dient voor onze nu volgende analyse. We zoeken naar regels die niet zozeer het al of niet voorkomen van bepaalde permutaties verklaren, maar die over de frequenties van alle 120 volgordes iets zeggen.

DFNTU	FDNTU	NDFTU	TDFNU	UDFNT 17
DFNUT	FDNUT	NDFUT 1	TDFUN	UDFTN 1
DFTNU	FDTNU	NDTFU	TDNFU	UDNFT 10
DFTUN	FDTUN	NDTUF	TDNUF 1	UDNTF 3
DFUNT	FDUNT 11	NDUFT 44	TDUFN 3	UDTFN
DFUTN	FDUTN	NDUTF 6	TDUNF	UDTNF 1
DNFTU	FNDTU	NFDTU	TFDNU	UFDNT 1
DNFUT	FNDUT 11	NFDUT 8	TFDUN 1	UFDTN
DNTFU	FNDTU	NFTDU	TFNDU	UFNDT
DNTUF	FNTUD 2	NFTUD 3	TFNUD	UFNTD
DNUFT 18	FNUDT 9	NFUDT 17	TFUDN	UFTDN
DNUTF 2	FNUTD	NFUTD	TFUND	UFTND
DTFNU	FTDNU	NTDFU	TNDFU 2	UNDFT 25
DTFUN	FTDUN	NTDUF 3	TNDUF 32	UNDTF 5
DTNFU	FTNDU	NTFDU 2	TNFDU 5	UNFDT 1
DTNUF	FTNUD	NTFUD	TNFUD 11	UNFTD
DTUFN	FTUDN	NTUDF 2	TNUDF 11	UNTDF
DTUNF	FTUND	NTUFD	TNUFD 1	UNTFD
DUFNT 4	FUDNT 6	NUDFT 9	TUDFN	UTDFN
DUFTN	FUDTN	NUDTF 3	TUDNF 1	UTDNF
DUNFT 14	FUNDT 3	NUFDT	TUFDN	UTFDN
DUNTF 1	FUNTD	NUFTD	TUFND	UTFND
DUTFN	FUTDN	NUTDF	TUNDF	UTNDF
DUTNF	FUTND	NUTFD	TUNFD	UTNFD

TABEL 1 Frequenties van de 120 volgordes

Daar onze regels de vorm van (grove) optionele permutatie-transformaties met gewichten zullen hebben, moeten we eerst vaststellen wat we als de dieptestructuurvolgorde nemen:

5. ≠ NDUFT ≠

We zouden elk van de 120 volgordes als standaardvolgorde kunnen nemen, maar er is er ëën die zich duidelijk als zodanig aanbiedt. De hoogste frequentie van de 41 voorkomende types heeft de volgorde NDUFT (onderwerp, bepaling van tijd,

[p. 350]

bepaling van plaats, ‘faculteitsbepaling’ en ‘titelbepaling’). Maar een andere opstelling van de gegevens levert deze volgorde nog overtuigender. In tabel 2 op p. 351 zijn de dertig bigrammen van de zes elementen D, F, N, T. U en ≠ (de ≠ is het teken voor de begrenzing vóór en achter een vijf-letter-karakteristiek) aangegeven. Verticaal staan daar de eerste elementen van elk bigram en horizontaal de tweede. Men leest uit deze tabel bijvoorbeeld af dat het bigram FD de frequentie 30 heeft: 30 maal volgde in een promotiebericht een D direct op een F. De gutallen in de horizontale rij achter ≠ geven aan hoe vaak D, F, N, T en U als eerste optraden; de verticale kolom getallen onder ≠ hoe vaak ze als laatste element optraden. De tabel heeft de bijzonderheid dat de maxima van de zes kolommen samenvallen met de maxima van de zes rijen. Daarom kunnen we de basisvolgorde ook trachten te vinden door eerst te zoeken welk element het vaakst op de ≠ volgt. Dat is de N. Dan kijken we wat het vaakst op de N volgt: de D; en wat het vaakst op de D volgt: de U; op de U volgt het vaakst de F; op de F volgt het vaakst de T, en op de T volgt het vaakst de ≠. De rij van maximale bigramman ≠NDUFT≠ is een toegestane volgorde. De bigrammen uit tabel 2 kunnen we de ‘gerichte affiniteiten’ noemen. Op eenvoudige wijze is uit die tabel af te leiden hoe de tabel van de (ongerichte) affiniteiten tussen paren elementen er uit ziet: door optelling van de paren getallen die ten opzichte van de diagonaal gespiegeld liggen. Het affiniteitsgetal maakt duidelijk hoe vaak twee elementen naast elkaar staan, in willekeurig welke volgorde. Maximale affiniteit hebben T en ≠ (namelijk 277) en D en U (namelijk 251). De affiniteiten geven ons wel aanwijzingen omtrent de op te stellen regels, maar niet voldoende (let bijvoorbeeld op de behandeling van N in § 9 die alle bigrammen verstoort).

Als enige basis-regel nemen we dus de herschrijfregel:

(0) S➙≠NDUFT≠

Alle andere volgordes willen we met optionele permutatie-transformaties hieruit afleiden. In de volgende vier paragrafen doen we dat. Een ander zou het wellicht anders doen. Onze oplossing werd pas bereikt na het proberen van vele andere benaderingen. Een alternatief moet met onze oplossing concurreren op 1) kortheid van beschrijving (wij gebruiken 4, of 5, transformaties en twee gewichten) en 2) voorspellende waarde. Hier komen we in § 10 op terug.

6. T en ≠

Met T willen we hetzelfde doen als met P in § 4. Van de 41 (op de 120 mogelijke) typen in tabel 1 die een positieve frequentie hebben zijn er 28 die T in eerste of laatste positie hebben. Dat lijkt onvoldoende reden om te postuleren dat T altijd naast ≠ staat. Maar naar de frequenties kijkend is dat wel geoorloofd: 277 van de 311 tekens hebben T initiëel of finaal. De affiniteit tussen T en ≠ is groter dan van enig ander paar. Bovendien blijkt er een overeenstemming tussen de voorkomens van ≠;Tx≠; en ≠;xT≠ (waarbij x een permutatie is van DFNU): Op één geval na (NUFD) komt ‡Tx‡ alleen voor als ‡xT‡ voorkomt. Onze transformatie wordt dus:‡xT‡ ➙≠Tx≠. Aangezien het de eerste transformatie is die we opstellen (en de transformaties geordend zullen zijn) kunnen we hier x door de basisvolgorde DNUF vervangen. We willen de optionele transformatie een getal meegeven dat de kans aangeeft dat hij wordt toegepast. Op grond van onze gegevens (68 berichten

[p. 351]

hebben de vorm ‡Tx‡ en 209 Je vorm ‡xT‡) kiezen we als 1/4. Onze eerste transformatie is:

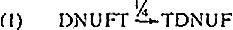
De vooropplaatsing van T blijkt niet afhankelijk te zijn van de (soms aanzienlijke) iengte van T.

We gaan nu verder met de 48 vijf-letter-karakteristieken die T vooraan of achteraan hebben (en waarvan er 28 een positieve frequentie hebben) met de hoop dat de syntactische restricties die we daarin ontdekken ook gelden voor de in frequentie veel geringere overige typen, en dat de plaats van de T geen grote invloed heeft op de plaats van de overige elementen.

Na eliminatie van T blijven D, F, N en U over. Bestudering van tabel 1 maakt het aannemelijk dat de N apart behandeld kan worden (§ 9) en dat van D, Fen U de F tegenover het paar D, U staat. We beginnen met F:

7. F en (D en U)

Wanneer we de T en N uit de vijf-letter-karakteristieken weglaten valt het op dat F niet tussen D en U in wil staan. Ook bij de dertien types waar T niet aan een uiteinde stond, en die we verwaarloosden, is dat het geval. De gevallen waar DFU toch voorkomt zijn vaak te interpreteren als een U die onder een F hoort (‘aan de faculteit F van de universiteit U’); maar niet in bericht 5 van week 1 op p. 355! De bepalingen van tijd en plaats worden niet graag gescheiden door de ‘faculteltsbepaling’.

Als we de onderlinge volgorde van D en U uitstellen tot de volgende paragraaf, dan hoeven we voor het bepalen van het gewicht waarmee F vóór of achter DU of UD komt, alleen te kijken naar de frequenties van Fy en yF (waarbij y een permutatie is van DU). Uitgaande van de basisvolgorde DUF hebben we dus een regel nodig die deze volgorde omzet in FDU. Gezien de frequenties en onze voorliefde voor gewichten 1/2 en 1/4 opteren we voor de transformatie:

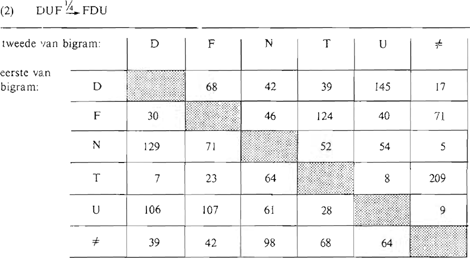
tabel 2 Affiniteiten tussen de elementen

[p. 352]

8. D en U

D en U vertonen grote affiniteit (alleen die tussen T en ‡ is groter. De vier volgordes van de drie elementen D, F en U waarbij de F niet tussen D en U in staat, zijn qua frequentie het best te benaderen door de transformaties:



waardoor de verhouding DUF:UDF:FUD:FDU dan wordt als 4:2:1:1. Maar omdat we in de vorige paragraaf F geheel isoleerden kunnen we dat niet doen. In plaats daarvan kiezen we voor de verhouding DU/UD de simpele transformatie:



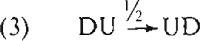
die in combinatie met regel (2) de vier volgordes geeft in de verhouding 3:3:1:1. Essentiëel is dat (3) pas toegepast wordt als (eventueel) regel (2) is toegepast. Immers, (2) eist de volgorde DU om de F te kunnen verplaatsen. De nummering van de transformaties is dus een wezenlijke.

Precieser analyseren zou ook een samenhang van de tegenstelling DU/UD met de plaats van de N opleveren. Maar wij behandelen nu N geheel apart:

9. N

In de basisvolgorde NDUFT is met (1) aan T de vrijheid geschonken om vooraan te gaan staan, met (2) en (3) worden D, F en U gepermuteerd. Nu mag de N in de aldus ontstane rij NXYZ (waarbij XYZ een permutatie is van DFU) nog 1, 2 of 3 plaatsen naar rechts opschuiven. Om de frequenties in ons materiaal zo goed mogelijk te benaderen (bij onze beperkte keuze van gewichten) leken de volgende transformaties het beste:

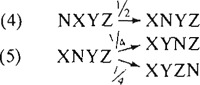
Deze twee, of drie (of men regel (5) als één of twee transformaties wil tellen is een kwestie van smaak) transformaties zorgen dat N op de eerste, tweede, derde en vierde plaats komt te staan (afgezien van T) in de verhouding 4:2:1:1. In ons materiaal is die verhouding 141:65:28:43.

Regel (5) kan alleen toegepast worden als (4) werd toegepast. Het is niet mogelijk om regel (5) in tweeën te splitsen, omdat de resulterende frequenties dan anders worden.

Hiermee zijn de optionele transformaties met gewichten voltooid. Welke claim leggen we daar nu mee?

[p. 353]

theoretische frequentie (op 256)	echte frequentie (op 277)
DFNU 0	0
DFUN 0	0
DNFU 0	0
DNUF 24	19
DUFN 12	7
DUNF 12	14
FDNU 4	0
FDUN 4	12
FNDU 8	11
FNUD 8	9
FUDN 4	6
FUND 4	3
NDFU 0	3
NDUF 48	76
NFDU 16	13
NFUD 16	28
NUDF 48	20
NUFD 0	1
UDFN 12	17
UDNF 12	11
UFDN 0	1
UFND 0	0
UNDF 24	25
UNFD 0	1

tabel 3 Theoretische en echte frequenties van permutaties van DFNU

10. Wat de regels claimen

Recapitulerend stellen we deze regels voor:

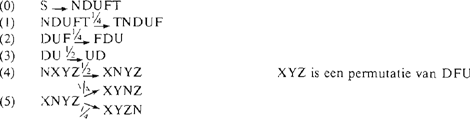
Natuurlijk leveren deze regels niet precies ons materiaal op. Ze genereren 32 verschillende types. Om een vergelijking te maken tussen de theoretische en de echte waarde hebben we op 256 basisvolgordes de transformaties toegepast (de kleinste verkregen frequentie is dan 1). In tabel 3 vindt u de theoretische en de echte waarden van de frequenties van de 24 permutaties van DFNU.

De gewichten zijn voor precisering vatbaar, maar ook al zouden ze alle exact zijn, dan betekent dat nog in het geheel niet dat de combinatie van de vier transformaties precies het materiaal oplevert.

Wat claimen we wel met onze regels? We claimen dat de samensteller van ‘Hora est’ het volgend jaar best een heel andere frequentieverdeling over de 120 mogelijkheden kan laten zien maar dat:

[p. 354]

0)	de hoogstfrequente volgorde NDUFT zal zijn;
1)	in 90% van de gevallen de T initiëel of finaal zal zijn;
2)	F slechts bij 2% tussen D en U in zal staan;
3)	er geen groot verschil tussen de volgordes DU en UD zal zijn;
4)	de volgorde NXYZ frequenter zal zijn dan XNYZ;
5)	de volgorde XNYZ frequenter zal zijn dan XYNZ en dan XYZN.

Laat wie dit leest zorgen dat de samensteller van ‘Hora est’ niet gewaarschuwd wordt. Mocht de rubriek ingrijpend veranderen dan zijn onze claims ook te testen op de andere helft van het academische jaar 1973/74, of op voorgaande jaren; maar dat zal op een argwanende lezer minder indruk maken.

11. Invloed van de primaire bron

De rubriek ‘Hora est’ moet gebaseerd zijn op de berichten die de voorlichtingsdiensten van de universiteiten naar de pers toesturen. Het zou denkbaar zijn dat de stijl daarvan bepaalt hoe het bericht in ‘Elseviers Weekblad’ kwam. In die voorlichtingsberichten ontbreekt het element U in elk afzonderlijk promotiebericht.

Van de Universiteit van Amsterdam konden we de primaire bron voor de samensteller van ‘Hora est’ zien, en we slaagden er niet in enige invloed op de Amsterdamse promotieberichten te vinden.

[p. 355]

[p. 356]

12. Stijl

Er bestaan twee diametrale opvattingen over wat stijl is. In de eerste opvatting (J.P. Thorne: ‘Generative grammar and stylistic analysis’ in J. Lyons (ed.): ‘New horizons in linguistics’, Pelican book, 1970) wordt stijl gezien als de wijze waarop in een tekst de dieptestructuren elkaar opvolgen. In de tweede opvatting wordt stijl gezien als de individuele wijze waarop een schrijver de optionele transformaties vaker of minder vaak dan normaal toepast. De waarheid ligt niet in het midden tussen deze twee opvattingen, maar in een combinatie van beide. Ook is het mogelijk dat bij de ene schrijver (Hemingway) de eerste, en bij de andere schrijver (Vestdijk) de tweede methode vruchtdragend is. Bovendien zijn er nog stijlkenmerken die onder geen van beide vallen.

Bij onze promotieberichten is de stijl volgens de eerste opvatting uiterst monotoon: 311 maal dezelfde dieptestructuur. De samensteller van ‘Hora est’ moet de door hem zozeer gewenste afwisseling dan ook bereiken door het toepassen van optionele transformaties. Dat hij bij die maniakale zucht tot variatie toch gebonden blijkt aan bepaalde regels hopen we in het bovenstaande aangetoond te hebben.

Voor een meer zinvol stijlonderzoek zouden van een aantal optionele transformaties de ‘normale’ gewichten bekend moeten zijn, waarna bepaald kan worden in hoeverre een bepaald stuk proza andere gewichten vertoont. Pas dan kunnen uitspraken als ‘Die schrijver gebruikt veel passieve zinnen’, ‘Die schrijfster gebruikt veel inversies’ exact gemaakt worden.

Voor de samensteller van ‘Hora est’ geldt ongetwijfeld dat hij alle optionele transformaties overmatig zwaar gebruikt.

13. Gewichten bij optionele transformaties

Sta ons toe dat we nu van de wij-vorm in de ik-vorm overga. Al jaren bepleit ik grammaticale regels van getallen te voorzien, al weet ik ook niet precies hoe. Bij optionele transformaties lijkt het redelijk om ze een gewicht tussen de 0 en de 1 mee te geven, dat de kans aangeeft dat hij zal worden toegepast. Verplichte transformaties worden daarmee tot grensgevallen van optionele transformaties, namelijk die met het gewicht 1. Bij de opstelling van transformaties (en de bepaling van hun volgorde) kan dat geven van gewichten invloed hebben (zie de paragrafen 7, 8 en 9). Als het gewicht afhankelijk is van een bepaalde eigenschap van de structurele beschrijving, dan moet de optionele transformatie opgesplitst worden in meerdere transformaties die allemaal dezelfde structurele verandering bewerkstelligen, maar met verschillende gewichten.

Bij de kleine hoeveelheden materiaal die ik had heeft het weinig zin om de gewichten met grote precisie te bepalen. Bewust beperkte ik me tot twee gewichten (1/2 en 1/4), waarmee overigens door herhaling elke breuk bereikt kan worden. Een concurrerende oplossing zou liefst met evenveel gewichten (eventueel andere: 1/3 en 2/3) moeten werken.

Pas na omvangrijke taaltellingen heeft het zin de gewichten precies te bepalen, en krijgt het zin om van significante afwijkingen te spreken. Ik heb geen statistiek gebruikt.

Amsterdam, 15 juli 1974