De Revisor. Jaargang 25

(1998)– [tijdschrift] Revisor, De– rechtenstatus



[pagina 130]
Gerrit Krol Formalistische grappen Wiskunde is de wetenschap van het ware. Ze doet uitspraken die onder alle omstandigheden waar zijn. De stelling van Kuhn dat de wetenschap zich van tijd tot tijd schikt naar een nieuw paradigma, waardoor oude kennis moet worden herzien en herroepen, geldt niet voor de wiskunde. Eenmaal bewezen, altijd waar. Wiskunde is tijdloos. Wie wiskunde bedrijft, ‘beitelt aan de eeuwigheid’. Hij maakt dingen die er voordien niet waren en doet daarover uitspraken die waar zijn. Wiskunde is een uitvinding. Anderen zeggen: wiskunde is een ontdekking. Want wiskunde is waarheid, en waarheid vind je niet uit, maar ontdek je. Wiskunde is een taal, vinden weer anderen, en een taal is een uitvinding. Wiskunde, zeggen nog weer anderen, is cumulatief en consistent: nooit zal een bewezen stelling het veld hoeven ruimen voor een andere stelling. Wiskunde is, nogmaals, invariant onder de Kuhntransformatie. Toch heeft ook de wiskunde haar revoluties gekend. Zo is na de uitvinding van de niet-Euclidische meetkunde rond 1830, door o.a. Lobatsjefsky, de wiskunde langzaam overgegaan van een aanschouwelijke wetenschap in een conceptuele wetenschap. In de aanschouwelijke wiskunde heeft het oog nog een stem; ook zonder bewijs zie je dat iets waar is. In de conceptuele wiskunde kun je niet meer op je oog vertrouwen. Dat komt doordat in de conceptuele wiskunde - om een voorbeeld te noemen - het woord ‘lijn’ niet langer alleen maar lijn hoeft te betekenen en ‘evenwijdig’ niet langer alleen maar evenwijdig. Als je meetkundige stellingen bewijst, kijk je niet langer naar de figuur, maar naar de woorden die deze figuur beschrijven. Woorden worden tot symbolen, tot formules, die je kunt manipuleren als onderdelen van een machine. Om te kunnen worden begrepen, moet het bewijs tot op het bot worden ontleed, ontdaan zijn van elke visuele suggestie. Het ideale bewijs is een reeks formules die feilloos door een automaat kunnen worden begrepen en getoetst. Zo'n automaat werd gesuggereerd, in 1899, door David Hilbert, die daartoe de hele Euclidische meetkunde had geformaliseerd. De automaat bestond uitsluitend op papier, de mens zelf kan immers heel goed voor automaat spelen. Hilbert beweerde dat de symbolen die hij gebruikte stuk voor stuk zo eenduidig waren, zozeer blindelings door ‘het apparaat’ werden begrepen, dat het geen verschil maakte of je er nu punten, lijnen en vlakken mee bedoelde, dan wel, zoals hij zei, ‘stoelen, tafels en bierpullen’ - dat maakte niets uit.
[pagina 131]
Als je in het Euclidische, parabolische parallellenaxioma het getal 1 vervangt door 2, of 3, of 4, krijg je het hyperbolische parallellenaxioma: gegeven een punt en een rechte lijn, dan gaan er door dat punt minstens twee rechte lijnen evenwijdig aan de gegeven lijn. Omdat dat ook tafels en bierpullen mogen zijn, is er niets op tegen in die rechte lijnen halve cirkels te zien, met hun middelpunten op een rechte lijn. Noem deze rechte lijn ‘de horizon’. 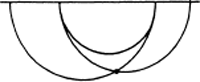Evenwijdig zijn twee cirkels als ze elkaar op de horizon raken: Jaren geleden stuitte ik in Die Naturwissenschaften op een artikel waarin te lezen stond dat voor sommige van onze waarnemingen de hyperbolische meetkunde adequater is dan de Euclidische. Deze bewering werd geïllustreerd door een voorbeeld uit de cinematografie. Op een rechte weg rijdt een auto. Wij staan aan de rand van die weg, misschien wel met de duim omhoog. De auto rijdt ons voorbij. Hoe nemen wij die auto waar? Zet een camera voor je neus en volg de auto. Draai nu de film af, of de videoband, en je ziet dat de rechte weg op het moment dat de auto je passeert een tamelijk scherpe hoek maakt. 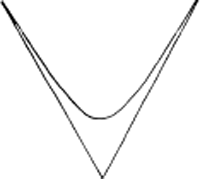De weg is getransformeerd in een hyperbool: De rechte weg maakt een hoek, omdat de camera een hoek maakt. Iets soortgelijks laat zich waarnemen langs de spoorrails.
[pagina 132]
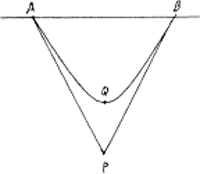
De waarnemer staat in punt P, op een rail. De andere rail, AQB, lijkt een slag te draaien. P ziet de rail AQB, hoewel verbogen, als één geheel. De rail waar hij zelf op staat kan hij niet als één zien, die ziet hij als twee verschillende rails. P zegt: ik zie door P twee rails gaan, evenwijdig aan de rail AQB. En de nieuwe wiskunde zegt: gegeven een lijn I en een punt P, dan zijn er twee lijnen door P evenwijdig aan I. Soms kun je volstaan met een enkele stelling uit de projectieve meetkunde. Wittgenstein heeft het in zijn Tractatus (3.032) over de onmogelijkheid de coördinaten aan te geven van een punt dat niet bestaat. Helaas! Het snijpunt van twee evenwijdige lijnen is zo'n punt. Het bestaat niet, maar toch kun je het zien: als het punt waar twee evenwijdige spoorstaven elkaar op de horizon snijden. Je kunt het tekenen en de coördinaten ervan laten zich berekenen. Maar het kan ook anders. We kunnen de begrippen ‘punt’ en ‘lijn’ uitbreiden tot ‘Punt’ en ‘Lijn’. Met Punt P bedoelen we voortaan: een punt of een richting en met Lijn L: een lijn of de verzameling van alle richtingen. Zo zou je allerlei uitzonderingen kunnen ondervangen. Dat verfraait de wiskunde. In het bijzonder zou je elk nieuw soort element (lijn op oneindig, wortel uit min 1), elk begrip (evenwijdigheid) een rechtmatig bestaan geven. Er zijn gevallen van uitbreiding waarmee bijna iedereen vertrouwd is. Denk aan de gewone getallen. Eerst waren er alleen de positieve gehele getallen, 1, 2, 3 enzovoort. De rest ‘bestond’ niet, 7 van 5 aftrekken ‘kon niet’. Dat verschil ‘bestond niet’. Totdat de negatieve getallen werden uitgevonden, en ook de breuken. Zo ontstond een systeem waarin allerlei uitspraken mooier waren geworden: steeds minder uitzonderingen. Op deze manier vermijd je dat dingen die eerst ‘niet bestaan’ later, door gebruik, weer wel bestaan. De wiskunde, die uitgaat van het evidente en bouwt met triviale middelen, is een methode ons te laten kennis maken met het onmogelijke - als nieuwe mogelijkheid. Zo is de wortel uit een negatief getal (bijvoorbeeld √ - 1) iets dat ‘niet kan’, omdat een kwadraat altijd positief is. We noemen het ‘imaginair’. Wat dat betekent weten we niet, maar er is plaats voor. We kunnen ermee rekenen: √ - 1 × √ - 1 = -1. We hebben nu dus twee soorten getallen. De ene soort noemen we reëel en de andere imaginair. De ene soort tekenen we op een horizontale lijn, de andere op een verticale.
[pagina 133]
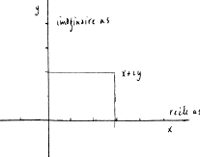
Als we √ - 1 kortheidshalve schrijven als i, geldt i² = -1. Het symbool i staat voor imaginair. Je kunt het ook tekenen, in de zojuist gedefinieerde tweedimensionale ruimte. Zo laat deze figuur reële getallen (x) zien, imaginaire getallen (iy) en combinaties daarvan, de zogenoemde complexe getallen (x + iy). In het complexe vlak zijn dingen mogelijk die in het gewone, alledaagse vlak niet mogelijk zijn. 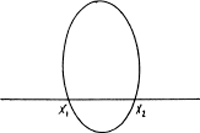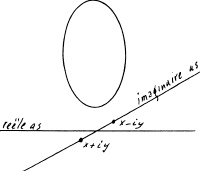Zo zien we onderstaande ellips de rechte lijn snijden in twee reële punten: Als we imaginaire getallen toelaten kunnen we beweren dat elke ellips en rechte lijn twee punten gemeen hebben, ook al schijnen ze elkaar op het oog niet te snijden:
[pagina 134]
De twee onzichtbare snijpunten laten zich lokaliseren door complexe getallen. Het tweedimensionale getal x + iy helpt ons dingen te begrijpen die we anders niet zouden begrijpen. Via de beroemde vergelijkingen van Maxwell begrijpen we nu hoe elektriciteit stroomt en hoe ze verweven is met magnetisme. Zonder het zogenaamd niet-bestaande getal i zouden we ons dat nooit goed hebben kunnen voorstellen. We hebben nu het getal i, waarmee we goed kunnen rekenen in het complexe vlak. Misschien is er, ter uitbreiding van het complexe vlak, vervolgens een getal j, waar we ook goed mee kunnen rekenen. Een getal in de vorm van het driedimensionale x + iy + jz. Naar zo'n hypercomplex getal is jaren gezocht, maar er is geen manier gevonden om het te construeren. Er was geen verband tussen i en j te bedenken, dat dit getal als het ware opspande. Wel kwam er iemand (Hamilton, 1843) voor de dag met een vierdimensionaal getal: v + ix + jy + kz, met drie imaginaire coëfficiënten i, j en k waarvoor geldt: i² = j² = k² = -1, ij = -ji = k, jk = -kj = i, ki = -ik = j. Hij noemde deze getallen quaternionen. Het zijn vierledige vectoren met wonderlijke, nooit eerder gekende rekenregels. Ze schijnen een uitstekende basis te vormen voor de quantummechanica en voor het begrip van de structuur van atomen. Als we nu, uitgaande van het evidente, langs een logische weg terechtkomen in het imaginaire, het ongehoorde en het onmogelijke - zouden we dan ook niet, uitgaande van het onmogelijke, logischerwijs kunnen terechtkomen in het evidente? Sinds Escher is de wereld goed op de hoogte van zogenoemde ‘onmogelijke figuren’. Figuren die je wel kunt tekenen, maar die je je niet kunt voorstellen als je de tekening een driedimensionale interpretatie geeft. Op papier is er meer mogelijk dan in werkelijkheid. 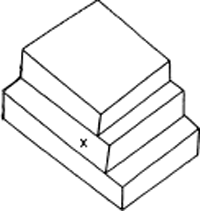Als je van deze tekening de linkerkant bekijkt, zie je twee boeken op elkaar gestapeld. Bekijk je de rechterhelft, dan zie je er drie. Dat dit mogelijk is komt doordat wi1 het vlak aangegeven met x links als
[pagina 135]
horizontaal zien en rechts als verticaal - hetzelfde vlak. Een tekening staat ons toe - en bovenstaande tekening dwingt ons ertoe - hetzelfde ding op twee elkaar uitsluitende manieren te zien. Zo kan deze tekening ons uitleggen, hoe het mogelijk is dat wij bij een correcte, wetenschappelijke verklaring van de natuur op strijdigheden stuiten. Een voorbeeld. Licht, weten we sinds Einstein - en ook eigenlijk sinds Newton -, bestaat uit deeltjes. Hoe meer deeltjes, des te meer licht. Tegelijk weten we sinds Maxwell - en ook eigenlijk sinds Huygens -, dat licht zich verspreidt zoals golven zich verspreiden wanneer je een steen in het water hebt gegooid: in de vorm van cirkels. Gooi je twee stenen in het water, dan zullen daar waar twee cirkels elkaar ontmoeten, de golven elkaar wat men noemt annihileren, daar zal het water niet bewegen. Met licht heb je dat ook. Op plaatsen waar twee keer zoveel licht valt zal het, in bepaalde omstandigheden, donker zijn. Hoe is dat te rijmen met de deeltjestheorie? Hoe kunnen twee deeltjes samen nul deeltjes zijn? Het is duidelijk dat beide visies strijdig zijn met elkaar. En toch zijn ze beide waar. Hoe is dat nou mogelijk? Heel eenvoudig, als je bedenkt dat de verklaring van een verschijnsel niet alleen bepaald wordt door het verschijnsel zelf, maar ook door de route die je, redenerenderwijs, volgt. Elke route creëert zijn eigen semantiek, zijn eigen beeldspraak. Bij de deeltjestheorie ga je bij wijze van spreken linksom, bij de golftheorie rechtsom. Je komt, links- dan wel rechtsom, uit bij hetzelfde verschijnsel, waar je verschillende verklaringen voor hebt gevonden en het is helemaal niet gezegd dat die verklaringen met elkaar in overeenstemming zijn, waarom zouden ze. Waarom zouden twee ware uitspraken elkaar niet kunnen tegenspreken? 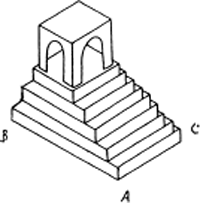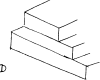Deze onlogische gedachte, waar de wetenschap zo langzamerhand mee heeft leren leven, laat zich begrijpen via een tweede illustratie: een trappenheuvel, die links (B) drie treden telt, vóór (A) vijf en rechts (C) negen. Hoe ziet nu de achterkant (D) van de heuvel eruit? Als je linksom loopt, kom je uit op twee treden:
[pagina 136]
Loopje rechtsom, dan kom je uit op 9 + 9 - 1 = 17 treden. Beide omwegen zijn correct, uiteraard, en hun uitkomsten ook. Natuurlijk, het venijn zit niet in de staart, maar in de kop - en wel in de interpretatie van het verticale/horizontale vlak. In de natuurkunde kan ons dat overkomen. Het voert ons tot de genoemde tegenstrijdigheden. We doen er ons voordeel mee. We hebben het over ‘golven die bestaan uit deeltjes’, of over ‘deeltjes met een golfkarakter’. Ook in de wiskunde overkomt het ons dat we onszelf tegenspreken (de beide figuren laten het immers zien), maar in de wiskunde dienen tegenstrijdigheden om aan te tonen datje uitgangspunten of denkmethoden fout zijn. ‘Een wiskundige interpreteert niet,’ heb ik eens geschreven. Daar was niet iedere wiskundige het mee eens. Je kunt immers de formule y = 3x + 5 interpreteren als een algebraïsche vergelijking, maar ook als een rechte lijn - twee geheel verschillende dingen, die elkaar overigens niet bijten, maar ondersteunen. Mathematische concepten en theorieën vullen elkaar aan ‘omdat het open systemen zijn’. 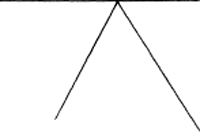(Ik heb het vermoeden dat dit de Kuhn-invariantie van de wiskunde verklaart.) De wiskunde bestaat uit elementen als lijnen, cirkels, getallen en klassen enerzijds, en stellingen, uitspraken, bewijzen, waarheid anderzijds. Zowel elementen als stellingen kunnen ons voorkomen als evidenties. Dat 2 + 2 gelijk is aan 4 is evident - als je kunt tellen. Dat de twee scherpe hoeken in gelijk zijn is evident. De gewone, Euclidische meetkunde neemt een aantal evidenties als axioma's (onbewezen stellingen) en wordt vandaaruit opgebouwd door bewijzen. Die bewijzen overtuigen door exactheid en welbespraaktheid. En doordat je dingen ‘ziet’. 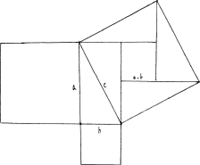Een voorbeeld. Je kunt de stelling van Pythagoras bewijzen als volgt:
[pagina 137]
Het vierkant op de schuine zijde heeft als oppervlak c². Datzelfde vierkant laat zich verdelen in vijf stukken zoals aangegeven. De vier driehoeken in dat vierkant hebben elk als oppervlakte: basis maal halve hoogte, oftewel ½ab. Gezamenlijk bedraagt hun oppervlakte: 2ab. Het vierkantje in het midden, daarvan zijn lengte en breedte: a - b. De oppervlakte van dit gebied is lengte maal breedte, oftewel (a - b)², oftewel a² - 2ab + b². Alle vijf oppervlakken samen zijn: 2ab + a² - 2ab + b² = a² + b². De oppervlakte van het geheel was c². Dus a² + b² = c². 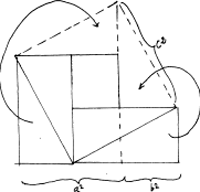Er bestaat een soortgelijk bewijs, waarbij niet gerekend hoeft te worden: Typisch een bewijs dat de informatie van de wijzende vinger nodig heeft (de pijlen). Hoe een bewijs er formeel uit moet zien, daarover zijn de wiskundigen het niet gauw eens. Ik lees (Gillies e.a., Revolutions in Mathematics): ‘Je kunt zeggen dat geen enkel bewijs uit 1800, gemeten naar de standaards van omstreeks 1900, nog geldigheidswaarde heeft. 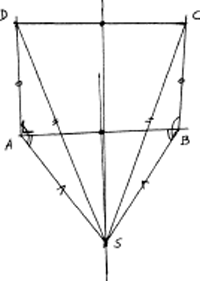De standaards van 1900 zijn, op hun beurt, vandaag al niet acceptabel meer.’ Dit lijkt me maar ten dele waar. Van de toepassingen van meetkunde op fysica is de analytische meetkunde, die stamt uit de tijd van Descartes, al eeuwenlang een bevredigende methode gebleken. De moeilijkheid zit 'm in het hanteren van begrippen als ‘binnen’, ‘buiten’, ‘tussen’, ‘links’, ‘rechts’, ‘een beetje’, en dergelijke, waarbij men aanneemt dat de getekende figuur dat wel duidelijk maakt. Een bekend geval waarin dat tot fouten leidt, volgt hier.
[pagina 138]
De hoek bij A is recht, die bij B een heel klein beetje groter. De stukken AD en BC zijn precies even lang. De middelloodlijnen van AB en CD snijden elkaar in S. Bijgevolg is AS = BS, DS = CS, en doordat ook AD = BC, zijn de driehoeken SAD en SBC congruent. Bijgevolg is hoek DAS gelijk aan hoek CBS. Omdat S op de middelloodlijn van AB ligt, is ook hoek SAB gelijk aan hoek SBA. Door optelling blijkt dat hoek DAB gelijk is aan hoek CBA. Het is ons dus niet gelukt de hoek bij B een klein beetje van de rechte hoek te laten verschillen! Waar zijn wij ontspoord? (Aanwijzing: teken de hoek bij B een stuk groter.) De redeneringen worden steeds preciezer. Woorden krimpen ineen tot afzonderlijke symbolen en, in tegenstelling tot wat je daardoor zou verwachten: de bewijzen worden steeds langer. Wat vroeger één regel in beslag nam, vraagt nu niet zelden een hele bladzijde. Deze ontwikkeling lijkt nergens, in geen enkele fase, op een revolutie, zelfs niet op een evolutie, maar - om een veel geciteerde woordspeling te gebruiken - op een sterk vergrote resolutie, een term uit de cartografie. Het gaat daarbij niet om de stelling - de waarheid daarvan staat wel vast - maar om de precieze structuur van het/een bewijs. Het handmatige formalisme van Hilbert en Russell (in zijn Principia Mathematica) is vervangen door een mechanisme dat ongevoelig is voor de betekenis van symbolen en geen last heeft van ‘bedoelingen’ - de computer. Alleen die staat garant voor de uiteindelijke juistheid en waarheid. Een geavanceerde bewijsroutine, voortgaande op de ideeën van Hubert, is het programma AUTOMATH, ontwikkeld in Eindhoven onder leiding van De Bruijn. Het heeft een buitengewoon grote resolutie; het is alsof je de Himalaya met een microscoop bekijkt. Je herkent de afzonderlijke elementen niet meer. Je ontdekt dat axioma's niet noodzakelijk evident zijn. Bijvoorbeeld, om te bewijzen dat (3 + 4) + 5 = 3 + (4 + 5) wordt uitgegaan van axioma's voor de aftrekking, hier aangeduid door voorbeelden: 3 - 0 = 3 3 - 3 = 0 3 - (4-5) = 5 - (4 - 3) en van een definitie van de optelling, aangeduid door het voorbeeld: 3 + 4 = 3 - (0 - 4) Het bewijs bestaat uit welgeteld tien stappen. En de programmeur/schrijver vervolgt: ‘We hebben bovenstaand bewijs expres al zo geformuleerd dat het een beetje gaat lijken op de
[pagina 139]
manier waarop AUTOMATH werkt. Maar het is nog lang niet precies genoeg. (...) Voor de lezer is het duidelijk dat we het derde axioma hebben toegepast op een term uit het linkerlid, en hij ziet onmiddellijk welke term het betreft. Voor een computer is dat niet zo vanzelfsprekend. (...) En dan zitten we nog met het probleem dat AUTOMATH moet gaan zoeken in de tekst naar de zinnen die bepaalde veronderstellingen waar maken.’ U ziet, het automatische bewijs graaft zich steeds dieper in. De automaat zoekt het bewijs door alle zinnen en veronderstellingen op te sporen die het bewijs hun onmisbare medewerking verlenen. Hoe geheel anders had ik mij dat voorgesteld toen ik als twintigjarige las wat je met een computer kon doen! Met een computer zou je alles kunnen bewijzen, de hele wiskunde. De wijzende vinger, de betoogtrant zou hebben plaats gemaakt voor een puur formalistische tekst, die door de computer kon worden gelezen, begrepen en goedgekeurd. De stelling van Pythagoras zou, ontdaan van alle redeneringen, slimme sluiproutes, berekeningen, hulplijnen en herhalingen, gereduceerd zijn tot zoiets als vier eieren in een kievitsnest. Het bewijs van ‘Pythagoras’, teruggebracht tot vier bits! Zoals in zekere zin de natuurkunde is teruggebracht tot de vier elementaire krachten en de ‘vier’ elementaire deeltjes: atomen, protonen, neutronen en elektronen. Het is dus geheel anders uitgekomen. Een zin is waar als hij lijkt op een andere ware zin - in woord (rijmwoord) of in beeld (rijmbeeld). Je zou dat het syllogisme van de gelijkenis kunnen noemen. Ook in de wiskunde wordt dit syllogisme wel eens toegepast. 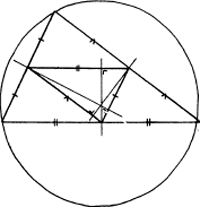De stelling dat de hoogtelijnen van een driehoek door één punt gaan, bewijs je eenvoudig door in de hoogtelijnen de middelloodlijnen van een ‘omgeschreven driehoek’ te zien, en dat die door één punt gaan zie je als je in dat punt het middelpunt van de omgeschreven cirkel ziet: Als je in iets dat je bewijzen moet iets anders ziet dat waar is, hoef je het bewijs niet meer te leveren. Ook de grote wiskundigen werken zo. Poincaré maakt melding van de relatie tussen tussen de algebraïsche functies van Fuchs Z - > (AZ + B)/(CZ + D)
[pagina 140]
en de hyperbolische meetkunde van Lobatsjefsky. ‘Tussen deze twee theorieën,’ schrijft hij, ‘ogenschijnlijk zover van elkaar verwijderd, bestaat een diepe analogie.’ Une analogie profonde. Het verschil tussen Poincaré en mij is onder andere dat hij dingen zag waar ik nooit opgekomen zou zijn. Een zin is ook waar, als wat je leest lijkt op wat je, vaak zonder het te weten, al wist en je doet verzuchten: ja, hoe waar. (Dit is meer een literaire dan een mathematische zucht. Waarom eigenlijk?) De meest elementaire uitspraak is de wet van de identiteit: a = a Ik heb altijd gedacht dat dit een typisch logische wet was, alleen toe te passen op de wiskunde. De literatuur zou er te fijn voor zijn gebouwd. Literatuur is meerduidig enzovoort. Maar juist daarom kan de literatuur wel wat ‘hardheid’ gebruiken: de syntaxis van de taal, de voorgeschreven woordvolgorde bijvoorbeeld (harder dan de bewijsregels uit de wiskunde!). En zeker ook elementen uit de logica. a = a is een logische wet, van toepassing op de gewoonte, in de literatuur, de personen een naam te geven. Die namen kunnen verzonnen zijn, maar eenmaal A blijft iemand doorgaans A heten. De ‘Arthur’ op bladzij 21 van De tranen der acacia's is dezelfde als de ‘Arthur’ op bladzij 50. Deze mogelijkheid tot identificatie draagt in sterke mate bij tot de geloofwaardigheid van een verhaal. Maar pikanter wordt dat verhaal als halverwege of aan het einde A dezelfde blijkt te zijn als B. Of als blijkt dat (De donkere kamer van Damocles) Dorbeck niemand anders is dan Osewoudt. Of als tot het einde toe niet duidelijk is wie precies deze Dorbeck was. Als iemand van P naar Q loopt en hij bevindt zich in P, dan is hij niet in Q. Eenmaal in Q is hij niet meer in P. Je kunt dit een wandelende waarheid noemen. De lijnen a en b snijden elkaar in S. Even later zie ik dat a en b elkaar niet snijden, maar kruisen, met wandelend snijpunt S. Wat je beschrijft is niet een toestand, maar een gang van zaken, of een verhaal. Een verhaal is - anders dan een wiskundig bewijs - niet consistent. Het is een reeks van lokale waarheden: waar is alleen de zin die je op dat moment leest. Je leest ‘Jan loopt in de Kalverstraat.’ En even later lees je ‘Jan zit in de trein naar Haarlem.’ Beide zinnen kunnen waar zijn, alleen niet tegelijk. In de literatuur is dat geen probleem. Want geen mens kan twee zinnen tegelijkertijd uitspreken. In de wiskunde kunnen niet beide zinnen waar zijn. Want, zoals gezegd, de wiskunde is tijdloos.