De Revisor. Jaargang 12

[p. 44]

Piet Meeuse
Pythagoras, of de metamorfosen van een hersenschim I

1 De posthume lotgevallen van Pythagoras

Volgens de overlevering zouden de pythagoreeërs drie soorten met rede begaafde wezens hebben onderscheiden, te weten: goden, mensen en ‘zulken als Pythagoras’. Als deze doctrine van de meester zelf afkomstig is kan een vooruitziende blik hem niet worden ontzegd, want de derde categorie mag dan niet uitblinken door duidelijkheid, ze geeft in elk geval een sprekend voorbeeld. En eerlijk is eerlijk: wie de sporen nagaat die de pythagorese traditie in de geschiedenis van onze cultuur heeft getrokken zal moeten toegeven dat die derde categorie haar bestaansrecht in de loop der eeuwen wel heeft bewezen; ergens tussen mensen en goden heeft hij een stelling betrokken waarmee elke middelbare scholier, tot voor kort althans, gedwongen was kennis te maken.

De vraag wie Pythagoras in deze bevoorrechte categorie eventueel gezelschap zouden mogen houden laat ik hier maar rusten, want het voorbeeld op zich is interessant genoeg: geen filosoof na hem - en hij was het zelf die dat woord introduceerde - heeft het ooit zover gebracht dat hij op een vergelijkbare wijze het voorwerp werd van een cultus en een legendevorming die tot in onze tijd doorwerkt. Deze ‘Hyperborese Apollo’, de man ‘met de gouden dij’, in wie sommige moderne onderzoekers een Griekse sjamaan menen te hebben ontdekt, vormt een van de fascinerendste raadsels in de geschiedenis van het Europese denken. Als vermeend grondlegger van de wiskunde werd hijzelf tot object van die andere, hogere vorm van wiskunde die ‘geschiedenis’ heet en waarvan de wetmatigheden wel altijd onachterhaalbaar zullen blijven: tijd en toeval wissen in sommige gevallen blijkbaar precies zoveel uit als nodig is om uit de resterende gegevens een even onverwoestbare als vruchtbare formule te produceren.

Dat leven en leer van Pythagoras tot zo'n ‘formule’ geworden zijn, die zelfs na 2500 jaar nog creatieve interpretaties uitlokt en ook in het denken over kunst al sinds eeuwen een opmerkelijke rol speelt, hoop ik hierna aan te tonen met een aantal voorbeelden uit het grensgebied tussen literatuur en filosofie.

De zekerheid over bepaalde historische feiten lijkt soms omgekeerd evenredig aan de kracht waarmee de verbeelding erin wortelschiet. Maar waarom gebeurt dat wel in het ene, en niet in het andere geval? Waarom niet in het geval van Thales van Milete of Herakleitos en wel in dat van Pythagoras? De verbeelding die werkzaam is in de overlevering heeft blijkbaar haar eigen redenen en op die redenen hoop ik hier wat meer licht te werpen.

Wanneer Eduard Zeller als wetenschappelijk onderzoeker aan het begin van onze eeuw ironisch constateert dat de bronnen van 1000 jaar na de dood van Pythagoras beduidend meer over hem weten te melden dan de oudste bronnen - en ze derhalve als onbetrouwbaar terzijde schuift - dan vergeet hij dat die produktiviteit van de verbeelding, zoals die in de uitbundige legendevorming tot uiting kwam, op zichzelf al veelzeggend is. Een verleden dat op zo'n manier meegroeit met de tijd bevat kennelijk iets dat aktueel blijft, iets dat uitnodigt tot een voortdurend hernieuwde bewerking.

Uit de geschriften van Porphyrius, Jamblichus en Proclus is in elk geval op te maken dat Pythagoras zich 800 à 1000 jaar na zijn dood in de status van een halfgod mocht verheugen. Maar zelfs voor Empedocles, die nauwelijks een eeuw na hem leefde, kon daarover al weinig twijfel bestaan.

Wie de historische Pythagoras ook geweest moge zijn en wat zijn leer ook precies behelsd mag hebben - zeker is dat het nageslacht in hem een goddelijke wijsheid heeft vermoed, want zo'n langdurige en fantasievolle scheppingsarbeid besteedt het mensdom doorgaans uitsluitend aan leven en leer van godsdienststichters. Het eigenaardige is alleen, dat Pythagoras geen godsdienststichter was. Daarvoor was zijn leer blijkbaar toch net iets te aristocratisch, te intellectueel. Hij vormt, kortom, een moeilijk classificeerbaar geval, waarvoor een aparte categorie op zijn plaats lijkt. Met een been in de religieuze wereld van Orphische mysteriën, Apolloverering en Demetercultus, en met het andere in de nieuwe wereld van filosofie en wetenschap, staat hij als een eenmalige verschijning aan de horizon van onze cultuur. En zijn legende is dan ook niet zozeer het produkt van de volksverbeelding als wel grotendeels het werk van geschoolde intellectuelen.

Maar waarom juist hij? Waarom niet een andere presocraticus, of Plato? Het antwoord zou misschien kunnen liggen in het feit dat hij geen enkel geschrift heeft nagelaten. Dat onderscheidt hem weliswaar van vrijwel al zijn collega-filosofen en dat vergrootte de speculatieve mogelijkheden - maar ook Socrates schreef niets. De verklaring moet elders liggen. Wat er van zijn leer werd overgeleverd moet de verbeelding geprikkeld hebben en dat kan - achteraf gezien - niets anders zijn geweest dan de unieke combinatie van getalsoperaties met mystieke, muzikale en astronomische ideeën, die een breukloze eenheid suggereert van kwantitatief en kwalitatief denken. Het is die harmonie van wiskundige, muzikale en kosmischreligieuze interessen die tot in onze tijd het archetypisch ideaalbeeld van de pythagorese filosofie vormt.

[p. 45]

Maar helaas: niemand weet meer precies hoe het allemaal in elkaar paste. Het moderne Pythagorasonderzoek moet genoegen nemen met resultaten die voornamelijk bestaan uit onduidelijkheden, onzekerheden en wankele hypothesen. Behalve de leer van de zielsverhuizing en de ontdekking van getalsverhoudingen in de muzikale consonanties¹ is er vrijwel niets dat met enige zekerheid aan hem persoonlijk kan worden toegeschreven. Zelfs zijn beroemde stelling moest hem tenslotte ontnomen worden. De feiten die over zijn leven bekend zijn en waarover een zekere consensus bestaat geven niet meer dan een rudimentair houvast: het zijn de verbrokkelde fundamenten van wat ooit een van de grote tempels van het Griekse denken moet zijn geweest. Weliswaar is die tempel, zoals gezegd, met veel voortvarendheid, vernuft en fantasie talloze malen op papier gereconstrueerd, waarbij ze steeds uitbundiger vormen aannam, maar geen van die reconstructies is historisch betrouwbaar.

Iets meer valt er, dankzij Aristoteles, te zeggen over de leer van zijn volgelingen in de eerste 150 jaar na zijn dood. Dat blijkt, logisch gezien, een niet erg coherent geheel: er is een getalsleer, geformuleerd als een kosmogonie, een zielsleer, een kosmografie (van Philolaos), en de leer van de mathematische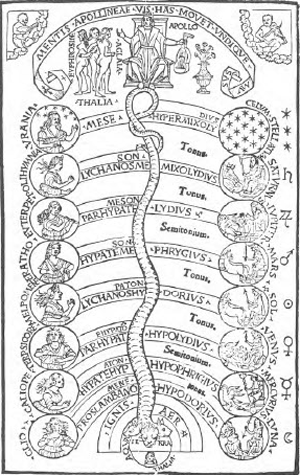

De muziek der sferen. Uit Gafurius, Practica musice 1496

verhoudingen in de muzikale consonanties. Deze elementen waren onderling verbonden (bijvoorbeeld in de doctrine van de ‘harmonie der sferen’), en werden bovendien aangevuld met een reeks pythagorese leefregels en raadselspreuken: de zgn. ‘gulden verzen’.

Een centrale plaats lijkt de getalsleer in te nemen: deze beschrijft hoe de getallen ontstaan uit de twee oerprincipes (archè), nl. de grens en het onbegrensde. Het eerste wordt als manlijk en oneven, het tweede als vrouwelijk en even beschouwd. Uit de inwerking van beide principes op elkaar ontstaat dan het Ene, of de 1 - die overigens niet als een getal wordt beschouwd. Dit Ene is zowel even als oneven en daaruit ontstaan, door een herhaalde begrenzing van het grenzeloze, de getallen én de wereld. Want de dingen ‘zijn’ volgens de pythagoreeërs getallen.

Wat dat precies moest betekenen, daarover heeft Aristoteles zich tevergeefs het hoofd gebroken (zoals in zijn voetspoor opnieuw vele moderne onderzoekers). De enige die er een oplossing voor vond - maar die werd door Aristoteles verworpen - was Plato, die ervan maakte dat de dingen afleidbaar zijn uit getallen. Met zijn leer van de ‘idee-getallen’ (die we overigens alleen uit de tweede hand kennen, omdat ze behoorde tot zijn omstreden ‘ongeschreven leer’) werd Pythagoras grondig geplatoniseerd. Dat wil zeggen: geïnfecteerd met Plato's ideeënleer.

Deze drastische herinterpretatie kan gezien worden als een vervalsing van de oorspronkelijke leer, maar evengoed kan ze beschouwd worden als een ‘face-lift’ waarmee de wijze van Samos weer tweeduizend jaar vooruitkon als filosoof. Want de pythagorese traditie na Plato grijpt voornamelijk terug op de geplatoniseerde Pythagoras van de Academie. Hier blijkt dat de overlevering, in handen van degenen die zich beschouwen als de voortzetters van de traditie (en zo beschouwde de late Plato zich ook), in de eerste plaats gericht is op het levend houden van het erfgoed. En dat betekent een voortdurende ontwikkeling en aanpassing ervan. Zo is Plato te beschouwen als een van de eersten die een eigen creatieve interpretatie van de pythagorese leer leverden, met name in zijn Timaios.

En hoe verder de historische Pythagoras uit het zicht verdween, hoe creatiever en inventiever de interpretaties werden - literair gesproken althans, want filosofisch gezien ging het na Plato voorlopig weer bergafwaarts. Neoplatonici als Porphyrius, Jamblichus en Proclus bleken weinig last te hebben van wetenschappelijke of filosofische twijfels: zij schreven als bewonderaars en maakten Pythagoras tot de zegelbewaarder van een goddelijke wijsheid waarin arithmetica, geometrie, muziek en astronomie in hun onderlinge verbondenheid garant stonden voor de intellectuele harmonie van ziel en kosmos.

Zo ging Pythagoras, voorzien van een onaantastbare autoriteit, de middeleeuwen in: de meester van het quadrivium, beschikkend over bovennatuurlijke gaven, de personificatie van wat het oude heidendom aan goddelijke wijsheid had kunnen vergaren. Toen de renaissance wat nieuw licht in de duisternis begon te werpen nam hij naast Orpheus, Hermes Trismegistus en Plato een plaats in op de eregalerij van heidense wijzen (de zgn. Prisca Theologia). De pythagorese legende, waarin leven en leer tot een fabuleus geheel waren versmolten, was

1 Zelfs dat laatste wordt betwijfeld. Zie bijv. J.A. Philip, Pythagoras and early Pythagoreanism, Hfdst. 8 (Toronto, 1966)

[p. 46]

voornamelijk een produkt van de late oudheid maar bleek nog zo levenskrachtig dat ze niet alleen de middeleeuwen overleefde maar zelfs weer opbloeide in de 15de en 16de eeuw. En met het aanbreken van de nieuwe tijd worden de posthume lotgevallen van Pythagoras eigenlijk pas echt interessant.

In de 16de eeuw treedt een scheiding der geesten op onder de geleerden, die raakt aan de kern van de pythagorese leer: de oude, symbolische en kwalitatieve getalsopvatting komt tegenover een nieuwe, mathematisch-funktionele getalsopvatting te staan. Anders gezegd: een mystiek-beschouwelijke tegenover een mathematisch-wetenschappelijke. Om het conflict in twee namen toe te spitsen: Giordano Bruno tegenover Galileo Galilei. En in dit conflict wist de legendarische wonderdoener zijn wetenschappelijk gezicht alleen te redden dankzij de mathematische face-lift die Plato hem gaf.

Maar de vraag rijst of Pythagoras vanaf dat moment eigenlijk niet twee gezichten vertoont. Zijn er geen twee Pythagorassen? De ene een getalsmysticus, die al in de late oudheid een alliantie was aangegaan met gnosis en kabbala en de ander een wiskundige met zeldzaam vooruitziende intuïties? De eerste, met wie Bruno's wetenschapsopvatting gelieerd was, leek verder voorbestemd voor een schemerige, esoterischesthetische carrière, terwijl de tweede zich aan Galilei's zijde in de rijen van de wetenschap mocht scharen (zij het op een bescheiden plaats, in de schaduw van Plato). Maar zo gemakkelijk laten die twee zich niet scheiden, zoals nog zal blijken. Uiteindelijk is er toch maar één Pythagoras, aan gene zijde van zo'n onderscheid.

De scheiding der geesten waarover ik sprak had overigens niet alleen betrekking op de getaisopvatting maar betrof ook de kennistheoretische kwestie die kunsten en wetenschappen tenslotte rigoureus van elkaar scheidde: de kennistheoretische aanspraken van de magie (: in de intellectuele renaissanceopvatting) kwam frontaal in botsing met de kennistheoretische aanspraken van de empirisch-mathematische methode. En met die aanspraken van de magie waren die van de imaginatio nauw verbonden. In Bruno's wetenschap vormden magie en verbeelding, onlosmakelijk verbonden, het voornaamste instrument van de kennisverwerving, en zijn speculatieve filosofie bezat dan ook een sterke artistieke component. Galilei daarentegen reduceerde alle kennis tot het strikt kwantitatieve: meten en wegen. Dat Bruno aan het kortste eind trok is algemeen bekend. Maar minder bekend lijkt de logische consequentie van zijn nederlaag, namelijk dat zijn intellectuele erfenis - en dat is de erfenis van een hele traditie: die van het speculatieve (neo)platonisme van Ficino, Pico della Mirandola en anderen, met al zijn mystieke en gnostische ingrediënten - automatisch toeviel aan die disciplines die voortaan ook van het wetenschappelijk kennen in strikte zin waren uitgesloten: de kunsten. Daarin werkte die erfenis dan ook door, inclusief Pythagoras. (En niet alleen in muziek en architectuur waarin hij zich al een plaats veroverd had.)

Men ziet: Pythagoras is niet voor één gat te vangen. Bij gebrek aan schriftelijke autoriteit van de meester zelf had de overlevering meer dan 2000 jaar vrij spel gehad om het beeld te modelleren van de ‘ideale Wijze’: een mens die niet alleen een religieus, maar ook een wetenschappelijk en een esthetisch ideaal belichaamde.

Boëthius en Pythagoras rekenend met geschreven getallen en een abacus

En die formule zou wel eens sterker kunnen blijken dan alle scepsis van filologen en wetenschapshistorici, want ook na de grondige ontluistering van zijn legende in onze eeuw blijkt de aantrekkingskracht van deze Pythagoras nog volop werkzaam: in geschriften van auteurs als Hermann Broch, Thomas Mann en in ons land Harry Mulisch speelt hij een intrigerende rol. Maar eerst wil ik de aandacht vestigen op een veel vroeger geval van pythagorese inspiratie: Novalis.

2 Novalis' magische wiskunde

Na de wetenschappelijke revolutie werkt Pythagoras het levendigst door in de kunst. Weliswaar blijft zijn invloed ook nog wel bespeurbaar in de wetenschap (bij Kepler bijvoorbeeld) en treffen we er in de filosofie van de volgende eeuwen nog wel sporen van aan (bij figuren als Leibniz, Franz von Baader en Schelling), maar belangwekkende creatieve interpretaties moeten we sindsdien vooral zoeken in de theoretische beschouwingen van kunstenaars.

De dichter Georg Philipp Friedrich von Hardenberg (1772-1801), beter bekend als Novalis, viel na zijn vroege dood al snel de twijfelachtige eer te beurt verheerlijkt te worden als het prototype van ‘de romantische dichter’: een lyricus, jong gestorven en vervuld van een ‘Sehnsucht’ naar het Oneindige. Pas toen geleidelijk zijn nagelaten notities en fragmenten begonnen te verschijnen werd dat beeld stukje bij beetje genuanceerd en het is eigenlijk pas sinds de editie van zijn werk door Kluckhohn en Samuel (1929) dat er een definitieve doorbraak plaatsvond naar een heel andere waardering van Novalis. Zijn nalatenschap vormt verreweg het omvangrijkste

[p. 47]

deel van zijn oeuvre en daaruit rijst een heel ander beeld op dan dat van de kwijnende romantische ‘Schwärmer’.

In 1798 schreef zijn vriend Friedrich Schlegel: ‘Hardenberg ist dran, die Religion und die Physik durcheinander zu kneten. Das wird ein interessantes Rührei werden!’ En inderdaad - een interessanter roerei dan wat Novalis in zijn theoretische notities brouwde zal men in de geschiedenis van literatuur en filosofie niet snel aantreffen. Hij roerde trouwens nog veel meer door elkaar dan alleen ‘Religion’-en ‘Physik’: de posthuum gepubliceerde notities en fragmenten bestrijken zo ongeveer alle wetenschappen en kunsten; ze vormen een pièce de résistance waarop zowel literatuurwetenschappers als filosofen voorlopig nog niet uitgestudeerd zijn.

Van een grondige studie van dit geheel - dat in de meest recente uitgave van Hans Joachim Mähl meer dan 800 pagina's omvat - kan hier natuurlijk geen sprake zijn. Ik zal me voornamelijk richten op de notities die verzameld zijn in Das Allgemeine Brouillon en ik moet me ertoe beperken, de pythagorese tendens daarin te belichten. Daarbij is het onvermijdelijk dat die wat overbelicht wordt ten koste van allerlei andere aspecten in dit complexe geheel. Laat ik dus om te beginnen vaststellen dat de namen van Kant, Fichte en Hemsterhuis in zijn aantekeningen veel prominenter vertegenwoordigd zijn dan die van Pythagoras, die maar sporadisch opduikt. En toch speelt de Hyperborese Apollo in zijn denken een belangrijker rol dan op het eerste gezicht lijkt. In de notities van Das Allgemeine Brouillon (hierna afgekort als AB), die de voorbereiding vormden van een fantastisch encyclopedisch project, is een pythagorese oriëntatie onmiskenbaar.

Hoewel Pythagoras hierin niet meer dan enkele malen genoemd wordt zijn bijvoorbeeld de notities waarin Novalis zich bezighoudt met analogieën tussen wiskunde, muziek en taal erg talrijk en het begrip ‘harmonie’ mag welhaast een sleutelwoord genoemd worden voor de hele onderneming.

Zo noteert hij bijvoorbeeld onder het kopje musikalische mathematik: ‘De combinatorische analyse leidt tot fantaseren met getallen - en onderwijst de getallen-compositiekunst - de mathematische generale bas. (Pythagoras. Leibniz.) De taal is een muzikaal ideeëninstrument.’ (AB 547)²

De term ‘combinatorische analyse’ verwijst naar een bepaalde richting in de wiskunde, die ten tijde van Novalis een kortstondige bloei beleefde in Duitsland en een poging behelsde om Leibniz' ideeën over een ars combinatoria (door hem op zijn beurt ontleend aan Ramon Lull, 1236-1315) verder uit te werken. Zo'n gegeven op zich is al een indicatie voor Novalis' verreikende ambities. Zijn ‘encyclopedie’ beoogde niet zozeer een systematische ordening van alle kennis maar moest leiden tot een ‘Erfindungskunst’ die het mogelijk maakte, uit bekende gegevens ook onbekende af te leiden. De methode daarvan moest op de een of andere wijze een ‘mathematische’ zijn: ‘De basis van alle wetenschappen en kunsten moet een wetenschap en kunst zijn - die men met de algebra kan vergelijken -’ (AB 90). Maar wat voor wiskunde heeft hij daarmee op het oog? In een notitie waarin de naam van Pythagoras opnieuw valt, heet het: ‘wiskunde. Innerlijke levendigheid van de wiskunde. Magie van de getallen. Mystieke leer van Pythagoras - personificatie van de 3 - van de 4 etc.’ (AB 348).

Novalis

Waar hij precies op uit is wordt van een andere zijde verduidelijkt in notities als de volgende: ‘magie. (Mystieke taaltheorie). Sympathie van het teken met het betekende. (Een van de grondgedachten van de kabbalistiek.) De magie is van de filosofie heel verschillend en vormt een wereld - een wetenschap - een kunst op zich. Magische astronomie, grammatica, filosofie, religie, chemie etc. Spiegelrepresentatietheorie (“Wechselrepraesentationslehre”) van het universum. Emanatietheorie. (Gepersonifieerde emanaties.)’ (AB 137).

En: ‘Overal ligt, naar het mij voorkomt, een grammaticale mystiek aan ten grondslag - die heel gemakkelijk de oorspronkelijke verbazing over taal en schrift kon opwekken. (De wilde volkeren houden ook nu nog het schrift voor toverij.)’ (AB 138.)

Hoe kryptisch Novalis zich in zijn notities ook vaak uitdrukt, het is duidelijk dat het hem te doen is om die ‘grammaticale mystiek’ die hij overal als de grondslag vermoedt. De taal van de getallen, de taal van de muziek, de taal van de woorden - het zijn allemaal grammaticale systemen die elkaar spiegelen en het gaat erom, die ene universele grammatica te ontdekken die aan al die verschillende talen ten grondslag ligt. Dat is zijn ‘Wechselrepraesentationslehre’. Hij wil alle wetenschappen en kunsten onder één (poëtische èn systematische) noemer brengen en is daarom in zijn notities voortdurend op zoek naar analogieën en correspondenties tussen de meest uiteenlopende kennisgebieden. Hij droomt van een universele ‘Combinationslehre’, ofwel een ‘Construktionslehre des schaffenden Geistes’.

In Das Allgemeine Brouillon hebben we te maken met een groots

2 Ik citeer (en vertaal) uit Band 2 van de Novaliseditie van Hans Joachim Mähl, Hanser Verlag, München 1978. Terwille van de leesbaarheid laat ik alle haakjes - op plaatsen waar afgekorte woorden zijn vervolledigd - weg. Cursiveringen in de tekst zijn onderstrepingen van Novalis zelf. (De nummers verwijzen naar notities, niet naar pagina's.)

[p. 48]

opgezette poging, een synthese tot stand te brengen tussen de innerlijke en de uiterlijke wereld (de tegenstelling innerlijk/uiterlijk keert voortdurend terug in zijn aantekeningen). Romantisch geformuleerd: een synthese tussen natuur en geest. Wat er van die poging resteert doet zich bijna twee eeuwen later op het eerste gezicht voor als een waar pandemonium van speculatieve invallen en bizarre associaties, en in de ogen van een sceptische twintigste-eeuwer moet zo'n onderneming wel naief en warhoofdig lijken.

Toch is ze al veel minder vreemd wanneer men haar ziet in de context van de ‘Kopernikanische Wendung’ die Kants filosofie in zijn tijd teweegbracht en die de bloeiperiode van het speculatieve Duitse idealisme inluidde met Fichte, Schelling en Hegel. Ook deze filosofen, en iemand als Hölderlin, waren bezeten van het idee, die grote synthese tot stand te kunnen brengen waarmee, in de termen van het Tübinger drietal, het ‘Reich Gottes’, of in Novalis' woorden ‘das Goldene Zeitalter’ aan zou breken. Na Fichtes radicalisering van de Kantiaanse filosofie ziet deze enthousiaste generatie van jonge filosofen en dichters het als de taak van de filosofie, een nieuwe eenheid van alle wetenschappen te bewerkstelligen op basis van Fichtes uitgangspunt. Kants transcendentale subject wordt bij hem als ‘ik’, als handelend subject, tot de uitdaging, de wereld opnieuw te denken. Maar dan vanuit een ‘praktisch’ ofwel ‘moralisch’ vertrekpunt (in de zin van Kants praktische postulaten).

Net als in de Italiaanse renaissancefilosofie van Pico della Mirandola wordt denken als scheppen begrepen en de vrijheid van het subject als de morele imperatief om een integrale eenheid in het kennen tot stand te brengen: alle wetenschappen moeten tenslotte uitmonden in die ene ‘oceaan’ die de poëzie is (Schelling).

Tegen die achtergrond zien Novalis' speculaties er al veel minder excentriek uit. Bovendien moet ook de schok die de Franse Revolutie teweegbracht ingecalculeerd worden: niet alleen in de studeerkamers van filosofen, ook in de samenleving lijkt zich een Copernicaanse wending te voltrekken. Het tijdperk van de Aufklärung en de analytische rede lijkt uit te monden in de opgave, een nieuwe, alomvattende synthese tot stand te brengen die ook de samenleving grondig zal veranderen.

Het is verleidelijk, hier verder in te gaan op de opmerkelijke parallellen die de renaissancefilosofie biedt. Maar ik kan hier slechts in het voorbijgaan opmerken, dat ook toen artistieke en visionaire impulsen een belangrijk aandeel hadden in de doorbraak naar een nieuw denken. Ook toen speelde de speculatieve filosofie een centrale rol en ook toen ging het minder om een specifiek theoretisch probleem dan om de totaliteit van het leven. Zo bezien kan het nauwelijks toeval zijn dat juist dichters als Novalis en Hölderlin een intrigerende rol hebben gespeeld in de opbloei van het Duitse idealisme.

Maar van alle Duitse idealisten is Novalis de enige die die opgave van een nieuwe, grote synthese in pythagorese zin probeert te realiseren. En als ‘pythagorees’ beschouw ik dan niet alleen zijn pogingen om wiskunde, muziek en taal als analoge systemen te begrijpen, maar meer in het algemeen ook zijn streven de kwalitatieve en de kwantitatieve dimensies in het kennen met elkaar te verbinden. Overal is hij bezig de exacte wetenschappen (wis- en natuurkunde) middels analogieën en correspondenties te vervlechten met fenomenen als poëzie, muziek en religie.

Daarbij legt hij een opvallende voorkeur aan de dag voor exacte, mathematische terminologie. Zo wil hij het onbekende kenbaar maken en omgekeerd het bekende, het gewone, de glans van het geheim teruggeven. Hij noemt dat, in een aantekening uit 1798 (Vorarbeiten, 105) ‘romantisieren’. De term is bedriegelijk, want: ‘Romantiseren is niets anders dan een kwalitatieve potentiëring. Het lagere zelf wordt in deze operatie met een beter zelf geïdentificeerd. Zoals wijzelf zo'n kwalitatieve potentiereeks zijn. Deze operatie is nog geheel onbekend. Wanneer ik het alledaagse een verheven betekenis, het gewone een geheimzinnig aanzien, het bekende de waardigheid van het onbekende, het eindige een schijn van oneindigheid geef, dan romantiseer ik het - omgekeerd is de operatie voor het hogere, onbekende, mystieke, oneindige - dit wordt door deze koppeling gelogaritmiseerd - het krijgt een gangbare uitdrukking. (-)’

Het woord ‘romantiseren’ krijgt hier een heel wat preciezere inhoud dan we gewend zijn eraan toe te kennen. Een uitdrukking als ‘logarythmisirt’ maakt duidelijk dat het om iets anders dan romantische ‘schwärmerei’ gaat. En elders noteert hij nog eens: ‘Romantiseren, gelijkend op het algebraïseren.’ (AB 10).

Ook een notitie onder het kopje mathematik und grammatik sluit daarbij aan: ‘Over de logaritmen - de eigenlijke taal is een logaritmensysteem. Zouden de tonen niet in zekere zin logaritmisch voortschrijden.’ (AB 643). Het woord ‘taal’ (Sprache) lijkt hier in een overdrachtelijke zin gebruikt, maar zoals verderop zal blijken brengt hij ook de verbale taal met wiskunde in verband.

Nu is het idee van de verwantschap van wiskunde en muziek sinds Pythagoras vrijwel een traditioneel gegeven (en het is aardig, in dit verband Leibniz te citeren die de muziek ‘eine verborgene arithmetische Übung der Seele’ noemde, ‘welche dabei nicht weiss dass sie mit Zahlen umgeht’), maar Novalis wilde die verwantschap dus ook tot de taal uitgebreid zien. En hij doelde daarbij niet op een logische of filosofische begrippentaal (zoals Leibniz die in zijn characteristica universalis probeerde te ontwikkelen) maar op de taal als zodanig, en in het bijzonder ook op de poëzie. Dat blijkt bijvoorbeeld wanneer hij de taal een ‘muzikaal ideeëninstrument’ noemt. Die verwantschap met de muziek impliceert een paradoxale combinatie van vrijheid, spel, en wetmatigheid: ‘De dichter, de redenaar en filosoof spelen en componeren grammaticaal.’ (AB 547). En elders: ‘De dichter gebruikt de dingen en woorden, als loetsen en de hele poëzie berust op actiev associatie van ideeën - op zelfwerkzame, opzettelijke, ideële loevalsproduktie - (toevallige - vrije aaneenschakeling.)’ (AB 953).

Dergelijke notities hebben hem tot de grote initiator van de moderne poëzie gemaakt, maar zijn eigenlijke taalopvatting wordt er nauwelijks door verhelderd. Is het toch de eigenlijke taal (die van de woorden) die hij een logaritmensysteem noemde, of moeten we afgaan op AB 495: ‘grammatica. De taal is Delphi.’? Dat lijkt in een heel andere richting te wijzen. Pas wanneer we de Monolog, een kort tekstje uit 1798, erbij halen wordt die ambivalentie opgeheven: ‘Als men de mensen

[p. 49]

maar begrijpelijk kon maken,’ zegt hij daar, ‘dat het met de taal gesteld is als met de mathematische formules - zij vormen een wereld op zich - ze spelen slechts met zichzelf, drukken niets anders uit dan hun wonderlijke natuur en juist daarom zijn ze zo expressief - juist daarom spiegelt zich in hen het zeldzame spel van de verhoudingen der dingen. (-) Zo is het ook met de taal - wie een fijn gevoel heeft voor haar toepassing, haar maat (“Takt”), haar muzikale geest, wie in zichzelf de fijnzinnige werking van haar innerlijke aard verneemt en zijn tong of zijn hand daarop beweegt, die zal een profeet zijn (-)’

Het is deze taalopvatting die Novalis' baanbrekende betekenis als poëzietheoreticus bepaalt: hij begrijpt de taal als een autonoom systeem dat in de eerste plaats naar zichzelf verwijst. De woorden ‘spelen slechts met zichzelf’, zoals wiskundige formules. Daarin ligt dus haar overeenkomst met wiskunde en muziek en dat verklaart zijn hardnekkige koppeling van dit drietal.

Wat zijn filosofische speculaties een extra pythagorees accent verleent is het feit dat hij aan die verwantschap een kosmische betekenis toekent: alles is taal voor hem. Voor het begrijpen van zijn filosofische intenties is de volgende notitie dan ook van cruciaal belang: ‘grammatica. De mens spreekt niet alleen - ook het universum spreekt - alles spreekt - oneindige talen./Leer van de signaturen.’ (AB 143).

Deze poëtische overtuiging vormt het uitgangspunt van Novalis' speurtocht naar de ‘grammatica’ van het universum en hij is ervan overtuigd dat de menselijke geest de sleutel daartoe moet bevatten. Die sleutel ligt mogelijk verborgen in de ‘leer van de signaturen’. Een betekenisvolle verwijzing, want die verbindt het ‘magische idealisme’ van Novalis (de term is van hemzelf) met de speculatieve traditie van het neoplatonisme, waarin religieuze, wetenschappelijke en esthetische idealen zich al van oudsher verbonden. Wat Novalis voornamelijk onderscheidt van zijn neoplatoonse geestverwanten is echter zijn poging tot mathematisering van hun speculatieve en visionaire ideeën. Het is precies deze combinatie van mystieke, of zelfs magische denkbeelden met een sterke hang naar mathematische systematiek, die de kern vormt van zijn denken. En tegelijkertijd verklaart dit de pythagorese oriëntatie ervan: eenzelfde combinatie ligt immers ten grondslag aan het pythagorese wereldbeeld van de Timaios en sindsdien waren pythagorisme en neoplatonisme altijd sterk verweven.

Dat brengt ons overigens terug op de vraag wat hij precies onder wiskunde verstond. Wanneer we bij hem bijvoorbeeld een mathemathische definitie van God aantreffen - ‘God is nu eens 1.∞ - dan weer 1/∞ - dan weer 0’ (AB 933) - dan heeft dat veel weg van spielerei en kun je betwijfelen of dat wat hij wiskunde noemt wel samenvalt met dat wat beroepsmathematici eronder verstaan.

Andere uitspraken klinken weer koel-modern: ‘Alle wetenschappen moeten wiskunde worden,’ schrijft hij in zijn Freiberger Naturwissenschaftliche Studien (FNS 5). ‘De wiskunde tot nu toe is slechts de eerste en gemakkelijkste uiting of openbaring van de ware wetenschappelijke geest.’ Maar dan vervolgt hij: ‘Het getallensysteem is een voorbeeld van een echt taaltekensysteem - Onze letters moeten getallen, onze taal rekenkunde worden. Wat zouden de pythagoreeërs toch onder getalskrachten hebben verstaan?’

Ook zijn idee van wiskunde wordt dus bepaald door die ambivalentie van het mystiek-magische enerzijds en wetenschappelijke exactheid anderzijds. En de oriëntatie die de vraag naar ‘getalskrachten’ verraadt wordt in latere aantekeningen bevestigd. Enkele citaten uit Mathematische Fragmente (1799/1800):

‘De huidige wiskunde is weinig meer dan een speciaal empirisch organon (-) Getallen zijn, net als tekens en woorden, verschijningen, representaties katexoxin. (-) Echte wiskunde is het eigenlijke element van de magiër. In de muziek verschijnt ze formeel, als openbaring - als scheppend idealisme. (-) Men kan een groot rekenaar zijn, zonder vermoeden van de wiskunde. De echte wiskundige is per definitie een geestdriftige. Zonder geestdrift geen wiskunde. (-) Zuivere wiskunde is religie. De wiskunde bereikt men slechts door een theofanie.’ Wat zijn opvatting van ‘echte wiskunde’ onderscheidt van de vakmatige wiskunde die de wetenschap hanteert, maakt hij duidelijk wanneer hij schrijft: ‘In het Morgenland heeft de echte wiskunde haar thuis. In Europa is ze tot louter techniek verworden.’ (p. 790/791).

Dit zijn de roemruchte notities die bekend geworden zijn als de ‘Hymnen an die Mathematik’ en die aanvankelijk door de commentatoren als ‘poëzie’, of ‘poëtische onzin’ werden afgedaan. Eckhard Heftrich concludeert in zijn studie Novalis. Vom Logos der Poesie dat pythagorese en kabbalistische getalsmystiek mede bepalend lijken voor wat Novalis verstaat onder ‘echte wiskunde’. En die conclusie lijkt niet in strijd met die van Martin Dyck in Novalis and Mathematics. ‘Wanneer,’ zo reconstrueert de laatste Novalis' gedachtengang, ‘de zuiver filosofische speculatie over de aard van het universum zich, in de geest van de wiskunde, ontwikkeld had tot natuurwetenschap, de alchemie tot chemie, de kwakzalverij tot medische wetenschap, de astrologie tot astronomie en, meer in het algemeen, speculatieve takken van kennis zich ontwikkeld hadden tot systematische wetenschappen met logische structuren en een empirische basis, waarom zou het dan niet mogelijk zijn dit proces voort te zetten en religie, magie, muziek, of zelfs poëzie te mathematiseren? In dat proces van mathematisering moest echter de wiskunde zelf verbreed en verdiept worden, in het verlengde van Descartes' zoeken naar een “mathesis universalis” en Leibniz' zoeken naar een “arithmetica universalis”. De universele rekenkunde moest alle mentale operaties, zowel die van de wil als esthetische ervaringen, en alle kennis omvatten.’³

Zo kwam Novalis tot zijn concept van een ‘magische wiskunde’. Dat wil zeggen: een wiskunde, verheven tot de status van een universele symbolentaal, die zowel kunst als wetenschap en religie zou omvatten. Een symbolische taal waarin mens en natuur op een volmaakte wijze zouden communiceren.

Uit zulke ideeën concludeerde men al snel dat Novalis nogal lichtvaardig omsprong met de wiskunde en dat hij er als dichter wel niet veel van begrepen zou hebben. Maar zulke conclusies bleken meer te zeggen over romantische vooroordelen ten aanzien van het dichterschap dan over Novalis'

3 Zie Martin Dyck, Novalis and Mathematics, Chapel Hill (V.S.) 1960

[p. 50]

ideeën. Dycks studie toont aan dat Novalis zeer goed op de hoogte was met de stand van zaken in de wiskunde van zijn tijd. Zijn interesse daarin was echter meer van filosofische dan van technische aard en dat voerde hem tot ver buiten de grenzen van het vakgebied.

Daarmee is de relatie tussen wiskunde en magie natuurlijk nog allerminst verklaard. En toch is die combinatie niet zo vreemd en onlogisch als ze op het eerste gezicht lijkt. Käte Hamburger heeft er in haar studie Novalis und die Mathematik⁴ al op gewezen dat zijn magiebegrip rechtstreeks samenhangt met zijn Kantstudie. Kant voerde in zijn Kritik der reinen Vernunft het bestaan in van synthetische oordelen a priori en het is de scheppende functie van deze synthetische oordelen a priori die Novalis fascineert. In het Kantiaanse begrip van de synthesis ziet Novalis het creatieve, scheppende principe bij uitstek, en ook magie is voor hem een synthetisch, scheppend handelen. Wanneer dan volgens Kant alle mathematische oordelen synthetische oordelen a priori zijn, dan is daarin, voor Novalis, hun verwantschap met de magie (en met het artistieke scheppen, dat er rechtstreeks mee samenhangt) gegeven.

Maar wat beide noties, magie en wiskunde, bovendien verbindt, is de mysterieuze aard van het getal, waarop Novalis in zijn notities meermalen terugkomt: ‘Merkwaardige, geheimzinnige getallen. Toen het tellen nog nieuw was, moesten vaak voorkomende getallen bij het tellen van werkelijke dingen - karakteristieke, blijvende getallen als bijvoorbeeld de 10 vingers etc. - en andere frappante getalsfenomenen de verbeeldingskracht van mensen wel op de levendigste manier bezighouden en haar in de wetenschap van de getallen een diep verborgen schat van wijsheid - een sleutel op alle gesloten deuren van de natuur doen vermoeden.’ (AB 787). En elders: ‘Al het uit niets geschapen reële, zoals bijvoorbeeld de getallen en de abstracte uitdrukkingen, heeft een wonderlijke verwantschap met dingen van een andere wereld (-) met een poëtische, mathematische en abstracte wereld.’

De mysterieuze aard van het getal prikkelt dus de verbeeldingskracht omdat men er een verborgen wijsheid in vermoedt, omdat getallen in verbinding staan met een ‘andere wereld’, volgens Novalis. Bij die ‘andere wereld’ hoeft niet gedacht te worden aan een ‘hogere’ of transcendente wereld: het is de wereld van de geest, waarvan we zelf deel uitmaken, zonder de geheimen ervan te kennen: ‘Wij zoeken het ontwerp van de wereld - dit ontwerp zijn wijzelf - Wat zijn wij? Gepersonifieerde almachtige punten.’ (Vorarbeiten, 74). En notitie nr 115 in diezelfde Vorarbeiten luidt: ‘Wij zullen de wereld verstaan wanneer we onszelf verstaan, omdat wij en zij integrerende helften zijn. Godskinderen, goddelijke kiemen zijn wij. Eens zullen we zijn wat Onze Vader is.’

Op die correspondentie tussen mens en wereld, tussen microen macro-kosmos, berust zijn conceptie van magie. Zijn definitie daarvan klinkt alsof het er een van de verbeeldingskracht had kunnen zijn: ‘Magie is = (de) kunst, de wereld van de zintuigen willekeurig te gebruiken.’ (Vorarb. 109).

Zo komen we een merkwaardige verwantschap op het spoor tussen de getallen (en in het verlengde daarvan: de wiskunde), de verbeeldingskracht en de magie. En in de geschiedenis van de filosofie wordt die verwantschap bevestigd door de analoge positie die deze uiteenlopende begrippen - magie, getal, verbeeldingskracht - in de loop der tijden en in verschillende filosofische systemen hebben ingenomen. Alle drie vormen ze, mutatis mutandis, de verbindende schakel tussen de wereld van de geest en de wereld van de zintuigen. Dat zou een verklaring kunnen zijn voor die eigenaardige ambivalentie in de betekenis van getallen, die nu eens naar de ene, dan weer naar de andere kant doorslaat.

Te beginnen bij de oude pythagorese getalsmystiek, die beide componenten verenigde, kunnen we vaststellen dat die een paar eeuwen later bij Archytas en Plato is gerationaliseerd in wiskundige zin. Omstreeks het begin van onze jaartelling wordt ze opnieuw gemystificeerd (neopythagorisme en neoplatonisme), in de 15de en 16de eeuw magisch geïnterpreteerd en met de imaginatio verbonden (Pico, Bruno), vervolgens opnieuw gerationaliseerd tot wiskunde door Galilei, Descartes en Leibniz, en tenslotte andermaal gemystificeerd en met ‘Einbildungskraft’ en magie verbonden door Novalis bij het begin van de 19de eeuw.

Net als woorden en muzikale klanken bezitten getallen voor Novalis een kwalitatieve (‘magische’) dimensie, die de sympathetische samenhang van al het bestaande uitdrukt. Daarom sluiten begrippen als magie en wiskunde elkaar in zijn ogen niet uit, maar in. De ware wiskunde is voor hem niet de technisch-instrumentele, maar de filosofisch bezielde wiskunde, die uitdrukking is van de ‘Sympathie des Weltalls’ waarover hij in zijn Mathematische Fragmente spreekt.

In Novalis' opvatting betekent dat geen afwijzing van de moderne, wetenschappelijke wiskunde, maar een vollediger en diepgaander interpretatie ervan. Zo herkrijgt de wiskunde die poëtische en ‘magische’ kwaliteit die zij vermoedelijk ook voor de oude pythagoreeërs bezat.

‘De poëtische filosoof is en état de Créateur absolu,’ noteert hij ergens. ‘Een cirkel, een driehoek worden al op deze wijze gecreëerd. Ze bezitten geen andere eigenschappen als die de vervaardiger hun toekent. (-) dus ook, wanneer de wiskundige werkelijk iets doet wat juist is, doet hij dat als poëtische filosoof.’ (AB 758). In deze notitie treffen wiskunde, kennen en scheppen samen. En opnieuw fungeert hier de wiskunde als model. Ook noemt hij ergens de wiskunde een ‘echte wetenschap’ omdat ze ‘gemaakte kennis’ behelst. En: ‘Het echte denken verschijnt als een maken - en is dat ook.’ (AB 710). De dichter, de filosoof en de wiskundige vinden elkaar dus in het maken. Dat ‘maken’ is een vrije, scheppende daad en in zoverre dat een willekeurig gebruik van de wereld van de zintuigen inhoudt is het ook ‘magie’ in de zin van Novalis' definitie. Wanneer hij het woord ‘magiër’ gebruikt betekent dat dan ook zoveel als: dichter, wiskundige en filosoof tegelijk. In de theoretische speculaties van Novalis krijgt de poëzie dus haar oorspronkelijke betekenis van poièsis (: maken, voortbrengen) terug en wint tegelijkertijd een kennistheoretische betekenis. Want: ‘Wij weten iets alleen - in zoverre wij het uitdrukken - i.e. maken kunnen.’ (Vorarb. 267). Hier verschijnt dus het idee van de dichter als maker, de ‘calculerende dichter’, dat in de ontwikkeling van de moderne poëzie-opvattingen zo'n belangrijke rol heeft gespeeld.

Bekende uitspraken als die van Baudelaire (‘... dat de ver-

4 Opgenomen in: Käte Hamburger, Philosophie der Dichter, Stuttgart 1966

[p. 51]

beelding het wetenschappelijkste van alle vermogens is, omdat alleen zij de universele analogie begrijpt, of dat wat een mystieke religie de correspondentie noemt.’) of van Yeats (‘De wereld weet niets omdat zij niets gemaakt heeft, wij weten alles omdat we alles gemaakt hebben.’) zijn geheel in de geest van Novalis' reflecties - al hebben ze die ook niet gekend. En zelfs Rimbauds radicale uitspraak dat de dichter zich ziende (of: ziener) moet maken door een langdurige, grenzeloze en beredeneerde ontregeling van alle zintuigen lijkt een wat verwrongen echo van Novalis' definitie van magie.

In dit filosofisch labyrint zijn we Pythagoras ondertussen een beetje uit het oog verloren, lijkt het. Zo pleegt dat te gaan met hersenschimmen: ze zijn overal en nergens. Toch zwerft zijn geest overal rond, want al geeft het hier besprokene bij lange na geen compleet beeld van de rijkdom van zijn reflecties, het vormt wel zoiets als het centrale zenuwstelsel ervan: en Novalis' magische wiskunde is op allerlei manieren verbonden met de pythagorese wetenschappen van het quadrivium. Het accent valt daarbij sterk op wiskunde (arithmetica en geometrie) en muziek, maar ook de astronomie ontbreekt niet. Zij moet zelfs ‘Grundlage aller physikalischen Wissenschaften’ worden (AB 1104) en in AB 460 gaat hij nog verder wanneer hij haar tot het paradigma van alle theorie verheft en Fichte uitroept tot de ‘tweede Copernicus’ van het innerlijke ‘Weltsystem’. Ook de muziek speelt zo'n paradigmatische rol. Hij ziet haar overal weerspiegeld en spreekt niet alleen van ‘musikalische Mathematik’, maar ook van ‘musikalische Physik’ (AB 387) en zelfs van ‘chemische Musik’ (AB 826), om van de verwantschappen tussen muziek en taal verder maar te zwijgen. Elk van de pythagorese wetenschappen kan in zijn ‘Wechselrepraesentationslehre’ de rol van paradigma vervullen. En wanneer hij opmerkt: ‘De muzikale verhoudingen lijken mij in de ware zin des woords de grondverhoudingen van de natuur te zijn.’ (Fragmente und Studien 1799/1800, nr 65) - wie zou dan nog aan de pythagorese inspiratie van zijn filosofisch roerei kunnen twijfelen?

Er is, tenslotte, in Novalis' notities nog een bijzonder motief te vinden, waarbij ik even wil stilstaan, omdat ook dit blijkbaar samenhangt met een pythagorese oriëntatie. Dat is het oude, gnostische motief van het god-worden. Het is te vinden in allerlei verspreide notities. In de Fichtestudien (p. 202) noteert hij: ‘De tot op heden (vigerende) begrippen van God waren tamelijk juiste ideeën van de mens - qua intelligentie.’ In het Allgemeine Brouillon: ‘Als onze intelligentie en onze wereld harmoniëren - dan zijn wij God gelijk.’ (AB 78) en onder het kopje zukunftslehre: ‘Alles wat van God gezegd wordt bevat de menselijke toekomstleer. Iedere machine, die nu nog van het grote Perpetuum Mobile leeft, moet zelf perpetuum mobile - ieder mens die nu van God en door God leeft, moet zelf God worden.’ (AB 320). Maar de kernachtigste formulering van dit motief is wel te vinden in de Vorarbeiten (248) waar hij kortweg zegt: ‘God wil goden.’

Zover gaan dus de totaliteitsaanspraken van zijn encyclopedisch project: de mens moet god-gelijk worden. Dat is geen vermetele opstand tegen de goden - of God - maar dat ligt, in Novalis' visie, binnen zijn mogelijkheden en het is zelfs zijn bestemming: ‘God wil goden.’

Nu leerde ook Pythagoras volgens de oude overlevering dat de mens zich door een strenge ethische en intellectuele discipline tot een goddelijke status kon verheffen en het is waarschijnlijk dat zijn leer van de onsterfelijke ziel daarop was toegespitst. De ziel was immers van goddelijke oorsprong en kon tot die oorsprong terugkeren wanneer ze een zuiveringsproces doormaakte. In de Dionysische (en andere) mysteriereligies kon dat bereikt worden door een tijdelijke identificatie in de extase, maar in de pythagorese leer (evenals in latere gnostische leren) wordt dat een levenslang proces: de extase wordt vervangen door de theoria: de contemplatie van de universele orde, waarbij de (menselijke) microkosmos de goddelijke orde van de macrokosmos moet weerspiegelen.⁵

Hier ligt de oorsprong, zowel van de magie-opvatting van renaissancefilosofen als Ficino, Pico en Bruno, als van het romantische magieconcept van Novalis. En het is ook op grond van dit emancipatorische idee van de principiële godgelijkheid dat ‘zulken als Pythagoras’ een aparte categorie claimden tussen goden en mensen in. Het aardige en leerzame van een dergelijke emancipatie schuilt in het elitaire karakter ervan: het is niet voor iedereen weggelegd. Men zal er het nodige voor moeten presteren. Ook volgens Novalis krijgt een mens zijn godgelijkheid bepaald niet cadeau. Het is een ideaal dat op z'n minst een grote intellectuele en creatieve inspanning vergt.

Dat er een rechtstreeks verband bestaat tussen dit gnostische motief van het god-worden en het verlangen naar een alomvattende, universele kennis - en dat dat verlangen tenslotte niet anders is dan het verlangen naar een volmaakte harmonie van mens en wereld - lijkt voor de hand te liggen.

Even voordehandliggend is de moderne reactie op zulke idealen: zulke romantische illusies worden met minzame ironie besproken, want het is al sinds lang een uitgemaakte zaak dat de wetenschap met zulke pretenties definitief heeft afgerekend. Niet alleen is het absoluut onmogelijk, volgens de communis opinio, dat een mens nog alle kennisgebieden zou kunnen overzien en beheersen, maar bovendien is het uitgesloten, ze hoe dan ook met elkaar in overeenstemming te brengen. (Het ironische van dit ‘wij-weten-wel-beter’ is echter dat wát wij beter weten alleen maar is, dat wij het niet-meer-zo-goed weten.)

Des te verrassender is het daarom, te constateren dat er ook na die kortstondige, romantische euforie van het Duitse idealisme (waarvan Novalis' onderneming deel uitmaakt) nog steeds sporen zijn te vinden van een dergelijk ideaal, waarin bovendien de contouren van die pythagorese ‘formule’ herkenbaar zijn. Maar het is symptomatisch dat dit pythagorese denken intussen is verbannen naar het onduidelijke grensgebied (of moet ik zeggen: niemandsland?) ergens tussen kunst en wetenschap. En dat was in Novalis' tijd eigenlijk al niet anders. Hoe strenger de gebieden van kunst en wetenschap werden afgebakend, hoe minder plaats er bleef voor een interdisciplinair denken als het pythagorese.

Niettemin schreef iemand als Hermann Broch in zijn uitvoerige studie Hofmannsthal und seine Zeit (1947/1948): ‘De domei-

5 Zie Cornford, Mysticism and science in the Pythagorean tradition, opgenomen in: Mourelatos, The Presocratics, New York 1974

[p. 52]

nen van het kennen en van het dichten, ja zelfs van de droom, lopen onophoudelijk in elkaar over. Novalis wist van de pythagorese verwantschap tussen de poëtische logica en het mathematisch denken.’ Dat die verwantschap ook Broch zelf hardnekkig heeft beziggehouden zal nog blijken.

‘De scheiding tussen dichter en denker,’ schreef Novalis, ‘is slechts schijnbaar - en in beider nadeel.’ (AB 717).

Of de wens hier de vader van de gedachte is of niet - in elk geval lijkt ook Pythagoras voor het vaderschap ervan in aanmerking te komen en als zodanig is zijn rol nog niet uitgespeeld.

(wordt vervolgd)