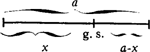De Revisor. Jaargang 2

[p. 44]

Géza Frid
De gulden snede en de vormverhoudingen in de kunst

Ik zit aan mijn schrijfbureau te werken en kijk af en toe naar buiten. Ik zie het raam, dat zoals de meeste van dit type, in drieën is verdeeld, ongeveer als hiernaast.

Het valt mij op, dat de plaatsing van de horizontale scheidingslijn (b) het oog bijzonder bevredigt. Ik neem de moeite om op te staan, haal de centimeter uit de kast en verricht enkele metingen; het blijkt dat lijn b lijn a precies op het punt van de gulden snede verdeelt.

Herinnert u zich nog, lezer, uit de wiskundelessen op de middelbare school, de definitie van de gulden snede? De gulden snede (sectio aurea) is die verdeling van een lijn waardoor de gehele lengte in dezelfde verhouding staat tot het langste deel, als dit langste tot het kortste. Als men de hele lijn met a aanduidt en het onbekende langste deel met x, dan zal het kortste deel a-x zijn:

Men kan dit als volgt noteren:

a : x	=	x : (a - x)
x^2	=	a (a - x)
x^2 + ax - a^2	=	o
x	=	½a (-1 ± √5)

Daar een lijnstuk geen negatieve waarde kan hebben, vervalt de waarde ½a (-1 - √5), dus x = ½a (-1 + √5) = a × 0,61803398875...

Hieruit kan men de praktische conclusie trekken dat men na vermenigvuldiging van de gehele lengte met 0,618... het langste gedeelte als uitkomst krijgt. Een merkwaardige verdeling dus (ergens tussen ½ en ⅔, doch dichter bij ⅗) die echter, zoals bij bovengenoemd vensterraam, steeds een bevredigend resultaat voor het oog oplevert. En niet alleen voor het oog, maar eveneens voor geest en gemoed - en hier raakt het probleem ‘gulden snede’ ons onderwerp: de vormverhoudingen in de kunst.

Het is alom bekend dat de architect bij de constructie van een bouwwerk niet slechts in esthetisch, doch ook in geometrisch opzicht wel degelijk met de gulden snede (g.s.) rekening moet houden. De g.s. openbaart zich volgens velen in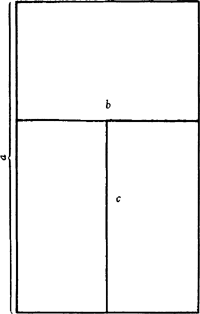



zijn meest aantrekkelijke vorm bij de gotische bouwkunst.

In hoeverre de beeldhouwer gebonden is de g.s. in zijn evenwichtsberekening te betrekken, is mij niet bekend;¹ evenmin weet ik of de g.s. bij de compositorische verdeling van een schilderij, bij de dosering van lijn en kleur, bewust of onbewust een rol speelt. Ook het onderzoek naar de eventuele aanwezigheid van de g.s. in de vormverhoudingen der literatuur stuit op moeilijkheden. Wat moet men hier immers als maatstaf nemen? De tijd die het voorlezen van een gedicht, een novelle, een roman en de opvoering van een toneelstuk duurt, of het aantal woorden (of lettergrepen)?²

Veel gemakkelijker is dit onderzoek in de muziek. Hier vormen ongetwijfeld het ritme, de maat, en het aantal metrische waarden (en niet de tijdsduur) de lengte van een muziekstuk. Wil men dus de g.s. van een compositie vaststellen, dan neemt men het aantal maten - in moderne werken

1 Men heeft aangetoond, dat de Lansdrager van Polykleitos in al zijn verhoudingen volgens de g.s. is geconstrueerd.

2 Ofschoon niet tot een der kunsten maar tot de denksport behorend, levert het schaakspel ten opzichte van de g.s. duidelijke gegevens op. Hier is het het aantal zetten van de gehele partij, dat men dan met 0,618 moet vermenigvuldigen om de g.s. te vinden. Afgezien van grove fouten, die de partij tot een voortijdig einde zouden kunnen brengen, valt de g.s. - althans in de partijen van de grote schaakmeesters - meestal op het hoogtepunt van de strijd.

[p. 45]

waar veel maatwisseling voorkomt, de metrische eenheden (kwarten of achtsten) - en men vermenigvuldigt dit getal met 0,618. Telt een stuk bijvoorbeeld 145 maten, dan valt de g.s. (145 × 0,618 = 89,610) in de 90e maat.³

De Hongaarse musicoloog Ernö Lendvai, een kenner bij uitnemendheid van Béla Bartóks oeuvre, heeft in Bartóks werken omtrent de rol van de g.s. verbazingwekkende ontdekkingen gedaan. In zijn boek Bartók stilusa (Bartóks stijl, Zenemükiadó, Boedapest 1955), waarin hij speciaal twee werken van de meester, te weten de Sonate voor twee piano's en slagwerk en de Muziek voor snaarinstrumenten, slagwerk en celesta aan een nauwkeurige analyse onderwerpt⁴, komt hij tot de volgende verrassende resultaten: in beide werken, maar vooral in de Sonate, zijn de vormverhoudingen van de kleinste details (de opbouw van de verschillende thema's afzonderlijk, de onderlinge relaties van het thematisch materiaal en de verhoudingen in de doorwerkingen enzovoort) tot de grootste proporties van de diverse delen zelf en ook naast elkaar, volkomen aan de getallen van de g.s. onderworpen. Ik zal u de details besparen en geef hier slechts de verhoudingen in het groot: de g.s. van de gehele sonate valt tot op de achtste precies (!) op de grens tussen het eerste en tweede deel. In cijfers uitgedrukt: het gehele werk bestaat uit 804 hele waarden,⁵ ofwel 6432 achtsten; de g.s. valt op de 3975e achtste - het laatste akkoord van deel I. Dit komt ook overeen met de psychologische opbouw van de sonate: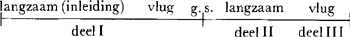

En nu de drie delen afzonderlijk:

Deel I	443 maten	g.s.	274e maat: reprise van het hoofdthema
Deel II	92 maten	g.s.	56e maat: het muzikale hoogtepunt
Deel III	420 maten	g.s.	260e maat: het hoogtepunt van de reprise

In de Muziek voor snaarinstrumenten, slagwerk en celesta zijn de verhoudingen ten opzichte van de g.s. minder spectaculair. Toch valt het op dat in deel I (88 maten) de g.s. precies op het culminatiepunt valt (de 56e maat in es - de meest verwijderde toonsoort van het uitgangspunt in a) en in het laatste deel (293 maten) op het moment van het afbreken van het dansritme, het begin van de doorwerking. Tellen we het aantal maten van het gehele werk op, dan blijkt dat de g.s. precies op de grens tussen II en III valt. Dus wederom:

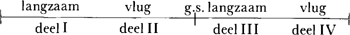
Wij zien hoe Bartók hier, bewust of onbewust, de g.s. als belangrijke factor van vormelement gebruikt. Ook in het eerste deel van het Divertimento voor strijkorkest valt de g.s. letterlijk op het begin van de reprise en in de Contrasten voor klarinet, viool en piano (deel I) eveneens. Maar het merkwaardigste is, dat Bartók in zijn bekend pianostuk Allegro barbaro gebruik maakt van de zogenaamde Fibonacci-cijfers!

En wat symboliseren de getallen van Fibonacci? Niets anders dan de g.s. in de meest vereenvoudigde vorm in hele cijfers uitgedrukt; zij brengen steeds een getal, dat de som is van de twee voorafgaande: 1-2-3-5-8-13-21-34-55-89 enzovoort. De fis-mol begeleidingsfiguren van het Allegro barbaro komen hier namelijk, steeds als de melodie ophoudt, in precies hetzelfde, toenemende aantal maten voor (3-5-8-13) als bovengenoemde cijfers dit aangeven. - Zou het in het oog vallend gebruik hiervan erop wijzen, dat Bartók de g.s. ook in zijn grote werken bewust heeft gehanteerd? Dit verrassende element in de composities van Bartók was voor mij aanleiding het oeuvre der klassieke meesters uit dit oogpunt te onderzoeken: de grote werken van Haydn, Mozart en Beethoven, de volledige beheersers der vormkunst, bij wie van een bewust gebruik der g.s. dunkt mij geen sprake kan zijn. Welnu, na het doorkijken van een groot aantal hunner symfonische werken en kamermuziek kwam ik tot de conclusie dat de g.s. zich hier eveneens steeds in de buurt van het keerpunt (hoogte- of dieptepunt) der compositie bevindt - het verschil is haast nooit meer dan 16 maten ervoor of erna - namelijk bij grotere vormen (sonate of groot rondo) bij de reprise, in menuetti of scherzi tussen trio en da capo, in langzame delen bij de reprise of op het dynamische hoogtepunt en in variatievormen meestal voor of na de langzame variatie. En ook bij de werken der romantici vond ik - ofschoon met ruimer verschil - een opvallende nabijheid tussen wiskundig en muzikaal hoogtepunt.

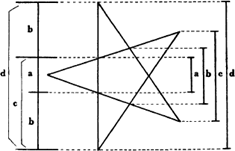
De g.s. is een begrip dat geheel uit de natuur en haar veelheid van vormen is voortgekomen. Fibonacci vond bij het bestuderen van de vruchtbaarheid der konijnen zijn bovengenoemde g.s.-achtige cijferreeks terug.⁶ Ook in de spiraalvorming der bloemstelen zijn deze cijfers steeds aanwezig. Een der schoonste voorbeelden van de g.s. is ongetwijfeld het zogenaamde pentagram - in de middeleeuwen boven de huisdeur bevestigd om de duivel af te weren - waarin alle verhoudingen op de g.s. zijn gebaseerd:⁷ Ook Goethe maakte in Faust dankbaar gebruik van de duivelafwerende functie van het pentagram (eerste deel, Studirzimmer):

Mephistopheles

Gesteh' ich's nur! Dass ich hinausspaziere,
Verbietet mir ein kleines Hinderniss,
Der Drudenfuss auf eurer Schwelle.

3 Ik geef de raad aan concertinstellingen, impressario's, enz. de pauze der concerten ongeveer op de g.s. van de avond te houden. Hier gaat het vanzelfsprekend niet om het aantal maten, doch om de tijd. De tijdsduur van het gehele programma × 0,618 geeft dan de g.s. (Dit houdt natuurlijk niet in, dat de pauze het hoogtepunt van het concert zou moeten zijn!)

4 Zie ook mijn artikel Twaalf contra twaalf in: M. en M. december 1957.

5 Hierbij wordt ermee rekening gehouden, dat in de uitgave van Boosey and Hawkes de aanduiding van maat 411 (laatste deel) niet juist is.

6 Een stelling van Lendvai, die ik echter bij bio- en zoölogen niet bevestigd kon krijgen.

7 De vijfstraligheid speelt overigens bij het planten- en primitieve dierlijk leven altijd een belangrijke rol; ook bij het uitrekenen van het getal 0,618... komt de wortel van vijf te pas (zie het begin van dit artikel).

[p. 46]

d : c = c : b = b : a = 1 : 0,618

Faust

Das Pentagramma macht dir Pein?
Ei, sage mir, du Sohn der Hölle,
Wenn das dich bannt, wie kamst du denn herein?
Wie ward ein solcher Geist betrogen?

Mephistopheles

Beschaut es recht! es ist nicht gut gezogen;
Der eine Winkel, der nach aussen zu,
Ist, wie du siehst, ein wenig offen.

Bij deze overpeinzingen kwam ik op de gedachte, of de g.s. misschien ook in het leven van de mens, en vooral in het veelbewogen leven van de scheppende kunstenaar (en andere belangrijke figuren uit het openbare leven) een bepaalde taak zou vervullen. Mijn onderzoekingen leidden tot resultaten die de factor toeval tot het minimale reduceren. Eerst neem ik de voornaamste (overleden) componisten vanaf Haydn tot onze dagen, waarbij ik ook degenen vermeld, wier leven (en dood) mijn berekeningen niet ondersteunen.⁸

	g.s.
Haydn (1732-1809)	1779-'80	Niets bijzonders gevonden; of misschien de kennismaking met zijn grote liefde, Luigia Polzelli.
Mozart (1756-1791)	1778	Parijs, de dood van zijn moeder; kennismaking met de familie Weber te Mannheim, terugkeer naar Salzburg.
Beethoven (1770-1827)	1804-'05	Fidelio en Eroica; keerpunt in zijn scheppingswerk.
Schubert (1797-1828)	1816	Het ontstaan van de Vierde en Vijfde symfonie; de eerste grote werken van zijn volledig meesterschap.
Mendelssohn (1809-1847)	1832-'33	Hebriden-ouverture en de Italiaanse symfonie; de eerste uitvoering van de Sommernachtstraum te Londen, begin van zijn wereldroem.
Schumann (1810-1856)	1838-'39	Kinderszenen; verloving met Clara Wieck.
Chopin (1810-1849)	1834	Niets bijzonders gevonden.
Liszt (1811-1886)	1856	Weimar, bezoek van Berlioz; het ontstaan van de Graner Messe, zijn eerste kerkelijke compositie.
Wagner (1813-1883)	1854-'55	Kennismaking met de filosofie van Schopenhauer; Mathilde Wesendonck. De eerste conceptie van Tristan und Isolde.
Verdi (1813-1901)	1867	Don Carlos, overgang van zijn populaire opera's naar een andere stijl.
Brahms (1833-1897)	1872	Dood van zijn vader; blijvende vestiging in Wenen.
Debussy (1862-1918)	1896	Niets bijzonders.
Ravel (1875-1937)	1911-'12	Voltooiing en première van Daphnis et Chloé.
Bartók (1881-1945)	1920-'21	Contract met Universal Edition, hetgeen de verspreiding van zijn werken in de gehele wereld betekende.
Pijper (1894-1947)	1926	Het ontstaan van zijn chef d'oeuvre: de Derde symfonie.

Nu nog enkele (willekeurige) grepen uit het leven van schilders, schrijvers en - voor de curiositeit - van een ‘heerser’:

Rembrandt (1606-1669)	1645	Vanaf dit jaar is Hendrikje Stoffels op zijn schilderijen te herkennen.
Goya (1746-1828)	1796	Zijn terugkeer tot het leven na zijn zware ziekte, waar hij zijn doofheid van overhoudt.

8 Het uitrekenen van de g.s. van een mensenleven geschiedt op de gebruikelijke wijze: treedt de dood bijvoorbeeld op 70-jarige leeftijd in, dan valt de g.s. (70 × 0,618 = 43,26)

[p. 47]

	g.s.
Goethe (1749-1832)	1800	Hoogtepunt van zijn vriendschap met Schiller; genezing van zijn levensgevaarlijke ziekte.
Tolstoi (1828-1910)	1879	Zijn religieuze crisis, die zijn verder leven en werk in een totaal andere richting drijft.
Napoleon (1769-1821)	1801	Benoeming tot Eerste Consul; het begin van zijn volledige heerschappij.

En zo kunnen wij nog doorgaan en ons steeds verbazen, dat de g.s. in het leven der eminenten bijna altijd op een belangrijk keerpunt valt.

Maar nu gaan wij de zaak omkeren: veronderstel, dat in het werk de g.s. bekend is en de gehele lengte niet. Om deze uit te rekenen, moeten wij dan de ons bekende afstand door 0,618 delen: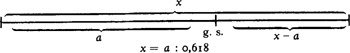

Hieruit volgt, dat een ervaren componist het werk, dat hij onder handen heeft, gemakkelijk aan de regels van de g.s. kan onderwerpen en hierdoor het meest zuivere vormevenwicht kan bereiken. Op het moment dat hij voelt, dat zijn compositie het keerpunt heeft bereikt (of dit een hoogte- of dieptepunt is, hangt van het karakter van het werk af), moet hij de aanwezige maten (of kortere waarden) optellen en dit getal door 0,618 delen. Dan krijgt hij de juiste lengte van het geheel; hij weet dus precies hoeveel maten hij nog te schrijven heeft en dan is het een kwestie van routine, om deze op de juiste manier te realiseren - de inspiratie zal hierbij heus niet te kort komen.

Nog een stap verder is het om dezelfde procedure bij nog levende tijdgenoten toe te passen. Aangezien slechts een betrekkelijk klein aantal mensen hun 80ste jaar beleven, is men dus pas na zijn 50ste jaar - 50 is ongeveer de gulden snede van 80 - in staat om zijn levensloop zodanig te overzien, dat het keerpunt van zijn leven met enige zekerheid als gulden snede kan worden uitgekozen. Een griezelige aangelegenheid, voor bijgelovige en fatalistische personen niet aan te bevelen!

Wat mijzelf betreft, heb ik deze stap aangedurfd en na rijpe overweging heb ik de preciese datum der g.s. van mijn levensloop op 16 febr. 1949 - ik was toen in mijn 45ste jaar - vastgesteld. Het is dus op mijn 72ste jaar, exact uitgerekend (rekening houdende met de schrikkeljaren) op 16 dec. 1976, dat ik het tijdelijke met het eeuwige zou verwisselen.

De heimelijke overtuiging dat dit zou kloppen, draag ik al meer dan 20 jaar met me mee. Door allerlei omstandigheden, o.a. door enkele in latere periode plaatsgevonden hoogtepunten en vooral op aandringen van familie en vrienden, ben ik van mijn oorspronkelijke g.s.-datum teruggekomen en heb ik de ‘fatale dag’ naar een later tijdstip uitgesteld. Maar ergens in mijn binnenste geloof ik nog steeds aan de eerste versie en wacht nu met belangstelling en zonder angst de verdere gebeurtenissen af.