Ons Erfdeel. Jaargang 36

[p. 721]

Recente Nederlandse ontdekkingen in de fysica
Huub Eggen

HUUB EGGEN
werd in 1948 geboren te Maastricht. Hij studeerde fysische geografie. Is voorlichter bij de Stichting voor Fundamenteel Onderzoek der Materie (FOM). Hij publiceerde artikelen over wetenschap en techniek, is vertaler van enkele populair-wetenschappelijke boeken en mede-auteur van een boek over de Space Shuttle.
Adres: Van Musschenbroekstraat 54, NL-3514 XL Utrecht

’Ik vertel mijn studenten vaak, als ze het in deze wereld niet zo meer zien zitten, dat er twee dingen zijn die mijn leven de moeite waard maken: Mozart en quantum mechanica’. Die uitspraak is afkomstig van de beroemde Amerikaanse natuurkundige Victor Weisskopf. De quantummechanica, waarvoor de grondslag in het begin van deze eeuw werd gelegd, heeft iets geheimzinnigs dat net als bizarre fenomenen uit de sterrenkunde een breed publiek aanspreekt. Er is momenteel een geweldige hausse in boeken over natuurkunde en met name over de zogeheten ‘nieuwe natuurkunde’. In de New York Times van 2 februari 1989 stond een artikel onder de kop: ‘Tophoeken van 1988: spionnen en fysica’. Diverse boeken over natuurkunde waren geweldige verkoopsuccessen in dat jaar.

Het mysterieuze van de quantummechanica wordt voornamelijk bepaald door het feit dat deze theorie ‘een logica vereist die niet direct afgeleid kan worden uit de dagelijkse ervaring’, zoals de Amerikaanse Nederlander professor Abraham Pais, die wereldbekendheid geniet als Einstein-biograaf, een interview met het Nederlandse dagblad Trouw zei. Er is geen enkele analogie te maken tussen onze wereld en de quantumwereld. De quantummechanica is een bouwwerk van formules dat heel goed experimentele waarnemingen beschrijft, maar dat daarom nog niet automatisch tot begrip leidt. De in 1988 overleden Amerikaanse natuurkundige en Nobelprijswinnaar Richard Feynman zei eens: ‘Ik denk dat ik veilig kan zeggen dat niemand de quantummechanica begrijpt’. Toch heeft ieder meer met de quantummechanica te maken dan men denkt. Dankzij de quantummechanica begrijpen wij hoe de zon aan haar energie komt. Op de quantummechanica is de werking van computers en compact disc-spelers gebaseerd. ‘Mensen merken er dus wel wat van, maar ze weten niet dat ze het merken’, aldus Pais in het eerder genoemde interview in Trouw.

[p. 722]

Tegelijk golf en deeltje

Eén van de bekendste elementen uit de quantummechanica is het zogeheten golfdeeltjes-dualisme. Een deeltje, laten we zeggen een elektron, kan zich manifesteren als deeltje maar ook als golf. In onze dagelijkse wereld kunnen we elektronen zonder problemen als deeltjes beschouwen. De elektriciteitsleer kan met elektronen als deeltjes uitstekend uit de voeten. Gaan we echter naar elektronen kijken op het niveau van atomen, dan voldoet de deeltjesbeschrijving niet meer. Elektronen moeten dan als golfverschijnsel worden beschreven. Om dit te illustreren zullen we twee recente experimenten van Nederlandse onderzoekers bekijken, die binnen de natuurkunde wereldwijd de aandacht hebben getrokken. Praktische toepassingen hebben de uitkomsten van die experimenten niet, daarvoor zijn ze te fundamenteel van karakter.

Onlangs namen onderzoekers van het FOM-Instituut voor Atoom- en Molecuulfysica in Amsterdam en de Universiteit van Amsterdam de beweging van één elektron in een atoom waar. Het mag heel raar klinken, maar zij waren de eersten in de wereld die dit deden en hun prestatie haalde vrijwel alle kranten in Nederland. De bijzondere prestatie, die pas nu mogelijk was door de ontwikkeling van een geavanceerde lasertechniek, koppelt de klassieke mechanica en de quantummechanica aan elkaar.

Bijna iedereen zal het klassieke atoommodel kennen. Dat ziet eruit als een soort planetenstelsel. Rond de atoomkern bewegen elektronen, op verschillende afstanden van de kern vandaan. De elektronen kunnen niet op elke willekeurige afstand staan. Ze moeten zich houden aan bepaalde, door de theorie heel nauwkeurig voorgeschreven banen. Onder invloed van licht kunnen ze van baan veranderen, maar vroeg of laat zullen ze altijd terugkeren naar de baan waarin ze thuishoren. Zo kan worden uitgerekend dat een bepaald elektron in een rubidium-atoom met behulp van een zeer kortstondige laserpuls in een grote, excentrische baan gebracht kan worden. Na een tijdbestek van 10^-11 seconde (eenhonderdmiljardste seconde) keert dat elektron terug naar zijn oorspronkelijke plaats, dicht bij de atoomkern. Als het elektron precies op datzelfde moment opnieuw met een laserpuls wordt bestookt, zal zijn baan zo groot worden dat het uit het atoom ontsnapt. Een detector zal dan een signaal meten.

Nu geldt in de kleine wereld van atoomkernen en elektronen de klassieke mechanica

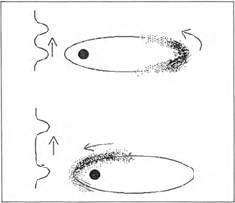
Een elektron als een ‘klontje waarschijnlijkheid’.

[p. 723]

niet meer. Slechts de quantummechanica beschrijft de gebeurtenissen rond de atoomkern op de juiste manier. Het gedrag van elektronen kan beschreven worden in termen van golven. Deze golven zijn ruimtelijk uitgebreid, een paar duizend keer groter dan een atoom, dus atoomkern plus de ruimte erom heen waarin de elektronen rondlopen. Hoewel elke golf afzonderlijk heel uitgebreid is, is de som van alle golven samen dat niet. Bijna overal doven de golven elkaar via interferentie uit. Er is maar een klein gebied waar de golven elkaar juist versterken en vanuit de klassieke mechanica gezien is dat juist de plaats waar het elektron is. In de klassieke beschouwing draait het elektron baantjes rond de kern; die beweging is nu quantummechanisch gezien de verplaatsing van de plek waar de golven elkaar het meest versterken. Die plek werd door één van de onderzoekers omschreven als een ‘klontje waarschijnlijkheid’.

Een van de - voor ons gevoel - bizarre consequenties van de quantummechanica is namelijk dat de plaats en de snelheid van een deeltje nooit tegelijk exact bepaald kunnen worden. Wordt de plaats bepaald, dan kan er geen preciese uitspraak over de snelheid gedaan worden en omgekeerd. Zolang de onderzoeker niet precies gaat kijken waar het elektron zich bevindt, kan hij over de plaats slechts een uitspraak doen in termen van een grotere of een kleinere waarschijnlijkheid dat het elektron zich er werkelijk zal bevinden als hij gaat meten. Overigens komt het definitieve antwoord pas als het moment van meten aangebroken is. Het elektron is er dan wel of niet. In het ‘planeetmodel’ van een atoom zou op elk moment precies voorspeld kunnen worden waar het elektron zich ophoudt, in de quantummechanische benadering kan dat per definitie niet. Omdat in het experiment in Amsterdam werkelijk elektronen uit hun atoom werden weggeschoten, werd de plaats van die elektronen dus werkelijk bepaald en zo gaan hier resultaten uit de klassieke mechanica en de quantummechanica op fraaie manier in elkaar over.

Elektronen golven door een poort

Een tweede voorbeeld van een effect uit de quantummechanica komt uit onderzoek dat door wetenschappers bij de Technische Universiteit Delft en Philips werd gedaan. Dit onderzoek maakte gebruik van het feit dat met geavanceerd technieken steeds kleinere materiaalstructuren gemaakt kunnen worden. Het gaat dan om afmetingen van ver beneden de eentienduizendste millimeter. De achtergrond van dit soort onderzoek is de belangstelling vanuit de micro-elektronica voor zeer kleine afmetingen van structuren. De snelheid van computers bijvoorbeeld kan toenemen wanneer de afstanden tussen elementen op een chip heel klein gemaakt worden. Zoals al opgemerkt neemt de quantummechanica de plaats van de klassieke mechanica in wanneer we in het rijk van heel kleine afmetingen komen. In het onderzoek aan heel kleine structuren wordt de vraag hoe elektronen zich gaan gedragen, van groot belang. Als model is gekeken naar het gedrag van elektronen die gedwongen worden door een uiterst smal kanaaltje te lopen. De elektronen kunnen dan alleen maar vooruit of achteruit. Het kanaaltje werd vervaardigd door een poort van elektrisch geleidend materiaal te maken. Door over die poort een elektrische spanning te zetten, kan de breedte ervan voor elektronen worden gevarieerd. Die ervaren de poort dan als een nauwere of minder nauwe doorgang. Om na te gaan hoeveel elektronen die doorgang passeren, wordt de geleiding gemeten. Die is een maat voor de hoeveelheid passerende elektronen. Volgens het klassieke model zou de geleiding lineair moeten toenemen wanneer de doorgang breder wordt. Wie een waterkraan opendraait, weet dat er maar een dun straaltje water komt als de kraan een beetje openstaat en dat de straal dikker wordt naarmate we de kraan verder openzetten. Omdat de opening, de poort, in het Delftse experiment heel nauw gemaakt zou worden, wist de onderzoeker die de experimenten uitvoerde, dr. Bart van Wees (^o1961), al bij voorbaat dat er dan door het golfkarakter van

[p. 724]

de materie quantummechanische effecten zouden gaan optreden. De grote vraag was echter welke. Tot zijn verrassing bleek de geleiding in mooie, regelmatige stapjes toe te nemen, naarmate de doorgang breder gemaakt werd. Dat kon alleen maar het verwachte quantumeffect zijn. De afmeting van de doorgang was in de orde van de golflengte van de elektronen gekomen. Daarbij treedt interferentie van golven op, net zoals in het eerder beschreven experiment in Amsterdam. Dat betekent dat er alleen maar elektronen door de poort kunnen komen, als de breedte van die poort gelijk is aan een passende golflengte. Het is te vergelijken met het staan op een trap. Je kunt maar op één bepaalde trede staan en niet er tussen in, aldus Van Wees in het blad Delta van de Delftse universiteit. Van Wees en collega's kregen hun resultaat binnen twee maanden gepubliceerd in een gezaghebbend Amerikaans tijdschrift, hetgeen uitermate snel is.

Atomen verplaatsen met licht

Het is niet alleen maar quantummechanica wat in de moderne natuurkunde de klok slaat. Recent hebben twee eigenlijk heel klassieke experimenten internationaal opvallende resultaten opgeleverd. Beide experimenten hebben

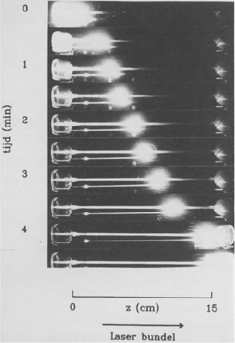
Een wolkje natriumatomen wordt met behulp van een laserbundel door een gas geduwd.

met licht te maken. In het eerste geval blijkt (laser)licht gebruikt te kunnen worden om atomen te verplaatsen, in het tweede geval is een heel nieuwe manier van voortplanting van licht ontdekt.

Aan het verplaatsen van atomen met licht, dat in het Engelstalige internationale jargon van de fysica als light-induced drift (LID) bekend staat, is aan de Rijksuniversiteit Leiden, in samenwerking met Russische theoretici, opmerkelijk onderzoek gedaan. Het verplaatsen van atomen is in een gasmengsel, dus een mengsel van verschillende soorten atomen met ieder hun eigen specifieke afmetingen, in principe het gemakkelijkst te realiseren. In een gas bewegen atomen in alle mogelijke richtingen. Afzonderlijke atomen botsen wel 100 miljoen keer per seconde met andere atomen. Daarbij wordt hun bewegingsrichting steeds veranderd. Kijken we bijvoorbeeld naar een gas dat uit natrium- en xenonatomen bestaat. Onze

[p. 725]

aandacht richt zich op de natriumatomen. Normaal verkeren die atomen in de zogeheten grondtoestand, waarbij ze hun kleinste afmeting hebben. Wanneer we ze zouden bestralen met (laser)licht van een heel bepaalde golflengte, worden de buitenste elektronen van de natriumatomen heel even in een iets grotere baan om de kern van het atoom gebracht. De natriumatomen heten dan aangeslagen; hun afmeting is dan iets groter dan voorheen.

In hun experiment hebben de onderzoekers het gasmengsel bestraald met laserlicht van een golflengte die net boven de golflengte zit waarbij de atomen worden aangeslagen. Er gebeurt dan zoals verwacht niets, behalve met die atomen die tegen de richting van de laserbundel in bewegen. Die atomen zien door hun beweging (het bekende Doppler-effect) de golflengte van het inkomende licht iets verschoven, tot precies de golflengte waarbij ze wel worden aangeslagen. Omdat aangeslagen atomen iets groter zijn dan hun broertjes in de grondtoestand, hebben ze een iets grotere kans om te botsen met een xenonatoom. Daardoor ondervinden die aangeslagen natriumatomen een grotere weerstand bij hun beweging door het xenongas. Het resultaat hiervan is dat de natriumatomen die naar de laserbron toe bewegen, meer worden afgeremd dan de natriumatomen die in andere richtingen bewegen. Omdat alle natriumatomen zo vaak per seconde botsen en dan van bewegingsrichting veranderen, zullen ze het ene moment tegen het laserlicht in bewegen en het volgende moment weer met het licht mee. In het eerste geval worden ze aangeslagen, in het tweede geval niet. Netto beweegt elk natriumatoom echter gemakkelijker met de laserstraal mee, zodat er een stroming optreedt weg van de laserbron. In de experimenten in Leiden is een snelheid van circa 14 meter per seconde gehaald. In een glazen buis kan men dan een bolletje natrium zien wegschieten, puur doordat er een laserstraal in het gas gericht wordt. Door de golflengte van het laserlicht net iets te kort te maken, kan men de natriumatomen naar de laser toe ‘zuigen’. Voor de experimenten is een laser nodig die uitermate nauwkeurig afgestemd kan worden op de gewenste golflengte. Die techniek hadden de Russische onderzoekers niet tot hun beschikking en de wetenschappers in Leiden wel. Omdat de lasertechniek overal steeds beter wordt, komen allerlei soorten experimenten, die tot voor kort alleen op papier mogelijk waren, nu binnen het bereik van de onderzoekers. Dat levert voortdurend nieuwe spectaculaire resultaten in het manipuleren van atomen en moleculen.

Op jacht naar het witte gat

Het tweede voorbeeld van een experiment met licht dat internationaal de aandacht heeft getrokken, is een onderzoekproject dat aan de Universiteit van Amsterdam onder leiding van professor Ad Lagendijk wordt uitgevoerd. Het gaat om zogeheten lokalisatie van licht, een geheel nieuw fenomeen dat een optisch analogon is van het gedrag van elektronen in een vast materiaal.

Het begon voor Lagendijk een paar jaren geleden, toen hij op een conferentie in Den Haag naar een voordracht van een Amerikaan zat te luisteren. Die had het over lokalisatie van elektronen, een verschijnsel dat verklaart waarom de elektrische geleiding in een vaste stof vaak anders blijkt dan verwacht. Elektrische geleiding in een materiaal is niets anders dan verplaatsing van elektronen door dat materiaal. Hoe beter dat gaat, hoe beter de geleiding. Als over een perfect kristal een elektrisch veld wordt aangelegd, dan moet in principe de geleidbaarheid van dat kristal oneindig zijn. In de praktijk is dat nooit zo, want er zijn altijd wel fouten in de kristalstructuur. Een vrij bewegend elektron wordt door zo'n fout, bijvoorbeeld een atoom op een verkeerde plaats of een te groot atoom op de plek waar een kleiner hoort te zitten, uit zijn koers gekaatst. Zo'n verstoorde beweging is elektrische weerstand. Een maat voor de geleidbaarheid is de zogeheten gemiddelde vrije weglengte, de afstand die elektronen gemiddeld kunnen afleggen, zonder met een vreemd atoom in botsing te komen. In een perfect kristal is die afstand oneindig groot. Hoe meer wanorde er in een kristal is, hoe kleiner de gemiddelde vrije weglengte.

[p. 726]

Professor A. Lagendijk (^o1947).

In deze redenering stelde Nobelprijswinnaar professor Philip Anderson in de jaren '60 de vraag of er een benedengrens is aan de gemiddelde vrije weglengte. Wat gebeurt er als je de wanorde in een kristal oneindig groot maakt? Het antwoord is dat er inderdaad een benedengrens is aan de gemiddelde vrije weglengte, maar daarvoor moet het elektron niet meer als een deeltje worden beschouwd, maar als een golf, zoals de quantummechanica dat doet. Zodra de golflengte van het elektron groter wordt dan de gemiddelde vrije weglengte, dan kan het elektron niet meer golven. Het botst al weer met een deeltje dat het op zijn weg ontmoet, voordat het één golfbeweging vol gemaakt heeft. De grens die Anderson zocht, wordt bereikt als het elektron zo vaak botst dat het zich niet meer voort kan planten. Het elektron dat zich op een bepaalde plaats bevindt, komt daar niet meer vandaan. Dit fenomeen noemde Anderson lokalisatie.

Elektronen die zich gedragen als golven, produceren na elke botsing een nieuw golffront. De oude fronten blijven echter bestaan, onafhankelijk van de nieuwe beweging van de elektronen. Een vast materiaal zit dus vol met golffronten die met elkaar kunnen interfereren. De fronten zullen elkaar meestal uitdoven, maar kunnen elkaar ook versterken. Onhandig bij het rekenen aan dit gedrag is het feit dat in een vast materiaal het kristalrooster altijd aan het trillen is. Niet alleen lokalisatie heeft daarom invloed op de elektrische weerstand van het materiaal, ook het trillen van het rooster speelt mee.

Dat schoot Lagendijk allemaal door het hoofd, toen hij naar die Amerikaan zat te luisteren. Opeens realiseerde hij zich dat je van die complicaties af zou zijn als je in plaats van elektronen licht zou gebruiken voor experimenten. Licht heeft zowel het karakter van deeltjes als van golven en kan dus uitstekend als model dienen voor het elektronengedrag. Nog herinnert Lagendijk zich de opwinding van dat moment, toen zich bij hem, en kennelijk als enige in die zaal, die mogelijkheid en de verregaande betekenis van zo'n experiment opdrong. ‘Lokalisatie van licht is op zich een heel fundamenteel fenomeen. Verder is de overeenkomst met elektronen ook heel fundamenteel. Bovendien heeft iedere fysicus de drang om te unificeren. Elke diepgaande analogie is dan heel welkom’.

‘Bij licht kun je iets doen, wat bij elektronen niet te doen valt’, zegt Lagendijk, ‘namelijk de terugkeerwaarschijnlijkheid meten. Dan moet ik eerst even iets uitleggen. De kans dat een elektron op een plaats terugkomt waar

[p. 727]

het eerder geweest is, noemt men de terugkeerwaarschijnlijkheid. Deze waarschijnlijkheid is een essentiële grootheid die altijd wel in het spel is. Alleen, bij lokalisatie is de terugkeerwaarschijnlijkheid 100 procent. Ik gebruik vaak het volgende beeld. Een zeeman is naar de kroeg en zijn vrouw komt erachter waar hij uithangt. Ze gaat naar dat café toe om hem naar huis te halen. Bij aankomst ziet ze haar man al op de stoep, in beschonken toestand waggelend van hot naar haar. Een ‘random walk beweging’ zouden natuurkundigen zeggen. Ze holt naar hem toe en begint aan hem te sjorren. De man is echter sterker dan zij en zet elke keer weer een stap in een richting die zij niet wil. Het enige wat zij voor elkaar krijgt, is dat ze hem steeds weer die ene stap terugtrekt. In welke richting de man ook een stap zet, zijn vrouw trekt hem terug en het resultaat van alle geharrewar is dat ze steeds weer uitkomen op het vertrekpunt. De terugkeerwaarschijnlijkheid is honderd procent geworden. De zeeman is gelokaliseerd’.

Theoretici weten dat zoiets ook gebeurt met golven in een vast materiaal. De golffronten die door interferentie uitdoven, zijn de elektronen die in het materiaal opgesloten raken. Alleen golven die, in tegengestelde richting, precies hetzelfde pad afleggen, zullen elkaar altijd versterken. ‘En welke golven zijn dat? Dat zijn de golven die in hun vertrekpunt terugkomen. Dus is er een grote terugkeerwaarschijnlijkheid en bij licht moet dat leiden tot verstrooiing precies terug naar de lichtbron waarmee je je experiment doet. Als je dat kunt meten, dan bewijs je in ieder geval dat dit mechanisme werkt en dat lokalisatie van licht moet kunnen bestaan. Wij in Amsterdam waren de eersten in de wereld die dit experiment voor licht bedachten’.

Om het effect van terugkeer van licht te bereiken, moest een stof gemaakt worden waarin de materiaalfouten die in kristallen zo belangrijk zijn, worden nagebootst. Voor licht betekent dat het veroorzaken van breking. De oplossing bleek water te mengen met heel kleine polystyreenbolletjes, die biologen bijvoorbeeld gebruiken om microscopen te ijken. Ook suspensies van titaandioxide (zeg maar witte verf) werken heel goed. De experimentele opstelling is van een haast ontnuchterende eenvoud.

Door de experimenten is het mechanisme van terugkeer van licht naar de lichtbron aangetoond. Zwakke lokalisatie wordt dat genoemd. Doel van de verdere experimenten is sterke lokalisatie te krijgen. Dat is technisch veel moeilijker te realiseren. De gemiddelde vrije weglengte moet immers kleiner zijn dan de golflengte van het licht en dat kan alleen bereikt worden door het experimenteermedium heel dicht te maken en voor een groot verschil in brekingsindex te zorgen tussen de vloeistof en de bolletjes waaraan het licht moet verstrooien. Als de sterke lokalisatie werkt, dan komt er geen licht meer in het medium en het licht dat erin zit, komt er niet uit. Dat doel is wat Lagendijk de jacht op het witte gat noemt. Hij en zijn medewerkers zijn met een reeks van experimenten op weg naar dat doel.

Het lokalisatie-onderzoek is heel fundamenteel van aard en van groot belang voor meer inzicht in al die verschijnselen waar golven en voortplanting van golven een rol spelen. Die verschijnselen doen zich niet alleen voor in de optica, maar ook in de microelektronica, waar zulke kleine schakelingen gemaakt worden dat ze de golflengte van een elektron krijgen. Voortplanting van licht vormt niet alleen een analogon voor elektrische weerstand (in termen van verstrooiing), maar ook voor geleiding (door te meten hoeveel licht door het medium heen komt). ‘Het is allemaal heel bijzonder’, zegt Lagendijk. ‘De Maxwell-vergelijkingen, die uit de vorige eeuw stammen en die voortplanting en verstrooiing beschrijven, zijn de best bestudeerde vergelijkingen uit de natuurkunde. Toch hebben we iets heel nieuws gevonden!’.

Kathedralen van de natuurkunde

Van een geheel andere orde zijn de experimenten die bij het Europese centrum voor deeltjesonderzoek CERN in Genève worden uitgevoerd. Hier wordt in een deeltjesversneller van een geweldige omvang en een duizelingwekkende complexiteit gespeurd naar de meest elementaire bouwstenen van de materie.

[p. 728]

Nobelprijswinnaar dr. Simon van der Meer (^o1925).

Aan het huidige succes van CERN heeft de Nederlander dr. Simon van der Meer een flinke steen bijgedragen. Voor zijn werk ontving hij in 1984, samen met dr. Carlo Rubbia, de huidige hoogste man bij CERN, de Nobelprijs voor de natuurkunde.

In deeltjesversnellers jagen onderzoekers deeltjes op tot een snelheid die in de buurt komt van de lichtsnelheid. Wanneer bij een dergelijke snelheid deeltjes met elkaar botsen, komen verschijnselen aan het licht die informatie geven over de meest fundamentele eigenschappen van de materie. Nu is het niet eenvoudig deeltjes tot de benodigde geweldige snelheid op te jagen. Men maakt gebruik van de elektrische lading van deeltjes om ze met behulp van magneetvelden te manipuleren en te versnellen. Hoe sneller de deeltjes bewegen, hoe moeilijker ze in de versneller op hun koers te houden zijn. Wie zich probeert voor te stellen hoe hij deeltjes die met een snelheid van zeg 260.000 kilometer per seconde voorbijrazen, in toom moet houden, zal zich realiseren dat zoiets geen eenvoudige opgave is. Van der Meer nu heeft een techniek ontwikkeld om dat toch te doen. Zijn techniek houdt geen rekening met afzonderlijke deeltjes, maar werkt met de hele deeltjesbevolking die op elk moment door de versneller raast. Er kan voor al die deeltjes een gemiddeld gedrag beschreven worden en door daar correctiemaatregelen op uit te voeren, zullen alle deeltjes gemiddeld in het gareel gehouden worden. Die techniek blijkt heel goed te werken. Hij wordt ook gebruikt voor experimenten met de nieuwe versneller LEP bij CERN, die zeer onlangs tot een fundamenteel resultaat in de natuurkunde hebben geleid.

Wie iets te weten wil komen over de meest fundamentele eigenschappen van de materie, moet omstandigheden creëren waarin deeltjes enorm veel energie hebben. Daarom wordt het bestuderen van elementaire deeltjes ook wel hoge-energiefysica genoemd. In de natuur komen hoge-energie-omstandigheden nauwelijks voor. Bij het begin van het heelal, in de gebeurtenis die bekend staat als de ‘Big Bang’, was er echter alleen maar hoge energie. Uit wat er toen gebeurde is alle materie in ons universum ontstaan. Om de fundamentele krachten te kunnen begrijpen, die de aard van alle materie bepalen, moeten daarom omstandigheden worden gemaakt die lijken op die in het heelal, onmiddellijk na de Big Bang. Dat kan in beperkte mate met de grote deeltjesversnellers die er momenteel op de wereld zijn.

Wanneer de materie tot op het meest elementaire niveau wordt ontleed, blijkt de

[p. 729]

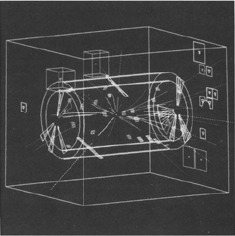
Een registratie van een kracht-overbrengend deeltje (het Z^o-deeltje). Voor het meetbaar maken van dergelijke deeltjes kregen Simon van der Meer en Carlo Rubbia in 1984 de Nobelprijs voor Natuurkunde, (foto CERN).

natuur te bestaan uit een aantal deeltjes die kennelijk de bouwstenen van ons heelal zijn. Die deeltjes noemt men elementaire deeltjes. In de jaren '60 begonnen natuurkundigen steeds meer van die deeltjes te ontdekken, totdat er uiteindelijk zoveel waren dat twijfel rees of al deze deeltjes wel werkelijk elementair waren. Op grond van die twijfel zijn theoretischnatuurkundigen een model gaan ontwikkelen dat nu bekend staat als het standaardmodel. Uit dat model volgt dat er drie, of misschien vier generaties elementaire deeltjes moeten zijn, waarbij elke generatie acht leden telt. Waarom dat zo is, weet nog niemand. Uit het model volgt ook dat er fundamentele krachten tussen de deeltjes werkzaam zijn; die krachten worden door een bepaald soort deeltjes overdragen. Drie van die krachten spelen zich af op het niveau van atomen, atoomkernen en deeltjes in de kernen; de vierde kracht is de zwaartekracht. Natuurkundigen hopen dat die vier krachten ooit binnen één theorie beschreven kunnen worden.

Voor het accepteren van de standaardtheorie is het noodzakelijk dat het bestaan van de fundamentele krachten en in het bijzonder de overdragende deeltjes experimenteel wordt aangetoond. Het werk waarvoor Rubbia en Van der Meer hun Nobelprijs kregen, behelsde het daadwerkelijk opsporen van drie van die kracht-overdragende deeltjes. Uit een heel nauwkeurig onderzoek van die deeltjes kan verder een uitspraak worden gedaan over de vraag of er niet toch meer dan drie generaties deeltjes zijn. De theorie laat die mogelijkheid op zich toe. Bij CERN is nu zeer onlangs, met de nieuwe deeltjesversneller LEP die in de zomer van 1989 in gebruik werd genomen, met zeer grote waarschijnlijkheid vastgesteld dat er inderdaad maar drie generaties deeltjes zijn. Daarmee hebben die experimenten een fundamentele zekerheid aan de natuurkunde toegevoegd.