Jaarboek Monumentenzorg 1993

[p. 15]

Steven Surdèl
‘Met passer en winkelhout’
over de mythe der middeleeuwse ‘Baugeometrie’

Het onderstaande artikel beslaat een onderwerp waarover de specialisten tot in een vrij recent verleden menig verhit debat hebben gevoerd: het gebruik van strikt geometrische, al dan niet symbolische verhoudingen bij het ontwerpen van middeleeuwse architectuur.
Ofschoon deze kwestie inmiddels zo goed als beslecht is door een fijnzinnige studie van de Duitse ingenieur Konrad Hecht (1918-1980), is diens werk buiten de Duitstalige landen nooit erg bekend geworden. In Nederland bleef de aandacht beperkt tot een uitvoerige bespreking door W.F. Denslagen uit 1982 (‘Geometrie in de Gotische bouwpraktijk’, Bulletin KNOB, 131-147), die nog steeds kan worden aanbevolen als een goede inleiding (in opzet en gevolgtrekking bestaat overigens een sterke overeenkomst tussen deze bespreking en de onderstaande bijdrage. Deze overeenkomst berust louter op toeval, daar beide auteurs onafhankelijk van elkaar hebben gewerkt).
Eigen lezing van tekstbronnen en de nieuwste litteratuur, alsook persoonlijke gesprekken met geïnteresseerden (onder wie Dhr. Denslagen) hebben bij de schrijver de mening doen post vatten, dat het geen overbodige luxe is om de belangrijkste argumenten nogmaals op een rijtje te zetten. Al was het maar om het jarenlange werk van Konrad Hecht de eer te geven die het toekomt.

Eudes de Montreuil, meester-metselaar.

Inleiding

Geometrie in de middeleeuwse bouwpraktijk is een thema dat veel onderzoekers tot schrijven heeft aangezet^*. Wie tijd genoeg heeft om de uitgebreide hoeveelheid litteratuur eens door te bladeren, komt onder de schrijvers niet alleen architecten en kunsthistorici tegen, maar ook wiskundigen, filosofen, theologen en musicologen.^1. ‘Vogels van diverse pluimage’ zou men bijna zeggen, met in hun gevolg een bonte stoet aan voorstellen over het al dan niet mystieke karakter van de maten en verhoudingen van middeleeuwse (kerkelijke) architectuur.

Tegenover deze ‘heiligverklaring’ heeft de schrijver van dit artikel gemeend positie te moeten kiezen als advocatus diaboli. Niet met de pretentie veel nieuws aan te kondigen, waar het noodzakelijke denkwerk voor een belangrijk deel reeds door anderen is verricht, maar wel met de voldoening een ontnuchterende bijdrage te mogen leveren die niet voor louter ingewijden is geschreven. Wie de bronnen voor de middeleeuwse bouwkunde namelijk niet - of slechts oppervlakkig - kent, blijkt vaak te vallen voor allerlei romantische hypothesen over hetgeen aan de materiële architectuur voorafging: het bouwkundig ontwerp. Hypothesen die steunen op de vooronderstelling, dat tijdens de middeleeuwen ontwerpmethoden zouden zijn toegepast die volstrekt afweken van de hedendaagse, ‘pragmatische’ bouwpraktijk. Eenieder die vandaag de dag wel eens een bouwtekening onder ogen heeft gehad zal gemerkt hebben, dat het lijnenspel van een ontwerp met behulp van de rekenkunde op papier wordt gezet: de maten die langs een liniaal worden afgepast zijn immers vaak afzonderlijk in de tekening ingeschreven. Bovendien blijkt uit de legenda bij de tekening, dat het ontwerp volgens een vaste schaalverhouding is uitgewerkt. Met het oog op de dagelijkse praktijk zijn deze gegevens

* Dit artikel is een uitgebreide en verbeterde versie van ‘De mythe van de Middeleeuwse “Baugeometrie”’ in: Decorum. Tijdschrift van kunst en cultuur (Kunsthist. Inst. R.U. Leiden) jrg. X,nr 1/jan. 1992, 3-12 en nr 2/april 1992, 49.

1. De beste litteratuuropgaven vindt men achtereenvolgens in: (algemeen:) Hermann Graf, Bibliografie zum Problem der Proportionen. Literatur über Proportionen, Maß und Zahl in der Architektur, Bildender Kunst und Natur, Speyer 1958; (architectuur:) Paul von Naredi-Rainer, Architektur und Harmonie. Zahl, Maß und Proportion in der abendländischen Baukunst, Köln 1982, 232-283 (hierna als: von Naredi-Rainer 1982); (architectuur middeleeuwen:) Konrad Hecht, Maß und Zahl in der gotischen Baukunst, Hildesheim/New York 1979, 105-112, 265-269 en 470-484 (hierna als: Hecht 1979).

[p. 16]

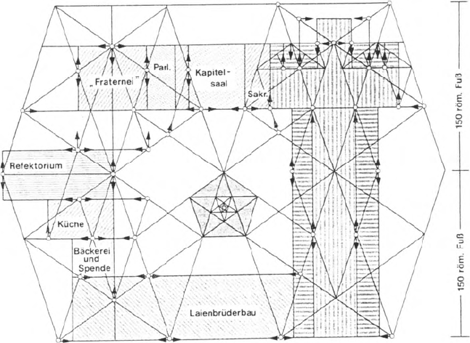
1 Eberbach, plattegrond van het Cisterciënzerklooster (v.a. ca. 1145). Geometrisch patroon naar Spieß (in: von Naredi-Rainer 1982, 201).

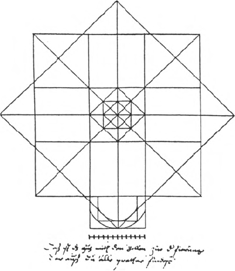
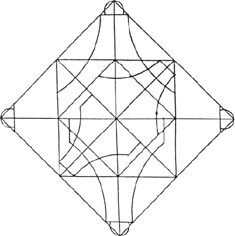
beslist onmisbaar, omdat de tekening immers moet dienen als communicatiemiddel: de uitvoerder en de bouwvakkers moeten er precies uit kunnen aflezen, hoeveel maateenheden zij op de werf moeten uitzetten.

Nu is het nog niet zo lang geleden dat veel architectuurhistorici ervan overtuigd waren, dat zo'n rekenkundige of aritmetische ontwerpmethode tijdens de middeleeuwen niet of nauwelijks werd toegepast. Sterker nog, sommigen onder hen aarzelden niet te stellen dat middeleeuwse bouwmeesters niet eens hoefden of konden rekenen; dezen zouden zich, als devote kinderen van een theocentrische samenleving, louter hebben laten inspireren door getallen die in de Heilige Schrift worden genoemd, onderwijl driftig manipulerend met passer en winkelhaak aan geheime ontwerpschema's vol drie-, vier-, acht- of twaalf- hoeken, desnoods gecombineerd met andere geometrische figuren (voor enkele typische uitspraken zie noot ^2.). Bij gebrek aan historisch bewijsmateriaal trachtten de aanhangers van deze hypothese de door hen veronderstelde ontwerpschema's naar eigen inzicht te reconstrueren (bijv. afb. 1 en 2). Dergelijke schema's, die in de vaklitteratuur sinds lang geliefd zijn, kunnen echter uit de aard der zaak niets bewijzen: de makers ervan hebben immers - zo blijkt - steeds gewerkt op basis van een soort ‘secundair’ bronnenmateriaal, zoals foto's of opmetingstekeningen. Aldus blijft het maar zeer de vraag, of zulke bouwmaten uit de tweede of zelfs derde hand wel een nauwkeurige afspiegeling mogen heten van hetgeen bijna altijd verloren is gegaan: de authentieke werktekeningen.

Het loont dan ook de moeite om de geometrische these eens op houdbaarheid te testen en wel aan de hand van de meest populaire onder de ontwerpschema's, de quadratuur en de triangulatuur: hypothetische patronen van uit elkaar afgeleide vierkanten of gelijkzijdige driehoeken, waarbij de plaats van de hoekpunten bepalend zou zijn geweest bij het uitzetten van grote bouwmaten als plattegrondbreedten of schiphoogten (vgl. afb. 3 en 4 met 2 en 5). Men leest er het eerst over in de publicaties van Georg Dehio en Gustav von Bezold, waaronder Die kirchliche Baukunst des Abendlandes ( 1887-1902) wel de bekendste is (afb. 5). Hypothesen en tekeningen uit beider werk zijn in de loop van deze eeuw door velen aangehaald en nagevolgd.^3. Ten onrechte, zoals de volgende bezwaren mogen aantonen.

2. Om de argumenten en de toonzetting van de belangrijkste publicaties over deze Baugeometrie enigszins tot de lezer te laten doorklinken, heb ik in de noten enkele typerende uitspraken willen citeren. Zo leest men over het gebrek aan rekenkundige kennis onder middeleeuwse bouwmeesters onder meer het volgende:
‘Der Vorrang der Geometrie in der abendländischen Mathematik der Antike und des frühen Mittelalters ergibt sich auch aus dem Umstand, daß schriftliches Rechnen sehr erschwert, ja fast unmöglich war (...)’ (Edgar Wedepohl, Eumetria. Das Glück der Proportionen, Maßgrund und Grundmaß in der Baugeschichte, Essen 1967, 252); ‘But we may note the general conclusion (...) that stereotomical problems were solved by mediaeval masons primarily through the physical manipulation of geometrical forms by means of the instruments and tools available to the masons. These were rule-of-thumb procedures, to be followed step by step, and there were virtually no mathematical calculations involved. (...) This non-mathematical technique I have labelled constructive geometry (...) It becomes evident that “the art of geometry” for mediaeval masons meant the ability to perceive design and building problems in terms of a few geometrical figures (...)’ (Lon R. Shelby, ‘The Geometrical Knowledge of Mediaeval Master Masons’, Speculum. A Journal of Mediaeval History 47 ( 1972), 395-421, passim); ‘Ce qu'on peut dire, en tout cas, c'est que toutes les méthodes fondées sur le calcul sont à rejeter parce que nous savons bien que les connaissances mathématiques, jusqu'à la fin du XIVe siècle, étaient fort élémentaires. Pour ce qui est des méthodes fondées sur des constructions géométriques, il n'en va pas de même: assurément les architectes étaient curieux de tracer au compas, à la règle, à l'équerre.’ (Pierre du Colombier, Les chantiers des cathédrales. Ouvriers, Architectes, Sculpteurs. Nouv. éd. rev. etaugm., Paris 1973, 93) (hierna als: du Colombier 1973);
‘(...) De basis van het ontwerp lag in de zogenaamde constructieve geometrie, waarbij men manipuleerde met vierkanten, cirkels en driehoeken, om lijnen en punten te verkrijgen van waaruit de details vastgesteld konden worden. (...) Het was voor geen enkele (lees: meester-) metselaar nodig om de theoretische basis te kennen van wat hij deed en hij hoefde ook niet aan te tonen dat zijn oplossing wiskundig juist was. Wat hij wel moest weten, was hoe je de figuren moest draaien om het gewenste vierkant te bereiken (...).’ (Nicola Coldstream, Meestermetselaars, Kampen en Turnhout 1992, 34; vert. van Masons and Sculptors, London, British Museum Press 1991).

3. Zie in het bijzonder Maria Velte, Die Anwendung der Quadratur und Triangulatur bei der Grund- und Aufrißgestaltung der gotischen Kirchen. Inaugural-Dissertation an der hohen Philosophisch-Historischen Fakultät der Universität Basel (= Basler Studien zur Kunstgeschichte, hrsg. von Prof. Josef Gantner, Bd. VIII), Basel 1951.

De ‘ongrijpbaarheid’ van irrationele geometrie

Om dit verhaal moeilijk te maken moet er hier op worden gewezen, dat de verhoudingen van veel geometrische figuren niet in eindige getallen kunnen worden uitgedrukt. Bij quadratuur bijvoorbeeld gaat men er van uit, dat een willekeurige maat is uitgezet als de diagonaal van een vierkant (afb. 3). Nu wordt de verhouding van deze diagonaal tot een zijde van het vierkant ‘irrationeel’ genoemd, omdat zij niet anders dan bij benadering kan worden aangegeven (zijde: diagonaal = 1 : √2, ofwel 1 : 1,4142...).

Hetzelfde dilemma geldt voor de triangulatuur, waarbij een maat wordt beschouwd als de hoogtelijn van een gelijkzijdige driehoek (afb. 4); ook hier is de verhouding van de basis tot de hoogtelijn rekenkundig

[p. 17]

2 Amiens, westfaçade van de kathedraal (13de-15de eeuw). Geometrisch patroon naar Lawlor (in: Lawlor 1982, 93).

[p. 18]

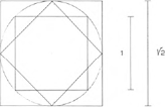
3 Voorbeeld van een quadratuurschema (tek. v.d. auteur).

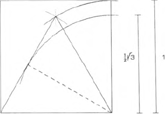
4 Voorbeeld van een triangulatuurschema (tek. v.d. auteur).

5 Bologna, San Petronio, schiptravee (1390-ca. 1480). Triangulatuur volgens Dehio (in: Hecht 1979, 127).

[p. 19]

6 Het visioen van abt Gunzo van Cluny (ca. 1180). Omtekening bij Conant (in: Kenneth John Conant, ‘Mediaeval Academy Excavotions at Cluny, IX: Systematic Dimensions in the Buildings’, Speculum. A Journal of Mediaeval Studies vol. 38/1 (jan. 1963, 29).

kundig ‘ongrijpbaar’ en moet zij worden uitgedrukt als 1:1/2√3 of 1:0,8660...

Bij het ‘reconstrueren’ van een geometrisch ontwerpschema heeft dit automatisch tot gevolg, dat zelfs de meest betrouwbare opmetingstekening per definitie onbruikbaar is, zeker waar het om grote afmetingen gaat: het is immers nooit mogelijk om - met de eindige getallen die bij een nameting nu eenmaal worden opgeschreven - zonder afwijking terug te rekenen tot de ‘schommelende’ waarden die ooit met behulp van een passer zouden zijn uitgezet. Wil men zulks toch proberen, dan kan men meestal ‘uitrekenen’ wat men maar wil.

Rechtlijnige adepten van de Baugeometrie hebben van dit bezwaar eigenlijk nooit zo'n punt gemaakt. Om de veronderstelde ontwerpschema's enigszins plausibel te doen lijken, nam men bij het terugrekenen dikwijls zijn toevlucht tot een - vanzelfsprekend willekeurige - ‘tolerantiemarge’; ook is het voorgekomen dat moeilijk in te passen opmetingsresultaten ten behoeve van ‘de door de bouwmeester gekozen’ verhoudingen werden aufgeschönt. En eigenlijk moest dat ook wel, wilde men het voor waar houden dat de vermeende passermanipulaties niet alleen op het tekenbord, maar ook op de bouwwerf werden uitgevoerd: bij het uitzetten van complete plattegronden en opstanden zouden dan palen en koorden hebben volstaan, waarmee de bouwvakkers het ontwerpschema op ware grootte en zonder enig rekenwerk zouden hebben kunnen uitspannen (men leze ook hier weer de citaten onder noot ^4.).

Ter illustratie van deze visie is het aardig hier te wijzen op een twaalfde-eeuws document, dat ter ondersteuning van geometrische hypothesen nogal eens is afgedrukt: een afbeelding, met hagiografisch commentaar, van abt Gunzo van Cluny, die in een droom door de patroonheiligen van zijn abdij zou zijn geïnformeerd over de maten van een nieuw te bouwen abdijkerk (afb. 6). Menig voorstander van de Baugeometrie heeft er zonder meer de conclusie uit getrokken, dat het onder middeleeuwse bouwmeesters niet gebruikelijk zou zijn geweest om op schaal te tekenen. De theorie van het geometrisch ontwerpen wil immers, dat bouwmaten slechts met koorden en palen werden uitgezet langs een afgeleide reeks passerconstructies; aldus zouden de bouwvakkers op de werf slechts de eerste maat van zo'n reeks (in het Duits: de Grundmaß) daadwerkelijk hebben moeten uitmeten, waarna de ‘schaal’ voor de overige maten vanzelf zou hebben vastgelegen (zie de citaten onder noot ^5.).

4. Deze toch wel fantasierijke voorstelling van zaken vindt men onder andere bij de volgende auteurs: ‘Werkzeichnungen (...) gaben die Möglichkeit, die gleichen Systeme, welche schon im Plan vorgezeichnet waren, (...) in sehr großem Maßstab auf dem Bauplatz aufzureißen, so daß man die daraus abzuleitenden Höhenmaße mit absoluter Genauigkeit (!) entnehmen konnte.’ (Paul Booz, Der Baumeister der Gotik, München/Berlin 1956, 94);
‘Wir wissen, daß der mittelalterliche Architekt alle Maßverhältnisse seines Bauwerks mit mathematischen, d.h. geometrischen Mitteln bestimmte. Genauer: von einem Grundmaß (...) ausgehend, entwickelte er alle anderen Maße mittels geometrischer Figuren, die am Bauplatz mit Hilfe von Schnüren und Pflöcken festgelegt wurden.’ (Otto von Simson, Die gotische Kathedrale. Beiträge zu ihrer Entstehung und Bedeutung, 2e herz. en vertaalde dr., Darmstadt 1972, 292);
‘Nicht nur zur Größenbestimmung der Kreise, (...) benützte man das gleichseitige Dreieck, sondern vor allem zur Realisierung der Entwurfsfigur auf der Baustelle: durch die Zerlegung der Entwurfsfigur in leicht einzufluchtende (...) Dreiecke konnte man die bei Zirkelschlägen über große Weiten unweigerlich auftretenden Ungenauigkeiten vermeiden (sic!); der entscheidende Vorteil aber lag darin, alle wesentliche Punkte des aufgehenden Bauwerks von Fixpunkten (...) aus einmessen zu können.’ (von Naredi-Rainer 1982, zie noot 1).

5. Men leze:
‘The architect, therefore, placed no value at all on plotting his drawings in a determined scale. That does not mean that he could get along without them entirely. He had at least to indicate the length in feet for the first measure that he prescribed, and it was then, so to speak, the preordained fate of the building whether a foot in that locality was, for example, 29 cm or 30 cm long. But for the further course of his work it was not important to be able to express every distance between two points of the structure in arithmetical quantities; he had only to determine the interval geometrically.’ (Paul Frankl, The Gothic. LiterarySources and Interpretations through Eight Centuries, Princeton N.Y. 1960, 51);
‘(...) So far as the design of plans and bays was concerned, these minor differences in unit would not effect the proportionate geometry involved. Except that the absolute size (...) would differ within certain limits, a building could be made from the drawings by the use of any recognized standard.’ (John Harvey, The Mediaeval Architect, London 1972, 108-109);
‘(...) Als men de basislengte eenmaal had vastgesteld (...) konden de verhoudingen opgesteld worden. (...) Men kwam tot deze verhoudingen door het roteren en halveren van vierkanten. Het maakte niet uit dat ze op irrationele getallen gebaseerd waren, omdat alles zonder wiskunde werd opgezet. (...) De grootte van het bouwwerk hing dus af van de grootte van de basiseenheid.’ (Coldstream 1992, 38, zie noot 2).

De ‘verhullende’ stijl van de tekstbronnen

Nu is de aanleiding tot al deze theorieën niet alleen gelegen in de menselijke fantasie, maar evenzeer in het gemis aan gedetailleerde bronnen. Uit de middeleeuwen zijn - het mag bekend zijn - nauwelijks theoretische geschriften bewaard over contemporaine bouwkunde, en men mag zich afvragen of kennis van dit onderwerp, althans met enige frequentie, eigenlijk wel op schrift werd gesteld: een wijdverbreid analfabetisme onder leken maakte immers, dat scholing in de artes mechanicae tot laat in de middeleeuwen vrijwel uitsluitend mondeling kon geschieden.^6. Wat bewaard is zijn de zogeheten werkmeesterboeken en modellenboeken uit de gotische en laatgotische stijlperioden, maar zij bieden de lezer geen volledig uitgewerkte, samenhangende architectuurtheorie.^7. In verband met de quadratuur zullen wij er dadelijk nog op terugkomen.

Wie informatie zoekt over het werk op de bouwwerf vóór de vijftiende eeuw is derhalve voor het merendeel aangewezen op een groot aantal ‘losse’ mededelingen in teksten als kloosterkronieken, heiligenlevens en reisverslagen.^8. Maar bij het raadplegen van dergelijke bronnen dient men er wel goed rekening mee te houden dat zij doorgaans niet zijn opgesteld uit interesse voor het menselijk vernuft, maar ter rechtvaardiging van een christelijke ideologie. Met andere woorden: ‘bekeren’ ging vóór ‘constateren’,

6. Vroege uitzonderingen daargelaten, geven de overgeleverde tekstbronnen eerst vanaf ca. 1200 te kennen, dat behalve de geestelijkheid en de hogere adel ook een toenemend aantal lieden uit de lagere standen leerde lezen en schrijven. Zij die een handwerk leerden en doorgaans te arm waren om zich duur perkament of een klerk te verschaffen, moeten gewend zijn geweest aan mondelinge kennisoverdracht (hetgeen dikwijls van vader op zoon geschiedde). Voor meer informatie zie: Pierre Riché, Recherches sur l'instruction des laïcs du IXe au XIIe siècle, Cahiers de civilisation médiévale, Xe-XIIe Siècles, t. V (1962), 175-182, alsook de interessante studie van Herbert Grundmann, Litteratus - illitteratus. Der Wandel einer Bildungsnorm vom Altertum zum Mittelalter, Archiv für Kulturgeschichte, Bd. 40, Heft 1 (1958), 1-65. Zie ook Harvey 1972 (noot 5), spec. 87-95.
Voor (het ontbreken van) architectuurtheorie tijdens de middeleeuwen raadplege men het fraaie standaardwerk van: Hanno-Walter Kruft, Geschichte der Architekturtheorie. Von der Antike bis zur Gegenwart, 3e herz. dr. München 1991, 31-43, met een gedetailleerde bibliografie op p. 663-664, 677 en 713. Zie ook: Georg Germann, Einführung in die Geschichte der Architekturtheorie, Darmstadt 1980, spec. 29-31, met een bibliografie op p. 256-259 (nota: 3e herz. dr. ibid. 1993).

7. In de litteratuur is de meeste aandacht tot dusver uitgegaan naar de werkmeesterboeken. De volgende standaardwerken over dit onderwerp bevatten echter ook verwijzingen naar publicaties over de modellenboeken: Hans R. Hahnloser, Villardde Honnecourt. Kritische Gesamtausgabe des Bauhüttenbuches ms.fr. 19093 der Pariser Nationalbibliothek, Zweite, revidierte und erweiterte Ausgabe, Graz 1972; Ulrich Coenen, Die spätgotischen Werkmeisterbücher in Deutschland. Untersuchung und Edition der Lehr schriften für Entwurf und Ausführung von Sakralbauten, München 1990 (= Beiträge zur Kunstwissenschaft, Bd. 35), met een goede bibliografie op p. 391-407 (hierna als: Coenen 1990); Hubertus Günther e.a., Deutsche Architekturtheorie zwischen Gotik und Renaissance, Darmstadt 1988, met een bibliografie op p. 207-222 (hierna als: Günther 1988).

8. Een analyse van middeleeuwse tekstbronnen over het bouwen geeft: Martin Warnke, Bau und Überbau. Soziologie der mittelalterlichen Architektur nach den Schriftquellen, 2e dr. Frankfurt 1976 (fotomech. herdr. ibid. 1984), met bronnenuitgaven in de bibliografie op p. 217-229.

[p. 20]

feitelijkheid stond niet voorop. Het betreft hier een voor de middeleeuwen karakteristieke schrijfpolitiek, die wellicht nog het krachtigst tot uitdrukking komt in de bekende bouwverslagen van abt Suger van Saint-Denis (1081-1151):

(vert.) ‘Omdat aan de voorkant (...) de nauwe hal werd ingeklemd door tweelingtorens die noch zeer hoog, noch zeer fors waren, begonnen we met Gods hulp dit gedeelte aan te pakken, (...) Steunend op Gods onschatbare raad en onweerlegbare hulp, vorderden wij met dit zo grote en kostbare werk in zo'n mate dat wij (...) moesten bekennen in onze overdaad: heel onze bekwaamheid komt van God. (...) Door een gave van God werd een nieuwe steengroeve ontdekt, die zeer sterke steen voortbracht zoals in kwantiteit en kwaliteit nog nooit in deze streken was gevonden’^9..

Het geschiedde echter niet alleen in de middeleeuwen dat feiten nogal eens schade leden door verdichting: ook in later tijd - met name in de ‘romantische’ negentiende eeuw - vormden uitspraken als die van Suger voor menig publicist een makkelijke aanleiding om gewaagde speculaties op te stellen over allerlei naïef-symbolische intenties van kerkstichters en hun bouwmeesters.^10.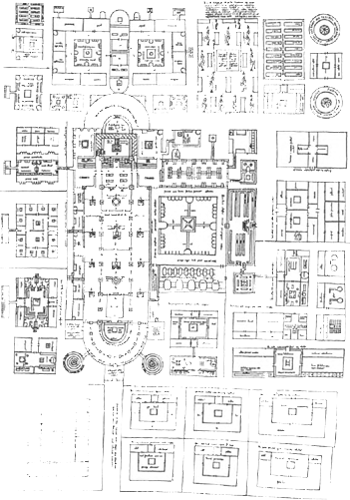

7 Sankt-Gallen, ontwerptekening voor een kloosterplattegrond; (vermoedelijk een copie) tussen 826 en 830. Inkt op perkament (in: Hecht 1983, 15).

9. Voor de Latijnse tekst met commentaar en een Engelse vertaling, zie de bekende uitgave van: Erwin Panofsky, Abbot Suger. On the Abbey Church of St.-Denis and its Art Treasures, second edition by Gerda Panofsky-Soergel, Princeton N.Y. 1979. De Nederlandse passages van het citaat zijn gekozen uit: Paul le Blanc e.a., Suger en St. Denis. Over de bouw van de nieuwe kerk 1140-1144. Cand. werkgr. Kath. Univ. Nijmegen 1979 (niet in druk).

10. Onder de vele ronkende verhalen mogen de volgende als voorbeeld dienen:
‘Und also mußte, was Gott zu dienen hatte (...), nach den ewigen Gesetzen hergestellt werden, die der Gottheit waren (...). Kritisch genommen, ist das heut noch der Bann der Menschheit, den kein Rationalismus lösen wird. Von der Menschheit Anfängen her hat er sich in überirdisch ausgedeuteten Symbolen figuriert (...). Nahezu Regel ist, daß chordienstliche Räume mit Sechseckelemente eingewinkelt waren, Schatzkammern, sonstige als fest vermeinte Räume und Türe mit den Mitteln des Goldenen Rechtecks (...). Der Figurierungsmethode ist vom Standpunkt damaliger Symbolgläubigkeit nicht abzusprechen. Chor und Altarhaus stellen sich unter das Zeichen für Christus (...) und Schatzkammern und Türen gegen unbefugten Zutritt, Diebstal, böse Geister und sonstiges Unheil unter das Pentagramm, den Drudenstern. In beiden Fällen hält man oft, ja meist die Handhabung des einschlägigen Dreiecks für ausreichend, ohne das die Vollfigur herauszukommen braucht (...)’ (Bartholomäus Hanftmann o.s.b., ‘Die Benediktiner als Architekten bis in die Zeit der Gotik. Ihr Werkschuh zu 0,3329 M.’, Studien und Mitteilungen zur Geschichte des Benediktiner-Ordens und seiner Zweige 48 (1930), 231 en 242);
‘Der germanische Norden hatte in der π-Triangulatur sich selber wiedergefunden (...) Denn in Proportion und Triangulation offenbarte sich ihm das geheimnisvoll wirkende Walten der Gottheit, deren Kraft die ganze Natur durchseelt und im Gleichgewicht erhält. Demgemäß umschließt diese Proportionalität, d.h. die π-Triangulation, das ganze Geheimnis der mittelalterlichen Bauhütten (...)’ (Otto Schubert, Gesetz der Baukunst, Leipzig 1954, 38).

[p. 21]

Portret van ‘werckmeester’ Matthes Roriczer door Hans Holbein de Oude (XVd). Parijs, Bibliothèque Nationale. Gewassen pentekening (in: Coldstream 1992, 35).

Maar het beeld van een haast kinderlijke, door louter godsvrucht bevlogen architectus of magister operis kan en mag geen stand houden. Men stelle zich alleen al de omstandigheid voor, dat een bouwmeester uit de aard van zijn beroep steeds verantwoordelijkheid draagt voor de beheersing van bepaalde bouwkosten. Dat is heden ten dage zo en het was in de middeleeuwen niet anders. Ook uit deze als ‘duister’ bestempelde eeuwen zijn verslagen bewaard van kostenberekeningen, van bestellingen van bouwmaterialen en van uitkeringen van een gepast loon aan de arbeiders; allemaal taken dus, die men aan een rekenkundig analfabeet beter niet zou overlaten.^11. Het is dan ook niet zo moeilijk om de geometrische these, zoals zij hiervóór in haar strengste variant is beschreven, te ontkrachten. Hele reeksen bestuurlijke verordeningen en bouwcontracten tonen namelijk overduidelijk aan, dat middeleeuwse bouwmeesters wel degelijk gewend waren om met rekeneenheden en bouwmaten om te gaan (in het toenmalige bouwvak geschiedde dit overigens op basis van een twaalfdelig, soms ook zestiendelig voetenstelsel^12.). Zo bevat de beschrijving van een ontwerp uit 1447 voor het complex van King's College te Cambridge maar liefst 53 maatopgaven.^13. Een aanmerkelijk ouder maar niet minder illustratief voorbeeld is de bekende Karolingische kloosterplattegrond van Sankt-Gallen (826-830), waarin vijf ontwerpmaten zijn ingeschreven (afb. 7).^14.

Mededelingen met maatopgaven zijn er genoeg en het opvallende is, dat de gewenste afmetingen vrijwel steeds zijn opgegeven in hele, soms ook

11. Goede voorbeelden van dit soort tekstbronnen vindt men onder andere in: Victor Mortet & Paul Deschamps, Recueil de textes relatifs à l'histoire de l'architecture et à la condition des architectes en France au moyen-âge, XIIe - XIIIe siècles, Paris 1929; Louis Francis Salzman, Building in England down to 1540, 2e dr. Oxford 1967 (hierna als: Salzman 1967), en tenslotte Jean Gimpel, Les bâtisseurs de cathédrales, 2e herz. dr. Bourges 1976 (in het Nederlands vertaald als De bouw van een kathedraal, Utrecht en Antwerpen 1960).

12. Over de precieze lengten van klassieke en middeleeuwse maten valt niet veel met zekerheid te zeggen. Achttiendeeeuwse vergelijkingstabellen tussen het metrieke en het voetenstelsel geven voorde lengte van één voet schommelende waarden op, variërend van ca. 26,5 cm tot ca. 34 cm. (zie: Hans-Joachim von Alberti, Maß und Gewicht. Geschichtliche und tabellarische Darstellungen von den Anfängen bis zur Gegenwart, Berlin (DDR) 1957; m.b.t. Nederland, zie: J.M. Verhoeff, De oude Nederlandse maten en gewichten,. 2e dr. Amsterdam 1983, alsook: K.M.C. Zevenboom, Theorie over de ontwikkeling van de Nederlandse voet- en ellematen, Amsterdam 1964.
De reden voor het onderling afwijken van oude maateenheden moet zeker worden gezocht in het ontbreken van een gestandaardiseerd ijkwezen. Daardoor kon het voorkomen dat de lengte van bijvoorbeeld een voet- of ellemaat van streek tot streek - en mogelijkerwijs dus ook van de ene ploeg bouwvakkers tot een andere! - verschilde.

13. Zie: Salzman 1967 (noot 11), 520.

14. Wat betreft de discrepantie tussen deze maatopgaven en de schaal van de plattegrond raadplege men een tweede magnum opus van Konrad Hecht, Der St. Galler Klosterplan (posth. uitg.), Sigmaringen 1983, spec. 25-56, 87-89 en 319-336, met een uitvoerige bibliografie.

[p. 22]

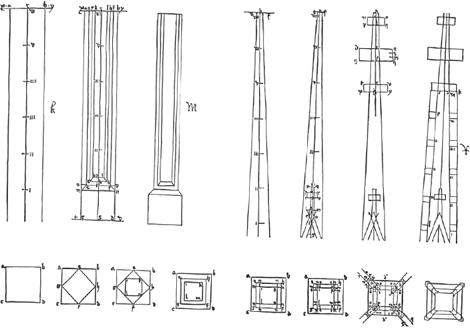
8 Matthes Roriczer, methode voor het ontwerpen van pinakels met behulp van een quadratuurschema. Uit het puechlen der fialen gerechtikait, Regensburg 1486 (in: Günther 1988, 40-41).

eenvoudig gedeelde aantallen; moeilijke breuken, die bij de verhoudingen van passerconstructies toch vaak zouden zijn opgetreden, komen in de genoemde tekstbronnen niet voor (vgl. noot 8). Zou men er desondanks toch van willen uitgaan dat middeleeuwse bouwmeesters hun ontwerpen op een strikt geometrische wijze vervaardigden, dan moet men daaraan verbinden dat alle overgeleverde opdrachten waarin voet- en duimmaten zijn genoemd voor hen geen enkele zin zouden hebben gehad. Een overweging die bijna vanzelf leidt tot de vraag, wat er dan wel toe geleid mag hebben dat zovelen zich hebben laten overtuigen van een puur hypothetische dominantie van de quadratuur en de triangulatuur.

De quadratuur

Voor een antwoord op deze vraag kan men uitstekend terecht bij een knappe, helaas niet al te bekende studie van de Duitse ingenieur Konrad Hecht, getiteld Maß und Zahl in der gotischen Baukunst.^15. In de uitgave in boekvorm, die de liefhebber confronteert met de spanning van een wetenschappelijke ‘rechtszaak’, vindt men glashelder uiteengezet dat bouwkundig ontwerpen in de middeleeuwen geen zaak was van halve mystici, maar van pragmatische, in de praktijk geschoolde vaklieden. Gezien de uitvoerigheid van Hechts doortimmerde betoog leek het verstandig, in deze bijdrage niet méér samen te vatten dan hetgeen hij heeft blootgelegd aan de wortels van de quadratuur en de triangulatuur. Voorzover het de quadratuur betreft zal men de bron moeten zoeken bij de Duitse Werkmeisterbücher en Musterbücher uit de vijftiende en zestiende eeuw, die betrekking hebben op laatgotische bouwstijlen. Zoals eerder al is opgemerkt zijn het geen volledig uitgewerkte handboeken voor bouwkunde; de inhoud bestaat overwegend uit al dan niet gedetailleerde tekeningen van onderdelen van gebouwen, die in de ‘wercmeesterboecken’ vergezeld gaan van een didactisch commentaar.^16. Dit commentaar maakt duidelijk dat de tekeningen moesten dienen ter illustratie van een groot aantal, min of meer losse, vuistregels: de strekking ervan draagt een zuiver praktisch, ad hoc-karakter en doet vermoeden, dat bouwmeesters hun kennis als een soort aide-mémoire nogal willekeurig plachten te bundelen.

Zo op het eerste gezicht lijken de werkmeesterboeken vóór de geometrische these tout court te pleiten, omdat er quadratuurschema's in zijn afgebeeld (afb. 8). Bovendien getuigen de getekende

15. K.H., ‘Maß und Zahl in der gotischen Baukunst’, Abhandlungen der Braunschweigischen Wissenschaftlichen Gesellschaft, resp. jrg. 21 (1969), 215-326; 22 (1970), 105-263; 23 (1971), 25-236. In 1979 zijn deze drie artikelen fotomechanisch herdrukt in één band, met aangepaste paginering (Hildesheim/New York, Georg Olms Verlag). In de voetnoten bij dit artikel wordt telkens verwezen naar deze ééndelige uitgave (als: Hecht 1979).

16. Zie Coenen 1990 (noot 7), een zeer welkom boek, waarin voor het eerst een samenvattende en overzichtelijke bespreking van alle werkmeesterboeken is geboden. Diplomatische transcripties ontbreken niet.

[p. 23]

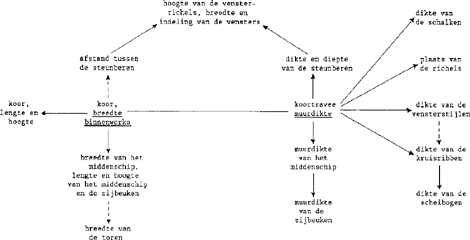
9 Lorenz Lechler, af te leiden ontwerpmaten voor een gotische kerk. Naar aanwijzingen uit zijn Unterweisung an seinen Sohn Moritz, passim. Afschrift uit 1593 naar een origineel uit 1516 (vgl. Hecht 1979. 178).

voorbeelden - ondanks de relatief jonge datering - vaak van een oudere, zuiver gotische traditie. Maar wie de inhoud van de onderscheidene bundels in zijn geheel overziet zal merken, dat de betreffende schema's alleen werden toegepast bij het werken met relatief kleine ontwerpmaten. De reden hiervan was gelegen in een typische werkwijze, waarbij de maten voor kleine onderdelen volgens min of meer traditionele verhoudingen werden afgeleid uit de maten voor grotere delen. Opdat de lezer zich hier een goede voorstelling van kan maken volgen hier enkele citaten en afbeeldingen uit het werkmeesterboek van Lorenz Lechler uit ‘1516’, dat van alle exemplaren de meest uitvoerige informatie biedt.^17.

Lechler was één van de werkmeesters die stelden, dat alle maten van een kerkgebouw direct of indirect moesten worden afgeleid uit de binnenwerkse breedte van de koortravee (zie het overzicht van afb. 9); deze breedte stelde hij voor op 20 of 30 voet (ca. 6 of 9 m). Een kleinere maat, bijvoorbeeld de dikte van de zijmuren van het koor, moest dan als volgt uit de koorbreedte worden afgeleid:

‘(...) Item ein khor der 20 Schueh weidt ist, Im liecht, vnd ist der stein guet, so mach die mauern zwen Werkhschueh dickh, ist aber d(er) khor von Eydlen gehauen steinwerckh, so brich im ab 3 Zoll, ist den fauller stein so gib im 3 Zoll zue der dickh der Mauren (...) Item Ein khor 30 Schueh weidt, 3 Schueh dickh die mauern (...)’.^18.

(vert.) ‘Bij een koor met een binnenwerkse breedte van 20 voet (moet je als volgt te werk gaan): is de steen van goede kwaliteit, maak dan de muren twee voet dik; bestaat het muurwerk uit steen van een bijzondere kwaliteit, maak dan de muren 3 duim smaller; is de steen slecht, dan moet je de muren 3 duim dikker maken (...) Bij een koor met een (binnenwerkse) breedte van 30 voet moeten de muren 3 voet dik zijn (...)’

Uit dit citaat blijkt duidelijk dat de diktemaat voor de koormuren niet op een geometrische manier werd gekozen, maar aan de hand van een gewone rekenkundige verhouding: in principe als het tiende deel van de binnenwerkse koorbreedte. Al naar gelang de kwaliteit van de steensoort zijn er dan vier mogelijkheden voorgesteld om de muurdikte in voet en duim af te leiden: 1′9″, 2′, 2′3″ en 3′ (in cm resp. ca. 52,5, 60, 67,5 en 90).

Bij dit rekensommetje bleef het niet. Twee nog kleinere maten, te weten de diepte van dikke en slanke vensterstijlen, moesten weer worden afgeleid uit de dikte van de muur:

‘(...) darnach so teill die mauer Dickhung des khorsz In drey teill, derselbige teil eines nimb, vnd teil dasselbig teil wider in siben teil, dasz ist der rechte alt Pfosten zu allen gebeien, Wiltu aber einen Iungen Pfosten machen, den man Offs bra(u)cht, so thue zwey teil von den siben teil, so bleiben dir fünff teill, dieselbige fünff teil bedeut(en) den Iungen Pfosten (...)’.^19.

(vert.) ‘(...) deel vervolgens de muurdikte van het koor in drie delen, neem daarvan één deel en verdeel dat weer in zeven delen; zo krijg je de juiste traditionele vensterstijl voor alle gebouwen. Wil je daarentegen een moderne vensterstijl maken - die men dikwijls nodig heeft - trek dan twee delen van de zeven delen af; je houdt dan vijf delen over, en die vijf delen zijn bestemd voor de moderne vensterstijl (...)’

Afbeelding 10.1 laat zien wat hier is beschreven. Men ziet dat Lechler twee vierkanten overhoeks heeft getekend, waarvan de zijden gelijk zijn aan de dikte van de muur; deze diktemaat heeft hij, conform de aanwijzingen in het citaat, onderverdeeld in 21 delen. Aan weerszijden van de as op de middellijn zijn telkens zeven eenheden aangegeven (ofwel éénderde van de muurdikte), die elk de diepte van een dikke of traditionele vensterstijl bepalen (de Alt Pfosten); vijf ervan geven de dieptemaat aan van een

17. De oudste versie van dit werkmeesterboek is sinds 1856 getiteld ‘Des Meisters Lorenz Lacher Unterweisung an seinen Sohn Moritz’ (Historisches Archiv der Stadt Köln, Sign. W * 276). Oorspronkelijk geschreven in 1516, is zij overgeleverd in een afschrift van Jakob Facht (of: Feucht) von Andernach uit 1593. Een tweetal iets jongere handschriften, die veel beknopter zijn, dateert uit de jaren rond 1600 (zie Coenen 1990, 174-266).

18. Coenen 1990, 95-99 (hs. Keulen fol. 43v). Zie tevens het commentaar van Hecht 1979, 179.

19. Coenen 1990, 114-116 (hs. Keulen fol. 44r en v). Zie tevens het commentaar van Hecht 1979, 185.

[p. 24]

10.1 Lorenz Lechler, voorbeeld van een quadratuurschema met enkele profielen van mallen (in: Hecht 1979, 186).

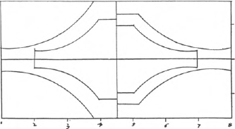
10.2 Lorenz Lechler, verhoudingen van dikke en slanke vensterstijlen (in: Hecht 1979, 187).

slanke of moderne stijl (de Iung Pfosten). De mallen voor het profiel van de stijlen ziet men getekend aan de bovenkant van de figuur. In een tweede tekening vindt men deze mallen nogmaals afgebeeld, waarbij de respectieve schaalverhoudingen door vergroting beter uitkomen (afb. 10.2).

Bij de rekenkundige verhouding die Lechler wenste was het niet moeilijk om de afmeting van de dikke vensterstijl nog op een eenvoudige manier in duimen uit te meten. Deelt men namelijk - wederom volgens de aanwijzingen in het citaat - de dikte van de koormuur door 7/21 e (ofwel 1/3e), dan levert dat als uitkomst achtereenvolgens 7″, 8″, 9″ en 12″ op (in cm ca. 17,5, 20, 22,5 en 30); maten, die tijdens het werk op de bouwwerf gewoon langs de maatstok konden worden afgepast.

Maar bij de maat voor de slanke vensterstijl lukte dit niet meer: het 5/7e deel van de dikke stijl (of het 5/21e van de muurdikte) liet geen indeling in ronde duimen meer toe. En het was dan ook eerst hier, dat Lechler zijn toevlucht placht te nemen tot de techniek van de passerconstructie. Het rekenkundig dilemma werd daarbij op een vernuftige manier omzeild:

‘(...) auf das du das der Leichter verstehn magst, so hat der alt Pfost siben teill, vnd der lung Pfost fünff teill, vnd wirt der Iung Pfost aus dem alth Pfosten genummen, wan du die fierung in drey teil geteillet hast, so reisz ein Andere fierung durch die grosse fierung vber Orth durcheinander zweimall so hastu breide und lenge.’^20.

(vert.) ‘(...) opdat je dit makkelijker zult begrijpen: de traditionele vensterstijl heeft (een diepte van) zeven delen, en de moderne vensterstijl (een diepte van) vijf delen. En om nu de moderne stijl uit de traditionele stijl afte passen moet je, nadat je het vierkant (overlangs) in drie delen hebt verdeeld, twee keer een ander vierkant overhoeks uitzetten in het grote vierkant; zo krijg je (de verhoudingen voor) de breedte en de lengte.’

Wat hiermee is bedoeld ziet men op afbeelding 11.1, waarin Lechler opnieuw twee vierkanten overhoeks heeft getekend. Eén ervan is ingedeeld in negen kleinere, waarvan de zijde telkens twaalf duim bedraagt ofwel één voet (het onderschrift luidt: Daß ist der schuh mitt den zollen zue d(er) fierung darauß du alle pretter findest/(vert.) ‘Ziehier de voet met de (indeling in) duimen bij het vierkant waaruit je (de maten voor) de mallen kunt afleiden’). In het middelste vierkant is vervolgens een quadratuurschema ingetekend (so reiß ein Andere fierung durch die grosse fierung vber Orth durcheinander zweimall). Dit schema, nu aangevuld met de contouren van de mallen (de pretter) voor de vensterstijlen, is in vergrote vorm nogmaals afzonderlijk weergegeven (afb. 11.2).

Vergelijkt men nu de geometrisch geconstrueerde afmetingen met de maten die Lechler op de gewone rekenkundige manier tot onwerkbare breuken had afgeleid, dan blijken beide in verhouding vrijwel exact overeen te komen. Weliswaar treden er tussen de aritmetische en de geometrische waarden in absolute zin kleine verschillen op, maar zij zijn dermate miniem dat men ze met het blote oog nauwelijks zou kunnen waarnemen.^21.

Het grote voordeel van deze ‘kleine quadratuur’ was dus, dat er - zowel op de tekentafel als op de werf - niet met ingewikkelde breuken gerekend hoefde te worden: door het quadratuurschema in een vloer uit te krassen, kon men maten voor kleine onderdelen

20. Coenen 1990, 114-116 (hs. Keulen fol. 44v). Zie tevens het commentaar van Hecht 1979, 185.

21. Bij de geometrische constructie verhouden de diepten van de moderne en de traditionele vensterstijl zich als 1:√2 = 0,7071: 1 in plaats van de oudtijds - en ook door Lechler - gebruikte ‘benaderde’ waarde 5:7 = 0,7143:1. Bij een muurdikte van 90 cm (voorgesteld voor 3 voet) levert dit een fout op van slechts 2,15 mm (mededeling G. Berends). Het spreekt vanzelf dat dit verschil onverantwoord groot wordt indien men benaderde waarden zou willen gebruiken bij het reconstrueren van quadratuur- en andere geometrische schema's over grote maten als die van plattegronden en opstanden.

[p. 25]

11.1 Lorenz Lechler, quadratuurschema (op basis van een koormuur van 3 voet dik) (in: Hecht 1979, 189).

11.2 Lorenz Lechler, quadratuurschema voor het ontwerpen van dikke en slanke vensterstijlen (in: Hecht 1979, 189).

12 Het gebruik van een vloerpasser op de bouwwerf. Walter Ryff (Gualtherius Rivius), Der Architectur fürnembsten, notwendigsten, angehörigen Mathematischen und Mechanischen Künst... Nürnberg 1558 (in: Hecht 1979, 150).

zoals vensterprofielen en pinakels desgewenst met een passer ‘uit het schema nemen’. Zeer waarschijnlijk is het dan ook dit procédé geweest, dat in statuten van middeleeuwse bouwmeestersgilden soms omschreven is als het nehmen aus dem Grunde (afb. 12).^22.

Anderzijds moet de aanhangers van de ‘grote’ quadratuur dratuur worden voorgehouden, dat de methode volkomen ongeschikt zou zijn geweest voor het uitzetten van complete plattegronden en opstanden (cf. noten 4 en 21). Het laat zich immers aanzien wat er zou gebeuren, indien men - zonder ook maar enige vorm van nameting - een quadratuurschema van de vereiste omvang zou hebben moeten uitspannen: koorden of linten zouden onder hun eigen gewicht steeds iets zijn doorgezakt, de precieze verhoudingen van het schema zouden al spoedig zijn ‘zoekgeraakt’, de maten van het ontwerpschema zouden op geen enkele manier gecontroleerd kunnen worden en het zou onmogelijk zijn geweest om het muurwerk overal ‘von Fixpunkten aus’(von Naredi-Rainer) te laten aansluiten.

22. Interessant op dit punt zijn bijvoorbeeld de zogeheten ‘Verordeningen’ van Regensburg uit 1459, waarin men leest:
‘Item es sol auch kain werchman Maister noch parlierer oder gesell niemants, wie der genannt sey, der nit vnsers hantwerchs ist, auff kainem auszueg vntterweisen, zu nemen aus dem grundt.’ (vert.) ‘Of men nu werkman, meester, uitvoerder of gezel is; niemand, om zo te zeggen, die ons beroep niet uitoefent mag aan de hand van een uittreksel (lees: modellenboek?) uitleggen, hoe men (een maat) neemt uit een vloerfiguur.’
Dit besluit is dikwijls geciteerd ter ondersteuning van de stelling, als zou geometrisch ontwerpen een tak van het middeleeuwse bouwvak zijn geweest waarover een beroepsgeheim lag. De uitdrukking nemen aus dem grundt heeft men dienovereenkomstig wel willen lezen als ‘het op geometrische wijze afleiden van (alle) hoogtematen uit een plattegrond’. De werkmeesterboeken tonen aan dat deze interpretatie niet klopt. Bovendien is in de betreffende passage helemaal geen sprake van een beroepsgeheim onder vakgenoten; er staat immers, dat het unterweisen aus einem auszueg niet door iemand mag geschieden, der nit vnsers hantwerchs ist. Met andere woorden: het geven van enig bouwkundig onderricht zou slechts voorbehouden mogen zijn aan lieden met een gedegen praktische vakkennis. Het geciteerde besluit moet dan ook eerder worden beschouwd als een doodgewone waarschuwing tegen knoeiwerk (men vindt het in een oude teksteditie van Joseph Neuwirth, ‘Die Satzungen des Regensburger Steinmetzentages nach dem Tiroler Hüttenbuch von 1460’, Zeitschrift für Bauwesen 46 (1896), col. 201-218).
Voor enige litteratuurhistorische kanttekeningen bij de meer juridisch geformuleerde geschriften als Baumeisterbücher en Hüttenbücher, zie Coenen 1990, 12.

Stornaloco en de ‘triangulatuur’

Natuurlijk kunnen tegen de hypothese van de triangulatuur dezelfde bezwaren worden aangevoerd (vgl. afb. 5). Theoretisch beschouwd zou deze bijdrage hier dan ook kunnen worden afgesloten, ware het niet dat oningewijde lezers zeker nog gewaarschuwd mogen worden om alert te blijven bij het zien van een oude tekening, die al tijdens de renaissance ten onrechte is geïnterpreteerd als een authentiek voorbeeld van middeleeuwse triangulatuur: het schema met een meetkundige weergave van een maatindeling voor de Dom van Milaan uit 1391 (afb. 13).^23. De tekenaar van dit schema was een man namens Gabriele Stornaloco, een discrelus vir, expertus in arte geometriae en afkomstig uit Piacenza. In de verslagen van de Milanese Domfabriek leest men, dat hij door de Raad van dit orgaan naar Milaan was

23. Het schema van Stornaloco werd opnieuw ontdekt in 1887 en voor het eerst als natekening afgebeeld door: Luca Beltrami, La Certosa di Pavia, z.pl. 1895, 42. Zie verder Hecht 1979, spec. 145-157, met een interessante kritiek van von Naredi-Rainer in diens boek uit 1982 (zie noot 1), 209-210, spec. noot 235.

[p. 26]

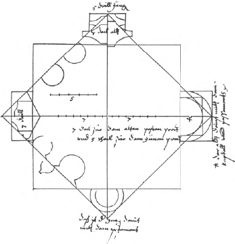
13 Gabriele Stornaloco, meetkundig schema met een maatindeling voor het schip van de Dom van Milaan. Natekening door Beltrami uit 1895 (in: Hecht 1979, 28).

ontboden causa discuterteli cum inzigneriis dictae fabricae de dubiis altitudinis et aliorum de quibus dubium erat inter dictos inzignerios (vert.) ‘(..) ommet de bouwkundigen van de voornoemde fabriek te overleggen over hun bedenkingen betreffende de hoogten alsmede over andere kwesties waarover onder voornoemde bouwkundigen twijfel bestond.’^24. Stornaloco moest dus uitkomst brengen in een dilemma, waar het de oogtematen van de Dom betrof; volgens de verslagen vreesden sommigen onder de bouwmeesters gevaar voor instorting, indien de oorspronkelijk voorgestelde hoogte voor het schip zou worden aangehouden.

Omdat men met de bouw van de kerk al was begonnen, moest Stornaloco uitgaan van de maten waarmee de plattegrond reeds was uitgezet. Deze maten zijn bekend: men vindt ze ingeschreven in een tekening van de Bolognese bouwmeester Antonio de' Vincenti, die hij kort vóór 1391 moet hebben vervaardigd (afb. 14). Het is belangrijk hier op deze tekening te wijzen, omdat men er uit kan opmaken dat de plattegrond van de Dom was uitgezet op basis van een vaste regelmaat: voor de hartafstand tussen de zuilen, alsook voor de binnenwerkse maten, had men telkens veelvouden gekozen van 16 Milanese ellen.^25. Aan de hand hiervan is het meer dan waarschijnlijk, dat het ontwerp van de plattegrond over een soort rasterpatroon was getekend.^26.

Dezelfde indeling vindt men terug in het schema van Gabriele Stornaloco. In vergelijking met Antonio de' Vincenti, die de plattegrondmaten in Bolognese voet heeft aangegeven, heeft hij voor het schip vrijwel dezelfde breedte opgegeven, zij het nu in 96 Milanese el, ofwel zes ‘rastereenheden’ (vgl. noot 25 en afb. 13). De overige verhoudingen lijken daarentegen op een geometrische manier te zijn gekozen: het opgaande werk is immers ondergebracht in een patroon van vierkanten en gelijkzijdige driehoeken. De hoogtemaat van het middenschip bijvoorbeeld komt overeen met de hoogtelijn van de grootste driehoek ABC; vervolgens lijkt de indeling van deze hoogtemaat maatgevend te zijn geweest voor de hoogte van de gewelfaanzetten.

Echter: hoezeer deze interpretatie ook door de tekening lijkt te worden bevestigd, zij staat of valt met het bewijs dat Stornaloco enkel en alleen met passer en winkelhaak moet hebben gewerkt. Wie een dergelijk bewijs overbodig vindt zal zich met gemak kunnen scharen onder diegenen, die het schema altijd dankbaar hebben geaccepteerd als het oudste document voor een vermeende triangulatuur.

Nu heeft Stornaloco bij het schema een toelichting geschreven, waar de meeste onderzoekers in het geheel geen aandacht aan hebben besteed.^27. Zouden zij dat wel hebben gedaan, dan zou het eerder aan het licht zijn gekomen dat het schema nooit is opgezet

24. De bekendste itgave van de Milanese bouwverslagen is die van G. Cantù (ed.), Annali della Fabbrica del Duomo di Milano dall'Origine fino al presento (3 dln.), Milano 1877-1880. Voor een interpretatie van deze verslagen vergelijke men Hecht 1979, 161-170 met James Ackerman, ‘“Ars sine scientia nihil est” - Gothic theory of architecture at the Cathedral of Milan’, The Art Bulletin 31 (1949), 84-111.

25. De' Vincenti heeft de plattegrondmaten, die hij waarschijnlijk zelf heeft kunnen nameten, aangegeven in de voor hem gebruikelijke Bolognese voetmaat van ca. 38,22 cm. Aan de hand van deze bijzonder grote voetlengte heeft Hecht voor één Milanese el een metrieke waarde van 61,34 cm kunnen berekenen (zie Hecht 1979, 159-160).

26. Hecht 1979, 159. Voor een vergelijkend onderzoek naar de toepassing van rasterpatronen tijdens de vroege middeleeuwen, zie: Hecht 1983 (noot 14), 41-47, met een tweetal hypothetische voorbeelden.
Uiteraard is het op rekenkundige wijze uitzetten van een rasterpatroon (vgl. ons hedendaagse millimeterpapier) niet hetzelfde als de puur geometrische passerconstructie van een quadratuurschema!

27. De tekst van deze toelichting is bedorven in zoverre, dat enkele getallen in later tijd veranderd moeten zijn. Wat in het originele document heeft gestaan valt niet meer precies na te gaan, vermits het bij een brand in 1906 verloren is gegaan. Zie hierover Hecht 1979, 147-151, met verwijzingen naar: Erwin Panofsky, ‘An Explanation of Stornaloco's Formula’, The Art Bulletin 27 (1945), 61-65 (als aanhangsel bij Paul Frankl's ‘The Secret of the Mediaeval Masons’, ibid., 46-60), alsook naar: Guy Beaujouan, ‘Calcul d'expert, en 1391, sur le chantier du Dôme de Milan’, Le Moyen Age 69 (1963), 555 vv (hierna als Beaujouan 1963).

[p. 27]

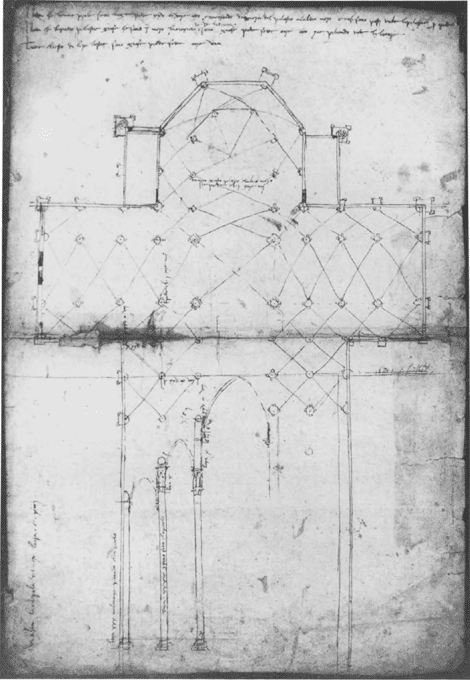
14 Antonio de' Vincenti, plattegrond met een doorsnede van de Dom van Milaan. Pentekening (verm. 1389-'90) (in: H. Siebenhüner, Deutsche Künstler am Mailänder Dom, München 1944, 94).

[p. 28]

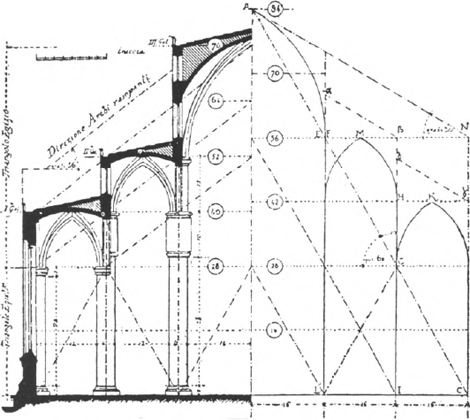
15 Luca Beltrami: Milaan, Domkerk. Doorsnede van het schip met een meetkundige vergelijking tussen verschillende ontwerpmaten (links conform het plan van de bouwkundigen; rechts zoals voorgesteld door Stornaloco) (1895) (in: Hecht 1979, 156).

als een passerconstructie: het diende enkel ter illustratie van een algebraïsche berekening. De woorden van de schrijver zelf mogen dit duidelijk maken: ‘Bassis trianguli est linea B C et est latitudo eclexie, scilicet LXXXXVI quantitatum. Erit ergo linea A D que est altitudo sumitas eclexie radix dix dc dcc mxx xxvii sesara quie tregesime, quod est aliquid minus de LXXXIIII quam divisi in sex partes in figuris triangularibus ac etiam in figuris quadrangularibus, prout patet in corpore majori eclexie, et trianguli incipiunt ab unitate secundum naturam triangulorum.’^28.

(vert.) ‘De basis van de driehoek is de lijn B C; deze lijn staat voor de breedte van de kerk, namelijk 96 quantitates (lees: ellen, St.S.). Aldus zal de lijn A D - deze geeft de hoogte aan tot het hoogste punt van de kerk - de wortel uit 10 600 700 1020 (?) anderhalf maal 27 zijn, omdat het een dertigste is, hetgeen iets minder is dan 84 (el); dit heb ik in zes delen verdeeld in driehoekige en ook in vierhoekige figuren, zoals men in het grotere deel (lees: het middenschip) van de kerk kan zien. De driehoeken beginnen vanuit de eenheid (d.w.z. van het raster), conform de eigenschap van driehoeken’.

Ondanks de verwarrende - en deels omstreden - rekensom blijkt duidelijk uit de toelichting, dat Stornaloco's ‘triangulatuur’ nooit verder heeft gereikt dan een eerste, voorlopige schets in de vorm van een gelijkzijdige driehoek. Hij schrijft immers het lijnenspel van het schema eerst voltooid te hebben, nadat hij de hoogtemaat voor het schip als een verhouding had berekend: aliquid minus de LXXXIIII, QUAM DIVISI IN SEX PARTES in figuris triangularibus ac etiam in figuris quadrangularibus.

Wat hij had berekend, omschreef Stornaloco als ‘iets minder dan 84 el’ (ca. 51,5 m, zie noot 25). Dit betekent, dat hem voor de hoogte van de gewelfaanzetten veelvouden van veertien el voor ogen hebben gestaan; ‘dit heb ik verdeeld in zes delen’. Het betekent ook dat hij er, als expertus in arte geometriae, goed van op de hoogte was dat de hoogte van een gelijkzijdige driehoek met een basis van 96 el (ca. 59 m) niet kan worden uitgedrukt in een geheel getal; daarom rondde hij de uitkomst (volgens de verhouding in het citaat 83,13 of 83,2 Milanese el) iets naar boven af.^29.

De reden hiervoor moet zijn geweest, dat het voor een adviseur in een moeilijk bouwkundig dilemma weinig zin zou hebben gehad om de leden van de Domfabriek een maatindeling in onhanteerbare breuken voor te schotelen. Uit de Milanese bouwverslagen blijkt ook, dat men ter plekke gewend was om bouwmaten aan te geven in hele en halve eenheden.^30. De manier bovendien, waarop in diezelfde verslagen over het schema is geschreven, maakt duidelijk dat men zich bepaald niet gebonden achtte aan een al dan niet sacrosancte Baugeometrie. Een voorbeeld.

Op 1 mei 1392 kwamen veertien bouwmeesters van

28. De redactie is van Frankl en Panofsky 1945, 53 (zie noot 27). De volledige tekst van Stornaloco's toelichting geeft Hecht 1979, 148-150, met aansluitend commentaar.

29. Tegenwoordig is het bekend dat de hoogte van een gelijkzijdige driehoek met een basislengte ‘I’ gelijk is aan 1/2√3 ofwel 0,866025 (in het geval van de Milanese Domkerk 83,13 el bij een basis van 96 el).
In de uitdrukking ‘quie tregesime’ (lett.: ‘omdat het een dertigste is’) heeft Beaujouan 1963 een bevestiging gezien van zijn vermoeden, dat Stornaloco voor het berekenen van de verhouding 1:1/2√3 de benaderde waarde 30:26 heeft gebruikt, hetwelk bij een basis van 96 el een hoogtemaat van 83,2 el oplevert (zie Hecht 1979, 151).

30. Een overtuigend aantal voorbeelden vindt men bij Hecht 1979, 151-155.

[p. 29]

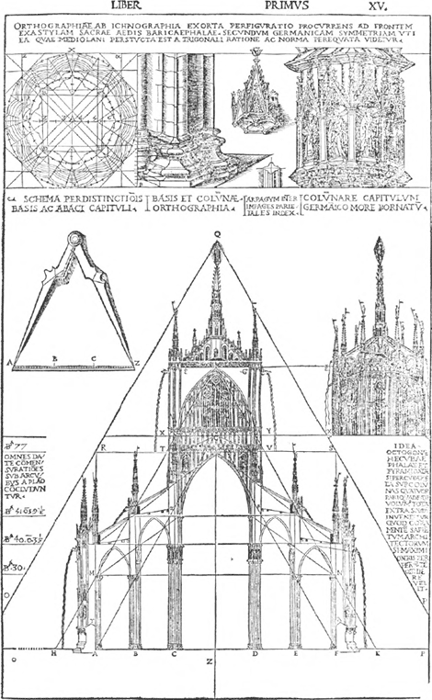
16 Cesare Cesariano, triangulatuurschema over een doorsnede van het schip van de Dom van Milaan; eerste versie. Houtsnede, 1521 (in: Cesare Cesariano, Vitruvius de Architectura: Nachdruk der kommentierten ersten italienischen Ausgabe (Como 1521), München 1969).

[p. 30]

de Domfabriek in conclaaf bijeen om over het voorstel van Stornaloco te beraadslagen. Eén van de gestelde vragen werd als volgt genoteerd:

‘Dubium: Utrum ecclesia ipsa non computando in mensura tiburium fiendum debeat ascendere ad quadratum an ad triangulum?’^31.

(vert.) ‘Kwestie: Moet de kerk zelf - de nog te bouwen vieringtoren in de afmeting niet meegerekend - volgens de vierhoek of volgens de driehoek oprijzen?’

Verscheidene onderzoekers hebben in deze vraag een duidelijke verwijzing gelezen naar de toepassing van quadratuur en triangulatuur in de bouwpraktijk van alledag.^32. Het besluit van de vergadering wijst daar echter in het geheel niet op. De bouwmeesters besloten namelijk het advies van Stornaloco maar ten dele te volgen, waarmee diens ‘triangulatuur’ op losse schroeven kwam te staan. Zijn voorstel om de gewelfribben over de buitenste zijbeuken te laten aanzetten op een hoogte van tweemaal veertien el werd gehandhaafd; maar vanaf dat niveau koos men voor een kleinere regelmaat van twaalf el, hetgeen uiteindelijk ook werd verwezenlijkt. Wanneer men nu deze verhoudingen schematisch weergeeft, dan wordt het duidelijk dat met ad quadratum geen zuivere vierkanten zijn bedoeld, maar vierhoeken of rechthoeken (met zijden van resp. 16:14 en 16:12 el, zie afb. 15). Dat er met de uitdrukking ad triangulum daarenboven zou zijn gezinspeeld op een ingeburgerde, symbolische methode van bouwkundig ontwerpen, lijkt gezien de toelichting van Stornaloco niet erg aannemelijk; een zuiver pragmatische afweging met betrekking tot de statica lijkt - hoe primitief ook - eerder voor de hand te liggen. Maar hoe dit ook zij, één ding kan worden vastgesteld: een geometrische ontwerptekening, gemaakt om op de werf te worden gebruikt, is het schema van Stornaloco nooit geweest.

31. Cantù 1877, dl. 1, 68 (zie noot 24).

32. Voorbeelden, in chronologische volgorde, zijn onder andere de publicaties van Dehio & von Bezold 1901 (zie de inleiding van deze bijdrage, p. 16), Ackerman 1949 (zie noot 24) en du Colombier 1973 (zie noot 2).

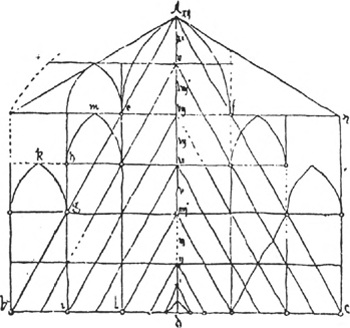
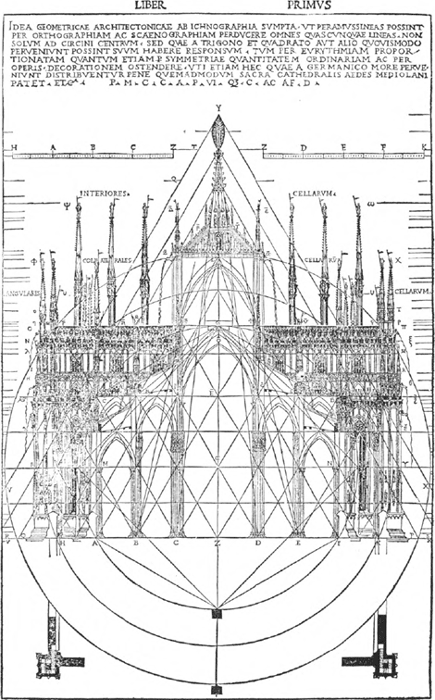
Cesariano en het ontstaan van de mythe

Ofschoon de eigentijdse bouwverslagen dus onomstotelijk aantonen dat de Dom van Milaan niet ad triangulum werd gebouwd, is de kerk in documenten van iets jongere datum vreemd genoeg wel als zodanig afgebeeld; een gegeven dat hier zeker vermeld moet worden, aangezien het ons uiteindelijk brengt bij de oorsprong van de geometrische ontwerphypothesen.

De vader van de mythe is de Milanese bouwmeester Cesare Cesariano geweest, die onder meer bekend is geworden door zijn vertaling uit 1521 van de De architectura libri X, rond 25 v.Chr. geschreven door zijn Romeinse collega Vitruvius. Ofschoon nu deze Vitruvius in al zijn Tien Boekdelen niets heeft behandeld wat zich enigerwijs met triangulatuur laat vergelijken, liet Cesariano zijn uitgave vergezeld gaan van een houtsnede van de Milanese Dom, zoals die naar zijn mening volgens de triangulatuur moest zijn ontworpen en gebouwd (afb. 16).

Wie de bijgevoegde afbeelding eens goed bekijkt zal al gauw beseffen, dat Cesariano volstrekt onkundig moet zijn geweest van het feit dat Stornaloco's voorstel uit 1391 maar ten dele was gerealiseerd. Op de houtsnede is namelijk te zien, dat hij de hoogtemaat van het middenschip zonder meer heeft geïnterpreteerd als de hoogtelijn van een gelijkzijdige driehoek (met als basis A-F). Daarenboven heeft hij nog twee driehoeken ingetekend, waarvan de basis in geen enkel logisch verband staat tot de indeling van de plattegrond. Waar het kader van deze driehoeken het opgaande werk doorkruist, zijn ook nog eens bouwmaten opgegeven die met de werkelijkheid niet overeenkomen.^33. Bij zijn poging om over een afbeelding van reeds bestaande architectuur een ‘passend’ geometrisch schema te leggen blijkt Cesariano dus al - hoe kan het ook anders - met dezelfde elementaire problemen te hebben geworsteld als al zijn navolgers. Cesariano's geloof in de juistheid van de zaak moet desondanks hardnekkig zijn geweest. Hij vervaardigde namelijk een tweede opstand in houtsnede, waarbij hij zijn uiterste best deed om het lijnenspel van pijlers, bogen en dakspitsen in een scala van geometrische figuren te vangen (afb. 17). Een hardnekkigheid, die Konrad Hecht en anderen in direct verband hebben uitgelegd met het schema van Stornaloco. Brengt men namelijk het ingewikkelde lijnenspel van de tweede houtsnede terug tot de meest essentiële verhoudingen, dan blijkt het in principe op dezelfde manier te zijn opgezet als het betreffende schema uit 1391 (vgl. afb. 13 met afb. 17).

Volgens Hecht kan deze gelijkenis weinig anders betekenen dan dat Cesariano het schema moet hebben gekend. Minder waarschijnlijk daarentegen is, dat hij tevens op de hoogte is geweest van de begeleidende tekst die dit schema juist begrijpelijk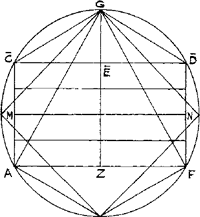

17 Cesare Cesariano, geometrisch patroon over een doorsnede van de Dom van Milaan, tweede versie. Houtsnede, 1521 (in: Cesare Cesariano, Vitruvius de Architectura: Nachdruk der kommentierten ersten italienischen Ausgabe (Como 1521), München 1969). Toegevoegd is een figuur met de belangrijkste lijnen van het patroon.

33. Dergelijk ‘alchemistenwerk’ van Cesariano is door Hecht uitvoerig ontleed: zie Hecht 1979, 129-140.

[p. 31]

[p. 32]

moest maken (zie hiervóór, noten 27 en 28); derhalve moet hij in Stornaloco's patroon van driehoeken en rechthoeken een soort ‘maatsleutel’ hebben gezien en hield hij het schema op zichzelf voor een heuse ontwerptekening.^34. Zouden velen hem in deze vergissing niet zijn gevolgd, dan zou de boeiende publicatie van Konrad Hecht waarschijnlijk nooit zijn geschreven.^35.

Ter bekering van de laatste esotherische geesten laat ik het slotwoord dan ook graag aan de meester zelf:

Der zum Baumeister bestimmte Konrad (von Cleve) und der Zimmermeister Wilhelm bestiegen im Herbst 1375 mit dem Baupfleger zusammen den südlichen Westturm der Stiftskirche (van Xanten, St.S.), um an Ort und Stelle den Bau des letzten Turmgeschosses zu bereden. ‘Konrad nam die nötigen Maß für seinen Riß’ (lees: bouwtekening), reiste nach Cleve zurück und übersandte von dort seinen Riß (...).

Die beiden Architekten fanden ein unvollendetes Bauwerk vor, das sie weiterführen sollten; beide machten sich die Mühe, am Bestehenden Maße zu nehmen. Weshalb? Die These behauptet doch, aus dem Grundmaß seien alle Baumaße eindeutig und mit der größten Genauigkeit hervorgegangen und überdies habe dieses Maßverfahren, das unter dem Siegel des Hüttengeheimnisses jedem Meister bekannt gewesen sei, die vorbestimmte Gestaltung des Bauwerks über lange Bauzeiten und selbst über Bauunterbrechungen hinweg sichergestellt. Weshalb griffen Konrad und Wilhelm dennoch zu Meßlatte und Zollstock? War etwa das die Bauarbeiten lenkende Grundmaß samt der zugehörigen Proportionsfigur (...) in Vergessenheit geraten? Mag sein - aber weshalb überzeugten sich die beiden (...) von der Länge des Grundmaßes nicht dort, wo man das Grundmaß eines Turmes zu suchen pflegt, am Fuß des Turmes nämlich, sondern stiegen nach oben, um in der Höhe Maß zu nehmen? Wollten sie etwa aus den mit Meßlatte und Zollstock näherungsweise ermittelten irrationalen Meßwerten die Proportionsfigur und aus dieser das Grundmaß zurückgewinnen? Wenn ja - wie sollte das geschehen, wo sich doch eine Proportionsfigur mit der Meßlatte unmöglich ermitteln läßt?

(Maß und Zahl in der gotischen Baukunst, 245-246).

Tekst en afbeeldingen zijn voor een deel getrokken uit mijn doctoraalscriptie, get. Bouwkundig ontwerpen in de Middeleeuwen. Een bespreking van de litteratuur, aangevuld met een onderzoek naar de oorspronkelijke voetmaten van de Pieterskerk te Utrecht (Kath. Univ. Nijmegen, aug. 1988). Het is hier dan ook zeker de plaats om mijn erkentelijkheid uit te spreken jegens Dr. H.A. Tummers (Instituut Kunstgeschiedenis der Kath. Univ. Nijmegen), em. Prof.dr.ir. C.L. Temminck Groll (destijds Techn. Univ. Delft), ir. G. Berends en G.W.C. van Wezel (beiden Rijksdienst voor de Monumentenzorg Zeist), alsmede aan Prof.dr. A.J.J. Mekking (destijds Rijksuniv. Utrecht), die niet geaarzeld hebben om de schrijver bij tijd en wijlen stimulerende - zij het soms pijnlijke - hoofdbrekens te bezorgen.

34. Ter vergelijking van twee recente opinies, zie Hecht 1979, 141-145 en Germann 1980, 33-34 (zie noot 6).

35. Dat de vermaningen van Hecht en anderen tegen de geometrische these niets aan actualiteit hebben verloren, toont het prachtige stalenboek van geometrische wichelarij van: Robert Lawlor, Sacred Geometry. Philosophy and Practice, London 1982. Op welke wijze deze auteur achtenswaardige gebouwen als de Parthenon te Athene en de kathedraal van Amiens geometrisch heeft onteerd, toont hij op p. 29 en 93 aldaar (het laatste hier als afb. 2). Wie zich evenmin heeft laten overtuigen is Günther Binding, die in de bibliografie van zijn recente publicatie Baubtrieb im Mittelalter (1993) enerzijds verwijst naar Hecht 1979, maar anderzijds op p. 345-349 - in een geometrische interpretatie van de twaalfde-eeuwse palts te Gelnhausen - nu juist laat zien hoe het niet moet...