Hollands Maandblad. Jaargang 1992 (530-541)

Denken en rekenen
Peter Wesly

Geld: ik ben er dol op. Het oppotten en dagelijks tellen verschaft me evenveel plezier als uitbundig geld uitgeven. Onverdiend geld in de schoot geworpen krijgen is al even bevredigend als met hard werken geld verdienen. Niet minder aardigheid heb ik erin om alles wat los en vast zit in geld uit te drukken: wat de schade zou zijn geweest als dat vliegtuig niet op een flat in de Bijlmer maar op het Rijksmuseum was neergestort, hoeveel het moet hebben gekost om Amsterdam op te delen in deelraden, welk vermogen ik nu zou hebben als mijn betovergrootvader een tientje voor zijn betachterkleinkind op de bank had gezet.

Die neiging, de monetaire variant van het pythagoreïsme, komt voort uit mijn algemenere lust in tellen en meten. En als ik nóg diepere lagen van mijn lustleven aanboor, vind ik de ultieme verklaring voor de opgebiechte aberraties: ik wil altijd gelijk krijgen. Omdat de medemens geen redelijk wezen is, hoef je het met argumenten meestal niet te proberen (al wil een drogreden nog wel eens uitkomst bieden, maar die heeft het bezwaar dat je het gelijk dat je krijgt niet tevens hébt). Afgezien dan van één soort argumenten: cijfers. Het behoort tot de hogere verrukkingen die het leven ons te bieden heeft wanneer je aan drie kwartier borreltafeldiscussie een einde kunt maken door te zeggen: allemaal goed en wel, maar 100 miljoen jaar geleden was er allang leven op aarde. En de argumenten waar zelfs de grootste botterik voor zwicht, zijn die waarin de cijfers worden voorafgegaan door $, f of £. ‘Kost het

[p. 7]

f 1000, -? Dan zie ik er van af.’

Maar als je rekent, moet je het wel goed doen. Met ‘goed’ bedoel ik nu niet in de eerste plaats dat je geen rekenfouten moet maken, maar dat je niet domweg moet rekenen. Dat is wat economen nogal eens doen. Soms is het zelfs hun credo. Zo schrijft E.J. Bomhoff: ‘Laten de economische experts maar aangeven hoe landen, bedrijven en individuen nog efficiënter kunnen worden, terwijl geestelijke leiders ons wijzen op onze morele verplichtingen. Ook dan kan de economische wetenschap nog nuttig bijdragen aan de discussie over inkomensverdeling en ontwikkelingshulp, net zo goed als de afdeling weg- en waterbouw van de Technische Universiteit kan adviseren over stormvloedkering in Bangladesh. Maar evenmin als de weg- en waterbouw orthodox, egoïstisch of niet “groen” genoeg zou zijn, omdat de cycloon in Bangladesh nog zoveel slachtoffers eist, valt de economische wetenschap te verwijten dat er in de Derde Wereld zoveel armoede is.’^1. Hier zit een belangrijke kern van waarheid in: niet de economie zelf is slecht, zomin trouwens als zij goed is; evenals de techniek kan zij ten goede of ten kwade worden aangewend, levert zij alleen maar middelen om door de burgers of politici gestelde doelen te verwezenlijken.

Maar de geciteerde econoom misleidt ons toch. Hij doet het voorkomen alsof economen niets anders doen dan modellen doorrekenen ten behoeve van beslissers. De praktijk is heel anders: economen bepleiten zélf maatregelen en soms hele politieke stelsels. Zij doen dat niet als burgers maar als economen, daarbij graag suggererend dat hun conclusies, immers resultaat van streng gereken, onontkoombaar zijn. Om deze beschuldiging te adstrueren een voorbeeld.

Twee jaar geleden betoogde een andere econoom, J. Tinbergen^2., dat het probleem van de duurzaamheid, dat wil zeggen het probleem van de eindigheid van de natuurlijke hulpbronnen, eenvoudig kan worden opgelost door een geleidelijke produktiviteitsverbetering. Uitgangspunt is handhaving van het huidige levenspeil^3., dus mijn radiatoren mogen per jaar evenveel calorieën blijven afgeven en u mag per jaar evenveel vluchten naar de zon en de sneeuw blijven maken. Hoe werkt Tinbergens wonderlamp van Alladin?

Wie voortgezet onderwijs heeft genoten, herinnert zich hoe hij in of rond zijn veertiende jaar kennis maakte met de meetkundige reeks: een reeks getallen die je krijgt door van een bepaald getal uit te gaan, daarvan het kwadraat te nemen, dan de derde macht, enzovoort:

a, a², a³, a⁴,...

In toepassingen van meetkundige reeksen gaat het meestal om hun som. Als de reeks eindig is, dus een laatste term aⁿ heeft, dan is die som natuurlijk ook een eindig getal. Als de reeks geen laatste term heeft maar oneindig (‘zolang je wilt’) voort is te zetten, dan heeft zij alleen een som in het geval dat a kleiner is dan 1. De som van zo'n oneindige reeks met a < 1 is:



Stel nu, schrijft Tinbergen, dat het jaarlijkse gebruik van een of andere natuurlijke hulpbron op dit moment v is. Laten we verder aannemen dat de technici erin slagen het rendement van de machines die op v lopen zo te verbeteren dat het gebruik van v ieder jaar met een vast percentage afneemt. Volgend jaar is het verbruik dan nog maar dv, waarin d de fractie is die met dat percentage overeenkomt (is bijvoorbeeld het percentage 2, dan is d 0,98). In het jaar na het volgende is het verbruik d²v, enzovoort. Omdat d kleiner is dan 1, heeft de (met v vermenigvuldigde) meetkundige reeks die zo ontstaat een eindige som: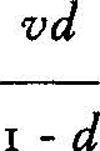

Als bijvoorbeeld d = 0,98 (dat wil zeggen het verbruik neemt met 2 procent per jaar af), dan is deze som gelijk aan 49d. Dat betekent dat we voor eeuwig voldoende steenkool (of welke andere hulpbron dan ook) hebben mits aan twee voorwaarden is voldaan: 1. de techniek stelt ons inderdaad in staat om ieder jaar hetzelfde te doen met 2 procent minder steenkool, en 2. de huidige wereldreserve is ten minste 49v.

Vervolgens geeft Tinbergen enkele werkelijke cijfers voor energiegebruik, wereldreserves en rendementsverbeteringen (globaal 1,7 procent, dus d = 0,983) in de afgelopen jaren, om daaruit te concluderen dat we voor altijd onderdak zijn mits we per jaar niet meer dan 1/59 van onze resterende energievoorraden verbruiken^4.. Een hele opluchting.

Tenzij we het volgende bedenken. Er is één ding dat onze knappe technici niet voor elkaar krijgen: de wetten van de natuurkunde veranderen. Die wetten houden in dat er grenzen zijn aan rendementsverbetering. Wat de grenzen zijn verschilt van proces tot

1. ‘Armoe komt niet door economen’, NRC Handelsblad 27 mei 1991.

2. ‘Zuinig aan met energie’, NRC Handelsblad 22 juni 1990. Op 27 juli 1990 gaf Tinbergen in de brievenrubriek van dezelfde krant een belangrijke correctie, maar die verandert niets aan mijn bezwaar. Ik heb dit bezwaar op 6 juli 1990 in NRC Handelsblad uiteengezet, maar uit een (persoonlijke) reactie van prof. Tinbergen maakte ik op dat ik hem de strekking van mijn betoog niet duidelijk had weten te maken.

3. Een ander uitgangspunt, ook geen kleinigheid, is dat de bevolking van de aarde niet verder toeneemt. Tinbergen noemt dit uitgangspunt zelf maar bespreekt het verder niet. Hetzelfde geldt voor milieu-effecten.

4. Dit is de conclusie op 22 juni 1190, zie noot 2. Die van 27 juni 1990 heeft niet op alle energie maar alleen op olie betrekking, en is daarvoor nog veel ‘gunstiger’.

[p. 8]

proces, maar voor alle processen geldt dat een rendement van 100 procent onmogelijk is. Wat de techniek ons nog allemaal brengt weet ik niet, maar mag ik redelijkerwijs verwachten dat over dertig jaar, als ik misschien nog leef, de huidige produktie kan worden gehaald met 60 procent van het huidige energiegebruik (0,983 tot de 30ste macht is namelijk 0,60)? En dat over negentig jaar, als mijn verhoopte kleinkinderen oud maar misschien nog niet dood zijn, hetzelfde kan met 21 procent van het huidige verbruik (0,983⁹⁰ = 0,21)?

Het is allemaal erg onwaarschijnlijk, te meer omdat veel processen nu al een behoorlijk rendement hebben. Een goede cv-ketel haalt op z'n gemak 80 procent. Als jaar in jaar uit de hoeveelheid brandstof die nodig is om mijn kamer zo warm te houden als het er nu is met 1,7 procent kan worden teruggedrongen, dan is al over dertien jaar een (onmogelijk) rendement van 100 procent bereikt. En daarna? 100 procent moge technisch of fysisch onmogelijk zijn, meer dan 100 procent rendement is zelfs theoretisch, dat wil zeggen ‘logisch’ of ‘voor God’, onmogelijk.

Tinbergens berekening klopt dus wel, en zijn cijfers over wereldvoorraden en dergelijke zullen ook wel in orde zijn, maar zijn conclusie dat we per jaar met een gerust hart 1/59 van onze energievoorraden mogen consumeren, berust op een verzwegen praemisse die kant noch wal raakt: de veronderstelling dat we tot in lengte van dagen het rendement van onze machines met een vast percentage kunnen blijven verbeteren. Zonder deze veronderstelling leiden dezelfde cijfers ongetwijfeld tot de tegengestelde conclusie: dat het huidige niveau van energieconsumptie veel te hoog is.

Het voorbeeld toont ons een van de meest bezochte intellectuele valkuilen: de redenering is vlekkeloos, dus we moeten de conclusie wel aanvaarden. Op de eerste bladzijde van elk logicaboek kun je lezen dat daartoe iets meer nodig is: de waarheid van de praemissen. De vlekkeloze redenering zorgt slechts voor behoud van waarheid: als de praemissen waar zijn, dan is de conclusie onontkoombaar. Dat economen ex cathedra aanbevelingen doen als de in het voorbeeld genoemde, is overigens een meer dan intellectueel gevaar.

De intellectuele leefregel die hier wordt overtreden, luidt: gebruik je verstand, niet de formule. Dat ook sommige economen deze leefregel voorstaan, blijkt uit de kritiek die John Maynard Keynes rond 1930 leverde op het boek Prices and Production van F.A. von Hayek, ook al een beroemde econoom: hij vond dat boek een voorbeeld van hoe een blindelings voortredenerend logicus die van een verkeerde veronderstelling uitgaat, in het gekkenhuis terecht kan komen.