Hollands Maandblad. Jaargang 1981 (398-409)

[p. 32]

Meetkundige taalkunde
Battus

- kun je over alles een artikel schrijven?
- ja
- schrijf dan over Geometrische Linguistiek

0 inleiding

De meetkunde wordt beheerst door twee principes: invariantie en abstractie, waartussen trouwens verband bestaat. Ik bespreek in 1 de invariantie in de meetkunde, in 2 de abstractie. In 3 kijk ik in hoeverre de taalkunde te karakteriseren is door het begrip invariantie, en in 4 doe ik hetzelfde voor abstractie.

Tot hier toe is de parallel tussen meet- en taalkunde een metaforische, of een parallel die het gevolg is van het feit dat in àlle wetenschappen invariantie en abstractie een rol spelen.

Maar er blijkt op één gebied een interessant dubbel wederzijds direct verband te bestaan tussen enerzijds een bepaalde axiomatische opbouw van een meetkunde met duale eigenschappen, en anderzijds de twee diametrale grondslagen van de linguistische semantiek - dit komt in 5 aan de orde.

1 invariantie in de meetkunde

Meetkunde, dat zult u zich herinneren, gaat over punten, lijnen, vlakken, driehoeken, cirkels. In elke wetenschap is van belang om vast te stellen wanneer twee dingen gelijk geacht worden. In de chemie zijn twee isotopen gelijk, in de fysika juist niet.

Het opvallende van de meetkunde is nu dat er niet één begrip van gelijkheid tussen meetkundige objecten bestaat, maar een hele ladder. Er is een grote verzameling van meetkundes ieder met een eigen gelijkheidsbegrip.

Op het laagste niveau is een driehoek uitsluitend gelijk aan zichzelf (gegeven de invariantie in de tijd die we bij fysische objecten vaak aannemen). Elke twee driehoeken zijn dus verschillend. Dit is geen erg interessant niveau.

De middelbare-schoolmeetkunde, door Euclides nauwkeurig beschreven, kan gekarakteriseerd worden als de congruentie-meetkunde: twee driehoeken zijn gelijk als de ene op de andere gelegd kan worden. Meestal staat men daarbij een wenteling in de ruimte toe, zodat de driehoeken 3 en 4 evenzeer gelijk zijn als de driehoeken 1 en 2.

Congruente driehoeken hebben gelijke vorm en oppervlak. Men kan bewijzen dat als drie onafhankelijke elementen van twee driehoeken gelijk zijn (even lange zijdes, of twee zijdes met de hoek ertussen), dat dan die twee driehoeken gelijk zijn.

Maar de middelbare-schoolmeetkunde is eigenlijk wat ruimer. Op het bord tekent de leraar driehoek 5, en in het schrift tekent de leerling driehoek 6. Ze hebben dezelfde vorm (bij een driehoek betekent dat: dezelfde hoeken), maar niet meer hetzelfde oppervlak. De centimeter speelt in de middelbare-schoolmeetkunde geen rol - die kende Euclides trouwens niet. Elk recht lijnstukje kan als eenheid van lengte dienen. Door tekeningen, film, televisie, zijn wij gewend aan het feit dat goedgelijkende afbeeldingen niet levensgroot hoeven te zijn.

In de schoolmeetkunde spelen evenwijdige lijnen een belangrijke rol. Als zij niet bestonden, zouden we de prettige eigenschap hebben dat elk tweetal lijnen elkaar in één punt snijdt. Men zegt wel dat een paar evenwijdige lijnen elkaar ‘in een oneindig ver punt snijden’. Om precies te zijn: alle aan elkaar evenwijdige lijnen snijden elkaar in het ene punt (P in figuur 7); andere daaraan niet evenwijdige lijnen gaan niet door dat punt. Deze manier van spreken is nuttig en zichtbaar te maken door de (oneindig verre) lijn waarop alle punten liggen die als snijpunten van evenwijdige lijnen dienen, te beschouwen als een gewone lijn. Door het tekenpapier oneindig ver te schuiven zien we in figuur 8 wat in figuur 7 niet getekend kon worden.

Deze zienswijze maakt de vlakke meetkunde veel eenvoudiger: twee lijnen hebben nu altijd een snijpunt. Er is niet langer verschil tussen een ellips, een parabool, en een hyperbool. Het is, zoals blijkt uit de prentjes 9, 10 en 11, slechts de vraag waar en in hoeveel punten een ellips de ‘oneindig verre rechte’ snijdt.

Hier gebeurt meer dan spielerei: allerlei eigenschappen van lijnen in ellipsen zijn nu in direct verband te brengen met soortgelijke eigenschappen van lijnen in parabolen en hyperbolen.

Behalve deze, ‘projectieve’, meetkunde zijn er nog ontelbaar veel andere meetkundes: met een eindig aantal punten, met meer dimensies, met anti-Euclidische eigenschappen. De ruimste van deze meetkundes, gezien het standpunt van wat gelijk geacht wordt, is de topologie. In

[p. 33]

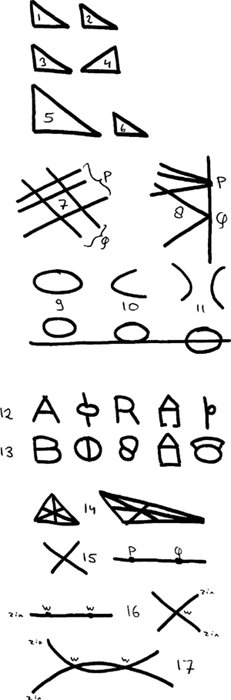die meetkunde zijn de figuren uit 12 alle onderling gelijk, maar ongelijk aan de figuren uit 13, die weer alle onderling hetzelfde geacht worden. Invariant bij de elementen van 12 is dat ze allemaal twee eindpunten hebben, en twee driesprongpunten, en dat ze één ‘zwart te kleuren’ cirkelgebiedje bezitten.

In de projectieve meetkunde blijft een figuur dezelfde, hoe hij ook ten opzichte van de oneindig verre rechte wordt geschoven. In de gelijkvormigheidsmeetkunde blijft een figuur dezelfde hoe hij ook in een vlak, loodrecht, vergrootapparaat geprojecteerd wordt. In de topologie blijft een figuur dezelfde hoe je hem ook uitrekt of indeukt, zolang je maar niet plakt of knipt.

Natuurlijk zijn de trappen van invariantie ook te zien als trappen van abstractie, maar in de meetkunde versta ik onder abstractie toch iets anders:

2 abstractie in de meetkunde

Vlakke meetkunde spreekt wel over punten, lijnen, en driehoeken, maar gaat absoluut niet over stippen, strepen, en getekende driehoeken. De meetkundige objecten zijn pure bedenksels. De meetkundige redenering mag dan ook nooit een beroep doen op de aanschouwing. Welke driehoek je ook tekent, altijd zullen de drie lijnen uit de hoekpunten naar de middens van de ertegenover gelegen zijden elkaar in één punt snijden. Wie dat voor honderd verschillende driehoeken heeft gedaan, is ervan overtuigd dat het altijd zo is. Uit fysische beschouwingen, en zelfs uit esthetische, is ook tot de conclusie te komen dat de drie ‘zwaartelijnen’ elkaar in één punt moeten snijden. Maar voor de meetkundige snijdt dat allemaal geen hout. Zij wil een bewijs. Als voor dat bewijs alleen logica gebruikt mag worden, dan kan het niet geleverd worden: logica kent geen driehoeken. Daarom heeft de meetkundige startstellingen, ‘axioma's’, waarvan zij de waarheid, voorlopig en zonder metafysiek, aanneemt. De kunst is nu om met zo weinig mogelijk axioma's zoveel mogelijk interessante dingen te bewijzen. Het kan een meetkundige werkelijk niets schelen of drie lijnen elkaar in een punt snijden. Maar de vraag hoe dit mooi bewezen kan worden, en wat er daarna weer voor een bewijs in aanmerking komt, dat houdt haar bezig.

In de axioma's komen natuurlijk de woorden voor waarmee de elementaire meetkundige objecten worden aangeduid. Maar de meetkundige mag geen eigenschappen van die objecten gebruiken die niet in de axioma's staan. De houding van de ambtenaar tegen iemand zonder geboortebewijs: ‘U bent niet geboren’ is de normale meetkundige houding.

[p. 34]

In het bijzonder is het mogelijk om de elementaire meetkundige objecten anders te tekenen dan traditioneel gebruikelijk. We deden dat al bij de tekeningen 8 tot en met 10. Zo kan ook in het Euclidische, dat wil zeggen ons oude vertrouwde, vlak een tekening worden gemaakt van de niet-Euclidische meetkunde, waarin bijvoorbeeld de som van de hoeken in een driehoek niet langer 180 graden is. De lijnen in die niet-Euclidische meetkunde teken je als halve cirkels. Twee lijnen die elkaar op de buitengrens snijden noemen we evenwijdig. Zo'n tekening noemt men wel een ‘model’ van het axiomastelsel.

Een axiomastelsel van de projectieve meetkunde zou kunnen zijn:

axioma 1 Door twee punten gaat precies één lijn.

axioma 2 Twee lijnen snijden elkaar in precies één punt.

(figuur 15)

We voeren het werkwoord ‘incideren’ in, dat als onderwerp een punt of een lijn kan hebben. De zinnen ‘het punt P ligt op de lijn l’ en ‘de lijn l gaat door het punt P’ schrijven we nu als: ‘P incideert met l’ of ‘l incideert met P’.

De axioma's worden in deze schrijfwijze:

axioma 1': Twee punten incideren met precies één lijn.

axioma 2': Twee lijnen incideren met precies één punt.

Met behulp van de drie elementaire meetkundige objecten punt, lijn en incideren, zijn nu alle andere te maken, zoals bijvoorbeeld driehoek.

Nu geldt de volgende metameetkundige stelling:

Als je in een meetkundige stelling alle voorkomens van het woord ‘punt’ vervangt door het woord ‘lijn’, en alle voorkomens van het woord ‘lijn’ door het woord ‘punt’, dan krijg je een stelling die even waar is als de oorspronkelijke.

De waarheid van deze metageometrische verrassing is niet moeilijk in te zien. Als de oorspronkelijke stelling bewezen kon worden, schrijf dat bewijs dan op. Vervang in het bewijs overal ‘punt’ door ‘lijn’, en ‘lijn’ door ‘punt’. Overal waar je axioma 1' gebruikte, gebruik je nu axioma 2'. En waar je axioma 2' nodig had roep je nu axioma 1' te hulp. Andere axioma's met ‘punt’ en ‘lijn’ zijn er niet. Je krijgt dus nu een bewijs voor de getransformeerde stelling.

Men noemt dit proces ‘dualiseren’; het is een ook in andere gebieden van de wiskunde voorkomende manier van ‘één betalen, twee halen’. Ontdek dat het duale van een driehoek weer een driehoek is!

De meetkundige abstractie gaat dus zover dat hij punten en lijnen met elkaar verwisselen kan, als dat in de axioma's kan. Nergens verschijnt een expliciete definitie van wat punten en lijn nu ‘eigenlijk’ zijn. Hun eigenschappen worden slechts impliciet in de axioma's vastgelegd.

3 invariantie in de taalkunde

Ook in de taalkunde is het begrip ‘gelijkheid’ tussen taalkundige objecten veel ruimer dan in de omgangstaal. Op het laagste niveau is elke uiting natuurlijk uniek. Twee uitingen zijn dus verschillend. Dit is geen erg interessant niveau. Met grote moeite slaagt de linguist erin om twee uitingen die ‘hetzelfde klinken’ gelijk te noemen.

De Utrechtse a klinkt anders dan de Amsterdamse a, maar voor het begrip ‘Nederlandse zin’ wordt van dat verschil afgezien.

In een taal wordt tussen de zin ‘Gisteren was ik daar’ en ‘Ik was daar gisteren’ een verband gelegd. Voor de fonoloog zijn dit twee verschillende zinnen. Maar voor een syntacticus zijn dit misschien twee verschijningsvormen van eenzelfde zin. Zelfs de twee bepaald niet gelijkbetekenende zinnen ‘Was ik daar gisteren?’ en ‘Ik was daar gisteren’ zijn, als je maar hoog genoeg gaat, ‘gelijk’.

De zin ‘Ik was daar gisteren’ en ‘I was there yesterday’ zijn op het niveau van de betekenis ‘gelijk’.

Taalkunde is, anders dan meetkunde, een empirische wetenschap die te maken heeft met feiten die er al liggen voor de taalkunde begon. Maar de taalkundige kan zijn objecten toch aanzienlijk fatsoeneren, niet alleen wat betreft de vraag ‘Wat noem ik gelijk’, maar ook door abstractie:

4 abstractie in de taalkunde

Tussen de Aristotelische tweedeling van een zin in subject en predikaat en de herschrijfregel uit de transformationele grammatica

S → NP VP

bestaat een principieel verschil. De symbolen S, NP en VP zijn slechts hulpsymbolen bij het vervaardigen van een zin. Zij hebben geen intrinsieke betekenis. Aristoteles dacht bij subject en predikaat zelfs niet aan iets taalkundigs, latere taalkundigen deden dat wel, maar in de transformationele taalkunde hebben zij in zich even weinig belang als de vraag of je een punt in de meetkunde P of Q noemt. Het is misschien handig om de regels

S → NP VP

NP → Jan, Piet

VP → loopt, zweet

zo op te schrijven, maar precies even goed is het drietal:

[p. 35]

S → VP NP

VP → Jan, Piet

NP → loopt, zweet

De vraag in hoeverre de taalkundige vrij is te abstraheren, is onder taalkundigen nog niet uitgevochten. Er zijn er die bezwaar maken tegen een uitspraak als: de uitgang achter de stam in de eerste persoon enkelvoud tegenwoordige tijd is nul. Mij lijkt het dat elke abstractie geoorloofd is die tot aantrekkelijke resultaten leidt. Vergeleken met de abstractie in de natuurkunde is de abstractie in de taalkunde nog niet eens begonnen.

5 semantische dualiteit

Er bestaan twee, diametrale, grondslagen voor de semantiek (geïllustreerd in figuur 16):

1e grondslag. De betekenis van een woord wordt gevonden in een lexicon, waarin geen zinnen staan, maar alle relevante eigenschappen van het woord.

De betekenis van een zin wordt gevonden door de betekenissen van de er in voorkomende woorden in het lexicon op te zoeken, en met behulp van de syntactische bouw van de zin daaruit de zinsbetekenis af te leiden.

[p. 36]

2e grondslag. De betekenis van een woord wordt vastgesteld door de zinnen waarin dat woord voorkomt. Op de een of andere manier kennen we de betekenis van elke zin. Kijken we nu hoe een woord in allerlei zinnen optreedt dan leert ons dat de betekenis van het woord.

Bij beide standpunten zijn problemen. In de taalkunde volgt men meestal het eerste. Met name Montague doet dat. Joos en Wittgenstein zijn aanhangers van het tweede standpunt. In de kindertaalverwervingskunde hoor je vaak het tweede standpunt (de ‘eenwoordszin’). In woordenboeken wordt de betekenis van een woord dikwijls aangegeven door enkele goedgekozen voorbeeldzinnen waarin het voorkomt.

In 2 leerden we een zuiver geval kennen van semantiek volgens de 2e grondslag: de betekenis van de woorden punt en lijn werd uitsluitend vastgelegd door twee zinnen, de axioma's. (Merk op dat van die twee zinnen de waarheid werd aangenomen, iets dat in de bovengenoemde 2e grondslag niet genoemd werd, maar juist in de eerste wel een rol speelt).

De plaatjes 15 en 16 lijken op elkaar. Laten we proberen ze gelijk te maken.

Twee lijnen gaan door één punt. Twee zinnen kunnen natuurlijk best geen, of méér dan een woord gemeen hebben. De zinnen zijn, in het vlak getekend, eerder de kromme lijnen uit figuur 17.

Is het mogelijk om onze zinnenverzameling zo in te perken dat twee zinnen elkaar in niet meer dan een punt snijden? Dat lijkt geen al te gekke abstractie, want als het zo was dat een woord altijd samen met een ander woord in een zin voorkwam, dan is het waarschijnlijk verstandig die twee woorden als één woord te beschouwen (bijvoorbeeld: ‘verzenen’ en ‘slaan’)

Is het aan de andere kant teveel gevraagd dat bij ieder tweetal woorden er een uniek bepaalde zin is die ze bevat? Als ons dat lukt hebben we:

1"	Twee zinnen hebben precies een woord gemeen.
2"	Twee woorden liggen in precies een zin. Denkt u hier eens een maand over na.