|
| |
| |
| |
René de Borst
Jules Verne als ingenieur
Inleiding
De boeken die Jules Verne in de tweede helft van de negentiende eeuw heeft geschreven, vormen een goede weerspiegeling van de geest van de tijd waarin hij leefde, waarin het geloof in wetenschappelijke en technische vorderingen een centrale plaats in het denken innam. Met technische innovaties - al zal men toen dit woord niet gebezigd hebben - als de stoommachine en wetenschappelijke doorbraken als de leer van het elektromagnetisme beweegt Jules Verne zich met zijn boeken in een hoofdstroom van maatschappelijk denken. De vraag is in hoeverre hij meer betekende. Was hij profetisch of visionair? Hoewel een allesomvattend antwoord op deze vraag in deze bijdrage niet nagestreefd zal worden, zal gepoogd worden aan de hand van een bespreking van Vernes De reis naar de maan een indruk te geven of hij visionaire gedachten ontvouwd heeft en, evenzeer belangrijk, in hoeverre fysische principes ten grondslag lagen aan de sciencefictionachtige verhalen die hij gepubliceerd heeft en in welke mate de getallen die hij noemt, soms schijnbaar goed beargumenteerd, maar soms ook heel terloops genoemd, realistisch zijn.
| |
De reis naar de maan
De reis naar de Maan is geïnstigeerd door de zogenaamde ‘Gun club’. De leden van deze club hebben een grote passie voor artillerie. Na het aflopen van de Amerikaanse Burgeroorlog is het met technische innovaties op dit gebied echter wat kalmer geworden. Op een gegeven moment komt Impey Barbicane, de president van de Gun club, op het fantastische idee om een kanon te construeren, zo krachtig dat het een capsule kan afschieten die op de Maan zal landen. Scepsis alom. Zo noemt een zekere kapitein Nicholl vijf redenen waarom de Gun club er nooit in zal slagen een dergelijk project succesvol te voltooien. Ze variëren van heel praktische redenen, zo- | |
| |
als dat de Gun club het benodigde kapitaal nimmer bijeen zal krijgen, tot heel technische, bijvoorbeeld dat het kanon zal springen bij het afvuren. Op dit laatste aspect wordt in dit artikel nog nader ingegaan.
Uiteraard komt in het optimisme van die tijd het geld bijeen en ontploft het kanon niet bij de lancering. Na lancering van de capsule, met aan boord zowel de voorvechter van het project, Impey Barbicane, zijn criticus kapitein Nicholl als Michel Ardan, een Fransman (!) die op een gegeven moment uit het niets komt opdagen, wordt de capsule licht uit zijn baan gebracht door de aantrekkingskracht van een onbekend hemellichaam. Als gevolg hiervan landt de capsule niet op de Maan, maar maakt een aantal rondjes eromheen, waarna hij terugkeert richting Aarde en uiteindelijk in de Stille Oceaan neerkomt. Geheel overeenkomstig de procedures in het Amerikaanse Apollo-programma van een eeuw later, wordt de bemanning vervolgens opgepikt door een Amerikaans marineschip.
| |
Enige opmerkelijke zaken
Zoals hierboven reeds aangestipt, zijn er enige opmerkelijke overeenkomsten tussen de maanreis zoals Verne deze beschreven heeft en de maanreizen binnen het een eeuw later plaatsvindende Apolloprogramma. Het oppikken van de drie ruimtereizigers door een Amerikaans marineschip in de Stille Oceaan is natuurlijk een detail, maar de lanceerplaats is dat allerminst. In beide gevallen is dat Florida. Dit is geen toeval, aangezien dit een gunstige lanceerplaats is. Hieraan liggen dan ook echte berekeningen ten grondslag, uitgevoerd door Vernes neef Henri Garcet, een wiskundige. Deze heeft evident de zwaartekrachtswet van Newton, die toen al bijna twee eeuwen bekend was, gebruikt om de berekeningen aan de baan uit te voeren. Dit blijkt bijvoorbeeld uit de in het boek genoemde tijdsduur, die met circa 200 uur effectieve reistijd niet veel uitgaat boven de ongeveer 120 uur van de Apollo 8.
Heel opmerkelijk is ook de keuze voor het materiaal aluminium voor de capsule. Bedenkend dat men pas zestig tot zeventig jaar na verschijning van De reis naar de maan vliegtuigen uit dit materiaal is gaan construeren, mag dit gerust een revolutionaire gedachte worden genoemd. Opmerkelijk is al dat eraan gedacht is dat een capsule uit gietijzer veel te zwaar zou worden. Het zijn dit soort details die Vernes boeken een zo sterke werkelijkheidszin geven. Interessant is ook dat Verne voor een capsule met een diameter van on- | |
| |
geveer 3 meter uitkomt op een massa van m = 10.000 kilogram. Zowel diameter als massa komt nauw overeen met die van de latere Apollo-capsules, die een massa hadden van ruim 12.000 kilogram.
| |
De mechanica van Newton
Verne en verwanten die hem bij de daadwerkelijke berekeningen hielpen, voerden hun berekeningen uit op grond van degelijke fysische principes. Voor De reis naar de maan zijn dat de mechanicawetten van Newton. Deze grote wis- en natuurkundige heeft in zijn Philosophiae Naturalis Principia Mathematica uit 1687 de grondslagen gelegd voor de mechanica, de leer van de beweging en vervorming van lichamen en de krachten die daarop uitgeoefend worden en daarbinnen heersen. Zij worden nog steeds onderwezen in de bovenbouw van middelbare scholen over de hele wereld en vormen een belangrijk fundament van hedendaagse ingenieursopleidingen als in de luchtvaart- en ruimtevaarttechniek, de werktuigbouwkunde, civiele techniek en maritieme techniek. In het bijzonder Newtons gravitatiewet, die zegt dat de aantrekkingskracht tussen twee lichamen evenredig is met hun massa's, maar omgekeerd evenredig is met het kwadraat van de afstand tussen twee lichamen, speelt een cruciale rol in berekeningen van satellietbanen en ruimtereizen. Ongetwijfeld heeft Vernes neef deze wetmatigheid toegepast in zijn berekeningen.
Het bekendst is waarschijnlijk de zogenaamde Tweede Wet van Newton, die stelt dat de kracht die op een lichaam uitgeoefend wordt, gelijk is aan de massa van het lichaam maal de versnelling die het als gevolg van deze kracht ondergaat. Deze wet zal hierna gebruikt worden voor een globale berekening van de afmetingen van het kanon, zodanig dat het bij afvuren inderdaad niet uit elkaar springt. Dit is een aspect waarop Verne in zijn boek niet echt ingaat, hij postuleert uit de losse pols een wanddikte van 2 meter. Inderdaad, de methoden om dit goed te berekenen waren destijds nog niet voorhanden: zij werden pas rond de Tweede Wereldoorlog ontwikkeld. Toch heeft de wanddikte waarop Impey Barbicane uitkomt bij extrapolatie van bestaande kanonontwerpen een redelijke orde van grootte.
| |
Het kanon: hoe realistisch was dit?
Het kanon waarmee de ruimtecapsule afgeschoten wordt, heeft een
| |
| |
inwendige diameter van D = 3 m en een wanddikte van d = 2 m. De lengte van de loop, die rechtstandig in de aardbodem gegoten is, bedraagt L = 270 m. Ongeveer een kwart van de loop is gevuld met het explosief, schietkatoen, zodat de capsule ongeveer 200 meter in de kanonsloop moet afleggen.
Een belangrijk gegeven is de door Verne genoemde startsnelheid van 15.000 m/s. Deze snelheid is nodig om aan het Aardse zwaartekrachtveld te ontsnappen en is waarschijnlijk uitgerekend door Vernes neef, Henri Garcet. De drukverdeling die op de wanden van het kanon ontstaat ten gevolge van de explosie, is uitermate complex en computermodellen om dit proces te simuleren zijn nog in volle ontwikkeling. Interessant is dat de ontwikkeling van deze simulatiemodellen in de jaren zestig van de twintigste eeuw een sterke impuls hebben gekregen door het Apollo-programma. De eindige-elementenmethode, een belangrijke vertegenwoordiger van dit soort simulatiemethodieken, is nu niet meer weg te denken uit de ingenieurspraktijk en wordt toegepast op uiteenlopende problemen als botssimulaties van auto's, de stormvloedkeringen in de Oosterschelde en in de Nieuwe Waterweg, het ontwerp van vliegtuigen als de nieuwe superjumbo van Airbus, de A380, enzovoorts.
Al is de werkelijke drukverdeling op de wanden heel moeilijk precies uit te rekenen, een globale voorspelling van de orde van grootte van deze druk en van de hieruit volgende spanningen die in de wanden optreden, is redelijk eenvoudig te maken. Hiertoe doen we een paar aannamen. Als eerste postuleren we dat de gasdruk ten gevolge van de explosie constant blijft in de tijd dat de capsule zich in de loop bevindt en dat deze druk ook overal in de loop dezelfde waarde heeft. Voorts vervangen we het gietijzer door staal. Gietijzer, vanaf het einde van de achttiende tot ver in de negentiende eeuw frequent toegepast, bijvoorbeeld bij de Coalbrookdale-brug stammend uit 1779, de eerste metalen brug, heeft als vervelende eigenschap dat het vrij bros is. Staal is veel taaier, en deze eigenschap maakt het mogelijk om de in de twintigste eeuw ontwikkelde plasticiteitstheorie toe te passen bij de berekening. Plasticiteit is de eigenschap van metalen dat zij relatief grote vervormingen kunnen ondergaan alvorens te breken, een beetje vergelijkbaar met boetseerklei. Deze eigenschap maakt het mogelijk te veronderstellen dat de spanning in de wand bij bezwijken van het kanon overal gelijk is, zie bijvoorbeeld de figuur hiernaast, waar een dwarsdoorsnede van het kanon is geschetst met de spanningen in de wand en de gasdruk.
Als we aannemen dat het kanon net niet bezwijkt bij de explosie, dan is de totale kracht die per strekkende millimeter kanonsloop
| |
| |
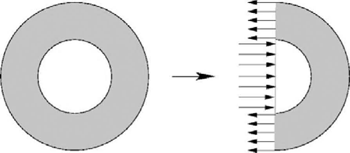
Dwarsdoorsnede van een kanonsloop (links) en halve dwarsdoorsnede met de daarop werkende drukken en spanningen (rechts).
opgevangen kan worden: 4000 · 1 · 210 = 840 · 10 3 Newton [N]. Het getal 210 N/mm 2 komt van de maximale spanning die staal per vierkante millimeter kan weerstaan. Bij een inwendige diameter van 3000 millimeter levert dit een maximale gasdruk op van 840 · 103 / 3000 = 280 N/mm 2.
De totale kracht die het gas dan op de capsule uitoefent, is gelijk aan deze gasdruk maal de oppervlakte van de onderkant van de capsule: 280 N/mm2 · π · 1500 mm2 ≈ 2.000.000.000 N. Met de Tweede Wet van Newton vinden we vervolgens de versnelling door deze kracht te delen door de massa van de capsule: m = 10.000 kg. Dit geeft een versnelling a ≈ 200.000 m/s2. De verblijftijd in het kanon kan worden berekend op grond van de aanname dat de gasdruk, en derhalve ook de versnelling, constant zijn in de loop van de tijd. Voor een dergelijke eenparig versnelde beweging geldt dat de afgelegde afstand gelijk is aan de helft van de versnelling maal het kwadraat van de verblijftijd. In herinnering roepend dat het stuk kanonsloop dat niet met schietkatoen gevuld is ongeveer 200 meter bedraagt, is de verblijftijd t = √ (2 · 200 / 200.000) ≈ 0,045 s. De snelheid waarmee de capsule de loop verlaat, is dan, wederom uitgaande van een eenparig versnelde beweging, het product van versnelling en verblijftijd: v = 200.000 · 0,045 = 9000 m/s. Dit is weliswaar kleiner dan de benodigde ontsnappingssnelheid van 15.000 m/s, maar toch van een vergelijkbare orde van grootte. Bij een wanddikte van ongeveer 5,5 meter zouden de geweldige krachten van de explosie door het kanon opgevangen kunnen worden, uiteraard binnen het kader van deze vereenvoudigde berekening.
Het grootste probleem is echter niet het intact blijven van het kanon, maar de enorme versnelling waar de reizigers aan onderworpen worden: bij een wanddikte van 2 meter reeds twintigduizend keer de Aardse zwaartekrachtversnelling. Om dit getal in per- | |
| |
spectief te plaatsen, dient men te bedenken dat goedgetrainde straaljagerpiloten in beschermende kleding maximaal tien keer de versnelling van de zwaartekracht kunnen doorstaan zonder bewusteloos te raken. Het drietal zou de lancering nooit overleefd hebben. Verne lijkt zich van dit probleem bewust, aangezien dit precies een van de argumenten is die Barbicanes criticus, kapitein Nicholl, noemt. De mogelijkheid om de schok via dempers op te vangen wordt genoemd, maar dit onderschat de enorme versnelling die hier gegenereerd wordt.
| |
Besluit
Veel van de ideeën van Jules Verne waren redelijk onderbouwd door berekeningen op solide fysische grondslagen. Zo ook die in De reis naar de maan, waar de orde van grootte van de genoemde getallen vrij realistisch blijkt te zijn, ook voor de afmetingen van het kanon, terwijl deze met de kennis van Vernes tijd nog niet echt te berekenen waren.
Maar op verschillende punten loopt Verne heel lichtvoetig heen over overigens wel gesignaleerde problemen, zoals de enorme versnelling bij de lancering, de koude en het ontbreken van zuurstof in de ruimte, en de grote hitte die zich ontwikkelt door de wrijving met de lucht van de atmosfeer, met name bij terugkeer in de dampkring (de capsule van aluminium zou gesmolten zijn). Veel van deze problemen betreffen het welzijn van de reizigers en je zou kunnen zeggen dat Verne behept was met hetzelfde gebrek dat technici en ingenieurs soms wel door de maatschappij verweten wordt, namelijk dat de apparaten die zij construeren technisch wel knap zijn, maar niet altijd gemaakt zijn voor mensen.
De betekenis van Vernes werk voor de vooruitgang van wetenschap en techniek kan echter niet genoeg benadrukt worden. Hele generaties zijn erdoor geïnspireerd geraakt en tot ver in de twintigste eeuw heeft dit technisch-wetenschappelijke ontwikkelingen en de maatschappelijke acceptatie ervan gestimuleerd.
|
|