De Gids. Jaargang 152

[p. 290]

H.H. Kubbinga
Stof en vlak: Beeckman en Escher

Een klassiek probleem uit de geschiedenis van de filosofie is de eventuele deelbaarheid van alles wat op het eerste gezicht de oneindigheid in zich lijkt te dragen. Zo kan men het verschijnsel ‘tijd’ opsplitsen tot eeuwen, jaren, maanden, enz., dus tot steeds kleinere eenheden, waarbij de vraag zich vanzelf opdringt of er mogelijk een kleinste tijdseenheid bestaat, of dat dit natuurverschijnsel tot in het oneindige deelbaar is. Een zelfde vraag kan gesteld worden voor wiskundige zaken als lijn, vlak en ruimte: is een lijn opgebouwd uit punten, een vlak uit lijnen, een ruimte uit vlakken? Zij doen zich voor als ‘continua’: bij eerste beschouwing verwacht men ononderbrokenheid, vanaf het allerkleinste tot aan het allergrootste, en grenzeloosheid: bij elk kleinste kan men altijd iets kleiners voorstellen van dezelfde aard, bij elk schijnbaar grootste iets nog groters. Men kan ze gemakkelijk onderscheiden van ‘discontinua’, zoals bij voorbeeld de reeks der gehele getallen: een dergelijk iets is weliswaar naar boven en naar beneden onbegrensd, echter de opeenvolging is niet continu, maar sprongsgewijs: elke term is ‘discreet’. Het is van belang te weten dat het probleem niet afgedaan heeft. Begin deze eeuw kwam vast te staan dat het natuurkundige begrip ‘energie’ als een discontinue grootheid moet worden opgevat (Max Planck; 1900). Tegenwoordig neemt men overigens aan dat de meeste fysische grootheden discontinu van aard zijn, oftewel, zoals men zegt, ‘gequantiseerd’ zijn. Over het verschijnsel ‘tijd’ lopen de meningen nog steeds uiteen. Tien jaar geleden werd nog in de New Scientist gemeld dat de Amerikaanse fysicus Robert Ehrlich tot de slotsom was gekomen dat er ook een kleinste tijdseenheid moest bestaan, het zogenaamde chronon.

Van oudsher heeft ook het begrensde of onbegrensde karakter van de deelbaarheid van de waarneembare materie ter discussie gestaan. Zoals bekend meenden de Griekse atomisten (Demokritos, Leukippos, Epikouros) dat de materie niet tot in het oneindige deelbaar is, maar bestaat uit kleinste eenheden, de atomen. Aan deze atoomleer werd een complete kosmogonie opgehangen: een theorie over het ontstaan van het heelal. Op dit niveau liggen natuurwetenschap, filosofie en religie kennelijk zeer dicht bij elkaar. Nog steeds immers hebben ontwikkelingen in de deeltjesfysica, het wetenschappelijk frontgebied waar men zoekt naar de allerkleinste bouwsteentjes van de materie, directe consequenties voor de opvattingen over de vorming van het heelal.

In zijn commentaren op de atomisten meende de eveneens Griekse filosoof Aristoteles (384-322 v.Chr.) te kunnen volhouden dat de waarneembare materie wèl tot in het oneindige deelbaar was: hoe klein ook de hoeveelheid, een stof als ‘water’ houdt nooit op ‘water’ te zijn. Elders in zijn werk besloot Aristoteles echter tot het bestaan van groottegrenzen, zowel naar boven als naar beneden. Hierbij redeneerde hij ongeveer als volgt. De wereld om ons heen bestaat uit min of meer individuele eenheden, zoals mensen, leeuwen, eiken, enz. Deze eenheden zijn zowel naar boven als naar beneden van begrensde grootte: men ziet geen volwassen mensen met een lengte kleiner dan,

[p. 291]

zeg 50 cm of groter dan, zeg, 250 cm. Wat voor die eenheden als geheel geldt, moet noodzakelijkerwijs ook voor de onderdelen gelden waaruit ze bestaan, zoals bij voorbeeld ‘vlees’ en ‘been’. Een stuk vlees kan dus niet kleiner zijn dan een bepaald minimum en tegelijkertijd niet groter dan een bepaald maximum. Er bestaat dus een zeker grootte-traject waarop iets ‘vlees’ of ‘been’ kan zijn. Gedurende de middeleeuwen hebben de volgelingen van Aristoteles zich vooral het hoofd gebroken over de benedengrens: waardoor wordt die benedengrens bepaald en hoe valt zij te rijmen met de ogenschijnlijke homogeniteit van een stof als water? De meningen bleven verdeeld, zoals onder andere gebleken is uit het werk van de natuurfilosoof A.G.M. van Melsen.

Het is interessant te zien dat de atomisten er evenmin in geslaagd zijn zo'n benedengrens te definiëren. Voor hen, zowel als voor de aristotelianen, waren de dingen in de natuur individuele zaken en als zodanig opeenhopingen van atomen, waarbij de aard van het ding in kwestie werd bepaald door soort en aantal van de benodigde atomen, alsmede door de ruimtelijke structuur waarin ze verenigd zijn. Het verschil tussen, bij voorbeeld, een aluinkristal, een klompje goud en een hazewindhond zat hem dus in soort, aantal en ordening der atomen, waarbij men eenvoudig voorbijging aan het feit dat bij splijting van het kristal of het klompje de aard van de stof niet verloren gaat, hetgeen niet gezegd kan worden van levende wezens. Ondanks het aureool van vooruitstrevendheid en keiharde wetenschappelijkheid dat wetenschapshistorici doorgaans aan het atomisme toekennen, was het fysischchemisch gezien nauwelijks bruikbaarder dan het vermaledijde aristotelianisme. Tot zover de filosofische achtergrond.

De wetenschapshistoricus Hooykaas heeft gewezen op de bijdragen van de alchemisten aan de totstandkoming van de chemische deeltjestheorie. Zijns inziens waren het vooral de praktiserende chemici die, ongehinderd door filosofische vooroordelen, hun theorieën vormden naar de eisen van hun dagelijkse laboratoriumervaring en dit volgens een traditie die terugging op de artsen en ingenieurs van het Alexandrië van voor het begin van onze jaartelling. De alchemisten waren in elk geval een heel eind op weg gekomen, zonder evenwel een volledig bevredigende oplossing voor het probleem van de stofsoort te hebben gevonden. Zo zou een stof volgens de grote alchemist Geber (dertiende eeuw) worden gekenmerkt door bepaalde soorten deeltjes - zwavel en kwik -, in een bepaalde getalsmatige verhouding en in een bepaald ruimtelijk patroon. Het superieure theoretische kader waarin deze Geber zijn gedachten ontwikkelde verdient in breder kring bekendheid, omdat de alchemist nog maar al te vaak wordt gezien als het klassieke voorbeeld van een warhoofdig najager van hersenschimmen.

Zoals wij zagen is het probleem van de deelbaarheid van de materie ten nauwste verwant aan dat van de stofsoort: wat maakt een stof tot ‘water’ en beneden welke grootte-grens houdt een hoeveelheid water op ‘water’ te zijn? Een eerste werkelijk doeltreffende oplossing van dit probleem, de crux van natuur- en scheikunde, werd aangedragen door de Zeeuwse natuurfilosoof Isaac Beeckman, van wie in 1988 wordt herdacht dat hij vierhonderd jaar geleden werd geboren. Volgens Beeckman, in zijn tijd de evenknie van erkende grootheden als Descartes en Galilei, dient men een hoeveelheid van een stof als goud op te vatten als een opeenhoping van uiterst kleine deeltjes, welke laatste hij vergeleek met levende wezens als mens en dier. Deze onderling vrijwel identieke kleine deeltjes zouden opgebouwd zijn uit vier soorten atomen, die van de klassieke elementen Aarde, Water, Lucht en Vuur. De deeltjes zijn dus net als gelijksoortige levende wezens niet volstrekt gelijk. In de biologie spreekt men van ‘variabiliteit’: het verschijnsel van de individuele verschillen binnen de soort (grootte, haarlengte en -kleur, geluid, bewegingssnelheid, enz.). Volgens Beeckmans theorie wordt de ‘variabiliteit’ van de kleine deeltjes van een stof veroorzaakt door geringe verschillen in grootte en vorm van de samen-

[p. 292]

stellende atomen. Hier is het voldoende te wijzen op de allesbeheersende analogie tussen de kleine karakteristieke deeltjes van een stof, die Beeckman overigens ‘fysische homogenea’ (‘homogenea physica’; 1620) noemde, en biologische individuen. De driedimensionale ruimte zoals die wordt ingenomen door de waarneembare materie moet men dus opgevuld denken met entiteiten die Beeckman zich voorstelde naar het voorbeeld van levende wezens. Zoals een diersoort tot uitdrukking komt in de individuen die ertoe behoren, moet Beeckman hebben gedacht, zo komt een stofsoort tot werkelijkheid in zijn ‘fysische homogenea’, in zijn moleculen dus.

Strikt genomen moet men dus van een nieuwe stofsoort spreken zodra er één ‘homogeneum’ van bestaat. Vandaar dat men Beeckmans ‘homogenea’ kan betitelen als substantiële individuen, dat wil zeggen als de noodzakelijke èn voldoende voorwaarde voor het bestaan van een stofsoort. In dit opzicht staan zij aan het begin van een natuurwetenschappelijke traditie die via René Descartes (1596-1650), Georg Ernst Stahl (1659-1734) en John Dalton (1766-1844) heeft geleid tot de moderne molecuultheorie.

Wat Beeckman veronderstelde voor de drie dimensies van het stoffelijke continuüm heeft de graficus Maurits Cornelis Escher (1898-1972) tot leidende gedachte gehad bij de uitwerking van zijn studies van de opvulling van de twee dimensies van het platte vlak, zoals recentelijk aan het licht gekomen is. Wij doelen hier in het bijzonder op de ‘Vlakverdelingen’ waarin hij een plat vlak van onbepaalde afmetingen laat ontstaan uit een aaneenschakeling van op dier en mens geïnspireerde wezens zonder dat ook maar enige tussenruimte overblijft. Voor een uitputtende analyse hiervan verwijs ik graag naar MacGillavry's Symmetry aspects of M.C. Escher's periodic drawings (Utrecht 1965, 1976²). Bij de uitwerking van zijn ‘vlakverdelingen’^* had Escher kunnen volstaan met een geometrische figuur te kiezen van zodanige vorm dat daaruit een vlak zou kunnen ontstaan. Een zeshoek, bij voorbeeld, of een vierkant. Door middel van inkleuring zou hij dan, althans in principe, dezelfde symnmetrieregels tot uitdrukking hebben kunnen brengen als hij feitelijk gedaan heeft. Dit was hem kennelijk niet genoeg. Hij koos om overigens nooit bekend geworden redenen voor min of meer imaginaire wezens, waarin veel van dier en mens herkend kan worden. Aldus werden zijn vlakke ‘continua’ tweedimensionale opeenhopingen van ‘platlanders’, tweedimensionale dier- of mensachtige individuen. Sommige van zijn vlakken zijn samengesteld uit wezens die op de kleur na aan elkaar gelijk zijn. Beroemd zijn de hagedissen. Zo beroemd zelfs dat zij tegenwoordig op computerschermen worden nagebootst, zoals de hierbij afgedrukte prent laat zien.

In dit verband dringt de vraag zich op of Escher, een van de meest met het spel der dimensies vertrouwde kunstenaars aller tijden, zich ooit gewaagd heeft aan de opvulling van drie dimensies uitgaande van driedimensionale eenheden. Voor zover uit catalogi of anderszins gepubliceerd werk valt op te maken is dit niet of nauwelijks het geval geweest. Wèl heeft hij zich intensief beziggehouden met de opvulling van driedimensionale oppervlakken, al dan niet begrensd. Bekend zijn de beukehouten bol waarvan het oppervlak werd gevuld met twaalf identieke vissen (‘Bol met vissen’, 1940) en de betegelde zuil in de Nieuwe Meisjesschool in Den Haag (1959); verwant hieraan zijn het in hout uitgesneden twaalfvlak met op elk zijvlak een in reliëf geciseleerde, vijftallig symmetrische bloem (‘Veelvlak met bloemen’, 1958) en het regelmatige twintigvlak dat hij van een opdruk van schelpen en zeesterren voorzag en dat als koekblik zijn weg naar de wereld gevonden heeft (1963). Wat men aan de opvulling van drie dimensies door middel van driedimensionale eenheden in zijn werk tegenkomt is zeer beperkt van omvang. Zo bij voorbeeld in de litho ‘Platwormen’ (1959) waar hij de drie dimensies op continue wijze vult met

* Aanvankelijk sprak Escher van ‘vlakvullingen’.

[p. 293]

regelmatige acht- en viervlakken (in de aantalsverhouding 1:2). Over de omvang van het probleem kan men zich overigens gemakkelijk een idee vormen. Ieder ziet in dat een stapeling van kubussen tot een continuüm kan leiden, dat wil zeggen tot een zodanige opvulling van de ruimte dat er geen ‘gaten’ open blijven. Bij een stapeling van bollen lukt dit niet; er blijft hoe dan ook lege ruimte over. Met alleen achtvlakken lukt het ook niet; met alleen viervlakken evenmin. Een combinatie van achten viervlakken - in de al genoemde verhouding 1:2 - is echter wèl ruimtevullend. Het meetkundige probleem van de ruimtevulling is als zodanig zeer oud; als men uitgaat van éénsoortige eenheden komen de kubus en het blok in aanmerking, alsmede het parallellepipedum en de croissantachtige figuur die ontstaat als men een achtvlak laat versmelten met twee viervlakken. Op grond van zijn werk in twee dimensies zou men nu van Escher een uitputtende analyse hebben mogen verwachten van alle mogelijkheden in drie dimensies, te meer daar het hier om een probleem gaat dat in de geschiedenis van de kristallografie een belangrijke rol heeft gespeeld. Rond 1800 namelijk stelden de kristallografen hun kristallen voor als stapelingen van moleculen, waarvan zij de ruimtelijke vorm langs meetkundige weg probeerden te bepalen (René-Just Haüy). Uit het onderzoek bleek, in de loop van de negentiende eeuw, dat de molecuultheorie niet voor alle stoffen opgaat. Zo ontstond uit de molecuultheorie - als een aanvulling daarop - de zogenaamde roostertheorie, die wij hier verder buiten beschouwing laten. Hoe dit ook zij, het probleem van de opvulling van drie dimensies met driedimensionale eenheden zal Escher niet hebben aangesproken of - hoe onwaarschijnlijk ook - zijn krachten te boven zijn gegaan. Met enig recht had men anders werk van hem mogen verwachten waarin stapelingen van op dier en mens geïnspireerde driedimensionale wezens de ruimte vulden, zoals elders de ‘platlanders’ zijn ‘Vlakverdelingen’ bevolken. Over Beeckman gesproken...!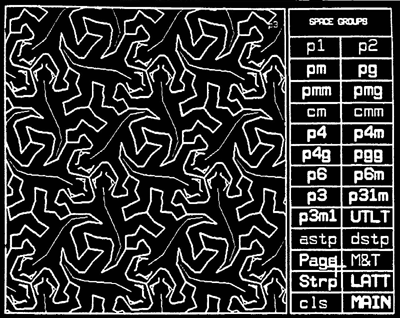

‘Studie van de ornamentiek van het platte vlak: interactief programma voor de analyse van de kristallografische groep van het platte vlak’, R. Farinato, L. Loreto en M. Tonetti (Rome). Uit: M. Calvesi, M. Emmer en medewerkers, I frattali - la geometria dell'irregolare, Rome, Istituto della Enciclopedia Italiana, 1988, p. 65.