De Gids. Jaargang 112
(1949)– [tijdschrift] Gids, De–
[pagina 106]
| |||||||||
Pythagoras en de PythagoreërsInleidingHet is voor ons, nuchtere moderne mensen, bijna niet te geloven, welk een enorme invloed Pythagoras en zijn adepten op het geestelijk leven der antieke wereld en daardoor ook op het onze hebben uitgeoefend. De bewaard gebleven Pythagorese fragmenten maken op ons de indruk van een verward mengelmoes van religie, bijgeloof, mystiek en wetenschap: wij kunnen ons nauwelijks meer voorstellen, dat men dit eens als filosofie au sérieux genomen heeft. En toch sloot Plato zich (volgens Aristoteles) in de meeste punten bij de Pythagoreërs aan, en Aristoteles acht het nodig, hun leerstellingen (die hij in zijn jeugd blijkbaar ook heeft aangehangen) met de grootste ernst te bestrijden. Plato's leerlingen schreven boeken vol over Pythagorese wijsheid. Eeuwen later namen de Neopythagoreërs en Neoplatonici deze ideeën weer op, en de kerkvaders ondergingen er sterk de invloed van. Kepler knoopt in zijn Harmonia mundi weer bij de Pythagoreërs aan, en zelfs Goethe bezingt nog in de Faust de harmonie der sferen. Zo mogelijk nog meer dan op de filosofie hebben de Pythagoreërs op de exakte wetenschappen hun stempel gedrukt. Vier mathèmata, d.w.z. leervakken omvatte hun program: Getallentheorie, harmonieleer, meetkunde en astronomie. Hun astronomie moet men vooral zien tegen de achtergrond van de in hun tijd, de 5de eeuw, heersende materialistische, atomistische physica. Volgens Anaxagoras en Demokritos waren de hemellichamen slechts dode stenen, overgelaten aan het blinde toeval, heen en weer geslingerd door druk en stoot in de werveling der atomen. De Pythagoreërs daarentegen gingen van de verheven opvatting uit, dat het heelal door een goddelijke macht volgens getallen harmonisch geordend was, dat de planeten bezielde hogere wezens waren, die volgens hun goddelijke natuur eenparige cirkelbewegingen volvoerden; immers het goddelijke is eeuwig en blijft zichzelf steeds gelijk, en de cirkelbeweging is de enige begrensde beweging, die eeuwig onveranderd kan duren. Zij stelden daarom de vraag, hoe de verschijnselen der planeten door geordende cirkelbewegingen verklaard kunnen worden. Om deze vraag draait de gehele Griekse theoretische astronomie, en ook Kopernikus en Kepler, de grondvesters van de moderne astronomie, gingen van deze vraag uit. Doordat de Pythagoreërs aldus naar de wiskundige wetten zochten, die de kosmos beheersen, werden | |||||||||
[pagina 107]
| |||||||||
zij, en niet de atomisten, de eigenlijke voorlopers van de moderne wetenschap. Zij legden in hun mathèmata de grondslag voor het bewonderenswaardige bouwwerk der Griekse mathesis, waarop onze gehele wetenschap berust. Maar daarnaast waren de Pythagoreërs vurige gelovigen. Zij geloofden in de onsterfelijkheid der ziel, die van goddelijke oorsprong is, en na het doorlopen van de cyclus der wedergeboorten eens tot God zal wederkeren. Zij vereerden Pythagoras, die hun de weg tot bevrijding der ziel uit deze smartelijke kringloop had gewezen, als een soort halfgod, verwant aan Apollo. Zij vertelden elkaar de wonderen, die hij op aarde verricht had: hoe hij op twee plaatsen tegelijk was verschenen, hoe hij een beer tot het vegetarisme had bekeerd, hoe de rivier Kasa voor hem uit zijn bedding was opgestaan en hem ‘Heil, Pythagoras!’ had toegeroepen, hoe hij Abaris de pijl van Apollo had afgenomen, die geen sterfelijk mens hem kon ontrukken. Zij leefden in gemeenschap van bezit volgens bepaalde leefregels: zij aten geen vlees en geen tuinbonen en ze brachten geen bloedige offers. Na door dit reine leven hun ziel gereinigd te hebben, werden zij ingewijd in het mysterie der getallen en vonden daardoor de weg tot de mystieke vereniging der ziel met God. Het streven naar wijsheid (filosofie) was voor hen een soort godsdienst, want wijsheid is het kenmerk van het Goddelijke. Door deze merkwaardige verbinding van mystiek en wetenschap onderscheidde het Pythagorisme zich van andere mysteriediensten, die in dezelfde tijd (6de eeuw) in Italië en Griekenland zo grote aanhang verwierven. Een ander punt van verschil is de ethische inslag, die het Pythagorisme met het Christendom gemeen heeft. Terwijl namelijk bij de andere mysteriën, zoals die van Eleusis, de inwijding slechts een uiterlijke deelneming aan een bepaalde ritus vereiste, was de bedoeling van het ‘Pythagorese leven’ de innerlijke verheffing der ziel, de navolging van God. De zin van het vegetarische leven bijv. is het overwinnen van de moordlust en het vermijden van broeder- en vadermoord, want alle levende wezens zijn verwant, en in een dier, dat men doodt en opeet, kan immers de ziel van vader of broeder huizen. In de laat-Hellenistische tijd ging nog eenmaal een golf van religieus mysticisme over de antieke wereld. Het is algemeen bekend, hoe in de keizertijd vóór en tegelijk met het Christendom allerlei mysteriediensten zich over de wereld verbreidden. Ook de Pythagorese leer, en in samenhang daarmee het vegetarisme, komen in deze tijd tot nieuw leven. Natuurlijk blijft de oorspronkelijke leer der Pythagoreërs daarbij niet onveranderd: in deze | |||||||||
[pagina 108]
| |||||||||
tijd werden immers allerlei religieuze en filosofische stromingen zonder veel logische scrupules met elkaar vermengd, en zo vinden we in het Neopythagorisme ook allerlei Platonische en nog latere elementen. Het is niet altijd gemakkelijk te onderkennen, welke ideeën van echt Pythagorese oorsprong zijn, maar zeker is, dat het oude Pythagorisme, al is het dan na een zekere transformatie, een geweldige invloed op de gedachtenwereld van deze met mystiek en religie doordrenkte tijd heeft gehad. En deze dingen zijn niet alleen voor deze mensen, die al zo lang dood zijn, van belang, maar zij gaan ook ons aan, want in deze sfeer is ook het Christendom ontstaan. Maar ook op tovenarij en bijgeloof heeft de Pythagorese leer een onmetelijke invloed gehad. Volgens Herakleides van Pontos zou Pythagoras Abaris in de ‘tovenarij door middel van getallen’ hebben ingewijd. Hoe bijgelovig de Pythagoreërs waren 'ziet men uit leefregels als:
Met het vertellen van merkwaardigheden der Pythagoreërs zou ik nog wel een tijdje door kunnen gaan. Zo verhaalt men bijv. dat de adepten, die nog niet volledig ingewijd waren, de Meester niet mochten zien, maar alleen door een gordijn zijn stem mochten horen. Maar ik denk, dat het bovenstaande al voldoende is om belangstelling voor Pythagoras en zijn leer te wekken. Wie was deze supermens en wat leerde hij? | |||||||||
PythagorasPythagoras van Samos was de zoon van Mnesarchos. Men neemt meestal aan, dat hij omstreeks 570 geboren is. Maar Aristoxenos, van wie deze datering afkomstig is, is nogal onbetrouwbaar, en Eratosthenes, de zéér conscientieuze bibliothecaris van Alexandrië, de grondvester van de wetenschappelijke chronologie, vertelt ons, dat Pythagoras als knaap met lange haren bij de 48ste Olympische spelen (dus in 588) door de scheidsrechters van de vuistkamp der jongens werd uitgesloten | |||||||||
[pagina 109]
| |||||||||
(waarschijnlijk omdat hij nog niet 13 jaar was). Toen hij hierom werd uitgelachen, viel hij volwassenen aan en versloeg ze. Eratosthenes neemt dus aan, dat hij nabij 600 v. Chr. geboren is. Het verhaal zelf behoort blijkbaar tot de legenden, die Pythagoras' bovenmenselijke kracht moeten aantonen.Ga naar voetnoot1) Pythagoras moet veel gereisd hebben. Volgens de redenaar Isokrates bezocht hij Egypte en leerde allerlei wijsheid van de Egyptenaren. Men zegt, dat hij door de Perzische koning Kambyses, toen deze Egypte veroverde, gevangen genomen werd en naar Babylon gebracht, waar hij 12 jaren bleef en door de priesters in allerlei mysteriën werd ingewijd. Volgens Aristoxenos kwam hij ook met ‘Zaratas den Chaldeër’ (= Zoroaster of Zarathustra) in aanraking. Neanthes, een compilator uit de 3de eeuw v. Chr., vertelt, dat Pythagoras in zijn jeugd in Syrië door Chaldeërs (d.w.z. Babylonische sterrenkundigen) werd onderwezen. Al deze verhalen betekenen slechts, dat men reeds in de oude tijd Orientaalse elementen in de leer van Pythagoras vond en daarom aannam, dat hij met de wijzen van het Oosten in aanraking was geweest. En inderdaad, hoe meer wij van de Babylonische meetkunde, algebra en astronomie leren kennen, des te meer aanrakingspunten vinden wij met de leer van de Pvthagoreërs. Aan die reisverhalen kan dus heel goed iets waars zijn. Hij keerde naar Samos terug, bleef echter niet in Ionië, maar vestigde zich in Kroton, een Griekse stad in Zuid-Italië. Hier predikte hij zijn heilsleer en verzamelde een schaar van enthousiaste volgelingen om zich. Van alle zijden, ook uit de omliggende barbaarse streken, zelfs uit Rome kwamen de vereerders tot hem, als men Aristoxenos ditmaal mag geloven. De Pythagoreërs behoorden meestal tot de aanzienlijke families, oefenden dus vanzelf op het aristokratische staatsbestel van Kroton een grote invloed uit. De broederschap was vooral een religieuze, geen politieke organisatie, maar toch ligt het voor de hand, dat de leden de staatszaken met elkaar bespraken en naar buiten eensgezind optraden. Volgens Aristoxenos had de organisatie de leiding van de politiek in Kroton in handen. Voegt men hierbij, dat ze een zeer bijzonder leven leidden - het ‘Pythagoreïsche leven’, waar Plato van spreekt - en zich beter achtten dan de anderen, dan begrijpt men gemakkelijk, dat zij zich vijanden maakten, die zich tegen hun politiek keerden. Een zekere Kylon stelde zich aan het hoofd van een partij, die de politieke macht van de Pythagoreërs wilde breken. Wat er precies gebeurd | |||||||||
[pagina 110]
| |||||||||
is, weten wij niet, want de overlevering aangaande deze onlusten is zeer verward.Ga naar voetnoot1) Pythagoras zelf, die blijkbaar niet al te veel met de politiek te maken wilde hebben, week tijdig uit naar Metapontion. Ook hier genoot hij buitengewone eer en bleef er tot zijn dood. Zijn huis werd als tempel aan de Muzen gewijd. Omstreeks het midden van de 5de eeuw kwamen de Pythagoreërs in verscheidene steden van Italië nog eens tot grote politieke macht. Zij vormden de kern van het aristokratische verzet tegen de opkomende demokratie. In Kroton kwam het tot een gewelddadige opstand, waarbij het huis, waarin de Pythagoreërs vergaderden, in brand werd gestoken en bijna allen het leven lieten. Ook uit andere steden moesten de Pythagoreërs wijken: zij vluchtten naar Rhegion en van daar naar Griekenland. Omstreeks 410 predikte Philolaos in Thebe; zijn discipelen hielden volgens Aristoxenos nog lang aan de Pythagorese tradities vast. In Tarente was echter een groep Pythagoreërs achtergebleven, die onder leiding van de voortreffelijke Archytas, de vriend van Plato, belangrijk wiskundig werk verrichtten. In de Atheense komedie worden nog in het midden van de 4de eeuw de ‘Pythagoristen’ om hun gekke leefregels bespot. Pythagorese mysteriediensten vindt men nog lang daarna in Italië. Maar laten wij tot Pythagoras en zijn leer terugkeren. Reeds zijn tijdgenoten oordeelden zeer verschillend over hem. Herakleitos schrijft: ‘Veelweterij brengt nog geen verstand met zich mee; anders zouden Hesiodos en Pythagoras het immers hebben gekregen’. Xenophanes drijft de spot met zijn leer der zielsverhuizing en verwantschap van alle levende wezens: ‘Men zegt dat, toen hij eens ergens langs kwam, waar een hondje werd mishandeld, hij medelijden kreeg en sprak: Houd op met slaan, want het is de ziel van een vriend, die ik herkende aan zijn stem’. Empedokles daarentegen is vol bewondering en toont zich een geestdriftig aanhanger van Pythagoras' leer. Hij schrijft in zijn gedicht ‘Reinigingen’; ‘Er leefde onder hen een man van bovenmatige zienergave, die de grootste rijkdom van geest verworven had en in alle soorten wijsheid uitblonk. Want als hij met zijn gehele geest ernaar streefde, kon hij zonder moeite alles onderscheiden wat er was geweest in zijn tien, ja wel twintig mensenlevens’. De grote gave van Pythagoras volgens Empedokles was dus de Anamnesis, de herinnering aan zijn vroegere levens. De heilige | |||||||||
[pagina 111]
| |||||||||
Hippolytos ontleent (Refutatio I 3) aan Empedokles de mededeling, dat Pythagoras ‘zeide, dat hij vroeger Euphorbos geweest was, die aan de Trojaanse oorlog deelnam, en dat hij zijn schild’ (dat in een tempel werd bewaard) ‘herkend had’. De dichter Ion van Chios zegt, dat iemand die bij zijn leven moed en eergevoel heeft getoond, ook na zijn dood voor zijn ziel een heerlijk leven zal hebben ‘indien inderdaad Pythagoras boven alle mensen uit inzichten heeft verworven’. Ook Herodotos, de geschiedschrijver, spreekt met respekt van Pythagoras en noemt hem ‘één van de beste Helleense sophisten’. Het woord sophist, wijsheidsleraar, had in die tijd nog geen slechte klank. Al deze getuigenissen, hoe verschillend van toon ook, komen toch naar de inhoud met elkaar overeen. Allen schrijven unaniem de leer der zielsverhuizing aan Pythagoras toe, en of men nu verachtelijk van ‘veelweterij’ spreekt of bewonderend van ‘veelzijdige wijsheid’, het komt toch allemaal hierop neer, dat Pythagoras veel wist en allerlei wijsheid aan zijn discipelen verkondigde. Maar waarin bestond dit weten? Waren het slechts mystieke ervaringen en religieuze openbaringen over het lot der ziel in haar eeuwige kringloop, of doceerde Pythagoras ook wiskunde en exakte wetenschappen, zoals de latere overlevering ons wil doen geloven? | |||||||||
De leer van PythagorasDe enige betrouwbare samenvatting van de leer van Pythagoras is van Dikaiarchos, een tijdgenoot van Aristoteles, afkomstig. Dikaiarchos vertelt eerst over de vier toespraken, die Pythagoras tot de raad, de jonge mannen, de kinderen en de vrouwen van Kroton richtte. Maar wat hij zijn eigen discipelen leerde, daarvan weet Dikaiarchos niet veel te zeggen, omdat zij daarover het zwijgen moesten bewaren. Slechts de volgende punten zijn volgens hem bekend: ‘In de eerste plaats zei Pythagoras, dat de ziel onsterfelijk is, en dat de zielen in alle andere soorten levende wezens overgaan, vervolgens, dat alle dingen die eenmaal gebeuren in een kringloop wederkeren en er niets werkelijk nieuws is, en dat alle bezielde wezens verwant genoemd moeten worden’. Veel nieuws leren wij hier niet uit. Zou dit werkelijk alles zijn? Men heeft vroeger veel waarde gehecht aan een uitvoerig résumé, dat Diogenes Laertios aan Alexander Polyhistor ontleent. Hierin worden de leer van de bolvorm van de aarde en allerlei andere leerstukken aan Pythagoras toegeschreven. Maar | |||||||||
[pagina 112]
| |||||||||
men heeft onmiskenbaar Stoïcijnse invloeden in de terminologie gevonden en de leer van de onbepaalde tweeheid, waarmee het stuk begint, is zeer zeker van Plato en niet van de Pythagoreërs afkomstig: juist door dit leerstuk onderscheidt Plato zich (volgens Aristoteles) van de Pythagoreërs! Verder heeft E. Frank overtuigend aangetoond, dat de leer van de bolvorm van de aarde ten tijde van Plato nog nieuw was en dus onmogelijk aan Pythagoras toegeschreven kan worden. Het excerpt van Alexander is dus van nul en gener waarde. Verder zijn er nog fragmenten uit de ‘drie boeken van Pythagoras’ over physica, opvoeding en staatkunde, maar dit zijn vervalsingen: Pythagoras heeft geen geschriften nagelaten. Dan is er nog een mooi verhaal van Pythagoras, die in een smidse kwam en in de tonen der vallende hamers de akkoorden oktaaf, quint en quart herkende. Hij woog de hamers en vond, dat hun gewichten zich als 1:2, 2:3 en 3:4 verhielden. Thuis gekomen, voerde hij ‘zeer nauwkeurige experimenten’ met snaren uit, die hij met gewichten in deze verhoudingen belastte en vond weer dezelfde akkoorden. Dit alles is natuurkundig onzin. Moeten we meer waarde hechten aan de wiskundige stellingen die men op Pythagoras' naam pleegt te schrijven? Proklos zegt, dat Pythagoras de leer van het irrationale en de 5 regelmatige veelvlakken vond, maar volgens een ander, veel betrouwbaarder bericht kenden de Pythagoreërs er slechts drie, nl. tetraëder, kubus en dodekaëder, en de leer van het irrationale is zeker van later datum. Toen Pythagoras de rechthoekige driehoek met zijden 3, 4, 5 vond, moet hij ter ere van deze ontdekking een stier geslacht hebben. Maar wij weten uit véél beter bron, dat Pythagoras het slachten van stieren streng verbood. Ook dit verhaal is dus zeer verdacht. Met ontzetting zult U nu misschien vragen: Is dan de beroemde stelling van Pythagoras soms ook niet van hem? Inderdaad, de Griekse getuigenissen hieromtrent zijn uiterst vaag en twijfelachtig. Maar hier komen ons nu goddank de Babylonische bronnen te hulp. In spijkerschriftteksten uit de tijd van Hammurapi (1700 v. Chr.) wordt het beroemde Theorema toegepast, en omstreeks 200 v. Chr. werden de oudbabylonische wiskundige methoden nog steeds in Mesopotamië gebruikt. Het is dus zeer goed mogelijk, dat Pythagoras ‘zijn’ theorema in Babylon heeft leren kennen en dat hij de eerste was, die het in Griekenland bekend gemaakt heeft. | |||||||||
[pagina 113]
| |||||||||
Kritiek en hyperkritiekWij hebben zo juist gezien, hoe verward en onbetrouwbaar de Griekse getuigenissen over Pythagoras en de zijnen zijn. Het ziet er hopeloos uit, door deze doolhof van vervalsingen, fantasieën en legenden de weg te vinden tot de enkele geloofwaardige mededelingen, die er wellicht nog tussen verborgen zitten. Daarom is het volkomen begrijpelijk, dat in de laatste tientallen jaren een kritische stroming de overhand kreeg, die al deze verhalen uit veel later tijd eenvoudig overboord wilde werpen en zich tot de mededelingen van tijdgenoten en gefundeerde conclusies uit de werken van Plato en Aristoteles en de wiskundige vakliteratuur wilde beperken. Het verst in deze richting is E. Frank gegaan, die in zijn boek ‘Plato und die sogenannten Pythagoreer’ (Halle 1923) een scherpe scheidingslijn trekt tussen Pythagoras en de ‘zogenaamde Pythagoreërs’, de mathematici om Archytas van Tarente. De oude Pythagoras heeft volgens hem met exakte wetenschap niets te maken. Hij was een wegwijzer naar nieuw zedelijk leven, maar geen mathematicus. Mogelijk dat hij een zekere neiging tot getallenmystiek heeft bezeten, en dat dit religieuze getallenbijgeloof bij de latere Pythagoreërs de beoefening der wiskunde in de hand heeft gewerkt, maar de eigenlijke wetenschappelijke wiskunde, harmonieleer en astronomie zijn volgens Frank pas omstreeks 400 in de kring van Archytas ontstaan. De toeschrijving van allerlei wiskundige ontdekkingen en filosofische theorieën aan Pythagoras en oudere Pythagoreërs is een legende, die door latere Pythagoreërs en Platonici in omloop is gebracht om aan hun leer het aanzien van oude wijsheid te geven. Archytas en de zijnen zijn volgens Frank niet eens echte Pythagoreërs, maar experimenteel-natuurwetenschappelijke onderzoekers in moderne zin, die Aristoteles dan ook slechts ‘zogenaamde Pythagoreërs’ noemt. Er is veel van grote waarde in het werk van Frank. Zijn bewijs, dat de astronomie een jonge wetenschap is, is volkomen overtuigend. Zijn opvatting, dat de Pythagoreërs als mannen van wetenschap au sérieux genomen moeten worden, dat zij geen archaïsche theorieën verkondigen, maar op de hoogte van hun tijd waren, is juist. Het methodische beginsel, aan authentieke getuigenissen van tijdgenoten en aan de wetenschappelijke vakliteratuur de voorkeur te geven boven latere, oncontroleerbare verhalen, is uitstekend. Maar in zijn hyperkritische houding gaat Frank soms te ver. Hij verwerpt te veel, wat in zijn theorie niet past en hij onder- | |||||||||
[pagina 114]
| |||||||||
schat de tijd, die voor de ontwikkeling van de wiskundige wetenschappen nodig is. Deze kunnen niet in één enkele generatie uit de grond worden gestampt. Zeer juist schrijft E.J. Dijksterhuis (De Elementen van Euclides I, p. 81): ‘Het is niet onmogelijk, dat Frank, die blijkbaar meer philoloog dan mathematicus is, onwillekeurig geneigd is geweest, de geestesarbeid, die aan de opbouw van de Euclidische meetkunde vooraf heeft moeten gaan, te onderschatten en dat hij daardoor te weinig oog heeft gehad voor het aandeel, dat de vijfde eeuw in de ontwikkeling der wiskunde moet hebben gehad’. Frank komt in strijd met de feiten, als hij de grote wiskundige Hippokrates van Chios, die een generatie vóór Archytas leefde, een ‘Mathematiker kaum vor 400’ noemt. Het werk van Hippokrates bewijst, op welk hoog wetenschappelijk niveau de wiskunde toen reeds, omstreeks 430, stond. Nog lastiger voor de theorie van Frank is de oude Pythagoreërmathematicus Hippasos, die volgens de beste bronnen, die volkomen met elkaar in overeenstemming zijn, omstreeks 500 leefde. Frank probeert weliswaar, deze datering verdacht te maken door er andere getuigenissen naast te stellen, die tot andere data leiden, maar deze zijn volkomen onbetrouwbaar. Deze Hippasos nu construeerde een regelmatig dodekaëder in een bol; hij voegde aan de drie fundamentele akkoorden oktaaf, quint en quart er nog twee toe en onderzocht de getalverhoudingen van deze akkoorden, o.a. door experimenten met volle en half lege vazen; ook moet hij zich met de harmonische middelevenredige bezig hebben gehouden. Wanneer Frank nu meent, dat deze ontdekkingen ‘op zijn vroegst in de tijd onmiddellijk vóór Archytas’ vallen, dan is dit alleen te verklaren uit zijn vooropgezette mening, dat de Pythagorese wiskunde vlak voor Archytas eigenlijk pas begint. Ik acht deze constructies en berekeningen omstreeks 500 heel goed denkbaar. Wat bijv. het dodekaëder betreft: er is juist in Italië een dodekaëder van speksteen van Etruskische origine uit de tijd vóór 500 gevonden. Ik kan ook overigens niets verdachts in de berichten omtrent Hippasos vinden. Hippasos is geen legendarische persoon, maar de eerste der volgelingen van Pythagoras, die zich speciaal met de exakte wetenschappen heeft bezig gehouden: de eerste der ‘mathematici’ onder de Pythagoreërs. | |||||||||
Akousmatikoi en MathematikoiEr waren namelijk onder de latere Pythagoreërs twee secten: de Acusmatici en de Mathematici. De Acusmatici waren ortho- | |||||||||
[pagina 115]
| |||||||||
doxe gelovigen: zij hielden zich streng aan de heilige leefregels en aan de plicht tot zwijgen. Het zwaartepunt van de leer van Pythagoras lag volgens hen niet in de wiskundige wetenschappen, maar in de Akousmata, de heilige spreuken van religieuze en zedelijke inhoud, waarvan Aristoteles er een aantal heeft opgetekend. De Mathematici daarentegen, waartoe Archytas en de zijnen behoren, waren meer filosofen en mannen van wetenschap. Door streven naar wijsheid, filosofie, trachtten zij de goddelijke wijsheid te benaderen en zo de godheid naderbij te komen. Zij namen het met de plicht tot zwijgen niet zo nauw. Om deze reden werd Hippasos, die de een of andere wiskundige ontdekking publiceerde, van de orde der gelovige Pythagoreërs uitgesloten. Zo ontstond de splitsing in de Mathematikoi, de volgelingen van Hippasos, en de Akousmatikoi. Deze splitsing is ook volkomen begrijpelijk. Tussen de exakte wetenschap en de mystiek bestaat nu eenmaal een spanning, die vroeger of later tot een scheuring moest leiden. Van tweeën één: òf men beschouwt de goddelijke openbaring als de bron van Pythagoras' wijsheid, dan heeft het geen zin om door eigen denken deze wijsheid verder te ontwikkelen. Òf men beschouwt Pythagoras volgens zijn eigen maxime niet als wijze, maar als filosoof, als zoeker naar wijsheid, en men gaat op zijn voetspoor zelfstandig verder zoeken, maar dan is niet de goddelijke openbaring, maar de rede de hoogste rechter in wetenschappelijke vragen, dan kan men ook verder gaan dan Pythagoras en is niet aan zijn leer als dogma gebonden. Verder: Als men in ernst wetenschap wil bedrijven, kan men deze wetenschap niet geheim houden: men moet kennis nemen van de resultaten van anderen en kan daarbij zijn eigen mening niet verzwijgen. Voor de orthodoxen was deze publicatie heiligschennis. Vandaar, dat het reeds kort na de dood van Pythagoras tot een scheuring kwam. | |||||||||
De vier leervakken: 1. harmonieleerDat de wetenschap der Pythagoreërs zich niet plotseling, maar geleidelijk heeft ontwikkeld van Pythagoras en Hippasos af tot op de hoogte, die zij ten tijde van Archytas en Plato had bereikt, blijkt het duidelijkste bij de Pythagorese muziektheorie. De resultaten van mijn onderzoek hieroverGa naar voetnoot1) kunnen als volgt worden samengevat: De opvolgende stadia in de normale ontwikkeling van een | |||||||||
[pagina 116]
| |||||||||
natuurwetenschap zijn: ervaring, theorie, experiment. De dagelijkse ervaring leert, dat een snaar, tot op de helft of ⅔ of ¾ verkort, een toon geeft, die een oktaaf of quint of quart hoger ligt. Analoog geeft een aulos, een klarinet, bij verdubbeling van de lengte een toon, die een oktaaf lager ligt. Dit wisten de instrumentmakers natuurlijk al lang. Uit deze ervaringsfeiten besloot Pythagoras, dat aan de intervallen oktaaf, quint en quart de getalverhoudingen 2:1, 3:2 en 4:3 beantwoorden. Deze zijn vervat in het viertal getallen 1, 2, 3, 4: de ‘Tetraktys’, die reeds door de oudste Pythagoreërs als een heilig mysterie werd vereerd. ‘Wat is het orakel van Delphi? De Tetraktys! Want zij is de toonladder der sirenen’, zo luidt een zeer oude spreuk, een Akousma. En de eed der Pythagoreërs luidde: ‘Wij zweren bij hem, die onze ziel de tetraktys heeft toevertrouwd, de bron en de wortel der eeuwige natuur’. De intervallen oktaaf, quint en quart zijn inderdaad fundamenteel voor de antieke muziek. De vier ‘onveranderlijke snaren’ van de lyra: Hypatè, Mesè, Paramesè, Netè werden steeds volgens deze intervallen gestemd: Hypatè en Netè vormden een oktaaf, die door de Mesè in quart + quint, door de Paramesè in quint + quart werd verdeeld. Pythagoras verkreeg deze tonen volgens de overlevering, door een liniaal in twaalf gelijke delen te delen en er een snaar over te spannen. Deze snaar gaf de laagste toon: die der Hypatè aan. Verkortte hij de snaar tot negen, acht of zes van de twaalf delen, dan verkreeg hij de tonen der Mesè, Paramesè en Netè. De overige tonen van de toonladder werden ten tijde van Pythagoras meestal verkregen door van de Mesè een quart naar boven te gaan, dan een quint naar beneden, dan weer een quart naar boven en weer een quint naar beneden. Pythagoras berekende intervallen van deze ‘diatonische’ toonladder als volgt:(Hypatè) 256/243 9/8 9/8 (Mesè) 9/8 (Paramesè) 256/243 9/8 9/8 (Netè). 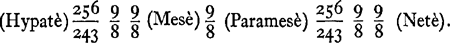 Het inzicht, dat de belangrijkste intervallen der muziek aan de verhoudingen der getallen 1, 2, 3, 4 beantwoorden, was voor de Pythagoreërs van buitengewoon belang. Zij zagen er de bevestiging in van hun these: ‘Alles is volgens getallen geordend’. Hippasos merkte op, dat van de vier getallen 6, 8, 9, 12 de middelste twee het harmonisch en het rekenkundig gemiddelde tussen de beide uitersten vormen. Deze beide gemiddelden vormen steeds met de uitersten een evenredigheid, in dit geval: 6:8 = 9:12. | |||||||||
[pagina 117]
| |||||||||
Voor ons zijn dit nuchtere betrekkingen tussen getallen, maar voor de Pythagoreërs was dit alles goddelijke wijsheid, bewonderenswaardige harmonie tussen de getallen en de natuur. Hoor maar, hoe Aristoteles, die in zijn jeugd sterk onder de invloed der Pythagorese ideeën stond, over deze dingen spreekt: ‘De harmonie is hemels: zij heeft een goddelijke, heerlijke, wonderbaarlijke natuur. Zij wordt door vier termen voort gebracht en houdt twee gemiddelden in: het rekenkundige en het harmonische. De grootte en de verschillen van haar termen verschijnen volgens het getal en de geometrie, want zij bestaat uit twee tetrachorden’. Nu zet hij de eigenschappen der gemiddelden aan het voorbeeld 6:8 = 9:12 uiteen, en eindigt met de woorden: ‘Zo is zij (de toonladder) met al haar delen in overeenstemming met de natuur gevormd, namelijk uit het even, het oneven en het even-oneven’ (d.w.z. de één). De Pythagoreërs demonstreerden de getalverhoudingen der intervallen aan het ‘monochord’; een over een liniaal gespannen snaar, die met de hand of door een verschuif baar plankje verkort kon worden. Nog op zijn sterfbed, zo zegt men, maande Pythagoras zijn discipelen aan, het monochord te beoefenen. Maar hieruit mag men niet concluderen, dat de Pythagoreërs de getalverhoudingen der intervallen uitsluitend als verhoudingen van lengten van snaren of blaasinstrumenten definieerden. Dat deze opvatting niet juist is, blijkt reeds hieruit, dat aan de hoogste toon van een interval soms het kleinste, maar soms ook het grootste getal wordt toegekend. Sommigen, zo zegt Theon van Smyrna, zochten de getalverhoudingen in de lengten, anderen in de gewichten, weer andere in de snelheden en nog anderen in holle ruimten. Wat met dit laatste bedoeld is, blijkt uit het verhaal, dat Theon er direct op laat volgen: Hippasos nam twee gelijke vazen, vulde de ene half en liet de andere leeg en verkreeg zo de samenklank van de oktaaf. De Pythagoreërs meenden blijkbaar, dat de getalverhoudingen 2:1 etc. zozeer bij het wezen der intervallen oktaaf etc. behoren, dat men empirisch steeds deze getalverτhoudingen zal vinden, onverschillig of men nu lengten, spanningen, snelheden of luchtruimten meet. Bij de spanningen klopte dit wel niet, maar dat weet men dan aan de onvolkomenheden van de empirie. Juist om deze onvolkomenheid wendde men zich van de empirie af en trachtte een zuiver theoretische motivering voor de getalverhoudingen der symphone intervallen te geven, uitgaande van de veronderstelling, dat met ‘symphone’ intervallen, wier tonen met elkaar samensmelten, noodzakelijkerwijs verhoudingen overeenkomen, die met één getal kunnen worden benoemd, te | |||||||||
[pagina 118]
| |||||||||
weten verhoudingen als van een geheel getal tot de eenheid of van een geheel getal tot het voorafgaande. Uit deze en dergelijke veronderstellingen leidde men reeds vóór Archytas zuiver logisch af, dat aan de intervallen oktaaf, quint en quart de verhoudingen 2:1, 3:2 en 4:3 moeten overeenkomen. Archytas zelf trachtte, zeer spitsvondig, met nog minder hypothesen uit te komen, maar in zijn redenering schuilt een denkfout. Hij staat trouwens wel meer met de logica op gespannen voet. Archytas was een brillante, veelzijdige geest: filosoof, geometer, getallentheoreticus, musicus, uitvinder, staatsman en wat niet al, maar het strenge logische denken was zijn zwakke punt. Archytas heeft ook door het rekenkundig en harmonisch gemiddelde de getalverhoudingen 5:4 en 6:5 voor grote en kleine terts en die voor enkele andere intervallen gevonden. Op grond hiervan heeft hij de belangrijkste toonladders, die in zijn tijd in zwang waren, uitgerekend. Ptolemaios noemt hem met recht de grootste Pythagorese muziektheoreticus. Aristoxenos, die ingebeelde kwast, die zichzelf als de eerste werkelijke muziektheoreticus beschouwde en alles wat vóór hem was gedaan volslagen waardeloos achtte, verweet de Pythagorese muziektheoretici dat ze niet van de feiten uitgingen, maar zuiver theoretisch erop los speculeerden. Om deze kritiek te weerleggen, hebben de ‘canonici’ door zorgvuldige experimenten met een verbeterd monochord de juistheid van de leer der getalverhoudingen experimenteel bevestigd. | |||||||||
2. GetallentheorieDe harmonieleer geeft ons niet alleen de duidelijkste kijk op de geleidelijke ontwikkeling van de wetenschap der Pythagoreërs, maar zij is voor ons nog in ander opzicht van belang: uit de redeneringen over getallen, die Archytas in zijn harmonieleer toepast, kunnen wij zien, welke trap van ontwikkeling de arithmetica toen al bereikt had. Hierbij blijkt, dat de knappe logische opbouw van de leer der evenredigheden en van de deelbaarheid der getallen, die we in boek VII van de Elementen van Eukleides vinden, reeds vóór Archytas voltooid was. Nog ouder is de leer van even en oneven uit boek IX, die bekroond wordt door een beroemde stelling over ‘volmaakte getallen’, d.w.z. over getallen, die gelijk zijn aan de som van hun delers. Deze stelling luidt: Indien de som van een meetkundige reeks met reden 2 een priemgetal is, bijv. 1 + 2 = 3 of 1 + 2 + 4 = 7 of 1 + 2 + 4 + 8 + 16 = 31 | |||||||||
[pagina 119]
| |||||||||
dan levert deze som, met de laatste term vermenigvuldigd, een volmaakt getal op, bijv.: 2.3 = 6 of 4.7 = 28 of 16.31 = 496. Inderdaad is 6 gelijk aan de som van zijn delers: 6 = 1 + 2 + 3, en net zo bij 28 en 496. Iets dergelijks zijn de ‘bevriende getallen’ zoals 220 en 284, waarvan elk gelijk is aan de som van de delers van de ander. Toen men Pythagoras eens vroeg wat een vriend is, zei hij ‘een tweede ik’ en noemde de bevriende getallen 220 en 284. Hiermee betreden wij het uitgebreid terrein van de getallenmerkwaardigheden: dingen, die wiskundig meestal niet veel om 't lijf hebben, maar waar de Pythagoreërs een verheven, mystieke betekenis aan hechtten. In het werk van Nikomachos van Gerasa vindt men talloze dergelijke onderwerpen behandeld: volmaakte en bevriende getallen, driehoekige, rechthoekige en veelhoekige getallen, kubus- en pyramidegetallen, klassifikatie van gehele getallen en van breuken, allerlei gemiddelden..., alles zonder bewijzen, aan voorbeelden uiteengezet, waarbij Nikomachos op naïef-beminnelijke wijze telkens weer in vervoering geraakt over de wonderbaarlijke harmonie, die op dit terrein heerst. Zo merkt hij op, dat het dubbele van een driehoekig getal, zoals bijv. 1 + 2 + 3 + 4 = 10 (zie figuur) telkens een rechthoekig getal n(n + 1) oplevert, dat een rechthoekig getal zoals 4 × 5 meetkundig middelevenredig is tussen twee opeenvolgende vierkante getallen (16 en 25), en een vierkant getal weer rekenkundig middelevenredig is tussen twee opeenvolgende rechthoekige getallen (bijv. 16 tussen 12 en 20); verder dat door optelling van de oneven getallen juist de vierkante getallen ontstaan (bijv. 1 + 3 + 5 = 9) enz. Dit soort arithmetica is véél primitiever dan wat wij bijv. in de Elementen van Eukleides (omstreeks 300 v. Chr.) vinden, en nauw verwant aan de Babyloniche wiskunde. Zo bijv. vindt men niet alleen de quadraat- en kubusgetallen, maar ook de ‘paramekepipedongetallen’ n2(n + 1) van Nikomachos in Babylonische tabellen weer terug. Neugebauer heeft eens het vermoeden geuit, dat alles wat men ‘Pythagorees’ pleegt te noemen, beter ‘Babylonisch’ genoemd kan worden. Het doet mij genoegen, de lezers van ‘de Gids’ het nieuwste snufje op dit gebied te kunnen meedelen. Door een | |||||||||
[pagina 120]
| |||||||||
onlangs gepubliceerde spijkerschrift-tekstGa naar voetnoot1), is Neugebauers vermoeden volkomen bevestigd. De traditie schrijft aan Pythagoras het volgende middel toe om rechthoekige driehoeken met gehele getallen tot zijden te vinden: Neem een oneven getal m als kleinste zijde, dan is (m2 - 1):2 de tweede rechthoekszijde en (m2 + 1):2 de schuine zijde. Welnu, het oud-Babylonische tablet ‘Plimpton 322’ geeft een hele lijst van zulke driehoeken, die volgens een dergelijke, zelfs nog iets algemenere regel zijn berekend. Om samen te vatten: Pythagoras leerde allerlei wonderbaarlijke eigenschappen van getallen, grotendeels aan de Babylonische wetenschap ontleend; zijn leerlingen, te beginnen met Hippasos, maakten er een logisch opgebouwde wetenschap van. | |||||||||
3. MeetkundeOok de meetkunde der Pythagoreërs was een logisch opgebouwde wetenschap: wij weten bijv., hoe zij de stelling bewezen, dat de som van de hoeken van een driehoek gelijk is aan twee rechte hoeken. En ook in de meetkunde vinden wij de invloed van de Babylonische wetenschap, met name van de hoog ontwikkelde Babylonische algebra. De Pythagoreërs waren namelijk volgens Eudemos de uitvinders van de ‘aanpassing van oppervlakken met overschot en met defect’, dat zijn meetkundige constructies ter oplossing van vergelijkingen van de eerste en tweede graad. Nu kenden de Babyloniërs reeds sinds de tijd van Hammurapi (1700 v. Chr.) de algebraïsche oplossing van deze vergelijking volgens hetzelfde recept, dat wij op school leren. Dit zou op zichzelf nog niets bewijzen, maar NeugebauerGa naar voetnoot2) heeft overtuigend aangetoond, dat de constructies, die de Grieken toepasten, niet anders zijn dan vertalingen van de Babylonische formules in de taal der meetkunde. De Babyloniërs rekenen hun oplossing stap voor stap voor, in deze trant: Als van twee onbekende grootheden gegeven zijn het verschil en het product, halveer dan het gegeven verschil, verhef de helft in het quadraat, tel er het gegeven product bij op, trek de wortel, en tel er het halve verschil bij op, dan krijg je de eerste onbekende, of trek het ervan af, dan krijg je de tweede. Het Griekse constructievoorschrift komt hier nauwkeurig mee overeen: Als men een rechthoek wil construeren, waarvan gegeven | |||||||||
[pagina 121]
| |||||||||
zijn het oppervlak en het verschil basis min hoogte, of, zoals de Grieken zeggen, als men een gegeven oppervlak wil ‘aanpassen’ aan een gegeven lijnstuk, zodat er een vierkant ‘overschiet’, dan halveert men het gegeven lijnstuk, construeert op deze helft een vierkant, enz. Wanneer de Babyloniërs een wortel trekken, zeggen de Grieken: Verander het oppervlak in een even groot vierkant en neem daar de zijde van. De meetkundige oplossing geldt ook voor het geval dat de wortels der vergelijking niet meetbaar zijn, in welk geval men langs de weg der berekening slechts een benaderde oplossing kan geven, maar meetkundig een exakte. Om de exaktheid, niet om de aanschouwelijkheid hebben de Griekse mathematici aan de meetkundige inkleding de voorkeur gegeven. Pythagoras zelf had als Ioniër allicht een nauwer contact met het Oosten dan zijn discipelen in Italië. Ik neem daarom aan, dat hij het zelf geweest is, die de algebraïsche oplossing der vierkantsvergelijking van de Babyloniërs geleerd heeft, en dat de latere Pythagoreërs dit alles meetkundig geformuleerd en bewezen hebben. Met behulp van deze meetkundige algebra hebben de Pythagoreërs ook de ‘gulden snede’, d.w.z. de verdeling in uiterste en middelste reden, en de regelmatige vijf- en tienhoek geconstrueerd. De stervijfhoek was hun herkenningssymbool. Het Babylonische vraagstuk van de derde wortel, dat eveneens rekenkundig niet steeds exakt opgelost kan worden, leidde in meetkundige formulering tot het beroemde Delische probleem van de ‘verdubbeling van de kubus’. Hiervoor heeft Archytas een bewonderenswaardige stereometrische constructie gevonden met behulp van een ruimtekromme, die door een draaiende halve cirkel op een cylinder wordt uitgesneden. Wie meer van deze dingen wenst te weten, die verwijs ik naar mijn boek: ‘Ontwakende Wetenschap’, dat juist bij Noordhoff verschijnt. | |||||||||
4. AstronomieAl heel lang (minstens sinds 783 v. Chr.) kenden de Babyloniërs de dierenriem met zijn 12 tekens, en wisten zij, dat zon, maan en planeten in deze gordel hun banen beschrijven, van West naar Oost, tegengesteld aan de dagelijkse beweging der vaste sterren. Tussen 548 en 535, dus juist ten tijde van Pythagoras, werd de dierenriem ook in Ionië, door Anaximandros, bekend gemaakt; ook enkele sterrenbeelden in de buurt van de dierenriem | |||||||||
[pagina 122]
| |||||||||
hebben de Grieken van de Babyloniërs overgenomen. De Babyloniërs wisten ook, dat de morgen- en avondster slechts twee verschijningsvormen waren van één godin, de godin van de liefde. De Grieken schrijven de ontdekking van de identiteit van morgen- avondster soms aan Pythagoras, soms aan Parmenides toe. Het zou al heel verwonderlijk zijn, als Pythagoras, die de Babylonische algebra kende, de Babylonische astronomie, de actueelste Babylonische wetenschap, waar de Babyloniërs zelf religieuze betekenis aan toekenden, niet had gekend. Alle bronnen zijn het erover eens, dat hij de loop der sterren wist, en men kan zich zijn ‘veelweterij’, als de sterrenkunde daar niet toe zou behoren, moeilijk voorstellen. Alkmaion, de beroemde arts uit Kroton, die jong was, toen Pythagoras oud werd, en wiens denkbeelden in vele opzichten aan die van de Pythagoreërs verwant waren, leerde ‘dat de planeten zich tegengesteld aan de vaste sterren van West naar Oost bewegen’. Wij kunnen met zeer grote waarschijnlijkheid aannemen, dat ook Pythagoras dit leerde, temeer omdat de Pythagoreërs ten alle tijde, tegen de heersende materialistische werveltheorieën in, aan de leer van de eigenbeweging der planeten hebben vastgehouden. Zoals ik in de inleiding heb trachtten duidelijk te maken hangt de leer van de cirkelbeweging der planeten ten nauwste samen met de opvatting, dat de planeten bezielde, goddelijke wezens zijn. Bij Plato is dit verband zo nauw, dat hij het feit dat de planeten zich in cirkels volgens wiskundige wetten bewegen, als overtuigend bewijs voor het bestaan der goden aanvoert. Immers, als de planeten slechts dode stenen waren, meegesleurd door de wervelbeweging der atomen, heen- en-weer geslingerd door druk en stoot, zoals materialisten aannamen, hoe zouden zij dan hun zuivere cirkelbewegingen kunnen uitvoeren, nota bene in vlakken, die scheef staan ten opzichte van de richting van de wervelbeweging? Welnu, de opvatting dat de planeten bezield en goddelijk zijn, vindt men zowel bij de Babyloniërs als bij Alkmaion weer, en de traditie schrijft deze mening ook uitdrukkelijk aan Pythagoras toe. Hier hebben wij nu eens een geval, waarin ook de meest kritisch auteur de traditie gelijk moet geven. Waarschijnlijk behoren tot de oudste Pythagorese astronomie ook nog speculaties over het ‘grote jaar’, dat is volgens Plato de periode, na welks afloop alle planeten tot hun uitgangspunt terugkeren. Er zijn verschillende grote jaren, die aan verschillende Pythagoreërs en niet-Pythagoreërs toegeschreven worden. De overlevering is nogal verward, maar dergelijke speculaties vinden we ook in de Babylonische teksten. | |||||||||
[pagina 123]
| |||||||||
Maar wat men verder nog aan Pythagoras pleegt toe te schrijven: het meetkundige wereldbeeld der latere Pythagoreërs, met een bolvormige aarde in het midden, waaromheen de planeten op verschillende afstanden hun scheve cirkelbanen beschrijven, die alle worden meegenomen door de dagelijkse beweging van de hemel, dit wereldbeeld, dat Plato ons in de Staat en de Timaios beschrijft, is zeer zeker van later datum. Vóór 430 of hoogstens 440 kan het nauwelijks zijn opgesteld, want dan had Demokritos er rekening mee moeten houden. Volgens Demokritos en zelfs nog volgens de Atheense astronoom Meton, die tegen het eind van de 5de eeuw leefde was de aarde een platte of uitgeholde schijf. Maar deze theorie is zo slecht in overeenstemming met de feiten, dat een verlichte geest als Demokritos, die volkomen op de hoogte van zijn tijd was, zijn opvatting had moeten laten varen, indien de leer van de bolvorm in zijn tijd al had bestaan. Trouwens, Plato zelf laat Sokrates zeggen, dat hij deze leer pas laat heeft leren kennen. Bij dit wereldbeeld behoort ook de ‘harmonie der sferen’. Elke planeet geeft door zijn sneller of langzamer beweging een toon, en deze tonen vormen een toonladder, een ‘harmonie’. De kosmos wordt wel vergeleken met een lyra met 7 snaren, dat zijn de banen van de planeten (zon en maan incluis). Men moet niet denken, dat deze harmonie een dichterlijke toevoeging is: neen, zij is een essentieel deel van de mathematische theorie van de kosmos. Immers uit deze harmonie kan men de verhoudingen van de afstanden der banen berekenen! Bij een langere snaar behoort immers een lagere toon, en de getalverhoudingen der tonen van de toonladder zijn gelijk aan de verhoudingen van de lengten van de snaren, d.w.z. van de baancirkels. Die Pythagorese volgorde der planeten, van binnen naar buiten, was: Maan Mercurius Venus Zon Mars Jupiter Saturnus. Aan de planeten met de langzaamste eigenbeweging werden dus de grootste banen toegekend, in overeenstemming met het feit, dat volgens Archytas bij een langzamere beweging steeds een lagere toon behoort. Maar nu trad een moeilijkheid op: de snelheid der planeten in hun banen is niet constant, de tonen zouden dus ook geleidelijk hoger en lager moeten worden. Maar dan zou de toonladder vals worden! Bovendien, zo redeneerden de Pythagoreërs volgens Geminus: Een goddelijk wezen blijft zichzelf steeds gelijk en kan dus niet nu eens sneller en dan langzaam lopen. Daarom stelden de Pythagoreërs de vraag: Door welk samenstel van eenparige | |||||||||
[pagina 124]
| |||||||||
cirkelbewegingen kan de schijnbare onregelmatigheid van de planetenbeweging verklaard worden? De zon heeft slechts een kleine schijnbare onregelmatigheid: deze kan verklaard worden, door de cirkelbaan van de zon excentrisch te nemen. Een andere mogelijke verklaring, die ook op Venus en Mercurius van toepassing bleek te zijn, is de ‘epicykelhypothese’. Een epicykel is een cirkeltje, welks middelpunt een grotere cirkel om de aarde doorloopt. Een planeet, geplaatst op een epicykel, heeft twee bewegingen: een draaiing om het middelpunt van de epicykel en een draaiing mèt dat middelpunt om de aarde. De middelpunten der epicykels van Mercurius, Venus en de zon liggen voortdurend op één lijn met de aarde en voltooien hun omloop dus in dezelfde tijd, namelijk in één jaar. Daardoor verschijnen Mercurius en Venus nu eens ten Westen, dan weer ten Oosten van de zon, maar zij kunnen zich nooit ver van de zon verwijderen. Ik meen, uit de geschriften van Plato en andere bronnen te kunnen aantonen, dat de Pythagoreërs deze theorie (voor Mercurius, Venus en de zon) al vóór 380 opgesteld hebben. Voor de buitenste planeten probeerden ze ook wel iets dergelijks, maar dat lukte niet zo vlot. Behalve hun twee bewegingen op de epicykel en mèt de epicykel om de aarde, nemen de planeten ook nog aan de dagelijkse omwenteling van de hemel deel: elk heeft dus volgens deze voorstelling drie bewegingen tegelijk. Dit is een heel ingewikkeld mechanisme, vandaar dat Hiketas van Syracuse omstreeks 360, aan voorstellingen van Philolaos aanknopend, een andere theorie ontwierp, waarin elke planeet slechts één enkele cirkelbeweging had. Het geniale idee van deze theorie was, dat zowel de dagelijkse wenteling van de sterrenhemel als de onregelmatigheden van de zichtbare planetenbeweging als schijneffecten verklaard kunnen worden, wanneer men slechts aan de waarnemer zelf, dus aan de aarde, een beweging toekent. De aarde staat in deze theorie niet in het middelpunt, maar in het midden is het vuur. De aarde draait in één dag om dit vuur, en wel zo, dat altijd dezelfde kant van de aarde naar het vuur is toegekeerd, zodat wij, die aan de andere kant zitten, het niet kunnen zien. Door deze draaiing schijnt het, alsof alle hemellichamen zich dagelijks in tegengestelde richting draaien. Bovendien bekijkt de waarnemer elke planeet telkens weer van een ander punt uit, zodat de planeten, ook wanneer ze zich in werkelijkheid gelijkmatig in een cirkel bewegen, schijnbaar onregelmatig lopen. Hierdoor kunnen, althans in principe, de onregelmatigheden der planetenbeweging verklaard worden. De perioden klopten nog wel niet, maar Hiketas | |||||||||
[pagina 125]
| |||||||||
hoopte, dat het mettertijd wel zou lukken, de stralen van de banen en de omlooptijden zo te kiezen, dat alles in orde zou komen. En hierin vergiste hij zich niet. Deze theorie wordt door Aristoteles aan ‘de zogenaamde Pythagoreërs in Italië’ toegeschreven. Andere schrijven het op naam van Philolaos, maar Philolaos was een warhoofd en in zijn tijd, vóór 400, was zo'n geraffineerde astronomische theorie nog niet mogelijk. Twee andere, van elkaar onafhankelijke mededelingen noemen de naam Hiketas, en Hiketas leefde inderdaad omstreeks 350. Hij was tyran van Leontini en vocht wel tien jaar lang tegen zijn collega Dionysios, tyran van Syracuse. Heath meent dat zo iemand wel geen tijd voor astronomische studie zal hebben, en neemt daarom naast deze vechtjas Hiketas van Syracuse nog een andere Hiketas van Syracuse aan, die Pythagoreër en astronoom was, en ongeveer gelijktijdig met de vechtjas geleefd moet hebben. Maar ik zie geen noodzaak voor deze verdubbeling: de vechtersbaas kan zich in de tien voorafgaande jaren best met astronomie bezig hebben gehouden. Om de tegenstrijdige mededelingen over Philolaos en Hiketas te verklaren, moet men wel aannemen dat Philolaos een fantastische, half mythische cosmologie heeft uitgedacht, met het heilige, goddelijke vuur in het midden van de kosmos. Aristoteles schrijft ergens, dat volgens de Pythagoreërs de plaats in het midden de voornaamste plaats was en aan het voornaamste element, het vuur toekwam, en niet aan de aarde. Aan deze ideeën nu knoopte Hiketas aan bij de uiteenzetting van zijn astronomisch stelsel, en hij beriep zich daarbij waarschijnlijk uitdrukkelijk op de eerwaardige Philolaos. Vandaar dat het stelsel nu eens op zijn naam, dan weer op die van Philolaos wordt geschreven, en dat Aristoteles er zich met een onbepaalde aanduiding: ‘Die in Italië, de zogenaamde Pythagoreërs’ afmaakt. Dat was dus de derde astronomische theorie, die de Pythagoreërs opstelden. Maar nog was hun scheppend vermogen niet uitgeput! Sommige Pythagoreërs stelden zich voor, dat het centrale vuur niet buiten, maar binnen in de aarde zit, en dat het de aarde van binnen uit verwarmt en zo het leven op aarde mogelijk maakt. De aarde wentelt om dit vuur, dus om haar eigen as, en daardoor schijnt het weer, alsof de hemel om ons wentelt. Men verbindt met de aswenteling der aarde de namen der Pythagoreërs Hiketas en Ekphantos, maar het is mogelijk, dat Ekphantos slechts een dialoogpersoon bij Herakleides van Pontos is. Vol bewondering zien wij, wat een voortreffelijke astronomen de Pythagoreërs waren. Op hun ideeën berust de gehele Griekse | |||||||||
[pagina 126]
| |||||||||
theoretische astronomie. De door hen gestelde vraag, door welk samenstel van cirkelvormige bewegingen de verschijnselen der planeten verklaard kunnen worden, was voor Eudoxos de aanleiding, zijn kunstig stelsel van wentelende sferen uit te denken. Een leerling van Plato, Herakleides van Pontos, combineerde het Pythagorese denkbeeld van de cirkelbeweging der aarde met het eveneens Pythagorese denkbeeld der aswenteling en gaf aan de aarde beide bewegingen tegelijk, waardoor alle verschijnselen voortreffelijk verklaard konden worden. Aristarchos behoefde slechts de straal van de baan van de zon, die bij Herakleides nog willekeurig was, nul te stellen om het helio-centrische stelsel te verkrijgen. Apollonios, Hipparchos en Ptolemaios, die om astronomische en fysische redenen de geocentrische opvatting prefereerden, konden door combinatie van de Pythagorese hypothesen van excenter en epicykel zelfs de onregelmatigste bewegingen van Mars en de maan heel behoorlijk voorstellen. Maar ook de astronomie van de nieuwe tijd ging van dezelfde ideeën uit. Kopernikus ontleent bewust de voorstelling van de wenteling der aarde aan de Pythagoreër Hiketas; overigens werkt hij evenals Ptolemaios met epicykels en excenters. Het denken van Kepler, de vader van de moderne astronomie, is geheel en al doordrenkt met Pythagorese ideeën. Op Keplers werk berust echter de mechanica van Newton, en hierop weer de gehele moderne natuurwetenschap. B.L. van der Waerden
(Slot volgt) |
|

