De Gids. Jaargang 87

[p. 293]

De ontwikkeling van de meetkunde tot wetenschap bij de Grieken.

De Indiërs noemden dvija, ‘tweemaal-geborene’ den wijze, die uit het gewone leven ontwaakte tot het hoogere bewustzijn, die boven aardsche belangen zich verhief en kwam tot pañña, ‘het weten’ en dan tot vimutti, ‘de bevrijding’. In dien zin zou men de wiskunde dvija kunnen noemen, want eeuwen lang reeds werden enkele van haar stellingen in de praktijk toegepast vóór ze zich haar bestaan bewust werd en zich begon te ontwikkelen tot wat wij nu wiskunde noemen.

Wanneer men bedenkt dat het Griekenland was, waar de sophoi, de practisch-wijzen, die hun kennen verstonden om te zetten tot een kunnen op het gebied van politiek en eigenbelang, met der tijd plaats moesten maken voor de philosophoi, voor hen wie belangelooze liefde tot de wijsheid dreef, bij wie de wijsheid zich zelf tot doel was, dan zal men niet verwonderd zijn te bemerken, hoe ook de wiskunde aan den Griekschen geest haar tweede geboorte dankt.

Over deze periode, waarin deze omvorming van een aantal nuttige handgrepen met behulp van lijn en hoeken tot één hecht systeem tot stand kwam, laat zich meer vermoeden dan aanwijzen, zooals te verwachten is, waar het een proces betreft dat onbewust verliep en dus eerst beseft kon worden toen het voltooid was. Maar toen het zoover was, waren met den loop der eeuwen de meeste gegevens over die vroegere stadia reeds verloren gegaan.

Toch lijkt uit wat behouden bleef de afgelegde weg nog weer te vinden. Wanneer hij begint valt moeilijk aan te wijzen, want

[p. 294]

al waren er enkele van de bouwstoffen, de wiskunde was er nog niet. Oorspronkelijk werd naar bewijzen in het geheel niet gevraagd; de werkmethoden met koord en maatstok ontleenden haar bestaansrecht alleen aan het feit, dat het voorgeslacht hen had erkend en hieraan dat ze, zelf kinderen der ervaring, door nieuwe ervaringen steeds weer ten naaste bij bevestigd werden. Langzamerhand is toen gemerkt dat, in sommige gevallen, ze door het bewustzijn behalve gekend ook eenigszins begrepen konden worden, dat er dus iets vanzelfsprekends in hen viel aan te wijzen, dat als tweede bevestiging een - nog heel kleine - plaats vroeg naast wat we het drastische bewijs konden noemen. Hier begint de lange ontwikkeling, die de sanctie door de werkelijkheid meer en meer tot tweede argument maakt en ten slotte zelfs ook daar waar de ervaring zich schijnbaar verzet, haar theoretisch bewijs handhaaft en wijst op de slechts betrekkelijke juistheid van onze waarneming.

In Egypte is het bij het beginstadium gebleven, waarin een overpeinzing over hoeken en lijnen nog bezijden het directe nut voor tempelgrondafbakening en dergelijke, een lichte voldoening aan het verstand gaf over het logisch bevredigende der motiveeringen. Zooals het lang duurde eer de philosophie besefte dat het niet aanging het denkvermogen zoo maar aan te wenden op een philosophischen inhoud, zonder eerst de werkwijze van dat denken te hebben onderzocht, zoo had men ook op wiskundig gebied reeds verschillende resultaten bereikt zonder nog een vaag idee te hebben van de eischen waaraan een bewijs behoort te voldoen.

Uit Egypte is één boek bewaard gebleven, het rekenboek van Ahmes uit de 19de eeuw voor Christus, dat volgens eigen ondertitel geschreven is naar voorbeeld van geschriften uit de dagen van Amenemhat III. Dit boek tot maatstaf stellen van de kennis dier dagen mogen we niet, want wat Ahmes' bedoeling was is onduidelijk. Immers, wat te denken van een werk dat wetenschappelijk aldus begint: ‘Voorschrift om te geraken tot kennis van alle duistere dingen, alle geheimen die in de dingen liggen opgesloten’, en dat eindigt met de aansporing: ‘Vang ongedierte, muizen, levend onkruid, talrijke spinnen. Bid Ra om warmte, wind en hoog water.’ Dat lijkt weinig op onze opvatting van een leerboek, maar een boeren-

[p. 295]

almanak kan het evenmin geweest zijn, daar er naast enkele werkelijk landelijke sommen over voer voor koeien en ganzen toch ook echte rekenkundige vergelijkingen, lijnverhoudingen bij piramiden en zelfs geometrische reeksen behandeld worden. Maar toch toont het boek wat men in dien tijd in ieder geval aan stellingen kende en ook wat men - ten onrechte - meende te kennen. In hoofdzaak komt het neer op een oplossing voor de cirkelquadratuur waarbij π r² aan (16/9 r)² gelijk werd gesteld. Verder de seqt-rekening, dat is de becijfering van wat wij de cosinus en tangens zouden noemen van enkele, bij de piramide voorkomende hoeken en waarvan de uitkomst bij meting bleek te kloppen met de overeenkomstige verhoudingen bij een twaalftal piramiden.

Daartegenover stond echter - een typisch bewijs hoe de wiskundige resultaten der Egyptenaren op benadering door waarneming berustten - een foutieve formule voor de oppervlakte van driehoeken nl. O = basis × halve som der opstaande zijden en evenzoo voor het gelijkbeenig trapezium O = een opstaande zijde × de halve som der evenwijdige zijden; terwijl bovendien hun onkunde zich verraadt, waar ze een eenigszins groot gelijkbeenig trapezium door nieuwe evenwijdige lijnen in deelen snijden en van deze elk afzonderlijk het oppervlak berekenen, alsof dit een ander, minder onjuist resultaat zou opleveren. Dat deze fouten niet onder den naam van vergissing bij de heel vele verdere vergissingen van Ahmes mogen geboekt worden bewijst de tempelinscriptie van Edfu, 1800 jaar na Ahmes ingegrift, waar het oppervlak van de meest willekeurig vierhoekige stukken land gelijk gesteld wordt aan het product van de halve sommen der overstaande zijden! En dat, terwijl toen reeds tweehonderd jaar te voren Euclides de Elementa geschreven had, en wel geschreven in Alexandrië!

Dit alles wijst er op dat het in Egypte bij het onnauwkeurig beschouwen der figuren is gebleven; iets wat, hoe weinig ook op een bewijs lijkt zoekt men in Ahmes' rekenboek tevergeefs. Op aanschouwing uitsluitend berust dan ook hun systeem om een wand door elkaar loodrecht snijdende lijnen in vierkanten te verdeelen voor het gemak bij het vergrooten van het model volgens welk de muur versierd moest worden. Van een coördinatenstelsel is hier geen sprake.

[p. 296]

Het hierboven gezegde geeft, meen ik, een anderen zin aan de vraag in hoeverre de eerste vondsten, die op naam van Grieken staan, ontleeningen uit Egyptische kennis zijn. Gewoonlijk antwoordt men hierop alsof een stelling, die reeds bij de Egyptenaren bekend schijnt, zoo zonder meer door de Grieken is overgenomen. Anderzijds geeft men toe, dat de wiskunde eerst in handen van de Grieken een wetenschap is geworden, doch bedenkt niet dat dit beteekent dat de wiskunde geheel van de Grieken is, want een onwetenschappelijke wiskunde is ondenkbaar en het was nog allerminst wiskunde wanneer in Egypte de harpedonapten, om hun tempel rechte hoeken te geven, een ring van koord, waarin op gelijke afstanden twaalf knoopen waren gelegd, zoo spanden, dat er een (rechthoekige) driehoek uit ontstond met de lengten drie, vier en vijf als zijden. Zoo moet de vraag dus eer deze zijn: hoe is bij de Grieken de behoefte van het denken aan argumenteering voor het begríp zoo sterk geworden dat iets geheel nieuws: het wetenschappelijk bewijs, zich bij hen heeft ontwikkeld en dat juist aan een stof, welke, omdat ze practisch nuttig was en oplossingen gaf wier onnauwkeurigheid geen hinderlijke onjuistheden schiep (fouten die men bovendien ook aan de onvolmaaktheid der meetinstrumenten kan hebben toegeschreven) zoo weinig aanleiding tot theoretische beschouwing scheen te geven?

Gaan we nu in het kort de eerste Grieksche mathematici in volgorde langs:

Thales ontdekte de gelijkheid van de overstaande hoeken bij twee elkaar snijdende lijnen; de gelijkheid der basishoeken bij den gelijkbeenigen driehoek; de gelijkheid der twee deelen waarin een middellijn een cirkeloppervlak verdeelt. Niet tegen onze verwachting bij dezen eersten overgang van Egyptische kunde-door-aanschouwing naar Grieksch weten-door-begrip, voegt Proclus, een commentator van Euclides uit de vijfde eeuw onzer jaartelling, hier aan toe, dat de eerste dier drie stellingen door Thales gevonden maar eerst door Euclides bewezen is, terwijl op datzelfde aflezen uit de teekening lijkt te wijzen dat Thales bij zijn formuleering der gelijke basishoeken in de tweede stelling, deze homoia, ‘van gelijke gedaante’ noemt, waar lateren bij hoeken steeds van isa ‘van gelijke grootte’ spreken.

[p. 297]

Het komt dus hierop neer, dat Thales' vondsten alle reeds voor het oog waarschijnlijk, daarom misschien door de Egyptenaren onbewust en dus ongenoemd toegepast zijn, zoodat zijn verdienste hierin ligt dat hij het eerst den wetenschappelijken eisch stelde ook het vanzelfsprekende met name te noemen. Zoo wordt ook een andere opmerking van Proclus begrijpelijk: ‘Thales vond veel zelf, tot veel andere dingen wees hij bovendien den weg aan wie na hem kwamen door ze deels algemeener, deels helderder voor oogen te stellen.’ Van andere, hoogstbetrouwbare zijde worden we gewaarschuwd dat ‘algemeener stellen’ niet al te ruim op te vatten daar ‘de oude wiskundigen bijvoorbeeld voor elken vorm van driehoek een afzonderlijk bewijs betreffende de grootte van de som der hoeken hadden.

Na Thales wordt eerst van Pythagoras weer iets zakelijks op wiskundig gebied bericht. Maar, wat hij en wat zijn leerlingen ontdekten onderscheidt de overlevering niet. Eerbied deed zijn jongeren zwijgend hun vondsten met 's meesters naam verbinden en hier vermocht geen onbescheiden speurzin van het nageslacht aan het daglicht te brengen wat zíj wilden dat verborgen zou blijven.

Wat dan op zijn naam staat is, voorzoover het dit onderzoek aangaat, het volgende: Pythagoras spreekt met nadruk uit dat de wiskunde iets hoogers is dan hulpmiddel voor de praktijk; hij maakt het tot een belangrijk onderdeel van de opvoeding; hij ook is de eerste die zich philosophos noemt. Volgens Iamblichus veranderde hij den naam geometrie - landmeetkunde - in historia - onderzoek - wat, gezien de aan practisch nut herinnerende oude benaming geenszins ongeloofwaardig klinkt. Pythagoras verder hoorde in de wiskunde de taal der goden waarmee deze symbolisch hun wezen openbaarden aan hem die dit zelfstandig gedachtenspel, dat zich in hem ontwikkelde maar waar zijn wil geen invloed op had, als stille toeschouwer vermocht te vatten. Naast een helder besef van het ordenend vermogen van de wiskunde, dat hem het materiaal van deze wetenschap zulk een belangrijke plaats in de wereldorde deed toekennen, begreep hij, hoe de wiskunde zelf ook streng geordend diende te worden. Vandaar de indeeling naar hun eigenschappen van lijnen, hoeken, figuren en getallen in vele groepen, waarvan enkele

[p. 298]

op den duur onvruchtbaar bleken en in onbruik geraakten, al vinden we ze tot het einde harer dagen in de neo-Pythagoreesche mystiek terug.

Een gevolg van dit ordenen was, dat Pythagoras het eerst het belang van definities inzag. Jammer, dat ons geen enkele van zijn definities is bewaard gebleven. Waarschijnlijk zouden we er een sterk steunen op de aanschouwing in hebben weergevonden; want zelfs nog Plato definieert de rechte lijn als die lijn, waarvan het tusschenliggende aan het begin- en eindpunt in den weg staat (of: in het licht staat).

De befaamde stelling van Pythagoras, die de ontdekking van het irrationeele beteekent zal in ander verband nog ter sprake komen.

De uitbreiding en systematiseering door Pythagoras van wat men aan wiskundige kennis bezat, had twee groote gevolgen: dat men boven de voor het oog terstond evidente stellingen uitkwam en dus aan het abstracte bewijs steeds strenger eischen stelde én dat men merkte geen eigenlijk beginpunt te hebben. Vandaar een onderzoek naar de grondslagen, wier ontdekking en nauwkeuriger bestudeering uit der aard gelijken tred hield met de ontdekking en daarna verfijning van de bewijsmethode. Vooral het pas ontwaakte besef, dat men ook het vanzelfsprekende uitdrukkelijk stellen moest met daarop volgend de gewaarwording dat die vanzelfsprekendheid veelal slechts schijnbaar was, moet veel hebben bijgedragen tot een aldoor dieper afdalen in de beginselen tot men eindelijk gedwongen was een aantal axioma's op te stellen, de niet bevredigende, doch niet verder te herleiden, beweringen, die men dan maar, uit gebrek aan beter, als punt van uitgang voor het systeem nam, wel bewust dat het een concessie van de zijde van den leerling was, als hij op het axioma, de ‘vordering’ van zijn leermeester, deze beweringen zonder meer te laten gelden, inging.

Verliest dus de vraag, wat de Grieken in wetenschappelijk opzicht aan Egypte dankten haar belang, veel meer op den voorgrond komt nu het onderzoek of er naast den anderen aanleg der Grieken nog verdere factoren zijn geweest, welke de Grieken het mogelijk maakten, zoo snel tot een hooge wetenschap te vervormen wat in Egypte eenige duizenden jaren lang een onveranderlijken vorm had gehad. Mij nu

[p. 299]

lijkt, dat het in teekening brengen van de meetkundige vragen hierbij een zeer belangrijke factor is geweest en dit reeds dadelijk om twee redenen:

Ten eerste omdat we zien hoe bij de Egyptenaren de teekening uiterst primitief is. Zoo wordt bij het vraagstuk van de cirkelquadratuur nevenstaande onbeholpen teekening gevoegd, met in het midden het Egyptische cijfer voor negen, welke eerst duidelijk wordt als men er de redeneering, die bij een ander cirkeloppervlak-vraagstuk staat, naast legt, n.l.: ‘Neem af 1/9 van 9, dat is 1, rest 8, vermenigvuldig het getal 8 met 8, dat is 64’, m.a.w. de teekening geeft weer wat men krijgt als men over den cirkel een vierkant aanbrengt, welks zijden 8/9 van de middellijn tot lengte hebben. De vier cirkelsegmenten die buiten dit vierkant uitsteken zijn achterwege gelaten; de teekening dient alleen om het oog te overtuigen (!) dat het weggelatene in oppervlak nabij zal komen aan de vier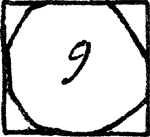

Fig. I.

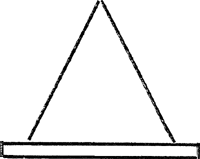Fig. II.

stukken, welke het quadraat grooter is dan de gemutileerde cirkel.

Waarom de teekening alleen weinig aan de ontwikkeling der Egyptische meetkunde kon meehelpen, toont de reeds genoemde seqt-rekening nog veel duidelijker. Hier wordt de verhouding berekend tusschen de lengten van een opstaande rib (bij Ahmes pir-em-us d.i.: ‘het uitkomen uit de zaagsnede’ genaamd, een naam welke, overgegaan op het geheel, de oorsprong werd van ons woord piramide) en van de lijn die het voetpunt van die ribbe met het middelpunt van het grondvlak verbindt, dus de helft is van een diagonaal van dat grondvlak. Dit is natuurlijk alleen met behulp van het perspectief duidelijk weer te geven. Maar hier gaat de Egyptenaar niet toe over. Hij brengt de piramide in teekening (Fig. II) zuiver van terzij gezien maar op een basis, die naar weerszij uitsteekt. Dat het meetkundige denken, dat juist in zijn begin zoozeer behoefte er aan heeft zich de figuur te

[p. 300]

kunnen voorstellen, over de zoo geschapen moeilijkheden niet heen heeft kunnen komen, is begrijpelijk.

De tweede reden, waarom ik de teekening zulk een belangrijke rol in de ontwikkeling der meetkunde toeschrijf is het feit, dat bij de Grieken, ondanks hun aanleg tot abstractie en daarmee tot generaliseeren, toch nooit de algebra bewust is uitgewerkt. Bij Euclides vindt men alle formules weer van de lagere algebra, doch meetkundig uitgedrukt en bewezen. Evenredigheden zijn hem altijd verhoudingen van lengten en oppervlakken geweest.

Welk een groote plaats de figuur in nam, vinden we voor de oudste tijden terug o.a. in het vele spreken over het merkwaardige verschijnsel, dat er drie regelmatige figuren (gelijkzijdige driehoek, vierkant en regelmatige zeshoek) bestaan, die de ruimte rond een punt geheel vullen. Voor later tijd leert het het woordgebruik, de benamingen die op een oorspronkelijke bijgedachte aan een teekening wijzen. Zoo wordt er geregeld gesproken van driehoeksgetallen, vierhoeksgetallen etc., quadraat en kubus, veelhoekige- en piramidale getallen.

Typisch komt het ook uit in het lijfwoord der Pythagoreërs: ‘schama kai bama all' ou schama kai triobolon’, ‘een nieuwe stelling beteekent een stap vooruit maar niet een geldelijk voordeel’, de oudste triumphkreet van de wijsheid om de wijsheid, waarin een stelling eenvoudig een ‘figuur’ genoemd wordt. Toen dan ook de Pythagoreërs tot de ontdekking kwamen van het irrationeele, d.i. bemerkten dat er geen gemeenschappelijke maat ten grondslag lag aan rechthoekzijde en hypotenusa, de lengte van de een dus niet in die van de ander was uit te drukken en daarmee de oude opvatting, als zou een quantiteit een som van eenheden zijn, op zij zette, toen heeft deze vondst zulk een indruk gemaakt op het van de behoefte aan aanschouwelijkheid nog niet vrij geworden denken, dat velen in de Eleatische leer de wanhoopsdaad zien van het verstand, dat zich door het irrationeele gedwongen ziet zich zelf te weerspreken en nu den noodstap doet naar ontkenning van veelheid en beweging. En van hem, die deze vondst had bekend gemaakt en zoo het eerst het gebod van zwijgen der Pythagoreërs, gesymboliseerd in het verbod zegelringen met godenbeeltenis te dragen, dat is: zijn opvatting en kennis betreffende de goden niet openlijk met zich te

[p. 301]

dragen noch ook haar onder de menigte te brengen, van hem dan die dit gebod vergeten had heette het, dat hij tot straf door een schipbreuk ellendig was omgekomen.

Als een eindpunt en hoogtepunt in het zuivere denken staat dan Aristoteles, die... ook al van de aanschouwelijkheid niet los kan komen in zijn pogen, de ruimte als iets anders dan het ledige aan te toonen, waar hij omgekeerd moet erkennen, dat als de ruimte dan dus wél íets is en wanneer alles wat is, ruimte inneemt er dan ook een ruimte moet zijn die door de ruimte wordt ingenomen en zoo voort tot in het oneindige. Voorts bedenke men hoe Aristoteles nog spreekt van de zes dimensies: omhoog, omlaag, naar voren, naar achteren, rechts, links, terwijl hij het peil der kennis zijner tijdgenooten die hij tot hoorders en lezers had, verraadt, waar hij het noodig acht er den nadruk op te leggen dat de wiskundige het niet heeft over de figuren zelf, die hij teekent, doch dat ze hem altijd symbool zijn.

Ook het terugschrikken der ouden voor het invoeren van het begrip der oneindigheid lijkt gedeeltelijk gevolg van het nog niet vrij zijn van de behoefte aan voorstelbaarheid.

Voorts denke men aan den loculus Archimedius, een soort legwerk, door Archimedes bedacht, waarvan de figuren tot een quadraat en verschillende andere figuren kon worden gelegd, vrucht dus van pogingen van Archimedes, om regelmatige figuren te snijden in kleinere waarin andere figuren zich eveneens lieten verdeelen, iets wat sterk aan Plato's fantasieën over den bouw van het heelal uit driehoeken doet denken.

Van groot belang zou het daarom zijn wanneer we van den beginne af aan de ontwikkeling van de meetkundige teekening konden nagaan. De reeds weergegeven uitlating van Proclus, dat Thales den weg tot verschillende bewijzen aanwees door ze helderder voor oogen te stellen (aisthetikoteron) wijst op den invloed, welke deze wijze op dit gebied gehad heeft. Enkele aanwijzingen geeft verder de bestudeering van de cirkelindeeling in den loop der tijden. Zoolang de beschaving nog op laag pijl staat vindt men de deeling in vieren door twee onderling loodrechte middellijnen (behalve in ornamenten het duidelijkst te zien in wagenafbeeldingen met vier-spakige wielen). Bij de Etrusken vindt men nagenoeg niets anders,

[p. 302]

evenzoo op de oudste Grieksche vazen met wagenafbeeldingen, de François-vaas bijvoorbeeld. Alleen op Melisch vaatwerk komt het zesspakige wiel voor, welke te teekenen geen meetkundige kennis vereischt en berust op de ontdekking, dat men de straal juist zes keer als koorde op den omtrek kan afzetten.

In Babylonië verwacht men de zes-deelige als de gewone, immers uit Mesopotamië is de deeling van den cirkel in 360 graden tot ons gekomen; daar ook noemen de kleitabletten getallen in het zestigtallig stelsel. Daarom verrast het, daar meest de deeling in achten te vinden Zoo is het zonnesymbool in acht sectoren verdeeld, evenveel armen telt het oud-Babylonische spijkerschriftteeken voor ‘god’.

Bij koning Ashurnasirpal is echter de dertien-deeling op armbanden en hoofdsieraad regel, evenzoo op rosetten uit den tijd van Salmanassar, tezamen met het achtspakige wiel. Deze dertien-deeling is heel wonderlijk, daar ze neerkomt op een indeeling in hoeken van ongeveer 27⅔ graad, wat alleen met een gradenboog te vinden is. Mogelijk is deze hoek bij benadering ontleend aan de sterren, want 28 graden is ongeveer de verplaatsing, die men voor elke ster vindt bij twee waarnemingen op hetzelfde oogenblik van den nacht, doch met als tijdsverschil den tijd die tusschen twee nieuwe-maansnachten verloopt. Meer waarschijnlijk is het dat men, naar bepaalde lengteverhoudingen der zijden onderling, driehoeken construeerende, toevallig een hoek gevonden heeft die, dertien keer rond één hoekpunt uitgezet, de ruimte om dat punt ten naastebij bleek te vullen. Aan de gezochte grootte komt zeer nabij de helft der grootste van de beide scherpe hoeken der beroemde rechthoekige driehoek met de zijden: drie, vier en vijf. Deze hoek is n.l. slechts ruim één graad kleiner dan de gezochte. Maar nog veel geringer wordt de fout, minder zelfs dan een halve graad, wanneer men de helft neemt van den grootsten scherpen hoek van een rechthoekigen driehoek, waarvan de eene rechthoekzijde anderhalf maal de lengte der andere heeft.

Meer gegevens over de ontwikkeling van het wiskundig teekenen zouden misschien de handschriften kunnen brengen. Het is bekend dat de monniken bij het copiëeren van oude handschriften de illustratie's - ik denk hier in het bijzonder

[p. 303]

aan de Latijnsche comedie - meest nauwkeurig nateekenden. Ditzelfde is. ook van wiskundige figuren niet onmogelijk. Voor ons onderzoek zou dit van belang zijn wanneer we afschriften van de oudere wiskundige werken bezaten. Tot nog toe is dit niet het geval, maar wellicht bevatten de palimpsesten er nog enkele. Het schijnt wel dat, wanneer zuinigheid de monniken er toe bracht een oud geschrift met puimsteen af te schuren om het voor nieuw gebruik geschikt te maken, hun hand het eerst naar de plank bestemd voor de exacte wetenschappen greep. Zoo is een palimpsest het door Heiberg in 1906 bij Constantinopel gevonden geschrift van Archimedes dat, door hem voor zoover doenlijk ontcijferd, een uiterst belangrijk document is geworden, daar het bewees dat Archimedes reeds systematisch integraalrekening toepaste, een werkwijze sindsdien verloren gegaan en eerst door Newton en Leibnitz opnieuw ontdekt. Maar de tekst en vooral de teekeningen hebben door het uitwisschen zwaar geleden. Voor deze en andere palimpsesten kan dan ook van groote waarde worden een methode, door een Italiaansch geleerde, Prof. Perugi het vorig najaar ontdekt, om de oudste hand weer leesbaar te maken. Reeds te voren had een uitvinding op dit gebied door Kögel goede resultaten gegeven, maar de bestraling van het handschrift met ultraviolette stralen, hiertoe noodzakelijk, bracht aan het stuk groote schade toe en was tevens niet voor herhaling vatbaar, zoodat een hernieuwde bestudeering voor goed onmogelijk werd. Nu is het groote voordeel der nieuwe vinding, dat Prof. Perugi voldoende heeft aan een goede negatieve foto van het handschrift. Uit deze haalt hij de beide teksten in afzonderlijke positieve afdrukken zonder het oorspronkelijke perkament in handen te hebben gehad. Zijn werkwijze komt dus neer op het afdrukken volgens een nieuwe manier van een gewoon negatief¹⁾. De

1) Dit maakt begrijpelijk dat de beteekenis er van zich niet tot palimpsesten beperkt: ook Röntgen-foto's zijn door hem zoodanig verscherpt, dat in enkele gevallen geneeskundigen er hun diagnose juister door stellen konden.
Ook van volkomen onleesbaar geworden handschriften zijn door hem op deze wijze goed leesbare afdrukken gemaakt. Zoo behoorden tot de eerste resultaten enkele tot op dien dag onbekende pagina's uit Gaius. Reeds gaf hij uit de zoo verscherpte palimpsest van de Fasti Consulares uit Verona en het geschrift: De Trinitate van St. Hilarius uit de Vaticaan-Bibliotheek.

[p. 304]

dag waarop een wiskundig werk aan deze behandeling onderworpen wordt, kan een zijn van groot belang niet alleen voor de geschiedenis dezer wetenschap maar voor heel ons begrijpen van de eerste ontwikkeling van het wetenschappelijk denken in het algemeen.

H.M.J. Oldewelt.