De Gids. Jaargang 76

[p. 319]

Rekenwijze voor de praktijk van evenredige vertegenwoordiging.

In het Gids-artikel van 1 Nov. '11: ‘De verdeeling der zetels over de verschillende partijgroepen bij evenredige vertegenwoordiging’ trof mij de opmerking op pag. 336: ‘Maar m.i. bewijzen die wiskundige betoogen weinig meer, dan dat de wiskunde in deze zaak geen uitspraak kan doen.’

Zóó opgevat, als zoude aan de wiskunde alléén in dezen niet het eerste en het laatste woord zijn, zou ik de juistheid dezer uitspraak niet durven betwisten, echter, gelijk ze daar staat in verband met wat de schrijver van de toepassing der wiskunde op het vraagstuk meêdeelt, doet zij onwillekeurig de vraag rijzen: kan het ook zijn, dat bij die ‘wiskundige betoogen’ de wiskunde even weinig betrokken is, als bij de in het artikel beschreven stelsels van Fruin, D' Hondt e.a.?

Laatstgenoemde rekenwijzen toch verdienen den naam wiskundige-oplossing al even weinig als zoovéél in de praktijk gebruikelijke loopjes en kunstjes ter oplossing van reken- of meetkundige vraagstukken zoo goed en zoo kwaad als het gaat zonder toepassing van wiskundige beschouwing en berekening.

Als voorwaarde voor evenredige vertegenwoordiging behoort te worden gesteld deze, dat de verhouding van het aantal kiezers tot dat der vertegenwoordigers voor alle groepen zoo na mogelijk dezelfde zij.

De schrijver van bovengenoemd artikel stelt de vraag, welker oplossing deze voorwaarde eischt, volkomen op dezelfde wijze (pag. 336).

Zoo na mogelijk dezelfde zij: immers, daar aan iedere groep slechts een geheel aantal zetels, geen onderdeel daar-

[p. 320]

van, kan worden toegewezen, is volkomen evenredigheid in het algemeen onbereikbaar.

De fouten - noodzakelijke derhalve -, welke bij de verdeeling gemaakt worden, worden gemeten niet door de fraktie van een' zetel, welke eenige partij in vergelijking met eene andere te veel of te weinig ontvangt, maar door de verhouding van die fraktie tot het aantal zetels - in het algemeen geen geheel getal dus - dat haar in vergelijking met die andere partij toekomt. M.a.w. die fout wordt bepaald door het gedeelte (het percentage) van het haar - in vergelijking met wat aan een andere partij wordt toegewezen - toekomende, dat elke partij te veel of te weinig ontvangt.

Gesteld aan eene partij met 3000 kiezers worden 3 zetels toegewezen, aan eene andere 6400 stemmen uitbrengende - welke dus naar evenredigheid op 6,4 zetels aanspraak heeft - 6 zetels, aan een derde 2400 kiezers tellende - in vergelijking met de eerste dus recht hebbende op 2,4 zetels - 2 zetels, zoo worden beide laatste partijen door haar dien 0,4 zetel te onthouden niet in gelijke mate te kort gedaan, de eene toch voor 1/16 de andere daarentegen voor ⅙ van het haar toekomende; evenredig vertegenwoordigd waren zij, ten opzichte van elkaar wel te verstaan, wanneer beiden een zelfde deel van haar door haar getalsterkte aangewezen aandeel werd onthouden, zoo, wanneer eene partij recht hebbende op 6,75 zetels 6, eene andere, welke op 2,25 zetels aanspraak maakt, 2 zetels erlangt.

In andere bewoordingen is het zwaartepunt van de quaestie als volgt aan te duiden: de verhouding in getalsterkte der partijen moet in de verhouding van het aantal vertegenwoordigers van elk dier partijen tot uitdrukking komen, en nu is het duidelijk, dat dit in mindere mate het geval zal zijn, wanneer de zwakste partij een fraktie van een' zetel moet derven, dan wanneer der sterkste partij een zelfde fraktie wordt gekort.

De vraag wordt dus: het aantal zetels zoodanig te verdeelen, dat het percentage, hetwelk de minst begunstigde partij in vergelijking met de ruimst bedeelde te kort komt, zoo gering mogelijk zij.

Een eenvoudige wiskundige formule ter oplossing van het

[p. 321]

vraagstuk is niet te geven, doch het zal niet veel hoofdbreken kosten, om in ieder voorkomend geval de oplossing tastenderwijze te vinden, zooals uit de toepassing op een enkel voorbeeld kan blijken. Bovendien is de vraag eenig en alleen welke verdeeling de juiste is, niet: welke wijze van verdeeling den minsten arbeid vordert.

Onderzoeken we, hoe de verdeeling behoort te geschieden in het geval in boven aangehaald artikel ondersteld.

Partijen	A.	B.	C.	D.	E.	Totaal
Stemmen	500	370	220	120	70	1280
Theor. verdeeling	3,12	2,31	1,38	0,75	0,44	8 zetels
Prakt. verdeeling	3	2	2	1	0	8 zetels
Proc. te-veel	÷ 12/312 ÷ 31/231 + 62/138 + 25/75 ÷ 44/44

Partij C wordt dus bij deze verdeeling der zetels het meest bevoordeeld: voor 62/138 = 0,45, partij B - E buiten beschouwing gelaten - het sterkst benadeeld: voor 31/231 = 0,13.

Eerstgenoemde krijgt 1 zetel op 110 kiezers toegewezen, naar evenredigheid heeft dus B aanspraak op 370/110 × 1 of 3,36 zetel, komt dus in vergelijking met C 1,36 zetel of 1,36/3,36 van het haar toekomende d.i. 0,41 te kort, welke maximumwaarde voor het procentsgewijze te kort van eenige partij in vergelijking met eene andere we kortheidshalve de fout noemen, voluit: de grootste betrekkelijke procentsgewijze fout in de verdeeling.

Werd onderstaande verdeeling gevolgd:

Partijen	A.	B.	C.	D.	E.
Prakt. verdeeling	3	3	1	1	0
Proc. te veel	÷ 12/312 + 69/231 ÷ 38/138 + 25/75 ÷ 44/44

zoo werd - afgezien weer van het aandeel van E - partij C de meest benadeelde en wel voor 0,28, met een ruim tweemaal zoo groot tekort dus als B bij de vorige verdeeling, terzelfder tijd echter werd de meest begunstigde partij - thans D - met een kleiner bedrag bevoordeeld dan de ruimst bedeelde bij de eerst gekozen verdeeling n.l. 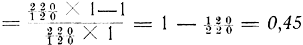met 0,33, het zou dus kunnen zijn, dat de fout kleiner geworden en de laatste verdeeling de juiste was, de fout blijkt echter grooter geworden de eerste verdeeling is dus de aangewezene.

[p. 322]

We lieten partij E buiten beschouwing; brengen we ook haar tekort in rekening, zoo wordt de fout bij beide verdeelingen gelijk 1, onafhankelijk dus van de verdeeling der zetels over de andere partijen, onafhankelijk ook van de waarde door de theoretische verdeeling voor E aangewezen; de waarde van de fout voor E in de verdeeling, in het algemeen voor een partij, welke geen zetel ontvangt, kan dus zonder meer geen maatstaf zijn ter beöordeeling van de meerdere of mindere juistheid der verdeeling.

We hebben echter te onderzoeken, wat de fout voor E wordt, wanneer haar een zetel wordt toegekend, dan ontvangt zij méér dan het dubbele van het haar in vergelijking met andere partijen toekomende, meer dan 100 % te veel, de fout voor E is dan grooter dan 1, grooter dan de waarde van die fout - in tegengestelden zin -, wanneer E geen zetel bekomt, in welk geval die fout tevens de maximumfout in de verdeeling is; aan partij E - en in het algemeen aan een partij, welke theoretisch op minder dan de helft van een zetel aanspraak maakt - behoort dus geen zetel te worden toegewezen.¹⁾

Bij de eerst beschouwde verdeeling - welke derhalve de praktisch-juiste is gebleken - wordt voor de verschillende

1) De vraag kan worden gesteld, of het inderdaad minder juist is E met meer dan 1/1 of zelfs 2/1 of meer van het haar toekomende te bevoordeelen dan haar 1/1 van het haar toekomende te kort te doen, in het eerste geval ontvangt zij ruim 2/1 of 3/1 enz. van haar rechtmatig aandeel, in het laatste geval 0/1 daarvan, in het eerste geval verhoudt zich dus haar werkelijk aandeel tot haar rechtmatig als 1 tot omstreeks ½ of ⅓ enz., in het laatste geval als 1 tot oneindig groot. Zonder daarop verder in te gaan zij opgemerkt, dat de moeielijkheid waarschijnlijk slechts te ondervangen is door elke partij minstens één zetel doch aan de stemmen van afgevaardigden ter vergadering van verschillende partijen ongelijke waarden toe te kennen. Gesteld een partij, welke theoretisch op 0,1 zetel aanspraak maakt, kon zich door 1 afgevaardige doen vertegenwoordigen, terwijl eene andere, wie de theoretische verdeeling 3,6 zetels toewijst, slechts met 3 zetels werd bedeeld, zoo zou aan de stem van eerstbedoelden afgevaardigde slechts de waarde 0,1 behooren te worden toegekend, aan die van elk der laatstgenoemden de waarde 3,6/3 = 1,2. Het gevaar, dat bij eene dergelijke regeling het aantal partijen gelijk aan dat der kiezers werd, is niet denkbeeldig.

[p. 323]

partijen het getal kiezers door éen afgevaardigde vertegenwoordigd als volgt:

Partij	A.	B.	C.	D.
Aantal kiezers voor één afgev.	167	185	110	120

Deze getallen - in het Gids-artikel van den heer H. Onnen Sr. partijquotiënten geheeten - verhouden zich onderling gunstiger dan bij eenige wijze van verdeeling in dat artikel beschreven, noodzakelijkerwijze: immers de voorwaarde, dat de verhouding der partijquotiënten zoo na mogelijk gelijk 1 zij, is de voorwaarde, dat de verhouding van het aantal kiezers tot dat hunner vertegenwoordigers zoo na mogelijk voor alle partijen dezelfde zij, in anderen vorm gesteld, - is identiek met deze, dat het aantal zetels, dat eenige partij in vergelijking met een andere naar haar getalsterkte beoordeeld procentsgewijze te kort komt, zoo gering mogelijk zij.

Ter onderlinge vergelijking volgen hier in een tabel vereenigd de cijfers berekend volgens de door den heer Onnen beschreven stelsels en de boven bepaalde, door K.F. (methode der kleinste fout) aangeduid.

Stemmen	500	370	220	120	70
Zetels volgens { Gr.R.	3	2	1	1	1
Zetels volgens { D.' H.	4	3	1	0	0
Zetels volgens { S.L.	3	3	1	1	0
Zetels volgens { K.F.	3	2	2	1	0

Bepalen we de verdeeling der zetels nog voor een geval uit de praktijk gekozen: de Belgische verkiezingen van 1900. We laten daarbij de verdeeling in kiesdistrikten ter zijde, zoodat de sterkte der partijen over het gansche land gemeten inderdaad door het aantal harer vertegenwoordigers in de Kamer zoo goed mogelijk wordt uitgedrukt.

In totaal werden daarbij uitgebracht:

Katholieken	995066 stemmen,
Christen-dem.^n	55737 stemmen,
Liberalen	465264 stemmen,
Progressisten (Rad.^n).	33840 stemmen,
Socialisten	467350 stemmen,

[p. 324]

behalve de stemmen van eenige andere frakties, die om hun gering aantal buiten beschouwing kunnen blijven, en beschikten partijen te zamen over 152 zetels.

Groepeeren we de cijfers in onderstaande tabel.

	A.	B.	C.	D.	E.
Part.^n	Kath.^n	Chr.-dem.^n	Lib.^n	Prog.^n	Soc.^n
Stemmen	995066	55737	465264	33840	467350
Theor. verd.	74,98	4,20	35,06	2,55	35,21
Prakt. verd.	75	4	35	3	35
Proc. te-veel	+ 2/7498 ÷ 20/420 ÷ 6/3506 + 45/255 ÷ 21/3521

Partijen D en B zijn de resp. meest en minst begunstigde bij deze verdeeling en wel voor + 3/17 en ÷ 1/21, de fout is derhalve: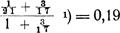

¹⁾ = 0,19 ruim.

Verdeelen we daarentegen de zetels als in de navolgende tabel:

Part.^n	A.	B.	C.	D.	E.
Theor. verd.	74,98	4,20	35,06	2,55	35,21
Prakt. verd.	74	5	35	3	35
Proc. te-veel	÷ 98/7498 + 180/420 ÷ 6/3506 + 45/255 ÷ 21/5321,

zoo wordt B de meest bevoorrechte met een grooter te-veel dan de meest bevoorrechte partij (D) bij de vorige verdeeling, het grootste tekort is thans echter aanzienlijk verminderd en wel tot 49/3749 (bij A) tegen 1/21 te voren, wellicht zal dus deze verdeeling gunstiger en derhalve de juiste blijken.

De fout wordt thans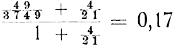 ruim, inderdaad kleiner dan te voren, de laatste verdeeling behoort dus te worden gevolgd.

De uitkomsten, die we in dit geval door toepassing der in het artikel van den heer Onnen verklaarde stelsels verkrijgen, wijken allen van de hier berekende af. Om het overzicht te vergemakkelijken, zijn ze met de laatste in onderstaande tabel samengevat:

1) Hoe men tot deze uitdrukking voor de fout komt, zal den lezer òf duidelijk òf onverschillig zijn.

[p. 325]

Stemmen...	995066	55737	465264	33840	467350
Zetels volgens {Gr.R.	75	4	35	3	35
Zetels volgens {D.'H.	76	4	35	2	35
Zetels volgens {S.L..	75	4	35	3	35
Zetels volgens {K.F.	74	5	35	3	35

De uitslag dier Belgische verkiezingen volgens het bestaande kiesstelsel was:

Partijen	Kat.^n	Chr.-dem.^n	Lib.^n	Progr.^n	Soc.^n
Zetels.	86	1	32	2	31,

zoodat de regeeringspartij met 86 leden tegen 66 van de andere partijen, de oppositie, in de meerderheid bleef, terwijl zij naar haar getalsterkte gerekend met 4 stemmen in de minderheid had behooren te zijn: 74-78 (K.F.). Bij de verdeeling van het land in provinciale kiesdistrikten ware met toepassing van het stelsel van evenredige vertegenwoordiging de uitslag geweest, dat de regeering eene meerderheid van 2 stemmen had verkregen: 77-75, - een voorbeeld, hoe de verdeeling in distrikten - ook bij een overigens juiste toepassing van het stelsel van evenredige vertegenwoordiging - tot gevolg hebben kan, dat de samenstelling der vertegenwoordiging een volkomen onjuist beeld geeft van de werkelijke partijverhoudingen: de meerderheid aan de zwakste partij kan verzekeren.

H.J.C.G. Eilbracht.

Naschrift.

Gaarne maak ik gebruik van de mij aangeboden gelegenheid, om naar aanleiding van de door den heer Eilbracht voorgestelde rekenwijze eene enkele opmerking te maken.

De schrijver acht het blijkbaar van zelf sprekend, dat, wanneer twee partijen van ongelijke sterkte hetzelfde breukdeel van een zetel te kort komen, de zwakkere partij meer benadeeld wordt, dan de sterkere. Dit geven echter de voorstanders van de methode der grootste resten niet toe, en de pennestrijd tusschen de heeren La Chesnais en Macquart in de Revue Rose is wel een bewijs, dat noch vertoogen, noch voorbeelden, noch wiskundige beschouwingen in staat zijn aan een dezer twee opvattingen de zege te bezorgen.

[p. 326]

Ik herinner nog eens aan het gezegde van Sainte Laguë: ‘c'est un argument de sentiment, et non pas de logique, qui nous conduit à adopter l'un des systèmes plutôt que l'autre’.

Overigens heeft de redeneering van den heer Eilbracht, dunkt mij, veel aantrekkelijks. Men overtuigt zich gemakkelijk, dat, wat de schrijver ‘de fout’ noemt, niets anders is, dan hetgeen de verhouding van het kleinste partijquotiënt tot het grootste minder is dan de eenheid, zoodat volgens hem die verdeeling der zetels voor de beste gehouden moet worden, waarbij de verhouding tusschen het grootste en het kleinste partijquotiënt het gunstigst is.

Volgens de methode-d'Hondt moet de verdeeling der zetels zoo plaats hebben, dat het partijquotiënt van de meest bevoorrechte partij grooter is, dan het voor elke andere partij worden zou, wanneer deze er één zetel bij kreeg; terwijl in het systeem van Sainte-Laguë de fouten in de kieskrachten tot een minimum worden teruggebracht.

Is de schrijver er in geslaagd, overtuigend aan te toonen, dat zijne zienswijze inderdaad juister is, dan die van d'Hondt en van Sainte-Laguë? Of moet men ook hier aan het ‘argument de sentiment’ een overwegenden invloed toekennen? Ik geloof het laatste. Men kan van elke methode het vóór en tegen zoo scherp mogelijk in het licht stellen; maar welke betrekkelijke waarde men aan de verschillende vóór- en nadeelen gehecht wil hebben, is een kwestie van persoonlijke opvatting.

Bij de rekenwijze van den heer Eilbracht staat tegenover het voordeel van de gunstige verhouding tusschen het grootste en het kleinste partijquotiënt o.a. het nadeel, dat hare toepassing een inspannenden en tijdroovenden arbeid eischt. Wie zich hiervan eenig denkbeeld wil vormen, beproeve eens 32 zetels volgens de theorie van den heer E. te verdeelen over 5 partijen met resp. 8000, 6000, 5050, 2950 en 1000 stemmen. Er is heel wat gecijfer noodig, om tot de slotsom te komen, dat ‘de fout’ niet kleiner gemaakt kan worden dan ⅓ en dat er drie verschillende verdeelingswijzen zijn, waarbij zij deze minimumwaarde heeft.

H. Onnen Sr.