De Gids. Jaargang 71

[p. 366]

Is tweemaal twee hetzelfde als vier... of is het iets anders?
Een populair-filozofische beschouwing.

Volgens een onzer groote geleerden op het gebied der filozofie ligt in een eenvoudige bewering als ‘tweemaal twee is vier’ een tegenstrijdigheid besloten, een raadselachtig onhelder iets, dat alleen langs den weg van diepgaande (liefst Hegeliaansche) filozofie tot klaarheid kan worden gebracht.

De groote vraag is namelijk deze: Is ‘tweemaal twee’ inderdaad gelijk aan of identiek met ‘vier’? 1^o. Zoo ja, hoe is het dan mogelijk, dat het eene zóó, het andere zùs benoemd wordt, dat men aan 't begin en aan 't slot van de bewering verschillende woorden gebruikt, die zonder twijfel ook moeten dienen om verschillende voorstellingen op te roepen, terwijl ieder ziet en voelt, dat die verschillende woorden en dus ook die verschillende voorstellingen op hun plaats absoluut noodzakelijk en onvermijdelijk zijn - hoe is dat mogelijk of verklaarbaar, wanneer werkelijk het eene hetzelfde, absoluut hetzelfde¹⁾ is als het andere? Hoe kan men in 't algemeen het eene ('t zij dan meer of minder gelijkstellend) met het andere vergelijken en er tegenover plaatsen als het eene en het andere eigenlijk en wezenlijk één en hetzelfde zijn? - 2^o. Zoo neen, wat wordt dan eigenlijk met de geheele bewering ‘tweemaal twee is vier’ bedoeld? Is het eenvoudig een onwaarheid of moeten we de ongerijmdheid aanvaarden, dat het tegelijk een waarheid en een onwaarheid is?

1) Over het begrip ‘hetzelfde’ in 't algemeen wensch ik elders uitvoerig te handelen.

[p. 367]

Reeds lange tijd, ik meen ongeveer acht jaar geleden, toen professor Bolland in een kort tijdschriftartikel dit raadsel opgaf, heeft mij de kwestie geïnteresseerd. Nu ik zie, dat Z.H. Gel. onlangs weer, in de openingsrede van zijn colleges te Amsterdam¹⁾, dezelfde vraag heeft opgeworpen en er onmiddellijk aan verbonden deze tweede vraag: ‘Hoe kan men op verschillende wijze hetzelfde denken en zeggen?’, in welke vraag volgens hem het thema van Hegel's filozofie gelegen is, nu wil ik trachten op de eerstgenoemde vraag een afdoend antwoord te geven, een antwoord zonder drukkende diepzinnigheid, maar dat aanspraak maakt op duidelijkheid, beslistheid en waarheid.

Volgens mijn meening ligt er in de bewering ‘tweemaal twee is vier’ voor een gewoon denkend mensch geen mysterie en kan er op de vraag of tweemaal twee identiek is met vier wel degelijk en beslist een ondubbelzinnig antwoord gegeven worden. Dat antwoord is namelijk: Neen, ‘tweemaal twee’ is niet hetzelfde als ‘vier’; het is iets heel anders.

Ik zal hier in teekening brengen ‘tweemaal twee’:



En nu zal ik in teekening brengen ‘vier’: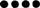

Is dat hetzelfde of iets anders? Licht zal men er toe komen hierop te antwoorden: ‘'t Is hetzelfde.... op een scheiding of een leege ruimte na, die niets is, is 't hetzelfde, - 't is iets anders in schijn, door een bizondere schikking of groepeering, die niets wezenlijks is - maar in werkelijkheid is 't hetzelfde, absoluut en volkomen hetzelfde.’

Deze oordeelvelling, ik durf het als gewoon denkend mensch met stelligheid verklaren, is onwetenschappelijk, oppervlakkig en onwaar. De scheiding of de leege ruimte is namelijk niet eenvoudig niets; de schikking of groepeering van deelen of leden is een factor, een meetellend iets in 't geheel der gesteldheid van een ding. ‘'t Zelfde’ anders geschikt of gegroepeerd is... niet hetzelfde. ‘'t Zelfde’ mèt een scheiding of ruimte of zònder die scheiding of leege ruimte zijn twee en niet één.

Tot overtuiging van hen, die 't in 't algemeen hiermee niet

1) Uitgegeven bij A.H. Adriani te Leiden.

[p. 368]

eens mochten zijn, heb ik hier een paar kolossale argumenten, enkele weinige uit duizend, die mogelijk zijn.

Stellende, dat de schikking of de groepeering geen factor, niet iets meetellends is, dan is... zóóveel pond verfstoffen van die en die soorten gelijk aan alle schilderijen van het Rijksmuseum te Amsterdam.

Stellende, dat de schikking of de groepeering geen factor, niet iets meetellends is, dan zijn... zoo of zooveel gamma's, door een eerstbeginnend muziekleerling afgetrommeld, gelijk aan de mooiste symfonie van Beethoven, vertolkt door de allerkranigste virtuoos.

Stellende, dat de schikking of groepeering... enz., dan is... het Engelsche, Duitsche, Italiaansche woordenboek gelijk aan Milton's Paradise lost, Göthe's Faust en Dante's Inferno.

Dit zijn argumenten op 't gebied der Kunst. Maar ook op 't gebied der ‘exacte wetenschappen’ zijn de bewijzen gemakkelijk te vinden. In de meetkunde kan men uit twee gegevene driehoeken, door ze op verschillende wijze met elkaar te vereenigen, geheel uiteenloopende figuren doen ontstaan. De scheikunde maakt ons bekend met in tal van opzichten verschillende substantiën, die elk uit volkomen gelijke aantallen atomen van volkomen dezelfde elementen (maar op verschillende wijze tot molekulen gegroepeerd) zijn opgebouwd.

Stellende, dat de schikking of groepeering niets afdoet, is... de chaos gelijk aan de meest volmaakte wereldorde.

Door de bovengegevene redeneering meen ik al vast aan de eene kant van mijn vaarwater de Scylla, het gevaar aan de gelijkstelling der beide zaken verbonden, gelukkig te zijn ontzeild. Maar nu de Charybdis, het gevaar, dat verbonden is aan de niet-gelijkstelling der beide. - Toegegeven, dat ‘tweemaal twee’ niet hetzelfde is als ‘vier’, maar iets anders... wat bedoelen we dan in 's Hemels naam met de heele bewering ‘tweemaal twee is vier’? Deze vraag eischt een eenigszins uitvoeriger antwoord, maar mag toch (naar mijn persoonlijke meening) niet onder de werkelijk moeielijke vragen gerekend worden.

Heel lang wordt het niet. Ik begin mijn redeneering als volgt. Bij de normaal-natuurlijke zinnelijke waarneming en bij de normaalnatuurlijke vorming van voorstellingen is de algemeene toestand deze, dat alle verschillende eigenschappen van alle verschillende

[p. 369]

dingen of zaken tegelijk en zonder schifting hun indrukken bijbrengen en zoodoende op ieder gegeven oogenblik tot de bontste verscheidenheid van voorstellingen leiden. - Dat is de normaalnatuurlijke toestand bij de zinnelijke waarneming en de vorming van voorstellingen... maar nu is er in het menschenleven iets, dat redeneering heet. Redeneering nu is een eigenaardige combinatie van voorstellingen, waarbij tegelijkertijd een schifting plaats heeft, die van dien aard is, dat van de verschillende eigenschappen der dingen of zaken telkens een groot aantal meer of minder opzettelijk wordt weggedacht of voorbijgezien, als niet bestaand achterwege gelaten. Bij de normale redeneering van de gewoonnatuurlijke, onwetenschappelijke mensch is de wegdenking enz. ongeregeld en oogenblikkelijk, d.w.z. een en dezelfde soort van wegdenking of voorbijziening geldt alleen voor één bepaalde redeneering bij een bepaalde gelegenheid en is daarna verdwenen. - Intusschen... er zijn abnormale uitzonderingsmenschen, die men geleerden of wijsgeeren of meer in 't algemeen wetenschappelijke menschen noemt. Wat is een geleerde of wijsgeer, wat is een wetenschappelijk mensch? Antwoord dit: Het is een meneer, die zich met zeer veel moeite heeft aangewend in bepaalde gevallen geregeld, in massa zaken of toestanden of eigenschappen van die en die bepaalde soorten niet te zien, niet te hooren, niet te voelen, als niet bestaand te laten liggen, in weerwil van de indrukken die hem door de zinnen worden geleverd. - Deze heeren hebben den grond gelegd tot iets, wat men wetenschap noemt. Wetenschap is geregelde redeneering, d.w.z. voorstellingen verbinding met standvastige, gereglementeerde wegdenkingen en voorbijzieningen. - De wetenschap zoekt algemeene, bovenzinnelijke waarheid door geregelde wegdenking van bizonderheden uit de zinnelijke waarnemingswereld. Het verschillende karakter van verschillende wetenschappen bestaat hierin, dat elk harer bij het wegdenken van zaken op een eigene afzonderlijke manier te werk gaat. Verschillende wetenschappen denken niet dezelfde soorten van zaken en bepaaldelijk ook niet evenveel verschillende soorten van zaken weg. - De kultuurgeschiedenis of de aardrijkskunde denken minder weg dan de biologische dier- en plantkunde, deze minder dan de anatomie, deze minder dan de physika, chemie en mechanika, deze minder dan de meetkunde en deze laatste minder dan de leer der getallen.

[p. 370]

Laten we ons nu maar eens tot de achterste of meestwegdenkende wetenschappen bepalen. De meetkunde denkt van de geheele zinnelijke wereld alles weg behalve ruimte-uitgebreidheid en vorm, - de getallenleer denkt ook deze inzoover weg, dat er niets van overblijft dan lengte-uitgebreidheden van verschillende uit volkomen eigenschaplooze stippen bestaande stiplijnen, welke lengte-uitgebreidheden men getallen noemt. - De meetkunde wil en kan niet anders doen dan uit-, in-, af- en rondmeten; de getallenleer niet anders dan tellen, voorttellen, terugtellen enz. onder allerlei verschillende omstandigheden

En nu kom ik terug tot de bewering: ‘tweemaal twee is vier’. Wat wordt daarmee bedoeld? Naar mijn meening is het dit: ‘tweemaal twee’ en ‘vier’ zijn verschillende voorstellingen, genomen uit de beschouwingen van redeneerende, maar niet wetenschappelijke menschen, dus van menschen, die uit de wereld der zinnelijke waarneming ongeregeld wegdenken. - De bewering ‘tweemaal twee is vier’ echter is geen bewering uit diezelfde beschouwingen; het is een bewering van de wetenschap der getallenleer. En die bewering wil niets anders zeggen dan dit, dat bij toepassing van die eigenaardige, in wegdenken van bizonderheden bestaande voorstellingenschifting, die speciaal aan de getallenleer eigen is, dat bij toepassing daarvan ‘tweemaal twee’ op 't zelfde neerkomt, d.w.z. precies even goed is en precies dezelfde diensten kan doen als ‘vier’.

Om dit goed te begrijpen kan het zijn nut hebben eens terug te keeren tot onze vroeger gegevene opmerkingen aangaande het Rijksmuseum, de symfonieën van Beethoven enz. Wat we daar debiteerden waren zeker wel buitengewoon grove onwaarheden. Maar zeer belangrijk is het op te merken, dat ook de daar tegenover elkander geplaatste zaken op 't zelfde neerkomen, zonder schade in elkanders plaats kunnen dienst doen... als men maar de rechte wetenschap daarvoor uitzoekt, d.w.z. die wetenschap, die zich juist die bepaalde blind-, of doof- of gevoelloosheid heeft aangeschaft, waardoor tusschen de daar tegenover elkander staande zaken alle onderscheid als geheel onbelangrijk verdwijnt. Zooveel pond verf is niet gelijk aan de schilderijen van 't museum... maar de scheikunde zegt: ‘Voor mij maakt het verschil niets uit.’

[p. 371]

Zooveel gamma's zijn niet gelijk aan de symfonie, maar de physika zegt: ‘Ik heb aan 't eene precies even veel als aan het andere.’

Ligt er nu, vraag ik ten slotte, ligt er nu een ondoorgrondelijk raadsel of mysterie in het feit, dat van twee of meer niet aan elkander gelijke zaken onder zekere omstandigheden het eene in plaats van het andere dienst kan doen? Zoo ja, dan strekt zich dit raadselachtige uit over tal van gelijkstellingen uit het dagelijksch leven, waarin waarschijnlijk zelfs prof. Bolland nooit iets raadselachtigs heeft gezien. Een leeuw ‘is 't zelfde’ als een tijger... in zoover, dat de ontmoeting met ieder van beide hetzelfde gevaar aanbrengt van te worden opgepeuzeld. Veenendaal - De Klomp ‘is 't zelfde’ als Ede - Wageningen... inzoover, dat je voor allebei die stations te Utrecht moet overstappen. - Een broodmes, een hartsvanger, een vouwbeen en een vizitekaartje ‘zijn 't zelfde’... inzoover, dat alle vier bij het opensnijden van een boek kunnen dienst doen. - Gebruik van morfinepillen ‘is 't zelfde’ als lektuur van sommige minder onderhoudende geschriften... inzoover als men van beide gaat slapen, enz. enz.

Het feit, dat ‘tweemaal twee’ niet hetzelfde is als ‘vier’ wil ik tot besluit nog door enkele duidelijke voorbeelden toelichten.

Hoeveel vingers heeft het menschelijk lichaama 't Juiste antwoord op deze vraag is stellig niet ‘twintig’, maar wel ‘viermaal vijf’, of liever nog ‘tweemaal tweemaal-vijf’. Twintig vingers heeft een mensch alleen bij een heel bizondere, eenzijdige beschouwing. B.v. bij de Kannibalen (zoo heb ik me laten vertellen) geeft men aan het opperhoofd van de stam de afgehakte vingers en teenen van een buitgemaakte Engelsche tourist gebraden op een schotel... dat zijn goed geteld twintig smakelijke kluifjes.

Dat verder ‘viermaal drie spiegeleieren’ iets heel anders is dan ‘driemaal vier spiegeleieren’, ‘vijfmaal zes grein kinine’ iets heel anders dan ‘zesmaal vijf grein kinine’ en ‘tweemaal drie schelknopdrukken’ iets heel anders dan ‘driemaal twee schelknopdrukken’, zal wel respectievelijk door alle kellners, alle apothekers en alle portiers zonder eenig bezwaar worden toegegeven.

J.M. Hoogvliet.