De Gids. Jaargang 35

[p. 414]

Aangeboren waarnemingsvormen.

II. Ruimte en tijd.

Bij onze voorafgaande beschouwing is ons gebleken, dat het vraagstuk van het causaalverband zich nog altijd bevindt ter plaatse, waar Hume en Kant het hebben gelaten. De eene helft der empirische wijsgeeren sluit zich onverholen bij Hume aan; de andere helft ontkent op onhoudbare gronden de verdienste, die er in zijne vraag ligt, en streeft er met alle krachten naar, de wetenschap van het menschelijk kenvermogen terug te voeren naar het lagere standpunt, waarop zij voor Hume stond. Wij zagen verder, dat men ongelijk heeft in de bewering, dat Hume's theorie zou kunnen worden wederlegd door zoo eenvoudige opmerkingen, als de waarheid, dat niet alle opvolgen een gevolg zijn is; eene waarheid, die Hume ongetwijfeld alleen daarom niet bespreekt, omdat hij niet kon verwachten, dat men hem zou bestrijden met zoo weinig beteekenende argumenten. De schimmen van Kant en Schopenhauer mogen mij vergiffenis schenken voor dit oordeel, dat ik niet nalaten kan over eene beschouwing te vellen, die ook zij gesteund hebben door hun gezag, dat door mij zoo hoog wordt vereerd. In de volgende bladzijden wensch ik een meer uitvoerig en beter toegelicht overzicht te geven van de oplossing van Hume's vraagstuk, die gedeeltelijk door Kant, gedeeltelijk door Schopenhauer, is gegeven. De toelichting van die oplossing moet toch zeer onvolledig en weinig overtuigend blijven, zoolang men slechts vraagt naar den oorsprong van het causaalverband,

[p. 415]

waarbij wij ons tot nu toe, althans in hoofdzaak, hebben moeten bepalen. Eerst als men de beide andere waarnemingsvormen, ruimte en tijd, opneemt in den kring van het onderzoek, kan de juistheid van de leer van Kant duidelijk worden voor personen, die niet reeds tamelijk wel bekend zijn met zijne philosophie. Het hoofdstuk van zijne Kritik, dat over tijd en ruimte handelt, is door hem geschreven op zoo uitstekende wijze, dat men zou kunnen volstaan met naar dat hoofdstuk te verwijzen, indien men verzekerd kon zijn, dat ieder de Kritik der reinen Vernunft bij de hand had. Daar echter deze onderstelling niet tot de veroorloofde behoort, en men veeleer zou kunnen vermoeden, dat de meeste belangstellende lezers wel bekend zijn met de argumenten tegen de leer van Kant, maar niet met de geschriften van Kant zelf, kan ik mij niet onttrekken aan de minder aangename taak, om de hoofdstelling van zijne Transcendentale Aesthetik uiteen te zetten in eene beschouwing, die zeker veel minder treffend zal zijn dan zijne eigene woorden.

Al onze kennis, zoowel die van het menschelijk individu, als die van het menschelijk geslacht, begint met de ervaring. Maar de mensch bepaalt zich niet tot de besluiten, waartoe zijne ervaring hem gemachtigd heeft. Ten aanzien van sommige deelen zijner kennis twijfelt hij niet aan zijne bevoegdheid tot beweringen, die de ervaring hem nimmer kan hebben aan de hand gedaan. Aan sommige soorten van waarheden kent hij algemeene geldigheid toe en noodzakelijkheid, dat is ondenkbaarheid van hun tegendeel. Dat hij deze eigenschappen toekent aan zijne logische axioma's en aan zijne analytische oordeelen, kan niet verwonderlijk worden genoemd. Zijne drie logische axioma's zijn toch blijkbaar de wetten, die zijne rede moet volgen bij de abstractie van hare afgetrokken begrippen uit de gegevens der ervaring. Zijne analytische oordeelen zijn niets anders dan de onderlinge vergelijking en rangschikking van die abstracte begrippen, die hij zelf gemaakt heeft en volkomen kent. Het is natuurlijk, dat hij bij die vergelijking en rangschikking met apodictische zekerheid spreekt. Maar wel mag het zonderling heeten, dat hij drie soorten van synthetische oordeelen als even algemeen en noodzakelijk beschouwt. Die drie soorten van oordeelen zijn: a. Iedere verandering heeft eene oorzaak, een oordeel, dat als geheel ongelijksoortig met de andere, op zich zelve eene geheele klasse vormt, b. som-

[p. 416]

mige zijner oordeelen over den tijd, en al de stellingen van rekenkunde en algebra, die gezamenlijk op de aanschouwing van den tijd berusten, c. sommige oordeelen over de ruimte, en al de stellingen der meetkunde, die gezamenlijk berusten op de aanschouwing der ruimte.

De eerste klasse der synthetische oordeelen, die door ons als noodwendig en algemeen worden beschouwd, bevat dus niets anders dan de wet van oorzaak en gevolg, die wij voor ons doel het best kunnen uitdrukken door de stelling, dat bij gelijke omstandigheden gelijke verschijnselen ontstaan. Er is niet veel nadenken toe noodig om in te zien, dat deze formule identisch is met de zooeven genoemde: Iedere verandering heeft eene oorzaak. Zij legt alleen meer nadruk op het feit, dat een verschijnsel, eene verandering, nimmer wordt voortgebracht door eene enkele verandering, maar altijd door een toestand, die ten gevolge van een aantal veranderingen geworden is, eene som van omstandigheden, van welke wij volgens onze onnauwkeurige spreekwijze nu eens de laatst gewordene, dan weder de meest in het oog vallende, de oorzaak noemen. Nu gebeurt het dikwijls dat iemand twijfelt aan de waarheid van deze wet der causaliteit, wanneer zij hem in abstracten vorm wordt voorgelegd. Daar echter niemand aan de geldigheid van dezelfde wet twijfelt bij hare toepassing op ieder bijzonder geval, zoo is het alleen aan de onvolkomenheid van het vermogen om te abstraheeren toe te schrijven, dat zoo vele menschen aarzelen in de erkenning van de wet der causaliteit in het algemeen. Buiten haar is er geen enkele stelling over de stoffelijke of over de geestelijke wereld, die wij voor algemeen en noodwendig aanzien. Dat twee stoffelijke punten elkander aantrekken in rechte reden van hunne massa's en in omgekeerde reden van het vierkant hunner afstanden, is wellicht de stelling, die na de wet der causaliteit de meest algemeene is. Toch heeft zelfs deze stelling niet de eigenschap van algemeen geldig en noodzakelijk te zijn. Het heeft nimmer aan personen ontbroken, die beweren, dat de werking der gravitatie eigenlijk zou moeten uitgedrukt worden door eene andere functie van den afstand, ten einde het mogelijk te maken ook de moleculaire werkingen door dezelfde formule uit te drukken. En anderen hebben het niet overbodig geacht te onderzoeken, of de wet der gravitatie ook geldt buiten de grenzen van het zonnestelsel. Aan de geldigheid van de wet der causaliteit daaren-

[p. 417]

tegen twijfelt in concreto niemand. Men zou eene dwaasheid begaan, als men de juistheid van deze wet experimenteel wilde onderzoeken, daar toch geen enkel experiment waarde kan hebben, als men niet mag aannemen, dat de natuur aan zich zelve gelijk blijft, dat dus gelijke oorzaken gelijke gevolgen hebben.

In de tweede plaats kennen wij algemeenheid en noodzakelijkheid toe aan sommige oordeelen, die betrekking hebben op den tijd, dat is, volgens Kant, op den waarnemingsvorm, waarin zich de verschijnselen der innerlijke waarneming voordoen. Wij kunnen niet nalaten te meenen, dat sommige onzer oordeelen over den tijd algemeen en noodzakelijk zijn, en kennen dezelfde algemeenheid en noodzakelijkheid toe aan al de stellingen der rekenkunde en der algebra, wetenschappen, die, volgens Kant, op onze aanschouwing van den tijdvorm berusten. Men moet deze aanschouwing van den innerlijken zin waarmede Kant hetzelfde bedoeld heeft, wat men later innerlijke waarneming genoemd heeft, niet met de gewone, zintuiglijke, uitwendige aanschouwing verwarren. De keuze van den naam aanschouwing (Anschauung) voor de wijze, waarop wij ons bewust worden van de waarheden, die ons de innerlijke waarneming levert, heeft dikwijls aanleiding gegeven tot misverstand, daar de naam aanschouwing als van zelve aan eene zichtbare gedaante doet denken. Zoo hebben dan ook velen gemeend, dat Kant met de namen aanschouwing en zinnelijkheid (Sinnlichkeit) niets anders bedoelde dan de zintuiglijke waarneming en het vermogen daartoe. De spreekwijze van Kant wordt echter gerechtvaardigd, als men bedenkt, dat er in geen enkele taal een woord te vinden is ter benoeming van de intuïtieve voorstellingen van de innerlijke waarneming, dat niet tevens gebruikt wordt voor de abstracte voorstellingen of begrippen. Toch is de werkzaamheid van onzen geest bij beiden geheel verschillend. De voorstellingen van den inwendigen zin, die wij als een individueel gevoel van vreugde, van haat, van verachting, waarnemen, verschillen geheel en al van de abstracte begrippen scherpzinnigheid, laagheid, gebeurtenis. Om slechts een enkel verschil aan te wijzen: de laatsten bewegen ons zeker lang zoo krachtig niet, wanneer zij in den loop van onze beschouwingen in ons bewustzijn treden, als de eerstgenoemde individueele voorstellingen, of, als men verkiest, gewaarwordingen van den inwendigen zin. Zij stemmen echter in dit op-

[p. 418]

zicht overeen, dat zij zich geen van beiden aan ons kenvermogen voordoen als eene zichtbare gedaante, in een bepaalden vorm. Ook de abstracte begrippen, wier voorwerpen tot de uitwendige wereld behooren, hebben dezelfde eigenschap. Al kunnen wij ons toch gemakkelijk bij het denken van deze begrippen een der intuïtieve aanschouwingen voorstellen, die onder het begrip behooren, zoo kunnen wij het toch even goed nalaten. Wij kunnen uren lang over een mensch redeneeren zonder dat zich zijne uitwendige, zichtbare gedaante aan ons voorstellingsvermogen vertoont. Terecht beschouwt nu Kant de waarneming der individueele gewaarwordingen van den inwendigen zin als iets geheel anders dan de waarneming der begrippen. De eerste noemt hij bij gebrek aan een beter woord aanschouwing, maar de aanschouwing van den innerlijken zin; de tweede noemt hij het denken.

De voorstellingen van den inwendigen zin doen zich aan ons voor als aanwezig in den tijd, die van den uitwendigen zin als aanwezig in tijd en ruimte. Het denkbeeld, dat wij ons van den tijd vormen is nu van geheel anderen aard dan onze abstracte begrippen. Willen wij van een begrip komen tot een der aanschouwelijke voorstellingen, of tot een der lagere begrippen, die in den omvang van het eerste begrip behooren, dan moeten wij den inhoud van dat begrip niet verdeelen, maar aan dien inhoud eenige bepaling toevoegen. Uit het begrip gewerveld dier geraken wij bijv. tot het lagere begrip vogel, door bij den inhoud van het eerste de praedicaten warmbloedig en eierleggend te voegen. Om daarentegen het denkbeeld van een bepaalden, individueelen tijd te verkrijgen, moeten wij niet bij het denkbeeld ‘tijd in het algemeen’ eene bepaling toevoegen, maar wij moeten dat denkbeeld naar beide richtingen beperken, zoowel naar voren als naar achteren. Terwijl het algemeene begrip eene abstractie is, die uit de individueele voorwerpen verkregen wordt door sommige hunner bepalende omstandigheden te laten vallen, is daarentegen de tijd, de geheele tijd, de som der afzonderlijke, individueele tijden. Abstraheeren wil bij onze beschouwing van een individueelen tijd van zijn eenig kenmerkend verschil met andere individueele tijden, zijne lengte, dan houden wij geenszins een abstract begrip ‘tijd in het algemeen’ maar eenvoudig niets over. Ieder, die het wil beproeven zal bevinden, dat wanneer hij uit zijne voorstelling van een bepaalden duur, eene minuut

[p. 419]

bijv., het denkbeeld van hare bepaalde lengte wil laten vervallen, hij òf niets overhoudt, òf wel bezig is zich een anderen begrensden tijd voor te stellen. Om deze redenen is het volgens Kant geheel verkeerd den tijd als een begrip te beschouwen. Zooals de ruimte de vorm is, waarin zich alle voorstellingen van den uitwendigen zin voordoen, zoo is de tijd de vorm der voorstellingen van den inwendigen zin. Over den tijd bezitten wij nu eenige algemeen geldige, noodwendige waarheden. Wij meenen zeker te weten, dat verschillende tijden niet tegelijk kunnen zijn, maar alleen na elkander. Ook kunnen wij het niet over ons verkrijgen te twijfelen aan de waarheid, dat twee verschillende tijden niet gescheiden kunnen zijn door iets, dat zelf geen tijd is, en meenen wij op dezen grond, dat de tijd continue is en tot in het oneindige deelbaar. Wij kunnen ons niet voorstellen, dat de tijd een begin zou hebben gehad, of ooit een einde zou nemen.

Op de aanschouwing van den inwendigen zin berust de rekenkunde. Deze stelling, die thans weder paradox kan schijnen, wordt gemakkelijk ingezien, wanneer men bedenkt, dat geen getal ons bewust kan worden, anders dan door successie. Zoolang wij ons een getal duidelijk voorstellen, zoolang wij ons daarvan volkomen bewust worden, stellen wij ons de opvolging der eenheden voor, die dit getal uitmaken. Twee omstandigheden zijn er, die het inzicht in deze waarheid eenigermate bemoeilijken. De eerste omstandigheid is de volgende. Ons bewonderenswaardig tientallig stelsel maakt het ons mogelijk een groot getal even goed te gebruiken, alsof wij er eene heldere voorstelling van hadden. Zoo kunnen wij even goed 27 en 24 bij elkander optellen als 2 en 3. Dat echter onze voorstelling van die groote getallen toch niet helder is, zal ieder bemerken, die beproeven wil zich 27 knikkers of 27 centen of 27 punten voor te stellen. Een, twee, drie of vier eenheden kan hij zich gemakkelijk voorstellen, maar bij de hoogere cijfers blijkt de zwakheid van zijn voorstellingsvermogen en de noodzakelijkheid van het talstelsel ten duidelijkste. Zelfs zullen de meeste menschen ontdekken, waarom sommige volken het slechts tot een vijftallig stelsel hebben kunnen brengen; het vereischt reeds eene groote inspanning zich zeven eenheden tegelijk voor te stellen. Bij het nemen van de proef zal ieder tevens bemerken, dat wij ons onder het woord ‘tegelijk voorstellen’ volstrekt niet moeten denken aan werkelijke

[p. 420]

gelijktijdigheid, maar dat zelfs onze voorstelling van het getal twee bestaat in de voorstelling van eene opvolging. Wij zeggen echter nog, dat wij ons zeven eenheden tegelijk voorstellen, als wij in staat zijn zonder in de war te raken de achtereenvolgende voorstelling der zeven eenheden met groote snelheid eenige malen te herhalen.

De tweede omstandigheid, die ons beletten kan de waarheid in te zien van de leer, dat de rekenkunde berust op de aanschouwing van den tijdvorm, is deze. Wij kunnen bij onze voorstelling van getallen veel beter onze eenheden kiezen uit de uitwendige wereld dan uit de inwendige. Als wij voor onze eenheid een knikker nemen, hebben wij veel minder moeite om tot de duidelijke voorstelling van het getal 6 te komen, dan het geval zou zijn, als wij een bepaald gevoel van onlust voor onze eenheid kozen. Wij nemen dan ook altijd een zichtbaar voorwerp als eenheid, wanneer wij ons een getal willen voorstellen. Maar de zichtbaarheid van onze eenheid, het feit dat zij ruimte inneemt, doet niets ter zake. Wij kunnen die ruimte zoo groot en zoo klein nemen, als wij willen. Alleen de opvolging der gelijksoortige eenheden geeft ons de voorstelling van het getal. Deze opvolging geschiedt nu in ons kenvermogen natuurlijk uitsluitend in den vorm van den tijd, niet in dien der ruimte, waarin geen opvolging mogelijk is. Bij kleinere getallen, 3 en 4 bijvoorb., zou men kunnen twijfelen of wij ons niet onmiddellijk het getal kunnen voorstellen in de ruimte, zoodat wij ons bij het getal 3 de drie eenheden niet opvolgend maar gelijktijdig voorstellen. Bij grootere getallen blijkt echter de noodzakelijkheid van eene successie zeer duidelijk, en ook bij de kleinere bemerken wij bij eene meer nauwkeurige innerlijke waarneming, dat onze voorstelling zelfs van het getal twee, slechts mogelijk is als de voorstelling van eene opvolving, dus in den vorm van den tijd.

Alle stellingen van rekenkunde en algebra hebben het karakter van noodwendigheid en algemeenheid. Wij weten niet alleen, dat 3 + 2 = 5 en (a + b)² = a² + 2ab + b²; maar wij weten ook, dat het altijd zoo zijn zal, en wij kunnen ons onmogelijk het tegendeel denken. Uit begrippen laten zich deze waarheden niet bewijzen; zoolang men niets anders beschouwt dan het abstracte begrip drie en het abstracte begrip twee, kan men onmogelijk de eerste stelling inzien. Om die stelling te

[p. 421]

bewijzen, moet men die begrippen construeeren; men stelt zich drie punten en twee punten of drie knikkers en twee knikkers voor, en ziet, wat hunne vereeniging voortbrengt. Om de waarheid in te zien van alle stellingen der rekenkunde nemen wij proeven met onze geconstrueerde begrippen; het doet bij die proeven niets ter zake of wij ons de abstracte begrippen der getallen aanschouwelijk maken door werkelijke dingen, of wel door voorstellingen van deze werkelijke dingen. De uit komst van zoodanige proefneming beschouwen wij als eene noodzakelijke en algemeene waarheid.

De derde klasse van de synthetische oordeelen, die wij als algemeen en noodzakelijk beschouwen, bevat eenige onzer oordeelen over de ruimte, en de stellingen der meetkunde, die gezamenlijk op de aanschouwing der ruimte berusten. Wij meenen bijv. met zekerheid te weten, dat verschillende ruimten niet na elkander zijn, maar wel te gelijker tijd. Wij kunnen onmogelijk twijfelen aan de waarheid, dat twee ruimten niet gescheiden kunnen zijn door iets, dat geen ruimte is, en stellen ons daarom de ruimte voor als continue en tot in het oneindige deelbaar. Wij kunnen ons geen begrensde ruimte voorstellen, buiten welke geen ruimte meer zijn zou. Wij weten met zekerheid, dat de ruimte drie afmetingen heeft. Al deze stellingen zijn algemeen en noodzakelijk; algemeen, omdat wij er niet aan twijfelen, dat zij overal en ten allen tijde zullen gelden, noodzakelijk, omdat het ons onmogelijk is hun tegendeel te denken. Wij vermogen wel in woorden te verklaren, dat voor andere wezens, dan wij zijn, de ruimte misschien zeven afmetingen zou kunnen hebben; maar wij zijn geheel buiten staat om ons eenig denkbeeld te maken van de wetenschap van dergelijke wezens. Nu ligt het verschil tusschen eene denkbare en eene ondenkbare woordverbinding hierin, dat wij bij de eerste in staat zijn de aanschouwelijke voorstellingen te vereenigen, die in abstracto door de begrippen worden uitgedrukt, terwijl deze vereeniging bij de tweede onmogelijk is. Zoo zijn de woordverbindingen een gouden berg van 1000 meters hoogte, eene deugdzame koe, denkbare begrippen, wier voorwerpen niet in de werkelijkheid worden aangetroffen. Daarentegen zijn een ongewerveld gewerveld dier, een vierkante cirkel ondenkbare woordverbindingen. Tot dezelfde afdeeling behoort nu ook eene ruimte, die zeven afmetingen zou hebben; zij bevat een onderwerp en een praedicaat, die elkander

[p. 422]

opheffen. Alleen blijkt de tegenstrijdigheid eerst, wanneer men de begrippen wil construeeren¹.

De ruimte is geen begrip, evenmin als de tijd een begrip is. Want, om van de ruimte, in het algemeen genomen, te komen tot de individueele ruimten, moet men niet aan de ruimte, in het algemeen genomen, eenige nadere bepaling toevoegen, maar men moet die ruimte in drie richtingen beperken. Ons denkbeeld van ruimte is dus niet verkregen door abstractie uit de individueele ruimten; de ruimte in het algemeen is het geheel der individueele ruimten. Zij is de waarnemingsvorm van den uitwendigen zin. Onze algemeen-geldige en noodzakelijke stellingen over tijd en ruimte leiden ons toch met zekerheid tot de bewering, dat tijd en ruimte niets anders zijn dan vormen, waarin het kenvermogen de stof opneemt, die ons door het niet-ik wordt geleverd. Want, waren zij iets anders, hoe zouden wij dan bij mogelijkheid zoo apodictisch kunnen spreken over hunne eigenschappen, zelfs over eigenschappen, die de ervaring ons nimmer kan aantoonen, zooals de oneindige deelbaarheid en de continuïteit? Zijn zij de aangeboren vormen van ons waarnemingsvermogen, dan is het duidelijk, dat onze oordeelen over deze vormen dezelfde absolute zekerheid hebben als onze logische axioma's, die ontwijfelbaar zijn, omdat onze rede niet bij machte is in strijd met hare aangeboren denkwetten te denken. En als ruimte en tijd geen waarnemingsvormen zijn, wat zijn zij dan wel? Individueele voorstellingen zijn zij zeker niet, want wij nemen wel bepaalde tijden en bepaalde ruimten waar, maar nimmer den tijd of de ruimte. Abstracte begrippen zijn zij, blijkens het voorgaande; nog veel minder. Nu bevat ons bewustzijn niets anders dan individueele voorstellingen, begrippen en de verschillende combinatiën van voorstellingen onderling, van voorstellingen en begrippen, van begrippen onderling. Niemand zal tijd en ruimte voor een van deze com-

1 Eenige weinige dingen, die men zich niet kan voorstellen, moeten als denkbaar worden erkend. Zij zijn de hypothetische vermogens van het nietik, dat in onze voorstellingen wordt voorgesteld, en de hypothetische vermogens van het ik, de krachten en de waarnemingsvormen. Hoogstens kan men zich aanschouwelijke voorstellingen ontwerpen, die met de genoemde dingen eene verwijderde overeenkomst hebben. Zoo is bijv. de gewaarwording, die ons de samentrekking der spieren geeft, voor ons een beeld van de kracht, de gedachte, dat de luchttrillingen als geluid worden waargenomen, een beeld, waardoor wij onze opvatting van het niet-ik in de vormen van ruimte en tijd tot op zekere hoogte aanschouwelijk kunnen makeu.

[p. 423]

binaties, voor een oordeel of voor eene redeneering, aanzien. Bepaalde ruimten en bepaalde tijden komen als individueele voorstellingen voor, maar leiden ons niet, zoo als alle andere individueele voorstellingen doen kunnen, tot abstracte begrippen van tijd en ruimte. Ter verklaring van dit vreemde feit blijft er geen andere onderstelling over dan de meening van Kant. Die bepaalde plaats en die bepaalde tijd, waarin wij onze zinnelijke voorstellingen waarnemen, zij hebben niets te maken met het niet-ik, maar zij zijn niets anders dan de beperking van onze algemeene voorstelling van ruimte en tijd binnen zekere grenzen, eene beperking die op voor ons onbekende wijze wordt teweeggebracht door den aard van het niet-ik. Is ons kenvermogen reeds voor het ontstaan der ervaring met de vatbaarheid voorzien om zelf de aanschouwing van ruimte en tijd voort te brengen, dan laat het zich verklaren, waarom deze twee denkbeelden eene zoo geheel eigen plaats in ons kenvermogen innemen en met geen ander element daarvan kunnen vergeleken worden. Dat onze oordeelen over tijd en ruimte algemeen en noodzakelijk zijn, is, naar de leer van Kant, volkomen natuurlijk; wij hebben in die oordeelen toch niet te maken met iets, dat van ons afhankelijk is, maar alleen met de subjectieve, aangeboren vormen van onze waarneming.

Op de aanschouwing van den uitwendigen zin berust de meetkunde, de wetenschap van de ruimte. Al hare stellingen zijn toepasselijk op de stoffelijke voorwerpen, omdat deze allen niets anders zijn dan voorstellingen, die in den vorm der ruimte zijn opgenomen. Geheel valsch is de meening, dat de stellingen der meetkunde zouden berusten op de waarneming der uitwendige, zichtbare wereld. Dat de kortste weg om van een punt tot een ander punt te geraken, altijd en overal zal gegeven zijn door de rechte lijn, die deze twee punten verbindt; dat twee rechte lijnen elkander slechts eenmaal kunnen ontmoeten; dergelijke waarheden liggen geheel buiten het bereik van onze beperkte ervaring. Die stellingen berusten wel op aanschouwing, maar op eene aanschouwing, die wij van de ervaring geheel moeten onderscheiden. Want, zoodra wij de waarheid der mathematische stellingen hebben ingezien, twijfelen wij niet langer aan hunne algemeenheid en noodzakelijkheid. Zien wij daarentegen duizendmaal, dat eene kraai zwart is, dan besluiten wij uit die dikwijls herhaalde waarneming volstrekt nog niet tot eene algemeene stelling, en blijven blauwe

[p. 424]

kraaien voor ons even denkbaar, al bestaan zij niet in de werkelijkheid. De aanschouwing, waarop de mathematische waarheden berusten, noemt Kant de aanschouwing a priori, in tegenstelling van de empirische aanschouwing of ervaring. De eerste naam is in zooverre ongelukkig gekozen, als hij aanleiding heeft gegeven tot de opvatting, alsof deze aanschouwing a priori reeds vóór de ervaring bij het kind zou aanwezig zijn. Die opvatting volgt echter niet noodzakelijk uit de meening van Kant; de aanschouwing a priori ontwikkelt zich tegelijkertijd met de empirische aanschouwing, maar zij behoort er van te worden onderscheiden, omdat wij aan hare uitspraken een geheel ander gewicht toekennen, dan aan de uitkomsten der gewone, empirische aanschouwing. In Kant's eigen werken wordt deze vraag niet opzettelijk besproken, voor zoover mij bekend is. Wel heeft men zijne leer vrij algemeen opgevat in dier voege, dat de aanschouwing a priori reeds bij het kind in volmaakten vorm aanwezig zou zijn, en daardoor een ruim veld geopend voor de kritiek. Maar bij Kant zelven zal men geene uitspraken van die soort vinden. Slechts heeft hij niet genoeg gelet op de wenschelijkheid, om over dit punt duidelijk te spreken. Misschien ook heeft hij de wenschelijkheid der behandeling van dit onderwerp wel ingezien, maar haar toch moeten achterwege laten, omdat de physiologie hem nog geen enkel gegeven aan de hand deed, dat hij bij deze vraag zou hebben kunnen gebruiken.

De redeneering van Kant is dus, in korte woorden samengevat, de volgende:

a.	Wij bezitten een zeker aantal synthetische oordeelen, waaraan wij algemeenheid en noodwendigheid toeschrijven; deze oordeelen zijn de wet van het causaalverband, sommige onzer meeningen over tijd en ruimte, al onze wiskundige stellingen.
b.	De bloote ervaring kan ons slechts leeren, dat zekere waarheid tot nog toe altijd gegolden heeft, nimmer dat zij noodwendig is en altijd gelden zal.
c.	Onze kennis, die zich buiten het gebied der mogelijke ervaring uitstrekt, kan niet uit begrippen verkregen zijn. Ruimte en tijd zijn toch in het geheel geen begrippen, en ook de wet der causaliteit is niet uit begrippen te bewijzen.
d.	Deze kennis berust, wat tijd en ruimte aangaat, op aanschouwing a priori.

[p. 425]

e.	Die aanschouwing a priori zou ons onmogelijk algemeene en noodwendige waarheden kunnen leeren kennen, als zij zich niet uitsluitend bezig hield met de subjectieve zijde der verschijnselen, met de aangeboren waarnemingsvormen van het subject.
f.	Daar zich nu alle mogelijke dingen aan ons kenvermogen voordoen in de vormen van tijd en ruimte, is het duidelijk, dat wij niets anders kennen dan onze voorstellingen van de dingen, niet de dingen zelven.

Tot de laatste stelling was Berkeley reeds vroeger langs veel korteren weg gekomen; zij is de meest evidente waarheid, waaraan niemand kan twijfelen, die eenigermate tot bezinning geraakt is. Op zich zelve echter is zij eene vrij onbelangrijke waarheid, die slechts van gewicht wordt wanneer men, als Kant, beproeft de subjectieve elementen onzer voorstellingen van de objectieve te scheiden.

Het zou een onbegonnen werk zijn, al de argumenten te onderzoeken, die zijn ingebracht tegen de redeneering van Kant. Niemand zal van mij verlangen, dat ik in eene uitvoerige beschouwing treed van den Aenesidemus, waarin de leer van Kant aan eene zoo scherpzinnige en soms zoo billijke kritiek wordt onderworpen. Habent sua fata libelli. Ofschoon de Aenesidemus een voortreffelijk boek is, strekt zijn invloed zich toch niet meer zoo ver uit, dat het noodig zou zijn het boek te bestrijden. De krachtigste strijders tegen de leer van Kant, die in Nederland bekend zijn en gelezen worden, zijn zonder twijfel Mill en Opzoomer. De eerste heeft in navolging van Hobbes, durven verklaren, dat de mathematische waarheden op ervaring berusten. De tweede heeft zijne instemming betuigd met de gronden van die bewering. Hunne denkbeelden over het causaalverband heb ik reeds aan eene uitvoerige kritiek onderworpen. Wanneer ik thans nog zal hebben aangetoond, dat al hunne argumenten tegen de aprioriteit van ruimte en tijd niets anders zijn dan min of meer verborgen sophismen, zal ik gelooven mijne rechtvaardiging van Kant en Schopenhauer te hebben voltooid.

Zooals reeds uit het vroeger behandelde blijkt, zijn de aanvallen der empirische wijsgeeren voornamelijk, zoo niet uitsluitend gericht tegen de stelling van Kant, dat de ervaring ons geen algemeenheid en noodzakelijkheid kan leeren kennen. Reeds bij mijne beschouwing van het causaalverband kwam

[p. 426]

de meening van Opzoomer ter sprake, dat de ervaring ons wel degelijk algemeenheid en noodzakelijkheid kan aanwijzen, zoo dikwijls zij ons namelijk oorzaken leert kennen. Op die plaats is door mij toegestemd, dat wij werkelijk in zoodanige gevallen aan de uitkomsten van onze ervaring tot op zekere hoogte algemeenheid toekennen, maar aangetoond, dat de vraag van Hume en Kant niet was naar hetgeen wij werkelijk doen, maar naar den grond, waarop wij het doen. Daar de onjuistheid van elke empirische afleiding van de wet van oorzaak en gevolg kon worden aangewezen, bleek het ons, dat wij nog altijd staan voor de vraag van Hume. Thans echter moet ik er de aandacht op vestigen, dat deze uitspraak van Opzoomer ook nog in een ander opzicht volkomen onvoldoende is. Ook onze wiskundige stellingen zijn algemeen en noodzakelijk. Zou nu de ervaring ons bekend hebben gemaakt met de oorzaken van die wiskundige stellingen? Men zou gelooven, dat Opzoomer het inderdaad meent, wanneer men ziet, op welke wijze hij Kant's denkbeelden over de mathematische stellingen bestrijdt. De zaak is van zooveel belang, dat ik mij een paar uitvoerige citaten moet veroorloven. Wij lezen dan bij Opzoomer:

‘Eindelijk beroept men zich daarop, dat de mathematische waarheden algemeen en noodzakelijk zijn. De ervaring kan ons immers slechts met een beperkt aantal gevallen bekend maken, en ons leeren, dat iets zoo is, maar nooit, dat het zoo moet zijn en het tegendeel ondenkbaar is. Doch reeds in mijne vorige verhandeling heb ik deze redeneering wederlegd, en, zoo ik hoop, bewezen, dat de algemeenheid en noodzakelijkheid van waarheden niet het minst tegen haar ontstaan uit de ervaring kan betoogen. Ik mag hier dus volstaan met naar het daar ontwikkelde te verwijzen’¹.

In de geheele tweede verhandeling over de Aangeboren Begrippen, waarin Opzoomer Kant's leer over tijd en ruimte beoordeelt, wordt geene andere verklaring gegeven van de mogelijkheid der algemeene en noodzakelijke wiskundige waarheden, dan de verwijzing naar de eerste verhandeling, die in mijne aanhaling voorkomt. In die eerste verhandeling vinden wij nu het vroeger beoordeeld betoog, dat de ervaring ons algemeenheid en noodzakelijkheid kan leeren kennen, als zij ons oorzaken aanwijst. Dat nu de schrijver bij de tweede verhande-

1 Opzoomer, Wetenschap en Wijsbegeerte, blz. 272.

[p. 427]

ling de strekking van zijn betoog in de eerste helder voor zich heeft gehad, en werkelijk gelooft, dat wij de oorzaken der mathematische stellingen kennen, blijkt uit de volgende redeneering, die in de eerste verhandeling voorkomt:

‘Noodzakelijke waarheden zijn die, waarvan wij weten, niet alleen dat, maar ook waarom zij waar zijn, dat is wier oorzaken wij kennen. En dat kennen der oorzaken, hoe velen wij er ook opnoemen, komt ten slotte toch altijd op onze waarneming, onze gewaarwordingen, neder. Zijn wij tot dezen opgeklommen, dan zijn wij aan het eind, en het antwoord op de vraag: waarom is het zoo? kan dan alleen zijn: het is zoo. Of waarop steunt de noodzakelijke waarheid, dat 2 + 2 = 4, dat is = 1 + 1 + 1 + 1 is? Alleen op waarneming, op gewaarwording;’ -¹.

Men ziet, er is niet aan te twijfelen of Opzoomer gelooft, dat wij de oorzaken der mathematische waarheden kennen. Onmiddellijk na zijne definitie van noodzakelijke waarheden als de zoodanigen, wier oorzaken ons bekend zijn, haalt hij als voorbeeld eene rekenkundige waarheid aan. Nu is echter eene oorzaak, ook volgens hem, niets anders dan een onveranderlijk, onvoorwaardelijk antecedent, waarop een verschijnsel geregeld volgt. Vragen wij dan: wat is het noodwendige constante antecedent, waarop de mathematische waarheid 2 + 2 = 4 geregeld volgt? Wat is de oorzaak van die waarheid? Men bemerkt, dat de vraag ongerijmd is. Er bestaan slechts oorzaken van gebeurtenissen, van toestanden in tijd en ruimte; ten aanzien der verhoudingen tusschen onze begrippen laten zich geen oorzaken opgeven. Er is geen oorzaak te noemen van ons oordeel, dat de koe een herkauwend dier is. Evenmin van de waarheid, dat twee rechte lijnen elkander slechts eenmaal kunnen snijden. Niet ten onrechte onderscheidde de voortreffelijke Hume onze kennis in twee hoofdafdeelingen, verhoudingen tusschen onze begrippen (relations of ideas) en feiten (matters of fact). Terecht meende hij, dat er alleen in de laatste afdeeling plaats is voor het causaalverband. Dat Opzoomer, ondanks dit alles, spreken kan van de oorzaken der mathematische waarheden, berust op de verwarring van twee geheel ongelijke dingen, de oorzaken (causae) en de bewijsgronden (rationes)². De vermelde gewaar-

1 Opzoomer, t.a.p., blz. 207 en 208.

2 Ik gebruik dit woord bewijsgrond hier ter plaatse en in het vervolg in den zin van het Duitsche Erkenntuissgrund, voor de meer bekende waarheid, waaruit wij eene minder bekende waarheid afleiden. Het is niet in alle opzichten voor dat doel geschikt, daar het ons al te veel aan de bewijsvoering der mathesis doet denken, terwijl het door mij ook wordt toegepast op de minder strenge besluiten door inductie en analogie, waarop onze meeningen gelwoonlijk berusten. Kengrond zon beter zijn, maar is niet gebruikelijk. Kenbron doet al te veel aan eene verzameling van gegevens denken, terwijl ik in ieder geval slechts een of eenige weinige gegevens op het oog heb. Ons woord reden valt in sommige gevallen met mijn bewijsgrond samen, maar wordt ook als synoniem met motief gebruikt, en is daarom voor mijn doel ongeschikt.

[p. 428]

wording is natuurlijk niet de oorzaak van de wiskundige waarheid, dat 2 + 2 = 4 is, maar zij is onze bewijsgrond voor die waarheid. Bij de feiten der ervaring kunnen wij zoowel naar de oorzaak, als naar den bewijsgrond vragen. Als wij het kwik in een thermometer zien stijgen, meenen wij dat het kwik warmer wordt. Het stijgen van het kwik is onze bewijsgrond voor zijne toeneming in warmtegraad, terwijl de oorzaak van die temperatuur-verhooging wellicht gelegen kan zijn in het wegtrekken van eene wolk, die voor de zon hing. Opzoomer is bij deze gelegenheid vervallen in een begripsverwarring die zeer dikwijls voorkomt, omdat wij dezelfde voegwoorden: omdat, daar, enz. gebruiken zoowel om eene oorzaak, als om een bewijsgrond aan te geven. Wij zeggen bijv.: de lamp brandt heden avond helder, omdat wij er betere olie in gedaan hebben, en bedoelen met ons omdat de aanwijzing van eene oorzaak. Maar als iemand ons vraagt, waarom wij denken, dat er een nieuw kousje in de lamp gedaan is, zullen wij evengoed antwoorden: omdat zij zoo helder brandt. Het tweede omdat geeft ons een bewijsgrond. In Schopenhauer's voortreffelijk boek: Ueber die vierfache Wurzel des Satzes vom zureichenden Grunde, vindt men deze begripsverwarring uitvoerig besproken, en de zonderlinge sophismen aangewezen, waartoe zij beroemde mannen gebracht heeft. Ook Whately handelt in zijne Logica vrij uitvoerig over de verwisseling van deze twee geheel verschillende begrippen.

Nu is de vraag, wat Opzoomer bedoeld kan hebben met zijne oorzaken, causae of rationes? In het vroeger modegedeeld betoog, dat op blz. 217 en 218 van zijn Wetenschap en Wijsbegeerte wordt gevonden, heeft hij zonder twijfel gewoonlijk aan werkelijke oorzaken, onvoorwaardelijke antecedenten, causae, gedacht. Bij de wiskunde echter bestaan deze niet; hij moet dus bij de wiskundige stellingen aan bewijsgronden, rationes, denken, zoo dikwijls hij van oorzaken spreekt. Nu is het

[p. 429]

niet moeilijk aan to toonen, dat niet iedere stelling, wier be wijsgrond ons bekend is, noodzakelijk is en algemeen. Van de waarheid, dat de lichamen elkander aantrekhen in rechte reden van hunne massa's en in omgekeerde reden van het vierkant hunner afstanden, is de volledige reeks der bewijsgronden door de vlijt der astronomer verzameld. Toch houdt niemand deze stelling voor algemeen en noodzakelijk. Van onze bewering, dat kraaien zwart zijn, is ons de bewijsgrond volkomen bekend; zij is de onmiddellijke uitspraak van ooze waarneming. Toch twijfelt men terecht aan de algemeenheid en noodzakelijkheid van deze stelling.

De uitvlucht, dat de natuur ons wet degelijk algemeenheid en noodzakelijkheid zou leeren kennen, als zij ons oorzaken aanwijst, was dus bij de bespreking van het causaalverband alleen onvoldoende, bij de behandeling der mathematische stellingen was zij ongerijmd. Want bij de stellingen der wiskunde kennen wij geen oorzaken, maar alleen bewijsgronden. En de omstandigheid, dat hare bewijsgronden bekend zijn, maakt eene stelling niet algemeen en noodzakelijk. Maar zelfs in geval wij eens wilden toestemmen, wat nimmer eenig verstandig mensch heeft toegestemd, dat eene stelling algemeenheid en noodzakelijkheid verkrijgt, als wij hare bewijsgronden leeren kennen; zelfs in dat geval is nog niet verklaard, hoe de mathematische waarheden ons noodwendig en algemeen kunnen toeschijnen. Want hun bewijsgrond is bij Opzoomer ten slotte de waarneming, de dikwijls herhaalde waameming. Dat 2 + 2 = 4 is, blijkt ons slechts, doordien ‘wanneer ik twee dobbelsteenen b.v. naast twee andere heb gelegd, mijne gewaarwording van het daardoor tot stand gekomene geheel dezelfde is, als wanneer ik naast één dobbelsteen er nog één heb gelegd, dan nog één, en dan nog één’¹. Dus is het de inductie, en wel de inductie per enumerationem simplicem, die ons niet de oorzaken, maar de bewijsgronden van de wiskundige stellingen zal leeren kennen. Nog eenmaal vraagt de onvermoeide Hume: Hoe weten wij toch, dat datgene, wat altijd nog zoo geweest is, ook in de toekomst zoo zijn zal en niet anders wezen kan?

Met het zoo even beschouwde betoog wordt door Opzoomer eene andere redeneering op zoodanige wijze vermengd, dat bet

1 Opsoomer, t.a.p., b1z. 208.

[p. 430]

moeilijk valt te zeggen, waar de eerste redeneering eindigt en de tweede begint. Nadat toch op blz. 206 en 207 de waarheid is toegelicht, dat alles, wat in de natuur geschiedt, noodzakelijk geschiedt, wordt hieruit de conclusie afgeleid, dat alle waarheden even noodzakelijk zijn¹. Daarop volgt de reeds beoordeelde onjuiste onderscheiding van de noodzakelijke waarheden als de zoodanigen, wier oorzaken ons bekend zijn. Uit de omstandigheid, dat het verschil tusschen de toevallige en noodzakelijke waarheden niet gelegen is in die waarheden zelven, maar alleen in de grootere of geringere volmaaktheid van onze kennis dier waarheden, wordt nu afgeleid, dat beider oorsprong dezelfde is, dat alle waarheden door de ervaring verkregen zijn. Ten slotte wijst de schrijver op het feit, dat men zeer dikwijls meeningen voor onmogelijk heeft verklaard, die toch later gebleken zijn mogelijk te wezen, en besluit hieruit, dat het beweren van de noodzakelijke waarheid eener stelling dikwijls niets anders is dan eene dwaling². De conclusie, die uit dit alles zou volgen, maar die door Opzoomer niet wordt uitgesproken, is geene andere dan de volgende. Dus zouden ook de waarheden, die wij thans voor noodzakelijke waarheden houden, ten slotte nog wel niet eens waar kunnen zijn.

De valsche redeneering, die in deze beschouwing verborgen is, behoort niet tot degenen, wier onjuistheid gemakkelijk is te ontdekken. Opzoomer geeft hier, in andere woorden, dezelfde redeneering, waarmede Mill in zijne Logica tegen Whewell tracht te betoogen, dat de waarheid eener stelling nog niet bewezen is, doordien het ons onmogelijk voorkomt, haar tegendeel te denken. Het is een onbegonnen werk, licht en orde te willen brengen in dezen chaos, als men niet begint met de intuïtieve kennis ten strengste van de abstracte te scheiden. Maar ook hiermede heeft men niet genoeg gedaan. Het is noodig in hoofdzaak de analyse van het menschelijk kenvermogen te verstaan, die door Schopenhauer is gegeven in de merkwaardige dissertatie, waarmede hij in 1813 te Jena promoveerde. Zonder de scherpzinnige onderzoekingen, die ons in de genoemde dissertatie worden medegedeeld over ‘die vierfache Wurzel des Satzes vom zureichenden Grunde’, zou ik mij niet durven wagen tegen dit argument van Mill en Opzoomer.

1 Opzoomer, t.a.p., blz. 207.

2 Opzoomer, t.a.p., blz. 210.

[p. 431]

Schopenhauer's klein, maar belangrijk, boek handelt over de verschillende beteekenissen, waarin de stelling gebruikt wordt, die de Duitschers Satz vom zureichenden Grunde (principium rationis sufficientis) noemen. Deze stelling luidt, zoo algemeen mogelijk uitgedrukt: Niets bestaat zonder grond, waarom het is¹. Hij meent, dat deze stelling gebruikt wordt in vier verschillende beteekenissen, die vóór hem nimmer met scherpte zijn onderscheiden. Soms toch, bij de verschijnselen van de zichtbare natuur, wordt met den grond, waarom iets bestaat, eene oorzaak bedoeld. Op de vraag, waarom het verschijnsel bestaat, waarom de verandering is ingetreden, antwoordt men in dat geval door een voorafgaand verschijnsel te noemen, waarop het andere onvoorwaardelijk volgt. In andere gevallen wordt er gevraagd naar den grond van onze oordeelen, van onze meeningen. Die grond is niet eene voorafgaande verandering, eene oorzaak, maar een of ander feit in ons bewustzijn, waaruit wij onze oordeelen afleiden. Een dergelijke bewijsgrond, ratio, kan zijn eene algemeene stelling, waarop ons oordeel berust, of wel eene gewaarwording. Onze meening, dat een persoon, wiens naam wij voor het eerst hooren noemen, niet volmaakt zal zijn, berust op de algemeene stelling, dat alle menschen hunne gebreken hebben; onze meening, dat keukenzout wit is, berust op onze gewaarwording. Het verschil tusschen oorzaken en bewijsgronden is reeds in het voorafgaande behandeld; een enkel voorbeeld moge voldoende zijn om toe te lichten, hoe noodig het is deze twee soorten van gronden te ouderscheiden. De rijke oogst, dien een korenveld ons levert, is onze bewijsgrond voor de vruchtbaarheid van den akker; daarentegen is de vruchtbaarheid van den akker de voornaamste oorzaak van de overvloedigheid van den oogst. Hier is dus het gevolg onze bewijsgrond voor het bestaan van de oorzaak, en even zoo in honderd andere gevallen. Wij zeggen nu, dat die akker vruchtbaar moet zijn, omdat de oogst zoo rijk is. Maar even goed kunnen wij verklaren, dat de oogst zoo overvloedig is, omdat de akker zoo vruchtbaar is. Dat nu de twee genoemde omdat's eene geheel verschillende beteekenis hebben, wordt dikwijls over het hoofd gezien. Ook onze vraag waarom? slaat even goed op den grond van onze meening als op de noodzakelijke voorwaarden van een natuurverschijnsel. Deze twee soorten van gron-

1 Nihil est sine ratione, cur potius sit quam non sit.

[p. 432]

den zijn natuurlijk lang vóór Schopenhauer bekend geweest, ofschoon zelden met scherpte onderscheiden; dat zij ook na Schopenhauer niet altijd met nauwkeurigheid uit elkander worden gehouden, is ons uit het bovenstaande gebleken. Nu zijn er echter gevallen, waarin men een grond voor eenig ding weet aan te geven, die noch eene oorzaak, noch een bewijsgrond is. Als men iemand vraagt: waarom zijn deze twee cirkels gelijk en gelijkvorming? - dan kan hij antwoorden: omdat de stralen van deze cirkels gelijk zijn. Nu is de gelijkheid der stralen zeker niet de oorzaak van de gelijkheid der cirkels. Evenmin kan men zeggen, dat die gelijkheid der stralen de bewijsgrond is van de gelijkheid der cirkels. Want de laatste gelijkheid laat zich niet door eene aaneenschakeling van begrippen van de eerste afleiden; onze bewijsgrond voor de gelijkheid der cirkels is niets anders dan de aanschouwing, die ons geen twijfel laat over het feit, dat twee cirkels, met gelijke stralen beschreven, gelijk zijn. Wel kan, als wij deze laatste stelling als bewezen aannemen, de gelijkheid der stralen in een bijzonder geval onze bewijsgrond worden voor de gelijkheid der cirkels; in zoodanig geval vervult toch de gelijkheid der stralen de plaats van den minor in het volgende syllogisme

Alle cirkels met gelijke stralen zijn gelijk en gelijkvormige figuren.
Deze twee cirkels hebben gelijke stralen
Dus zijn deze twee cirkels gelijk en gelijkvormige figuren.

Het was ons hier echter te doen om het bewijs van den major van bovenstaand syllogisme, en dat bewijs kan nimmer anders dan door de aanschouwing worden geleverd. Nu kan men echter niet volstaan met de aanschouwing, in het algemeen genomen, aan te wijzen als den grond der mathematische waarheden. Deze algemeene bewering zou wel niet onwaar zijn, maar zij is even onvoldoende, als wanneer men de ervaring in het algemeen aangaf als den grond van onze oordeelen over stoffelijke dingen. In iedere meetkundige figuur is de bepaalde verhouding van sommige harer deelen voldoende om de anderen volkomen te bepalen. Is bijv. in een driehoek de lengte van eene zijde, en de grootte der twee aanliggende hoeken gegeven, dan is daardoor de lengte der twee andere zijden en de grootte van den overblijvenden hoek volkomen bepaald. Deze bepaalde grootte van de laatstgenoemde elementen van den driehoek vindt

[p. 433]

haren grond in de bepaalde grootte der eerstgenoemde elementen. Op dezelfde wijze is nu ook de gelijkheid der stralen de grond van de gelijkheid der cirkels. Voor deze soort van gronden, die bij de aanschouwelijke bewijzen der mathesis de eenige zijn, ontbreekt het in iedere taal aan een passend woord. Schopenhauer noemt ze gronden van het zijn (rationes essendi) en onderscheidt er twee soorten van, de zijnsgronden in de ruimte en de zijnsgronden in den tijd. Zoo vindt de gelijkheid der zijden van een driehoek, van wiens hoeken twee aan elkander gelijk zijn, haren zijnsgrond in de gelijkheid der overstaande hoeken. Maar evengoed is de gelijkheid der zijden van een gelijkbeenigen driehoek de zijnsgrond voor de gelijkheid der overstaande hoeken. In den tijd is ieder oogenblik de zijnsgrond van het volgende; het tweede oogenblik kan slechts bestaan, als het eerste is voorbijgegaan.

Minder verschillend van de vorige is eene vierde soort van gronden. Wanneer iemand eene bepaalde handeling doet, vraagt men naar den grond, waarom hij die gedaan heeft. Op deze vraag antwoordt men door het noemen van een motief, van eene beweegreden. Die beweegredenen kunnen ongetwijfeld gerangschikt worden in de eerste klasse der gronden, onder de oorzaken. Zij zijn voorafgaande veranderingen, waarop de handeling onveranderlijk, onvoorwaardelijk volgt. Daar zij ons echter op geheel eigenaardige wijze, door innerlijke waarneming, hekend worden, verdienen zij eene afzonderlijke vermelding.

Nu beteekent het woord noodzakelijkheid niets anders dan het onvermijdelijk intreden van het gevolg, als de grond daarvoor bestaat. In verband met zijne verdeeling der gronden in vier rubrieken onderscheidt Schopenhauer vier soorten van noodzakelijkheid, a. physische noodzakelijkheid, het ontstaan van eene verandering als de toereikende oorzaak geworden is; b. logische noodzakelijkheid, de zekerheid van de conclusie als de praemissen zijn toegestemd; c. mathematische noodzakelijkheid, volgens welke de betrekking tusschen de verschillende deelen van de ruimte en van den tijd ons niet anders kan toeschijnen dan zij ons toeschijnt; d. moreele noodzakelijkheid, volgens welke ieder mensch bij een gegeven motief op zoodanige wijze handelen moet, als zijn eigenaardig karakter medebrengt, en niet anders handelen kan.

Na deze korte uiteenzetting van het onderscheid tusschen de verschillende beteekenissen, waarin het woord noodzakelijkheid

[p. 434]

gebruikt wordt, zal het mij wellicht mogelijk zijn den nevel te verspreiden, die over het vraagstuk der noodzakelijke waarheden hangt, en die zoo dik is, dat zelfs een Spencer kon betoogen, dat in ieder geval de waarheid eener stelling bewezen is, indien het ons onmogelijk is haar tegendeel te meenen. Van welken aard is toch de noodzakelijkheid in onze abstracte wetenschap, behalve in de mathesis? Zij is nimmer iets anders dan logische noodzakelijkheid. Op die noodzakelijkheid steunt de waarheid van onze analytische oordeelen; hun tegendeel is voor ons werkelijk ondenkbaar. Als ik aan een onderwerp geen andere praedicaten toeken, dan die, welke mijn begrip van het onderwerp samenstellen, dan is het tegendeel van mijne bewering voor mij werkelijk ondenkbaar. Op dezelfde noodzakelijkheid steunt de zekerheid van elke conclusie, zoodra de juistheid der praemissen is toegestemd, en de redeneering geen logische fout bevat. Bij de intuïtieve kennis daarentegen is de logische noodzakelijkheid nimmer aanwezig, maar wel eene der drie andere soorten van noodzakelijkheid. Dat het kwik zich bij verwarming uitzet, is een physisch noodwendig feit; dat de rechte lijn de kortste weg is tusschen twee punten, is mathematisch noodzakelijk; dat Brutus Caesar verwondde, was moreel noodzakelijk. Plaatsen wij ons nu op het standpunt der intuïitieve kennis, dan zijn alle feiten noodzakelijk, zooals Opzoomer terecht beweert. Gaan wij daarentegen over tot de abstracte beschouwing, dan kunnen zekere verschijnselen, op eene bepaalde wijze bezien, ons als toevallig voorkomen. Dat er op dit oogenblik een Kaffer sterft is een physisch noodwendig feit: het geschiedt niet zonder voldoende oorzaak. Maar dat hij juist sterft, nadat ik van mijn stoel ben opgestaan, is voorzeker toevallig. Elk physisch verschijnsel is noodzakelijk, wanneer men het beschouwt in verband met zijne oorzaak, met den geheelen toestand, die het verschijnsel heeft voortgebracht. Het is daarentegen toevallig, als men het beschouwt in verband met een ander verschijnsel, dat niet zijne oorzaak is, maar alleen gelijktijdig met zijne oorzaak. Dezelfde beschouwing geldt van alle handelingen; zij zijn noodwendig bepaald door hunne motieven, maar volgen toevallig op andere, gelijktijdige verschijnselen. Terwijl ons dus de physisch noodwendige en de moreel noodwendige feiten, uit zeker oogpunt bezien, als toevallig kunnen voorkomen, bestaat bij de mathematische stellingen de mogelijkheid van een toeval niet. Want in de bloote

[p. 435]

ruimte, het veld der meetkunde, bestaat geene opvolging; in den blooten tijd, het veld der rekenkunde, bestaat geen gelijktijdigheid. En het begrip van toeval vereischt zoowel het begrip opvolging als het begrip gelijktijdigheid. Want de tegenstelling van noodzakelijkheid en toeval bestaat alleen in het verschillend verband van twee gelijktijdige feiten tot een zelfde opvolgend feit.

Voor dengene, die onbekend is met de oorzaken of motieven van eenig physisch of moreel verschijnsel heeft het den vorm der toevalligheid; hij kan ook denken, dat het niet bestaat, zoolang hij de toereikende oorzaken van het verschijnsel niet kent. Kent hij wel de oorzaken, maar niet de oorzaken van die oorzaken, dan kan hij zich de oorzaken van het verschijnsel en dus ook het verschijnsel zelf als niet-bestaande denken. Daar wij nu nimmer aan het einde kunnen komen van ons onderzoek naar de voortgezette reeks der oorzaken van eenig verschijnsel, is er geen enkel physisch of moreel feit, waarvan het tegendeel ondenkbaar zou zijn. Wel wordt het al moeilijker en moeilijker het tegendeel van eenig verschijnsel te verwachten, naarmate wij het in meer gevallen onder de gegeven omstandigheden hebben zien plaats grijpen; maar ondenkbaar wordt dat tegendeel nooit. Men kan zich zonder moeite denken en men kan zich zonder moeite voorstellen, dat een uit het venster geworpen steen in de lucht zou blijven zweven, al kan men moeilijk gelooven, dat dit verschijnsel werkelijk zou plaats vinden. In de discussie tusschen Mill en Whewell zoowel als in de Psychologie van Spencer wordt de ondenkbaarheid van een verschijnsel verward met de zekerheid van onze overtuiging, dat het zal uitblijven. Tot die zekerheid geraken wij eigenlijk nimmer, maar in het geval van den steen en in vele dergelijke gevallen is toch de waarschijnlijkheid zoo groot, dat zij in de praktijk voor zekerheid kan doorgaan.

Het tegendeel van de mathematische waarheden is daarentegen letterlijk ondenkbaar. Dat twee rechte lijnen elkander in twee punten zouden ontmoeten, kunnen wij ons onmogelijk voorstellen. Evenmin kunnen wij ons denken, dat twee platte vlakken elkander zouden snijden volgens eene kromme lijn. Dit ligt aan de omstandigheid, dat wij, de meetkunst bestudeerende, de gronden van deze stellingen hebben leeren inzien. Niet de bewijsgronden (rationes), waarmede een onverstandig

[p. 436]

leeraar misschien zou kunnen beproeven zoo evidente waarheden te bewijzen, maar de zijnsgronden van Schopenhauer. Wij hebben ons voorstellingsvermogen zoo dikwijls bezig gehouden met rechte lijnen, dat de richting der twee lijnen in het kleine gedeelte, dat wij ons voorstellen, voor ons de zijnsgrond is voor de bepaling der plaatsen, die zij in hun verloop zullen innemen.

Met deze eigenaardigheid van onze wiskundige kennis staat de regelmatige, ongeschokte vooruitgang van deze wetenschap in verband, waardoor zij zich zoo onmiskenbaar van de natuurwetenschap onderscheidt. Bij de mathesis verdwijnt het verschil tusschen abstracte en intuïtieve kennis. Geen enkel abstract begrip wordt in haar gebied erkend, dat zich niet met onberispelijke nauwkeurigheid in conereto en intuïtief laat voorstellen. Hoe abstract hare stellingen ook schijnen mogen, zij zijn altijd getoetst door de onbedrieglijke intuïtieve kennis. Iedereen heeft op elk oogenblik de vrijheid zich van de juistheid eener abstracte mathematische stelling te overtuigen. Dat de verhouding der oneindig kleine aangroeiingen van de ordinaat en van de abscis in eenig punt eener willekeurige kromme lijn de maat is van den tangens van den hoek, dien de raaklijn, in dat punt aan de kromme lijn getrokken, maakt met de as der abscissen - deze stelling mag den oningewijde eene zeer abstracte waarheid schijnen. Toch kan iedereen, die de beteekenis kent der volkomen ondubbelzinnige woorden, die in de stelling gebruikt worden, zich, zoo dikwijls hij wil, een aanschouwelijk en nauwkeurig beeld ontwerpen van de abstracte begrippen, welke door die woorden benoemd worden. Hij erkent de waarheid van de stelling als de onmiddellijke uitspraak van zijne proefneming met zijne geconstrueerde begrippen. Daarom is het mathematisch denken niets anders dan zich voorstellen, en vallen op dit gebied de twee begrippen ineen, die anders zoo scherp moeten worden onderscheiden.

De natuurwetenschap daarentegen is niet zoo gelukkig als hare eerbiedwaardige zuster. Zij moet de bouwstof, door de intuïtieve kennis geleverd, opnemen in abstracte begrippen. Zij kan zich nimmer eene aanschouwelijke voorstelling ontwerpen, die met een van hare abstracte begrippen identisch is. Zij moet van haar eigenlijk domein, de abstracte waarheid, overgaan op het gebied der intuïtieve, aanschouwelijke, kennis, zoo dikwijls zij haar gebied wil uitbreiden. Bij elke van hare onderzoekin-

[p. 437]

gen moet zij de moeilijke vraag beantwoorden, in hoeverre de waargenomen verschijnselen het recht geven tot het opmaken van een algemeenen regel, eene vraag, die bij de mathesis bijna nimmer te pas komt. Telkens weder moet zij veranderingen aanbrengen in het dorre stelsel van hare algemeene regels, om het te schikken naar den onuitputtelijken rijkdom der aanschouwelijke wereld. Zeer dikwijls ontdekt zij, dat hare meest algemeene stellingen eene belangrijke wijziging moeten ondergaan; soms dwingt haar de vooruitgang der wetenschap de meest ingewortelde overtuiging geheel te verwerpen. Nadat men eene eeuw lang gemeend had, dat de lichamen bij hunne verbranding een bestanddeel verloren, bemerkt men eindelijk, dat zij bij die verbranding een bestanddeel in zich opnemen. Nadat men vele jaren lang den galvanischen stroom beschouwd had als de oorzaak van de chemische werking in de galvanische batterij, zien thans vele natuurkundigen in die chemische werking de oorzaak van den galvanischen stroom. De hoeveelheid der intuïtieve kennis, der waargenomen feiten, neemt onophoudelijk toe met verwonderlijke snelheid; van alles, wat eenmaal goed gezien is, gaat zeer weinig weder verloren. Maar de theorie. de abstracte wetenschap, is als het kleedingstuk, dat onophoudelijk veranderd moet worden naar den lichaamsbouw van den groeienden knaap, misschien, ook naar de wisselvalligheden der mode. De feiten, door Scheele ontdekt, behooren nog steeds tot de belangrijkste waarheden van de scheikunde; zijne theoretische beschouwingen passen ons even weinig als de jongenskiel aan den volwassen man.

Die scherpe tegenstelling tusschen de rustige, onafgebroken vermeerdering der bekende feiten en de plotselinge omwentelingen der natuurkundige theorieën, ontbreekt in de wiskunde geheel en al. Want bij de laatste bestaat er geen zoodanig verschil tusschen de feiten en de theorie, als de natuurkunde aanbiedt. Elke waarheid, die zich aan het buitengewone voorstellingsvermogen van Descartes of Leibnitz vertoonde, is ook thans nog een bestanddeel van den cursus, dien de beginnende beoefenaar der wiskunde doorloopt. Als het onderwijs in die wetenschap zoo goed mogelijk is ingericht, stelt het zich niets anders ten doel, dan elken leerling de reeds bekende waarheden tot zoo ver te laten zien, als zijn voorstellingsvermogen toelaat. Wat wij in de wiskunde theorie zouden kunnen noemen, is toch niets anders dan eene verzameling van de meest

[p. 438]

belangrijke waarheden, bij de natuurwetenschap daarentegen de systematische vereeniging der algemeene regels, die uit de feiten zijn afgeleid.

De wiskundige heeft dus in zich zelven al de gegevens, die noodig zijn om te beslissen over de waarheid zijner stellingen. Hij verwerpt als eene ongerijmdheid het tegendeel van alles, wat hij helder heeft ingezien. Descartes' criterium der waarheid, in de wijsbegeerte reeds sedert langen tijd verworpen, heerscht nog altijd in de wetenschap, die hij met zoo gewichtige ontdekkingen heeft vermeerderd. In de natuurwetenschap daarentegen is geen enkele verklaring ondenkbaar; zij kan hoogstens zeer onwaarschijnlijk zijn. Dat de conclusies van onze analytische oordeelen voor ons logisch noodwendig zijn, maakt natuurlijk geen uitzondering op den regel. Zij zijn noodwendig met betrekking tot onze begrippen; maar of deze begrippen volkomen in harmonie zijn met de aanschouwelijke natuur, kunnen wij nimmer beslissen. Wanneer dus zeer dikwijls eene verklaring als ondenkbaar is verworpen, die later bleek zeer aannemelijk te zijn, dan is dit feit eenvoudig toe te schrijven aan het misbruik van het woord ondenkbaar voor hoogst onwaarschijnlijk. Op dit misbruik steunt Spencer's verdediging van zijn algemeen postulaat. De noodzakelijke waarheden, die Kant bedoelde, zijn nu waarheden, wier tegendeel voor ons niet slechts in de hoogste mate onwaarschijnlijk, maar ondenkbaar is. Die noodzakelijke waarheden zijn gemakkelijk op te tellen. Zij zijn: vooreerst de logische axioma's der identiteit, der tegenstrijdigheid, van het buitengesloten derde; ten tweede, alle analytische oordeelen; ten derde, de stelling over den toereikenden grond (principium rationis sufficientis) in hare verschillende beteekenissen; ten vierde, alle stellingen der zuivere wiskunde.

Het verschil tusschen deze noodzakelijke waarheden, wier tegendeel ondenkbaar is, en de waarheden, die de ervaring ons levert, wier tegendeel alleen min of meer onwaarschijnlijk, hoogstens zeer onwaarschijnlijk, maar volstrekt niet ondenkbaar is, valt duidelijk genoeg in het oog. De bewering van Opzoomer, wier wederlegging niet wel mogelijk was, zonder de aanwijzing van de verschillende beteekenissen, waarin men het woord noodzakelijkheid gebruikt, heeft door de juiste onderscheidingen van Schopenhauer alle waarde verloren. Want, terwijl in Opzoomer's betoog telkens wordt gesproken over noodzakelijkheid,

[p. 439]

wordt nergens aangewezen, welke noodzakelijkheid hij op het oog heeft. Daarom kan men wel de woorden van zijne redeneering lezen, maar niet te weten komen, wat hij bedoeld heeft. De groote lengte van zijne redeneering, die zich over verscheidene bladzijden uitstrekt, maakt het mij onmogelijk al de plaatsen op te tellen, waar het woord noodzakelijk in geheel verschillende beteekenissen gebruikt wordt, terwijl de deugdelijkheid der redeneering van de beteekenis van dat woord afhangt. Een enkel voorbeeld moge voldoende zijn. Wij lezen op blz. 207: ‘Dat kool als graphiet en houtskool niet, als diamant wel doorzichtig is, moge toevallig heeten; wij weten reeds genoeg van den samenhang der natuur, om ook hier noodzakelijkheid, het bestaan van vaste wetten te erkennen, en ons overtuigd te houden, dat, wanneer wij met den moleculairen toestand dier stoffen bekend waren, de toevallige waarheid voor ons in eene noodzakelijke waarheid zou veranderd zijn.’ De lezer zal opmerken, dat de eerste noodzakelijkheid eene physische, de tweede eene logische is.

De gang van mijn onderzoek heeft mij hier gevoerd tot eene reeds vroeger geopperde stelling, wier waarheid door de empirische wijsgeeren moet worden ontkend. Zij is de volgende. In de wiskunde is al het denkbare werkelijk of althans mogelijk, in de natuur zijn de meeste denkbare dingen onmogelijk.

De laatste helft der stelling is gemakkelijk in te zien, en in het bovenstaande genoegzaam toegelicht. Stellen wij ons voor, dat wij eene geelectriseerde glasstaaf in de nabijheid brengen van een vlierpitten bolletje, dat aan een draadje is opgehangen en niet geëlectriseerd is. Nu leert ons de ervaring, dat het bolletje zich altijd naar de glasstaaf toe beweegt, en wij zullen, bij het nemen van de proef, geen andere beweging dan de genoemde kunnen verwachten. Maar iedere andere beweging blijft voor ons even denkbaar. Ik heb er niet de minste moeite in mij voor te stellen, dat het vlierpitten bolletje geheel in rust blijft, of dat het zich als een tol gaat draaien. of dat het zich zoo ver mogelijk van de glasstaaf verwijdert. Wel kan ik deze bewegingen niet verwachten, maar ze mij te denken, daarin is geen bezwaar.

De eerste helft der stelling vereischt nog eenige opheldering. Men kan namelijk wel iets zeggen, iets in woorden uitdrukken, wat wiskundig onmogelijk is, bijv. een rechthoekige gelijkzij-

[p. 440]

dige driehoek. Maar denken kan men zich eene dergelijke onmogelijkheid niet. Blijft men bij de woorden staan, dan heeft men nog niets gedacht; het wiskundig denken bestaat alleen in de constructie van de in woorden medegedeelde begrippen. Nu is er, voor zoo ver ik heb kunnen nagaan, in de wiskunde slechts ééne soort van beschouwingen, waarbij onmogelijke dingen denkbaar kunnen schijnen. Die beschouwingen zijn de bewijzen uit het ongerijmde. Wij kunnen, om een eenvoudig voorbeeld te nemen, een bewijs uit het ongerijmde geven van de stelling, dat in een driehoek, die twee gelijke hoeken heeft, de zijden over die hoeken gelijk zijn. Men onderstelt dan, dat de eene zijde grooter is dan de andere, terwijl de overstaande hoeken gelijk zijn, en bewijst dan gemakkelijk uit vroegere stellingen, of door de aanschouwing, dat de redeneering die op de gemaakte onderstelling berust, op eene ongerijmdheid uitloopt. Dus, zou men kunnen zeggen, is er bij het begin van deze redeneering een onmogelijk ding gedacht. Inderdaad heeft men echter bij den aanvang van het bewijs eene ondenkbare woordverbinding opgegeven, die ondenkbaar blijkt, zoodra men hare begrippen construeert. Nu is niet iedereen van nature even oplettend en even geschikt in het construeeren van mathematische begrippen. Vooral bij de beschrijvende meetkunst blijkt het groote verschil, dat er in dit opzicht tusschen de individu's bestaat. Verreweg de meesten geraken onvermijdelijk in de war, als zij beproeven zich de meer samengestelde bewerkingen dezer wetenschap voor te stellen. Voor leerlingen met een helder voorstellingsvermogen daarentegen is het meerendeel van hare stellingen bij den eersten aanblik evident. Nu zal men toch niet beweren, dat het omgekeerde van eene stelling der meetkunst denkbaar is, omdat zoo menigmaal een weinig belovend leerling gemeend heeft dat omgekeerde te denken, terwijl hij eigenlijk, den zwaren arbeid van het denken moede, niets anders heeft voor zich gehad dan eene ondenkbare woordverbinding. Het bewijs uit het ongerijmde is eene speculatie op de onvolmaaktheid van het voorstellingsvermogen van de meeste menschen. Zij worden er toe gedwongen te beproeven, of zij zich het onmogelijke ding kunnen voorstellen. Aan sommigen blijkt de onmogelijkheid van de constructie reeds voor het bewijs: anderen daarentegen zien de onmogelijkheid der constructie eerst in, wanneer men hen door de redeneering van het bewijs dwingt die constructie met

[p. 441]

grootere nauwkeurigheid te maken. Zoodra hunne voorstelling duidelijk is geworden, blijkt de onmogelijkheid van de gemaakte onderstelling, de ondenkbaarheid van de onbestaanbare wiskundige figuur. In de natuurwetenschap is het geheel anders. Als iemand een volledig inzicht heeft in de natuurwetten, volgens welke het kwik in de buis van Torricelli opgeheven blijft, kan hij zich nog altijd voorstellen, dat het naar beneden gaat, of ook dat de top der kwikkolom zich rhythmisch gaat bewegen op de maat eener muziek, die in een naburig vertrek gemaakt wordt. Ik heb ten minste geen de minste moeite mij het laatste verschijnsel voor te stellen, en toch ben ik volkomen bekend met de natuurwetten, die het tot eene noodzakelijkheid maken, dat de top der kwikkolom, althans voor onze oogen, rustig blijft staan, en waardoor het onmogelijk is, dat zij in den regel eene zoo vlugge beweging zou vertoonen, als mijne onbedwongen verbeeldingskracht haar zoo even deed aannemen.

De omstandigheid, dat in de wiskunde alles mogelijk is, wat duidelijk gedacht wordt, geeft aan de stellingen der wiskunde hunne ontwijfelbare zekerheid, ook ingeval de ervaring ze onmogelijk kan bevestigen. Terwijl men in de natuurwetenschap ook voor de meest gerechtvaardigde deductie uit bekende waarheden de bevestiging door de proefneming vordert, acht men in de wiskunde die bevestiging volmaakt overbodig. De meeste kromme lijnen, die de wiskunde bespreekt, zijn nimmer in de natuur waargenomen, en zelfs wanneer de natuur ons deze lijnen vertoonde, zou de ervaring ons nimmer de juistheid kunnen bewijzen van eene enkele der stellingen, aan wier waarheid de wiskundige niet kan twijfelen. Hoe zou de ervaring ons kunnen leeren, dat de inhoud van de cycloïde gelijk is aan driemaal den inhoud van den genereerenden cirkel, niet ongeveer driemaal, niet ten naaste bij driemaal, maar juist driemaal, niet meer en niet minder? Hoe zou zij ons de waarheid kunnen aantoonen van de stelling, dat de hyperbool hare asymptoten altijd nadert, zonder ze immer te bereiken? Geen wiskundige twijfelt aan de waarheid dezer stellingen. Daarentegen, volgens algemeen erkende chemische waarheden is het bestaan van een lichaam, dat men amylglycerine noemt, in de hoogste mate waarschijnlijk. Wat meer is, reeds heeft een geacht scheikundige beweerd dat lichaam te hebben verkregen, en zijne eigenschappen beschreven. Toch twijfelen vele scheikundigen

[p. 442]

aan het bestaan van dat lichaam en zijn niet voornemens zijne aanspraken op bestaanbaarheid te erkennen, voordat nog vele andere scheikundigen hetzelfde lichaam zullen bereid hebben.

Het antwoord, dat de empirische wijsgeeren op deze bedenkingen geven, is genoegzaam bekend. Het innemen van eene bepaalde ruimte, zoo luidt hun antwoord, is eene geheel algemeene eigenschap der lichamen; van onze vroegste jeugd af worden wij met de eigenaardigheden van die ruimte volkomen bekend. De waarneming leidt ons in de wiskunde, die zich slechts met eene enkele eigenschap der lichamen bezig houdt, weldra tot zekere algemeene eigenschappen van de ruimte, die, door eene langdurige ervaring bewezen, voor ons volkomen evidente waarheden worden. Uit die bekende waarheden trekken wij dan besluiten voor gevallen, die nimmer door ons zijn waargenomen. Zulke waarheden zijn de weinige axioma's van stelkunde en meetkunde, waaruit wij eene zoo groote opeenstapeling van gevolgtrekkingen afleiden. Dit antwoord is echter om twee redenen onbevredigend. Vooreerst omdat de ervaring, zoo zij ons al de axioma's kan hebben leeren kennen, ons nimmer kan geleerd hebben, dat deze axioma's ook gelden buiten de grenzen van het veld, waarover zich onze ervaring heeft uitgestrekt. Ten tweede, omdat er andere eigenschappen zijn, die de lichamen even standvastig vertoonen als de eigenschap van ruimte in te nemen. Elk lichaam heeft een bepaald gewicht, een bepaalden warmtegraad, eene bepaalde kleur. Hebben wij nu in het vervolg nog eene deductieve wetenschap te verwachten, die over het gewicht handelt, eene andere, die over de warmte spreekt, eene derde, die de kleur tot haar onderwerp heeft? Dit is zeker hoogst onwaarschijnlijk, wanneer men in aanmerking neemt, hoever de wetenschap der ruimte reeds gevorderd is. Als de mogelijkheid bestond, om over de andere algemeene eigenschappen der lichamen eene deductieve wetenschap te vormen, zou er zeker reeds lang een begin van zoodanige wetenschap te vinden zijn. Is er nu van dergelijke wetenschappen ook niet het geringste spoor te ontdekken, dan blijkt toch met zekerheid, dat de eigenschap van ruimte in te nemen, die alle lichamen vertoonen, zich niet alleen door haar algemeen voorkomen, maar ook nog op andere wijze van de overige eigenschappen onderscheidt.

Een laatste argument wordt door Opzoomer op verschillende

[p. 443]

plaatsen uitgesproken. Het komt hierop neer, dat, wanneer onze geest aan onze ervaring iets toevoegt, wij niet bekend zouden zijn met de natuur.

‘Juist daaruit, dat onze geest kennis van de natuur verkrijgt, trek ik het besluit, dat hij aan de hem geleverde stof niets bijvoegt, er niets aan verandert. Immers deed hij dit, dan ware het niet langer kennis van de natuur, maar het zou enkel eene fantaisie zijn, waarvoor de natuur slechts het thema had aangegeven’¹.

‘Stellen wij nu eens, dat ik het begrip van den tijd vóór de waarneming in mij heb, en de waargenomen verschijnselen in dat begrip moet opnemen, waar is het dan aan te wijten, dat ik ze soms na elkander, soms niet na elkander plaats? Ik plaats bijv. Kant na Aristoteles, maar verklaar Huygens voor tijdgenoot van Newton. Waarom? Is het, omdat werkelijk Newton en Huygens, maar geenszins Aristoteles en Kant, in denzelfden tijd geleefd hebben? Zoo ja, dan heb ik dus die personen niet in den tijd gezet, maar heb ze eenvoudig met den tijd, waarin zij leefden, en waaraan ik niets toe of afgedaan heb, in mijne voorstelling opgenomen. Ik heb alzoo den tijd tegelijk met hen, als den vorm hunner onderlinge betrekking, die nu eens deze, dan gene is, leeren kennen. Ware het anders, van waar dan de willekeur, waarmede ik in het eene geval ze tot tijdgenooten maak, in het andere ze na elkander plaats?’².

Is mijne uiteenzetting van de leer van Kant niet geheel onvoldoende geweest, dan is bestrijding van dit argument geheel overbodig. Het is in een anderen vorm dezelfde verkeerde opvatting van Kant's bedoeling, waarop ik in mijn artikel over Spencer gewezen heb. Volgens de meening van Kant zijn toch Newton, Huygens, Aristoteles en Kant niets anders dan voorstellingen, die reeds in tijd en ruimte geplaatst zijn. Dat Aristoteles vroeger leefde dan Kant wil niets anders zeggen, dan dat wij vroeger op Kant dan op Aristoteles zouden stuiten, wanneer het ons mogelijk was in het geheel der gegeven ervaring terug te gaan. Dit kunnen wij echter niet doen, omdat de levendige voorstellingen, die door den natuurlijken mensch beschouwd worden als werkelijke dingen; die onafhankelijk zijn

1 Opzoomer, t.a.p., blz. 221.

2 Opzoomer, t.a.p., blz. 270.

[p. 444]

van den waarnemenden persoon, zich altijd aan ons voordoen, in den tijdvorm van het tegenwoordige. Maar wij weten dat, indien ons kenvermogen was ingericht op zoodanige wijze, dat wij ook de voorstellingen, die wij in den verleden tijd plaatsen, op dezelfde wijze konden beschouwen als de levendiger voorstellingen, die ons onmiddellijk tegenwoordig toeschijnen, onze teruggang in de reeks der verleden voorstellingen ons vroeger zou leiden tot Kant, dan tot Aristoteles. Volgens het gewone spraakgebruik zegt men nu, dat Aristoteles vroeger leefde dan Kant, en men kan dit spraakgebruik gerust behouden, als men er maar geen verkeerde beteekenis aan geeft. De Aristoteles, die destijds leefde, behoorde tot dezelfde wereld der voorstellingen, waartoe de Aristoteles behoort, wiens beeld wij ons ontworpen hebben naar zijne werken en naar de berichten van zijne tijdgenooten. De gansche natuur, die Opzoomer op deze plaatsen tegen onze voorstelling overstelt, zij is niets anders dan het aaneengeschakeld en geordend geheel onzer voorstellingen. Eene meer juiste beoordeeling van het idealisme vinden wij bij Opzoomer in de eerste verhandeling van de Waarheid en hare Kenbronnen, al is ook daar de schadelijke invloed van de zoo even genoemde dwaling gemakkelijk aan te wijzen. Maar toch, tegen het grootste gedeelte van die verhandeling is niets in te brengen. Ik moet geheel instemmen met de woorden: ‘Buiten uwe voorstellingen komt ge nimmer. De raad, om ze aan de dingen zelf te toetsen, is dus volkomen onpractisch; het is de raad om iets te doen wat onmogelijk is’¹. Daar wij nu niet gelooven, dat er een Aristoteles of een Kant bestaat buiten de wereld van onze voorstellingen, ten minste in ieder geval niets kunnen weten van deze hypothetische personen, zou het onverstandig zijn te willen onderzoeken, of zij buiten onze voorstelling dezelfde verhouding hebben, die wij hun binnen onze voorstelling toeschrijven. In zijn blinden ijver tegen de leer, dat tijd en ruimte aangeboren waarnemingsvormen zijn, heeft Opzoomer in zijn Wetenschap en Wijsbegeerte den raad gevolgd, dien hij in de Waarheid en hare Kenbronnen terecht als onpractisch veroordeelt.

Waaraan het nu ligt, dat onze voorstelling Aristoteles door ons geplaatst wordt in een vroegeren tijd, dan onze voorstel-

1 Opzoomer, De Waarheid en hare Kenbronnen, blz. 17.

[p. 445]

ling Kant, daarvan laat zich evenmin eene oorzaak aangeven als van het feit, dat suiker zoet en azijn zuur is. Alleen bij de wiskunde, die uitsluitend handelt over onze subjectieve waarnemingsvormen, is alles met volkomen evidentie af te leiden uit eenige weinige axioma's. Bij de oplossing van een wiskundig vraagstuk, blijft ons geene vraag meer te beantwoorden over, wanneer wij deze axioma's als waarheden erkennen. Maar bij de verschijnselen in de stoffelijke en de geestelijke wereld blijft er altijd iets over, dat niet verder verklaard kan worden. Datgene, wat wij ons voorstellen in onze aangeboren waarnemingsvormen is ons nooit zoo volledig bekend, als die vormen zelven. Ook ons eigen lichaam behoort tot die voorstellingen: onze geest bestaat uit twee bestanddeelen, dat, wat voorgesteld wordt, en datgene, wat zich het voorgestelde voorstelt. Van dit laatste, het waarnemend subject, bemerken wij niets hoegenaamd. Het is de onbekende grootheid, die de oude psychologen met onzen geest verward hebben, wiens eenheid en onsterfelijkheid zij meenden te kunnen bewijzen door de eenheid van deze onbekende, die ons daarom alleen als ondeelbaar toeschijnt, omdat wij nimmer eenige eigenschap van haar kunnen waarnemen. Dit was de diepzinnige waarheid, waarmede Kant de oude metaphysica onttroond heeft in een der schoonste gedeelten van de eerste uitgave zijner kritiek, de paralogismen van de reine rede. Alles dus, wat wij kennen door de innerlijke waarneming, onze liefde en onzen haat, onze verachting en onze bewondering, dat alles is voorstelling van het onbekende subject. Wij zelven zijn, voor zoo ver wij ons zelven kennen, psychisch zoowel als lichamelijk, voorstelling van het waarnemend subject en staan in zooverre gelijk met al onze medemenschen. Want zij gelijken volkomen op ons in hunne uiterlijke gedaante, en zij vertoonen ons verschijnselen, waaruit wij kunnen afleiden, dat ook zij een geest hebben, gelijk aan den onzen. Wel hebben wij voor de laatste bewering geen absolute zekerheid, maar toch zoo groote waarschijnlijkheid, dat zij voor de praktijk met zekerheid is gelijk te stellen. Eene dergelijke groote waarschijnlijkheid is ook op elk ander veld, buiten dat van de mathesis, de analytische oordeelen, en de algemeene wet der causaliteit, het hoogste, wat voor ons te verkrijgen is.

Wat Opzoomer hier als natuur tegenover onze voorstelling plaatst, is de wereld der Noumena. In deze nu bestaat vol-

[p. 446]

gens Kant geen tijd, geen ruimte, geen causaalverband, geen Kant noch Aristoteles, Van overeenstemming tusschen die wereld der Noumena en de ons bekende wereld der Phaenomena kan geen sprake zijn.

Na de uitvoerige wederlegging der bezwaren, door Opzoomer aangevoerd tegen Kant's denkbeelden over tijd en ruimte, is het minder noodig de redeneeringen van Mill ieder afzonderlijk te onderzoeken. Wij vinden de argumentatie van Mill in de twee laatste hoofdstukken van het tweede boek zijner logica. Die hoofdstukken bevatten, behalve eenige denkbeelden over het hypothetisch karakter der mathematische wetenschap, welker juistheid voor ons tegenwoordig doel niet behoeft onderzocht te worden, twee argumenten tegen de meening van Kant. Vooreerst houdt Mill tegenover Whewell de bewering staande, dat de ervaring ons geleerd kan hebben, dat eene wiskundige waarheid niet anders kan zijn, dan wij haar aannemen. Om de juistheid van deze paradoxe bewering te doen inzien, tracht hij het bewijs te leveren, dat de ervaring ons niet alleen leert, dat twee snijlijnen elkander slechts eenmaal ontmoeten, maar ook, dat zij elkander niet voor de tweede maal kunnen ontmoeten. Ten tweede beweert Mill, dat eene stelling nog niet waar behoeft te zijn, omdat haar tegendeel ondenkbaar is. De redeneering, waarop deze laatste bewering berust, is reeds vroeger door mij onderzocht; ik geloof te hebben aangetoond, dat de strijd tusschen Mill en Whewell haren grond vindt in de verwarring van de begrippen ondenkbaar en in de hoogste mate onwaarschijnlijk. Mill heeft gelijk, wanneer hij wil zeggen, dat eene stelling waar kan zijn, al schijnt zij ons in de hoogste mate onwaarschijnlijk: Whewell, als hij beweert, dat eene stelling, die voor ons ondenkbaar is, onmogelijk waar kan zijn.

Het vraagstuk der twee snijlijnen komt ook bij Opzoomer voor, maar dient bij hem alleen als een voorbeeld ter verduidelijking van zijne reeds vroeger behandelde theorie aangaande het verschil tusschen noodzakelijke en toevallige waarheden. Bij Mill daarentegen staat het geheel op zich zelf. Hij wil ons in dit voorbeeld laten zien, hoe de ervaring ons apodictische zekerheid kan geven. Hij geraakt tot zijn doel door eene wijze van redeneeren, die waarschijnlijk aan Opzoomer eenigszins zonderling is voorgekomen, daar hij wel het andere argu-

[p. 447]

ment van Mill heeft overgenomen, maar diens beschouwing over de twee snijlijnen niet. Echter vinden wij in Opzoomer's werken de redeneering van Mill met geen enkel woord bestreden.

Een der meest sprekende eigenschappen der geometrische vormen is, volgens Mill, hunne vatbaarheid om zoo duidelijk in onze verbeelding te worden aanschouwd, dat onze voorstelling van het beeld even duidelijk is als onze beschouwing van de werkelijkheid. Van daar dat wij even goed kunnen experimenteeren met onze voorstellingen van de meetkunstige figuren als met de werkelijke figuren, die wij bijv. op een bord kunnen teekenen. Wij zouden echter niet gerechtigd zijn, de beschouwing van onze voorstelling der lijnen, hoeken, enz. in de plaats te stellen voor de beschouwing der werkelijke lijnen, hoeken, enz., wanneer wij niet door eene langdurige ervaring geleerd hadden, dat al de eigenschappen der werkelijke figuren volkomen getrouw worden teruggegeven door ons gedachtebeeld van die figuren.

Nu kunnen wij wel niet zien, dat twee snijlijnen elkander nooit weder ontmoeten, want om dat te zien zouden wij de beide lijnen met onzen blik tot in het oneindige moeten volgen. Maar wij kunnen toch, zonder zulks te doen, zeker weten, dat, wanneer zij elkander ontmoeten, of ook slechts elkander beginnen te naderen, dit niet op oneindigen, maar op eindigen afstand moet plaats vinden. Denken wij ons nu, dat de lijnen elkander beginnen te naderen, dan kunnen wij onze verbeelding op de plaats vestigen, waar deze nadering begint en ons een beeld ontwerpen van de figuur, die eene der lijnen of de beide lijnen op die plaats moeten vertoonen. Wanneer wij dit doen, of ons de algemeene uitkomsten van onze vroegere beschouwing van werkelijke lijnen in het geheugen terugroepen, zal het ons duidelijk blijken, dat eene lijn, welke, na zich eerst van eene andere lijn te hebben verwijderd, die andere lijn begint te naderen, op onze zintuigen den indruk maakt van eene gebogen lijn en niet van eene rechte¹.

1 Mill, A system of Logic. Sec^d. Edition, p. 308-311. Het bewijs is te lang om geheel geciteerd, of woordelijk vertaald te worden. Ik geef alleen het slot in Mill's eigen woorden. For though, in order actually to see that two given lines never meet, it would be necessary to follow them to infinity; yet without doing so we may know that if they ever do meet, or indeed if after diverging from one another, they begin again to approach, this must take place not at an infinite, but at a finite distance. Supposing, therefore, such to be the case, we can transport ourselves thither in imagination, and can frame a mental image of the appearance which one or both of the lines must present at that point, which we may rely upon as being precisely similar to the reality. Now, whether we fix our contemplation upon this imaginary picture, or call to mind the generalizations we have had occasion to make from former ocular observation, we shall either way be equally satisfied, that a line which, after diverging from another straight line, begins to approach to it, produces the impression on our senses, which we describe by the expression ‘a bent line’, not by the expression, ‘a straight line’.

[p. 448]

Het sophisme, in deze redeneering verborgen, is niet moeilijk te ontdekken, ook wanneer wij afzien van het moeilijk onderzoek naar de gronden, waarop Mill kan beweren, dat de lijnen elkander slechts op een eindigen afstand kunnen gaan naderen en niet op een oneindigen afstand. Die bewering steunt waarschijnlijk op de valsche opvatting, dat het oneindige iets positiefs zou zijn, terwijl het eenvoudig de afwezigheid van grenzen beteekent. Doch wij wenden ons liever tot de hoofdzaak. Men zal toestemmen, dat het betoog van Mill op het volgende neerkomt. ‘Wanneer wij ons twee lijnen voorstellen, die na zich eerst van elkander te hebben verwijderd, elkander weder gaan naderen, dan maakt ten minste eene van die lijnen op ons den indruk van eene gebogen lijn.’ Want zijn beroep op de algemeene uitkomsten onzer vroegere ervaring over werkelijke lijnen mag niet worden aangenomen. Onze ervaring heeft zich toch altijd alleen uitgestrekt over lijnen van zekere bepaalde lengte, maar niet over lijnen, die nog langer zijn, dan de langste, die wij ons denken kunnen. Ook wanneer iemand zijne ervaring over stoffelijke lijnen had uitgestrekt tot lijnen van 1000 meter lengte, dan heeft de ervaring hem alleen gemachtigd tot redeneeringen over de lijnen, die niet langer zijn dan 1000 meter. Over de lijnen, die 1001 meter lang zijn, heeft zij hem niets gezegd. Onder het woord oneindig, hier oneindig verlengde lijn, verstaan wij niets anders dan eene lijn, die langer is dan elke lijn, die wij ons kunnen voorstellen. Hoe uitgebreid nu onze ervaring over rechte lijnen ook zijn moge, over lijnen, die onbepaald verlengd zijn, kan zij ons geene algemeene regels aan de hand doen. Dus berust de kracht van Mill's bewijsvoering alleen in het onloochenbare feit, dat hoever wij ook de twee snijlijnen in onze voorstelling verlengen, wij ze elkander slechts kunnen doen naderen door ons de eene of beiden als gebogen voor te stellen. Maar nu heeft Mill zelf, van uit zijn standpunt zeer con-

[p. 449]

sequent, een oogenblik te voren erkend, dat de eigenschappen der lijnen in onze voorstelling alleen daarom gelden van werkelijke lijnen, omdat de ervaring ons de volkomen gelijkheid van de werkelijke lijnen en de lijnen in onze voorstelling heeft leeren inzien¹. Het is dus deze laatste bewering, die bewezen moet worden, maar die niet bewezen wordt. De ervaring heeft ons alleen bekend gemaakt met lijnen van eene bepaalde grootte; alleen door ons voorstellingsvermogen komen wij tot het denkbeeld van eene onbepaald verlengde lijn, eene lijn, die altijd nog iets langer is dan de langste, die wij ons kunnen voorstellen. Hoe kan ons nu de ervaring hebben geleerd, dat de besluiten, door ons uit de beschouwing van begrensde lijnen afgeleid, ook geldig zijn voor de onbepaald verlengde lijn, die de ervaring ons niet kan vertoonen?

Wat in dit geval, en in vele andere, de empirische wijsgeeren op een dwaalspoor gebracht heeft, is de omstandigheid, dat ook in de natuurwetenschap zeer dikwijls meeningen worden uitgesproken, en voor onbetwistbaar gehouden, over verschijnselen, die de ervaring nog niet heeft doen zien. Zij houden de redeneeringen op grond van onze wiskundige aanschouwing voor gelijksoortig met de gerechtvaardige deducties uit natuurkundige wetten. Toch is er tusschen die beiden een zeer wezenlijk verschil; de laatsten voorspellen wel dingen, die de ervaring nog niet getoond heeft, maar zij houden zich toch altijd op het gebied, waarop de ervaring mogelijk is. De eersten daarentegen overschrijden in het geval der snijlijnen, der asymptoten, der oneindige deelbaarheid en in duizenden andere gevallen de grenzen van alle mogelijke ervaring. Kiezen wij van de natuurkundige deductiën een voorbeeld, om het verschil duidelijk te doen inzien.

Het experimenteel onderzoek heeft bij alle permanente gassen twee wetten aan den dag gebracht, die de verandering bepalen van het volumen dezer gassen bij wijziging van de drukking en van de temperatuur. Zij zijn de bekende wetten van Boyle en van Gay-Lussac. De eerste wet zegt, dat het volumen van zekere gewichtshoeveelheid van het gas omgekeerd evenredig is aan de drukking, waaronder het zich bevindt. De

1 Mill, t.a.p., p. 310. And we should not be authorized to substitute observation of the image in our mind, for observation of the reality, if we had not learnt by long continued experience that all the properties of the reality are faithfully represented in the image.

[p. 450]

tweede wet zegt, dat alle permanente gassen bij verhooging der temperatuur eene vermeerdering van hun volumen ondergaan, die evenredig is aan de temperatuur-verhooging, aan het volumen van het gas en aan zekeren factor α, dien men de uitzettingscoëfficient van het gas noemt. Wij zien voor ons doel af van de kleine afwijkingen van deze wetten, die ook bij de permanente gassen voorkomen. Door middel van deze wetten is nu uit het volumen



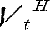van zeker gas, bij zekere temperatuur t en bij zekere drukking H, het volumen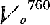



van dezelfde hoeveelheid gas bij de temperatuur van 0^o en den gemiddelen barometerstand gemakkelijk te berekenen. De beide wetten worden namelijk uitgedrukt door de volgende formule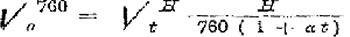

Door de toepassing van deze formule berekent men nu bijv. gemakkelijk, welk volumen eene zekere hoeveelheid zuurstof bij 0^o en 760 mm. drukking zal innemen, wanneer men haar volumen bij 20^o en 500 mm. drukking heeft gemeten. Nu heeft de ervaring waarschijnlijk niets geleerd over de veranderingen, die dat bepaalde volumen zuurstof ondergaat bij die bepaalde veranderingen van temperatuur en drukking. Toch aarzelt de natuurkundige niet zijne formule toe te passen, en twijfelt niet aan de juistheid van de uitkomst zijner berekening.

De empirische wijsgeer nu, die zoo vele andere zaken in het hoofd heeft, dat hij zijn minister voor natuurkundige zaken slechts enkele malen een paar uur ten gehoore kan ontvangen, heeft menigmaal dergelijke bewerkingen zien verrichten, en, geen tijd hebbende nauwkeuriger te onderzoeken, stelt hij ze op ééne lijn met andere bewerkingen, die zijn minister voor de wiskunde nu en dan voor hem gedaan heeft. Immers, zegt hij, ook mijn natuurkundige gaat verder dan de ervaring hem geleerd heeft, even als mijn wiskunstenaar in het geval der twee snijlijnen, en in zoo vele andere gevallen. Volkomen tevreden over de homogeniteit van zijn ministerie, begeeft hij zich aan de meer aristocratische werkzaamheden, die de levenstaak uitmaken van den constitutioneelen koning¹.

1 Ik heb mij, om de betrekking van den wijsgeer tot de beoefenaars der bijzondere wetenschappen op te helderen, in mijne lessen ook wel van de vergelijking met den constitutioneelen vorst en zijne ministers bediend. Terwijl in den vorst de eenheid der regeering zetelt, kan hij geen enkele regeerings- daad verrichten, waaraan het contraseign van een zijner ministers ontbreekt. Opzoomer, Wetenschap en Wijsbegeerte, blz. 74.

[p. 451]

Toch is het verschil tusschen de natuurkundige en de wiskundige deducties duidelijk genoeg. De eerste wagen zich in geen geval verder, dan mogelijke ervaring zich uitstrekken kan, en zelfs gelooft men niet aan de juistheid van deze deducties, dan wanneer de werkelijke ervaring zich zoover uitgestrekt heeft, als de deducties reiken. Slechts is het niet noodig, dat die werkelijke ervaring juist door denzelfden persoon gemaakt is, die de deducties afleidt. De wetten van Boyle en van Gay-Lussac zijn zoo nauwkeurig onderzocht door zoo vele geloofwaardige proefnemers, dat men het niet noodig vindt, zich telkens van hunne juistheid te overtuigen, als men ze wil toepassen. Wanneer thans nog natuurkundigen zich bezig houden met het onderzoek van deze wetten, dan doen zij zulks niet, omdat zij twijfelen aan hunne bruikbaarheid in de toepassing, maar omdat zij de kleine afwijkingen nauwkeurig willen leeren kennen, die alle gassen vertoonen; afwijkingen, die bij de permanente gassen zoo klein zijn, dat men ze bij verreweg de meeste toepassingen reeds daarom moet verwaarloozen, omdat de onvermijdelijke fouten bij de aflezing van het volumen, van de drukking en van de temperatuur nog grootere fouten in de uitkomst veroorzaken. Als dus de natuurkundige bij zijne onderzoekingen een besluit afleidt uit die wetten, dan is zijn besluit reeds vooraf door vele moeitevolle onderzoekingen gerechtvaardigd, die eens voor goed hebben uitgemaakt, tot hoe ver dergelijke besluiten door de ervaring worden bevestigd. Zoo hij verder gaat, dan de ervaring hem recht geeft, dan is het alleen hierin, dat hij meent, dat die wetten ook in zijn geval zullen toepasselijk zijn, dat hij gelooft aan de wet der causaliteit.

In enkele gevallen zal zich de natuurkundige ook besluiten veroorloven, die iets verder gaan dan de grenzen van het gebied, waarover zich de werkelijke ervaring op het oogenblik uitstrekt. Als er bijv. een nieuw permanent gas ontdekt wordt, zullen vele natuurkundigen, reeds voordat het onderzoek hun daartoe recht geeft, overtuigd zijn, dat ook het nieuwe gas aan de wetten van Boyle en Gay-Lussac zal gehoorzamen. De meerderheid intusschen is reeds zoo sceptisch geworden, dat ik vermoed, dat zij zelfs in dit geval met Montaigne zal zeggen:

[p. 452]

‘Que sais je? Reeds zag ik zooveel dingen gebeuren, die vroeger ongerijmd schenen, dat ik geen greintje vertrouwen meer heb in de regelmatigheid der natuur, en zelfs aan de wet der causaliteit zou willen vertwijfelen, als het mij maar niet onmogelijk was, dit te doen.’ Maar ook de gemoedelijke natuurkundige, die nog wel gelooven wil, dat er eenige orde in de natuur wordt gevonden, zal aan zijne meening niet meer dan een zekeren graad van waarschijnlijkheid toekennen, en hij zal zich wachten met zekerheid te spreken, totdat ook het nieuwe gas in dit opzicht onderzocht is. Zoo zal de natuurkundige zijne wet van het behoud van arbeidsvermogen, hoe groote waarschijnlijkheid zij ook moge hebben, over geen enkel gedeelte der natuurkunde uitbreiden, zonder zich eerst door moeilijke experimenten te hebben overtuigd, dat zijne besluiten, uit die wet afgeleid, door de ervaring worden bevestigd. Voordat die proefnemingen behoorlijk hebben plaats gevonden, zullen hem ook de meest waarschijnlijke conclusies slechts als nuttige wegwijzers dienen in het onafzienbare veld van het experimenteel onderzoek.

De wiskundige daarentegen spreekt met onwankelbare zekerheid niet alleen over dingen, die de werkelijke ervaring nog niet getoond heeft, maar ook over dingen, die de mogelijke ervaring nimmer toonen kan. De stelling, die de eigenschappen van de asymptoot eener hyperbool met onwederlegbare zekerheid aangeeft, moge hier als voorbeeld strekken. De natuur toont ons geen hyperbolen, niet eens brokstukken van hyperbolen; eene geheele hyperbool met hare asymptoten kan zij ons niet toonen, omdat zich die lijnen uitstrekken tot in het oneindige, dat wil zeggen, altijd nog verder dan wij ze ons kunnen voorstellen, wat natuurlijk veel verder is dan de natuur ze ons kan vertoonen. Wilde de natuurkundige een tegenhanger geven van de wiskundige conclusies, dan zou hij bijv. met apodictische zekerheid moeten spreken over een nieuw gas, dat hij zich in den dampkring van Sirius aanwezig dacht. Zelfs als hij zoo onverstandig was, dit te doen, zou hij nog de stoute vlucht der mathematische redeneering niet bereiken; hij spreekt dan toch nog maar van een gas, voor welks bestaan hij geen enkel empirisch bewijs heeft, en dat hij waarschijnlijk nimmer zal kunnen onderzoeken. De wiskundige daarentegen heeft de zekerheid, dat de voorwerpen, over welke hij oordeelt, onmogelijk door de ervaring zijn te bereiken.

[p. 453]

Vestigen wij eindelijk onze aandacht op eene onloochenbare waarheid, die bij de discussie over den oorsprong onzer denkbeelden over tijd en ruimte, voor zoo ver mij bekend is, tot hiertoe door de empirische wijsgeeren uit het oog is verloren en die toch in dit vraagstuk beslissend is. Ik heb het oog op de oneindige deelbaarheid en de continuïteit van tijd en ruimte. Hoezeer ik ook gezocht heb naar die bewering, ik heb bij geen enkel empirisch wijsgeer, en trouwens evenmin bij eenig niet-empirisch wijsgeer, de uitspraak kunnen vinden, dat tijd en ruimte geenszins tot in het oneindige deelbaar zouden zijn. Waarschijnlijk zouden er wel plaatsen te vinden zijn, waarin zij hunne overtuiging uitspreken, dat die oneindige deelbaarheid moet worden erkend, maar ook dergelijke plaatsen heb ik niet kunnen aantreffen. Wanneer zij dit vraagstuk niet bij toeval, maar opzettelijk vermijden, is hunne voorzichtigheid niet onverklaarbaar, want het levert ons een experimentum crucis, waarin hunne wijsbegeerte bezwijkt. Stemmen zij toch in met de bewering van alle wiskundigen en van alle menschen, wier denkvermogen de geringe oefening verkregen heeft, die noodig is om dit vraagstuk te beslissen; stemmen zij met deze allen overeen in de bewering, dat tijd en ruimte tot in het oneindige deelbaar zijn, dan is het ook duidelijk, dat zij niet langer kunnen volhouden, dat onze oordeelen over tijd en ruimte door de ervaring zijn verkregen. Want hoe zou ons de ervaring oneindige deelbaarheid kunnen toonen? Onze zintuigen zijn zoo grof, dat wij weldra moeten afzien van de empirische verdeeling onzer ruimtegrootheden, en eene empirische tijdsverdeeling kunnen wij in het geheel niet maken. Immers, onze empirische meting van den tijd bestaat in het meten van de ruimten, beschreven door een lichaam, dat zich met gelijkmatige, of zoo als men gewoonlijk zegt, met eenparige, snelheid beweegt. Hoe kan de ervaring ons dan geleerd hebben, dat wij bij het verdeelen der ruimte nooit zullen komen tot iets, dat twee ruimtedeelen van elkander scheidt, maar zelf geen ruimte is; bij onze verdeeling van den tijd nooit op iets, dat twee tijdsdeelen van elkander scheidt, maar zelf geen tijd is? Daar de ervaring ons dit nimmer kan geleerd hebben; daar zij ons zelfs geen verschijnselen vertoont, die met de oneindige deelbaarheid van tijd en ruimte eene verwijderde overeenkomst hebben, bevinden zich de empirische wijs-

[p. 454]

geeren voor het volgend dilemma. Of, onze meening over de oneindige deelbaarheid van ruimte en tijd is eene stelling, met wier inhoud zij moeten instemmen, die volkomen onbetwistbaar is. Maar dan is het ook zeker, dat ruimte en tijd geen dingen zijn, die wij uitsluitend door de ervaring hebben leeren kennen. Of, onze meening, dat ruimte en tijd tot in het oneindige deelbaar zijn, is eene ongegronde ideënassociatie, die door de ervaring niet is bevestigd, een droombeeld der bespiegeling, dat de empirische wijsgeer, die zich alleen door de uitspraken der ervaring laat leiden, als een metaphysisch wanbegrip moet verwerpen.

Ik weet niet, of er iemand zal gevonden worden, die de tweede helft van dit dilemma durft kiezen. Want, als er iets gezegd mag worden ondenkbaar te zijn, dan is het eene ondeelbare ruimte en een ondeelbare tijd. Elke ruimte toch heeft hare grenzen; iedere tijd zijn begin en zijn einde. Wij kunnen ons voorzeker die ruimte aangevuld denken door eene stofmassa, die bij de voor ons uitvoerbare bewerkingen niet gedeeld wordt; zoo stellen wij ons volgens de heerschende chemische theorie de atomen voor. Maar aan ieder, die het beproeven wil, zal het blijken, dat wij ons toch deze stofmassa en evenzoo de ruimte, waarin zij aanwezig is, als voor verdeeling vatbaar denken. Nu beteekent de oneindige deelbaarheid der ruimte niet, dat de ruimte tot in het oneindige gedeeld wordt, wat onmogelijk zou zijn, maar dat zij tot in het oneindige voor verdeeling vatbaar is. Over dit laatste laat ons de aanschouwing van de ruimte geen oogenblik in twijfel, en evenmin kunnen wij bij de aanschouwing van den tijd zijne oneindige deelbaarheid en continuïteit ontkennen. Wel moet ik erkennen, dat wij niet alleen tijd en ruimte, maar ook alle zinnelijk waarneembare eigenschappen als continue beschouwen, zoodat wij bijv. meenen, dat er tusschen twee warmtegraden altijd nog een oneindig aantal warmtegraden mogelijk zijn. Op onze overtuiging van de continuïteit van alle natuurverschijnselen berust de toepassing der mathesis op de physica. Maar toch blijven tijd en ruimte in dit opzicht eene afzonderlijke plaats innemen. Want uit de continuïteit van ruimte en tijd leiden wij onze wiskundige stellingen af, zonder er ooit naar te vragen, of de ervaring ze ook bevestigt. De continuïteit der sterkte van de waarneembare eigenschappen der lichamen wordt wel in onze natuurkundige redeneeringen gebruikt, maar wij vinden

[p. 455]

het toch altijd noodig de uitkomst van onze redeneering aan de ervaring te toetsen. Wij kunnen niet nalaten de voorstelling der continuïteit, die aan onze aangeboren waarnemingsvormen eigen is, ook op de gewaarwordingen toe te passen, die ons de ervaring leert kennen, en meenen bijv., dat eene bepaalde kleur door een oneindig aantal schakeeringen tot wit kan worden. Maar het feit, dat wij de intensiteit der kleur als eene continue grootheid moeten denken, leidt ons niet tot eene deductieve wetenschap der kleur, omdat wij in die eigenschap niet uitsluitend te doen hebben met een vorm onzer waarneming, maar tevens met den inhoud der gewaarwording, die eerst tot onze waarneming of voorstelling wordt, als wij haar in de vormen van ruimte en tijd opnemen.

De geschiedenis leert ons, dat de aanhangers van een wijsgeerig stelsel geen bezwaar hebben in de verdediging van tastbare ongerijmdheden, wanneer zij door een beslissend argument hunne geliefkoosde meening in gevaar zien. Met het oog op deze bekende waarheid, wil ik nog met eenige woorden aantoonen, welke de zonderlinge gevolgtrekkingen zijn, die met logische noodwendigheid volgen uit de bewering, dat wij niet met zekerheid kunnen oordeelen over de oneindige deelbaarheid van ruimte en tijd. Wordt ons toch de bevoeddheid ontzegd om gebruik te maken van deze waarheid en van de daarmede onafscheidelijk verbondene continuïteit van tijd en ruimte, dan moeten wij al de uitkomsten der differentiaal- en integraalrekening niet langer beschouwen als ontwijfelbare waarheden. Wij behooren dan veeleer de stellingen van deze wetenschappen te rangschikken onder de droomgezichten uit de transcendentale wereld, waarin het Absolute zijne vreemdsoortige oefeningen verricht, die zoo langen tijd met bovennatuurlijke zintuigen aanschouwd zijn door onze oostelijke naburen.

Want de infinitesimaal-rekening berust op de wet der continuïteit, hoe men haar beginsel ook wil afleiden, volgens Leibnitz, volgens Newton of volgens Lagrange. Misschien zou het reeds voldoende zijn de aanhangers van de wijsbegeerte der ervaring te herinneren aan de bekende bewijzen der infinitesimaal-rekening, om deze bewering toegestemd te zien. Daar ik echter niet geheel vrij ben van de vrees, dat de ingenomenheid met hunne wijsbegeerte hen zou kunnen bewegen de waarheid van mijne stelling eenvoudig te ontkennen, daar men zelfs bij Comte sommige zinsneden zou kunnen vinden, die bij eene oppervlakkige

[p. 456]

beschouwing tegen die stelling pleiten, zoo ben ik genoodzaakt mijne bewering nader toe te lichten.

Zooals bekend is vervangt men bij het gebruiken der infinitestimaal-rekening de grootheden, wier betrekking men wenscht te vinden, door zekere hulpgrootheden, wier betrekking gemakkelijker is te ontdekken, en uit wier bekende betrekking men die der eerste grootheden kan afleiden. Die hulpgrootheden worden ingevoerd volgens drie verschillende methoden, die echter in hunne uitkomsten geheel overeenstemmen. De eenvoudigste in de toepassing is de methode van Leibnitz, de moeilijkste die van Lagrange. Comte beweert, dat de laatste uit een wijsgeerig oogpunt meer voldoende is dan die van Newton, en vooral dan die van Leibnitz. Alleen de laatste schijnt mij werkelijk minder nauwkeurig te zijn, zoolang men haar beoordeelt naar de definities, die oorsponkelijk door haren ontdekker zijn gegeven. Beschouwt men toch met Leibnitz de ingevoerde hulpgrootheden als onmerkbaar kleinen, als zandkorrels tegenover de massa der aarde, dan kan men aan de uitkomsten der infinitesimaal-rekening niet meer de volstrekte nauwkeurigheid toekennen, die de overige stellingen der wiskunde kenmerkt, daar men niet kan beslissen, in welke gevallen de loop der bewerkingen de onmerkbaar kleinen tot bemerkbare grootheden zal hebben aaneengevoegd. Maar houdt men zich aan de betere definitie der hulpgrootheden, door Carnot voorgesteld, dan is de methode van Leibnitz even nauwkeurig als de beide andere. Carnot noemt eene grootheid oneindig klein, wanneer men haar zoo klein kan laten worden als men wil, zonder daarom genoodzaakt te zijn de eindige grootheden te veranderen, wier betrekking men wenscht te vinden¹. Als men deze definitie van de differentialen, van de oneindig kleinen, aanneemt, dan valt de uitkomst van Leibnitz' beschouwing zoo spoedig te zamen met die van Newton, dat men gewoonlijk eene vereeniging van beide methoden gebruikt ter uiteenzetting van de beginselen der differentiaal-rekening. Dat nu bij deze uiteenzetting de wet der continuïteit stilzwijgend ondersteld wordt, moge blijken uit de volgende beschouwingen, die ik uit Lobatto's differentiaal-rekening overneem.

1 Carnot, Réflexions sur la métaphysique du calcul infinitésimal, Sec^e. Ed. pag. 3.

[p. 457]

‘Onder oneindig kleine grootheid verstaan wij eene grootheid, die kleiner zij dan elke gegeven gelijksoortige grootheid; zij heeft dus geene bepaalde waarde, maar kan naar welgevallen tot hare limiet nul naderen.

Het denkbeeld van oneindig klein staat in nauw verband met dat van oneindig groot, waaronder men, gelijk bekend is, niets anders verstaat dan eene onbepaalde grootheid, steeds grooter zijnde dan elke andere denkbare grootheid van dezelfde soort. Indien bijv. de verhouding A/B tusschen twee veranderlijke grootheden A en B oneindig groot wordt, kan zulks ontstaan, hetzij uit eene grenzelooze toeneming van A, hetzij uit eene grenzelooze afneming van B. In dit laatste geval nu blijft A eene eindige, doch wordt B met betrekking tot A eene oneindig kleine grootheid.

Van veel belang is het hier aan te toonen, dat indien α en β oneindig kleinen zijn, voorstellende de gelijktijdige aangroeiingen van twee van elkander afhankelijke veranderlijke grootheden, de betrekking tusschen die oneindig kleinen vatbaar is voor eene limiet, welke, in het algemeen, eene eindige of bepaalde waarde verkrijgt. Deze eigenschap, waarin het grondbegrip der differentiaal-rekening opgesloten ligt, kan uit de beschouwing eener kromme lijn gemakkelijk aldus betoogd worden.

Zij MM' eene zekere kromme tot vergelijking hebbende



y = f (x). Laat PP' de eindige of bepaalde aangroeiing Δx voorstellen, welke de abscis OP = x van eenig punt M ondergaat, dan zal met de abscis OP' = x + Δ x, overeenstemmen de ordinaat M'P' = y + Δ y, zoodat Δ y de eindige aangroeiing M' N beteekent, welke de ordinaat y ondergaat bij den overgang van het punt M tot het punt M'. De aangroeiingen of veranderingen Δ x, Δ y der coördinaten x, y worden ook met de benaming van differentiën of eindige verschillen bestempeld. Zij zullen beide positief zijn, wanneer een aanwas van x tevens eene aangroeiing van y te weeg brengt, gelijk in de figuur het geval is. Het kan echter ook gebeuren, dat met eene positieve waarde van Δ x, eene negatieve van Δ y over-

[p. 458]

eenstemt, of omgekeerd, hetwelk van den loop der kromme en van den aard der gegeven functie afhangt. Heeft men bijv. y = a² / x, dan is het duidelijk, dat x niet kan toenemen zonder dat y gelijktijdig afneemt, of omgekeerd, zoodat Δ x en Δ y hier noodzakelijk van tegengestelde teekens zullen zijn. Niets belet intusschen om die differentiën beide als positief te beschouwen, dewijl de bewerking, waardoor de eene in functie der andere bepaald kan worden, van zelve het teeken doet kennen, waarmede Δ y, voor positieve of negatieve waarden van Δ x, moet aangedaan zijn. Nu heeft men, op grond van het hiervoren verklaarde, de vergelijking

y + Δ y = f (x + Δ x);

derhalve

Δ y = f (x + Δ x) - f (x),

waaruit verder volgt, voor de betrekking tusschen de gelijktijdige aangroeiingen der beide coördinaten van eenig onbepaald punt der kromme,

Δ y / Δ x = f (x + Δ x) - f (x) / Δ x

Bij het aanhoudend verminderen van Δ y en Δ x, zullen de punten M, M' blijkbaar elkander meer nabij komen. De teller en noemer van het voorgaande gebroken naderen elk in het bijzonder tot hunne limiet nul; doch met het gebroken zelve zal zulks niet eveneens gesteld zijn, dewijl het, in het algemeen, eene bepaalde en eindige waarde tot limiet verkrijgt.

Immers de verhouding Δ y / Δ x beteekent niets anders dan de trigonometrische tangens van den hoek door de koorde of snijlijn MM' met de as der x gevormd. Laat men nu het punt M' tot M naderen, dan zal de richting der snijlijn al minder en minder afwijken van die der raaklijn MQ aan het punt M, waardoor de richting der kromme in dat punt wordt aangewezen, zonder evenwel met die raaklijn te kunnen overeenkomen, zoolang Δ y en Δ x nog eenige eindige waarden, hoe gering ook, bezitten. De limiet van het gebroken Δ y / Δ x wordt alzoo voorgesteld door den tangens van den hoek MTX tusschen de raaklijn en het positieve deel van de as der x begrepen, en is blijkbaar afhankelijk van de plaats van het punt (x, y), omdat het in den aard eener kromme lijn ligt, aanhoudend van richting te veranderen. Zij kan dus beschouwd worden als eene

[p. 459]

functie van x, die wij door f₁ (x) zullen aanduiden. Dienvolgens stellen wij

Lim. (Δ y / Δ x) = f₁ (x).

Deze nieuwe functie heeft de benaming van afgeleide functie verkregen, uithoofde zij naar bepaalde regels, die wij straks verklaren zullen, uit de oorspronkelijke functie f (x) wordt afgeleid’¹.

In de aangehaalde woorden vinden wij het begin van de redeneering, waarmede Lobatto het bewijs levert van de stelling, waarop de differentiaal-rekening berust, dat de limiet der verhouding van de oneindig kleine veranderingen, die twee van elkander afhankelijke veranderlijke grootheden ondergaan, in het algemeen eene eindige waarde is. In ieder boek over differentiaal-rekening kan men hetzelfde betoog in andere woorden terugvinden. Nu is het niet moeilijk in te zien dat deze redeneering staat en valt met de wet der continuïteit. Door de beschouwing van de kromme lijn wil Lobatto aantoonen, dat de limiet van Δ y / Δ x, voor het geval dat het punt M' tot M nadert, gelijk is aan den tangens van den hoek MTX, en dus aan eene eindige waarde. Hij onderstelt daarbij, dat de snijlijn M'M in de raaklijn aan het punt M overgaat, wanneer het punt M' zich naar M bewegende eindelijk met dat punt samenvalt. Deze waarheid is ook volkomen evident wanneer wij mogen aannemen, dat de ruimte continue is, en dus ook de kromme lijn MM'. Wij kunnen in dat geval de snijlijn MM' om het punt M laten draaien en bij die draaiing het punt M' al de tusschenliggende punten der kromme laten doorloopen, totdat het met M samenvalt. Op dat oogenblik is de snijlijn MM' in de raaklijn TM overgegaan. Denken wij ons nu echter ter wille van het argument, hoezeer het ook tegen de mathematische aanschouwing indruise, dat de lijn MM' niet continue was, maar eene aaneenschakeling van ruimtedeeltjes, gescheiden door iets, wat geen ruimte meer is. Wij willen nu eens aannemen, dat wij bij het draaien de koorde MM' nog altijd door alle punten van de kromme lijn kunnen laten gaan, ofschoon wij hiervoor niet kunnen instaan als de ruimte niet continue is. Denken wij ons nu, dat de koorde MM' bij hare draaiing het ruimtedeeltje

1 Lobatto, Lessen over de differentiaal- en integraalrekening, blz. 4-6.

[p. 460]

bereikt heeft, dat van het punt M gescheiden is door iets wat geen ruimte is. Onze draaiende lijn is nu nog altijd niet ver genoeg gekomen in hare beweging, want Δ y, Δ x hebben nog altijd eindige waarden. Dat onze draaiende lijn eigenlijk op dit oogenblik volstrekt geen lijn meer is, daar zij twee ruimtedeeltjes zou moeten vereenigen, die niet meer door eene ruimte, maar door iets anders, zijn gescheiden - op deze kleinigheid kunnen wij niet letten, daar wij alle mathematische axioma's op zijde geschoven hebben om de ruimte als niet-continue te denken. Zoo behoeven wij er ons ook niet aan te storen, dat wij in onze niet meer continue ruimte het begrip van raaklijn geheel hebben verloren. Want eene raaklijn is volgens de wetenschap, die de ruimte als continue beschouwt, de rechte lijn, waarvan zich de kromme in het raakpunt minder verwijdert dan van eenige andere rechte. In de niet-continue ruimte zouden wij waarschijnlijk de raaklijn aan eene kromme verkrijgen door de twee opvolgende concrete ruimte-deeltjes van die kromme door eene rechte lijn te vereenigen. Maar wij krijgen in dat geval in elk punt der kromme twee verschillende raaklijnen en wij hadden vergeten, dat wij tusschen twee opvolgende punten der kromme geen lijn kunnen leggen, als de ruimte niet continue is. Kortom wij geraken in eene zoodanige opeenstapeling van zwarigheden, dat wij niet slechts de infinitesimaal-rekening, maar de geheele wiskunde als een wespennest van sophismen moeten verwerpen, als de ruimte niet continue is. Merken wij alleen nog op, dat het begrip oneindig klein zijne beteekenis geheel verliest, als de continuïteit der ruimte niet wordt toegestemd. Want hoe zal men de ruimte nog kleiner laten worden dan het concrete, ondeelbare ruimtedeeltje is? Kan dus de differentiaal-rekening niet afgeleid worden volgens de methode van Newton en Leibnitz, zonder het gebruik der oneindig-kleinen in de bovenstaande beteekenis - en ieder wiskundige zal toestemmen, dat die afleiding onmogelijk is - zijn de oneindig kleinen onbestaanbaar in eene ruimte, die niet continue is; dan moet of de differentiaal-rekening beschouwd worden als eene tastbare bedriegerij, of de continuïteit der ruimte worden erkend. Van den tijd, de natuurlijk voorkomende onafhankelijk veranderlijke geldt natuurlijk dezelfde conclusie.

Comte is de eenige onder de empirische wijsgeeren, die deze zwarigheid schijnt te hebben ingezien, al wordt zij niet uitdrukkelijk bij hem vermeld gevonden. Hij aarzelt niet het beginsel

[p. 461]

van Leibnitz ‘radicalement vicieux’ te noemen. De hoogere analyse heeft, als zij op deze wijze wordt opgevat, in mijn oog uit een wijsgeerig oogpunt het groote gebrek, dat zij werkelijk berust op die metaphysische beginselen, waarvan de menschelijke geest al zijne positieve theoriën met zooveel moeite ontdaan heeft¹. In het algemeen ziet Comte de metaphysica overal, waar hij een verschijnsel opmerkt, dat het geluk niet heeft zijne sympathie weg te dragen. Waarschijnlijk zal het den lezer, die geen Franschman is, vreemd voorkomen te hooren, dat de infinitesimaal-rekening op een metaphysisch beginsel zou berusten. Toch geloof ik, dat Comte's instinct hem hier ter plaatse terecht een steen des aanstoots voor de empirische wijsbegeerte heeft doen ontdekken. Zijn instinct, want tot het duidelijk inzicht, dat de wet der continuïteit eigenlijk de metaphysische stelling is, die hem onraad doet vermoeden, schijnt hij niet gekomen te zijn. Hij heeft ten minste veel minder bezwaar tegen de methode van Newton, die toch evenmin kan worden toegepast zonder de stilzwijgende erkenning van de wet der continuïteit. Alleen schijnt hem het beginsel der limieten een denkbeeld te zijn, waarbuiten de analyse zich moest kunnen houden. De invoering van dat begrip maakt in zijn oog eene te scherpe scheiding tusschen de gewone en de hoogere analyse.

Daarentegen vindt hij het zeer gelukkig, dat Lagrange eene afleiding der infinitesimaal-rekening gegeven heeft, die vrij is van elk metaphysisch denkbeeld en aan de eischen van den positieven wijsgeer voldoet. Wel moet hij erkennen, dat de beschouwing van Lagrange zich in de meer samengestelde gevallen bijna niet meer laat toepassen van wege hare moeilijkheid, zoodat ook Lagrange zelf in zijne Mécanique analytique tot de notatie van Leibnitz is teruggekeerd. Maar hij twijfelt er niet aan, of de methode van Lagrange zal mettertijd de eenige zijn, die gevolgd wordt, en de andere zullen alleen van een historisch belang zijn.

Comte's overzicht van de mathesis is, over het algemeen genomen, het schoonste gedeelte van zijn werk. Op deze plaats heeft hem echter zijne vrees voor de metaphysica op een dwaal-

1 L'analyse transcendante, ainsi conçue, présente, à mes yeux, cette grande imperfection philosophique, de se trouver encore essentiellement fondée sur ces principes métaphysiques, dont l'esprit humain a eu tant de peine à dégager toutes ses théories positives.
Comte, Cours de Philosophie Positive, 1, 264.

[p. 462]

weg geleid. Want, hoewel Lagrange inderdaad den schijn aanneemt van zonder eenige beschouwing van oneindig kleinen of limieten de afleiding der differentiaal-rekening te geven, komt hij toch niet tot zijn doel, zonder ter sluiks de hulp in te roepen van de wet der continuïteit. Neemt men nu de wet der continuïteit aan, dan is er althans geen bezwaar tegen de methode van Newton, met welke mij de verbeterde methode van Leibnitz in hoofdzaak schijnt samen te vallen. Dat nu Lagrange de wet der continuïteit moet erkennen, moge blijken uit een paar aanhalingen. Zoo vinden wij in § 14 van zijne Théorie des fonctions analytiques eene stelling bewezen, ‘die men moet beschouwen als een der hoofdbeginselen van de theorie, die wij willen uiteenzetten.’ Deze stelling zegt, dat men in de reeks

f (x) + ph + qh² + rh³ + ...... enz. = f (x + h)

de grootheid h altijd klein genoeg kan nemen om te verkrijgen, dat iedere term van de reeks grooter is dan de som van al de volgende termen. Natuurlijk zou deze stelling onmogelijk in het algemeen waar kunnen zijn, als men de grootheid h niet onbepaald kon doen afnemen. Evenzoo moet ook in § 110 en vlg. de hulp van de wet der continuïteit worden ingeroepen om tot het bewijs te komen van de stelling, dat de gederiveerde functie den tangens uitdrukt van den hoek, dien de raaklijn aan de kromme maakt met de as der abscissen.

De vrees voor de metaphysica, die er Lagrange toe bracht zijn beroemd werk te schrijven, en Comte in navolging van Lagrange de heldere en eenvoudige beschouwingswijze van Leibnitz als ‘essentiellement vicieux’ deed verwerpen, is een bedenkelijk verschijnsel voor de empirische wijsbegeerte in het algemeen, voor de empirische wijsbegeerte over tijd en ruimte in het bijzonder. Want men kan er zeker van zijn, deze groote wiskundigen gevoelden het, dat de wet der continuïteit een onverbreekbare slagboom is tegen alle positivistische denkbeelden. Zij meenden die wet der continuïteit te treffen in de onschuldige notatie van Leibnitz. Zeer opmerkelijk is het, dat Comte, die anders de belangrijkste beginselen der mathesis zoo nauwkeurig en zoo zorgvuldig bespreekt, de wet der continuïteit in het geheel niet vermeldt, noch om hare waarheid te erkennen, noch om haar te bestrijden.

[p. 463]

Zoo is dan de uitkomst van ons onderzoek, dat Kant's leer over tijd en ruimte berust op een voldoenden grondslag, het verschil tusschen de mathematische waarheden, die noodzakelijk en algemeen zijn, en de physische of psychische, die deze eigenschappen missen. Ik geloof er in geslaagd te zijn de nietigheid aan te wijzen van al de argumenten, waarmede men dezen grondslag voor zijn betoog heeft willen doen wankelen. Tegen de wijze, waarop hij zijne andere stellingen uit de behandelde stelling afleidt, heeft, voor zoo ver mij bekend is, geen empirisch wijsgeer eenig bezwaar geopperd¹. Ik kan dus volstaan met naar de Kritik der reinen Vernunft te verwijzen, zoo iemand meenen mocht, dat het transcendentale idealisme niet noodwendig volgt uit de erkenning van het verschil tusschen algemeene en noodzakelijke waarheden en, in zekeren zin, toevallige en niet-algemeene waarheden. Voor heden zal ik tevreden zijn, wanneer ieder lezer slechts wil toegeven, dat Kant gelijk had in zijne stelling, die ik hierboven aldus formuleerde:

De bloote ervaring kan ons slechts leeren, dat zekere waarheid tot nog toe altijd gegolden heeft, nimmer dat zij noodwendig is, en altijd gelden zal.

Wanneer hij dan het feit, dat onze wiskundige waarheden toch noodzakelijk en algemeen zijn, met deze stelling in verband brengt, zal zijne redeneering geen andere uitkomst kunnen geven, dan de erkenning, dat tijd en ruimte de aangeboren waarnemingsvormen zijn, waarin wij datgene opnemen, wat ons het niet-ik brengt. Dat dus deze geheele wereld, die wij aanschouwen, slechts bestaat, zoolang er een oog is, dat haar waarneemt, en slechts ontstaan is toen het eerste bewustzijn zich ontwikkelde.

Tot dus ver hebben wij alleen de bezwaren beschouwd, door de wijsgeeren der ervaring tegen de redeneering van Kant ingebracht. Door de wederlegging van al die bezwaren wordt zonder twijfel het pleidooi voor het transcendentale idealisme gewonnen. Toch kan het zijn nut hebben den oorlog op het vijandelijk terrein over te brengen, en nogmaals dringend te vragen aan de wijsgeeren der ervaring: wanneer onze denk-

1 Alleen Spencer maakt eene uitzondering. Zijne kritiek van Kant's redeneering is echter reeds in een ander artikel door mij zoo uitvoerig beoordeeld, dat ik mij hier ter plaatse tot eene verwijzing naar dat vroegere artikel kan bepalen.

[p. 464]

beelden over tijd en ruimte aan de ervaring ontleend zijn, hoe zijn zij dan wel verkregen? Uit onze waarnemingen geabstraheerd? Maar zij missen alle kenmerken der abstracte begrippen. Zijn zij dan intuïtieve voorstellingen? Maar wij nemen nooit iets anders waar dan bepaalde tijden en bepaalde ruimten. Zijn zij dan oordeelen? Zij gelijken er niets op. Of redeneeringen? Nog veel minder.

Ware de empirische wijsbegeerte een systeem, dan zou men wellicht door deze vragen te stellen de nietigheid van dat systeem kunnen aanwijzen. Maar de empirische wijsgeeren zijn op geestelijk gebied, om met Kant te spreken, eene soort van nomaden, die alle voortgezette bebouwing van den bodem verafschuwend van tijd tot tijd de goede gemeente verstrooien. Op de wijze der nomaden wagen zij zich met hunne lichte wapenen tegen den vasten burcht van het idealisme, maar als de volgeling van Kant hen in hunne eigene versterkte plaatsen wil bestoken, vindt hij in den regel wel vluchtende vrijbuiters, maar geen enkele vesting, door wier verovering hij zich voor latere aanvallen zou kunnen beveiligen. Zonder beeldspraak, de meeste empirische wijsgeeren geven in het geheel geen antwoord op de bovengenoemde vragen, of zij geven het zoo dubbelzinnig en zoo kort, dat het bijna onmogelijk is hen op grond van dat antwoord te overtuigen van dwaling.

In Duitschland maakt de school van Herbart zeker eene uitzondering, zoo men haar ten minste onder het gebied der empirische wijsbegeerte mag rekenen, wat mij minder gepast voorkomt, met het oog op de hevigheid, waarmede Herbart zelf het empirisme veroordeelt. Maar buiten Duitschland zijn mij slechts twee ervarings-wijsgeeren bekend, die beproefd hebben deze vragen, althans voor de ruimte, te beantwoorden. De eerste is Spencer, die echter maar voor een deel met de ervarings-hypothese instemt, de tweede is van der Wijck, die daarentegen volkomen rechtzinnig is in het geloof aan de wijsbegeerte der ervaring. Spencer's antwoord stemt overeen met dat van sommige hedendaagsche physiologen. Uit eene samenwerking van ons spiergevoel en van onzen tastzin zou de voorstelling der ruimte geboren worden. Zijne denkbeelden over dit onderwerp zijn zeker zoo merkwaardig, dat zij eene meer opzettelijke behandeling verdienen. Zij hangen echter al te nauw samen met de geheele leer van het ontstaan der waarneming om ze hier te kunnen bespreken. Dat zijn hoofdresul-

[p. 465]

taat valsch is, hoe belangrijk ook vele van zijne speciale opmerkingen zijn, blijkt reeds hieruit, dat de ruimte ons als een abstract begrip moest voorkomen, als zij ons bekend werd op de wijze, die Spencer beschrijft. Men beschouwe echter deze opmerking geenszins als een antwoord, waarmede ik zijne scherpzinnige onderzoekingen zou meenen te wederleggen; maar alleen als eene voorloopige aanwijzing, dat ik zijne denkbeelden nauwkeurig onderzocht heb zonder er door te worden overtuigd.

Wat nu van der Wijck's antwoord aangaat, het is niet zoo uitvoerig als dat van Spencer, maar zoo beknopt, dat wij het in zijn geheel kunnen citeeren. ‘De voorwerpen der wereld komen tot ons bewustzijn door middel van twee zintuigen hoofdzakelijk: het gevoel en het gezicht. Deze doen ons eindige dingen kennen. Nu is het duidelijk, dat niets mij verplicht op de verschillende eigenschappen van eenig ding tegelijkertijd te letten; ik laat ze alle buiten rekening op ééne na: zijne uitgebreidheid. Aldus verkrijg ik het begrip van eene bepaalde ledige plaats. Maar ik denk ook den vorm dier plaats weg. Nu houd ik het denkbeeld van uitgebreidheid in het algemeen over; niets meer dan dat. Al hare deelen, als zijnde zelve uitgebreidheden en niets anders dan dat, gelijken volkomen op elkander. Wanneer gij tot de grens van één dier deelen genaderd zijt, begint weder een ander deel, hetwelk geheel op het voorgaande gelijkt en dus op zijne beurt weder door een derde deel begrensd moet worden gedacht, en zoo tot in het oneindige voort. Wat ontbreekt er nu nog aan mijne voorstelling der ruimte? Is het niet gelukt haar uit de gegevens der ervaring af te leiden?’¹

Men bemerkt het duidelijk; voor van der Wijck is niets eenvoudiger dan de afleiding van de voorstelling der ruimte. Wel zijn de physiologen sedert honderd jaren bezig naar die afleiding te zoeken; wel meent slechts een enkele haar reeds gevonden te hebben en erkennen de meesten de onoplosbaarheid van het vraagstuk. Maar wie kan ook verwachten, dat zich aan de oogen van deze eenzijdige beoefenaars eener enkele wetenschap eene waarheid zal onthullen, die slechts zichtbaar kan worden voor den wijsgeer, die alle wetenschappen overziet? Verbijsterd door de stoutmoedigheid, waarmede hier in eene halve bladzijde

1 Van der Wijck, De oorsprong en de grenzen der kennis, blz. 26 en 27.

[p. 466]

eene oplossing gegeven wordt van een zoo moeilijk vraagstuk, hebben wij eenige minuten noodig om onze bewondering tot dat peil te matigen, waarop eene rustige beoordeeling van de voorgedragen afleiding mogelijk wordt. Bij die rustige beoordeeling blijkt ons al spoedig, dat wij niets anders voor ons hebben dan eenige woorden, waarin de schrijver het eigenlijk vraagstuk wel uit de verte nadert, maar toch niet eens aanraakt. Want wat houdt men toch wel over, als men den vorm eener ledige plaats wegdenkt, zooals de schrijver ons aanbeveelt? Zeker niet de ruimte in het algemeen, maar eenvoudig niets. Men zou de ruimte in het algemeen moeten overhouden, als deze ruimte een abstract begrip ware, maar men houdt niets over. Zoolang men zich ruimte voorstelt, stelt men zich eene begrensde ruimte voor. Dat de schrijver dit ook wel inziet blijkt uit de volgende zinsneden. Al de deelen van die uitgebreidheid in het algemeen, die hij heeft overgehouden, toen hij den vorm van zijne ledige plaats weg dacht, gelijken toch op elkander. Hoe kunnen nu uitgebreidheden, ledige ruimten, op elkander gelijken, anders dan door hun vorm? Dus had de schrijver alleen gezegd, dat hij den vorm zou wegdenken, maar hij had dien vorm wel degelijk in zijne gedachten behouden. Het doet er toch niets toe, of hij den vorm van het geheel, of den vorm van de deelen beschouwt; bij den laatsten vorm is hij juist even ver van de ruimte in het algemeen als bij den eersten. Dat nu de deelen van zijne uitgebreidheid nog altijd een vorm hebben, blijkt nog duidelijker in den volgenden zin, waarin hij tot de grens van een dier deelen nadert. Hoe kan men toch de grens naderen van iets, dat geen vorm heeft? Blijkbaar heeft hij niet begrepen, dat de ruimte in het algemeen niets positiefs is, maar even als het woord oneindig eenvoudig de afwezigheid van bepaalde grenzen te kennen geeft. Die ruimte in het algemeen nu bestaat uit de som van oneindig vele individueele ruimten. Ons denkbeeld van die ruimte wordt niet verkregen op de wijze der abstracte begrippen door het laten vallen van bijzondere omstandigheden, maar door de aaneenvoeging van individueele ruimten, verbonden met het bewustzijn, dat men die aaneenvoeging altijd nog verder kan voortzetten, hoe ver men haar ook voortgezet heeft. De eigenlijke vraag, die van der Wijck geheel over het hoofd ziet, is deze: Hoe kan de ervaring ons geleerd hebben, dat wij die samenvoeging der individueele ruimten onbepaald kunnen voortzetten,

[p. 467]

en dat wij elke individueele ruimte onbepaald, tot in het oneindige, kunnen verdeelen? Dat wij aan de oneindige grootte en de oneindige deelbaarheid der ruimte niet kunnen twijfelen, bewijst de mathesis, die zonder de erkenning van deze eigenschappen niet kan bestaan; de vraag is nu: kan de ervaring ze ons hebben leeren kennen?

Uit de waarheid van Kant's leer over ruimte en tijd volgt nu met waarschijnlijkheid, dat hij ook in het vraagstuk van het causaalverband recht heeft tegen Hume. Want zooals de onbetwistbare zekerheid der wiskundige waarheden ons leidt tot de aprioriteit van ruimte en tijd, zoo leidt ons de onwankelbare overtuiging van de onverbreekbaarheid der wet van oorzaak en gevolg tot de meening, dat ook zij niets anders is dan een vorm, waarin wij het niet-ik waarnemen, een vorm, die door het subject uit eigen middelen wordt voortgebracht. Maar terwijl de bijzonderheden van onze kennis aangaande tijd en ruimte ons geen twijfel laten over den oorsprong van deze eigenschappen der lichamen, bepaalt zich onze kennis van de wet der causaliteit, voor zoo ver zij algemeen en noodzakelijk is, slechts tot het bewustzijn, dat bij gelijke omstandigheden gelijke verschijnselen te wachten zijn; dat de wet in het algemeen gelden moet. Onze kennis van de werking der wet in bijzondere gevallen berust alleen op de ervaring. Daarom is het niet te ontkennen, dat zij, op zich zelve beschouwd, ons nog altijd laat zonder beslissend argument tegen de leer van Hume en van Spencer. Slechts door, als Schopenhauer, het bewijs te leveren, dat onze allereerste waarneming moet zijn voorafgegaan door de intuïtieve toepassing der wet van oorzaak en gevolg, kan met zekerheid worden aangetoond, dat ook de vorm der causaliteit met de vormen van ruimte en tijd behoort tot de waarnemingsvormen, die ons verstand, zonder daarvan bewust te zijn, moet toepassen om te komen tot de intuïtieve kennis van de wereld der voorstellingen, die voor den natuurlijken mensch den bedrieglijken schijn aanneemt van eene wereld der dingen op zich zelve.

Utrecht, Febr. 1871.

C.B. Spruijt.