De Gids. Jaargang 22

[p. 961]

Bibliographisch album.

Theorie der harmonisch-evenredige getallen, harmonische snijding der lijnen en der transversalen. Handboek ten gebruike van Gymnasiën, Instituten en tot zelfonderrigt, door S. van Logchem, Privaat-onderwijzer te Leyden. 's Gravenhage, Gebroeders van Cleeff. 1856, viii en 306 bl. 8^o.

Het bovenstaande boek werd mij door de Redactie van de Gids ter aankondiging toegezonden: ik achtte het niet ongeschikt voor de lezers van dit tijdschrift, in zoo verre zij niet door den titel van dit boek worden afgeschrikt, - en denzulken kan ik dit stukje ook niet ter lezing aanbevelen, - om daarbij over de zoogenaamde Nieuwere Meetkunde, die de Franschen thans Géométrie supérieure noemen, iets in het midden te brengen. Misschien dat deze opmerkingen den een' of anderen mogten opwekken tot het beoefenen van dit gedeelte der wiskunde: voor hen konde de bijgevoegde literatuur daarin behulpzaam wezen.

Hetgeen men gewoonlijk elementaire Meetkunde, ook wel Beginselen der Meetkunde, pleegt te noemen, dat door de ondervinding geijkt is als een der meest geschikte middelen tot de ontwikkeling van het verstand, en dat dien ten gevolge thans ook de vereischte plaats bij het middelbaar onderwijs heeft erlangd, - die Meetkunde is slechts een klein gedeelte der wetenschap, waaraan bij uitstek den naam van exacte wordt toegekend, ja zelfs van het eene deel daarvan, de Meetkunde. Zij behoort tot de Meetkunde in engeren zin, of wel tot de Meetkunde der Ouden, en behandelt slechts, wat het platte vlak betreft (in de Planimetrie), de regte lijn en den cirkel en de eigenschappen, die bij de onderlinge verbinding van deze ontstaan. Het meerendeel dier eigenschappen was reeds in ouden tijd bekend, en Euclides verzamelde die, ongeveer drie eeuwen vóór het begin onzer jaartelling, in zijne Elementen, een boek, dat thans nog veel voor het onderwijs pleegt gebruikt te worden, of althans den grondslag uitmaakt van de hedendaagsche leerboeken, al moge ongeveer dezelfde stoffe daarin op andere wijze zijn bewerkt. Zulk een synthetisch zamenstel van uit elkander volgende waarheden, waartusschen een goed geordend logisch verband bestaan moet, heeft voorzeker zijne eigen-

[p. 962]

aardige voordeelen bij het onderwijs, zoodat bij eene geschikte methode de goede gevolgen daarvan niet kunnen uitblijven.

De Meetkunde der Ouden omvatte echter nog meer, b.v. de leer van de regte lijn en van het platte vlak in de ruimte, en die van den bol, - dat is de Stereometrie, - de leer van enkele kromme lijnen, inzonderheid die der kegelsneden. Ook leerde de zoogenaamde methode van Exhaustie in sommige gevallen inhoud en omtrek van kromlijnige figuren bepalen.

Een geheel nieuw veld van beschouwingen opende Descartes¹ in de eerste helft der zeventiende eeuw, toen hij de Algebra op de Meetkunde leerde toepassen, waardoor de Analytische Meetkunde ontstond; en deze gaf wederom, op hare beurt, eerlang aanleiding tot de ontdekking van de Theorie der functiën, de Differentiaal-, Integraal- en Variatie-Rekening. Hierdoor werd eerst eene algemeene behandeling der kromme lijnen mogelijk, die voor de methode der Ouden ten eenenmale onbereikbaar was. Het is bekend, dat de grond van deze Analytische Meetkunde bestaat in de leer der coördinaten: laat ons kortelijk nagaan, waarin deze bestaat.

Het eenvoudigste geval is dat van twee regthoekige coördinaten. Laat b.v. twee lijnen, die loodregt op elkander staan, de vlakte van het papier in vier deelen scheiden: dan kan men de plaats van elk willekeurig punt, in de vlakte van dat papier gelegen, bepalen door de afstanden daarvan tot die beide lijnen, de coördinaten-assen genaamd: in dit bijzonder geval wordt de afstand tot de loodregte as abcis, die tot de horizontale as daarentegen ordinaat genoemd. Omgekeerd echter bestaan er voor eenige willekeurige ordinaat en abcis als gegevens, vier punten, die, symmetrisch ten opzigte der beide assen, in de vier gemelde gedeelten van het papier gelegen zijn: deze beschouwing gaf aanleiding tot de bepaling van positieve en negatieve grootheden. Rekent men de abcis ter regterzijde der loodregte as positief, dan wordt zij ter linkerzijde daarvan negatief; rekent men de ordinaat boven de horizontale as positief, dan wordt zij daaronder negatief; en op die wijze is dan elk der vier gemelde punten voor zich onderscheiden. Bij de onderstelling, dat een punt in het bovenste regtsche gedeelte van het vlak eene positieve abcis en ordinaat heeft, wordt de abcis negatief in het bovenste linksche gedeelte, terwijl de ordinaat ook daar positief blijft. Gaat men nu

1 R. Descartes, Géométrie. Paris, 1637. Hiervan is minder zeldzaam de uitgave door onzen van Schooten: Geometria à Renato des Cartes cum notis Florimondi de Beaune, in linguam Lat. versa et comment. ill op. Francisci à Schooten. Lugd. Bat., Maire, 1649, xii et 338 pag. 4^o *, of de tweede uitgave: Amstel., Elsevirios, II Partes, 1650, xiv et 520 pag., 1661, xviii et 424 pag. 4^o *^(a).

(a) De aanhalingen, die het sterretje (*) missen, heeft Ref. niet persoonlijk kunnen nagaan.

[p. 963]

over tot het benedenste deel aan de linkerhand, zoo blijft nu de abcis negatief, maar ook de ordinaat wordt negatief, terwijl eindelijk in het benedenste regtsche deel de ordinaat negatief blijft, en de abcis wederom positief wordt. Voor den positieven toestand gebruikt men het teeken + (plus), voor den negatieven het teeken - (minus). (Het dubbel gebruik van deze teekens, die ook gebezigd worden om de bewerkingen van optellen of aftrekken aan te duiden, heeft dikwerf aanleiding tot misverstand gegeven²)

Men kan derhalve, met inachtneming van dit plus- of minus-teeken der abcis en der ordinaat, de plaats van elk willekeurig punt in die ordinaten uitdrukken, of omgekeerd door middel van die ordinaten vinden. Noemt men nu de abcis b.v. x en de ordinaat y, en onderstelt men, dat y op eenigerlei wijze van x afhange, - of, zoo als men dit noemt, dat y eene gegevene functie van x zij, - dan kan voor elke waarde van x die van y worden berekend, en is alzoo het punt daarmede bepaald, dat met die waarde van x overeenstemt. Al die punten, overeenstemmende met alle mogelijke waarden van x, vormen nu in het algemeen eene kromme lijn (en deze kan alleen regt wezen, als y van den vorm a x + b is, waar a en b willekeurige, positieve of negatieve, standvastigen voorstellen). Deze is dus eene meetkundige voorstelling der vroeger gemelde functie van x, of omgekeerd, die functie van x is de algebraïsche uitdrukking van deze kromme lijn.

Het komt er nu slechts op aan, om na te gaan, welke analytische bewerking overeenkomt met eenige meetkundige constructie, en hierin bestaat de toepassing der hoogere Analyse op de Meetkunde. Zoo, kan men b.v. aan eene zekere gegevene kromme lijn eene raaklijn willen trekken, haar hoogste of laagste punt, of ook wel haren omtrek of inhoud willen bepalen, enz.: hiervoor schoten de krachten der lagere Analyse te kort, en men werd als van zelf gevoerd tot de ontdekking der Differentiaal- en Integraal-rekening, die in zulke bewerkingen moest voorzien.

Hebben de regthoekige coördinaten, en wel die in het platte vlak, hier als voorbeeld gediend, het gezegde geldt niet slechts ten haren opzigte: immers, ieder verband tusschen rigting en afstand in de ruimte, kan als grondslag van een coördinaten-stelsel worden aangenomen, mits daardoor slechts op eene ondubbelzinnige wijze de plaats van eenig punt in de ruimte of op het platte vlak kan worden bepaald. Het zoude te ver voeren, en het is ook niet noodig voor het doel van dit opstel, om deze verschillende stelsels van coördinaten na te gaan.

Maar nevens deze twee takken der Meetkunde, de Meetkunde in

2 Zie mijn stukje: Iets over de betrekking tusschen Meetkunde en Getallenleer. Deventer, de Lange, 1852, 30 blz. 4^o en 1 plaat *.

[p. 964]

engeren zin, of die der Ouden, en de Analytische Meetkunde, is er nog een derde tak ontsproten, de Nieuwere Meetkunde. Hoezeer deze reeds dagteekent van de school van den grooten Monge in het einde der vorige eeuw, is zij tot nog toe, inzonderheid in ons land, betrekkelijk minder bekend; en hiervan mag wel eene reden te zoeken zijn in de verschillende wijze, waarop vele onderdeelen, elk in het bijzonder, door verschillende schrijvers zijn uitgewerkt. Hier moge dus eene korte schets van hare ontwikkeling volgen.

Gaspard Monge voerde door zijne Géométrie Déscriptive³ een nieuw werktuig in de Meetkunde in, even als Descartes dit voor hem gedaan had door zijne leer der coördinaten. Deze Beschrijvende Meetkunde toch leert een stel regelen kennen, om hetgeen er in de ruimte voorvalt, terug te brengen op twee platte vlakken, die loodregt op elkander zijn geplaatst, en wel door middel van projectiën; maar Monge putte hieruit tevens eene methode, om eenige eigenschappen van figuren, die op het platte vlak plaats grijpen, af te leiden uit andere overeenstemmende waarheden in de ruimte: op die wijze ontwikkelde hij de theorie der gelijkvormigheidspunten, der polen en poollijnen. Wel was deze rigting reeds voor hem betreden door Desargues⁴ en Pascal⁵, ook naderhand door de la Hire⁶, le Poivre⁷ en Robert Simson⁸, maar Monge was de eerste, die deze beschouwingswijze tot eene methode verhief, en hare toepassing algemeen maakte.

Naast Monge evenwel staat Carnot, die evenzeer als opvolger van Desargues en Pascal te beschouwen is, maar zich bepaaldelijk toelegde op dat deel der wetenschap, dat den naam draagt van theorie der transversalen⁹, en waarvan de grondstelling is, dat een bundel lijnen, die

3 G. Monge, Géométrie Déscriptive. Paris, Baudouin. An 7 (1799), viii et 132 pag. 4^o et 25 pl. * - ej. op. Nouvelle édition avec un supplément, par Hachette. Paris, Klostermann, 1811, viii et 162 pag. 4^o et 22 pl.; viii et 120 pag. et 11 pl. * - ej. op. 4^e Ed. augmentée d'une théorie des ombres et de la perspective, par Brisson. Paris, Courcier, 1820, xx et 187 pag. 4^o et 28 pl. *. - De laatste 7^e uitgave is van 1847.

4 Over de verschillende werken van Desargues, die verloren gegaan zijn, kan men nazien: Bosse, Traité des pratiques géométrales et perspectives. Paris, 1665, 12^o.

5 Pascal, Essai pour les coniques, 1640, 7 pag. 8^o, opgenomen in Bossut's uitgave van diens werken: Oeuvres de Pascal, 1779.

6 De la Hire, Nouveaux élémens des sections coniques. Les lieux géométriques. La construction ou effection des équations. 1679, 12^o.
De la Hire, Nouvelle méthode en géométrie pour les sections des superficies coniques et cylindriques (Partie 2 des planiconiques). Paris, 1673.
De la Hire, Sectiones conicae in novem libros distributae. Paris, 1685, fol.

7 Le Poivre, Traité des sections du cylindre et du cône, considérées dans le solide et dans le plan, avec des démonstrations simples et nouvelles. 1704.

8 R. Simson, Sectionum conicarum, Libri V. Edinburgi, Rudimannos, 1735, viii et 204 pag. 4^o et 36 tab. * - ej. op. editio 2^a auctior. Edinburgi, Sands, 1750, viii et 224 pag. 4^o et 39 tab. *

9 L.N.M. Carnot, Mémoire sur la relation, qui existe entre les distances respectives de cinq points quelconques pris dans l'espace. - Essai sur la théorie des transversales. - Digression sur la nature des quantités dites négatives. Paris, Courcier, 1806, 112 pag. 4^o et 3 tables. *

[p. 965]

uit hetzelfde punt uitgaan, en eene lijn in eene zekere bepaalde verhouding verdeelt, ook alle andere lijnen, die door dien bundel worden getrokken, in dezelfde verhouding verdeelen zal. Maar niet minder is zijne verdienste door de vereenvoudiging, die hij in de wetenschap invoerde door zijn beginsel van correlatie¹⁰, en daardoor in eene figuur alle mogelijke gevallen eener stelling af handelde, waartoe vroeger even zoo vele figuren moesten gebezigd worden, b.v. door Stewart in zijne, tot dit gedeelte der Meetkunde behoorende, stellingen¹¹.

De rigting van Monge werd vervolgd door zijne leerlingen Dupin¹² en Hachette¹³; terwijl de theorie der transversalen, evenwel zonder van het grondbeginsel van correlatie gebruik te maken, werd uitgewerkt en toegepast door Servois¹⁴ en Brianchon¹⁵. Onder de benaming van Géométrie de la règle werd verder dit onderwerp door ve-

10 L.N.M. Carnot, De la correlation des figures de géométrie. Paris, Duprat, 1801, viii et 188 pag. 8^o et 4 pl. *
L.N.M. Carnot, Géométrie de position. Paris, an XI (1803), 4^o. Hiervan is minder zeldzaam de duitsche uitgave van Schumacher: L.N.M. Carnot, Geometrie der Stellung, übers. von H.C. Schumacher, II Th. Altona, Hammerich, 1810, 8^o, xiv und 366 S., 4 Taf.; iv und 386 S., 10 Taf. *; waarin tevens de Mémoire (zie noot 9) is opgenomen.

11 M. Stewart, Some general theorems of considerable Use in the higher parts of Mathematics. Edinburgh, 1746.
M. Stewart, Propositiones geometricae, more veterum demonstratae, ad Geometriam antiquam illustrandam et promovendam idoneae. Edinb., 1763, 8^o.
Over het eerste werk zie men: Breton de Champ, Journal de Liouville, T. 13. Ann. 1848, p. 281-332. Analyse de l'ouvrage de Stewart, intitulé: Quelques théorèmes généraux d'un grand usage dans les hautes mathématiques. *

12 Ch. Dupin, Développemens de géométrie. - Théorie. Paris, Courcier, 1813, xx et 374 pag. 4^o et 11 pl. *
Ch. Dupin, Applications de géométrie et de Mécanique. Paris, Bachelier, 1822, xxxv et 330 pag. 4^o et 17 pl. *

13 Hachette, Elémens de géométrie à trois dimensions. - Partie synthétique. Paris, Courcier, 1817, xii et 146 pag. 8^o et 2 pl. *

14 F.J. Servois, Solutions pen connues de différens problèmes de géométrie pratique. - Lettre de S. à F. Paris, Courcier, An 12 (1804), 79 et 29 pag. 8^o et 1 table. *

15 C.J. Brianchon, Journal de l'Ecole Polytechnique. Cah. 10, An 1802, p. 1-15. Solution de plusieurs problèmes de géométrie. *
C.J. Brianchon, Journ. de l'Ec. Polyt. Cah. 13, An 1806, p. 297-311. Mémoire sur les surfaces courbes du second degré. *
C.J. Brianchon, Mémoire sur les lignes du second ordre. Paris, Bachelier, 1817, 68 pag. 8^o et 4 tab. *
C.J. Brianchon, Application de la théorie des transversales, 1er (et seul) Cahier, Paris, Bachelier, 1818, iv et 62 pag. 8^o et 1 table. *

[p. 966]

len behandeld; en de ‘Annales de Mathématiques pures et appliquées’ van J.D. Gergonne, zoowel als de Cahiers van het Journal de l'Ecole Polytechnique werden de bewaarplaats van vele belangrijke hiertoe behoorende stukken; onder andere namen muntten vooral uit die van Gergonne, Poncelet, Bobillier, Durrande, Ferriot, Livet, Sturm, Sarrus, Vecten, enz.

Voorafgegaan door een opstel in de Annales van Gergonne¹⁶ opende het werk van Poncelet over de projectivische eigenschappen der figuren¹⁷ een geheel nieuw veld van beschouwing: het berustte gedeeltelijk op het grondbeginsel van dualiteit, dat, het eerste door Snellius¹⁸ gebruikt in het geval van den supplementairen Pooldriehoek in de Bolvormige Driehoeksmeting, ook door Gergonne als zijne uitvinding werd opgevorderd¹⁹. Dit grondbeginsel, door Poncelet genoemd dat der ‘polaires réciproques,’ leert ons twee figuren zoodanig in verband beschouwen, dat, wanneer eenige eigenschap in de eene figuur bewezen is, deze dan ook voor de tweede geldt, mits men punten in plaats van lijnen en omgekeerd lijnen in plaats van punten stelt. Naderhand werden onderscheidene hiertoe behoorende punten door Poncelet meer uitvoerig behandeld²⁰.

Poncelet maakt nog gebruik van een ander beginsel, dat der continuiteit, waarbij de eigenschappen eener figuur ook gerekend worden te blijven bestaan, al heeft de toestand der figuur opgehouden, die

16 J.V. Poncelet, Ann. de Math. T. 8, An 1818, p. 201-232. Solution de deux problèmes de géométrie, suivie d'une théorie des polaires réciproques et de reflexions sur l'élimination. *

17 J.V. Poncelet, Traité des propriétés projectives des figures. Paris, Bachelier, 1822, 425 pag. 4^o.

18 W. Snellius, Doctrinae triangulorum canonicae Libri IV, opus posth. a M. Hortenio ed. Lugd. Bat., 1627, 8^o.

19 Zie over dezen strijd o.a. Gergonne, Ann. de Math. T. 18, An 1828, p. 125-149. Réclamation de M. Poncelet, avec des notes. *

20 J.V. Poncelet, Ann. de Math. T. 16, An 1826, p. 349-360. Mémoire rélatif aux propriétés des centres de moyennes harmoniques. Rapport par M. Cauchy. *
J.V. Poncelet, Journ. v. Crelle, Bd. 3, J. 1828, S. 213-291. Mémoire sur les centres des moyennes harmoniques: pour faire suite au Traité des propriétés projectives des figures et servir d'introduction à la Théorie générale des propriétés projectives des courbes et surfaces algébriques. *
J.V. Poncelet, Journ. v. Crelle, Bd. 4, J. 1829, S. 1-71. Mémoire sur la théorie générale des polaires réciproques, pour faire suite au Mémoire sur les centres de moyennes harmoniques. *
J.V. Poncelet, Journ. v. Crelle, Bd. 8, J. 1832, S. 21-41, 117-127, 213-252, 370-411. Analyse des transversales appliquées à la recherche des propriétés projectives des lignes et surfaces géométriques, pour faire suite aux Mémoires sur les centres de moyennes harmoniques et la théorie générale des polaires réciproques. *

[p. 967]

tot deze eigenschappen aanleiding gaf. Ditzelfde beginsel heeft Gaultier²¹ ook gebezigd bij zijne behandeling der radicale assen, die later ook chordalen zijn genoemd. Hij stelde voorop, dat de gemeenschappelijke koorde van twee cirkels, die elkander snijden, de meetkundige plaats is van de punten, waaruit de raaklijnen, tot de beide cirkels getrokken, gelijk zijn: snijden nu de cirkels elkander niet, dan is er geene eigenlijke gemeenschappelijke koorde, maar daarvoor treedt dan de radicale as, met dezelfde eigenschap in de plaats. Hierom hebben de Duitschers haar ‘Linie der gleichen Potenze,’ of ook wel kortheidshalve ‘Potenzlinie’ genoemd²².

Allengs begon men zich meer op deze beschouwingen toe te leggen, en het beginsel van dualiteit werd op onderscheidene wijzen uitgewerkt: daarbij bleek het al spoedig, dat er, bij de transformatie van eene figuur in de overeenkomstige, twee gevallen konden plaats grijpen: of die transformatie was homographisch, - dat is, met een punt, of eene lijn of een vlak in de eerste figuur stemden weder een punt of eene lijn of een vlak respective in de tweede figuur overeen, - of zij was correlatif, - dat is, met een punt in de eerste stemde eene lijn in de tweede figuur overeen, en omgekeerd met eene lijn in de eerste een punt in de tweede. Zoo kwam Möbius uit de beschouwing van het zwaartepunt, waarin Ceva²³ hem reeds anderhalve eeuw was voorafgegaan, tot zijne leer van collineatie²⁴, die hij later nader uitwerkte²⁵ Deze behoort tot de eerste soort van dualiteit, de ho-

21 L. Gaultier, Journ. Ec. Polyt., Cah. 16, An 1813, p. 124-214. Sur les moyèns généraux de construire graphiquement un cercle déterminé par trois conditions et une sphère déterminée par quatre conditions. *

22 J. Steiner, Journ. v. Crelle, Bd. 1, J. 1826, S. 161-184, 252-288. Einige geometrische Betrachtungen. *
C.F. Arndt, Grunert's Archiv, Bd. 5, J. 1844, S. 115-151. Geometrische Untersuchungen über Potenzlinien, Potenzcentrum und Potenzkreis, Polarität, Aehnlichkeitspuncte und Aehnlichkeitsaxen. *

23 Jo. Ceva, De lineis rectis se invicem secantibus statica constructio. Mediol., Montia, 1678, viii et 84 pag. 4^o et 10 tab. *

24 A.F. Möbius, Der barycentrische Calcul. Leipzig, Barth, 1827, xxiv und 456 S. 8^o und 4 Taf. *

25 A.F. Möbius, Journ. v. Crelle, Bd. 4, J. 1829, S. 117-130. Von den metrischen Relationen im Gebiete der Lineal-Geometrie. *
A.F. Möbius, Journ. v. Crelle, Bd. 10, J. 1833, S. 317-341. Ueber eine besondere Art dualer Verhältnisse zwischen Figuren im Raume. *
A.F. Möbius, Journ. v. Crelle, Bd. 12, J. 1834, S. 109-133. Ueber eine allegemeine Art der Affinität geometrischer Figuren. *
A.F. Möbius, Journ. v. Crelle, Bd. 21, J. 1840, S. 70-73, 156-176. Anwendung der Statik auf die Lehre von den geometrischen Verwandtschaften. *
A.F. Möbius, Journ. v. Crelle, Bd. 24, J. 1842, S. 85-92. Entwickelung einiger trigonometrischer Formeln durch Hülfe der Lehre von den Doppelschnitts-Verhältnisse. *
A.F. Möbius, Journ. v. Crelle, Bd. 28, J. 1844, S. 1-9. Ueber die Zusammensetzung gerader Linien und eine daraus entspringende neue Begründungsweise des baryeentrischen Calculs. *

[p. 968]

mographische, en gaf naderhand tot de affiniteit der figuren aanleiding: Möbius gebruikte de anharmonische verhouding onder den naam van Doppelschnitts-Verhältniss, en pastte het beginsel der correlatie van Carnot bij zijne beschouwingen toe.

Magnus²⁶ en Steiner²⁷ ontwikkelden methoden, die tot de tweede soort van dualiteit, de correlative, behoorden, en Chasles leverde in zijn voortreffelijk historisch overzigt²⁸ eene belangrijke geschiedenis van het ontstaan der nieuwere Meetkunde, en van hetgeen reeds langen tijd vroeger, zelfs door de oudere Mathematici, b.v. reeds bij Pappus²⁹, met betrekking tot dit onderwerp gevonden was; voorts eenige wenken tot verdere uitbreiding en volmaking der verschillende methoden, en eindelijk in de daarbij gevoegde ‘Mémoire’ eene geheele theorie van het beginsel van dualiteit en van dat van homographie afgeleid uit de anharmonische verhouding, waarvan, zoo als later blijken zal, de harmonische verhouding slechts een bijzonder geval uitmaakt³⁰.

Maar nu ook begon men het reeds verkregene in de taal der analyse over te brengen, en daartoe boden zeker de verschillende betrekkingen goede gelegenheid aan: zoo wordt de collineatie door het systeem der vergelijkingen

26 L.J. Magnus, Journ. v. Crelle, Bd. 8, J. 1832, S. 51-63. Nouvelle méthode pour découvrir des théorèmes de géométrie. *
L.J. Magnus, Sammlung von Aufgaben und Lehrsätze aus der analytischer Geometrie. Berlin, Duncker und Humblot, 1833, xii und 660 S. 8^o, 4 T. *
L.J. Magnus, Sammlung von Aufgaben und Lehrsätze aus der analytischer Geometrie des Raumes, erste (einzige) Abth. Berlin, Dunckler und Humblot, 1837, ix und 518 S. 8^o. *

27 J. Steiner, Systematische Entwickelung der Abhängigkeit geometrischer Gestalten von einander, Theil 1 (einziger). Berlin, Fincke, 1832, 8^o.

28 Chasles, Aperçu historique sur l'origine et le développement des méthodes en géométrie; suivi d'un Mémoire sur deux principes générales de la science, la dualité et l'homographie. Bruxelles, Hayez, 1837, 852 pag. 4^o. *

29 Pappi Alexandrini, Mathematicae collectiones à Federico Commandino in Latinum conversae et commentariis illustratae. Bonon., de Duccys, 1660, viii et 490 pag. fol.

30 Chasles, Journal de Liouville, T. 2, An 1837, p. 388-405. Mémoire sur les diverses manières de généraliser les propriétés des diamètres conjugués dans les sections coniques. - Nouveaux théorèmes de perspective pour la transformation des relations métriques des figures. - Principes de géométrie plane analogues à ceux de la perspective. - Manière de démontrer dans le cône oblique les propriétés des foyers des sections coniques. *
Chasles, Journ. de Liouville, T. 12, An 1847, p. 1-40. Sur l'enseignement de la géométrie supérieure. - Discours d'introduction au cours de géométrie supérieure, fondé à la Faculté des sciences de l'Académie de Paris. Séance d'ouverture le 22 Décembre 1846. *

[p. 969]

,



,

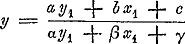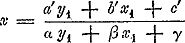en die der polaires réciproques door de vergelijking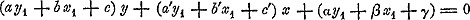

voorgsteld. Vooral in Duitschland won deze rigting veld; Plücker³¹ en Drückenmüller³² leverden Systemen von Verwandtschaft, zoo als deze sedert plegen genoemd te worden; onder onze landgenooten is de, voor de wetenschap te vroeg overledene, Swellengrebel in hunne voetstappen getreden³³.

Algemeener werd daarmede de belangstelling, en vooral in Duitschland werd veel gewerkt: laat ons slechts den arbeid aanhalen van Seydewitz over involutorische figuren³⁴ (in de rigting van Steiner), - van Grassmann, die de leer der centralen³⁵, als vervolg op de theorie

31 J. Plücker, Analytische geometrische Entwickelungen, II Bde. Essen, Baedeker, 1828, 1831, 4^o, viii und 272 S., 8 Taf.; xii und 294 S., 2 Taf. *
J. Plücker, Journ. v. Crelle, Bd. 5, J. 1830, S. 268-286. Ueber ein neues Princip der Geometrie und den Gebrauch allgemeiner Symbole und unbestimmter Coefficienten. *
J. Plücker, System der analytischen Geometrie auf neue Betrachtungsweise gegründet. Berlin, 1835.
J. Plücker, Theorie der algebraischen Curven. Bonn, Marcus, 1839, xvi und 256 S. 4^o, 4 Taf. *

32 N. Druckenmüller, Die Uebertragungsprincipien des analytischen Geometrie, erster (einziger) Bd. Trier, Lintz, 1842, xii und 260 S. 8^o, 1 Taf. *

33 J.G.H. Swellengrebel, Dissertatio mathematica inauguralis de quibusdam curvarum affinitatibus. Traj. ad Rhenum, Bosch, 1847, 95 pag. 4^o, 4 Tab. *
J.G.H. Swellengrebel, Journ. v. Crelle, Bd. 43, J. 1852, S. 245-282. Beitrag zur Lehre von den geometrischen Verwandtschaften. *
J.G.H. Swellengrebel, Neun verschiedene Coordinaten-Systeme in Zusammenhang untersucht. Bonn, Marcus, 1853, xii und 224 S. 4^o, 6 Taf. *
J.G.H. Swellengrebel, Analytisch-geometrische Untersuchungen. Bonn, Marcus, 1855, xii und 166 S. 4^o, 1 Taf.

34 Fr. Seydewitz, Grunert's Archiv, Bd. 4, J. 1844, S. 246-280; Bd. 5, J. 1844, S. 225-258, 331-334. Theorie der involutorischen Gebilde, nebst Anwendungen auf die Kegelschnitte. *
Fr. Seydewitz, Grunert's Archiv, Bd. 8, J. 1846, S. 1-46. Darstellung der geometrischen Verwandtschaften mittels projectivischer Gebilde. *
Fr. Seydewitz, Grunert's Archiv, Bd. 8, J. 1846, S. 115-148. Darstellung der geometrischen Verwandtschaften mittels projectivischer Gebilde mit besonderer Rücksicht auf die Theorie der höheren Curven. *
Fr. Seydewitz, Das Wesen der involutorischen Gebilde in der Ebene als gemeinschaftlicher Princip individueller Eigenschaften der Figuren. Heiligenstadt, 1846, 8^o, 11 Taf.

35 Grassmann, Journal v. Crelle, Bd. 24, J. 1842, S. 262-282, 372-380; Bd. 25, J. 1843, S. 57-83. Theorie der Centralen. *

[p. 970]

der poollijnen, analytisch behandelde - van Adams³⁶ en Wiegand³⁷, die de leer der transversalen, en hare onderdeelen, de harmonische snijdingen en de involutie meer bijzonder behartigden, - van Anger³⁸, die de leer der gelijkvormigheidspunten uitwerkte.

Werken, die deze wetenschap in haar geheel behandelden, bleven echter schaarsch: tot voor eenigen tijd waren het slechts Steiner's Systematische Entwickelung³⁹ en een werk van von Staudt⁴⁰; in de laatste jaren echter zagen nog de werken van Chasles⁴¹ en van Paulus⁴² het licht, die, elk zijne wijze, de verschillende, dikwerf op zeer onderscheidene wijze verkregen, uitkomsten bijeen hebben gebragt, en uit een zelfde beginsel afgeleid.

Laat ons nu zien, of het mogelijk zal zijn, den gang dezer methoden en het verband tusschen al het vroeger genoemde eenigzins duidelijk voor oogen te stellen. Wij moeten daartoe onze toevlugt nemen tot het vroeger uiteengezette begrip van coördinaten, hoezeer dit hier op eene geheel andere wijze moet worden toegepast.

Laat ons op eene regte lijn twee vaste punten, A en B, denken, dan is de plaats van elk willekeurig punt C, op die lijn gelegen, bepaald

36 C. Adams, Die Lehre von den Transversalen in ihrer Anwendung auf die Planimetrie. Winterthur, Steiner, 1843, vi und 138 S. 8^o, 12 Taf. *
C. Adams, Die harmonischen Verhältnisse, erster (einziger) Th. Winterthur, Steiner, 1845, iv und 288 S. 8^o, 4 Taf. *
C. Adams, Die merkwürdigsten Eigenschaften des geradlinigen Dreiecks. Winterthur, Steiner, 1846, viii und 112 S. 8^o, 2 Taf. *

37 A. Wiegand, Sätze über harmonische Verhältnisse. Halle, Schmidt, 1847, 24 S. 8^o, 1 Taf. *
A. Wiegand, Die merkwürdigen Punkte des Dreiecks mit Rücksicht auf harmonische Theilung, zweite Aufl. (des vorhergehenden). Halle, Schmidt, 1848, iv und 92 S. 8^o, 1 Taf. *
A. Wiegand, Die allgemeine goldene Schnitt und sein Zusammenhang mit der harmonischen Theilung. Halle, Schmidt, 1849, 16 S. 8^o. *
Hiermede is niet te verwarren:
Norzewski Roch, Nouvelle théorie des proportions et progressions harmoniques avec ses applications à la géométrie. Paris, Bachelier, 1852, 60 pag. 8^o, 2 pl. * Deze schrijver verstaat onder harmonische verhouding eene evenredigheid a:b = c:d, waarbij a + b + c = d is.

38 C.F. Anger, Betrachtungen über verschiedene Gegenstände der neueren Geometrie, II Hefte. Danzig, Homann, 1839 und 1841, 4^o, iv und 22 S., 3 Taf.; 28 S., 4 Taf. *

39 Zie noot 27.

40 G.K.C. von Staudt, Geometrie der Lage. Nürnberg, Bauer und Raspe, 1847, vi und 216 S. 8^o. * Hierop is onlangs een vervolg gekomen in zijne
Beiträge zur Geometrie der Lage. Nürnberg, Bauer und Raspe, 1856, vi und 129 S. 8^o. *

41 Chasles, Traité de géométrie supérieure. Paris, Bachelier, 1852, lxxxiii et 603 pag. 8^o, 12 pl. *

42 Chr. Paulus, Grundlinien der neueren ebenen Geometrie. Stuttgart, Paulus, 1853, xii und 364 S. 8^o, 10 Taf. *

[p. 971]

door de verhouding der afstanden AC:BC, mits men tusschen AC en CA onderscheid make, en dus b.v. de afstanden, genomen aan de regterzijde van de vaste punten, als positief, die aan de linkerzijde van die punten daarentegen negatief noemt. De genoemde verhouding, die men den Modulus van het punt C zoude kunnen noemen, is dus de positieve eenheid voor het punt, op oneindigen afstand aan de regterzijde gelegen, dewij alsdan beide afstanden oneindig (en dus gelijk) en tevens positief zijn, wanneer wij althans B ter regterzijde van A onderstellen; de modulus wordt steeds grooter, naarmate het punt digter bij B komt te liggen. Voor het punt B zelf wordt de noemer nul en de modulus daarmede oneindig. Ter linkerzijde van het punt B wordt de afstand BC, de noemer van de verhouding negatief, en zal dus, zoolang als het punt C tusschen A en B ligt, de verhouding negatief zijn, en wel van B naar A toe steeds in numerische waarde verminderen, dat is (bij B) van minus oneindig tot nul (bij A) veranderen; want bij dit laatste punt wordt de teller en dus ook de breuk zelf nul. Voor het punt, midden tusschen A en B gelegen, is de genoemde modulus minus de eenheid. Komt het punt C vervolgens ter linkerzijde van A, zoo wordt de teller AC van het gebroken mede negatief, zoodat de modulus zelf wederom positief wordt: bij A heeft deze, zoo als wij zoo even zagen, de waarde nul en klimt steeds totdat hij aan de eenheid gelijk zoude worden aan het punt, op oneindigen afstand ter linkerzijde van A gelegen. Uit het gezegde blijkt, dat de waarde van genoemden modulus, bij de beweging van het punt C, van de regter- naar de linkerzijde van + 1 door + ∞ (of - ∞) gaat, naar 0 en verder weder naar + 1, zoodat die beide uiterste punten eigenlijk hier als dezelfde te voorschijn komen, hetgeen ook in de beschouwingen der Nieuwere Geometrie telkens voorkomt. Tevens blijkt, dat de modulus alle mogelijke waarden doorloopt, en nergens dezelfde waarde heeft, zoodat wij derhalve met regt aannamen, dat de ligging van eenig punt door dien modulus werd bepaald. De punten A en B heeten daarbij toegevoegde punten (points conjugués).

Neemt men nu twee punten, C en C', op de lijn AB aan, zoo is de verhouding tusschen de beide overeenkomstige modulen, dat is de breuk AC/BC:AC'/BC'; juist de anharmonische verhouding van Chasles (door de Duitschers ook wel Doppelverhältniss genoemd). Daardoor is men nu in staat gesteld, om de punten C en C', in betrekklng tot de punten A en B gegeven, ook ten opzigte van elkander te beschouwen; en het is gebleken, dat deze anharmonische verhouding een zeer geschikt, maar ook een zeer krachtig werktuig was, om de figuren en hare eigenschappen te onderzoeken. Wordt de genoemde verhouding gelijk aan de negatieve eenheid, zoo ontstaat

[p. 972]

de harmonische verhouding; daaruit volgt al dadelijk, dat bij eene harmonische snijding één der beide punten C en C', die dan verwante punten kunnen heeten, tusschen de beide toegevoegde punten A en B, het andere daarbuiten moet liggen: anders toch konde de verhouding der beide modulen niet negatief zijn. Verder blijkt het dat, als het punt C b.v. op het midden tusschen A en B ligt, en dus de negatieve eenheid tot modulus heeft, alsdan het vierde punt C' de positieve eenheid tot modulus hebben moet (opdat de verhouding dier modulen minus één worde), en dus op oneindigen afstand, hetzij ter regter- of ter linkerzijde, zal moeten liggen.

Trekt men nu uit eenig punt van het vlak lijnen door de punten A, B, C, C', dan vormen deze eenen zoogenaamden straalbundel: en dan kan men aantoonen, dat tusschen de sinussen der ingesloten hoeken dezelfde verhouding bestaat als tusschen de segmenten der regte lijn AB; dat is, wanneer die lijnen respectivelijk door a, b, c, c' worden aangeduid, en een hoek tusschen twee lijnen p en q in het algemeen, volgens eene gewone schrijfwijze, door (p, q) wordt voorgesteld, - waarbij wederom, even als boven, onderscheid dient gemaakt te worden tusschen de hoeken (p, q) en (q, p), daar deze laatste het negatieve is van den eersten; zoodat dus eerst eene bepaalde draaijingsrigting als de positieve moet worden aangenomen, - dan heet de verhouding Sin. (a, c)/Sin. (b, c):Sin. (a, c')/Sin. (b, c') de anharmonische verhouding van dien straalbundel en is in waarde en teeken juist gelijk aan de anharmonische verhouding tusschen de overeenkomstig afgesneden segmenten der lijn AB. Hieruit volgt al dadelijk, dat elke willekeurige lijn door denzelfden straalbundel volgens dezelfde anharmonische verhouding moet gesneden worden.

Wordt deze verhouding wederom gelijk aan de negatieve eenheid, zoo verkrijgen wij eenen harmonischen straalbundel. Deelt nog hierbij de straal c den afstand AB midden door, dan moet het punt C', zoo als wij boven zagen, op oneindigen afstand ter regter- of ter linkerzijde liggen; dit punt C' is nu niets anders dan het snijpunt van de lijn c' met de lijn AB: dus loopt in dit geval de lijn c' evenwijdig aan die lijn AB.

Men kan ook meerdere punktenparen D en D', E en E', enz. op de regte lijn AB aannemen, zoodanig, dat hunne anharmonische verhouding ten opzigte der punten A en B steeds gelijk blijve aan die, welke voor de punten C en C' bestaat: alsdan heeft men op die lijn eene anharmonische verdeeling, waarbij alle eerste punten C, D, E, de punten der eerste reeks, en alle tweede C', D', C', die der tweede reeks mogen heeten. Het punt van eene dier reeksen, dat overeenkomt met het oneindig verwijderde punt der andere reeks, heet in die eerste

[p. 973]

reeks het Tegenpunt: van diens eigenschappen wordt een menigvuldig gebruik gemaakt.

Wanneer nu twee straalbundels door dezelfde punten van eene lijn AB gaan, zoo hebben zij, naar het boven aangevoerde, dezelfde anharmonische verhouding. En omgekeerd, als twee straalbundels dezelfde anharmonische verhouding hebben, en nog drie snijpunten van overeenkomstige stralen in dezelfde regte lijn liggen, alsdan moet ook het vierde snijpunt der beide overige overeenkomstige stralen in diezelfde regte lijn vallen.

Uit het gezegde volgt reeds, dat deze theorie de leer der transversalen en der harmonische snijdingen bevat, en men zal nog daaruit genoegzaam kunnen opmaken, welke voordeelige eigenschappen zij bezit als methode van onderzoek. Het is daarom, dat Ref. trachtte de grondbeginsels der Nieuwere Meetkunde zoo duidelijk voor te stellen als het korte bestek, waarop hij slechts aanspraak maken konde, hem veroorloofde, terwijl hij zich hier toch niet op een zuiver wetenschappelijk terrein konde bewegen. Maar nu ook eischt de laatste omstandigheid, uit den aard der zake, dat hij in het vervolg slechts het een en ander ter loops aanstippe: het geldt hier toch ook niet, een volledig begrip van den omvang eener wetenschap te geven, maar slechts zoodanige inzigten, als strekken kunnen, om dien omvang te doen gevoelen.

Hebben twee reeksen van punten of twee straalbundels de eigenschap, dat tusschen hunne clementen respective dezelfde anharmonische verhoudingen bestaan, zoo heeten deze homographisch. Liggen deze punten, b.v. zes A, A', B, B', C, C' (waarvan de A', B', C' telkens de toegevoegde de voorafgaande A, B, C zijn), op eene regte lijn, en wel in dier voege, dat de tegenpunten dier beide puntenreeksen op elkander vallen, zoo vormen zij eene involutie, dat is, de anharmonische verhouding van elke vier dezer punten is dezelfde, als die van hunne vier toegevoegde punten, b.v. die der punten A, A', B', C dezelfde als die van hunne toegevoegde A', A, B, C'. Men begrijpt verder, naar het bovenstaande, ligtelijk, hoe deze eigenschappen evenzeer gelden van straalbundels, die door zulke punten gaan.

Wanneer nu twee figuren de eigenschap bezitten, dat elk punt of elke lijn in de eene overeenstemt met een punt of met eene lijn in de tweede, en alsdan elke vier punten of elke straalbundel in de eerste met de overeenkomstige vier punten of met den overeenkomstigen straalbundel in de tweede telkens dezelfde anharmonische verhouding hebben, zoo heeten deze twee figuren homographische, ook wel collineaire.

Wanneer daarentegen twee figuren op zulk eene wijze tot elkander in betrekking staan, dat met elk punt in de eerste eene lijn in de tweede figuur overeenkomt, en wel met vier punten, die in de eerste

[p. 974]

eene regte lijn vormen, ook vier stralen in de tweede figuur, die in een en hetzelfde punt te zamen komen, zoodat dit punt wederkeerig overeenstemt met de lijn, waarop de vier punten in de eerste figuur gelegen waren, - en wanneer bovendien de anharmonische verhoudingen tusschen die vier punten en tusschen deze vier lijnen steeds dezelfde zijn, zoo heeten deze figuren correlative, of ook wel polaire.

Men onderscheidt nog wel als ouderdeelen der collineatie, de affiniteit, wanneer bij twee overeenkomstige puntenreeksen, de overeenstemmende afstanden telkens volgens dezelfde verhouding evenredig verdeeld zijn - de uniformiteit, als de voorgaande reden juist de eenheid is, - de gelijkvormigheid, wanneer de reden der evenredigheden in affine figuren bij alle puntenreeksen dezelfde is, - eindelijk de congruentie, ook wel gelijk- en gelijkvormigheid genoemd, als de laatste reden wederom de eenheid is.

Neemt men verder vier punten op den omtrek van eenen cirkel, dan zal de straalbundel, uit elk willekeurig punt van dien omtrek naar die vier punten getrokken, steeds dezelfde anharmonische verhouding hebben, afhangende van de ligging der vier genoemde punten. Verder leert men, dat wanneer eene koorde, om eenig vast punt, binnen den omtrek van den cirkel gelegen, rondgedraaid wordt, en op het verlengde van die koorde telkens het punt bepaald wordt, dat met het vaste punt ten opzigte van de beide snijpunten van den cirkel harmonisch verwant is, - alsdan dit vierde punt eene regte lijn beschrijft: deze is de poollijn of polaire van het vaste punt, dat dan den naam van pool ten opzigte van die lijn krijgt: en hiermede is de grondslag gelegd voor de theorie der Polen en Poollijnen.

Verder beheort ook hier de theorie der gelijkvormigheidspunten en die der radicale as of chordaal, als gemeenschappelijke koorde van twee cirkels, die elkander niet snijden. Nu kan men, en wel op onderscheidene wijze, tot de theorie der kegelsneden overgaan, in verband met transversalen en harmonische snijding. Zoo heeft de theorie der om- en ingeschreven veelhoeken bij kegelsneden hare ontwikkeling aan de Nieuwere Meetkunde te danken; het eerst werd zulk eene eigenschap bekend in het zoogenaamde Hexagramma mysticum van Pascal.

De Nieuwere Meetkunde heeft ons echter niet alleen voor de theorie der kegelsneden, maar ook ten opzigte van den cirkel en de regte lijn veel doen leeren. Zoo is bij de theorie der veelhoeken die der veelzijden ontstaan, die correlatieve figuren van de eerste zijn: stelt men als de definitie van eenen veelhoek een in stelling gegeven aantal punten, waarbij dan de onderlinge verbindingslijnen behooren geconstrueerd te worden - en op die wijze geraakt men tot het begrip van een volkomen veelhoek - zoo is de bepaling van eene veelzijde een in stelling gegeven aantal lijnen, waarbij nog de onderlinge snijpunten behooren geconstrueerd te worden.

[p. 975]

Uit de voorgaande korte ontwikkeling van den inhoud en de eigenlijke methode der Nieuwere Meetkunde ziet men, dat deze in den grond eigenlijk tot de leer der coördinaten behoort, maar die coördinaten, die hier uit twee punten langs dezelfde regte lijn worden gerekerd, geven aanleiding tot eene zoo verschillende methode, dat men wel gerustelijk deze Nieuwere Meetkunde als een afzonderlijk deel der wetenschap beschouwen mag. Maar ook tegenover de Meetkunde der Ouden staat zij, vooral in het opzigt van methode: munt deze uit door gestrengheid van vorm, de Nieuwere kenmerkt zich vooral door hare algemeene wijze van beschouwing. En te regt zegt Adams⁴³ van haar: ‘In der alten Geometrie ist es vorzugsweise der Verstand, welcher in Anspruch genommen wird; in der neuern muss die Schärfe des Verstandes mit der Kraft der Anschauung sich verbinden, um die einzelnen Wahrheiten wie den Zusammenhang dieser Wahrheiten in ihrem innersten Wesen und ihrer ganzen Ausdehnung zu erfassen.’

En nu willen wij nagaan wat wij in het boek vinden, dat aan het hoofd van dit opstel is aangegeven. Een Leerboek der Nieuwere Meetkunde is het niet, en daarvoor geeft het zich dan ook niet uit. Het doel daarvan is: ‘om de voornaamste eigenschappen (die de leerlingen hebben leeren kennen in de Leerboeken van Kempees, Lacroix of anderen) nog eens, doch langs een' anderen weg, weder voor den geest te brengen, hun te doen zien, hoe die kunnen dienen tot het ontdekken en bewijzen van nieuwe waarheden, welker bestaan zij uit eene naauwkeurige teekening der figuren, bij het oplossen van vraagstukken, reeds konden vermoeden.’ Men ziet het, schrijver volgt de methode der Oude Meetkunde en wil langs dien weg ‘de theorie der harmonische snijding der lijnen en die der transversalen behandelen, omdat daarin de grondslagen voor het hooger onderwijs, het Theorema van Pythagoras en de voornaamste eigenschappen der gelijkvormige figuren en van den cirkel zoo menigvuldig voorkomen.’ Hoezeer Ref. het nu wel met leedwezen ziet, dat schrijver niet liever de zoo eigenaardige methode der Nieuwere Meetkunde zelve verkoos, waardoor zijns inziens juist de vroeger geleerde eigenschappen telkens zoo treffend als gevolgen van geheel ongelijksoortige beschouwingen terugkomen, - zoo wil hij deze rigting van het boek als een gegeven rigtsnoer aanmerken en daarmede hetzelve doorgaan. Daartoe volge hier vooreerst eene korte opgave van den inhoud.

43 C. Adams, Die harmonischen Verhältnisse, Vorrede.

Afdeeling I. Theorie der harmonische getallen.

Blz. 1-17, § 1-35. 3 Vraagst. 7 Eigensch.

I.	Over de harmonische evenredigheden, blz. 1-7, § 1-15. 3 Vraagst. 3 Eigensch.

[p. 976]

II.	Over de harmonische reeksen, blz. 8-17, § 16-35. 4 Eigensch.

Afdeeling II. Theorie der harmonische snijding eener lijn.

Blz. 17-70, § 36-120. Werkst. 1-4. Stell. 1-22 (met 23 Gevolgen).

I.	Over de harmonische lijnen, harmonisch gelegene punten en de harmonische snijding eener lijn, blz. 17-26, § 36-55. 1 Werkst.
II.	Eigenschappen der harmonisch gesneden lijnen, bl. 27-41, § 56-75. 10 Stell. met 4 Gev.
III.	Over de harmonische pool, de harmonische stralen en hunne eigenschappen, blz. 41-52, § 76-89. 1 Werkst. 6 Stell. met 4 Gev.
IV.	Over de harmonische snijding van de regte lijn door den cirkel, blz. 52-59, § 90-99. 5 Stell. met 5 Gev.
V.	Over de gelijkvormigheidspunten, gelijkvormigheidsstralen, in verband met harmonische snijding, blz. 60-70, § 100-120. 2 Stell. met 10 Gev.

Afdeeling III. Theorie der Transversalen.

Blz. 70-246, § 121-393. Werkst. 1-17. Stell. 1-93 (met 117 Gevolgen).

I.	Over den driehoek met zijne transversalen, blz. 70-117, § 171-196. 25 Stell. met 39 Gev.
II.	Over de transversaal, in verband met gelijkvormigheidspunten, blz. 107-124, § 197-214. 7 Stell. met 6 Gev.
III.	Over de collineatie-punten, collineaire lijnen en collineaire driehoeken, blz. 125-135, § 215-234. 2 Werkst. 8 Stell. met 4 Gev.
IV.	De vierhoek met zijne transversalen, blz. 135-154, § 235-253. 12 Stell. met 7 Gev.
V.	Over de involutie en de anharmonische verhouding, blz. 154-166, § 254-272. 3 Stell. met 13 Gev.
VI.	De veelhoek met zijne transversalen, blz. 166-177, § 273-286. 6 Stell. met 8 Gev.
VII.	De cirkel met zijne transversalen. Pool en Poolijnen, blz. 177-184, § 287-298. 1 Werkst. 5 Stell. met 5 Gev.
VIII.	Over den cirkel met in- en omgeschreven veelhoeken, blz. 184-208, § 299-335. 5 Werkst. 10 Stell. met 18 Gev.
IX.	Over de transversaal, in verband met twee of meer cirkels. Chordaallijn en chordaalcirkel, blz. 208-246, § 336-393. 9 Werkst. 17 Stell. met 17 Gev. Aanhangsel. Oplossing van eenige (13) vraagstukken uit de praktische Meetkunst, blz. 247-264, § 394-409.

[p. 977]

De eerste Afdeeling bevat eene rekenkundige behandeling der harmonische getallen en behoort eerder in een Leerboek der Rekenkunde te huis. - Had de schrijver deze weggelaten, en vervolgens in de tweede Afdeeling de vierde Bepaling van harmonische snijding, die, naar de voorgaande uiteenzetting, toch wel de grond der geheele theorie is, vooropgesteld, dan had de volgende afleiding algemeener kunnen zijn. - De uitkomsten, in § 58-73 verkregen, worden op blz. 39 in een tafeltje bij elkander gesteld: deze grondformulen der harmonische snijding kunnen met vrucht gebruikt worden bij onderzoekingen over dit onderwerp. Ongaarne mist Ref. hier echter de eigenschappen van genoemde snijding ten opzigte van eenig willekeurig punt der lijn, en wel in het bijzonder ten aanzien van de punten, die den afstand van twee toegevoegde (of, volgens den schrijver, verwante) punten midden door deelen. - De bepaling van harmonische stralen, § 76, wordt eerst door Stelling XII, § 79, gewettigd. - Stelling XIII en XV (§ 83 en 88) zijn eigenlijk identiek dezelfde; dewijl de daarvoor gegeven bewijzen verschillen, geeft de schrijver dus wederom twee bewijzen voor dezelfde eigenschap, iets, dat hij meermalen, en zeer te regt, doet, daar zulke wezenlijk verschillende bewijzen gunstig op den leerling werken. - In deze Afdeeling behoorde, althans eerder dan zij willekeurig in de volgende worden gegeven, de bepalingen van anharmonische snijding en involutie. Zij staan daar, omdat zij bij de volgende stellingen gebruikt worden, maar volstrekt zonder eenigzins gemotiveerd te zijn, en dit is toch, minstens genomen, onbillijk jegens de hoofdgedachte, waaruit eigenlijk alles moest worden afgeleid; bovendien strekt het ook niet tot bevordering van geleidelijken gang. Vandaar dan ook misschien, dat de schrijver, tegen het begrip der zaak in, de anarmonische (bij vergissing schrijft hij zeker overal enarmonische) verhouding uit de involutie afleidt, terwijl deze integendeel slechts een bijzonderen toestand der anharmonische verhouding is, zoo als uit het hierboven ontwikkelde volgt. - In dezelfde derde Afdeeling komt ook de bepaling van collineaire lijnen willekeurig, zonder eenigen grond of oorzaak, voor; vandaar misschien ook, dat Bepaling 9 (§ 216) en Stelling 37 (§ 228) tegen elkander strijden. - De 10^de Bepaling (§ 218), van eenen volkomen vierhoek, behoort niet hier te staan, maar eerder onder Hoofdstuk IV, bij § 235.

Stelling III, blz. 77, is juist, maar hare omgekeerde Stelling IV, blz. 79, niet altijd, en de oorzaak daarvan ligt in de figuren, daar de schrijver de stellingen voor iederen stand der figuur afzonderlijk bewijst. Deze stelling geldt, wanneer alle drie transversalen inwendige zijn (zie Figuur 38 a), of wanneer er (bij 38 b) twee uitwendige met eene inwendige zijn, onder de voorwaarde, dat alsdan ééne der uitwendige, hetzij de andere uitwendige, hetzij de inwendige snijdt. Zij geldt daarentegen niet, als er twee transversalen inwendig, en eene

[p. 978]

uitwendig is, of als er drie uitwendige transversalen zijn, of als er, bij twee uitwendige en eene inwendige, alle transversalen onderling evenwijdig zijn. Ligtelijk is het beweerde uit de figuren op te maken. Wanneer b.v. (in Fig. 38 a) D regts van B in D, ligt (waarbij de verhouding van AD:BD, waar het hier op aankomt, toch dezelfde moet blijven⁴⁴), dan is er geen gemeenschappelijk snijpunt, daar BD, alsdan niet door C kan gaan; in dat geval zijn A, D, B, D, harmonische punten. Wanneer ten tweede, in Fig. 38 b, E ligt in het verlengde van AC buiten C in E, (zoodanig, dat weder de verhouding A E: C E niet verandere), alsdan gaat B E, niet door P, maar zijn weder de punten A, E, C, E, harmonisch gelegen. Eindelijk, als (in dezelfde Fig. 38 b) F beneden B in F, en D regts van B in D, ligt (altijd met de onderstelling, dat de verhoudingen tusschen de segmenten niet van waarde veranderen), dan kan het zeer wel gebeuren, dat AF,, BE, en CD, alle evenwijdig loopen: ook in dit geval is er alzoo geen gemeenschappelijk snijpunt.

Mogt Ref. deze aanmerkingen niet terughouden, aangenaam is het hem, overigens gerustelijk op den inhoud te kunnen wijzen, die den weetgierigen niet te leur zal stellen; reeds de namen van de schrijvers, die in het Voorberigt als bronnen zijn opgegeven, en waarvan vooral Adams veel gevolgd is, doen dit verwachten. Het kan geschiktelijk dienen om door zijne 34 Werkstukken, 123 Stellingen en 140 Gevolgen een denkbeeld te geven van de eigenschappen, die men thans kent omtrent transversalen, harmonische snijding en straalbundels, omtrent gelijkvormigheidspunten, omtrent pool en poollijnen, omtrent chordalen, en ook, hoezeer in mindere mate, omtrent volkomen veelhoeken en collineaire figuren. En als zoodanig moge het strekken tot eene opwekking, om de Nieuwere Meetkunde te beoefenen, die alle deze uitkomsten, en nog zoo vele meer, op eene meer algemeene wijze en langs meer geleidelijken, al zij het dan ook meer wetenschappelijken, weg doet vinden.

Wat ten slotte het uiterlijke van het boekje betreft, dit is volkomen in overeenstemming met de bekende rigting der uitgevers, en de zorg, die zij aan dergelijke werken besteden; het is goed en duidelijk gedrukt, schijnt weinige errata te bevatten (en dit zegt veel bij werken over Wiskunde) en is wezenlijk opgeluisterd door 176 en 18 in den tekst ingedrukte, zuivere, houtsnêe-figuren. Aan het einde van het boek is blz. 265-306 een zeer uitvoerige inhoud geplaatst, die veel tot nut en gemak bij het gebruik zal bijdragen.

Deventer, December 1856.

D. BIERENS DE HAAN.

44 Ten minste volgens de begrippen van den schrijver; naar de beginselen der Nieuwere Meetkunde wordt die verhouding dan van negatief positief, zoodat daarmede ook de onderstelling van teeken verandert.

[p. 979]

Rivier-polders in Nederland. Hunne gebreken en de middelen tot herstel, door B. te Gempt. Haarlem, A.C. Kruseman. 1857.

Die waant in dit boekje eene beschrijving van onze rivierpolders te vinden, zal teleurgesteld zijn.

Zij is ook op geene 94 bladzijden te geven.

In de ‘Bijdragen tot de Kennis van Gelderland’ van Sloet, beslaan de rivierpolders in die provineie alleen 240 bladzijden en daar wordt nog niet gehandeld over hunne gebreken en de middelen tot herstel.

Wat behelst het boekje dan?

Laat ons zien.

In eene soort van inleiding wordt een allertreurigst tafereel van den toestand der rivierpolders opgehangen. De polderlanden kunnen jaarlijks niet regelmatig worden bezaaid; de jaarlijksche opbrengsten staan in geene evenredigheid tot de zware lasten, die er op drukken; de welvaart vermindert; de armoede neemt toe; het geldt niet minder dan de keuze van pompen of vergaan.

De bron, de oorzaak van het kwaad moet men weten op het spoor te komen; men moet het in zijnen aard, uitgestrektheid en verderfelijken invloed leeren kennen, opdat men, overtuigd van de gebiedende noodzakelijkheid om het kwaad te keer te gaan en te bestrijden, de middelen aangrijpe, waarvan nog redding en uitkomst te verwachten is.

Men krijgt, dit lezende, medelijden met hen, die achter dijken wonen en noemt hen dwazen, die ƒ 1000 à ƒ 1500 en meer voor een bunder polderland geven.

Waarin is het kwaad gelegen?

In de kwel.

De gronden langs de rivieren, bestaan uit afwisselende lagen klei en zand, waartusschen in vele streken derrie ligt. Het zand is niet overal waterkeerend. Rijst het water hoog tegen de dijken, het kwelt er onder door, komt in de polders en rigt daar, als het niet door natuur of kunst gelost wordt, schade aan.

Doch slechts een klein gedeelte van de rivierpolders lijdt daar werkelijk nadeel door.

In de Over- en Neder-Betuwe - om ons slechts tot Gelderland te bepalen - het bovenste gedeelte van den Tielerwaard, Buren en het rijk van Nijmegen, en in het algemeen daar, waar geene molens zijn, heeft men er geene schade van.

[p. 980]

Langs den IJssel is de kwel weinig, langs de Hollandsche dijken in het geheel niet bekend.

Waardoor ontstaat het kwaad?

Door de bedijkingen.

Wij geven dit toe.

Zonder dijken geen kwel, doch er staat tegenover: zonder dijken geen bewoonbaar, granen voortbrengend land.

Wij meenden, dat de jammerklagten over het kunstmatig landbederven onzer voorouders tot de geschiedenis behoorden. Zij zijn voornamelijk gegrond op het onjuiste gevoelen, dat door de dijken de rivierbedden zich hebben verhoogd.

De S. kleeft dat gevoelen ook nog aan: eenmaal, zegt hij, zal de bedding der rivieren boven het maaiveld der binnenlanden zich verheffen.

Tot zijne verontschuldiging kan strekken, dat genoegzaam alle - niet alle, zoo als hij meent - waterbouwkundigen, van Velsen af tot Storm Buysing toe, het zelfde gevoelen aankleefden, doch andere, Brunnings, Goekoop, de Oud Soldaat, verhieven hunne stem er tegen.

Zij deden dit teregt.

Door de dijken is de stroombaan beperkt, verengd en aan het afstroomend water eene grootere snelheid gegeven, die zoowel het bezinken der stoffen, welke in het water zijn, belet als de ondiepten wegvoert. De ondervinding bevestigt dit. Uit de waterstanden, gedurende een tijdvak van 80 jaren waargenomen, is bewezen, dat de waterspiegel der rivieren, behalve van den IJssel, waar andere oorzaken werkten, niet verhoogd is. Had zich nu het bed verhoogd, dan moest de waterdiepte verminderd zijn, en dit is geenszins het geval. Staring heeft dit in zijn uitstekend werk: ‘de Bodem van Nederland,’ Dl. I, bl. 401 vlg., duidelijk uiteengezet. Vgl. ‘de Nederlandsche Hoofdrivieren,’ door een Oud Soldaat, 2^de Stuk, bl. 98 vlg.

Om het nadeel der bedijking aan te toonen, wijst de S., met Velzen, op den Nijl. Ongelukkig voorbeeld. Even als alle andere Nijlarmen, op ééne na, onbeduidend en onbevaarbaar zijn geworden, zoude zeer waarschijnlijk de Waal thans de eenige overgeblevene van den Rijn zijn en, de S. zegt het zelf, een groot deel der waarde van de polders ontstaat door hunne ligging aan bevaarbare stroomen.

De S. wil echter alle dijken niet wegcieren. Hij is zeer gestemd voor het plan van den Heer van Rechteren, om de wateren van Rijn, Waal en Maas, door het verlagen der dijken tot het hoogste zomerwater, over de polders heen te leiden.

Volgens dat plan zouden, meent de voorsteller, de dijken niet meer doorbreken, maar slechts overloopen. Doch zonden zij daardoor niet afloopen en wegdrijven?

[p. 981]

Hoe zoude men dan winterkoren durven verbouwen?

Het is waar, volgens de berekeningen van van Rechteren, zoude dat overloopen slechts gedurende 39 dagen in 50 jaren plaats vinden; doch wie zou de kans durven wagen?

Het ander voordeel, dat de S. in dat plan ziet, het verhoogen van den grond in de polders, is denkbeeldig en rust op een verkeerd begrip. In stroomend, vooral in snelstroomend water, bezinken de vaste stoffen, die het medevoert, niet. Dit vindt slechts plaats bij den noodigen stilstand van het water op de overstroomde landen.

De zwaarste stoffen, zoo als het los gewoelde zand, bezinken het eerste. Daardoor ontstaan langs de rivieren kanten, als het ware natuurlijke dijken, hooger dan het land, dat meer van de rivier verwijderd is. Daar vertoont zich na het wegvallen van het water een dun vlies van zoetwaterwier, waarin wat klei is blijven hangen, doch zoo weinig dat eerst na verloop van vele eeuwen eene ophooping merkbaar kan zijn. Staring, a.w.D. I, bl. 388.

De rivier-commissie van 1821 heeft dit feit ook opgemerkt, als onder anderen in het Arnhemsche en Velpsche broek, bij Arnhem, dat alle jaren des winters onder water wordt gezet.

Digt achter de sluizen bezinken de stoffen uit het water, maar meer binnenwaarts wordt geene ophooging waargenomen.

Dit zoude overal gebeuren wanneer men, zoo als de S. zich uitdrukt, ‘Gods water over Gods akker liet loopen.’

Toen men dijken aanlegde koos men, 't ligt in den aard der zaak, de reeds natuurlijk bestaande ophoogingen. Van daar dat het buitenland zoo dikwerf hooger is dan het binnenland, dat bijna in alle rivierpolders steeds binnenwaarts naar beneden helt.

De S. schuift verder de vele dijkbreuken op rekening van het verhoogen der dijken. De feiten wederspreken dit. In de jaren 1651, 1740, 1741 en 1744 zijn er met open rivieren zeer hooge waterstanden geweest, die telkens dijkbreuken ten gevolge hebben gehad. In 1824 rezen de rivieren, bij open water, even hoog en er vielen geene doorbraken.

De toestand der rivierpolders is over het algemeen zóó hopeloos, zóó allerjammerlijkst niet als de S. dien voorstelt, die den eenen polder voor, den anderen na, reeds onder zijne lasten ziet wegzinken.

Wij durven beweren, dat die toestand verbeterd is, nog voortdurend verbeter wordt, en dat het gevaar, om in de polders te wonen, steeds vermindert en verminderen zal door de dijken beter te rigten, tot het bekomen van een goed hoogwaterprofil; door het meer en meer aannemen eener gelijkmatige hoogte bij eene geëvenredigde zwaarte der dijken; door het wegnemen van beletselen op de dijken; door naauwlettend onderhoud, en door groote waakzaamheid bij hoogwater of ijsgang.

[p. 982]

Waardoor moet het kwaad geweerd worden?

Niet, zoo als men, volgens de redeneringen van den Schrijver, zoude verwachten, door het verlagen der dijken, maar door het aanwenden der stoomkracht.

Hierin zijn wij het met den S. eens. Waar het kwelwater nadeel doet, of het binnenwater niet goed en tijdig loozen kan, moet het dikwerf onvoldoend windgemaal vervangen worden door stoomgemaal.

Het geoctroyeerde van den Heer Fijnje is proefhoudend bevonden in den Maas- en Waalschen molenpolder van Wamel, Dreumel en Alphen en in den Bommelerwaard boven den Meidijk. Er zijn of worden er gebouwd in de polders Bommelerwaard beneden den Meidijk, Herwijnen en Culenborg.

Dit is eerstens een bewijs dat de polderlanden niet zóó arm zijn, dat de groote kosten van een stoomgemaal niet te dragen zijn, en ten anderen van de deugdelijkheid der vinding van den Heer Fijnje. Die voorbeelden zullen krachtiger werken dan de oppervlakkige beschrijving met twee teekeningen, die de S. van de machine te Dreumel geeft.

Doch aan een stoomgemaal op zich zelve heeft men niet genoeg. De verdeeling van het water en de opvolgende toevoer er van naar het gemaal, zijn onderwerpen van zeer veel belang, dikwerf zeer moeijelijk en met vele kosten te regelen.

Let men bijv. op de waterlossing van Maas en Waal, - waarvoor de S. kennelijk zijn boekje schreef en, pars pro toto, een gedeelte er van tot maatstaf voor alle rivierpolders nam - zoo als zij opgegeven wordt door Sloet, a.w., bl. 210 vlg. en op de daar medegedeelde plannen tot verbetering, dan ziet men dat daar eene zeer ingewikkelde zaak te ordenen is.

Eene zeer gunstige verandering is daar in de waterlossing gekomen. Door het digten van het kanaal van St. Andries is de waterspiegel van de Maas zeer verlaagd en daardoor het lozingsvermogen op die rivier zeer verhoogd. De S. zegt er niets van.

Hij bespreekt verder nog twee onderwerpen.

Het eene is het inlaten van rivierwater in de polders, om dezen te bemesten. In die, welke geheel of bijna geheel uit graslanden bestaan, zoo als het reeds vermelde Arnhemsche en Velpsche broek, de Ooy, de Willemspolders, waar het geschiedt, is het nuttig, doch hoe het toe te passen is op die uitgestrekte polders, waar de akkerbouw hoofdzaak is, kunnen wij niet bevatten.

Het andere onderwerp is het middel door den Heer Fijnje bedacht om de kwel te keeren. Het bestaat hierin om buiten langs de dijken, die het water doorlaten, een geul te graven, diep 1 à 2 en breed 0.50 à 0.75 ellen, en die met klei, welke geen water doorlaat, aan te vullen.

[p. 983]

Het kost den S. moeite, zijn oordeel over dit middel bepaaldelijk uit te spreken.

Niemand kan dit. Er moeten meerdere en uitgebreidere proeven genomen worden dan tot nu toe geschied is, en die, door Gedeputeerde Staten van Gelderland voorbereid, op kosten der provincie genomen zullen worden. De Provinciale Staten stellen daarvoor ƒ 2000 beschikbaar.

Het is opmerkelijk, dat slechts de eerste zandlaag onder de bovenste kleilaag water doorlaat. Wordt dit belet, het kwelwater is buiten den polder gesloten.

Had de S. dit gekend, hij zoude niet in de dwaling zijn gevallen, dat alle zandlagen afgesneden dienen te worden. Door boringen zal evenwel uitgemaakt moeten worden, of de zandlaag niet dieper ligt dan de Heer Fijnje aanneemt.

Bij het werkje is een kaartje gevoegd der polders van de Nederlandsche hoofdrivieren, met de landen die aan overstrooming onderhevig zijn.

Eene polderkaart zal wel in de eerste plaats de dijken moeten aanwijzen, en die deze niet kent, kan ze op dit kaartje niet vinden. Het is eerder een straat- en grindwegkaartje, daar de meeste begaande dijken als zoodanige wegen zijn geteekend.

De dijk, die de Ooy van de Duffelsche scheidt, is vergeten.

Op zoodanige kaart behooren ook de waterleidingen voor te komen. De S. heeft ééne blz. noodig om die van Maas en Waal op te geven en te verduidelijken.

En wat behelst nu het werkje?

Overdrevene voorstellingen. - Verkeerde beschouwingen.

In ons waterland zijn er zoo velen, die de eerste beginselen van waterloop en wat daartoe behoort of betrekking heeft, niet kennen, - zoo velen, die er geheel verkeerde begrippen over hebben. En toch moest het anders zijn, daar zoo velen geroepen worden om water te keeren en water te lossen.

Dit deed ons langer bij het geschrijf van den Heer te Gempt stil staan, dan het verdiende.

Tutus inter amnes.

[p. 984]

Opmerkingen over den invloed der wetgeving van voor 1795 op het Jagtregt in de provincie Groningen, door Mr. J.J. Cremers. Groningen, K. de Waard. 1856. 69 blz. 8^o.

Gelijk uit het voorwoord tot deze verhandeling blijkt, was zij oorspronkelijk niet tot de uitgave bestemd. De schrijver droeg dezelve voor in het welbekende genootschap ‘Pro excolendo jure Patrio’ te Groningen, en men moet o.i. deze bijzonderheid bij eene beoordeeling wel in het oog houden. Immers niet tot het publiek, ook buiten de provincie Groningen, sprekende, kon S. veel achterwege laten, hetgeen hij teregt vooronderstellen mogt aan zijn gehoor bekend te zijn; men mag echter vragen of S., tot de uitgave zijner verhandeling besloten hebbende en daarmede eene bijdrage tot de kennis van den vroegeren en tegenwoordigen toestand van het gewest zijner inwoning willende leveren, niet meer in het oog had mogen houden wie oorspronkelijk zijne hoorders waren, wie thans zijne lezers zouden zijn?

Het is bekend, dat gedurende de beraadslagingen in onze Tweede Kamer der Staten Generaal over de Wet tot regeling der Jagt en Visscherij, op voorstel van den toenmaligen Minister van Binnenlandsche Zaken Thorbecke, in Art. 54 dier Wet, in het bijzonder belang der provincie Groningen, eene bepaling werd opgenomen tot regeling van den toestand der eigenaren en vast beklemde meijers.

Op deze bepaling levert S., in bovengemelde verhandeling, een in vele opzigten belangrijke Commentaar, waaraan hij, na eene vlugtige beschouwing onzer tegenwoordige Jagtwet in betrekking tot het Reglement van Prinses Anna van 1752, eenige opmerkingen over de eerste artikelen, waarmede het Art. 54 dier wet in een onmiddellijk verband staat, laat voorafgaan. Hij vereenigt zich over het algemeen met de daarin vervatte bepalingen; alleen kan hij niet goedkeuren dat de wet, het beginsel vaststellende, dat in den regel niemand mag jagen op eens anders land zonder dezes vergunning, vordert dat deze vergunning schriftelijk zij. Ook in de beide Kamers der Staten-Generaal, bij de beraadslaging over Art. 2, deden zich hiertegen vele bezwaren op; wij zullen hier niet herhalen de argumenten voor of tegen die bepaling in het midden gebragt: wij gelooven die bezwaren niet van zooveel gewigt als die, welke zouden ontstaan, wanneer de vergunning enkel mondeling zou behoeven gegeven te worden. De

[p. 985]

Staat eischt toch niet te veel, wanneer hij, den grondeigenaar tegen ongenoodigde jagtlicfhebbers beschermende, van hem daarentegen, in zijn eigen belang, de geringe moeite vergt, wanneer hij iemand veroorlooft op zijn' grond te jagen, daartoe eene schriftelijke vergunning te geven. In geen geval echter kunnen wij het den S. toegeven, dat hier niet meer grond zou bestaan zulk eene schriftelijke vergunning te vorderen, dan bij den arbeider, die op mondelingen last eens anders oogst maait; voor dergelijk onderscheid bestaan o.i. wel zeer zeker goede regtsgronden. Immers het valt gemakkelijker iemands grond te betreden en daarop te jagen, dan eens anders oogst te maaijen, zonder vooraf daartoe verkregen vergunning; het laatste is eene schending van den eigendom, waartegen de strafwet waakt; het eerste zoude zulks zonder de Jagtwet niet zijn; hoe ligter een daad, die men wil beletten, te volvoeren is, des te gestrenger moeten de preventive maatregelen te dien opzigte zijn: zoo ook hier.

Evenmin kunnen wij instemmen met hetgeen S. zegt omtrent het doel dezer bepaling, noch met hem daarin eene verkeerde toepassing van het slot van Art. 625 Burg. Wetboek zien.

Teregt, zegt de Heer Cremers, liet de Jagtwet in Art. 54 de vraag, aan wien het Jagtregt toekomt, aan den eigenaar of aan den beklemden meijer, onbeslist. Aan de historische ontwikkeling dezer vraag, welke S. in laatstgemelden zin beantwoordt, is verder hoofdzakelijk zijn betoog gewijd.

Hij laat zijn onderzoek uitgaan van de twee volgende stellingen: ‘1^o. Het regt van beklemming is ontstaan uit het gewoon regt van huur en verhuur, en al de regten, die een losse huurder had op den verhuurder, kwamen ook den beklemden meijer toe op den beklemden grond.

2^o. Al had oudtijds de losse meijer niet het genot der jagt, moet dit thans aan eenen vast beklemden meijer evenzeer worden toegekend, als aan den vruchtgebruiker of erfpachter.’

Dit tweede punt laat S. onaangeroerd, dewijl, zegt hij, daaromtrent ieders oordeel veelal zal afhangen van zijne schatting, voor welke bezwaarlijk bewijzen zullen kunnen worden geleverd; waar de S. echter zegt, dat ieder onderzoek van de twee vermelde stellingen moet uitgaan, hadden wij gaarne ook de tweede meer ontwikkeld gezien, en zeker zoude zijn betoog aan belangrijkheid en volledigheid daaraan gewonnen hebben.

Tot toelichting der eerste stelling en ten einde aan te toonen wat in den regel den gewonen huurder naar oud regt toekwam, gaat S. eerst na, hetgeen de oude staatsinrigting van Groningen en de Ommelanden hieromtrent leeren, en wie in het algemeen over de jagt beschikte. Zeer belangwekkende bijzonderheden omtrent de innerlijke staatsregeling, de wetgevende en de regterlijke magt dier gewesten

[p. 986]

vindt men hier medegedeeld. Eenige uittreksels uit het protocol der Warfsvergaderingen, met welker zamenstelling S. zijne lezers bekend maakt, en uit de Oldambster Ordonnantiën van 18 September 1658 en 2 Februarij 1711, worden aan het einde van het boekje als Bijlagen vermeld.

Uit dit alles volgt klaarblijkelijk, hetgeen S. wilde bewijzen, dat de huurder in de Ommelanden en het Oldambt (en evenzoo in Groningen) zijn gehuurd land bejoeg en dat de beklemde meijer, als huurder, deze zelfde bevoegdheid heeft verkregen en behouden.

De kundige S. deelt thans nog eenige korte opmerkingen mede over het Jagtregt, afgescheiden van den grond. Zulk eene afscheiding, zegt hij, kan ook haren grond hebben in een privaat burgerlijk contract, en wij gelooven zijne bewering juist, dat, indien zulk een deugdelijk contract, ouder dan de tegenwoordige Jagtwet, geleverd is, de beklemde meijer, op grond van Art. 54 dier wet, bevoegd is, den afkoop, voor den duur van het contract van beklemming, ook van den eigenaar van een afgescheiden Jagtregt te vorderen.

Bij eene zeer belangrijke beschouwing der regale jagtregten, eerst meer in het algemeen, vervolgens meer bepaald van die in de Ommelanden, gaat S. kortelijk na wie aldaar vroeger, wie thans nog kunnen gezegd worden heerlijke jagtregten te hebben, en toont hij aan, hoezeer erkennende het verband tusschen de jagtregten of qualificatiën met de Jurisdictieregten (die in de 15^e en 16^e eeuw overal elders afgeschaft, alleen in de Ommelanden tot 1795 stand hielden), dat evenwel aan de Jurisdictie nimmer een eigenlijk jagtregt verbonden was. Ook later in een Naschrift tot deze verhandeling staaft hij dit gevoelen door eene vergelijking der regten van den Ommelander Jurisdictiehouder met die van den eigenaar der Heerlijkheid Tilburg, waaraan werkelijk zulk een Jagtregt verbonden was.

Maar, zegt S. verder, al ware het aan te nemen, dat eene uitsluitende jagtbevoegdheid een aloud en natuurlijk gevolg der Jurisdictieregten ware, ook dan zou zij niet als een verkregen regt door de wet moeten worden geëerbiedigd, maar integendeel als het uitvloeisel eener oude wet voor de latere moeten wijken, en zou de vraag overblijven, hoe, toen de Jurisdictie, de oorzaak, ophield, de Jagtbevoegdheid, het gevolg, is kunnen blijven bestaan? En waarom zou het heerlijke jagtregt, eene bevoegdheid welke de staatsregeling van vroegeren tijd gaf, meer een jus quaesitum zijn dan het kiesregt door onze tegenwoordige Grondwet geschonken en zeer zeker ten allen tijde afhankelijk van de wetgevende en grondwetgevende magt des Konings en der Staten-Generaal?

Ten slotte eindelijk en in verband met het voorgaande, onderzoekt S. in hoever de bewering waarheid bevat, dat de Jurisdictiehouders een heerlijk jagtregt herkregen door de besluiten van den Souverei-

[p. 987]

nen Vorst van 21 September 1814 en 8 Februarij 1815. Het feit valt niet te loochenen: werkelijk zijn sedert dien tijd vele Ommelander qualificatiën, en wel als zakelijke jagregten, op nieuw te voorschijn gebragt en uitgeoefend; maar S. ontkent dat zij in de aangehaalde besluiten bedoeld werden en beweert dat èn het bestaan van het Jagtregt èn het bezit nemen daarvan vóór dien tijd, moeten bewezen zijn. - Het al of niet bestaan der Heerlijke Jagtregten in genoemde streken is tot heden nog geen eigenlijk punt van regterlijke beslissing geweest; veel echter heeft S. in zijne verhandeling bijgebragt om de zaak in staat van wijzen te brengen. Een ieder, die belang stelt in de kennis van het bijzonder karakter en de historische ontwikkeling van het Jagtregt in Groningen, zij het boekje bijzonder ter lezing aanbevolen.

Mr. D.L.

Algemeene Geschiedenis van den wereldhandel, door H. Scherer. Uit het Hoogduitsch vertaald, met bijvoeging der aanteekeningen van Richelot en Vogel. Door N. Calisch. 1^ste Afl. Haarlem, A.C. Kruseman. 1858.

't Is voorwaar geene gemakkelijke zaak eene geschiedenis van den wereldhandel te schrijven. De kennis van de historische feiten alleen is daarvoor niet toereikende; ook de kennis van den handel dient het deel van hem te zijn, die zich aan dien arbeid waagt. Handelskennis toch moet de geschiedkundige mededeelingen in het ware licht stellen, en terwijl de gevolgen in de feiten vermeld zijn, de oorzaken daarvan opsporen en aantoonen. Zonder die handelskennis, zal eene handelsgeschiedenis eenzijdig en weinig belangrijk zijn, omdat hij die schrijft een juist oordeel over 't geen hij te boek stelt, mist.

Die moeijelijkheid wordt zoo sterk gevoeld, dat bijna niemand die taak aanvaardt. Hoogst beperkt is het aantal werken, die men goede handelsgeschiedenissen noemen mag. Van bijna ieder land afzonderlijk vindt men eene handelsgeschiedenis, van de geheele wereld maar zeer weinigen. Behalve Anderson en Macpherson in Engeland, moet men voor zoodanigen arbeid voornamelijk het oog naar Duitschland rigten; daar heeft men weder met stalen vlijt en ongekenden lust tot onderzoek de hand aan het werk geslagen, en nu liggen de twee lijvige boekdeelen van H. Scherer voor ons als een bewijs van die zucht tot werken. Van zijne hand eene geschiedenis van den handel te bekomen, zal niemand bevreemden. Wetenschappelijk gevormd

[p. 988]

en door de praktijk met den handel bekend, is reeds zijn naam op een boek van dezen aard eene aanbeveling. Wie als wij, voor 5 à 6 jaren, gretig de hand naar dit werk uitstak, toen het in Duitschland verscheen, zal voorzeker met ons het getuigenis afleggen, dat zijne verwachting niet teleurgesteld is. Bij degelijkheid van inhoud, zijn beknoptheid en aangenaamheid van vorm zoozeer het kenmerk van dit boek, dat het daardoor vooral onder een oneindig grooteren kring van lezers verspreid zal worden, dan menig misschien veel geleerder werk over hetzelfde onderwerp, maar waarin strenge wetenschappelijkheid den boventoon heeft en de lectuur moeijelijk en onaangenaam maakt voor den alleen praktischen man.

Reeds lang verwonderde 't ons, dat niet een onzer uitgevers, anders zoo tuk op het uitgeven van vertalingen van vreemde boeken, ook dit werk voor Nederland liet vertolken, en het prospectus van den Heer Kruseman, met de eerste aflevering, was ons dan ook uiterst welkom. Moeten wij die late verschijning wijten aan de vrees onzer uitgevers, om degelijke werken hier te lande uit te geven, daar de goede weinige, en de prullen vele koopers vinden, dan hopen wij dat die vrees ditmaal door eene goede uitkomst zal beschaamd worden. In een zoo bepaald commerciëel land, als Nederland mag genoemd worden, zullen toch waarlijk de koopers voor eene degelijke handelsgeschiedenis niet ontbreken? Die onderstelling zelfs zou eene beleedigende voor onzen handelsstand zijn!

Moge dit werk spoedig door het derde of laatste deel gecompleteerd worden, en weldra aan niemand onbekend zijn die zich koopman noemt, tot voordeel van handelaar uitgever en tevens.

De vertaling is vloeijend en juist en doet den Heer Calisch eer aan.

P.N.M.

(a) De aanhalingen, die het sterretje (*) missen, heeft Ref. niet persoonlijk kunnen nagaan.