De Gids. Jaargang 15

[p. 106]

Bibliographisch Album.

Lessen over de Differentiaal- en Integraal-Rekening door Dr. R. Lobatto. Eerste Deel. 's Gravenhage en Amsterdanm, bij de Gebr. van Cleef. 1851.

Wanneer men de aaneenschakeling en het verband nagaat tusschen de verschillende deelen der Wiskunde, tusschen de Analysis en de Geometrie, hare ouderdeelen en wederzijdsche toepassing, dan komt men gereedelijk tot het besluit, dat de Differentiaal- en Integraal-Rekening de hoofdschakel uitmaakt tusschen al deze aanverwante studievakken; den sleutel, die ons den weg opent, om in de hoogere, meer ingewikkelde deelen in te dringen: - een besluit, dat geregtvaardigd wordt door de plotselinge en krachtige uitbreiding der Wiskunde sedert de gewigtige uitvinding van Newton en Leibnitz, terwijl deze uitwerking slechts op zijde gestreefd wordt door den magtigen invloed, dien Descartes op de verbinding van Analysis en Geometrie heeft uitgeoefend. De Differentiaal- en Integraal-Rekening leerde ons de theorie en de eigenschappen der functien, der vergelijkingen, der reeksen, eigenlijk voor het eerst doorgronden, hetzij wegens de nieuwe gezigtspunten, waaruit het reeds bekende werd afgeleid, hetzij wegens den schat van nieuwe waarhedeu, door haar aan het licht gebragt; maar zij gaf ons ook voor de Geometrie de hulpmiddelen aan de hand, om den loop der kromme lijnen en alle bijzonderheden daarvan, om het beloop van lijnen van dubbele kromming en van gebogen oppervlakken met hunne eigenschappen te kunnen nagaan en bepalen; en wel uit dezelfde stelkundige formules, die ons de Analyse van Descartes had leeren kennen, om het verband tusschen meetkundige grootheden uit te drukken, en die dikwerf op zichzelve, bij dieper indringen in de eigenschappen der figuren en de betrekking daartusschen, te kort schoten, en hare hulp verder weigerden. Ja, het waren juist deze moeijelijkheden en belemmeringen, die aan eenen Newton in Engeland en aan eenen Liebnitz in Duitschland tegelijkertijd de aanleiding gaven, om kortere en meer algemeene regels voor het gewenschte gebruik uit te denken, en die alzoo de middelbare oorzaak van hunne uitvinding waren. Niet alleen heeft echter de Differentiaalen Integraal-Rekening aan hare eerste bestemming beantwoord, maar zij is tot een op zich zelf staand geheel geworden, dat een van de meest belangrijke en uitgebreide deelen der Wiskunde vormt, en zij heeft zoowel in de Analysis als in de Geometrie tot uitkomsten geleid, die men zeker vooraf verre was van te verwachten.

Uit het gezegde blijkt reeds ten duidelijkste, dat de strekking en de toepassing der Differentiaal- en Integraal-Rekening tweeledig is: eensdeels wordt

[p. 107]

zij gebruikt bij de theorie der functien, de Analysis in de meest uitgestrekte beteekenis; ten anderen wordt zij gebezigd en vertegenwoordigd bij de zoogenaamde Hoogere en Analytische Meetkunde, waarmede zij zeker in een naauw verband staat, zoo zelfs, dat een gedeelte van deze mede behoort tot de theorie der functien en daarvan, als het ware, gedeeltelijk de aanschouwelijke voorstelling is. Beide toepassingen evenwel zijn van groote uitgestrektheid en daarom vindt men veelal in eenig Leerboek der Differentiaal- en Integraal-Rekening op eene van beide in het bijzonder gelet, met althans gedeeltelijk voorbijgaan van de andere.

Onder de Leerboeken, die in onze taal zijn uitgekomen, verdient zeker dat van de Gelder - waarvan het 2^de Deel, hoewel voor een twintigtal jaren geschreven, echter eerst voor eenige maanden door de zorg van den Hoogl. Verdam in het licht gegeven is - eene eerste plaats; en wat de toepassing der Differentiaal-Rekening op de theorie der functien betreft, vindt men er nuttige en belangrijke bijdragen over de theoremata van Taylor, Maclaurin en Lagrange en hun gebruik, over de theorie der vergelijkingen en der reeksen, over interpolatie-methoden, als anderszins. Daarentegen missen wij in dat boek eene geregelde systematische behandeling van de theorie der kromme lijnen, waarvan slechts in het Eerste Deel eenige punten ieder op zich zelve worden behandeld, terwijl van de lijnen van dubbele kromming even als van de gebogen oppervlakken in het geheel geen gewag wordt gemaakt. Maar juist in dit opzigt leveren de boven aangekondigde Lessen over de Differentiaalen Integraal-Rehening van Dr. Lobatto de behandeling van eene leerstof, waaraan in onze taal behoefte bestond, en die voorzeker, mede en vooral door den trap van volkomenheid, waartoe zij in den laatsten tijd nadert, van groot belang is, zoowel voor de practische toepassing - daar toch eerst alzoo de kromme lijnen en gebogen oppervlakken gemakkelijk en met vrucht in het algemeen kunnen worden behandeld; - alsook en niet minder voor de theorie zelve, die in deze toepassing tevens hare verduidelijking en hare verklaring vindt. Hoewel nu van genoemd werk slechts het Eerste Deel verschenen is, wordt daarin de Differentiaal-Rekening afgehandeld en kan het alzoo eenigermate als een op zich zelf staand geheel worden beschouwd. Wanneer men namelijk zoowel de Rectificatie en Quadratuur der kromme lijnen en de Cubatuur der gebogen oppervlakken, alsook de toepassingen van de theorie der bijzondere en sommige bepaalde Integralen - welke toch eerst bij de Integraal-Rekening kunnen worden behandeld - uitzondert, vindt men hier de theorie der kromme lijnen, der lijnen van dubbele kromming en der gebogen oppervlakken, volledig uiteengezet; en onder genoemd voorbehoud zal eene korte opgave van den inhoud van dit boek - dat met regt kan gezegd worden het standpunt te vertegenwoordigen, waarop dat gedeelte der Wiskunde thans staat - de waarheid van het gezegde duidelijk kunnen aantoonen.

Om hierbij met meer gemak te werk te gaan, kan geschiktelijk de hoofdverdeeling van den Schrijver zelven worden gevolgd, namelijk:

I.	Les I-X. Differentiaal-Rekening voor de functiën met ééne verantwoordelijke grootheid.
II.	Les XI-XVII. Toepassing op de theorie der kromme lijnen.
III.	Les XVIII-XXII. Differentiaal-Rekening voor de functien met meer dan ééne onafhankelijk veranderlijke grootheid.
IV.	Les XXIII-XXXI. Toepassing op de theorie der lijnen van dubbele kromming en der gebogen oppervlakten.

Bij het doorloopen der behandelde stoffen, zal Ref. dan tevens gelegenheid hebben de eene of andere opmerking in het midden te brengen omtrent de behandeling zelve, als ook omtrent de orde bij de opeenvolging der onderdeelen in acht genomen.

[p. 108]

Eenen aanvang makende met de voorrede, zal wel ieder wiskundige den Schrijver toejuichen, die de leer der oneindig kleinen en wel, uit den aard der zake, in verband met de theorie der limieten, als grondslag der Differentiaal-Rekening aanneemt. Minder algemeen misschien zal de overeenstemming in gevoelen wezen bij het motiveren der hoofdverdeeling, hierboven voorgedragen, daar toch in den regel eerst de theorie der Differentiaal-Rekening voor functien met ééne, en vervolgens voor die met meerdere onafhankelijk veranderlijke grootheden wordt voorgedragen, om eerst daarna hare toepassing op kromme lijnen en gebogen oppervlakken te behandelen; op deze wijze toch is het verband ligter in te zien, dat tusschen de beide eerste punten bestaat, terwijl dan evenzoo ook de meetkundige toepassing in hare natuurlijke volgorde wordt uiteengezet. Ook Moigno nam deze volgorde aan in zijne Leçons de Calcul différentiel et intégral, - waarvan de beide eerste deelen te Parijs in 1840 en 1844 zijn uitgekomen en het laatste met belangstelling wordt te gemoet gezien -, en die zeker wel als voorbeeld ter navolging mogen dienen en ook plegen gebruikt te worden, zoowel wegens inhoud als wegens methode; slechts voegt hij achter ieder der beide eerste deelen hare analytische toepassing afzonderlijk. Zonder de verdeeling van den Schrijver met de redenen daarvoor opgegeven te willen afkeuren, gelooft Ref. toch, dat de gewone den voorrang verdient, waarvan in het vervolg ook wel de eene of andere aanmerking zal doen blijken.

Schr. bijvoeging van de fransche terminologie is niet zonder groot belang, daar toch vele, zoo niet de meeste der werken, inzonderheid over de behandeling der kromme lijnen en gebogen oppervlakken, òf in de fransche taal geschreven zijn, òf althans daarvan de terminologie hebben overgenomen: daarom vindt men dit ook hier, waar noodig, gevolgd.

I. Les I-X bevat de noodige verklaringen en bepalingen (Les I) en den zoogenaamden Algorithmus der Differentiaal-Rekening (Les II, III en IV), het onderzoek der waarde van onbepaalde uitdrukkingen (Les V), de beschouwing der reeksen van Taylor en Maclaurin (Les VI) en hare toepassingen (Les VII), de theorie der maxima en minima (Les VIII) en der ontbinding van gebrokens in eenvoudige (Les IX); eindelijk het veranderen der onafhankelijk veranderlijke grootheid (Les X).

Met het oog op de hoofdverdeeling, door Schr. ingevoerd, ware misschien eene andere volgorde in deze lessen wenschelijk geweest. Zoo behoort het onderwerp der Xde Les eerder bij den Algorithmus der Differentiaal-Rekening, en had gevoegelijk althans vóór de Vde Les kunnen komen. Even zoo zoude ook de IVde Les nict alleen wegens den inhoud zelven de IIIde hebben kunnen voorafgaan, - daar het behandelen van ingewikkelde functiën ook vóór de bekendheid met differentialen van hoogere orde kan gevorderd worden - maar dan was ook de zamenhang tusschen het differentieren van ingewikkelde en van zoogenaamde zamengestelde functien minder gebroken geweest, welk laatste nu, geheel op zich zelf, als eene hulpstelling in § 15 voorkomt.

Hierbij konde dan tevens het differentieren van de ingewikkelde functien met meer gemak en duidelijkheid zijn voorgedragen, dan wel thans heeft plaats gehad. Zoo komen in de IVde Les Blz. 46 de beide stellingen:

‘Door het differentieren der functie f (x, y) = 0, verkrijgt men blijkbaar eene uitkomst van den vorm P d x + Q d y = 0,’

en

‘Deze differentiaal vergelijking (nam. P d x + Q d y = 0) geeft tevens te kennen dat de functien P en Q ook afzonderlijk verkregen worden door f (x, y) te differentieren, als of y en x beurtelings standvastige waarden hadden.’

[p. 109]

zonder bewijs voor, dat hier toch niet ontbreken mogt; wanneer daarentegen na de stelling van Les II, § 15, Blz. 17, aangaande de functie van ééne functie eener veranderlijke grootheid, eene dergelijke ontwikkeling had plaats gegrepen voor y = F (z, v), waarin z en v beide functien van de onafhankelijk veranderlijke x voorstellen, dan had men (zie o.a. Navier, Résumé des Leçons d'Analyse données à l'Ecole Polytechnique, 1re Année, Page 42 etc.) verkregen:



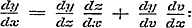
wanneer men nu y = 0 stelt, verkrijgt men de voorstelling eener ingewikkelde functie tusschen z en v, F (z, v) = 0, en, na eene korte herleiding, de partiele differentiaal-vergelijking boven aangehaald; bij welke handelwijze men tevens het voordeel heeft van het ontstaan der partiele differentiaalverhouding duidelijk te zien toegelicht. Hierbij kan tevens worden opgemerkt, dat Schr. bepaling van ingewikkelde functien niet volkomen juist is, daar elke vergelijking F (x, y) = 0 eene zoodanige ingewikkelde functie voorstelt, zonder dat het juist noodig is, de voorwaarde te stellen (zie IVde Les, § 34, Blz. 46),

‘dat het bezwaarlijk, zoo niet onmogelijk moet worden, y af te zonderen, of in eindigen vorm in x uit te drukken.’

Aan deze voorwaarde toch zoude bij eene ingewikkelde functie als bijv.



niet voldaan worden. Dat Schr. zich van tijd tot tijd op zijne ‘Lessen over de Hoogere Algebra’ eroept, kan voorzeker de bewerking veel bekorten, maar dan konden ook bal de eigenschappen der limieten als dáár bewezen ondersteld, en dus hier vermeden worden; - of, misschien nog beter, bij den aanvang van het boek, wegens haar groot gewigt, de voornaamsten bij elkander gevoegd zijn geworden, om daarop te kunnen verwijzen. Alzoo zoude de stelling op Blz. 11, Les I, § 9, N^o. 6, dat

‘de limiet van het produkt van twee of meer veranderlijke grootheden gelijk is aan het produkt der limieten, waartoe zij elk in het bijzonder naderen,’

als bewezen aaugenomen zijn, of de even belangrijke en gelijkluidende stelling aangaande de limiet eener som - waarop de genoemde berust, en die tevens naderhand o.a. § 14 wordt aangewend - tevens bewezen zijn geworden. Tot zoodanige grondstellingen, die naar den tegenwoordigen toestand der wetenschap eene hoofdrol spelen en als gronden dienen, waarop gemakkelijk de verdere theorie kan worden opgebonwd, - en die dan ook in vele nieuwere Leerboeken der Differentiaal-Rekening (zie o.a. O. Schlömilch, Handbuch der Differenzial- und Integral-Rechnung I, S. IV) voorop worden gesteld, - behooren:

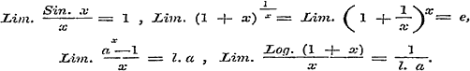
Was, behalve de aangehaalde stelling, de geheele § 9, -als bevattende eenige eigenschappen der oneindig kleinen van verschillende orde, - de vorige paragraphen, althans § 8 voorafgegaan, dan zoude zoowel de schijnbare onnaauwkeurigheid van formule (3) blz. 8 vervallen zijn, als in dat geval tevens het terugkomen daarop in § 10 overbodig zijn geweest.

Somtijds haalt schr. zijne ‘Lessen over de Hoogere Algebra’ aan, wanneer eene regtstreeksche oplossing te verkiezen ware geweest, bijv. bij het differen-

[p. 110]

tieren van de magtsgrootheid; dit geval toch is van zoo veel en zoo gewigtige toepassing, dat eene onafhankelijke behandeling (zoo als b.v. door Moigno geleverd wordt in zijne ‘Leçons Calcul. de diff. et integr.,’ Tome I, Page 9, en door Schlömilch in zijn ‘Handb. der Differenzialr.,’ Th. I, S. 26) niet geheel overbodig konde geacht worden. Bovendien is § 13, waarin de gevallen eener negatieve, gebrokene en negatief-gebrokene magt afzonderlijk worden nagegaan bij de onderstelling, dat de binominale reeks slechts voor eene geheele magt bewezen is, daarom reeds overtollig, daar het bewijs dezer gewigtige formule, - wanneer zij in de Hoogere Algebra zoo volstrekt en algemeen gegeven is, als de hoogte der wetenschap thans vordert, - voor elke magt in het algemeen moet gelden. (Men kan hierover nazien Smaassen, ‘Gronden der Hoogere Algebra’, 1849, blz. 69.)

Bij het bepalen der differentiaal van y = X : X₁ (X en X₁ beide functien van x zijnde), brengt Schr. (Les II, § 17, blz. 19) dit terug tot het geval van een produkt van twee zulke functien y = X × X₁^-1, welke wijze van behandeling zeer geschikt is, om de waarheid der regtstreeks verkregen uitkomst nader te bevestigen; echter moet de regtstreeksche afleiding steeds den voorrang behouden, ook wegens hare eenvoudigheid: immers stellende, zoo als gewoonlijk:



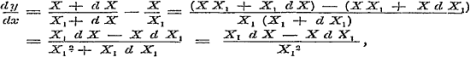
zoo verkrijgt men dezelfde uitkomst met meer gemak en grootere duidelijkheid, en wel onafhankelijk van eenige vroeger verkregen uitkomst.

Heeft men een gedurig produkt, dan neemt de schrijver, § 19, blz. 23, de Logarithmen: deze handelwijze is slechts geoorloofd, wanneer de faktoren vooraf tot de tweede magt zijn verheven, daar van de mogelijke negatieve faktoren geen' Logarithmus mag genomen worden, waardoor men tot onbestaanbare uitdrukkingen zoude geraken.

Vele voorbeelden van differentiatie worden hier aangetroffen, zoowel uitgewerkt ter toepassing der verkregen formules (blz. 20, 24, 28, 30), als ook ter eigene oefening (blz. 29, 31-34), en daaronder zal men voorzeker met belangstelling de differentialen der Logarithmen van de circulaire functien aantreffen.

Onder de volgende Lessen is inzonderheid de Vde - handelende over het onderzoek der waarde van uitdrukkingen, voorkomende onder eenen der onbepaalde vormen



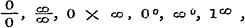
- zeer uitvoerig bewerkt; zij bevat wel alles, wat daarbij van belang zoude kunnen zijn, en ook hier volgt, blz. 68 en 69, eene reeks van 25 belangrijke voorbeelden ter eigene oefening. En zoo zijn wij dan genaderd tot den hoeksteen der Differentiaal-Rekening, het Theorema of de Reeks van Taylor en dat van Maclaurin, met de daarbij behoorende toepassingen. In de VIde Les vinden wij het theorema van Taylor afgeleid uit de waarde van F (x + n Δ x) in eene reeks naar de opvolgende Differentien van y = F (x) geordend; eene handelwijze echter, die voor het vinden eener zoo gewigtige ontwikkeling als genoemd Theorema naauwelijks zeker en voldoende genoeg kan gerekend worden. Daarop volgt evenwel de onafhankelijke, heuristische afleiding uit de formules

[p. 111]

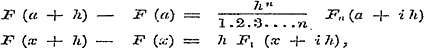
die eerst tot dat doel worden betoogd. Deze ontwikkelings-wijze heeft, behalve hare volstrekte juistheid en volkomen analytisch karakter, nog het eigenaardige voordeel van tevens de zoogenaamde rest der reeks te doen bepalen, waaruit men regtstreeks de convergentie of divergentie, met andere woorden de bruikbaarheid of ongeschiktheid der reeks kan nagaan. Deze rest, eerst onder den vorm



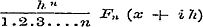
voorkomende, wordt daarna tot den anderen vorm



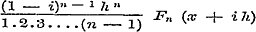
herleid.

De reeks van Maclaurin wordt telkens uit die van Taylor afgeleid door de achtervolgende substitutie van x = 0 en h = x; en hoewel ook deze laatste reeks als een gevolg der eerste wordt beschouwd, ware het misschien niet ongepast geweest, ook den weg aan te wijzen, waarop de reeks van Maclaurin dadelijk en onafhankelijk van de andere kan gevonden worden, iets, dat ligtelijk te doen is. Omgekeerd wordt aangetoond, dat elke convergerende reeks, die de ontwikkeling eener functie voorstelt, met de reeksen van Taylor en Maclaurin noodzakelijk moet overeenkomen.

Het geval, waarin x onbestaanbaar, dat is van den vorm a ± b √ - 1 zoude zijn, wordt hier niet overwogen, hoewel dit wel degelijk van groot belang is, wegens den merkwaardigen vorm der rest zoowel, als wegens de toepassingen, die van de reeks onder deze gedaante gemaakt kunnen worden.

In de VIIde Les worden de Theoremata van Taylor en Maclaurin toegepast op het ontwikkelen van functien in reeksen, geordend naar de opklimmende magten van het element; en daarbij worden, § 59, de gevallen overwogen, wanneer de ontwikkeling onmogelijk wordt, benevens de oorzaak van deze onmogelijkheid zelve. Onverwacht volgt hierop, § 61, eene methode naar het verbonden gebruik van deze theoremata en van de oude leerwijze der onbepaalde coefficienten, van welke laatste reeds zoo dikwerf het gevaarlijke en ongeoorloofde is aangetoond geworden. En dit kan hier weder ten stelligste blijken bij de ontwikkeling van de functie l { x ± √ (1 + x²)} naar die methode (blz. 89).

Daar toch



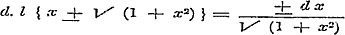
is, zoo geeft de onderstelling



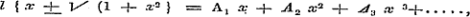
daar de term x⁰ ontbreekt, omdat ƒ (0) = 0 is, ook:



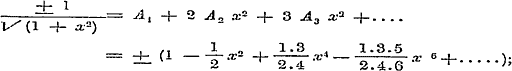
waaruit achtervolgens worden gevonden:



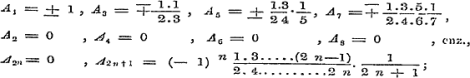
en dus

[p. 112]

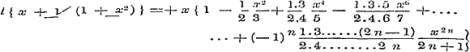
De limiet van de verhouding tusschen twee achtervolgende termen is:



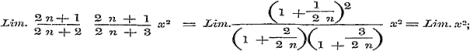
dus moet voor de convergentie slechts de voorwaarde bestaan

x² < 1 of 1 > x > - 1

Noemende kortheidshalve de gevondene reeks R, zoo is l. {x + √ (1 + x²} = R x, l. {x - √ (1 + x³ = - R x .... (x² < 1) welke laatste echter, als de Logarithmus van een negatief getal, onbestaanbaar zoude moeten zijn, en dit is eene tastbare ongerijmdheid. Dat de reeks nogtans convergent blijft, is daaruit te verklaren, dat zij niet de ontwikkeling van l. {x - √ (1 + x²}, maar wel die van ½ l. {x - √ (1 + x²}², of van de bestaanbare l. {- x + √ (1 + x²)} voorstelt, hetgeen ten overvloede nog blijken kan, door het negatief nemen van x in de eerste reeks l { x + √ (1 + x²)} = Rx, waardoor men wederom tot de laatst verkregene uitkomst geraakt.

Gereedelijk had in deze Les de betrekking tusschen de reeksen voor e^x, Sin. x en Cos. x, kunnen worden ontwikkeld; maar inzonderheid konde men hier, meent Ref., de ontwikkeling verlangen van de reeksen voor Tang. x, Cos. x, Sec. x en Cosec. x, waardoor dan tevens de gelegenheid zich had aangeboden, om iets over de Bernouilliaansche en Secanten-Coefficienten in het midden te brengen, die toch in de laatste vorderingen der wetenschap eene niet onbelangrijke rol spelen. Men zoude over deze merkwaardige functien kunnen nazien Schlömilch, ‘Handb. der Differenzialr.’ I, S. 229-245.

Eene uitvoerige theorie van de maxima en minima bij functien van eene enkele veranderlijke grootheid (in de VIIIste Les), wordt gevolgd door hare toepassing op enkele functien en op 16 belangrijke meetkundige vraagstukken, waarvan een gedeelte aan eigene bewerking zijn overgelaten. Als van zelf zoude Schr. hier tot de toepassing van dit eerste gedeelte der Differentiaal-Rekening op de vlakke kromme lijnen komen, indien niet hier de ontbinding van gebrokens in eenvoudige (Les IX) en de invoering eener nieuw onafhankelijk veranderlijke grootheid (Les X) waren tusschengeschoven. Over de verplaatsing der Xde Les is reeds vroeger gesproken, en de IXde konde zeer gevoegelijk achter de VIde zijn gevolgd; dan was bij de theorie der maxima en minina de toepassing op de Analysis geëindigd en die op de Meetkunde begonnen, om onafgebroken doorgezet te worden.

Wij zijn nu tot het tweede hoofddeel gekomen, waarin Les XI-XVII over de theorie der vlakke kromme lijnen wordt gehandeld, en wel vooreerst volgens hare vergelijking op regthoekige coördinaten-assen. Daarbij volgen de vergelijkingen der raaklijnen en normalen met hare bijzondere gevallen, de bepaling der lengte van de Tangens, de Subtangens, de Normaal en de Subnormaal elkander op, terwijl naderhand de differentiaal van den boog daarbij wordt ingevoerd, en over den hoek van contingentie en de regtlijnige asymptoten wordt gehandeld.

Dubbel is (§ 86, blz. 137) Schr. bepaling van deze laatsten, en twee metho-

[p. 113]

des zijn er ook, om haar bestaan na te gaan, waarvan men evenwel slechts die ontwikkeld vindt, waarbij de Asymptoot beschouwd wordt als eene lijn, ‘tot welke de kromme meer en meer nadert, zonder die lijn immer te kunnen snijden’: niet minder eenvoudig en dikwerf van nuttige toepassing is de andere manier, berustende op de eigenschap, dat de asymptoot ‘den stand der raaklijn op oneindig ver verwijderde punten voorstelt’, waarvoor dus de ordinaat of de abscis oneindig groot wordt; zoodat men hare vergelijking verkrijgt, door in die van de raaklijn, na eliminatie van x of y, y of x gelijk ∓ ∞ te stellen.

Vervolgens wordt nagegaan, of eene kromme lijn hare holle, dan wel hare bolle zijde naar de coördinaten-assen toekeert, en de theorie der buigpunten (points d'inflexion) breedvoerig ontwikkeld, en ook over de keerpunten van beide soorten (points de rebroussement) iets gezegd. Hier had misschien even zoo goed eene geregelde opgave behoord van de overige merkwaardige punten - die nu slechts als ter loops voorkomen in Les XII, § 97, 98, blz. 155 en vgg., waar wij de toepassing van de bovengemelde theorie aantreffen op verschiltes, de Conchoide enz. - van de dubbele en veelvoudige punten, ook knoopen genaamd (points doubles, multiples), waardoor derhalve verscheidene raaklijnen kunnen worden getrokken, van de eindpunten (points d'arret), van de afgezonderde punten (points isolés); terwijl daarbij nog gevoegd diende te worden eene bijzondere soort van keerpunten (points saillants), waarbij de differentiaalverhouding dy/dx voor eene zekere waarde der veranderlijke grootheid, plotseling van waarde verandert, en de beide raaklijnen derhalve eenen eindigen hoek te zamen vormen: al welke punten zulk eene gewigtige rol spelen in de beschouwing der kromme lijnen, en waarvan de theorie naauw verbonden is met die der gelijke wortels eener hoogere magts-vergelijking. Men kan hierover nalezen: Ekman, ‘de punctis singularibus curvarum algebraicarum simplicis curvaturae Disquisitio’, Par. 1842.

In de XIIIde Les worden de kromme lijnen tot hare poolvergelijking teruggebragt, en daarna dergelijke formules afgeleid als in Les XI, waarbij nog de loodlijn in lengte bepaald wordt, die uit de Pool op de raaklijn valt, en vooral als hulpgrootheid dikwerf van groote dienst is. Deze vergelijkingen leidt Schr., soms op velerhande wijze, onmiddelijk uit de figuur zelve af, terwijl eerst naderhand wordt aangegeven, op welke wijze zij door middel van de betrekkingen



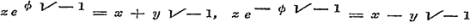
met de formules van Les XI zamenhangen: eene methode, die uitnemend geschikt is, om de ware beteekenis en het onderling verband der formules te leeren inzien. Als toepassing worden de Spiraal van Archimedes, de Logarithmische en hyperbolische spiraal, de kegelsneden, de Epicycloide en de Conchoide nagegaan.

De kromming, de kromtestraal, het middelpunt van den kromte- of ineensmeltingscirkel en de theorie der ontwondenen, vindt men in de XIVde Les behandeld, ten opzigte van het regthoekige coördinaten-stelsel; in Les XV daarentegen voor de polaire coördinaten: in beide gevallen worden de benoodigde vergelijkingen, zoowel uit de figuur als ook uit de reeds gegevene formules afgeleid, en op onderscheidene voorbeelden toegepast. Als eene bijdrage tot de geschiedenis van dit gedeelte der Wiskunde, is het misschien niet ongepast, op te merken, dat wij den oorsprong dezer theorie aan Jacobus Bernouilly verschuldigd zijn, terwijl de ontwondenen het eerst door onzen grooten Huygens zijn gebruikt (zie zijn ‘Horologium Oscillatorium,’ P. III).

[p. 114]

Les XVI handelt vervolgens over de kromlijnige aanrakingen van verschillende orden, met inachtneming van de gelijktijdige snijding, wanneer de graad der orde een evene is, en met toepassing op de gewone regte raaklijn, op den kromte-cirkel en de parabolische ineensmeltingskrommen; terwijl eindelijk in de XVIIde Les de theorie der omhullende kromme lijnen of Enveloppen gegeven, en in eenige toepassingen meer aanschouwelijk wordt gemaakt; daar deze theorie evenwel met die der bijzondere integralen ten naauwste tezamenhangt, zal men in de Integraal-Rekening hare verdere uitbreiding eerst kunnen afwachten. De beide laatste lessen gelden alleenlijk voor regthoekige coördinaten-assen: misschien ware het verband meer duidelijk geweest, indien eerst heir de XIIIde en XVde Les gesteld waren, wanneer men dan eerst de theorie der kromme lijnen volgens hare vergelijking op regthoekige coördinaten-assen bij elkander had gevoegd, om daarna die volgens de polaire coördinaten-vergelijkingen te doen volgen, die toch in vele opzigten als het ware op zich zelve staan.

De nu volgende Lessen XVIII-XXII zijn gewijd aan de Differentiaal-Rekening voor functien, met meer dan eene veranderlijke grootheid.

Nadat de gronden hiervan in de XVIIIde Les uiteengezet en volgens de figuur verder verklaard zijn, wordt deze theorie op homogene functien toegepast; op het einde van deze Les wordt de stelling bewezen (§ 141):

Indien men de gedeeltelijke differentiaalquotienten eener gelijkslachtige functie van den mden graad (u = F (x, y, z,...)) vermenigvuldigt met de veranderlijke grootheden, ten opzigte van welke zij genomen zijn, zal de som dezer produkten gelijk worden aan het m-voud der gegevene functie, dat is



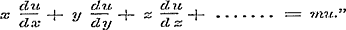
Maar dit betoog is niet zuiver, en levert slechts daarom eene goede nitkomst, opdat op het einde daarvan juist i = 1 genomen wordt. Nadat Schr.

F (ix, iy, iz,...) = i^m F (x, y, z,...) = i^mu

gesteld heeft (om aan de onderstelling eener homogene functie van den mden graad te voldoen) en vervolgens gemakshalve neemt

ix = x¹, iy = y¹, iz. = z¹, enz.,

verkrijgt hij, na differentiatie ten opzigte van i:



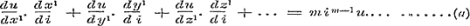
Dit is echter onwaar, terwijl het klaarblijkelijk wezen moet:



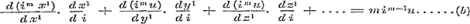
Wanneer men nu met schr. voortredeneert, en nagaat, dat



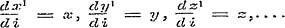
is, verkrijgt men door i = 1 te nemen, voor beide formules (a) en (b) de boven opgegevene waarheid.

In de XIXde Les volgt de ontwikkeling der hoogere differentialen, in de onderstelling van meerdere veranderlijke grootheden, en wordt hierbij opmerkzaam gemaakt op het gemakkelijke der symbolische vormen, en tevens op Schr. bekende Verhandeling ‘sur la théorie des caractérisques’ verwezen. Na in de XXste les een vrij kort overzigt te hebben gegeven aangaande de uitbreiding der reeksen van Taylor en Maclaurin, op functien van meerdere veranderlijke grootheden, gaat Schr. in de XXIste Les over tot het bepalen der maxima en

[p. 115]

minima bij zoodanige functien, - ook in de bijzondere gevallen, dat er zekere voorwaardenvergelijkingen gegeven zijn, waaraan de veranderlijken moeten voldoen, zoodat zij op zekere wijze van elkander afhankelijk zijn, - en de toepassing van de gevondene kenmerken op onderscheidene voorbeelden.

In de XXIIste Les wordt dit gedeelte der Differentiaal-Rekening besloten met de ontwikkeling van het teregt zoo beroemde theorema van Lagrange. Hiervan komt het bewijs aan Ref. niet onafhankelijk genoeg voor, en wel om de vroeger reeds gemaakte aanmerking, dat het gebruik van de leerwijze der onbepaalde coefficienten, hier wederom gebezigd, de uiterste omzigtigheid vordert en liever, zoo mogelijk, te vermijden is. Met geringe wijziging konde Schr. bewijs evenwel blijven gelden, zonder zich van deze coefficienten te bedienen, indien men te werk gaat zoo als o.a. Cournot, ‘Traité élémentaire de la Théorie des Fonctions et du Calcul infinitésimal’, Tome I, page 276, of ook zoo als Schlömilch, ‘Handb. der Differenzialr.,’ Th. I, Cap. IX. Nog meer heuristisch is de methode van Cauchy, waarover men kan nazien Moigno, ‘Leç. de Calcul Diff. et Intégr.’, Tome I, 18me Leçon. Hier had wel het bewijs nog behooren te volgen, dat èn het Theorema van Taylor èn dat van Maclaurin, beide in het Theorema van Lagrange, als bijzondere gevallen, zijn opgesloten, zoodat deze reeks zoowel in de Differentiaal- en Integraal-Rekening, als ook in de theorie der vergelijkingen van het hoogste belang, tevens nog eene algemeene voorstelling van genoemde reeksen is. In onze taal levert zeker De Gelder in zijne, door Schr. aangehaalde ‘Beginselen der Differentiaal-rekening,’ Tweede Deel, veel belangrijks en wetenswaardigs, waar hij, bl. 244-261, het Theorema van Lagrange afleidt, en blz. 297-373, toepast op het ontwikkelen van functien, op het oplossen der wortels van hoogere magts-, als ook van transcendentale vergelijkingen. Van beide laatste toepassingen vinden wij ook bij onzen Schr. eenige gevallen uiteengezet. Voor hem, die zich wil overtuigen, tot welke hoogte de theorie der vergelijkingen thans is opgevoerd, en wel voornamelijk door het gezamenlijk gebruik van het Theorema van Lagrange en de zoo belangrijke theorie der symmetrieke functien - welke toepassing eerst sedert den laatsten tijd van zoo veel gewigtigen invloed geweest is - is de lezing aan te bevelen van het werk van Serret, ‘Cours d'Algèbre Supérieure,’ Paris 1849.

Eindelijk zijn wij dan aan het laatste gedeelte gekomen: Les XXIII-XXXI, de theorie der lijnen van dubbele kromming en der gebogen oppervlakken bevattende, - dat zeker en wegens den inhoud op zich zelven genomen, en wegens de menigte belangrijke opmerkingen daarbij voorkomende, en wegens de duidelijke en geleidelijke behandeling van deze meer ingewikkelde theorien, de opmerking des lezers ten hoogste waardig is.

In Les XXIII vindt men, na eenige algemeene aanmerkingen en ophelderingen omtrent de lijnen van dubbele kromming, de vergelijkingen van de raaklijn en hare projectien, van het normaalvlak en van het krommingsvlak afgeleid, en deze op de gewone schroeflijn toegepast; terwijl in de XXIVste Les over den krommingshoek, den straal des kromte-cirkels, de hoofd-normaal, de coördinaten van het middelpunt des kromte-cirkels, het polaire oppervlak en de poollijnen met hare keerlijn, over de ontwondene, den wringingshoek en de daarmede zamenhangende tweede kromming, eindelijk over de buigpunten wordt gehandeld, alweder met toepassing op de gewone Schroeflijn. Deze afleiding is doorgaande zuiver analytisch; slechts enkele punten worden in de figuur aangewezen. Twee aanmerkingen zij het den Ref. geoorloofd, op deze Les te maken.

[p. 116]

Vooreerst had op blz. 295, § 168, ligtelijk het bewijs kunnen volgen, dat de kromtestraal van eenige kromme in de ruimte, in grootte en in rigting overeenkomt met den kromtestraal van de projectie dier gegevene kromme op het krommingsvlak. Wanneer men namelijk, gemakshalve, bijv. het coördinaten-vlak x y aan dit laatste evenwijdig stelt, wordt de kromtestraal R = ds³/Z, (waarbij de waarde van Z op blz. 290, § 166 voorkomt), de waarde des genoemden kromtestraals (Les XIV, § 109, blz. 177), terwijl ook de coördinaten van het kromte-middelpunt, volgens blz. 297



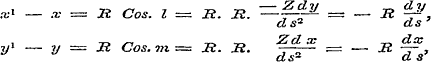
met de gezochte overeenkomen (zie Les XIV, § 112, blz. 181).

Wat, ten tweede, de tweede soort van buigpunt betreft, die gewoonlijk dubbel buigpunt (inflexion double) pleegt genoemd te worden, dit komt voor, wanneer twee opvolgende elementen der lijn van dubbele kromming in eene regte lijn liggen, en dus zoowel ε als ε¹ gelijk nul is: het tweede is echter geen gevolg van het eerste, zoo als Schr. bl. 303 aangeeft:

‘ε = 0, hetgeen van zelf medebrengt, dat ε¹ insgelijks = 0 zij.’

De onderstelling ε = 0 geeft volgens formule (4), blz. 295, X = 0, Y = 0, Z = 0, en daarvoor wordt ε¹ = 0/0. Neemt men nu gemakshalve hier het geval, dat d x standvastig is, dan wordt



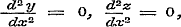
en formule (10), blz. 302 geeft:



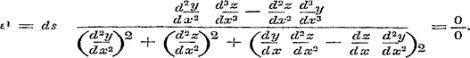
Dus op de gewone manier (zie Les V) teller en noemer differentierende:



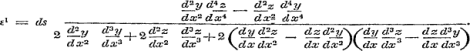
Dit is nog = 0/0. Dus weder de teller en noemer differentierende, en bedenkende, dat d²y/dx² = 0, d²z/d x² = 0 is:



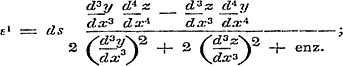
zoodat nu, om ε¹ = 0 te maken, noodzakelijk zijn moet:



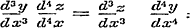
en dit is derhalve de voorwaarde, die behalve het nul zijn van ε gevorderd wordt, om ook ε¹ nul te maken, en een dubbel buigpunt daar te stellen.

[p. 117]

De XXVste Les besluit de theorie der lijnen van dubbele kromming met de aanrakingen van verschillende orden bij deze lijnen, en wel bepaaldelijk in toepassing op den kromtecirkel, waarvan de straal, de coördinaten van het middelpunt en het vlak zelf, op onderscheidene wijze bepaald worden.

Het eerst schreef over deze lijnen Clairaut, ‘Recherches sur les courbes à double courbure’, Paris 1731; terwijl later hunne theorie gewoonlijk tezamen met die der gebogen oppervlakken werd behandeld, tusschen welke dan ook in vele opzigten een naauw verband bestaat, zoo als in de volgende lessen genoegzaam zal blijken.

Met de XXVIste Les begint nu de theorie der gebogen oppervlakken, waarvan de vergelijking, even als die voor de raaklijn, het raakvlak, de normaal, en een normaalvlak, onder verscheidene onderstellingen worden ontwikkeld; de gevondene formules vinden dan hare eenvoudigste toepassing op den Bol, de Ellipsoide, de Hyperboloide met een blad en die met twee bladen, de Elliptische en Hyperbolische Paraboloiden, het cirkelvormig regte Kegelvlak, en het horizontale Schroefvlak. Bij het normaalvlak had geschiktelijk melding kunnen gemaakt worden van zijne doorsnede met het gebogen oppervlak, welke normale doorsnede (section normale) pleegt genoemd te worden, in tegenstelling van de overige schuinsche doorsneden (sections obliques), vooral daar deze benamingen later als bekend worden ondersteld.

Schr. gaat nu over tot de verschillende soorten of familien van oppervlakken, en de analytische kenmerken, waarnaar zij worden onderscheiden. Achtervolgens beschouwt hij in de XXVIIste Les de Cylinder-vlakken, de Kegelvlakken, de Omwentelings-oppervlakken, en in de XXVIIste de Regelvlakken, welke hij in Scheve en Ontwikkelbare Oppervlakken verdeelt, terwijl hij als eene ondersoort der eerste nog de Conoiden onderscheidt. Van iedere soort wordt zoowel de karakteriserende partiele differentiaalvergelijking, als ook de kenmerkende eindige vergelijking opgemaakt, en verder enkele bijzondere gevallen behandeld, waar zij aan eenige gegeven voorwaarden moeten voldoen, bijv. van om een gegeven oppervlak beschreven te zijn. Bij de beschouwing der ontwikkelbare oppervlakken wordt naar behooren aangetoond, dat zoowel de cylinder- als de kegelvlakken hiervan bijzondere gevallen zijn, en dan ook aan de vereischte voorwaarden-vergelijking voldoen.

Les XXIX handelt over de omhullende oppervlakken - waarvan de theorie eene voortzetting is van die der omhullende kromme lijnen, en dus, even als deze, in de Integraal-rekening eerst verder vervolgd kan worden - de karakteristieke, de kanaal-oppervlakken, het verband tusschen omhullende en ontwikkelbare oppervlakken, en de toepassing dezer theorie op de poollijnen eener lijn van dubbele kromming.

In de XXXste Les vindt men het voornaamste over de kromming der gebogen oppervlakken, - de bepaling van den straal van de coördinaten des middelpunts en van het vlak voor den kromtecirkel, van eene normale doorsnede, waaruit dan de voorwaarde voor het bol zijn des oppervlaks wordt afgeleid, - de bepaling der hoofd-doorsneden van de grootste en kleinste kromming, waarbij het dusgenoemde Theorema van Euler eene eenvoudige betrekking uitdrukt tusschen den kromtestraal (ρ), in elke willekeurige normale doorsnede met die (R en R¹), welke tot de hoofd-doorsneden behooren, te weten:



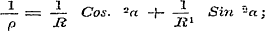
(zie blz. 364 formule (12)) - de toepassing hiervan op onderscheidene soorten van oppervlakken - het theorema van Meusnier omtrent de schuinsche doorsne-

[p. 118]

den, waarvan ook een geometrisch hetoog geleverd wordt, - de osculatie tusschen twee oppervlakken en hare voorwaarden, - de osculerende Ellipsoide, welke hier iets dergelijks is, als de kromtecirkel bij de kromme lijnen, terwijl daarbij van de Navelpunten en van de lijn der spherische krommingen (ligne ombilicale) gewag wordt gemaakt. Hier konde nog gewag zijn gemaakt van eenige bijzondere punten bij de gebogen oppervlakken, namelijk van de points de fluctuation (Golvingspunten?), waarbij de partiele Differentiaalverhoudingen van de eerste en tweede orde p en q bepaald, r, s en t daarentegen onbepaald zijn en van dy/dx afhangen: terwijl voor de ombilics de fluctuation (golvingsnavelpunten?) p, q en s gelijk nul, r en t gelijk (waardoor aan de voorwaarden van een navelpunt voldaan wordt), maar de partiele differentiaalverhoudingen van de derde orde van z, ten opzigte van x en y onbepaald en van dy/dx afhankelijk zijn.

De XXXIste en laatste Les eindelijk handelt over de theorie der krommingslijnen op de gebogen oppervlakken, het eerst door den grooten Monge opgemerkt, aan wien men den grond van vele nieuwe en merkwaardige bijzonderheden in de geheele leer der gebogen oppervlakken te danken heeft: daarbij worden tevens de lijnen van grootste helling, als ook de zoogenaamde waterpasse lijnen herdacht.

Hoezeer ook uit den aard der zaak de behandeling der gebogen oppervlakken slechts zeer kort konde wezen, om hier niet de grenzen van een Leerboek te overschrijden, vindt de Lezer toch niet alleen de hoofdzaken hier bij elkander, maar ook zal de studie van hare bewerking hem tevens in staat kunnen stellen, met deze theorie voort te gaan, waartoe dan ook eenige bronnen door Schr. worden opgegeven. Hieromtrent valt bij te voegen, dat het werk van Dr. Alings sedert met een tweede deel is voltooid, en met eene zeer belangrijke geschiedkundige bijdrage omtrent den opvolgenden vooruitgang der theorie van de kromming der gebogen oppervlakken en omtrent de daartoe behoorende literatuur besluit; zoodat dit werk allezins bij de studie van dit onderdeel kan aanbevolen worden. Verder zoude nog bij deze literatuur gevoegd kunnen worden:

Twee ‘Memoires’ van Tinseau, voorkomende in de ‘Mém.-prés. à l'Institut.’ Tom. IX.
Meusnier, ‘Mém. sur la courbure des surfaces. Mem.-prés.’ Tome X.
Lagrange, ‘Théorie des fonctions analytiques.’
Olivier, ‘Note de Géométrie sur les Paraboloides osculateurs,’ in het Journal de l'Ecole Polyt., Cah. 25.

Evenzeer als het bovenstaande overzigt dienen kan, om eenig denkbeeld te doen vormen omtrent het wezen en den inhoud der Differentiaal-Rekening, zal het ook strekken om het vroeger gezegde te staven, dat men in het Leesboek van Dr. Lobatto, inzonderheid met het oog op de meetkundige toepassing, eene volledige en bondige uiteenzetting, en eene grondige en duidelijke behandeling van deze studievakken aantreft, die, zoo als genoegzaam gebleken is, tot de tegenwoordige hoogte der wetenschap is opgevoerd. De lezing van dit boek zal verder den wensch doen ontstaan, dat het vervolg - hiermede in zoo naauw verband, niet alleen wat de theorie zelve, maar ook wat hare meetkundige toepassing betreft - niet lang achterwege moge blijven, maar tegelijk met het hier doorgeloopen deel moge strekken, om de studie van de zoo belangrijke als nuttige Differentiaal- en Integraal-Rekening te verligten, en den lust daartoe meer en meer op te wekken, gelijk daartoe een goed Leerboek zoo veel kan bijdragen.

[p. 119]

Om bij de lezing van het boek te huip te komen, volgt hier eene lijst van drukfeilen en misstellingen, die Ref. onder het lezen nog zijn voorgekomen, en waarvan het blijven bestaan, bij een wetenschappelijk werk van dezen aard, al zeer moeijelijk schijnt vermeden te kunnen worden.

Deventer, Mei 1851.

D. BIERENS DE HAAN.

[p. 120]

Het Vaandel. Tijdschrift voor onder-officieren. Eerste Jaargang. Delft. W.N.C. Roldanus. 1851.

De aankondiging van het hierboven genoemde Tijdschrift zal volstrekt geene beoordeeling zijn; daartoe bestaat het nog te kort. Dit alleen kunnen wij daarvan zeggen, dat de namen der oprigters en medearbeiders, namen van kundige en talentvolle officieren, ons de gegronde hoop doen koesteren, dat dit Tijdschrift een langdurig bestaan zal hebben, en immer door degelijkheid en belangrijkheid zal uitmunten.

Alleen reeds de uitgave van zulk een Tijdschrift voor onder-officieren is eene onderneming, die hoogen lof verdient, is eene nuttige, goede daad. Alles wat dáártoe strekken kan om meer kennis te verspreiden, meer militaire en zedelijke waarde te geven aan de onder-officiers van het Nederlandsche leger, moet onbepaald toegejuicht worden; want daardoor wordt de kracht van ons leger, het welzijn van ons Vaderland bevorderd.

Het is eene waarheid, die geen tegenspraak lijdt, dat een goed kader onder-officieren de sterkte van een leger uitmaakt; zulk een kader is vooral eene noodzakelijkheid bij een leger als het onze, dat altijd voor het grootste gedeelte uit jonge soldaten en uit militie zal bestaan. Het is verkeerd, bij de Nederlandsche krijgsmagt er naar te streven, om onder de soldaten een groot aantal vrijwilligers te willen hebben; ten minste bij de infanterie, het wapen dat drie vierde van de sterkte des legers uitmaakt, zal men die vrijwilligers niet in genoegzaam getal kunnen krijgen, of het gehalte zal slecht zijn; oude soldaten, in den goeden zin van het woord, zal men bij onze infanterie, in vredestijd, niet kunnen hebben; alleen de oorlog vormt die. Maar het is op de oefening en verbetering der militie en der schutterij, dat men zich met kracht moet toeleggen; en daartoe is het noodzakelijk dat men, vooral bij de infanterie, sterke en goede kaders heeft. Met een goed en genoegzaam sterk kader, kan men des noods van eenige honderde boeren, die nooit een geweer in handen hebben gehad, in weinig maanden tijds een goed bataillon vormen; hoeveel te meer zal men dit kunnen doen met militie, die reeds eene voorafgaande oefening heeft gehad. Maar alles hangt daarbij af van de kaders; wanneer in 1815 te Quatre-Bras de pas opgerigte Nederlandsche militie-bataillons zich zulk een onsterfelijken roem hebben verworven, door den kamp vol te houden tegen de overmagtige en oude troepen van Ney, dan is dit geweest, omdat die bataillons officieren en onder-officieren hadden, die ten volle berekend waren voor hunne taak. De deugdzaamheid van een kader maakt de deugdzaamheid van een corps uit; en hij, die wil, dat het Nederlandsche leger goed zij - en welk Ne-

[p. 121]

derlander wil dit niet! - moet dus alles aanmoedigen en toejuichen, wat kan medewerken om de waarde der officieren en onder-officieren te verhoogen.

Er is in de laatste vijf en twintig jaren zeer veel gedaan, om aan het Nederlandsche leger goede, uitmuntende officieren te verschaffen; voor de onder-officieren werd te weinig gedaan. Die gedeeltelijke verwaarlozing is zeker toe te schrijven geweest aan omstandigheden, die niet altijd van de regering afhingen; maar toch heeft die verwaarlozing een ongunstigen invloed uitgeoefend; en vooral het volslagen gemis aan vooruitzigt op bevordering, dat langen tijd loodzwaar op onze onder-officiers drukte, heeft nadeelig gewerkt op hun' stand, en gemaakt dat die stand, eenige jaren geleden, niet zóó zamengesteld was als hij het moest zijn.

Haasten wij ons er bij te voegen, dat ook daarin eene gelukkige verandering is gekomen. De regering heeft, aan de eene zijde door de oprigting van een Instructie-Bataillon, een uitmuntend middel daargesteld tot vorming van goede onder-officieren bij de infanterie; aan de andere zijde heeft zij, reeds sedert eenige jaren, een aantal onder-officieren de gelegenheid gegeven, om door het afleggen van een examen den officiersrang te verkrijgen. Beide maatregelen, vereenigd, kunnen niet anders dan heilzaam werken op den stand van onder-officier; het is nu een stand, waar vooruitzigt is op bevordering; een stand, die zich al meer en meer zal onderscheiden door beschaving, door karakter, door kennis, mogelijk niet uitgebreid, maar degelijk, maar praktisch; een stand, die al meer en meer uit goede elementen zal bestaan; een stand, dien de zoon van fatsoenlijke burgerouders gaarne zal intreden, omdat hij weet, dat hij daarop eer kan stellen, en omdat hem daardoor het vooruitzigt wordt geopend om, zoo zijne verdienste hem daartoe waardig maakt, tot de hoogste krijgsbetrekking te kunnen opklimmen. De slagboom, die eenige jaren lang den onder-officier belette den officiersrang te bereiken, is daardoor weggevallen; de afscheiding tusschen de beide rangen is daardoor verminderd; en het Nederlandsche leger loopt geen gevaar meer, zijne officieren uitsluitend uit de hoogere standen der maatschappij te moeten trekken.

Wij noemen dat een gevaar, en wij achten ons verpligt, dat woord toe te lichten.

Het is in ons oog altijd, ook bij de zamenstelling eens legers, verkeerd en nadeelig, uitsluitend te werk te gaan; de officieren, zoo als dit bij de Engelsche en Oostenrijksche legers plaats heeft, alleen te nemen uit de hoogere standen, uit den adel, de geldaristokratie, de magthebbenden, en geen partij te trekken van de krachten en vermogens, die men bij elken burgerstand vindt, maar vooral bij de burgerij in ons Vaderland. Onverstandig en onregtvaardig zou het zijn, hier op te treden als bestrijder der hoogere, als lofredenaar der mindere standen; zoo iets is volstrekt niet onze bedoeling. Integendeel, wij hebben achting, wij hebben hart voor die geslachten, wier geschiedenis als het ware is ingeweven in de geschiedenis van ons Vaderland; wij begrijpen den regtmatigen trots van die mannen, die, wanneer zij een slagveld noemen, de plaats noemen, waar een hunner voorvaderen een glorievol doodbed vond; wij achten ons gelukkig, wanneer wij bij ons leger de namen der Styrum's, der Wassenaers, der Aylva's ontmoeten, omdat wij verzekerd zijn, dat zij, die zulke namen dragen, juist in de luisterrijke da den van hun voorgeslacht een krachtigen prikkel hebben tot krijgsdeugd en dapperheid. Die geslachten, die van tijden her het voorregt hadden, in de oorlogsgevaren der prinsen van Oranje te deelen en meer dan andere hun bloed voor het Vaderland te storten, maken de eer en sterkte van dat Vaderland uit; en ieder ziet gaarne de waardige telgen uit die geslachten aan

[p. 122]

het hoofd van onze bataillons of als bevelhebbers onzer oorlogschepen. Maar ook daarin moet men niet uitsluitend zijn; men moet ook een weg banen voor de talenten, de krachten en vermogens, die bij den burgerstand aanwezig zijn; men moet wel in het oog houden, dat vooral die staud, bij ons, de uitstekendste mannen heeft opgeleverd, en dat die bevelhebbers, die aan het hoofd van Neêrlands legers en vloten door dapperheid en krijgsbeleid hebben geschitterd, zeer dikwijls mannen zijn geweest van geringe afkomst; - hunne kindschheid ging niet in gemak en weelde voorbij; maar in de harde school van armoede en ongeluk verwierven zij die vastheid van karakter en die geestkracht, welke onontbeerlijke hoedanigheden zijn in hem, die aan het hoofd van leger of staat met eere wil optreden.

Er is niets dat het leger meer populair maakt, en dat een geheel volk zich meer met hoogmoed aan dat leger doet aansluiten, dan de omstandigheid, dat onder zijne verdienstelijkste bevelhebbers zich mannen bevinden, uit de onbemiddelde klasse des volks voortgekomen, en alleen door eigen deugd en verdienste groot geworden. Zoo iets is een spoorslag voor allen; zoo iets doordringt allen met het bewustzijn, dat in het vrije Nederland de weg naar onderscheiding en eer voor allen openstaat, en dat men hier, om een man te beoordeelen, niet vraagt wie zijne voorouders zijn of tot welk geslacht hij behoort, maar alleen wat zijne daden zijn, en welke deugden en bekwaamheden hem regt geven op het vertrouwen en den eerbied zijner medebnrgers. Daarom juichen wij het toe, dat de betere toekomst, welke onzen onder-officieren is geopend, aan Neêrlands jongelingschap, zonder onderscheid, tot prikkel zal strekken, om hare krachten en geestvermogens aan het Vaderland te wijden, en in de krijgsdienst eene loopbaan van eer en roem te zien; daarom vinden wij het zoo verdienstelijk in de oprigters en schrijvers van dit nieuwe Tijdschrift, dat zij door dien arbeid krachtig willen medewerken, om beschaving, kunde en wetenschap bij de onder-officieren van het Nederlandsche leger te verspreiden, en hen daardoor voor te bereiden tot de nelangrijke betrekkingen, waartoe zij eenmaal welligt worden geroepen. Dat die arbeid lang moge worden voortgezet en steeds goede vruchten moge dragen!

Breda, 20 Mei 1851.

W.J. KNOOP.

[p. 123]

1. Korte verhandeling over het Pauperisme in Nederland, desxelfs oorzaken en de middelen, waardoor de voortgang van hetzelve kan worden gestuit. Door Mr. W. de Sitter, Advokaat bij het Provinciaal Geregtshof te Groningen. Groningen, F. Wilkens. 1850. 42 blz. 8^o.
2. De Armenverzorging in Nederland en het verschaffen van werk aan behoeftigen beschouwd, door Mr. W. de Sitter. Groningen, 1851. 70 blz. 8^o.

De twee in het opschrift genoemde werkjes van denzelfden schrijver hangen naauw zamen. In het eerste worden vlugtig de oorzaken onderzocht, waaraan het pauperisme, dat is, ‘de verarming, de langzamere of snellere vernietiging van maatschappelijke welvaart’ in Nederland, volgens het oordeel des schrijvers, moet geweten worden. Omstandigheden, die slechts van tijdelijken aard zijn, als: ziekte, duurte, misgewas, watervloed, oorlog, of welke enkel individuën aan den bedelstaf brengen, als: zedeloosheid, verlaafdheid aan spel of drank, worden wel als oorzaken genoemd van armoede, waardoor een individu buiten staat kan geraken in zijne behoeften te voorzien, maar zijn niet genoeg van algemeenen aard om de bron te kunnen zijn van het pauperisme, hetgeen van armoede streng te onderscheiden is. Dit is toe te schrijven aan overbevolking; niet echter in dien zin opgevat, alsof de aarde te vele bewoners telde, welke meening de schrijver dwaas en ongegrond acht, maar aan plaatselijke overbevolking, welke aanwezig is zoodra een groot deel der inwoners van een land, door gebrek, hetzij aan materiële, hetzij aan intellectuele vermogens, buiten staat is zich het noodige tot levensonderhoud te verschaffen. Zoodanige overbevolking nu bestaat in Nederland, dewijl er gebrek is aan arbeid, te weeg gebragt door gebrek aan kapitaal. De grondoorzaak van het in Nederland woedende pauperisme is alzoo de verkeerde inrigting van onze huishouding van staat, van welke dit gebrek aan genoegzaam kapitaal het gevolg is. Deze stelling is het, aan welker betoog het eerstgenoemde geschrift gewijd is. Een te hoog budget, door inrigting van den staat op te grootschen voet, daaruit ontstane tekorten, niet door bezuiniging, maar door het maken ven schulden bestreden, welke den rentelast steeds verzwaarden; belastingen, die voornamelijk den middelstand en nijvere klassen drukken; belemmering van den handel door den voortduur der vroeger nuttige Handel-Maatschappij, eindelijk de verkeerde regeling der Armenverzorging door de wet van 1818, en door de Koloniën der Maatschappij van Weldadigheid nog verergerd - ziedaar hetgeen de schrijver als zoo vele materiële oorzaken aanmerkt van pauperisme, aan welks voortplanting eindelijk nog de verkeerde rigting bij en inrigting van het onderwijs, naar zijn oordeel, krachtig heeft medegewerkt.

Uit die beschouwing over de oorzaken van het ontstaan, vloeijen van zelve de middelen voort tot wering van het pauperisme - het herzien namelijk

[p. 124]

van ons belastingstelsel, in al zijne deelen, en het verbeteren van de wetten op het Armwezen.

De ontwikkeling van dit laatste denkbeeld wordt beöogd in het tweede der bovengenoemde geschriften. De schrijver verklaart zich daarin volstrekt tegen eene armenverzorging van staatswege en wel op tweërlei grond. Vooreerst is zoodanige armenverzorging in strijd met het wezen van den Staat; zij ligt buiten het regt van den Staat en heeft, waar zij ingesteld werd, slecht gewerkt. Tot staving dezer stellingen wordt het wezen van den Staat onderzocht, hetgeen tot de uitkomst leidt, dat aan den Staat eene beschikking over het vermogen der ingezetenen slechts toekomt om regten te handhaven en storing in de zamenleving te voorkomen; maar dat eene Armenbelasting op te leggen niet tot zijne bevoegdheid mag gerekend worden, hetgeen tegen den heer Blaupot ten Cate (den eenigen hier genoemden voorstander van dat stelsel) verdedigd wordt. Het voorbeeld van Engeland wordt eindelijk ingeroepen, om aan te toonen, dat dit onregtmatige stelsei wrange vruchten oplevert, en zoowel het getal der behoeftigen als de kosten van bedeeling doet vermeerderen.

De tweede grond, waarom eene armenverzorging van Staatswege door den schrijver gewraakt wordt, geeft de geschiedenis aan de hand: in Nederland is die staatszorg geheel exceptioneel, de liefdadigheid was daar van oudsher de bron, die de middelen verschafte voor verpleging der behoeftigen. Tot dien toestand behoort de armenverzorging op nieuw teruggevoerd te worden; de armenverzorging geschiede op nieuw uit vrijwillige liefdegaven, beheerd door kerkbesturen, onder bescherming en toezigt van den Staat, die wel niet op eenmaal zijne thans onontbeerlijke bijdragen moet staken, maar door eene trapsgewijze vermindering der subsidiën een overgang behoort voor te bereiden van den tegenwoordigen toestand tot de natuurlijke en vrije werking der liefdadigheid. De armenverzorging worde geheel overgelaten aan de kerkelijke besturen, wier zelfstandigheid de Staat erkenne en handhave en die hij door strenge straffen op bedelarij ondersteune, terwijl tevens door wijze bepalingen eener wet de kring worde afgebakend, binnen welken de Diakoniën zich vrijelijk mogen bewegen. De wetgeving regele het domicilie van onderstand en bepale tot welk kerkgenootschap een behoeftige moet geacht worden te behooren; zij zorge dat de geschillen tusschen Diakoniën spoedig en kosteloos worden beslist; de Staat rigte scholen op voor lager en middelbaar onderwijs, en daarmede zal dan ook de staatspligt vervnld zijn. De particuliere liefdadigheid behoort dan het overige te doen en bijstand te verleenen: aan de eigenlijke armen door de Diakoniën, aan de nijvere behoeftigen, tijdelijk van werk ontbloot, door liefdadige vereenigingen tot werkverschaffing en patronaat. Dit laatste gedeelte is in ons oog het belangrijkste van dit geschrift, dewijl men daar, na eene scherpe veroordeeling der werkverschaffing door de Maatschappij van Weldadigheid, voorbeelden vindt van vereenigingen in Groningen en in Gouda, die aanvankelijk met het beste gevolg werkinrigtingen hebben tot stand gebragt, waarvan de medegedeelde bijzonderheden allezins opmerkelijk zijn. - Het overige echter bevat weinig, dat niet reeds door de Heeren Boer, Grevelink, Mackay en anderen ter bestrijding van de voorstanders eener Staats-armenzorg is aangevoerd. Enkel schijnt de Heer de Sitter een naauwer toezigt van Staatswege op de kerkelijke besturen wenschelijk te achten, dan door die schrijvers welligt zou gebillijkt worden.

[p. 125]

De Zeevaart der oude Volken, door wijlen J. ter Pelkwijk, A.L.M.J.U. et Philos. Dr., Ridder der Orde van den Nederl. Leeuw, Lid van Gedep. Staten der Prov. Overijssel, enz. Met aanteekeningen en bijlagen van H. van Blanken, Math. Mag. Phil. Nat. Doct., Lector in de Wisk. Wetenschappen te Zwolle. Met platen en kaart. - Uitgegeven ten voordeele der Stads-Armeninrigting te Zwolle. Gedrukt bij de Erven J.J. Tijl, te Zwolle. 1851. Bl. VIII en 100.

Weinige dagen voor de losbarsting der Belgische omwenteling, stond de Hr. ter Pelkwijk aan het Bestuur der Armen-inrigting te Zwolle, waarvan hij mede een ijverig lid was, het kopijregt af van eenige zijner ongedrukte verhandelingen en opstellen, ten voordeele van genoemde inrigting. Bij die stukken bevond zich onder anderen bovengenoemd werk, waarvan de uitgaaf trouwens sedert al dien tijd vertraagd bleef, uit vrees, gelijk men in het Berigt vermeld vindt, dat de kosten daarvan niet zouden gedekt worden, en men met regt zwarigheid maakte, na het overlijden van den Hr. t.P., om de penningen eener liefdadige instelling aan eene onzekere onderneming te wagen. Eerst nadat men zich op dit punt door eene goede inteekening verzekerd zag, gaf men eindelijk deze verhandeling in het licht. (Zóoveel ter opheldering van deze late verschijning.) - Van het drietal platen verder, waarmede de Heer van Blanken de uitgaaf vermeerderd heeft, is de laatste eene kaart van de Middellandsche Zee, waarop staat aangewezen: de scheepsweg van Athene naar Syracuse, in het jaar 415 V.O.I.; de scheepsweg van Paulus, van Caesarea naar Puteoli, en de scheepsweg der Kruisvaarders in 1217, van Cadix naar Syracuse. Men kan hieruit reeds ontwaren, dat aan de uitdrukking, op den titel, van oude volken, nog al eene ruime beteekenis gegeven wordt, en zoo handelt daarenboven zelfs een gedeelte van dit geschrift over de ontdekkingsreizen van Columbus en ook lateren. Doch daaromtrent merkt de schrijver aan, dat de zeevaartkunde, in dien tijd, der Portugezen en Spanjaarden, bij de hedendaagsche vergeleken, weinig grooter was dan die der oude, in betrekking tot de hunne, en in zoo verre kon zijne beschouwing zich mede tot de nieuweren uitstrekken.

Na eene beknopte en duidelijke inleiding over den oorsprong der Zeevaart en over de verschillende kustbewoners, die door hunne natuurlijke ligging het eerst en het veelvuldigst daarvan gebruik maakten, verdeelt hij zijn onderwerp in drie deelen, welke hij achtereenvolgens behandelt, als: 1^o. De scheepsbouw. 2^o. De scheepsbesturing. 3^o. De eigenlijke zeevaartkunde of stuurmanskunst. In dit eerste gedeelte komt vooral ter sprake de quaestie

[p. 126]

over het getal rijen en roeijers op de schepen der ouden en hunne onderlinge verhouding. Men vindt hier veel wetenswaardigs daarover bijeengehaald, zonder dat echter de opgeworpene zwarigheden omtrent een en ander worden opgelost. Jammer, altijd, dat wij hier geen gebruik zien gemaakt van Wachsmuth, doch vooral van Böckh. Overigens volgen hier nog belangrijke aanteekeningen over den inhoud der oude schepen, wat hunne bevrachting betreft.

Bij de scheepsbesturing handelt de S. voornamelijk over de werktuigen, die een vaartuig in beweging brengen, waarbij hij de minderheid der vroegeren, in dit opzigt, in korte trekken aanwijst.

Het derde deel doet bovenal de gewigtige voordeelen uitkomen, welke de uitvinding van het kompas, de zeekaarten, enz., eindelijk aanbragten, daar alle zeetogten vóor dien tijd zich in den regel slechts tot kustvaarten konden uitstrekken. Hierbij zijn verscheidene berekeningen gevoegd over den gemiddelden afstand, welken de vroegste zeevaarders in éen dag konden afleggen.

De beide bijlagen ten slotte bepalen zich: Over de omvaring van Afrika en de scheepvaart der bewoners van noordelijk Europa; de laatste stipt voornamelijk aan de bekendheid van Amerika vóor Columbus. Deze zijn, gelijk de titel aanwijst, van den Hr. v.B. De lezer van dit verslag ziet intusschen, waarover het hier aangekondigde werk, hetgeen wij overigens gaarne aanprijzen, mede om het goede doel aan de uitgaaf verbonden, hoofdzakelijk handelt. Met het oog op den titel zoekek men hier ook geenszins naar eene politisch-antiquarische beschouwing van het zeewezen der ouden in het algemeen, zoo als Böckh die uitvoerig gaf van Athene. Als eene afzonderlijke bijdrage hieromtrent zou men nog kunnen vermelden de verdienstelijke verhandeling van Mr. G. de Vries, Az., De foenoris nautici contractu iure attico (Harlemi, ap. A.C. Kruseman, 1842); terwijl al wie verder meer wenscht te weten van de zeevaart der ouden en de eerste groote ontdekkingsreizen, daarvoor opsla: Io. Alb. Fabricii Bibliographia antiquaria, alwaar, bl. 781 en volgende, onder den titel van: de commerciis et navigatione veterum, eene lange reeks van boeken daarover te vinden is.

Dr. C.A. ENGELBREGT.

[p. 127]

Broeder en Zuster, door de Schrijfster van Mary Barton. Uit het Engelsch. Amsterdam, P.N. van Kampen. 1851.

Een greep uit het leven om ons heen. Wie haar waagt, moet midden in dat leven verkeeren, of liever, opdat de blik helderer zij, verkeerd hebben. Hij moet zelf niet meer in het gelid staan, maar toch meê hebben gestreden en met scherpen blik, midden in het strijdgewoel, dikwerf door den kruiddamp heen, de feiten zijner wapenbroeders gâgeslagen, en de manoeuvres, bij aanval of terugtocht der bataillons, hebben begrepen. En dan, weêrgekomen van het slagveld, ingekeerd tot de stille binnenkamer, moet de fantazie het gebeurde terugroepen en de revue doen passeeren van het regelend oordeel, dat de baaiert ordent en in het verwarde strijdgewoel de taktiek des Generaals ziet vervuld.

De Schrijfster van ‘Broeder en Zuster’ schijnt echter niet dien strijd te hebben gekend, of, mocht zij het ook, niet het slagveld te hebben kunnen overzien, noch het plan van den Veldheer begrijpen.

Hare gave van opmerken was te zwak, om vele groepen om zich heen waar te nemen, en daarbij hare fantazie te onmachtig, om het verspreide onder één gezichtspunt te vereenigen. Haar werk heeft slechts ééne verdienste - schande over de hedendaagsche roman-literatuur, dat haar dit als verdienste moet worden toegerekend - er is een zin voor godsdienst en zedelijkheid in merkbaar, die in het voordeel der Schrijfster pleit en de kritiek ten deele verlamt.

Als kunstwerk verheft het zich niet boven het middelmatige; de gemoedelijkheid, die het geheel doorademt, releveert echter eenigzins de hier en daar zoo fletsche tinten.

De charakter-schildering is flaauw; en juist zij is de proefsteen van het talent. Dit alleen vermag individuën te scheppen, met een eigen leven, met een eigen geest, zich ontwikkelende in den loop der gebeurtenissen.

De Schrijfster van ‘Broeder en Zuster’ vermocht het niet.

De oude Jufvrouw Browne kán niet, zóó als ze hier wordt geschilderd, bestaan; ze schijnt ons bij wijle hatelijk, en toch merken wij elementen in haar op, die, zoo daarvan partij getrokken en ons een dieper blik in het harte gegund ware, ons een wezen had doen aanschouwen, dat wij hadden kunnen achten, ja lief hebben.

Grietje, haar dochter, noemen wij ten deele geslaagd. Slechts Anna, de oude meid, is met een paar fiksche trekken goed geteekend. De oude Heer Buxton is innerlijk onwaar en evenzoo de overigen.

De handeling schakelt zich wijders niet genoeg aan één, en is niet in staat de personen te doen bewegen. Slechts ééne pozitie is goed gekozen, is schoon uitgewerkt, voor zoo verre de charakterschildering het toelaat; het is, waar Grietje geplaatst wordt tusschen haar minnaar en haar broeder.

De stijl, - zoo veel ze te kennen is uit de wel korrekte maar ook stijve en dus niet schoone vertaling, is zonder verheffing, zonder gloed.

[p. 128]

Alles bewijst, dat de Schrijfster te weinig dichterlijk element bezit, om het haar omringende, - het dagelijksch leven, - te bezielen. De heide schijnt voor den kort-ziende dor, en toch, wierd het hem gegund de kracht van het oog te verdubbelen, hoe hij aan den horizon dien groenen zoom zou opmerken, welke de vlakte begrenst en als met een gordel omspant, - het zijn de immer groene dennebosschen, waar de ekster snatert, de rave krast en de meerle fluit; hoe hem het kale veld een bruin tapeet zou worden, hier lichter, daar donkerer getint; hoe hij, waar het hem dorre plagge scheen, de bloemekens zou bewonderen, die er de klokjens ten halve verbergen, waarover hommel of wesp begeerig heenzwiert.

De ‘Mary Barton,’ die der Schrijfster, naar 't schijnt, tot aanbeveling moet dienen, is mij geheel onbekend. Ik vermoed, dat die roman hooger zal staan dan deze, welke tot dat einde niet kan worden aangewend.