De Gids. Jaargang 14

[p. 644]

Bibliographisch album.

Beginselen der Differentiaal-, Integraal- en Variatie-Rekening. Een Leer-, Lees- en Studieboek, door Jacob de Gelder, in leven Hoogleeraar te Leiden. 's Grav. en Amst., Gebr. van Cleef. 1850.

Een ongewoon verschijnsel moge het zijn, dat een Leerboek der Differentiaalrekening, voor een vierde eeuw reeds grootendeels afgedrukt, thans nog in het licht wordt gegeven; niemand, die met des schrijvers naam eenigzins bekend is, zal niet den Hoogleeraar Verdam dank weten, dat hij het werk voltooid en in het licht gegeven heeft. Het boek, zoo als het daar ligt, vertegenwoordigt echter uit den aard der zaak twee, en wel twee zeer verschillende tijdperken eener wetenschap, welke in die laatste jaren zoo veel en in zoo onderscheidene rigtingen is uitgebreid geworden. Het eerste gedeelte met den tegenwoordigen toestand der wetenschap te vergelijken - hoe belangrijk dit ook konde zijn - hield Ref. voor ongepast, te meer, daar zulk eene noodzakelijkerwijze uitgebreide, en meer zuiver wetenschappelijke beschouwing niet voor dit tijdschrift zoude geschikt zijn; aan den anderen kant is het boek van veel te belangrijken inhoud, dan dat deze niet eenigermate diende bekend te worden. Ref. meende dus in het gegevene geval te kunnen volstaan met het boek vlugtig door te loopen, zich echter voorbehoudende van bij enkele punten wat langer te blijven stilstaan. Gemakshalve zal hier de hoofdverdeeling worden gevolgd, door de Gelder in ieder der beide Hoofdstukken met A tot D en met A tot G gemerkt.

Tot het plan van de Gelder, om een volledig stel Leerboeken voor alle deelen der Wiskunde te leveren, behoorde ook dat der Differentiaal- en Integraalrekening. Nadat hij in de voorrede van zijn zoo bekend Eerste Deel dezes Leerboeks (in 1823 uitgekomen) er den geest en inhoud van behandeld had, vervolgt hij dus, blz. xxxi: ‘Het tweede deel, dat reeds ter perse is, zal de toepassing der Differentiaalrekening of het practische gedeelte van dezelve bevatten: het derde deel de Integraal - en Variatie-Rekening; welke deelen zullen besloten worden met eene beknopte Geschiedenis der nieuwere

[p. 645]

ontdekkingen, sedert den tijd van Newton en Leibnitz tot nu toe, met eene raadgevende handleiding tot het lezen der merkwaardigste en nuttigste geschriften.’

De toepassing der Differentiaal-Rekening, hier in het tweede deel beloofd, en waarmede dus die rekenwijze in haar geheel wordt afgehandeld, is geenszins de gewoonlijk in de Leerboeken voorkomende, de toepassing namelijk op de theorie der kromme lijnen: deze toch had de schrijver reeds in zijn eerste deel opgenomen, en op de geschikte plaatsen ingelascht. Hier daarentegen vinden wij het Theorema of de reeks van Taylor, enkele punten uit de theorie der functien, de ontwikkeling der functien in reeksen en de behandeling dier reeksen beschouwd. De in de laatste jaren zoo zeer uitgebreide leer en toepassing der bepaalde integralen heeft, wel is waar, mede en wel voornamelijk bij deze onderdeelen eenen zeer gewigtigen invloed uitgeoefend, vooral in verband met de ontwikkelde leer omtrent de divergentie en convergentie van reeksen - het hier geleerde evenwel, de dnidelijke en grondige manier, waarop het wordt voorgedragen, is ten volle der moeite waardig, om naauwkeurig te worden nagegaan.

Vooraf echter dient in het algemeen aangemerkt te worden, dat, hoewel § 198-200 opzettelijk over de convergentie en divergentie van sommige reeksen gehandeld is, meerendeels het nagaan van convergentie of divergentie achterwege blijft, omtrent welke leer men dan ook eerst, sedert de Gelder zijn boek nederschreef, zoo veel gevorderd is; dit heeft ten gevolge, dat er verscheidene reeksen voorkomen, die thans bevonden zijn tot de niet-convergente en dus onbruikbare te behooren, zoo als b.v. blz. 386, de zes reeksen onder N^o. 5. - Gaan wij thans over tot de beschouwing van het eerste Hoofdstuk.

A. Dit is aan het Theorema van Taylor gewijd, en in de eerste plaats, § 175 en vgg., worden de gevallen overwogen, dat het voor bepaalde waarden der onafhankelijk veranderlijke te kort schiet; alsdan moet men de hulp der zeer kleine differentien inroepen, en komt alzoo zeer gemakkelijk tot de waarde der eerste of volgende differentien der afhankelijk veranderlijke grootheid. Na aangetoond te hebben, dat Lagrange van deze gevallen te regt zegt, dat dan de reeks van Taylor ‘est en défaut,’ dat is, ‘te kort schiet,’ hoewel zij niet van de waarheid afwijkt, maar slechts identiek wordt, - gaat de schr., § 181 en 182, bij een twintigtal kromme lijnen de gevallen na, waar dit voorkomt, en waar dus buig- of keerpunten, in het algemeen zoogenaamde bijzondere punten aanwezig zijn, - en welke kromme lijnen in die punten het naauwkeurigst met de gegevene overeenstemmen, terwijl als bijzondere gevallen daarvan de raaklijnen en asymptoten beschouwd worden.

B. Wanneer de betrekking tusschen beide veranderlijken ingewikkeld gegeven is, zijn er meerdere bezwaren: hunne oplossing en verscheidene nuttige wenken en opmerkingen vindt men bij de behandeling van een paar kromme lijnen. Na eene uitweiding over oneindig grooten en oneindig kleinen, § 186, als ook over de termen eener vergelijking, die voor zulke waarden van de

[p. 646]

veranderlijken eenen overwegenden invloed uitoefenen - alles door vele voorbeelden opgehelderd, - volgt, § 187-191, eene in 52 bladzijden beknopt en duidelijk uitgewerkte, volledige verhandeling over den analytischen Driehoek, die moet dienen, om de boven vermelde overwegende termen van eene vergelijking zeer gemakkelijk te bepalen, en daardoor o.a. de asymptoten en hunne gedaante, als ook den loop der kromme lijn in de nabijheid van bepaalde bijzondere punten op te maken. Ziehier eene korte schets van dit minder algemeen bekend hulpmiddel, die aan Ref. voldoende voorkomt om het nut en gemak daarvan te doen beoordeelen.

7	c
6	*	*
5	*	*	l
4	*	k	*	*
3	f	*	*	d	*
2	*	*	g	*	e	*
1	*	*	*	*	*	*	*
	a	*	*	h	*	*	*	b
		i	ii	iii	iv	v	vi	vii

In de nevensgaande figuur duiden de gewone cijfers de magten van y, de romeinsche die van x aan, welke respectivelijk in de horizontale en verticale kolommen als factoren voorkomen: zoodat b, c, e de plaats vervullen der termen x⁷, y⁷, x⁴ y²; a is de oorsprong, a b de voorname horizontale, a c de voorname verticale lijn, waaraan de gewone horizontale en verticale lijnen evenwijdig loopen; b c en evenwijdige lijnen worden diagonaallijnen, a d en evenwijdige, op de diagonaallijnen loodregt staande, contradiagonaallijnen genoemd; d k en f h zijn schuinsche lijnen; andere, die door a gaan, centraallijnen; lijnen, zoo als c d, e f, die a c en a b snijden, heeten parabolische, andere, zoo als e h, f l, die sleehts eene van beiden snijden, hyperbolische lijnen; de kant van eenige lijn, die naar den oorsprong gekeerd is, wordt binnenhant, de andere buitenkant genoemd. - Wil men nu eene vergelijking nagaan, zoo worden de daarin voorkomende termen in den driehoek aangeteekend; b.v. zouden in de figuur d, e, f, g, h, k en l de termen voorstellen der vergelijking:

x⁴ y² ± p x³ y³ ± q x³ ± r x² y⁵ ± s x² y² ± t x y⁴ ± y³ = 0.

De lijnen, door de buitenste termen getrokken, die dus alle andere insluiten, heeten grenslijnen, en worden alleen nagegaan, daar zij de overwegende termen bevatten; deze zijn hier: l e, e h, h f, f k l, welke respectivelijk als grenzen der vergelijking de

Parabool x^1 y^2 ± r x^2 y^5 = 0, of x^2 ± r y^3 = 0, voor x = y = ∞,

Hyperbool x^4 y^2 ± q x^3 = 0, of x y^2 ± q = 0, voor x = ∞, y = 0,

Parabool ± q x^3 ± y^3 = 0, voor x = y = 0,

Hyperbolen ± r x^2 y^5 ± t x y^4 ± y^3 = 0, of r x^2 y^2 ± t x y ± 1 = 0, of 2 r x y = ± t ± √ (t^2 - 4 ^r, voor x = 0, y = ∞,

in grootte en afmeting, maar niet altijd in stand, voorstellen.

Hier zij nog aangemerkt, dat fig. 39, op blz. 104 onderaan aangehaald, en den loop der aldaar en blz. 118-120 behandelde kromme lijn voorstellende, op de plaat niet voorkomt, terwijl Plaat III, fig. 39, eerst blz. 289 wordt gebruikt.

C. Dit handelt over het bepalen der waarden van functiën, die in zekere gevallen de onbepaalde vormen

0/0, ∞/∞, 0 × ∞, ∞ - ∞

[p. 647]

aannemen, hetgeen, § 193-196, in een dertigtal opgeloste voorbeelden genoegzaam wordt opgehelderd. Ref. mist hier echter het geval, dat eene functie y = p^q onbepaald wordt voor bijzondere waarden van p en q. Stelt men Log. y = z, Log. p = r, dan heeft men Log. y = q Log. p, z = q r, y = e^{q r} = e^{q Log. p} en in de drie voorkomende gevallen voor

1^o.	p = O, q = O, y = e^0 · - ∞;
2^o.	p = ∞, q = O, y = e^0 · ∞;
3^o.	p = 1, q = ∞, y = e^∞ · 0;

zoodat dus altijd de exponent van e, q. Log. p, volgens het derde der bovenvermelde gevallen (zie vraagstuk III, blz. 154) kan bepaald worden. Men vindt op deze wijze b.v. de waarden van

x^x voor x = 0	1;
x^1/ x voor x = ∞	1;
x^1/1- x voor x = 1	1/e.

Blz. 160 is voorbeeld 31 fautif opgegeven.

D. Eindelijk vindt men de convergentie der reeks van Taylor behandeld, en wel volgens de wijze van Lagrange betoogd, dat, wanneer f_n (a + i) tusschen a en a + i niet oneindig groot wordt, en p en q hare grootste en kleinste waarden voorstellen, de laatste term der reeks zal wezen

iⁿ/1.2.3....n. x, waarbij f_n (p) > x > f_n (q).

Omtrent dezen laatsten term, gewoonlijk de rest van de reeks van Taylor genoemd, is sedert meer onderzocht; Cauchy o.a. heeft in zijne ‘Lcçons sur le Calcul différentiel. Paris, 1829,’ bewezen, dat men voor x mag stellen: f_n (a + r i), waarbij r eene positive, gewone breuk beteekent.

Wij zijn gekomen tot het tweede Hoofdstuk, over het gebruik der Differentiaalrekening in verscheidene onderwerpen der algemeene Rekenkunde.

A. Eerstens vindt men verschillende manieren, om, naar de leer der onbepaalde coefficienten, door differentieren eenige functien in reeksen te ontwikkelen; dit geeft reeds dan veel gemak, wanneer polynomia tot zekere magten verbeven voorkomen, daar men, tot de Logarithmen overgaande en daarna differentierende, gemakkelijk de te behandelen functien verkrijgt; op die wijze worden, § 207. (1 + x)ⁿ, Log. (1 + x), a^x, Sin. x, Cos. x, Log. (a + b x + c x² + ....), e^{a x + b x2 + ....}, Sin. (a x + b x² + ....), Cos. (a x + b x² + ....), en eindelijk het schoone theorema van Girard ontwikkeld.

B. Uitgaande van de waarde van Cos. x ± Sin. x √ - 1, namelijk e^{± x √ - 1}, betoogt de schr. de goniometrische grondformulen, en komt verder door de leer der onbepaalde coefficienten en door inductie, - naderhand, § 209, door differentieren meer regtstreeks - tot de twaalf gewone reeksen voor de Sinussen en Cosinussen van de veelvouden eens boogs, en ein-

[p. 648]

delijk. § 210, tot de zeven reeksen voor de magten van den Sinus of Cosinus eens boogs.

C. Het theorema van Taylor wordt nu regtstreeks gebezigd, om eenige functie in eene reeks te ontwikkelen, door de differentiaalquotienten dier functie te berekenen en deze in de Taylor'sche reeks over te brengen; eene handelwijze, die, volgens de Gelder, ‘niet, gelijk de eerste (onder A behandeld), den vorm der reeks, in welke eene gegevene functie kan ontwikkeld worden, a priori onderstelt, en die, alhoewel zij in veel gevallen werkzamer schijnt te zijn dan de eerste, echter wegens hare volstrekte algemeenheid, in velerlei opzigten de voorkeur verdient.’ Daar evenwel nieuwere onderzoekingen geleerd hebben, dat het niet geoorloofd is eene functie aldus in eene reeks te ontwikkelen, zonder het bestaan eener zoodanige reeks eerst te hebben aangetoond, of althans naderhand bepaaldelijk de convergentie van eene aldus verkregene reeks na te gaan, vervalt die volstrekte algemeenheid, en is de hier gebruikte methode een middel, waarvan men althans een zeer omzigtig gebruik dient te maken. In dertien Voorbeelden, waarvan sommige op meer dan ééne wijze bewerkt zijn, wordt deze methode toegepast, waarbij verscheidene merkwaardige en nuttige kunstgrepen door den ervaren Analyst worden gebezigd.

D. Van het te regt dusgenoemde Theorema van Lagrange, van zoo veel gewigt bij de toepassing, vindt men hier, § 204, twee oplossingen of bewijzen, terwijl verder wordt aangetoond, dat het als een bijzonder geval het Theorema van Taylor houdt ingesloten.

E. Wat het gebruik der Differentiaalrekening in het oplossen van stelkundige en transcendentale vergelijkingen aangaat, wordt hier eerst de arbeid der wiskundigen vóór Lagrange nagegaan, om naderhand diens methode en hare toepassing vrij uitvoerig te behandelen.

Na eenige woorden over benaderingsmethoden vindt men, § 218, de eerste manier van Euler uiteengezet, berustende op het gebruik van Taylor's Theorema in de nabijheid van eenigen wortel; de overeenkomst van deze manier met de benaderingsmethoden van Newton en Halley, naarmate men twee of drie termen der reeks in rekening brengt, volgt gemakkelijk. Eene tweede manier van Euler, waarbij het verschil tusschen den benaderden en den waren wortel door eene reeks van oneindig kleinen van toenemende orde wordt voorgesteld, - en eene derde, waarbij uit de vergelijking y = f (x) gedacht wordt x = F (y) opgelost te zijn, en dan uit de eerste de differentiaal-verhondingen dezer laatste functie worden ontwikkeld - past de schr. op verscheidene vergelijkingen toe, waaronder ook transcendente. De gevallen van gelijke wortels, of van de zoodanige, welker verschil bekend is, worden § 222 en 223 behandeld.

F. De manier van Lagrange, om eenen wortel, of zelfs eenige willekeurige functie van dien wortel eener vergelijking in algemeene reeksen te ontwikkelen, die van de coefficienten der vergelijking afhangen, vindt men hier vooreerst § 225-228 uit zijn bekend en § 214 behandeld Theorema afgeleid, daar iedere vergelijking onder den vorm a - x + f (x) = 0 kan gebragt worden. Vervolgens wordt, § 229-232, gehandeld over de ontwikkeling van al de wortels der gegevene vergelijking in gelijksoortige reeksen, waarbij op het onderscheid der zoogenaamde eerste, tweede, derde en volgende wortels wordt gewezen; zoowel het geval van volkomene, als dat van onvolkomene vergelijkingen, waarmede eigenaardige zwarigheden sche-

[p. 649]

nen verbonden te zijn, worden behandeld en door voorbeelden opgehelderd, terwijl de vorm der reeks voor onbestaanbare wortels aanleiding geeft tot het beoordeelen van de convergentie of divergentie der aldus verkregen reeksen in § 233-235. Hierbij valt echter, blz. 348-351, het een en ander aan te merken.

Vooreerst verbetere men blz. 348, reg. 8, 7 en 5 van ond. aldus:

m + n + p + enz. = i,

am + bn + cp + enz. = u,

r + s + t + enz. = 1;

welke laatste verbetering ook voor blz. 349, reg. 11, geldt, waar dus, in plaats van = i; dus, te lezen is: = 1; dus. - Het gebroken, op die bladz., reg. 1, moet met a^{i v - i} vermenigvuldigd worden, en op reg. 19 en 21 heeft de grootheid tusschen de { }, die tot de ide magt verheven wordt, nog eerst a^{v - 1} tot factor. Blz. 350, reg. 2 van ond., leze men: Nⁱ = 1 + ω + ½ i θ² + ......

De behandeling van V, onder op blz. 349, houdt Ref. voor ongeoorloofd, daar, bij het verwaarloozen der termen g : i, andere van dezelfde orde r, s, t in den noemer der breuk behouden blijven. Men zoude in deze tegenwerping op de volgende wijze kunnen voorzien:

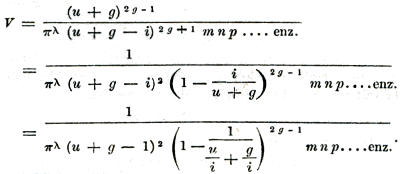
Indien nu z eenig groot of klein, maar niet oneindig getal voorstelt, zal u = z i zijn (dus z > 1) en dus:

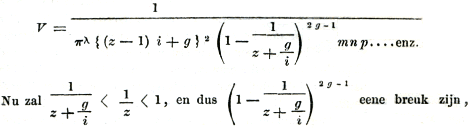
maar daar g, en dus 2 g - 1 een bepaald getal is, nooit oneindig klein worden. Daarentegen is {(z - 1) i + g}² voor i = ∞ een oneindig groot van de tweede orde: dus V voor i = ∞ een oneindig klein van de tweede orde; en evenzoo F √ V, de factor van Nⁱ, een oneindig klein der eerste orde; dezelfde uitkomst, die men blz. 350, reg. 12 van ond., verkregen vindt.

De verder afgeleide regel wordt, § 235, op twee trinomia toegepast, en daarbij worden vooral de wortels eener tweede magtsvergelijking ten opzigte van bestaanbaarheid of onbestaanbaarheid nader overwogen.

Daarna wordt, § 236 en 237, aangetoond, dat de voormelde methode ook

[p. 650]

op transcendentale vergelijkingen kan toegepast worden en daartoe het Problema van Kepler eenigzins uitvoerig nagegaan. Eindelijk vinden wij nog als toepassing de omkeering der reeksen kortelijk vermeld, en daarbij eenige bronnen van Literatuur aangegeven. Onder de vele, over dit punt handelende geschriften, is vooral merkwaardig: ‘die allgemeine Umkehrung gegebener Functionen, von Prof. Dr. Schlömilch. Halle, 1849;’ ook behoort hiertoe een voor eenige dagen aangekondigd werk, waarvan de titel is: ‘Kerz, die allgemeine Umkehrung der Reihen, nebst Anwendung derselben auf die vollstandige Lösung numerischer Gleichungen. Giessen, 1850.’

Wanneer men met de methode van Lagrange en haar verband met, en grootere volkomenheid door de theorie der symmetrische functien, alsmede met de vorderingen op dit veld, sedert het behandelde werd ter neder geschreven, nader wil bekend worden, is daartoe voorzeker de in 1819 door den bekenden Analyticus Serret uitgegeven ‘Cours d'Algèbre supérieure’ uitnemend geschikt.

G. Het laatste onderdeel handelt over het gebruik der Differentiaalrekening in de theorie der reeksen, en wel

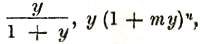I. over het transformeren derzelve, ten einde ze voor sommering geschikt te maken. Hiertoe wordt voor x achtervolgens gesteld 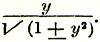. Maar ook

II. door differentieren kan uit ééne sommeerbare reeks eene menigte anderen worden afgeleid. Het duistere of liever tegenstrijdige, dat bij de definitie eener sommeerbare reeks, § 245 en in de noot op blz. 390 en 391, voorkomt, valt weg met het wegnemen der voorbeelden

Sin. x = x - ⅙ x³ + 1/120 x⁵ - enz.
en x + ½ x³ + ⅓ x⁵ + ¼ x⁷ + enz.

die aangevoerd worden, om niet sommeerbare reeksen voor te stellen, terwijl bij de eerste reeds dadelijk de som, namelijk Sin. x, wordt bijgevoegd, en de som der andere reeks ligtelijk blijkt te zijn: 1/ x Log. 1 / 1 - x². Latere wiskundigen evenwel (zie onder anderen ‘Prof. Schlömilch, Neue Methode zur Summirung endlicher und unendlicher Reihen, Greifswald, 1849,’ een boekje, waarvan de inhoud der lezing wel waardig is) strekken de bepaling veel verder uit, en noemen het voorstellen eener oneindige reeks onder den vorm van eene bepaalde integraal, dat is, van eene geslotene uitdrukking, het sommeren derzelve: kan dan zulk eene integraal door eene stelkundige of transcendentale functie worden voorgesteld - iets, dat niet altijd het geval is - zoo is de reeks gesommeerd volgens de vroegere, minder algemeene bepaling.

Van eene sommeerbare reeks worden nu andere afgeleid, door achtervolgens differentieren of integreren van de reeks zelve, of nadat zij eerst met eenige functie van x is vermenigvuldigd: en daarna wordt het belangrijke vraagstuk opgelost, om eene reeks te sommeren, nadat men al hare termen respectivelijk met de termen eener rekenkunstige reeks van zekere orde heeft vermenigvuldigd.

III. wordt, § 251, de sommerende term eener reeks bepaald, waarvan de algemeene term gegeven is, en worden de daarbij voorkomende Bernouil-

[p. 651]

liaansche Coefficienten nader overwogen; terwijl, § 252, de toepassing van deze benaderende sommeringsmethoden op een veertigtal reeksen volgt: - deze leert ons de dikwerf voorkomende constante C = 0,577 .... kennen; alsmede, blz. 431, de secanten-coefficienten, die echter aldaar genoemd worden: ‘eene nieuwe soort van transcendentalen, welker aard, natuur en onderlinge afhankelijkheid tot nog toe geheel onbekend is’ (sedert zijn zij, even als de Bernouilliaansche Coefficienten, volkomen bepaald): - ook het berekenen van groote produkten van den vorm 1.2.3.....x, en van groote Binomiaalcoefficienten wordt hier toegelicht.

Nadat in § 253 op den meer of minder bruikbaren vorm van den sommerenden term in eenige voorbeelden gewezen is, komt de Gelder, § 254, tot de bij eenige ontwikkeling, als het ware, toevalligerwijze gevonden sommen van anders moeijelijk te behandelen reeksen, en wel die, wier algemeene termen zijn:

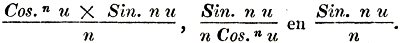
De regtstreeksche behandeling dezer laatste reeks is door de Gelder begonnen, en, hetgeen Euler naliet, door Prof. Verdam voltooid; hier derhalve eindigt de Gelders werk, voor zooverre het in druk verschenen was; de overige 112 bladzijden zijn ons door Prof. Verdam geschonken, en bevatten dus ook, zoo als Ref. boven aangaf, de uitdrukking van den tegenwoordigen toestand der wetenschap.

Vooreerst worden, § 255, de gevallen nagegaan, dat de termen der te sommeren reeks met afwisselende teekens zijn aangedaan, waarbij onderscheiden wordt, of het ranggetal van den laatsten term even, dan wel oneven zij; en daarvan eenige toepassingen gemaakt. Van de reeksen op blz. 475 gelde hetzelfde, als van die op blz. 386, daar de gegevene wederkeerige reeks slechts voor x² < 1 bestaat.

IV. vinden wij eene vrij uitvoerige verhandeling over het interpoleren van reeksen, en daarin een kort, maar algemeen en helder overzigt van de verschillende methoden, die hiertoe ook in latere tijden zijn aangewend. Na eenige ophelderingen omtrent de beteekenis, het doel en de manier van óf juiste, óf veelal slechts benaderende interpolatie, omtrent het ranggetal, zoowel volstrekte als betrekkelijke, en de empirische formulen - worden achtereenvolgens de gevallen behandeld van een of twee ranggetallen, die altijd ieder met gelijke verschillen opklimmen. § 260 bevat 12 Aanmerkingen, meest alle van het grootste gewigt, en om het voorstel van verschillende kanten te doen beschouwen, en vooral dienstig tot het gemak in de praktische berekeningen; van deze wordt ten laatste een voorbeeld gegeven in die eener interpolatie tusschen termen van eene tafel met dubbelen ingang.

Thans doet zich het meer ingewikkelde geval voor, dat de ranggetallen met ongelijke verschillen opklimmen. Voor de gevallen, dat er één of wel twee ranggetallen zijn, worden voornamelijk de uitkomsten van Newton en Lagrange kortelijk uiteengezet en verklaard, en daaruit eenige andere formulen afgeleid, ook voor het zoogenaamde interpoleren uit het midden. Nog vindt men de methode van Cauchy, voornamelijk dienende, om de uitkomsten van proeven of waarnemingen te kunnen behandelen, en op achtervolgende benaderingen berustende.

Na eene korte beschouwing over de vormende functien (fonctions génératrices) van Laplace en diens differentien ▽, en de toepassing daarvan op

[p. 652]

het problema der interpolatie, komt men, § 265, tot het algemeene vraagstuk, door Euler opgelost: om, namelijk, wanneer eene algemeene rij van getallen A, B, C, D, E,...... gegeven is, tusschen de termen der daaruit afgeleide reeksen

A, A + B, A + B + C,....... en A, A B, A B C,.......

andere te interpoleren. De oplossing van het eerste gedeelte van dit vraagstuk hangt van den algemeenen term der eerste reeks af, en verschilt naarmate men de oneindig verwijderde termen beschouwt, of als termen eener gewone rekenkundige reeks, of als termen eener rekenkundige reeks van hoogere orde, of als termen, waartusschen zulk eene wet niet bestaat; terwijl de oplossing van het tweede gedeelte tot het eerste wordt teruggebragt door het nemen der Logarithmen.

Ten laatste bevat § 267 de toepassing van het voorgaande op vijf reeksen van algemeenen, gewigtigen vorm.

Ref. meent hiermede de taak, die hij zich gesteld had, te hebben volbragt: om namelijk den schat van zaken, in dit boek bevat, de volledige wijze, waarop zij behandeld zijn, en de nuttige wenken, voor eigen toepassing daarbij gevoegd, hoofdzakelijk te doen kennen: welke vereeniging men elders te vergeefs zoude zoeken. Bovendien waarborgt de Gelder's wijze van uiteenzetten en verduidelijken, dat de lezing van dit boek niet alleen tot vermeerdering van wetenschappelijke kennis, maar ook tot leiding en opwekking van eigen studie zal kunnen strekken.

Deventer, September 1850.

D. BIERENS DE HAAN.