Forum der Letteren. Jaargang 1980

(1980)– [tijdschrift] Forum der Letteren– rechtenstatus

Natafelen met een automatische gesprekspartner Een aanzet tot automatisering J.P. Kerkhof

Samenvatting
In dit artikel worden voorwaarden gegeven voor het functioneren van een automaat als gesprekspartner in een afgebakende wereld.
Die voorwaarden betreffen voornamelijk het verloop van het gesprek met een automaat als actieve gesprekspartner. Raakpunten met de transformationeel-generatieve grammatica worden genoemd.

1. Inleiding

Het uiteindelijk doel van onderzoekingen op het gebied van kunstmatige intelligentie (artificial intelligence) is het geschikt maken van automaten voor communicatie in natuurlijke taal. Deze studie valt binnen genoemd gebied.

Onder een automaat verstaan we een machine, die in staat is ingewikkelde handelingen (operaties) uit te voeren met behulp van een rij opdrachten, die reeds in de machine opgeslagen zijn en dit zonder menselijke tussenkomst. Een telmachine is een automaat: in deze automaat is eenduidig en stapsgewijs aangegeven hoe b.v. het optellen gaat. Met andere woorden: in de telmachine is een procedure voor optellen opgeslagen.

Zoals met een telraam wordt bij de opdracht ‘3+3’ steeds weer het getal I bij de eerste drie opgeteld tot er bij de laatste drie niet een meer over is: de ‘+’ wordt uitgeveegd en aan de eerste rij enen wordt het getal ‘6’ toegekend. Zo gaat in principe het optellen in de automaat. Bij vermenigvuldigen (b.v. ‘4x3’) wordt vier maal gebruik gemaakt van de procedure van optellen (0+3+3+3+3).

Het rekeningen gebeurt in stapjes. Die stappen (procedures) worden in een gegeven volgorde door de machine uitgevoerd. Het in stappen volgen van een rij opdrachten gebeurt met een discrete machine. In een analoge machine werken functies (b.v. optellen) tegelijkertijd (zie J.J. van Amstel, 1976, p. 61 en verder).

Een handeling, die door een automaat uitgevoerd moet worden, wordt met behulp van een procedure verricht: dit geldt voor een rekenmachine, maar ook voor een taalmachine (zie hoofdstuk 2 van dit artikel).

Voor het nastreven van bovengesteld doel (met een automaat kunnen praten) zijn verschillende onderzoekingen, deelstudies mogelijk: dat zal ten dele uit hoofdstuk 2 blijken, ten dele, aangezien over draden, electriciteit of zand als ideale opslagplaats niet wordt gesproken. Het betreft hier mogelijke toepassingen van bestaande mogelijkheden. In hoofdstuk 2 zullen we de verschillende fasen vanaf het aanbieden van een zin aan de automaat tot het antwoord krijgen van de automaat belichten.

In hoofdstuk 3 wordt een algoritme gegeven voor het verloop van gesprekken binnen een in dat hoofdstuk aangegeven wereld.

Het betreft hier geen compleet pakket dat aan de machine aangeboden wordt. Voor de beschrijving van het gespreksalgoritme maken we gebruik van een Algol-achtige taal, waarbij niet alle begrippen in deze taal gedefinieerd zijn. Als het nu op den duur lukt een sprekende machine te fabriceren, betekent dit dan dat hiermee een verklaring van taalgebruik gegeven is, of dat ‘de geheimen van de menselijke geest ontsluierd zijn’? Een preciesere vraag: corresponderen de handelingen in de machine met die in de hersenen? Zijn de hersenen een discrete machine?

Hierop geven we geen antwoord en we vermoeden, dat we nog te weinig van de hersenen afweten om een serieus vergelijk met een taalmachine aan te durven.

Een andere preciesering van de eerste vraag: corresponderen de handelingen in de machine met de psychologische feiten?

R.C. Schank (1972, p. 17) hoopt dat zijn taalmodel, dat ten grondslag moet liggen aan een programma voor een sprekende automaat, nog eens psychologisch getest wordt, en natuurlijk, dat die test positief uitvalt.

E.B. Hunt (1976, p. 428) spreekt van een psychologisch georiënteerd model als o.a. de gebruikte algoritmes op intuïties berusten hoe men de taal zou kunnen begrijpen (comprehend!). Deze voorzichtige benadering steekt af tegen de visie van R.F. Simmons (1973, p. 65 en verder):

Volgens hem gaat het bij taalgebruik om het overdragen van de gevoelens (feelings) en ideeën (ideas). De taalgebruiker vertaalt als hoorder de boodschap van de spreker in zijn formuletaal en na verwerking en vertaling in natuurlijke taal komt er een antwoord aan de hoorder. Semantische netten (te vergelijken met conceptuele raamwerken, zie p. 131 van dit artikel) geven een model van ideeën. Dit standpunt is wel erg naïef, alsof de tussen liggende formule taal van de automaat correspondeert met zoals het ‘werkelijk’ bij de taalgebruiker gebeurt.

Alsof semantische primitieven aanwijsbaar zouden zijn, waarvan alle andere betekenissen door de taalgebruiker worden afgeleid.

Terecht zegt Winograd over het begrip ‘concept’ (Winograd, 1972, p. 26): ‘It is a fiction that gives us a way to make sense of data and to predict actual behaviour.’

Zó zien wij ook de status van de tussenstappen in de machine, van input (b.v. een vraag aan de machine) tot output (b.v. een antwoord van de machine). Dit is een pragmatische aanpak. Op de een of andere manier moet een automaat taal kunnen gebruiken, antwoord kunnen geven, zelf vragen kunnen stellen. Men kan trouwens van een theoretische constructie niet zeggen of zij waar is of niet; zij is allen wel of niet te gebruiken voor het beschrijven van verschijnselen en het voorspellen ervan.

Maar hoe moeten we de voorspellende kracht van een model interpreteren? We kunnen toch niet precies het verloop van een gesprek voorspellen? Uit de gespreksregels, die in hoofdstuk 3 worden gegeven, blijkt al dat dat in onze opzet niet mogelijk is (vanwege het gokelement).

Wel kunnen er minder vergaande voorspellingen gedaan worden. Men kan b.v. voorspellen wat er op een deel van de zin volgt (een missende syntactische categorie, of een missend betekenis-element, zie R.C. Schank, 1973, p. 189).

Nu moeten we wel onderscheid maken tussen voorspellingen van wat een sprekende machine gaat zeggen en wat een natuurlijke gesprekspartner gaat zeggen. Het hangt van de regels in de automaat af, wat deze gaat zeggen. In het gespreksalgoritme hebben wij de regel opgenomen dat de automatische gesprekspartner op een vraag van de natuurlijke gesprekspartner altijd een antwoord geeft. In een compleet programma zal dat in de praktijk ook altijd gebeuren.

Een verschil met een taaltheorie als de Transformationele-generatieve grammatica is, dat met een complete T.G.-theorie een nieuwe acceptabele zin beschreven moet kunnen worden, terwijl in A.I. (Artificial Intelligence) context met behulp van een theorie als reactie op de input-zin een acceptabele zijn als output uit de machine moet rollen. Een compleet systeem moet op alle acceptabele zinnen kunnen reageren. Niet alleen moet de zin, die er uit rolt, acceptabel zijn, hij moet ook wat betreft ‘inhoud’ in de context van het gesprek passen.

Alle A.I.-projecten hebben gemeen, dat het bij gesprekken met een automatische gesprekspartner moet gaan om het uitwisselen van informatie. Daar zijn twee verklaringen voor te geven:

in de eerste plaats zijn de A.I.-projecten, de vraag- en antwoordsystemen, gebaseerd op informatie-systemen (information-retrieval), waarbij het gaat om op automatische wijze informatie uit een gegeven bestand te krijgen;

in de tweede plaats is informatie-uitwisseling een machtig bindmiddel voor beschrijving en automatisering van gesprekken. Als je deze basis zou laten vallen, zou het programmeren van een automatische gesprekspartner wel erg moeilijk worden.

2. Van input naar output

Overzicht van de fasen van de door de automaat ontvangen zin tot de door de automaat geleverde zin als reactie hierop.

Een compleet model voor programmering van een automatische gesprekspartner houdt ook de vertaling in van gesproken taal naar geschreven taal. Met zo'n automaat zou je in spreektaal kunnen converseren.

Bij de meeste systemen wordt de fase van gesproken naar geschreven taal overgeslagen en wordt de text getypt aan de automaat aangeboden.

De ontvangen zin wordt in de automaat geanalyseerd en in dezelfde formuletaal vertaald waarin ook de gegevens van de automaat zijn geformuleerd. Input-zin en gegevens van de automaat worden vergeleken en afhankelijk van de uitkomst van de vergelijking wordt een antwoord geformuleerd, dat daarna vertaald wordt in natuurlijke taal.

Als het systeem compleet is, gebeuren deze stappen zonder menselijke tussenkomst.

Terug naar de input: de woorden van de input-zin zijn al gescheiden als ze getypt de machine worden aangeboden. Die woorden krijgen uit het lexicon van de automaat syntactische categorie aangehecht, en grammaticale en semantische kenmerken. Met behulp van die informatie wordt de zin ontleend. Ontleding geschiedt in de vorm van algoritmes. Computer-ontleding van de syntactische richting van de T.G. werkt per definitie ook met algoritmes. Het verschil met A.I.-ontleding bestaat hieruit, dat de eerste alleen met behulp van affixen en verbindingswoorden de structuur van de zin probeert te ontdekken. Het verbindingswoord ‘omdat’ is het sein dat er een bijzin volgt en de uitgang ‘aar’ wijst erop dat het betreffende woord een zelfstandig naamwoord is (zie hierover T. Winograd, 1972, p. 16).

Een belangrijk verschil tussen T.G. en A.I.: bij A.I. mag er maar één betekenis van de zin overblijven (R.C. Schank, 1973, p. 190-p. 191).

Alle mogelijke andere betekenissen vallen uit. Van de verschillende betekenissen

van ‘bank’ wordt die betekenis gekozen, die in de context past. Gaat het gesprek over geld en leningen, dan wordt door de automaat de betekenis ‘geldwinkel’ gekozen.

In uitgevoerde systemen wordt er rekening mee gehouden, dat ondanks het uitzeven van betekenissen m.b.v. de context, toch nog ambigue zinnen overblijven; de automatische gesprekspartner vraagt dan welke betekenis je bedoelt (Winograd, 1972, p. 12). Het uitzeven van ambiguiteiten vooronderstelt dat zinnen los van de omgeving meer dan één betekenis kunnen hebben.

In het systeem van Bronnenberg e.a. (1978, 1979, p. 128) worden eerst alle mogelijke syntactische structuren en betekenissen gevonden; daarna wordt er gezeefd, terwijl R.C. Schank het niet nodig lijkt te vinden dat een zin eerst op zijn ambiguiteiten bekeken wordt: ‘It should be clear then, that a system that operates in such a conceptually predictive manner, should, in principle never find more than one meaning for a given sentence at one time. Wheras this idea is contrary to the traditional one taken by researchers in this area in the past, we call again on the notion of human modeling as defence, that is: humans simply do not see all the ambiguities present in a given sentence at one time.’ (R.C. Schank, 1975, p. 191).

Voor de betekenisrepresentatie van de zin maakt Schank gebruik van conceptuele raamwerken (conceptual dependence). Tot de kenmerken van het werkwoord hoort óók een conceptueel raam. Daarin staat aangegeven welke casus bij het werkwoord horen, wil de zin als bewering compleet zijn (zie voorbeeld p. 131 van dit artikel). Met deze begrippen-klassen kunnen zinnen ontleed worden, maar hoe, vertelt Schank er niet bij, en ook niet hoe we van zo'n raamwerk in een prorgrammeertaal komen, een taal waarmee ook een automaat werkt als tussentaal. Een meest gebruikte programmeertaal is LISP 1.5 of een van zijn varianten (M. King en Ph. Hayes, 1976, Winograd 1972). Een zin wordt in relaties verdeeld en die relaties krijgen een naam mee: de relatienaam, die de functie van de argumenten aangeeft. De zin ‘Jan gaat naar de stad’ kan er in een LISP-variant als volgt uitzien (vgl. Winograd 1972, p. 24):

(Gaat Jan = RI) (Richting: RI naar de stad = R2)

De relatienamen (hierboven: Richting) lijken op de begrippenklassen van Schank. In principe gebeurt hetzelfde; de zinsdelen worden in hun relatie tot het hoofd werkwoord ontleed, de functie van die relatie wordt in de ontleding meegegeven.

Als eenmaal in een formuletaal is vertaald, wordt de input-zin met de lijst van Beweringen (L.B.) in de automaat vergeleken. In de L.B. is de kennis van de automatische gesprekspartner opgeslagen. Van die kennis kunnen nieuwe gegevens worden afgeleid. Dat gaat met behulp van inferentie-regels, die samen met het lexicon, de L.B., het geheugen van de automaat vormen.

Het vinden van afleidingen hoort onder de noemer ‘Problem solving’ van A.I. (zie E.B. Hunt, 1975, p. 208 en verder). Als eenmaal een antwoord is gevonden, wordt dat antwoord in natuurlijke taal vertaald.

3. Natafelen met automaten-Ellie

Enkele voorwaarden voor automatisering

In het systeem van Wingrad (1972) kan de robot antwoorden op vragen en eenvoudige opdrachten met zijn éne arm uitvoeren. Als een vraag na verwerking nog ambigu is vraagt de robot welke betekenis je bedoelt.

Een stap verder in de richting van een ‘natuurlijk gesprek’ is, dat de automatische gesprekspartner zelf vragen kan stellen en beweringen doen.

In dit hoofdstuk wordt een algoritme gegeven voor het verloop van een gesprek, waarin deze mogelijkheid verwerkt is.

Men kan alleen automatiseren, als het onderwerpgebied van het gesprek beperkt gehouden wordt: in het systeem van Bronnenberg e.a. (1978 1979) worden aan de automaat alleen vragen gesteld over computers bij Europese ondernemingen. De robot van Winograd kan alleen vragen beantwoorden over blokken en pyramiden, die op een tafel staan.

In principe zal het mogelijk zijn een hele encyclopedie in een automaat op te slaan, maar dat geeft nogal praktische problemen.

Onze wereld bestaat uit:

Een gezin met twee ouders: Jan en Ellie, en de kinderen Emmie (5), Petra (4), Piet (4) en Karel (2). De ouders zitten in de keuken. Ze hebben pas gegeten.

De kinderen spelen buiten op straat. Na het eten gaat Jan graag nog even de tuin in. Ellie zet meestal koffie en ze roept Jan als de koffie klaar is. Jan vond het eten lekker en niet te zout (hij heeft iets aan zijn hart). Na het eten rookt Ellie een gedraaide sigaret uit de pot shag. Het is mooi weer buiten.

We laten het gesprek vlak na het eten plaats vinden. De automatische gesprekspartner moet het aandeel van Ellie leveren. Voortaan noemen we de automaat: AutomatenEllie (A-Ellie).

Hier volgt een voorbeeld van een eenvoudig natafel-gesprek tussen Jan en Ellie:

Gesprek 1
Ellie:	Heb je genoeg gegeten?
Jan:	Ja.
	Het is mooi weer.
Ellie:	Zal ik koffie zetten?
Jan:	Graag, ik ga nog even de tuin in.
Ellie:	Ik roep je, als de koffie klaar is.

Met dit gesprek zou geheel geen informatie (zie p. 128 van dit artikel) uitgewisseld worden, als in het geheugen van A-Ellie alle gegevens van bovenstaand gesprek verwerkt zijn. Dit is niet het geval: in het geheugen van A-Ellie staat nog niet vermeld dat Jan genoeg gegeten heeft, dat wordt na het antwoord van Jan aangevuld in het geheugen van A-Ellie. Voor alle duidelijkheid zij gezegd dat we mogelijke gesprekken tussen Jan en Ellie als voorbeeld nemen met als gespreksstof hetzelfde beperkt aantal gegevens.

A.h.v. die gesprekken gaan we voorwaarden voor automatisering van de gesprekspartner (A-Ellie) formuleren. Ellie vraagt niet een tweede keer of Jan genoeg gegeten heeft. Zij vraagt alleen, wat ze nog niet weet. Voorkomen moet worden dat A-Ellie aan Jan vraagt:

A-Ellie: Wonen wij hier? (of)

A-Ellie: Hebben wij vier kinderen?

Het is ook ‘begrijpelijk’ dat A-Ellie over iets begint, dat staat te gebeuren: het koffiezetten.

Maar hoe moet dit in het geheugen van A-Ellie gerealiseerd worden?

In de L.B. (Lijst van beweringen over de toestand) kunnen leemtes in haar kennis

aangegeven worden. Als die leemtes opgevuld zijn, dan heeft A-Ellie niets meer te vragen.

Een andere mogelijkheid is dat aan de hand van het conceptuele raamwerk bij de werkwoorden in de L.B. nagegaan wordt welke begripsklassen in de L.B. van A-Ellie nog niet ingevuld zijn.

Laten we het volgend schema als conceptueel raam van ‘eten’ aannemen:

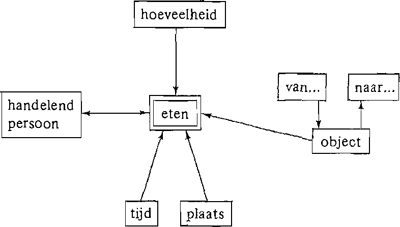
illustratie

Uit de L.B. van A-Ellie kunnen bijna alle begripsklassen ingevuld worden.

Ze eten iedere avond om zes uur. Hiermee is ‘tijd’ ingevuld.

Ze eten altijd in de keuken: hiermee is ‘plaats’ ingevuld; het eten gaat van het bord naar het inwendige van de handelende persoon: hiermee is ‘van...’ en ‘naar...’ ingevuld.

Wat nog niet ingevuld is: vond Jan het eten lekker, heeft hij genoeg gehad? Het nadeel van deze mogelijkheid is, dat eerst een algoritme bedacht moet worden, dat met behulp van L.B. en lexicon de leemtes opzoekt. En, waar houdt een raamwerk op? De raamwerken van verschillende werkwoorden zijn met elkaar verbonden.

Niet alleen in de L.B. staan beweringen over de toestand. Uit het lexicon kunnen ook beweringen over de toestand afgeleid worden.

Nemen we de volgende zin als voorbeeld:

Pudding kun je eten.

In het lexicon staat als (semantisch) kenmerk bij pudding ‘eetbaar’.

Uit het lexicon kan men de regel die ten grondslag ligt aan bovenstaande zin afleiden. In principe worden afleidingen niet in het geheugen vermeld. Als je ook afleidingen in het geheugen zou toestaan, zou je een eindeloze ruimte nodig hebben voor het opslaan van alle afleidingen.

De grens tussen lexicon en L.B. is vaag. In beide componenten staan gegevens over de beperkte wereld.

Hoe kunnen we voorkomen dat A-Ellie in een monoloog alle vragen stelt of dat ze alle beweringen doet, waarvan genoteerd staat dat Jan ze niet weet?

Mede hiervoor hebben we een algoritme ontworpen en in een Algol-achtige taal genoteerd:

1.	Gespreksalgoritme (x, y, A-Ellie, Jan);
2.	Variabelen (x, y); constanten (A-Ellie, Jan)

3.	Begin
4.	(A-Ellie = x) en (Jan = y) of (A-Ellie = y) en (Jan = x);
5.	(x beweert) of (x vraagt);
6.	Indien (x beweert) dan (ga naar 11) of (ga naar 9) of (x beweert =: x vraagt);
7.	(x vraagt =: y antwoord);
8.	(ga naar 9) of (ga naar 10) of (ga naar 11);
9.	(y =: x) en (x =: y);
10.	Ga terug naar 5;
11.	Eind.

In dit algoritme zijn de regels verwerkt, dat Ellie niet tweemaal achter elkaar, of vaker, vraagt, dat ze op een vraag van Jan antwoordt, dat ze na een antwoord van haar een bewering kan doen, en dan nog kan vragen, maar dat daarna Jan weer aan het woord komt.

Voorlopig gaan we er vanuit dat Jan dezelfde regels volgt, met dit verschil dat A-Ellie de aanwijzingen in de vorm van algoritmes ‘moet’ volgen.

In de routinedeklaratie wordt aangegeven welke procedure het betreft en welke variabelen en constanten een rol spelen. (regel 1 en 2).

De procedure zelf speelt zich tussen regel 3 en regel 11 af. Het teken ‘of’ duidt aan dat er tussen de zinnen die dit teken verbindt geloot moet worden. Als in regel 4 het eerste deel geloot wordt, dan krijgt x de waarde van A-Ellie en y krijgt de waarde van Jan.

Uit regel 5 blijkt dan dat A-Ellie het gesprek opent met een bewering of met een vraag.

Na een bewering (zie regel 6) kan in automaten-Ellie geloot worden dat het gesprek beëindigd is (ga naar 11), Jan kan het gesprek overnemen (ga naar 9), de waarden van x en y worden verwisseld, de volgende regel, regel 10, wijst weer terug naar 5, waar x (nu Jan) een bewering doet of een vraag stelt.

Als A-Ellie echter het tweede deel van regel 5 loot, dan wordt regel 6 overgeslagen, want (x vraagt) voldoet niet aan de gestelde voorwaarde (indien (x beweert)) in regel 6. Regel 7 is van toepassing: op een vraag volgt een antwoord van de ander (enz. ...).

Het gesprek is ten einde als (ga naar 11) wordt geloot; we kunnen uit het algoritme afleiden, dat een gesprek nooit met een vraag beëindigd wordt.

Het volgende ‘gesprek’ voldoet aan de in het gespreksalgoritme gegeven regels:

Gesprek 2
Jan:	Het is mooi weer.
Ellie:	De tabakspot is niet leeg.
Jan:	Ik ben met Piet naar de dokter geweest.
Ellie:	Wie zet er koffie?
Jan:	Ik heb genoeg gegeten.

In dit gesprek wordt niet op elkaars opmerkingen ingegaan. Het zou met bovenstaande algoritme een toevalstreffer zijn als wel een samenhangend gesprek met A-Ellie zou plaats vinden.

Gesprek 2 voldoet niet aan onze eisen (een eenvoudig natuurlijk gesprek met een automaat). Bij verdere uitwerking van het algoritme kan dit langs elkaar heen praten

vermeden worden. In de vorm van een diagram presenteren we een uitwerking van regel 7:

Diagram 1, uitwerking van regel 7 van gespreksalgoritme

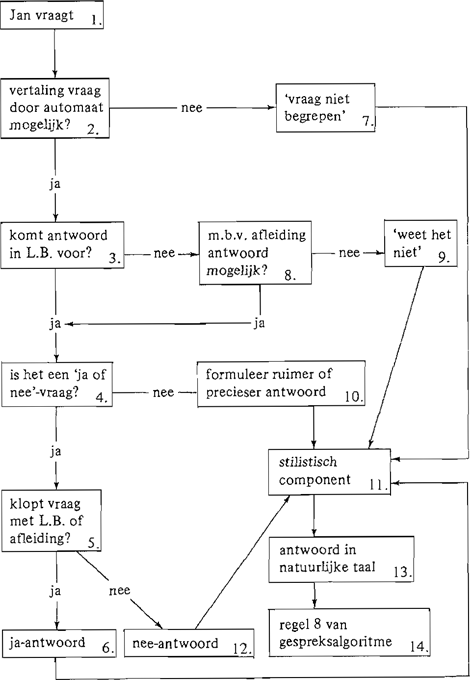
Men volge de pijlen van het diagram, met ‘Jan vraagt’ als begin. Als Automaten-Ellie

zou vragen, dan antwoordt Jan. Een geheel geformaliseerde procedure voor een antwoord heeft de natuurlijke gesprekspartner niet nodig voor een antwoord. En zo kunnen we hem niet programmeren. Wel verwachten we van hem dat hij enkele regels in acht neemt.

Als hij b.v. woorden gebruikt, die de automaat niet kent, dan kan zij de betreffende zin niet vertalen (zie blok 2 naar 7.). Uitbreiding van de mogelijkheden van Automaten-Ellie zou zijn, dat zij naar de betekenis van de voor haar nieuwe woorden vraagt.

Na een vertaalprocedure zal zij het nieuwe woord in haar geheugen (afd. lexicon) invoegen. De vraag moet in de taal van de L.B. vertaald worden. Dat gebeurt ook al weer in kleine stappen. Zie voor een uitgewerkt en op een machine toegepast model van Bronnenberg e.a. (1978, 1979, p. 245 en verder).

Als het antwoord (of precieser; de gegevens voor het antwoord) niet in de L.B. voorkomt, kan nog via inferentie geprobeerd worden de juiste gegevens te vinden (van blok 3 via blok 8 naar blok 4, zie diagram 1). Een stukje ‘problem solving’ in een kinderlijk stadium is hiermee aangegeven.

Als het met afleiding van gegevens ook niet lukt gaat de pointer (te vergelijken met aanwijsstok) naar blok 9. Je kunt op verschillende manieren het antwoord schuldig zijn; in het antwoord kan verwerkt worden, waarom je iets niet weet.

Als de vraag geen ‘ja of nee’-vraag (waarop je met ‘ja’ of ‘nee’ kan antwoorden) is, dan is het een voorbeeld van een zgn. ‘wh'-vraag (van het engels what, why, etc.).

B.v. waar zijn de kranten? waarom heb je de tabakspot niet gevuld? hoeveel aardappels heb je gegeten?

Op dergelijke vragen kan men een ruim of minder ruim antwoord geven. Zie het volgende gesprek:

Gesprek 3
1.	Jan:	Waar zijn de kinderen?
2.	Ellie:	De kinderen spelen buiten.
3.	Jan:	Dus Piet speelt ook buiten?
4.	Ellie:	Ja.
5.	Jan:	Hoe heb je dat klaargespeeld?
6.	Ellie:	Ik heb hem overgehaald.
7.	Jan:	Waarmee?
8.	Ellie:	Ik heb hem een nieuwe doos met wol beloofd als hij ook buiten ging spelen.
9.	Jan:	Buitenlucht doet de mens goed.
		Spelen de kinderen in de tuin?
10.	Ellie:	Nee, ze spelen op straat.

In Automaten-Ellie staat vermeld als (samengestelde) bewering, dat alle kinderen op straat spelen. Ze geeft een ruim antwoord (zin 2). Zo kan A-Ellie op de vraag van Jan wanneer zij met zorgenkind Piet naar de dokter is geweest, antwoorden: 's middags’, in plaats van het preciese tijdstip: ‘om drie uur 's middags’ (W. Lehnert 1978, p. 9, p. 49).

We gaan er van uit dat in de L.B. de preciese gegevens verwerkt zijn, omgekeerd kun je namelijk niet afleiden, b.v.: ‘s middags’ impliceert ‘om drie uur’.

Als een gegeven een element van een grotere verzameling is, kan ook die verzameling als antwoord gegeven worden. Dit geldt voor ‘plaats’, ‘tijd’-aanduidingen. In het lexicon kunnen dergelijke gegevens gevonden worden (vgl. met betekenissenboom). Ook

als het vragen naar oorzaak of reden zijn, kan een minder precies antwoord gegeven worden.

Nemen we de kwestie rond Piet (zie gesprek 3).

In Ellie's L.B. zijn in elk geval de volgende zinnen verwerkt:

‘Als Ellie Piet naar buiten stuurt, dan gaat hij niet. Hij zit altijd op zijn zolderkamertje met wol te spelen na het eten. Ellie wil dat hij buiten gaat spelen, want: de dokter heeft gezegd: buitenlucht is goed voor de mens. Ellie heeft Piet een nieuwe doos wol beloofd als ie buiten gaat spelen. Piet heeft gekozen voor nu buiten spelen en straks wol krijgen. Piet is naar buiten gegaan.’

Als het gesprek over Piet gaat kan A-Ellie direct de hele samenhang uit de L.B. geven. Ze kan een completer verhaal houden, als ze de reden geeft van het geloof in haar dokter, en in verband daarmee haar ideeën over leven en dood. Het kan niet anders of de zinnen in het geheugen raken op. We hebben voorlopig een woordenstroom van A-Ellie tegengegaan, door in de gespreksalgoritme te stellen, dat ze één bewering kan doen, en niet meer achter elkaar.

Wat is een bewering? Is de Bijbel geen complete afgeronde bewering? Zoals ook een compleet raamwerk bij R.C. Schank? We kunnen de term ‘Bewering’ operationeel maken door er een maximum aan elementaire zinnen uit de L.B. aan te verbinden (vgl. W. Lehnert, 1978, p. 116).

Maar terug naar het antwoord van Ellie op de vraag van Jan hoe ze het klaargespeeld heeft dat Piet buiten speelt:

A-Ellie zou de volgende antwoorden moeten kunnen geven:

A-Ellie:	Ik heb hem iets beloofd (of)
	Hij krijgt een nieuwe doos wol (of)
	Hij heeft zich laten overhalen.

Een deel van het hele verhaal kan ze als gedeeltelijk antwoord geven waarbij het waarschijnlijk is dat de natuurlijke gesprekspartner Jan vraagt, tot het beeld compleet is. Dat Ellie graag het kind naar buiten wil hebben, en waarom, kan hij aanvullen uit de wereld van opvattingen, die zij delen. Zo kan ook in de automaat de rest van een bewering van Jan met behulp van zinnen uit de L.B. aangevuld worden.

In het bovenstaand voorbeeld ‘weet’ de automaat ook dat Jan deze opvatting deelt. In de automaat moeten de zinnen, die beiden bekend zijn, als zodanig aangemerkt worden.

We hebben het al eerder gezegd: A-Ellie moet zo geprogrammeerd worden dat ze niet in algemene beweringen blijft hangen. Alleen in de context kan ze een algemene bewering doen, zoals Jan in het gesprek 3 doet:

Jan: Buitenlucht doet de mens goed.

Ook kan bij een tegenstelling tussen input-zin en een (afgeleide) zin uit de L.B. als reactie de betreffende (afgeleide) zin als output-zin gegeven worden, dat geldt niet alleen voor een algemene bewering maar ook voor een (voorlopige) bewering over een toestand (zie W. Lehnert, 1978, p. 169).

Gesprek 4
Ellie:	Ik heb zin in een sigaret.

Jan:	De tabakspot is leeg.
Ellie:	De tabakspot is niet leeg.
Jan:	Ik heb zelf gekeken in de pot.
Ellie:	Oh.

Input-zinnen worden op hun inconsistentie met zinnen uit het geheugen onderzocht (E.B. Hunt, 1975, p. 393).

Maar wat moet ze met een tegenstelling doen. Er moeten voorwaarden geformuleerd worden, waarop Ellie een zin uit haar geheugen corrigeert; vgl. het voorbeeld met de buiten spelende kinderen. Het is de eerste keer dat Piet 's avonds buiten speelt: hier vindt ook een aanpassing plaats in de L.B. als Ellie nog niet wist, dat alle kinderen buiten spelen. Deze opmerkingen kunnen we in een diagram verwerken, die als uitbreiding moet gelden van regel 5 van het gespreksalgoritme (zie p. 132).

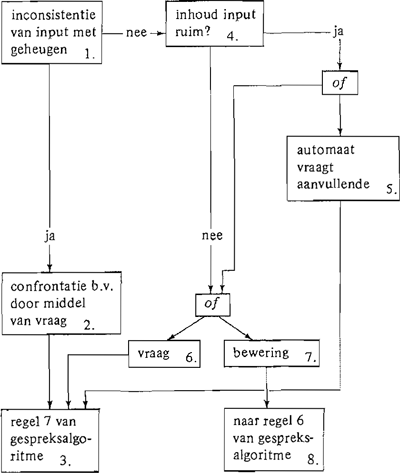
Het toevalselement is met deze uitvoering van regel 5 geringer geworden. We kunnen de gang van 4 naar 5 een grotere kans geven, dan van 4 naar (6 of 7). Als men het toevalselement geheel weg zou laten, zou het aandeel van de automatische gesprekspartner precies voorspeld kunnen worden, nl. wat ze als reactie op de input-zin geeft. In het

systeem, dat ons voor ogen staat, wordt door de automaat b.v. gegokt of ze wel of niet met een nieuw onderwerp begint (b.v. van ‘kinderen’ naar ‘eten’).

Ook in het stilistisch blok zal het gokelement een rol spelen, b.v. in de keuze tussen de volgende antwoorden als varianten van zin 10 in gesprek 3.

De kinderen spelen op straat.
Nee, de kinderen spelen op straat.
Nee, op straat.

Het gokelement zal geringer worden als een speciale stijl in de automaat geprogrammeerd wordt, b.v. met resultaat dat A-Ellie altijd korte zinnen gebruikt (nee, op straat). Als de inhoud van het antwoord is geformuleerd (in programmeertaal), dan wordt het stilistisch component in werking gesteld, te vergelijken met het transformationeel component van de school van Chomsky. Op het gebied van varianten zijn met behulp van het beschrijvingsapparaat van de T.G. opmerkelijke resultaten geboekt, die gebruikt kunnen worden voor het stilistisch component in een A.I. model. Er is wel het verschil, dat relaties als hierboven niet door de T.G. beschreven worden, aangezien de context niet in de transformatie-regels verwerkt is (een transformatie legt een stilistische relatie tussen twee zinnen, grof gezegd). Zonder context hebben bovenstaande zinnen niet dezelfde betekenis (de laatste heeft dan geen betekenis).

In dit stuk hebben we ons niet zozeer bekommerd om de details of een stukje programma geheel uitgewerkt.

Ons interesseert de vraag, hoe men een gesprek met een automatische gesprekspartner kan krijgen. We hebben enkele mogelijkheden gegeven.

4. Besluit

Het gokelement is een niet weg te denken factor bij het programmeren van een automatische gesprekspartner (zie hfdst. 3).

Het gespreksalgoritme is een niet-uitgewerkt en voorlopig algoritme, een middel om vat op het probleem te krijgen. Slechts een kleine klasse van natuurlijke gesprekken lopen volgens dit algoritme (hfdst. 3).

Het model dat we hier in grote lijnen geschetst hebben, kennen we geen waarde toe 41 van ‘psychologische realiteit’, of ‘competence-model’, zoals we ook niet durven te beweren, dat de hersenen een discrete machine zijn (hfdst. 2).

Bibliografie

Amstel, J.J. van, red.
1976	Computers en programmeren. E.I.T. diktatenserie 1.
Bronnenberg, W.J.H.J., S.P.J. Landsbergen, H.J.H. Scha, W.J. Schoenmakers, E.P.C. van Utteren e.a.
1978/1979	Phliqa-1, een vraag- en antwoordsysteem voor het in gewoon Engels raadplegen van een gegevensbank. Philips Technisch Tijdschrift, nr. 37, p. 241-251; 38, p. 282-297.
Chomsky, N.
1965	Aspects of the Theory of Syntax, M.I.T. Press.

Hunt, E.B.
1975	Artificial Intelligence.
King, M. & Ph. Hayes
1976	Programming in LISP, p. 235-282 van E. Charniak & Y. Wilks: Computational Semantics, Fundamental Studies in Computer Science 4.
Lehnert, W.
1976	The Process of Questioning Answering.
Schank, R.C.
1972	Conceptual dependence: A Theory of Natural Language Understanding, Cognitive Psychology 3, nr. 4.
1973	Identification of Conceptualizations Underlying Natural Language, p. 187- p. 247, van R.C. Schank & K.M.Colby.
Schank, R.C. & K.M. Colby
1973	Computer Models of Thought and Language.
Simmons, R.F.
1973	Semantic Networks: Their Computation and Use for Understanding English Sentences. p. 63-p. 113 van R.C. Schank & K.M. Colby.
Winograd, T.
1972	Understanding Natural Language, Cognitive Psychology, volume 3, nr. 1.

Vorige Volgende