Logo DBNL
De Boekenwereld. Jaargang 23 (2006-2007)

De Boekenwereld. Jaargang 23

(2006-2007)– [tijdschrift] Boekenwereld, De–rechtenstatus Auteursrechtelijk beschermd

Vorige Volgende

De werken van de meetkundige rekenmeester Sybrandt Hansz. Cardinael (1578-1647)
Proeve van een bibliografie*
Klaas Hoogendoorn

Een van de vermaardste rekenmeesters uit het Amsterdam van het begin van de zeventiende eeuw was Sybrandt Hansz. Cardinael. Geboren te Harlingen in 1578 en geadmitteerd als landmeetkundige bij het Hof van Friesland trok hij in 1605 naar Amsterdam. Daar bestond door de opbloei van handel en zeevaart een grote belangstelling voor onderwijs in praktisch wiskundige kennis. Hij werd er een hoog geacht schoolmeester en gaf niet alleen les in de rekenkunde en het boekhouden, maar ook in meer geavanceerde vakken als meetkunde, zeevaartkunde en astronomie. Met name zijn Hondert geometrische questien (Amsterdam, ca. 1612) stond op hoog niveau en diende de jonge Christiaan Huygens als leerstof. Daarnaast was hij in zijn tijd bekend door zijn ‘rekenhulpen’, tabellenboekjes die het berekenen vergemakkelijken. Onder meer toegepast bij het wijnroeien en het berekenen van rabatten.1 Vele van die boekjes zijn uiterst zeldzaam of verloren gegaan.

Na zijn dood in 1647 raakte hij geleidelijk uit het zicht. D. Bierens de Haan heeft einde negentiende eeuw in zijn Bouwstoffen zijdelings weer enkele mededelingen over hem gedaan.2 Zijn Bibliographie bevat een onvolledige lijst van door Cardinael gepubliceerde werken.3 Het is de Amsterdamse bibliothecaris H.F. Wijnman geweest, die in de jaren dertig van de vorige eeuw de auteur wat meer uit het vergeetboek haalde door zijn publicaties in Het Boek en het nnbw.4 Meer recent hebben J.A. van Maanen en M.H. Sitters het bijzondere van zijn meetkundige benaderingen laten zien.5 Ook hun onderzoek in archieven en studie aan meerdere overgeleverde handschriften van zijn leerlingen brengt nieuw inzicht in zijn betekenis.

Vondsten van een aantal tot nu toe onbekende drukken in buitenlandse bibliotheken en gegevens uit een oude veilingcatalogus leidden bovendien tot een herziening en aanvulling van de bibliografie van gedrukte werken. Onderstaande proeve van een bibliografie beoogt een volgende aanzet te zijn naar een zo compleet mogelijke bibliografie van deze bijzondere rekenmeester. Het wordt voorafgegaan door een reconstructie van de ontwikkelingsgeschiedenis van zijn werken.

Cardinaels vroege jaren

Sybrandt Hansz - de naam Cardinael werd pas later toegevoegd - werd in 1578 geboren in Harlingen, in een familie van Zuid-Nederlandse origine. In Friesland moet hij zijn kennis van de wiskunde verworven hebben. Daar verkreeg hij een admissie als landmeter van het Hof van Friesland en zal hij al een zekere bekendheid opgebouwd hebben als wiskundige.6 In 1605 vinden we hem echter in Amsterdam, waar hij de reeds bestaande school van Lieven Panten voortzet en in 1607 huwt met diens dochter Levijntje, eveneens afkomstig uit Harlingen.7

Aan de behoefte aan onderwijs in de exacte vakken kon de Latijnse school in het opkomende Amsterdam niet voldoen. Voor de zonen van kooplieden waren er de zogenaamde Fransoysche scholen, waarin naast onderwijs in schrijven, rekenen en boekhouden ook veel

aandacht aan de beheersing van de Franse taal werd geschonken.8 Toch valt de school van Cardinael niet in die categorie. Uit geen enkele publicatie blijkt Cardinaels kennis van de Franse taal, die door de Franse onderwijzers breed geëtaleerd placht te worden. De handschriften van zijn leerlingen behandelen onder meer onderwerpen als de Euclidische meetkunde, geometrische vraagstukken, de astronomie, de zeevaartkunde en het wijnroeien. Zijn onderwijs lag dus meer op middelbaar en hoger niveau en moet ook sterk op volwassenen gericht geweest zijn. Ook deed hij zelfstandig onderzoek op zeevaartkundig gebied. Hiernaast fungeert hij als beëdigd wijnroeier en verrichtte de eerder aangeduide werkzaamheden als landmeter.9

Tafelen van rabat

Het moet één van Cardinaels vroege specialismen geweest zijn praktisch bruikbare rekenhulpen te doen uitgeven. Ze vallen in de categorie van wat men in het Engels ready reckoners noemt: tabellenboekjes die iemand die de rekenkunde minder goed machtig was, maar die wel kon lezen, in staat stelde snel een antwoord te geven op een vraag in het handelsverkeer. Eén van die vragen had betrekking op het rabatteren: bijvoorbeeld welke korting op een prijs kan worden gegeven wanneer de klant eerder dan vereist betaalt? Bij rentepercentages van 8% en betalingstermijnen van meer dan drie maanden best van belang om te weten!

Cardinaels eersteling is zo'n rekenhulp, maar het is niet bewaard gebleven. Uit de veilingcatalogus van Isaac le Long blijkt dat al in 1606 van de hand van Sybrandt Hansz. te Amsterdam de Tafelen van rabat verschenen zijn.10 In dezelfde catalogus worden daarnaast drie exemplaren genoemd van een herdruk uit 1620. Geen van deze exemplaren is bij mijn weten bewaard gebleven.

Als eerst daaropvolgend is ons wel een dubbel blad met een Rabattafel overgeleverd. Het is ingevoegd in een exemplaar van het derde deel van de rekenboeken van Cardinael uit 1647 in de Universiteitsbibliotheek van Amsterdam, maar is niet aanwezig in een ander exemplaar of in volgende drukken. Die tabel, gevolgd door twee voorbeelden heeft als titel: ‘Van 't Rabat teghens 8 ten hondert in 't iaer, beginnende van 1 Maendt tot 42 Maenden toe.’

Pas in 1652 duikt een exemplaar in boekvorm op, uitgegeven als onderdeel van Jeremias Coghe's Specieboek. In 1662 moet er dan een niet meer gekende ‘bewerking’ zijn uitgegeven door de rekenmeester Johannes Maes. Wel zijn er exemplaren van een heruitgave hiervan uit 1667, nu onder de titel Rabatboek. Maes rept in zijn voorwoord, nog 1662 gedateerd, ‘over de 500 drukfouten uit de vorige (Coghes?) editie’ die hij gecorrigeerd zou hebben.

De Rabattafel uit 1647 bevat een eenvoudige tabel met twee uitgewerkte voorbeelden, waarbij nog een vermenigvuldiging moest plaatsvinden. In het Rabatboek staat die kleine tabel met de voorbeelden ook. Maar het werk is aangevuld met een tweede tabel. De gebruiker moest nog wel kunnen optellen; vermenigvuldigen was niet meer aan de orde.

Samenvattend: we weten van het bestaan van vijf uitgaven van het boekje; van twee uitgaven zijn exemplaren overgeleverd. We mogen echter aannemen dat dit gebruikswerkje vele malen is herdrukt en dat het gros van de exemplaren verloren is gegaan. We zullen verderop nog meer van die rekenhulpen tegenkomen.

Rest de vraag: is dit een origineel werk? Het antwoord moet negatief zijn. Gedurende het leven van Cardinael verschenen meerdere van dat soort boekjes.11 Het is echter in zijn compactheid wel uniek.



illustratie
Titelpagina van een der rabatboekjes naar ex. [G.L.] 1652 p.c. 1259.1 in de Senate House Library, University of London, Goldsmiths' Library of Economic Literature


De hondert geometrische questien

Na wat men een niemendalletje zou kunnen noemen, komen we nu bij Cardinaels belangrijkste boek: een doorwrocht werk waarin allerlei meetkundige vraagstukken op ingenieuze wijze opgelost worden zonder gebruik te maken van de in opkomst zijnde algebra.12 Zo adviseerde de kritische wiskundige Jan Jansz. Stampioen de Jongere in 1645 aan Constantijn Huygens om dit werk in het lesprogramma van Christiaan en diens broer Constantijn op te nemen.13 En blijkens Christiaan Huygens' nagelaten papieren heeft deze in zijn jonge jaren daadwerkelijk de tanden gezet in de oplossing van een aantal van deze vraagstukken. Overigens wel op algebraïsche wijze!

Alle edities zijn ongedateerd. De verschijningsdatum ervan moeten we afleiden uit secundaire bronnen. De belangrijkste daarvan is Jan Hendrik Jarichs van der Leys verhaal over zijn ontmoetingen met Cardinael naar aanleiding van Jarichs' poging de beloning van de Staten-Generaal te verkrijgen voor zijn methode voor het vinden van ‘Oost en West’.14 Hij tekende dit op in zijn Het gulden zegel der grote zeevaart dat in 1615 werd uitgegeven te Leeuwarden en blijkens het voorwoord in 1614 werd geschreven. Cardinael had in zeevaartkundige kringen kennelijk een groot gezag, want hij was samen met Willem Jansz Blaeu, Hendrick Reyersz en Hessel Gerritsz benoemd in de commissie die Jarichs' voorstel beoordeelde. Dat oordeel viel negatief uit.15

Ondanks Cardinaels ‘objectien’ tegen Jarichs' methode laat deze zich in zijn boek toch als volgt bewonderend uit over Cardinael:

Meester Sybrant Hansen een Vriese wt de Zee-Stadt Harlinghen haer alder Base seer vermaert inde tel ende meet-const oock so wytnemende in de selve als een in Hollant te vinden is ende te rechte nae een tweeden Ludolph geleken mach worden heeft onlanchs noch hondert zeer constighe Geometrische questien mette solutien laten wtgaen hij heeft mede een instrument onderhanden dat gedreven sal worden met sterke wateren waer met hij deur de tijt rekeninghe de Longitudo meent te vinden.16

Dit geeft aan dat de eerste uitgave van De hondert geometrische questien voor het einde van 1614 gedateerd moet worden.

Bierens de Haan is in zijn schattingen van de data in zijn Bibliographie niet erg eenduidig. Enerzijds noemt hij zonder voorbehoud 1616 onder het kopje ‘Cardinael’, anderzijds eveneens zonder voorbehoud 1612 onder het kopje ‘Sems’. Het werk van Cardinael wordt namelijk in alle uitgaven voorafgegaan door herdrukken van twee al eerder (in 1600) door Jan Bouwensz te Leiden gepubliceerde landmeetkundige werken van Johan Sems en Jan Pietersz Dou. Volgens de titel van die herdrukken van Sems en Dou hoort dat ook zo.17 Ook daar bevatten de titelpagina's geen jaar van publicatie. In de latere Bouwstoffen heeft Bierens de Haan zijn vermoeden toch gesteld op 1612.18 Bij gebrek aan beter en het ingeburgerd zijn er van (onder andere in de catalogi van bibliotheken) handhaven we daarom voor de eerste uitgave deze datum.19 We vermelden nog dat de stcn zich over de datering niet uitspreekt door op te merken dat alle edities van De hondert geometrische questien uitgegeven zijn in de eerste helft van de zeventiende eeuw.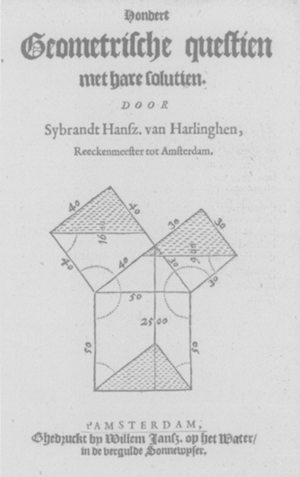



illustratie
Titelpagina van de tweede druk van de Hondert geometrische questien naar ex. 720 G 51 in de ub Leiden


De stcn geeft wel iets aan wat vroegere auteurs nooit expliciet hebben gemaakt, namelijk dat er vier onderscheiden drukken van deze combinatie zijn: twee bij Willem Jansz (Blaeuj

en twee bij Jan Jansz. (Janssonius). Afgezien van de voorwerken zijn die inhoudelijk nagenoeg identiek. Dat wil dus zeggen dat geen van de auteurs de moeite heeft genomen in de loop der tijd verbeteringen aan te brengen.

Van de twee bij Blaeu uitgegeven drukken is er één met en één zonder opdracht aan de stadhouders Prins Maurits en Graaf Willem Lodewijk. Die opdracht was ook al aanwezig in de editie van 1600. We kunnen daarom aannemen dat de uitgave met de opdracht de eerste herdruk is van de landmeetkunde en van De hondert geometrische questien de eerste druk. De tweede druk kan vervolgens voor 1623 gedateerd worden omdat Willem Jansz vanaf dat jaar meestentijds ‘Blaeu’ aan zijn naam toevoegde en de titel nog steeds Willem Jansz vermeldt. Bierens de Haan kende een convoluut waarin nog een ander werk van Dou was opgenomen, dat 1620 was gedateerd. Op basis daarvan heeft hij 1620 ook als datum toegewezen aan de landmeetkunde. We menen, dat ondanks de foute redenering - werken in een convoluut hoeven niet gelijktijdig gepubliceerd te zijn - ‘circa 1620’ geen slechte schatting is voor de tweede uitgave van Blaeu.

Nog moeilijker is de datering van de uitgaven bij Janssonius. Op het eerste gezicht lijkt het erop alsof deze weer eens - schaamteloos - een succesvolle uitgave van zijn buurman heeft gekopieerd. Merkwaardig is dan wel dat Janssonius de koperen platen van de titelgravures van de twee landmeetkundige werken van Blaeu heeft gebruikt: de afdrukken ervan zijn tot in detail identiek. Datzelfde geldt voor de gebruikte houtsneden in De hondert geometrische questien. De platen voor de octavo-uitgaven van Blaeu/Janssonius zijn overigens niet - zoals Pouls veronderstelt - afdruksels van de grotere koperen platen van de kwart-ouitgave van Bouwens uit 1600.20 Op een of andere wijze moeten die koperen platen van eigenaar gewisseld zijn. Kennelijk heeft Blaeu het verstandiger gevonden zijn investering in de drie werken te gelde te maken. Janssonius heeft de gravures nog wel laten bijwerken. Dat dit op de titelgravures van Blaeu niet te zien is, wijst erop dat de ongedateerde drukken van Blaeu van eerdere datum zijn dan die van Janssonius. De meest bijgewerkte titelgravure bij Janssonius vertegenwoordigt ook meteen de laatste uitgave. De druk bij Blaeu zonder opdrachten aan de stadhouders blijkt dan (wat we al vermoedden) de tweede en daar zien we ook de eerste foutjes in de houtsneden. Zie voor een illustratie hiervan bijlage v. Ook al omdat in Blaeus fondscatalogus van 1635 Blaeus druk nog steeds voorkomt, moeten we Janssonius' uitgaven aanmerkelijk later plaatsen dan tot nu toe gebruikelijk is.21 Zoals al door Pouls betoogd, lijkt het dan ook aannemelijk dat de drukken bij Janssonius tussen 1630 en 1660 de overbrugging vormen naar het in 1662 voor het eerst uitgegeven volgende leerboek De beknopte landmeetkonst van Matteus van Nispen.22 Daarom dateren we de twee drukken van de Hondert geometrische questien bij Janssonius op circa 1635 en circa 1645.23

 

In 1617 gaf Blaeu een Duitse versie uit van de Hondert geometrische questien in de vertaling van Sebastian Curtius of Kurz (1576-1659)). Curtius was een rekenmeester uit Neurenberg, die al in 1616 de landmeetkundige werken van Sems en Dou had vertaald en dat in 1618 nog eens zou doen voor Dou's versie van De zes boeken van Euclides. Hij zou later nog van zich laten horen door zijn Neues arithmetisches Compendium, dat dertien herdrukken beleefde.24

 

Veel later werden Cardinaels vraagstukken ook in Engeland bekend. Het tweede deel van de Practical geometry van de hand van een zekere Thomas Rudd in 1650 bevat zonder enige verwijzing 77 van de 101 vraagstukken van Cardinaels Hondert geometrische questien.25 Captain Thomas Rudd was als militair in de Nederlanden geweest en had er zo kennis mee kunnen maken. Van dit werk zijn slechts enkele exemplaren bekend in Britse bibliotheken. Hoewel

R.G. Archibald de afkomst van deze vraagstukken reeds in 1915 meldde in een artikel in het Nieuw Archief voor Wiskunde is dit feit pas onlangs in de vakpers doorgedrongen.

 

Cardinaels gezag was door de publicatie van de Hondert geometrische, questien duidelijk gevestigd. Dat blijkt uit het feit dat de vraagstukken van Cardinael steeds weer in andere werken terugkomen. Het blijkt ook hieruit, dat hij in 1617 te Amsterdam wordt benoemd tot professor in de wiskunde aan de Nederduytsche Academie van Samuel Coster. Zijn lessen aan deze academie schijnen bijzonder populair geweest te zijn, blijkens een door Wijnman geciteerd gelegenheidsgedicht.26 Ze hebben echter niet langer dan een jaar geduurd, omdat de Amsterdamse kerkenraad bezwaar had tegen de vrije opzet ervan.

Arithmetica

Het bekendst werd Cardinael door zijn Schoolboeken van de Arithmetica, die herhaaldelijk herdrukt werden, vanaf 1640 in vier delen uitgegeven. Ik heb het altijd merkwaardig gevonden dat dit werk pas aan het eind van het leven van Cardinael gepubliceerd werd, terwijl hij al zo lang werkzaam was als rekenmeester met een eigen school. Het was ook toen heel gebruikelijk om de te doceren stof te laten drukken ter ondersteuning van het onderwijs. En blijkens een later te behandelen voorwoord van dochter Levijntje bij de herdruk van het Boekhouden was dat ook voor Cardinael gangbare praktijk.



illustratie
Titelpagina van de oudst bekende druk van de Arithmetica van Cardinael naar ex. kb126,140 in de kb Kopenhagen


Dat Cardinael rond 1620 ook zo werkte, wordt bewezen door een uniek en tot nu toe onbekend exemplaar van een Arithmetica, ofte Reecken-konst uit dat jaar, dat ik aantrof in de Deense Koninklijke Bibliotheek. Het is gedrukt bij Abraham Biestkens, een drukker die we nog vaker in relatie tot Cardinael zullen tegenkomen. Deze woonde blijkens de titel ‘in

sinte Anne dwersstraet/ naest d'oude roo Kameel’ en nog niet, zoals later ‘op 't Water/ by de Kapel-steech/ inde Lelye onder de Doornen’. Kennelijk was de circa 1614 uitstekende relatie tussen Blaeu en Cardinael bij de uitgave van de Hondert geometrische questien en bij de behandeling van de casus Van der Ley wat verflauwd, en stapte Cardinael voor dit werkje naar een andere drukker.

De inhoud is overigens zeer bescheiden, zeker in vergelijking met soortgelijke werken van andere auteurs. Het behandelt de vier hoofdbewerkingen uit de rekenkunde voor gehele getallen. Daardoor komt het grotendeels overeen met het latere eerste deel uit de meerdelige uitgave, maar hier zonder de behandeling van het worteltrekken. Het is ook opvallend dat de meetkundige oriëntatie van de auteur nog zo weinig merkbaar is: het bevat geen figuren.

Niet uitgesloten kan worden dat er nog vroegere drukken van bestaan. In ieder geval is er wel een geheel gelijkende herdruk uit 1639. Tresoar in Leeuwarden bezit hiervan een wederom uniek en weinig gekend exemplaar, gedrukt in Haarlem by Hans Passchiers van Wesbusch.27 En waarom zou het tussen 1620 en 1639 niet nog meer drukken beleefd hebben?

Tafels van zilver en goud en tafels van wannigheid van vaten

In 1623 vinden we Cardinael opnieuw genoemd in de catalogus van Le Long met drie exemplaren van de Tafelen van silver en gout en wannigheit van vaten.28 Ik ken er geen exemplaren van en vond geen enkele andere referentie naar het eerste onderdeel. Het tweede onderdeel kennen we wel uit de bronnen. Isaac Beeckman noemt in zijn Journal de uitgave van 1623 expliciet en geeft aan dat Cardinael een oudere tabel nog heeft vereenvoudigd.29 Cardinael was zelf beëdigd wijnroeier. Van Dale definieert deze functie als: ‘beambte in openbare dienst die komt peilen hoeveel wijn er in de vaten bij slijters en verbruikers is, om de accijns die zij verschuldigd zijn te berekenen’. De wijnroeier zal overigens ook ingeschakeld zijn als objectieve instantie tussen koper en verkoper, ook bij andere vloeistoffen dan wijn.30 Zijn deskundigheid was met name nodig bij liggende ronde vaten. Wanneer het niveau in een aangebroken vat met een peilstok werd gemeten moest vervolgens de inhoud berekend worden. Cardinaels tabel gaf de inhoud als functie van het peil. Ook leerlingen van Cardinael hebben de tabel een wijdere verspreiding gegeven. Al is het werkje verloren, uit deze bronnen leren we Cardinael opnieuw kennen als een praktisch ontwerper van rekenhulpen.

Boekhouden

In 1632 komen we Cardinael opnieuw tegen in een werk op het gebied van het boekhouden. Ook van deze druk kennen we geen exemplaren, maar een bewerking ervan verscheen na Cardinaels dood in 1648. Het is blijkens het voorwoord door de bemoeienissen van zijn dochter Levijntje gepubliceerd.

‘Mijn Vader salig. Mr. Sybrant Hansz Cardinael heeft in druck uytgegeven seker Memoriael en Journael, voor die gene die int Boekhouden wilden oeffenen: en was van meeninge tot vol-tojinge der selve, het Schult-Boeck oock daar neffens te laten drucken, doch is door sijn overlyden verhindert. Evenwel, op dat de Liefhebbers, voornemelijck die 't aen ons hebben versocht, daer van niet mochten blyven verste-
ken, en wij oock het selve, ten dienste van onze Schole, die wy noch dagelijcx be-yveren en onderhouden, seer nodigh hebben, heeft ons goed gedacht, 't selve Schult-Boeck door den druck gemeen te maecken.’

Hiermee geeft Levijntje intussen meer informatie over het leven van haar vader dan deze ooit zelf publiceerde.31

Welnu, in de catalogus van de Staatsbibliotheek in Berlijn wordt van dit boekhoudboek een exemplaar, gedrukt in 1632, vermeld. Dit exemplaar is naar verluid in de Tweede Wereldoorlog verloren geraakt, maar de beschrijving in de catalogus is betrouwbaar genoeg om als bewijs te gelden voor het bestaan van deze druk. De titel is expliciet en wijkt af van die van de herdruk van 1648. De opgegeven drukker, Abraham Biestkens, werkte tot 1641 en gaf meer vroeg werk van Cardinael uit, zoals het eerdergenoemde rekenboekje uit 1620 en het vierde deel van de Arithmetica van 1640.32 Ik neem daarom aan dat er inderdaad een exemplaar van deze druk in Berlijn bewaard werd. Nu allerlei na de Tweede Wereldoorlog uit Berlijn weggevoerde werken toch regelmatig in Oost-Europese bibliotheken opduiken, zou dit exemplaar nog eens tevoorschijn kunnen komen.

Zoals aangegeven in het citaat bestond de druk uit 1632 uit twee delen en voegde Levijntje er in haar uitgave een derde deel, uit het manuscript van haar vader, aan toe. Blijkens Cardinaels eigen voorwoord op het eerste deel beoogt het een onderdeel te zijn van een ‘volkomen Instructie van Coopmans Boeckhouden’. Net als in andere boeken op dit gebied uit deze tijd bevat het vooral praktische voorbeelden en weinig theorie. Uit het werk blijkt echter dat Cardinael een goed boekhoudkundig inzicht gehad moet hebben.33 ‘Daghelijcksche wercken (die noodiger sijn)’ verhinderden hem het werk te ‘volbrengen’.

Mathematische bewijsredenen dat de aardkloot stilstaat

In 1635 gaf Cardinael een bestrijding uit van het Copernicaanse wereldbeeld. Het is een (late) reactie op de publicatie in 1629 van Philippus van Lansbergens Bedenkingen op de loop van de aardkloot. Het optreden van Galileo bracht de discussie over het nieuwe wereldbeeld eveneens onder het volk. Ook de doopsgezinden, waartoe Cardinael behoorde, plachten intensief deel te nemen aan discussies met een theologisch aspect.34

Het werkje werd in 1635 twee maal uitgegeven: in Amsterdam gedrukt door Cornelis Gerritsz. van Breughel, uitgegeven door Cardinaels zwager Salomon Savary, in Haarlem door Thomas Fonteyn. Het is waarschijnlijk dat deze laatste druk - waarbij de afdrukken van de houtsneden verschillen - een roofdruk is. Naast deze twee drukken worden nog twee andere uitgaven genoemd, waarvan het bestaan onzeker is. In de eerdergenoemde catalogus van de Berlijnse Staatsbibliotheek wordt een eveneens verdwenen exemplaar van een Amsterdamse druk uit 1625 bij Cornelis van Breughel genoemd. Blijkens Gruys zijn er van deze Van Breughel alleen tussen 1631 en 1635 drukken bekend. In 1625 zou zijn vader, Gerrit Hendricksz, het werk gedrukt hebben. Ook al omdat de discussie over het Copernicanisme in 1625 nog niet speelde lijkt het mij toe, dat hier een typefout in de catalogus is geslopen. Op gelijke wijze vermeldt Bierens de Haan een herdruk van 1655 bij Thomas Fonteyn te Haarlem. Maar deze drukte - wederom volgens Gruys - in 1655 te Amsterdam. Waar Bierens de Haan de druk van 1635 niet vermeldde, kunnen we gevoeglijk aannemen dat hier sprake is van een zetfout. De aanname dat er een herdruk in 1655 is geweest, is niet zo vreemd. Ettelijke scribenten die Bierens de Haans opgave overnamen, leggen het verband met de pennenstrijd van dat jaar en het volgende over het Copernicanisme, aangezwengeld door

Lambert van Velthuysen in zijn Bewijs dat het gevoelen van die geenen, die leeren der sonne stilstandt, en des aertrycks beweging niet strijdigh is met Godts Woord.35

Opvallend in het verzorgde werkje van Cardinael is dat deze vooral niet-theologische argumenten inbrengt. Zijn belangrijkste argument sluit aan bij de Aristotelische fysica en zegt dat een recht omhoog geschoten kogel bij een draaiende aarde tegen de ervaring in niet op zijn uitgangspunt zou terugkeren. Of Cardinael zijn redenering echt geloofde, werd betwijfeld door Dirk Rembrantsz van Nierop - die andere grote doopsgezinde rekenmeester - die ervan verhaalt dat Descartes Cardinael op zijn visie aangesproken had, waarop deze zich er vanaf maakte met het antwoord dat ‘hij dit om seeckere oorsaecke alsoo gestelt hadde’.36 Het zal wel zo geweest zijn dat de doopsgezinde Cardinael, die in 1641 formeel toetrad tot de orthodoxe groep van de ‘Vlamingen’, ten diepste de letterlijkheid van een aantal bijbelse teksten wilde vasthouden en daarover niet met Descartes wilde discussiëren.



illustratie
Titelpagina van de Haarlemse druk van de Mathematische bewijsredenen


Arithmetica in vier delen

Vanaf 1640 komt Cardinael met een nieuwe versie van zijn rekenboek. Het werk is uitgebreid en beslaat nu vier afzonderlijke delen en wordt meestal voorafgegaan door een blad met de titel Arithmetica, de gemeenschappelijke titelpagina. De afzonderlijke delen heten nu Het eerste (tweede, derde, vierde) School-Boeck van Mr. Sybrand Hansz. Cardinaels Arithmetica. Uit 1640 kennen we alleen het vierde School-Boeck, uitgegeven door Abraham Biestkens. Waarschijnlijk zijn de andere delen in dat jaar ook bij Biestkens uitgekomen, maar die zijn ons niet overgeleverd.

Van alle vier delen kennen we meerdere latere drukken. Rond 1644 wordt Everhard Cloppenburgh nog een keer als uitgever genoemd, maar de opvolger in de drukkerij van

Biestkens, Jan Jacobsz. Bouman blijkt dan de drukker te zijn. Diens naam komt daarna steeds weer voor op de titelpagina van de volgende drukken. In 1659, ver na de dood van Cardinael krijgt Bouman concurrentie van Michiel de Groot, die het werk nog meerdere malen zal uitbrengen, al of niet in combinatie met de Wed. Theunis Jacobsz. Lootsman.

Het verzamelwerk bevat vaak de verschillende delen in drukken uit verschillende jaren. Aangezien de eerste delen de hoogste omzetsnelheid hadden, moesten die vaker herdrukt worden dan het laatste. Zo bevat het exemplaar in de ub Chicago - vermoedelijk samengesteld in of na 1654 - achtereenvolgens de delen uit 1652, 1648, 1654 en 1640. Zodra de katernen van een deeltje op waren, werden nieuwe exemplaren gedrukt met op de bijbehorende titelpagina het betreffende jaar.



illustratie
Gemeenschappelijke titelpagina van een meerdelige Arithmetica


Bijzonder in de meerdelige uitgave is dat de vijf titelpagina's vaak meetkundige illustraties geven van rekenkundige bewerkingen. Die figuren zijn een soort handelsmerk van Cardinael. Bijlage vi laat deze houtsneden op titelpagina's zien.

Blijkens het derde deel (uit 1647) was Cardinael niet van plan het bij vier delen te laten. In dat boekje spreekt hij op pagina 91 over ‘ons Seste School-boeck’, waarin hij de interestrekening uit de doeken zou doen. Het vijfde wordt genoemd in Cornelis van Leeuwens Aenhangh genaemt den bril, voor de Amsterdamsche belachelijcke geometristen, 1663, p. 23. Van Leeuwen beweert daarin dat dit werk door Claes Hendriksz. Gietermaker in diens Tweede deel van de arithmetica ‘van Questie tot Questie/ van woort tot woort/ van cijffer letter tot cijffer-letter/ en van werck tot werck’ is overgenomen uit het vijfde deel van de Arithmetica.37 Het zou daarin dus overgeleverd zijn.

Maar ook de druk van het zevende tot en met het tiende deel waren gepland. Dat kan weer worden opgemaakt uit een mededeling van Levijntje Cardinael in haar voorwoord tot het eerder vermelde Schuldboek: ‘Van sijne Arithmetica zyn alleene vier deelen gedruckt, wy hoopen metter tijt en gelegentheyt in 't licht te geven mede de ses resterende.’ Daar is het echter nooit van gekomen. Ook de handschriften ervan zijn ons niet overgeleverd.

Na Cardinaels dood zijn er weinig veranderingen aangebracht in het werk. Bouman vond het nog wel nodig om Jillis Kok de druk van 1658 te laten corrigeren.38 Dat betreft overigens alleen het eerste deeltje. Kok viel geen dankbaarheid ten deel. Een leerling van Cardinael, Johannes Dauman, maakt in een concurrerende uitgave bij Michiel de Groot korte metten met deze uitgave:

‘want hy heeft de voornaemste Exempels niet alleen onghecorrigeert voor-by gegaen; maer oock sommige, die goede facit hadden, verstelt; oock sommighe in fouten grooter gemaeckt; gelijck men sien magh aende 72. in de multiplicatie,... De worteltreckinge (soo hy seit) heeft hy voor een ander over-ghelaten. Hier soude hy liever geseit hebben, dat hyse niet en verstont...’

Dezelfde Dauman zou volgens Bierens de Haans bibliografie in 1640 de Arithmetica in drie delen uitgegeven hebben. Wijnman acht dat weinig waarschijnlijk.39 Inderdaad, Cardinael leefde in 1640 en een leerling zal de redactie van een nieuwe uitgave niet tijdens het leven van de meester op zich hebben willen nemen.

In 1678 wordt het eerste deel nog een keer herdrukt. De titelpagina's vermelden ofwel M. de Groot ofwel de Wed. T.J. Lootsman. Hierna wordt het stil rond alle vier de delen. Het wordt dan al snel overvleugeld door het compactere werk van Bartjens.40

De interesse voor het werk is voor een rekenboekje uit die tijd relatief van korte duur geweest. Wat mag hiervan de oorzaak zijn? We dienen daartoe naar de inhoud te kijken.

Het eerste deel behandelt de basisbewerkingen voor gehele getallen, inclusief het worteltrekken en de regel van drie. Het tweede hetzelfde voor de breuken. Het derde deel behandelt dan weer de regel van drie. Het vierde geeft allerlei uitbreidingen op die regel van drie. Enkele dingen vallen daarbij op.

In de eerste plaats is het werk nogal wijdlopig. Wanneer in het tweede deel de ‘Divisie in 't ghebroken’ in 160 vraagstukken de verschillende bewerkingen op breuken afsluit, komt Cardinael met een ‘Lieve neerstighe Discipulen’, waarin hij opnieuw honderd oefeningen voorstelt. Kennelijk was dat zelfs voor de zeventiende-eeuwer te veel van het goede. Vergelijk dat met de sappige, glimlach oproepende vraagstukken van Willem Bartjens met diens gedichtjes tussendoor, die de inhoud van alle delen inclusief allerlei andere praktische zaken als de interestrekening en tarrarekening in één enkel deeltje had ondergebracht.

 

In de tweede plaats zijn de werken didactisch niet sterk. Het zijn meer verzamelingen van veel vraagstukken en ze bevatten weinig uitleg. Er worden zelfs geen definities van de basisbewerkingen gegeven. Sommige rekenkundige bewerkingen, zoals de ‘Multiplicatie in 't ghebroken’ worden zeven pagina's lang meetkundig geïllustreerd in houtsneden. Dat is uit meetkundig oogpunt erg interessant. Maar wat moet een praktische koopman daarmee?

Kortom: Cardinael heeft zijn werk te mooi willen maken en heeft het daardoor in die opzet niet kunnen voltooien.

Zou Wijnman dan toch gelijk hebben, dat er bij het verschijnen van de vierdelige Arithmetica nogal wat kritiek was? Hij citeert daarbij het vers dat Vondel kort voor 1644 op



illustratie
Titelpagina van het vierde deel uit 1640, nog zonder meetkundig titelvignet


Cardinael dichtte en waarin zijn leerlingen opgeroepen worden een cordon om hun meester te vormen:
 
Lyfwacht voor Meester Sybrant Hanssen Kardinael, den Vrieschen Euklides.
 
Aen zijn Scholieren.
 
 
 
De Vriesche Euklides hangt alleen
 
Van cijfferletters hecht aan een,
 
Bewaart toch Sybrant met u allen,
 
Bewaart dien Rekenschat getrouw:
 
Viel Kardinael van 't plat, hy zou
 
Aan cijfferletters stucken vallen.41

Tafels van traan

De catalogus van Le Long noemt nog een rekenhulp, nu uit 1643: Tafelen van Traan. De summiere aanduiding in die catalogus geeft weinig aanknopingspunten voor de inhoud. Er is echter een late herdruk van. In de Plimpton-verzameling van de Columbia University te New York trof ik een druk aan uit 1704. Het unieke exemplaar telt maar acht bladen, geeft enkele voorbeelden van de bepaling van de waarde van een hoeveelheid traan en vervolgens de tabel, die daarbij behulpzaam moet zijn. De walvisvangst had zich verplaatst van de Noordelijke IJszee naar de Groenlandse kust en de uitgever speelde daar mogelijk met de herdruk op in. In dit eenvoudige boekje leefde de naam van Cardinael tot in de achttiende eeuw voort.



illustratie
Titelpagina Traanboekje naar het enige bekende exemplaar plimp 511 1704 C14 in de Butler-Library van de Columbia University, New York


Tafels van terra

Ter afsluiting nog een andere rekenhulp: Tafelen van Terra, ofte afslag van de Lakenen/ en om te weten hoe veel per El komt te staen; seer dienstig voor alle Laken-kopers/ van nieuws oversten en verbetert. Ook hiervan is mij geen exemplaar bekend. Het is ongedateerd genoemd door Beughem onder ‘Cardinael’ in de alleroudste bibliografie van wiskundige werken.42 Omdat hij spreekt over een nieuwe uitgave moeten er meerdere drukken van geweest zijn. Naar de inhoud moeten we gissen.43

Besluit

Vanaf 1624 gaf Cardinael zijn lessen in de Nieuwestraat (thans Nieuwe Nieuwstraat, huidig nummer 20] in het huis toen bekend onder de naam ‘De Drie Vergulde Ossehoofden’. Hij stierf daar in 1647 op 69-jarige leeftijd. We nemen hier afscheid van deze wiskundige, die voor zijn vak geleefd schijnt te hebben. Vooral een begaafd meetkundige. Zeer praktijkgericht, gezien alle rekenhulpen die op zijn naam staan. Maar er nauwelijks op uit zichzelf te profileren. Hij liet zich niet lauweren met lofdichten: in al zijn werken staat er geen. Hij maakte er zelfs geen enkele tegen de ‘berispers’, die je in zo veel rekenboeken van zijn tijd tegenkomt. Maar het zijn anderen die respect voor hem hebben, hem loven en door hun geschriften doen voortleven. Dat getuigt van kwaliteit.

 

Zoals we gezien hebben werd zijn school nog enige tijd voortgezet door dochter Levijntje. Nog weer later waren er aan de school gerenommeerde rekenmeesters en zeevaartkundigen verbonden, zoals Abraham de Graaf (1657-1658) en Claes Heyndericks Gietermaker (1662).

 

‡Zonder de stimulerende discussies met Harry Sitters zou dit artikel niet geschreven zijn.


Vorige Volgende

Over dit hoofdstuk/artikel

auteurs