Geschiedenis van de wiskunde

[p. 191]

VIII. De negentiende eeuw

1.

De Franse Revolutie en de Napoleontische tijd schiepen bijzonder gunstige voorwaarden voor de verdere ontwikkeling van de wiskunde. Het pad voor de industriële revolutie op het Europese continent was nu geopend. Dit werkte gunstig op de groei van de natuurwetenschappen; nieuwe maatschappelijke klassen werden gevormd die belang hadden in wetenschap en techniek. Democratische ideeën wisten binnen de academische muren in te sluipen, oude en verouderde denkwijzen en levenswijzen werden bekritiseerd. Het gehele onderwijs moest hervormd en vernieuwd worden.

De nieuwe, onstuimige bloei van de wiskunde berustte niet zozeer op de technische problemen die de nieuwe industrie stelde. Engeland, het hart van de industriële revolutie, bleef, wat de scheppende wiskunde betreft, jaren lang vrijwel steriel. Het was in Frankrijk en wat later ook in Duitsland, dat de wiskundige wetenschappen het schoonste bloeiden - dus in die landen waar de ideologische breuk met het verleden het sterkst werd gevoeld, waar snelle economische en politieke veranderingen zich aan het voltrekken waren, waarbij de voorwaarden voor een moderne kapitalistische maatschappij werden geschapen. Nieuw leven kwam tot bloei aan scholen en universiteiten.

Men voelt die breuk ook in de Romantiek aan, en het zou interessant zijn de betrekkingen tussen deze stroming in de letteren en de kunst aan de ene zijde en die in de wiskunde anderzijds aan een nader onderzoek te onderwerpen. Hoe dit ook zij, zeker is dat de zich nieuw ontwikkelende wiskunde zich langzamerhand van de oude traditie emancipeerde, waarbij mechanica en astronomie als een soort van einddoel in de ontwikkeling der exacte wetenschappen werden beschouwd.

Ook algemeen gesproken begon de wetenschap zich meer en meer los te maken van de eisen die het praktische leven en het krijgswezen stelde. Wij krijgen de specialist, en die specialist was allereerst in de wetenschap om haar zelf geïnteresseerd. Ofschoon het verband met de praktijk nooit werd opgeheven, was deze vaak moeilijk te zien of verduisterd. Als nevenverschijnsel bij de toenemende specialisatie beginnen we nu ook tussen ‘zuivere’ en ‘toege-

[p. 192]

paste’ wiskunde te onderscheiden.¹

De wiskundigen van de negentiende eeuw leefden niet meer aan vorstelijke hoven en vonden slechts zelden hun weg tot de salons der aristocratie. Hun voornaamste beroep was niet meer het lidmaatschap van academies, zij waren gewoonlijk hoogleraren aan universiteiten en technische instituten, waar zij onderwijs gaven en hun salaris verdienden. Sommige grote wiskundigen als de Bernoulli's hadden alreeds enig onderwijs gegeven. Nu namen de onderwijsverplichtingen toe met de grote uitbreiding die het schoolsysteem kreeg, wiskundeprofessoren werden opvoeders en examinatoren. De geleerden werden daardoor nauwer met hun eigen nationale instituties verbonden, wat zich ook uitte in het feit dat hun publikaties steeds meer in de taal van hun land verschenen en steeds minder in het Latijn. Dit deed schade aan het internationalisme van de vorige eeuwen, doch niet zozeer dat internationale gedachtenwisseling onderbroken werd. De wiskundigen werden meer en meer specialisten in één bepaald (ofschoon nog zeer ruim) gebied, en waar men Leibniz, Euler, D'Alembert als ‘wiskundigen’ (‘géomètres’ in de terminologie van de achttiende eeuw) kan aanduiden, vinden we in Cauchy allereerst een analyticus, in Cayley een algebrist, in Steiner een meetkundige (zelfs een ‘zuivere’ meetkundige) en in Cantor de schepper van de leer der verzamelingen. De tijd was gekomen waarin we ‘mathematische fysica’ beginnen te krijgen, en waarin er goede vaklui in ‘mathematische statistiek’ of ‘mathematische logica’ optreden. Deze specialisatie werd alleen op het hoogste niveau van genialiteit doorbroken en juist door het werk van deze grootsten der groten, een Gauss, een

1 Het verschil in opvatting vond klassieke uitdrukking in een uitspraak van Jacobi over de ideeën van Fourier, die nog het nuttigheidsstandpunt van de achttiende eeuw innam: ‘Het is waar dat de heer Fourier van mening was dat het hoofddoel van de wiskunde in het openbare nut en in de verklaring van de natuurverschijnselen lag; maar een filosoof als hij had moeten weten dat het enige doel van de wetenschap de eer van de menselijke geest is, en dat van dit standpunt gezien een vraagstuk over getallen even waardevol is als een vraagstuk over de bouw van de wereld’ (le but unique de la science, c'est l'honneur de l'esprit humain, et sous ce titre une question de nombre vaut autantqu'une question du système du monde). In een brief aan Legendre sprak Gauss zich uit voor een synthese van beide opvattingen (1830, Werke i, blz. 454); hij paste de wiskunde op grootse schaal toe op astronomie, natuurkunde en geodesie, doch terzelfder tijd zag hij in de wiskunde de ‘koningin der wetenschappen’ en in het bijzonder in de getallenleer de ‘koningin der wiskunde’.

[p. 193]

Riemann, een Klein of een Poincaré ontving de wiskunde in de negentiende eeuw haar grootste inspiratie.

2.

Op de scheidingslijn tussen de achttiende en negentiende eeuw verheft zich de Olympische gestalte van Carl Friedrich Gauss. Hij was de zoon van een arbeider in Brunswijk, maar zijn vroege begaafdheid bracht hem onder de aandacht van de hertog van Brunswijk (uit de vaderlandse geschiedenis welbekend), die voor de opvoeding van het wonderkind zorg droeg. Na van 1795-'98 in Göttingen gestudeerd te hebben verkreeg de jonge Gauss in 1799 de graad van doctor in Helmstedt, waar J.F. Pfaff professor was (de man van het ‘probleem van Pfaff’). Van 1807 tot zijn dood in 1855 werkte hij ongestoord als directeur van de sterrenwacht en professor aan de universiteit te Göttingen. Zijn tamelijk streng isolement, zijn beheersing van de ‘zuivere’ als wel de ‘toegepaste’ wiskunde, zijn grote astronomische belangstelling en zijn voorliefde voor het Latijn als de taal waarin hij publiceerde, geven aan zijn figuur een achttiende-eeuws karakter, maar zijn werk als geheel ademt de geest van de nieuwe eeuw. Met zijn tijdgenoten Kant, Beethoven, Hegel en Goethe stond hij buiten de grote politieke strijd van zijn tijd, maar in zijn eigen gebied van de exacte wetenschappen wist hij aan de nieuwe ideeën op diepzinnige, doch ook klare wijze uitdrukking te verlenen.

De dagboeken van Gauss tonen dat hij reeds op zeventienjarige leeftijd merkwaardige ontdekkingen begon te doen. In het jaar 1795 ontdekte hij, bij voorbeeld, de kwadratische reciprociteitswet der getallentheorie, onafhankelijk van Euler en Legendre. Sommige van zijn vroegste ontdekkingen werden in zijn dissertatie van Helmstedt in 1799 en in zijn indrukwekkende Disquisitiones arithmeticae van 1801 gepubliceerd. Het proefschrift bracht het eerste strenge bewijs van de zogenaamde hoofdstelling der algebra (zie bldz. 178). Deze stelling, volgens welke een algebraïsche vergelijking van graad n minstens één en dus n wortels heeft, gaat terug op Albert Girard, de uitgever van de werken van Stevin (Invention nouvelle en algèbre, 1629). Later hadden D'Alembert, Euler en Lagrange een bewijs gewaagd, dat door Gauss werd verbeterd. Gauss hield van deze stelling, gaf later nog twee bewijzen en keerde in 1849 terug naar zijn eerste bewijs. Het derde bewijs (1816) maakte van complexe integralen gebruik en toont hoe vroeg Gauss de theorie der complexe getallen beheerste.

In de Disquisitiones arithmeticae bracht Gauss op zijn wijze alle belangrijke resultaten van zijn voorgangers samen en verrijkte ze

[p. 194]

met zulk een meesterhand dat men wel in deze Disquisitiones het begin van de moderne getallentheorie heeft gezien. De kern bestaat uit de theorie der kwadratische congruenties en vormen, en culmineert in de reciprociteitswet der kwadratische resten - dat ‘theorema aureum’ waarvoor Gauss het eerste volledige bewijs gaf. Gauss was even geestdriftig over deze wet als over de hoofdstelling van de algebra en publiceerde later nog vijf andere bewijzen, één werd na zijn dood nog tussen zijn papieren gevonden. De Disquisitiones bevatten ook Gauss' onderzoekingen over de cirkelverdeling, dus over de wortels van de vergelijking xⁿ = 1. Hier kwam de grote verrassing in de stelling dat de zijden van de regelmatige zeventienhoek met passer en lineaal kunnen worden geconstrueerd. Dit geldt voor alle regelmatige veelhoeken van n zijden zo n = 2 ^p + 1, p = 2^k, n priemgetal, k = 0, 1, 2, 3, ..., dus b.v. ook n = 257. Dit was een merkwaardige aanvulling van de Griekse meetkunde zoals we die uit Euklides kennen.

Gauss' belangstelling in de sterrenkunde werd opgewekt toen Giuseppe Piazzi in Palermo op 1 januari 1801, de eerste dag van de nieuwe eeuw, de eerste planetoïde ontdekte, die de naam Ceres kreeg. Van deze planetoïde konden slechts weinig observaties worden gemaakt, zodat het probleem ontstond de baan van een planeet uit een betrekkelijk klein aantal niet ver van elkaar af liggende observaties te bepalen. Gauss loste dit vraagstuk volledig op; het leidde tot een vergelijking van de achtste graad. Toen in 1802 Pallas, de tweede planetoïde, werd ontdekt, begon Gauss zich te interesseren in de seculaire storingen van de planeten. De reeks van onderzoekingen die met al deze verschijnselen samenhing, bevatte de Theoria motus corporum coelestium (1809), de verhandeling over de aantrekking van de algemene ellipsoïde (1813), een andere over mechanische kwadratuur (1814) en over seculaire storingen (1818), alsook Gauss' onderzoekingen met betrekking tot de hypergeometrische reeks (1812), die het mogelijk maakt een groot aantal functies vanuit één gezichtspunt te bekijken. Ze is de eerste stelselmatige studie van de convergentie van een reeks.

3.

Na 1820 begon Gauss zich levendig voor de geodesie te interesseren, dit naar aanleiding van de triangulatie van het koninkrijk Hannover, waaraan hij praktisch deelnam. Op karakteristieke wijze verenigde hij weer toegepaste met theoretische wiskunde. Een van zijn resultaten was zijn uiteenzetting van de methode der kleinste kwadraten (1821, 1823), die reeds door Legendre (1806) en Laplace tot een onderwerp van studie was gemaakt. Misschien

[p. 195]

zijn meest belangrijke wiskundige bijdrage uit dit tijdperk van zijn leven was zijn oppervlakkentheorie, die hij in de Disquisitiones generales circa superficies curvas (1827) uiteenzette, en die de differentiaalmeetkunde van een geheel ander standpunt bezag dan Monge. Deze theorie van Gauss was weer het gevolg van praktische overwegingen, in dit geval aan de hogere geodesie ontleend. Ze hield de aandacht gevestigd op de inwendige meetkunde van een oppervlak, die dus niet van de omringende ruimte afhangt, en waarbij kromlijnige coördinaten u en v op het oppervlak worden aangewend, om het lijnelement ds in een kwadratische differentiaalvorm uit te drukken: ds² = Edu² + 2Fdudv + Gdv². Hier bereikte Gauss weer een hoogtepunt, het theorema egregium, dat leert dat de totale kromming van een oppervlak alleen afhangt van E, F en G en hun afgeleiden en dus een buigingsinvariante is.

Zelfs in deze periode van ingespannen werkzaamheid in de praktische geodesie verwaarloosde Gauss zijn eerste liefde, de ‘koningin der wiskunde’ niet. In 1825 en 1831 verschenen zijn verhandelingen over bikwadraatresten. Deze vormen een voortzetting van de theorie der kwadraatresten in de Disquisitiones arithmeticae, maar een voortzetting met behulp van een nieuwe methode, de leer der complexe getallen. De verhandeling van 1831 bevatte niet alleen algebra, doch ook een rekenkunde der complexe getallen. Hierbij ontstond een nieuwe theorie van priemgetallen, waarin 3 een priemgetal blijft, maar 5 = (1 + 2i) (1 - 2i) niet langer priem is. Het getal 1 + 2i is een complex priemgetal. Met behulp van deze nieuwe getallentheorie kon Gauss vele duistere punten van de reële rekenkunde ophelderen. Zo bleek de kwadratische reciprociteitswet voor complexe getallen eenvoudiger dan voor reële. Het was in deze verhandeling dat Gauss voor altijd de geheimzinnigheid die de complexe getallen nog steeds hadden, verstoorde, doordat hij liet zien hoe complexe getallen door punten in het ‘vlak van Gauss’ kunnen worden voorgesteld. ¹

1 Vgl. E.T. Bell, Gauss and the Early Development of Algebraic Numbers, National Mathem. Magazine 18 (1944) 188, 219. A. Speiser, in zijn inleiding tot Eulers Opera i (28), bldz. xxxvii, heeft erop gewezen dat reeds Euler en andere wiskundigen na 1760 gedacht hebben in de geest die aan deze opvatting van Gauss ten grondslag ligt.
Een diagram van Gauss waarop de complexe priemgetallen zijn afgebeeld kan men o.a. vinden in het Tijdschrift Fortune (artikel ook in boekvorm uitgegeven). De idee, zulk een diagram te maken, kwam van B. van der Pol te Eindhoven (ca. 1943). Men heeft zelfs tafelkleedjes gemaakt met dit diagram als patroon.

[p. 196]

Een standbeeld in Göttingen stelt Gauss met zijn jongere medewerker Wilhelm Weber voor op het ogenblik dat zij bezig zijn de elektrische telegraaf te ontdekken. Dit gebeurde in de jaren 1833-'34 in de tijd dat Gauss begon de fysica te beoefenen. In die jaren voerde hij vele experimenten uit met het aardmagnetisme. Toch vond hij nog tijd voor een theoretische verhandeling van grote betekenis, zijn Allgemeine Lehrsätze in Beziehung auf die im verkehrten Verhältnisse des Quadrats der Entfernung wirkenden Anziehungs- und Abstöszungskräfte (1839-'40). In deze verhandeling werd de potentiaaltheorie als een eigen gebied in de wiskunde ingevoerd (de verhandeling van Green uit het jaar 1828 was toentertijd vrijwel onbekend gebleven). Men vindt er oppervlakte- en inhoudsintegralen met minimaalprincipes waarin men het zgn. beginsel van Dirichlet herkent. Gauss hield het bestaan van een minimum nog voor vanzelfsprekend, eerst later werd dit bestaan een onderwerp van veel studie, waaraan ten slotte Hilbert een exacte formulering heeft gegeven.

Gauss bleef werkzaam tot aan zijn dood in 1855. In zijn latere levensjaren wendde hij zich meer en meer tot de toegepaste wiskunde. Toch leveren zijn publikaties geen voldoende beeld van zijn volle grootheid. Door de publikatie van zijn dagboeken en van sommige zijner brieven is het gebleken dat hij enige zijner diepste gedachten nooit heeft bekend gemaakt. We weten thans dat Gauss reeds in 1810 de elliptische functies had ontdekt (eerst later herontdekt door Abel en Jacobi) en omstreeks 1816 in het bezit was van de niet-euklidische meetkunde (later herontdekt door Lobačevskiï en Bolyai). Hierover heeft hij zich slechts in enige brieven aan vrienden uitgelaten, en daaruit zien we dat hij kritisch stond tegenover alle pogingen het parallellenaxioma te bewijzen. Wars van alle polemieken wilde hij in het openbaar geen onderwerp aansnijden waarmee hij controverses kon veroorzaken. Hij schreef over wespen die hem dan om de oren zouden vliegen en van het ‘geschreeuw der Boeotiërs’, dat hij dan te horen zou krijgen. Maar hij betwijfelde de toen vrijwel algemeen aanvaarde leer van Kant die onze ruimtevoorstelling a priori voor Euklidisch hield; voor Gauss was de meetkunde van de werkelijke ruimte een natuurverschijnsel dat men experimenteel moest onderzoeken.

4.

Felix Klein, in zijn Entwicklung der Mathematik im 19. Jahrhundert heeft een vergelijking getrokken tussen Gauss en de vijfentwintig jaar oudere Franse wiskundige Adrien-Marie Legendre. Misschien is het niet helemaal fair om Gauss te vergelijken met een

[p. 197]

andere wiskundige, tenzij die tot de allergrootste behoort; maar we leren uit deze vergelijking hoezeer Gauss' ideeën ‘in de lucht hingen’, want Legendre heeft, op zijn eigen onafhankelijke wijze, vele vragen die Gauss bezighielden, ook onderzocht. Legendre was van 1775 tot 1780 docent aan de militaire school in Parijs en had later vele regeringsbetrekkingen. Zo was hij professor aan de Ecole Normale, examinator aan de Ecole Polytechnique en had administratieve posities.

Evenals Gauss heeft hij belangrijke onderzoekingen over de getallentheorie gepubliceerd (Essai sur les nombres, 1798; Théorie des nombres, 1830), waarin hij de kwadratische reciprociteitswet formuleerde. Hij schreef ook over geodesie en theoretische astronomie, was een even ijverig berekenaar van tafels als Gauss, schetste in 1806 de methode der kleinste kwadraten en bestudeerde de aantrekking van ellipsoïden - ook van de ellipsoïden die geen omwentelingsoppervlakken zijn. Hierbij voerde hij de ‘Legendre-functies’ in. Hij stelde evenals Gauss belang in elliptische integralen en integralen van Euler, en in de grondslagen en methoden der euklidische meetkunde.

In al deze gebieden drong Gauss dieper door dan Legendre, zo vond Legendre nooit de stelling van de regelmatige zeventienhoek, de elliptische functies en de niet-euklidische meetkunde. Toch deed Legendre werk van blijvende betekenis. Zijn leerboeken werden lange jaren druk gebruikt, vooral zijn Exercises du calcul intégral (3 dln, 1811-'19) en zijn Traité des fonctions elliptiques et des intégrales euleriennes (1827-'32), dat nog steeds een standaardwerk is. In zijn Elements de géométrie (1794) brak hij met het Platonische ideaal van Euklides en gaf een leerboek der schoolmeetkunde dat met de eisen van de toen moderne opvoeding rekening hield. Dit boek is dan ook zeer populair geweest, het is in verscheidene talen vertaald en vaak herdrukt; de invloed van dit boek is blijvend geweest.

5.

Men kan het nieuwe tijdperk in de geschiedenis van de wiskunde in Frankrijk misschien laten aanvangen met de oprichting van militaire scholen en academies, die in het tweede deel der achttiende eeuw plaatsvond. In deze scholen, waarvan er ook enige buiten Frankrijk bestonden (Turijn, Woolwich) werd op de wiskunde bij de opleiding van militaire ingenieurs en genieofficieren sterke nadruk gelegd. Lagrange begon zijn loopbaan aan de artillerieschool in Turijn, Legendre en Laplace doceerden aan de militaire school in Parijs, Monge aan de academie in Mézières, Carnot was een mi-

[p. 198]

litaire ingenieur. Napoleons belangstelling in de wiskunde dateert uit zijn studentenjaren aan de militaire scholen in Brienne en Parijs. Toen gedurende de Revolutie Frankrijk door buitenlandse legers werd bedreigd werd de behoefte aan een gecentraliseerde militaire ingenieursopleiding sterker dan ooit gevoeld. Dit leidde in 1794 tot de oprichting van de Ecole Polytechnique te Parijs. Spoedig begon deze school een leidende plaats in te nemen in de opleiding van ingenieurs van allerlei soort, zodat ze het voorbeeld werd van alle militaire ingenieursscholen die in de eerste jaren van de negentiende eeuw werden opgericht, in Nederland zowel als in de Verenigde Staten (West Point) en Rusland - ook al werd het militaire karakter van de Ecole Polytechnique bij andere technische hogescholen niet altijd overgenomen. Een wezenlijk bestanddeel van het leerplan was de studie van de zuivere en toegepaste wiskunde. Aan de Ecole Polytechnique werd niet alleen het onderwijs, doch ook het wetenschappelijk onderzoek met alle kracht ondersteund. Men trachtte de beste mannen van wetenschap aan de Ecole Polytechnique te verbinden, vele bekende Franse wiskundigen zijn studenten, examinatoren of professoren aan de Ecole Polytechnique geweest.¹

De opleiding aan zulk soort scholen eiste een nieuw soort geleerde - de leraar - en een nieuw soort van wetenschappelijke tekst - een leerboek. De geleerde verhandelingen voor de ingewijden, die zo kenmerkend waren voor de tijd van Euler, moesten vervangen worden door handboeken die geschikt waren voor het klasseonderwijs. Zo zijn een aantal van de beste leerboeken van de eerste jaren van de negentiende eeuw uit het onderwijs aan de Ecole Polytechnique of verwante instituten voortgekomen. Hun invloed heeft continu doorgewerkt tot in de huidige tijd. Een goed voorbeeld van zulk een leerboek is de Traité du calcul différentiel et du calcul intégral (2 dln., 1797) van Sylvestre François Lacroix, waaruit hele generaties hun infinitesimaalrekening hebben geleerd. Lacroix heeft ook vele andere leerboeken der wiskunde geschreven. We hebben alreeds van Legendres boeken gesproken; nog een an-

1 Vgl. C.G.J. Jacobi, Werke 7, bldz. 355 (voordracht van 1835). Over de oprichting van de Ecole Polytechnique: J. Fayet, La révolution française et la science 1789-1795 (Paris, 1960). Verder zie H. Wussing in Pädagogik 13 (1958) 646-662. Voor de wetenschappelijke achtergrond zie M.P. Crosland, The Society of Arcueil (Cambridge, Mass. 1967). Laplaces woning in Arcueil, niet ver van Parijs, was van 1806 tot 1813 een plaats waar geleerde personen tezamen kwamen.

[p. 199]

der voorbeeld is het leerboek der beschrijvende meetkunde van Monge, dat ook nog lang voor het onderwijs in dit vak voorbeeldig is geweest.

6.

Gaspard Monge, de eerste directeur van de Ecole Polytechnique, was de wetenschappelijke en pedagogische leider van de mannen van wetenschap die gedurende het Directoire, het Consulaat en het Keizerrijk met deze school waren verbonden. Hij was zijn loopbaan begonnen als docent aan de militaire school van Mézières (1768-'89), waar hem zijn voordrachten over vestingbouwkunde de gelegenheid boden de beschrijvende meetkunde als een bijzonder gebied van de wiskunde te ontwikkelen. Zijn boek Géometrie descriptive verscheen tussen 1795-'99.

In Mézières begon hij ook met de toepassing van de differentiaalrekening op de leer der ruimtekrommen en oppervlakken; zijn verhandelingen hierover werden later verzameld in de Application de l'analyse à la géométrie (1809), het eerste boek over de differentiaalmeetkunde, doch nog niet in de vorm waarin we die tegenwoordig bestuderen. Monge was een der eerste moderne wiskundigen die als specialist kan gelden: als meetkundige. Ook zijn behandeling der partiële differentiaalvergelijkingen is typisch meetkundig.

Door Monges invloed begon de meetkunde aan de Ecole Polytechnique te bloeien. In de beschrijvende meetkunde lag de kiem der projectieve meetkunde, en de toepassing van algebraïsche en analytische methoden op krommen en oppervlakken kwam de analytische meetkunde en de differentiaalmeetkunde ten goede. Jean Hachette en Jean-Baptiste Biot ontwikkelden stelselmatig de analytische meetkunde van kegelsneden en kwadratische oppervlakken, in Biots Essai de géométrie analytique (1802) beginnen wij onze huidige analytische meetkunde te herkennen; naar inhoud zowel als naam. Charles Dupin, een leerling van Monge, paste als jonge marine-ingenieur gedurende de Napoleontische tijd de methoden van zijn leraar op de oppervlakkentheorie toe, waarbij hij de asymptotische en geconjugeerde lijnen vond; de kromtelijnen waren reeds door Monge onderzocht. Dupin werd professor in de meetkunde in Parijs en werd later ook een bekend politicus en propagandist van de industrie. Hij vatte zijn meetkundige ontdekkingen samen in de Développements de géométrie (1813) en Applications de géométrie (1825), waar men de ‘indicatrix van Dupin’ en de ‘cycliden van Dupin’ bestuderen kan.

Monges naam is ook verbonden aan de vernieuwing van de

[p. 200]

scheikunde, waarbij zijn academische collega Lavoisier zulk een belangrijke rol speelde. Hij behoorde tot die groep van mannen die de samenstelling van water uit wat we nu waterstof en zuurstof noemen ontdekten (1783-'85), ook experimenteerde hij op het gebied van de uitzetting van gassen en de capillariteit. Gedurende de revolutie gaf hij advies aan de regering omtrent het maken van wapens en van buskruit. Ofschoon Monge een man van democratische opvattingen was, bleef hij trouw aan Napoleon, met wie hij in Egypte was (1798-'99) en in wie hij de man zag die de idealen van de Revolutie kon verwezenlijken. In 1815, bij de terugkomst der Bourbons, werd Monge ontslagen en hij stierf kort daarop. Doch Monges geest bleef heersen in de Ecole Polytechnique. Zo bleef er datzelfde nauwe verband tussen zuivere en toegepaste wiskunde bestaan dat er van de aanvang al geweest was. De mechanica werd druk beoefend, en de mathematische fysica begon zich eindelijk van de ‘katoptrika’ en de ‘dioptrika’ van de Ouden te bevrijden. Etienne Malus ontdekte in 1810 de polarisatie van het licht, later nam Augustin Fresnel Huygens' golftheorie van het licht weer op (1821). André-Marie Ampère, die met groot succes de partiële differentiaalvergelijkingen had bestudeerd, werd na 1820 een der grote pioniers van de nieuwe wetenschap van het elektromagnetisme. Uit deze beoefening der mathematische fysica kwamen ook resultaten voor de wiskunde zelve, we denken aan Fresnels golfoppervlak en aan Malus' meetkunde der lichtstralen, verbeterd door Dupin, en die weer vruchten afwierp voor de meetkundige optica en de meetkunde der stralencongruenties.

Lagranges Mécanique analytique werd zorgvuldig bestudeerd en de methoden daarin uiteengezet, werden op allerlei vraagstukken toegepast. De statica had Monge reeds vroeg geïnteresseerd en hij beoefende haar met zijn leerlingen ook vanwege haar meetkundige mogelijkheden; in de loop der jaren verschenen verscheidene leerboeken over dit vak, waaronder een van Monge zelf (1788, vele uitgaven). De meetkundige inhoud van de statica werd klaar tot uiting gebracht in het werk van Louis Poinsot, vele jaren lang een lid van de Franse Hoge Onderwijsraad. In zijn Elements de statique (1804) en zijn Théorie nouvelle de la rotation des corps (1834) voegde hij aan het begrip van de kracht dat van het koppel (draaimoment) toe, gaf een voorstelling van Eulers leer der traagheidsmomenten met behulp van een traagheidsellipsoïde en onderzocht de beweging van deze ellipsoïde wanneer het lichaam zich in de ruimte beweegt of om een punt draait. Victor Poncelet en Gustave-Gaspard Coriolis gaven aan het streng analytische karakter

[p. 201]

van Lagranges analytische mechanica een meetkundig gewaad, beide geleerden hebben met Poinsot ook de toepassing der mechanica op eenvoudige mechanismen behandeld. Een der resultaten van deze onderzoekingen is de ‘coriolisversnelling’, die optreedt wanneer een lichaam zich beweegt in een versneld systeem (1835).

Victor Poncelet was een der meest oorspronkelijke leerlingen van Monge. Toen hij als soldaat van Napoleons Grande Armée in 1813 in Russische krijgsgevangenschap geraakte, vond hij ruimschoots tijd om over de methoden van zijn leraar na te denken. Speciaal voelde hij zich aangetrokken door het zuiver synthetische in Monges meetkunde en zo werd hij tot een gedachtengang gevoerd die reeds twee eeuwen te voren Desargues had geïnspireerd. Poncelet werd de ontdekker van de projectieve meetkunde.

Hij zette zijn ideeën uiteen in de Traité des propriétés projectives des figures (1822). Dit omvangrijke boek bevat alle begrippen die deze nieuwe soort meetkunde karakteriseren, begrippen als dubbelverhouding, perspectiviteit, projectiviteit, involutie en zelfs de oneindig verre cirkelpunten. Poncelet liet zien dat de brandpunten van een kegelsnede kunnen worden beschouwd als snijpunten van de raaklijnen, door die cirkelpunten aan de kegelsnede getrokken. Ook vindt men in de Traité de theorie der veelhoeken die tegelijk door één kegelsnede omgeschreven en door een andere ingeschreven zijn (het zgn. sluitingsprobleem van Poncelet). Het verschijnen van dit boek werd gevolgd door zulk een geestdriftige bestudering van het nieuwe gebied, dat in weinige tientallen jaren de projectieve meetkunde een graad van ontwikkeling bereikte die haar tot een klassiek model van een afgerond wiskundig systeem zou maken.

Naast Poncelet behoorden ook Siméon Poisson, Joseph Fourier en Augustin Cauchy tot de leidende wiskundigen wier naam met de eerste tientallen jaren der Ecole Polytechnique waren verbonden. Alle drie toonden diepe belangstelling voor de toepassing van de wiskunde op de natuur- en werktuigkunde, en alle drie werden door deze belangstelling weer tot ontdekkingen in de ‘zuivere’ wiskunde gevoerd. Poissons produktiviteit blijkt uit de vele manieren waarop zijn naam in onze leerboeken voorkomt: hier ontmoeten we de haakjes van Poisson in de leer der differentiaalvergelijkingen, de constante van Poisson in de elasticiteitsleer, de integraal en de vergelijking van Poisson in de potentiaaltheorie. Deze vergelijking van Poisson, gewoonlijk ΔV = 4πρ geschreven, vond haar oorsprong in Poissons ontdekking (1812), dat de vergelijking van Laplace, ΔV = 0, slechts daar geldt waar geen massa's zijn; het

[p. 202]

exacte bewijs voor massa's van veranderlijke dichtheid werd eerst door Gauss in zijn Allgemeine Lehrsätze van 1839/'40 geleverd. Poissons Traité de mécanique (1811) was geschreven in de geest van Lagrange en Laplace, maar bevatte menige oorspronkelijke gedachte zoals het expliciet gebruik van de impulscoördinaten p_i = ∂T/∂q_i. Deze coördinaten hebben dan later in het werk van Hamilton en Jacobi een fundamentele rol gespeeld - en doen het nu nog.

Poisson schreef ook een boek over de waarschijnlijkheidsrekening (1837) dat wij reeds citeerden. Onder de vele resultaten die dit boek bevat vinden we de ‘wet van Poisson’ als benadering van de binomiale wet voor kleine waarschijnlijkheden. De grote betekenis van deze wet voor de statistiek, o.a. van straling en verkeer, is eerst in de twintigste eeuw begrepen.

Fourier wordt wel als de grondlegger van de mathematische fysica beschouwd. Hij heeft deze reputatie in de eerste plaats te danken aan zijn Théorie analytique de la chaleur, zijn analytische warmtetheorie (1822). Deze warmtetheorie is de theorie der warmtegeleiding, bepaald door de partiële differentiaalvergelijking ΔU = k∂u/∂t, die voor het geval van een ééndimensionale voortplanting van de warmte (door Fourier nog als stof, ‘calorique’, gedacht) als ∂²U/∂x² = k∂U/∂t kan worden geschreven. Deze vergelijking moet dan worden opgelost onder gegeven randvoorwaarden. De methoden die Fourier hierbij gebruikte waren zo algemeen dat zijn werk het prototype is geworden voor de behandeling van de gehele theorie der oplossingen van partiële differentiaalvergelijkingen onder gegeven randvoorwaarden. Daarbij demonstreerde Fourier het nut van trigonometrische reeksen, die in de voorafgaande eeuw het onderwerp waren geweest van een gedachtenwisseling tussen Euler, D'Alembert, Daniel Bernoulli en Lagrange. Fourier loste de moeilijkheden die zich ontwikkeld hadden althans in beginsel op: elke ‘willekeurige’ functie (waaronder Fourier een functie verstond die door een continu gebogen of recht lijnsegment of door een aantal van zulke segmenten kan worden voorgesteld) kan in een gegeven interval worden uitgedrukt door een reeks van de vorm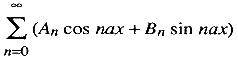

Ondanks het feit dat Euler en zijn collega's reeds over de al of niet juistheid van dit feit van gedachten hadden gewisseld, was Fouriers resultaat toch nog zo nieuw en frapperend dat hij in 1807, toen hij zijn ideeën het eerst bekend maakte, op scherp verzet

[p. 203]

stuitte, zelfs bij zulk een groot wiskundige als Lagrange.

Van nu af aan werden de ‘Fourier-reeksen’ langzamerhand een algemeen aanvaard en goed doordacht middel voor de oplossing van partiële differentiaalvergelijkingen met randvoorwaarden. Maar ze waren ook, van zuiver wiskundig standpunt beschouwd, verbazend interessant, omdat hun gedrag zo afweek van dat van reeksen van Taylor. Wat moest men onder een ‘willekeurige functie’ verstaan? Uit vragen als deze is het te verklaren dat de wiskundigen van de negentiende eeuw zich veel meer inlieten met de exactheid van hun bewijzen dan hun voorgangers, en dat zij ernstiger ernaar streefden de grondbegrippen der wiskunde te verhelderen.¹ Wat de Fourier-reeksen betreft werd deze verheldering door Dirichlet en Riemann gebracht, met consequenties die veel verder reikten dan die bijzondere reeksen.

1 P.E.B. Jourdain, Note on Fourier's Influence on the Conceptions of Mathematics, Proc. Intern. Congress of Mathem. (Cambridge, 1912) ii 526/527. Zie over Fourier ook J. Ravetz, Archives intern. de l'histoire des Sciences 13 (1960) 247-251.

7.

Cauchy's talrijke bijdragen tot de theorie van het licht en de mechanica zijn door het succes van zijn prestaties in de analyse wel wat in de vergetelheid geraakt, en toch mogen we niet uit het oog verliezen dat hij met zijn tijdgenoot Louis Navier tot de grondleggers der wiskundige elasticiteitstheorie behoort. Zijn roem berust echter in de eerste plaats op zijn theorie van de functies van een complexe veranderlijke, en op zijn streven naar exactheid in de analyse. Functies van een complexe veranderlijke waren wel eens vroeger opgedoken, bijv. bij D'Alembert, die in een verhandeling van 1752 over de weerstand in vloeistoffen zelfs tot de vergelijking werd gevoerd die we nu als die van Cauchy-Riemann kennen. Ook Euler was bezig geweest dit gebied te ontginnen. Onder de handen van Cauchy werd nu de complexe functietheorie van een toevallig hulpmiddel bij hydrodynamica, aerodynamica of oppervlakkentheorie tot een nieuw en zelfstandig onderdeel van de wiskunde opgebouwd. Cauchy's publikaties op dit gebied begonnen in 1814 en volgden elkaar in ononderbroken volgorde op. Een van zijn belangrijkste publikaties is de Mémoire sur les intégrales définies, prises entre des limites imaginaires (1825). Hier vindt men de integraalstelling van Cauchy en het begrip van het residu van een pool. De stelling dat iedere analytische functie f(z) om ieder punt z = z_o in een reeks van Taylor kan worden ontwik-

[p. 204]

keld, en dat die reeks in een cirkel van het complexe vlak convergeert, die door het naastbijgelegen singuliere punt gaat, werd in 1831 gepubliceerd, dus in hetzelfde jaar dat Gauss zijn arithmetische theorie der complexe getallen het licht deed zien. Laurents generalisatie van Cauchy's stelling over de reeksen van Taylor is van 1843, toen ze ook in het bezit van Weierstrass was. Deze feiten illustreren waarom de theorie van Cauchy geen weerstand in vakkringen had te overwinnen: vanaf haar begin is de theorie der complexe functies geaccepteerd, zelfs in de notatie die Cauchy had voorgesteld.

Cauchy behoort, met zijn tijdgenoten Gauss, Abel en Bolzano, tot de pioniers van de nieuwe exactheid in het wiskundig denken. De achttiende eeuw was in wezen een eeuw van mathematisch experimenteren geweest, waarbij de resultaten in overweldigend aantal zich ophoopten. Daarbij hadden de wiskundigen zich maar weinig beziggehouden met de grondslagen van hun wetenschap - ‘allez en avant, et la foi vous viendra’ (ga maar vooruit, het geloof zal wel komen) - deze aanmoediging wordt wel aan D'Alembert toegeschreven. En als deze wiskundigen, zoals Maclaurin, Euler of Lagrange, wel eens van hun gewetensbezwaren lieten blijken, waren hun redeneringen maar matig overtuigend. Nu echter was de tijd gekomen om zich consequent af te vragen wat de precieze zin van al die verkregen resultaten was. Wat was eigenlijk een ‘functie’ van een reële veranderlijke, die zich ten opzichte van een Taylor-reeks zo anders gedraagt als ten opzichte van een Fourier-reeks, en in welke betrekking stond ze tot een ‘functie’ van een complexe veranderlijke, die weer haar eigen gedrag heeft? Met vragen als deze kwamen alle onopgeloste kwesties in de grondslagen van de infinitesimaalrekening en in het vraagstuk van het bestaan van een potentieel en een actueel oneindige weer vooraan in het bewustzijn van de wiskundige.¹ Wat Eudoxos had gedaan in de tijd na de val van de Atheense democratie begonnen Cauchy en zijn exact denkende collega's in de periode van een snel groeiend

1 P.E.B. Jourdain, The Origin of Cauchy's Conception of a Definite Integral and of the Continuity of a Function, Isis 1 (1913) 661-703, vgl. ook Bibliotheca Mathematica 6 (1905) 190-207. Over Cauchy zie het uitvoerig verslag door H. Freudenthal in DSB iii (1971) 131-149, met vele anekdotes: ‘Cauchy beheerste niet de wiskunde, de wiskunde beheerste hem’. Verder: The Installation of Rigor in Analysis in M. Kline, Mathematical Thought from ancient to modern Times (New York, 1972), Hoofdstuk 40.

[p. 205]

industrialisme te voltooien. Dit grote verschil in maatschappelijke verhoudingen leidde tot grote verschillen in de wijze waarop de vraagstukken werden aangepakt: waar het succes van Eudoxos er op den duur toe leidde dat de wiskundige produktiviteit belemmerd werd, leidde het succes van de moderne hervormers tot nieuwe en verhoogde produktiviteit. Op Gauss en Cauchy volgden Weierstrass en Cantor, en op hen weer Hilbert en Lebesgue.

Cauchy ontwikkelde de grondslagen der infinitesimaalrekening op de manier waarop ze nu algemeen in onze leerboeken worden uiteengezet. Men kan zijn methode bestuderen in zijn Cours d'Analyse (1821) en de Résumé des Leçons données à l'Ecole Royale Polytechnique i (1823). Cauchy's methode berustte op het limietbegrip zoals D'Alembert dit al eens bij gelegenheid had gebruikt. Nu werd dit begrip op strenge wijze geformuleerd en door voorbeelden verduidelijkt. Zo toonde Cauchy aan wat de limiet (grenswaarde) is van sin α/α voor α = 0. Daarna definieerde hij een oneindig kleine veranderlijke als een veranderlijk getal dat nul als grenswaarde heeft. Dan eiste hij dat Δy en Δx ‘seront des quantités infiniment petites’ (oneindig kleine grootheden zullen zijn). Vervolgens schreef hij: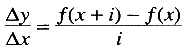

en noemde de grenswaarde voor i → 0 de fonction dérivée (afgeleide functie) y′ ou f′(x). Verder zette hij i = αh, waar α een oneindig kleine grootheid is en h een eindige grootheid: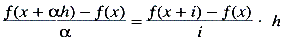

Dan werd h de différentielle de la fonction y = f(x) (differentiaal van de functie y) genoemd, en dy = df(x) = hf′(x); dx = h.¹

Cauchy gebruikte zowel de notatie van Lagrange als vele van zijn bijdragen tot de reële functietheorie zonder concessies te doen aan Lagranges ‘algebraïsche’ formulering van de afgeleiden. Zo nam hij de stelling van de gemiddelde waarden en het restlid van de Taylor-reeks over zoals Lagrange die geformuleerd had, doch de reeksen werden nu onder passend onderzoek naar hun conver-

1 Résumé i (1823), Calcul différentiel 13-27. Een nauwkeurig onderzoek van dit proces bij M. Pasch, Mathematik am Ursprung (Leipzig 1927), 47-73. Verder: J.V. Grabiner, The Origins of Cauchy's rigorous Calculus (MIT Press, Cambridge, Mass, 1981).

[p. 206]

gentie besproken. Verschillende convergentiecriteria in de theorie der oneindige reeksen zijn naar Cauchy genoemd. In zijn geschriften vindt men duidelijke sporen van een overgang tot die ‘arithmetisering’ van de analyse, die later de kern van Weierstrass' onderzoekingen zou uitmaken. Cauchy gaf ook het eerste existentiebewijs voor de oplossing van een differentiaalvergelijking en van een stelsel van zulke vergelijkingen (1836). Op deze manier maakte Cauchy althans een begin met die reeks van problemen en paradoxen te beantwoorden, die in de wiskunde reeds van Zeno's tijd af hadden rondgespookt, en hij deed het niet door die moeilijkheden te loochenen of te omzeilen, maar door een wiskundige techniek te scheppen die het mogelijk maakte ze recht te doen wedervaren.

Cauchy was evenals zijn tijdgenoot Honoré de Balzac, met wie hij een bijkans onbegrensde arbeidscapaciteit gemeen had, een legitimist en royalist. Beiden hadden zo'n diep inzicht dat ondanks hun reactionaire idealen hun werk ook voor latere generaties een grote betekenis blijft behouden. Na de revolutie van 1830 gaf Cauchy zijn leerstoel aan de Ecole Polytechnique op en bracht enige jaren door in Turijn en in Praag; in 1838 keerde hij naar Parijs terug. Na 1848 werd het hem niet moeilijk gemaakt: hij mocht blijven zonder de eed van trouw aan de nieuwe regering afgelegd te hebben. Zijn produktiviteit was zo enorm dat de Académie eenvoudig niet de publikatie van zijn artikelen kon bijhouden, zelfs niet in de wekelijks verschijnende Comptes Rendus. In 1826 begon hij zelfs zijn eigen tijdschrift uit te geven, de vijf delen bevatten alleen zijn eigen werk. Men zegt dat toen hij zijn eerste verhandeling over de convergentie van reeksen aan de Académie voorlegde, Laplace zo ongerust werd dat de grote man naar zijn kamer ijlde om de reeksen in zijn Mécanique céleste op hun convergentie te onderzoeken. Het schijnt dat hij geen belangrijke veranderingen hoefde aan te brengen.

8.

Dit Parijse milieu met zijn intensieve wiskundige bedrijvigheid bracht omstreeks 1830 een genie van de eerste rang voort, dat als een komeet even snel verdween als het verschenen was. Evariste Galois, de zoon van een burgemeester van een stadje bij Parijs, trachtte tweemaal tevergeefs als student tot de Ecole Polytechnique te worden toegelaten, en toen hij het ten slotte klaarspeelde in de Ecole Normale te komen, werd hij spoedig weer weggestuurd. Hij poogde met privaatlessen in de wiskunde aan de kost te komen, waarbij hij moeite had enig evenwicht te bewaren tussen zijn hartstocht voor de wetenschap en voor de democratie. Als republi-

[p. 207]

kein nam hij met vuur aan de revolutie van 1830 deel, bracht verscheidene maanden in de gevangenis door en werd kort daarop, éénentwintig jaren oud, in een duel gedood. Twee van zijn verhandelingen, die hij ter publikatie had aangeboden, raakten zoek op de schrijftafel van de redacteur, enkele andere werden pas lang na zijn dood gepubliceerd. Op de vooravond van het fatale duel schreef hij aan een vriend een verslag van zijn ontdekkingen in de leer der vergelijkingen. Dit ontroerende en diepzinnige document, waarin hij zijn vriend verzoekt die ontdekkingen in het geval van zijn dood aan het oordeel van vooraanstaande wiskundigen te onderwerpen, eindigde met de woorden:

‘Je zult Jacobi af Gauss in het openbaar verzoeken, hun oordeel te uiten niet over de waarheid, maar over de betekenis van deze stellingen. Daarna zullen er naar ik hoop, wel enige lieden zijn die het de moeite waard vinden dit gekrabbel te ontcijferen.’

Dit gekrabbel (ce gâchis) bevatte niet meer of minder dan de groepentheorie, sleutel tot de moderne algebra en de moderne meetkunde. De idee van deze theorie komt tot op zekere hoogte al bij Lagrange en de Italiaan Ruffini voor, doch bij Galois vindt men een doordachte, scherpomlijnde groepentheorie. Hier vindt men het fundamentele begrip van de permutatiegroep die wordt bepaald door de wortels van een algebraïsche vergelijking, en die door haar samenstelling op haar beurt het karakter van de wortels bepaalt. Galois wees op de beslissende rol die invariante ondergroepen spelen bij de vorming van de resolvente. Oude en eerwaardige vraagstukken, zoals de driedeling van de hoek, de verdubbeling van de kubus zowel als de oplossing van de vergelijkingen van de derde, vierde en algemene graad, vonden hun natuurlijke plaats in de theorie van Galois. Doch zijn laatste brief is, zover wij weten, nooit aan Gauss of Jacobi ter hand gesteld. Het wiskundige publiek kreeg haar niet eerder te zien voor Liouville in 1846 een aantal verhandelingen van Galois in zijn Journal de mathématiques publiceerde. Dat was omstreeks de tijd dat ook Cauchy over groepentheorie was beginnen te schrijven (1844-'46). Nu eerst begonnen enige wiskundigen zich voor de theorieën van Galois te interesseren. Maar eerst nadat in 1870 Camille Jordans Traité des substitutions verschenen was, gevolgd door de publikaties van Klein en Sophus Lie, is de betekenis van de theorie van Galois in wiskundige kringen algemeen erkend. Thans ziet men in haar een der schitterendste resultaten der negentiende-eeuwse wiskunde, waaraan deze theorie een

[p. 208]

groot omvattend beginsel heeft geschonken.¹

Galois had ook ideeën over de integralen van algebraïsche functies van één veranderlijke; integralen die we nu naar Abel noemen. Die laten ons zien dat er verband bestaat tussen de gedachtenwereld van Galois en van Riemann. We kunnen ons afvragen of de moderne wiskunde, als Galois was blijven leven, niet haar diepste gedachten uit Parijs en de school van Lagrange in plaats van uit Göttingen en de school van Gauss had kunnen putten.

1 H. Wussing, Die Genesis des abstrakten Gruppenbegriffes (Berlijn, 1969).

9.

De jaren van de Romantiek zijn rijk aan geniale jongemannen, wie slechts een korte levensduur was gegund, mannen, ‘die door de Goden bemind worden’. Wij ontmoeten een ander jong genie in Niels Henrik Abel, de zoon van een Noorse dorpspredikant. Abels kort bestaan verliep bijna zo tragisch als dat van Galois. Als student in Christiania (Oslo) geloofde hij een tijdlang dat hij de vergelijking van de vijfde graad had opgelost, maar in een geschrift van 1824 verbeterde hij zijn werk. Dit geschrift is beroemd geworden, omdat hier eindelijk de onmogelijkheid werd aangetoond een algemene vergelijking van de vijfde graad met behulp van radicalen op te lossen - een vraagstuk dat de wiskundigen reeds vanaf Bombelli en Viète heel wat hoofdbrekens had gekost. Overigens bestond er reeds een bewijs van de onmogelijkheidsstelling, dat in 1799 de Italiaan Paolo Ruffini had gegeven, maar Poisson en andere wiskundigen hadden dit bewijs nooit geheel aanvaard. Nu kreeg Abel een stipendium waardoor hij met enige vrienden naar Berlijn, Italië en Frankrijk kon reizen. Maar ondanks enige prettige reisavonturen kon de jonge wiskundige, die wat schuchter en teruggetrokken was, niet slagen de nodige contacten te leggen voor zijn toekomst. Hij leed aan chronisch geldgebrek, dat hem bleef kwellen ook toen hij naar Noorwegen terugkwam en een bescheiden academisch baantje kreeg. Hij verzwakte en stierf in 1829 op zesentwintigjarige leeftijd, op een tijdstip dat de geleerde wereld juist zijn genie begon te erkennen.

Abels baanbrekend werk bestrijkt vele gebieden: convergentie van reeksen, ‘Abelse’ integralen, algebraïsche vergelijkingen en elliptische functies. Zijn stellingen in de theorie der oneindige reeksen tonen dat Abel, evenals Cauchy, erin slaagde deze theorie op exacte grondslagen te construeren. ‘Kun je je iets verschrikkelijkers voorstellen dan de bewering dat 0 = 1 ⁿ - 2 ⁿ + 3 ⁿ - 4 ⁿ + etc.,

[p. 209]

waarbij n een geheel positief getal is?’ schreef hij aan een vriend en voegde eraan toe:

‘Er bestaat in de hele wiskunde nauwelijks een enkele oneindige reeks, waarvan de som op strenge wijze is bepaald’ (brief aan Holmboe, 1826).

Abels onderzoekingen over elliptische functies vonden plaats in een korte, maar spannende wedkamp met Jacobi. Gauss had in zijn persoonlijke aantekeningen al lang opgemerkt, dat de omkering van de elliptische integralen tot dubbelperiodieke functies voert, doch hij heeft zijn ideeën nooit gepubliceerd. Aan Legendre, die zoveel tijd en moeite had besteed aan elliptische integralen, schijnt dit feit geheel ontgaan te zijn en hij was diep bewogen toen hij als man op leeftijd van Jacobi's en Abels ontdekkingen op de hoogte werd gesteld. Abel, met al zijn tegenspoed, had het geluk in A.L. Crelle, een invloedrijke en vermogende constructie-ingenieur in Berlijn (hij heeft wegen gebouwd en ook de eerste spoorweg in Duitsland), een man te vinden die zijn talenten wist te waarderen. In het eerste deel van Crelles Journal für die reine und angewandte Mathematik verschenen niet minder dan vijf verhandelingen van Abel, in het tweede deel (1827) verscheen het eerste deel van Abels Recherches sur les fonctions elliptiques, waarmee de theorie der dubbelperiodieke functies begint.

Wij spreken van de integraalvergelijking van Abel en over de stelling van Abel over de som van integralen van algebraïsche functies, een stelling die tot de functies van Abel voert. Commutatieve groepen heten ook Abelse groepen, een naam die erop wijst hoe nauw de gedachtenwereld van Galois en van Abel aan elkaar verwant waren. Twee jongemannen, beiden omstreeks dezelfde tijd in Parijs, beiden onbekend aan of zelfs genegeerd door de oudere geleerde heren en beiden onder tragische omstandigheden gestorven - wij schijnen een roman van Balzac te lezen.¹

1 De levens van beide jongemannen zijn in interessante boeken beschreven, dat van Galois (in meer romantische vorm) door L. Infeld, dat van Abel (strikt biografisch) door O. Ore. Zie de literatuurlijst.

10.

In 1829, Abels sterfjaar, verscheen in Crelles Journal de Fundamenta nova theoriae functionum ellipticarum van Carl Gustav Jacob Jacobi. De auteur was een jeugdige hoogleraar aan de universiteit in Koningsbergen, toen een gedeelte van Pruisen. Hij was de zoon van een bankier in Berlijn en behoorde tot een intellectuele familie; zijn broeder Moritz, lid van de Academie in St.-Peters-

[p. 210]

burg, was de uitvinder van de galvanoplastiek en een der eersten die met elektromagnetische instrumenten experimenteerde. Jacobi studeerde in Berlijn en gaf van 1826-'43 onderwijs in Koningsbergen, waarna hij om gezondheidsredenen enige tijd in Italië doorbracht. Hij stierf in 1851, zesenveertig jaar oud, als hoogleraar in Berlijn. Hij was een geïnspireerde en liberale denker, een uitstekend docent en een wiskundige, wiens helder en oorspronkelijk denken, gepaard aan onstuimige energie, op vele gebieden der wiskunde vruchtbaar heeft gewerkt.

Jacobi baseerde zijn theorie der elliptische functies op vier functies die door oneindige reeksen waren gedefinieerd en die als thètafuncties bekend zijn. De dubbelperiodieke functies sn u, cn u en dn u zijn quotiënten van thètafuncties, zij voldoen aan bepaalde identiteiten en additietheorema's die lijken op die waaraan de sinus- en cosinusfuncties der gewone goniometrie voldoen. De additietheorema's der elliptische functies kunnen ook als toepassingen van Abels stelling over de som van integralen van algebraïsche functies worden beschouwd. Nu kon men zich dus afvragen of hyperelliptische integralen ook konden worden omgekeerd zoals elliptische integralen, die tot elliptische functies leiden. In 1832 publiceerde Jacobi het antwoord, dat luidde dat zulk een omkering mogelijk was met behulp van functies van meer dan één veranderlijke. Zo ontstond de theorie der functies van Abel in p veranderlijken, een theorie die vooral in de negentiende eeuw verscheidene beoefenaars vond.

Sylvester heeft aan de functionaaldeterminant de naam van Jacobi verbonden om Jacobi's werk op het gebied van de algebra en de eliminatietheorie te eren. De meest bekende verhandeling van Jacobi op dit gebied is zijn De formatione et proprietatibus determinantium (1841), waarmee de theorie der determinanten het gemeengoed der wiskundigen werd. Onze schrijfwijze van de determinanten is aan deze verhandeling ontleend, doch het begrip is ouder; dit gaat in beginsel terug op Leibniz (1693), op de Zwitserse wiskundige Gabriel Cramer (1750) en op Lagrange (1773); de naam gaat op Cauchy (1812) terug. Y. Mikami heeft erop gewezen dat de Japanse wiskundige Seki Kōwa dit begrip van de determinant voor 1683 reeds kende. Hier denkt men aan de ‘matrix’- methode, ontwikkeld door de Chinese wiskundigen van de Sung- periode, wier werk Seki goed heeft gekend.¹

1 Y. Mikami, On the Japanese theory of Determinants, Isis 2 (1914) 9-36, zie ook T. Hayashi, A brief history of the Japanese Mathematics, Nieuw Archief voor Wiskunde (2) 6 (1905) 296-361, 7 (1907) 105-163, en Mikami's ‘Development of mathematics in China and Japan’ (1913) 191-199. Volgens Needham, Science and civilization in China iii, 117 zegt men beter Seki Takakusu (met ziet ook Takakazu).

[p. 211]

Een uitstekende inleiding tot het werk van Jacobi krijgt men uit zijn mooie Vorlesungen über Dynamik, die in 1866 naar collegedictaten uit 1842-'43 zijn uitgegeven. Ze zijn in de traditie van de Franse school van Lagrange en Poisson geschreven, maar ze zijn vol nieuwe gedachten. Men kan hier Jacobi's onderzoekingen over partiële differentiaalvergelijkingen der dynamica vinden. Een interessant hoofdstuk van deze Vorlesungen bevat de bepaling van de geodetische lijnen op een ellipsoïde, die tot een betrekking tussen twee integralen van Abel voert.

11.

Jacobi's voordrachten over dynamica voeren ons tot een andere wiskundige wiens naam vaak met die van Jacobi verbonden wordt, tot William Rowan Hamilton (die men niet met zijn tijdgenoot, de Schotse wijsgeer uit Edinburgh, William Hamilton, moet verwarren). W.R. Hamilton was de zoon van een advocaat in Dublin, die als kind met zijn ouders uit Schotland was gekomen. Hij bezocht Trinity College in zijn geboortestad Dublin, waar hij in 1827, tweeëntwintig jaar oud, professor in de sterrenkunde werd en kort daarop ‘Astronomer Royal’ voor Ierland. Deze positie behield hij tot het einde van zijn leven, in 1865. Als knaap leerde hij de wiskunde van het continent, nog steeds iets bijzonders in het Verenigd Koninkrijk, door de studie van Clairaut en Laplace en bewees door zijn originele verhandelingen over optica en dynamica dat hij deze nieuwe wiskunde beheerste. Zijn theorie van de lichtstralen (1824) was veel meer dan alleen een differentiaalmeetkunde van lijnencongruenties, ze was tevens een theorie van optische instrumenten, die het Hamilton mogelijk maakte de zgn. conische refractie in tweeassige kristallen te voorspellen. Ze werd in 1832 door een van Hamiltons collega's experimenteel geverifieerd. In de verhandeling van 1824 treedt Hamiltons ‘karakteristieke functie’ op, die het grondmotief werd van zijn General Method in Dynamics van 1834-'35. De hoofdgedachte in deze methode was: optica en dynamica tezamen uit een enkel algemeen beginsel af te leiden. Euler had in zijn verdediging van Maupertuis er reeds op gewezen hoe men de stationaire waarde van de actie-integraal voor dit doel kon gebruiken. En zo toonde Hamilton aan, dat lichttheorie en dynamica twee verschillende manieren zijn om een bepaald variatieprobleem te bekijken. Hij vroeg naar de stationaire waar-

[p. 212]

de van een zekere integraal en beschouwde die als functie van haar grenzen. Dit was de ‘karakteristieke functie’, die voldoet aan twee partiële differentiaalvergelijkingen. Een dezer vergelijkingen, die gewoonlijk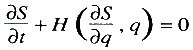

wordt geschreven, werd door Jacobi speciaal uitverkoren voor zijn theorie der dynamica en is nu bekend als de vergelijking van Hamilton-Jacobi. Hierdoor is de betekenis van Hamiltons karakteristieke functie een beetje in het vergeetboek geraakt, ofschoon het juist die functie was die de eenheid van mechanica en mathematische fysica had moeten teweegbrengen. Zo werd ze in 1895 door de astronoom Heinrich Bruns in de geometrische optica herontdekt, en als ‘eikonal’ treffen we haar aan in de theorie der optische instrumenten.¹

Het deel van Hamiltons werk over dynamica dat gemeengoed van alle wiskundigen en theoretische fysici is geworden, bevat allereerst de theorie der ‘kanonische’ vorm q̇ = ∂H/∂p, ṗ = -∂H/∂q, waarin Hamilton de vergelijkingen der dynamica schreef. Sophus Lie heeft dan later aangetoond hoe kanonische vorm en differentiaalvergelijking van Hamilton-Jacobi de overgang van de dynamica naar de contacttransformaties vormen. Deze ideeën van Hamilton, de wetten der theoretische fysica en der mechanica uit de variatie van een integraal af te leiden, hebben doorgewerkt, zodat ze ook in de relativiteitstheorie en de quantummechanica een fundamentele rol hebben vervuld. Men ontmoet ook hier steeds weer de ‘functies van Hamilton’.

Het jaar 1843 was een keerpunt in het leven van de koninklijke astronoom van Dublin. In dit jaar ontdekte hij de quaternionen, waaraan hij een belangrijk deel van zijn latere leven wijdde. Wij komen hier nog op terug.

1 Vgl. M. Herzberger, Geschichtlicher Abriss der Strahlenoptik. Zeitschrift für Instrumentenkunde 52 (1932) 429-435, 485-493, 534-542.

12.

Peter Gustav Lejeune-Dirichlet stond zowel met Gauss en Jacobi als met de Franse wiskundigen in nauw verband. Van 1822-'27 woonde hij als gouverneur in Parijs, en ontmoette in het huis van zijn patroon bekende Franse geleerden, onder wie Fourier, wiens warmteleer hij bestudeerde. Ook drong hij diep door in de gedachtenwereld van Gauss' Disquisitiones arithmeticae. Na zijn

[p. 213]

terugkeer naar Duitsland werd hij privaatdocent, eerst in Breslau, daarna in Berlijn, waar hij professor werd, en in 1855 volgde hij Gauss in Göttingen op; hij stierf reeds in 1859. Zijn persoonlijke bekendheid met de Franse zowel als met de Duitse wiskunde maakte het hem bijzonder goed mogelijk om zowel Gauss' getallentheorie als Fouriers reeksen te interpreteren. Dirichlets Vorlesungen über Zahlentheorie (gepubl. 1863) zijn nog steeds een der beste inleidingen tot Gauss' onderzoekingen in de leer der getallen, en bevatten ook vele nieuwe resultaten. In een verhandeling van 1840 liet hij zien hoe men de theorie der analytische functies in haar volle omvang op de getallentheorie kon toepassen; het was in deze onderzoekingen dat hij de ‘reeksen van Dirichlet’ invoerde. Hij generaliseerde ook het begrip van kwadratische irrationaliteiten tot dat van algemene algebraïsche rationaliteitsgebieden.

Dirichlet was de eerste die een streng convergentiebewijs gaf voor Fourier-reeksen. Dit was ook een bijdrage tot het probleem: de aard van een functie juist te begrijpen.¹ Hij voerde in de variatierekening het zgn. beginsel van Dirichlet in, waarbij het bestaan van een functie v, die de integraal ∫[v_x² + v_y² + v_z²]dt onder gegeven randvoorwaarden tot een minimum maakt, wordt gepostuleerd. Dit beginsel was een wijziging van een principe dat Gauss in zijn potentiaalthesis van 1839-'40 had ingevoerd, en later werd het door Riemann gebruikt als een uitnemend hulpmiddel om vraagstukken in de potentiaaltheorie op te lossen. Wij hebben reeds vermeld dat de geldigheid van dit beginsel later door Hilbert streng werd bewezen.²

1 A.E. Monna, The Concept of Function in the 19^th and 20^th Centuries, AHES 9 (1972) 51-84.

2 A.E. Monna, Dirichlet's Principle (Utrecht, 1975).

13.

Met Bernhard Riemann, Dirichlets opvolger in Göttingen, komen we tot de man die misschien meer dan enige andere man van wetenschap de loop van de moderne wiskunde heeft beïnvloed. Hij was de zoon van een plattelandspredikant en studeerde aan de universiteit in Göttingen, waar hij in 1851 promoveerde. In 1854 werd hij privaatdocent, in 1859 hoogleraar aan dezelfde universiteit. Evenals Abel had hij last van een zwakke gezondheid; zijn laatste dagen bracht hij in Italië door, waar hij in 1866 op veertigjarige leeftijd stierf. In dit korte leven publiceerde hij slechts een betrekkelijk klein aantal verhandelingen, maar iedere publikatie van zijn hand was - en is - belangrijk, en sommige van deze publikaties hebben nieuwe en vruchtbare gebieden opengelegd.

[p. 214]

In 1851 verscheen Riemanns proefschrift over de theorie der complexe functies u + iv = f(x + iy). Evenals D'Alembert en Cauchy vóór hem was hij door hydrodynamische beschouwingen beïnvloed. Hij beeldde het (xy)-vlak conform af op het (uv)-vlak en liet zien dat een functie bestond die een willekeurig enkelvoudig samenhangend gebied in het ene vlak in een enkelvoudig samenhangend gebied van het andere vlak, b.v. de eenheidscirkel, transformeert. Dit bracht hem tot het begrip Riemann-oppervlak en zo werden in de analyse topologische beschouwingen ingevoerd. Topologie was in die dagen nog een bijna maagdelijk terrein, waaraan J.B. Listing in 1847 een artikel in de Göttinger Studien had gewijd - Euler had het onderwerp alreeds eenmaal aangesneden in een artikel over het probleem van de zeven bruggen van Koningsbergen.¹ Riemann liet zien hoe gewichtig deze topologische beschouwingen in de theorie der complexe functies zijn. In dit proefschrift werd ook het begrip analytische functie verduidelijkt: haar reële en haar imaginaire doel moeten in een bepaald gebied aan de zgn. vergelijkingen van Cauchy en Riemann, u_x = v_y, u_y = - v_x, voldoen, en verder aan zekere voorwaarden met betrekking tot de rand en singulariteiten.

Riemann paste zijn ideeën toe op hypergeometrische functies en op functies van Abel (1857), waarbij hij vrij gebruik maakte van het beginsel van Dirichlet (zo noemde hij het). Hierbij ontdekte hij het geslacht van een oppervlak van Riemann als een topologische invariante, waarmee hij o.a. de functies van Abel kon classificeren. In een verhandeling, na zijn dood (1867) gedrukt, paste hij zijn ideeën op minimaaloppervlakken toe. Tot dit gedeelte van Riemanns werkzaamheid behoren ook zijn onderzoekingen over elliptische modulaire functies, thètareeksen in p veranderlijken en lineaire differentiaalvergelijkingen met algebraïsche coëfficiënten.

Bij zijn toelating tot privaatdocent bood Riemann niet minder dan twee gewichtige verhandelingen aan, de ene over trigonometrische reeksen en de grondslagen van de analyse, de andere over de grondslagen van de meetkunde. In de eerste verhandeling onderzocht Riemann de voorwaarden van Dirichlet voor de convergentie van Fourier-reeksen. Een van die voorwaarden was de ‘integreerbaarheid’ van de functie. Maar wat is de betekenis van het ‘bestaan’ van een integraal? Cauchy en Dirichlet hadden deze

1 Uit deze eerste tijd dateren ook de voor de topologie belangrijke wetten van Kirchhoff (1846-49) en het werk van Möbius en Listing over eenzijdige oppervlakken (1858).

[p. 215]

vraag reeds op hun manier beantwoord. Riemann verving hun definities door een nieuwe, die meer omvattend was en die wij kennen als de definitie van de ‘Riemann-integraal’. Eerst in de twintigste eeuw bleek dat het voor vele doeleinden beter was, deze integraal te vervangen door de Lebesgue-integraal (1902).

Riemann bewees verder dat functies, door Fourier-reeksen gedefinieerd, zeer goed in het bezit kunnen zijn van een oneindig aantal maxima en minima, iets dat wiskundigen van een oudere school niet in een functie zouden hebben aanvaard. Het begrip ‘functie’ begon zich nu toch wel zeer los te maken van dat van de curva quaecumque libero manus ductu descripta van Euler.¹ In zijn colleges gaf Riemann een voorbeeld van een continue functie zonder afgeleiden; in 1875 werd een voorbeeld van zulk een functie, door Weierstrass ontdekt, gepubliceerd. In die dagen weigerden de meeste wiskundigen om zulke functies au sérieux te nemen, ze spraken van ‘pathologische’ functies. De moderne analyse heeft aangetoond hoe fundamenteel zulke functies zijn, zodat Riemann ook hier de vinger heeft gelegd op een belangrijk wiskundig verschijnsel.

De andere verhandeling van 1854 is een onderzoek naar de hypothesen die aan de meetkunde ten grondslag liggen. Riemann voerde de ruimte in als een topologische uitgebreidheid van een willekeurig aantal afmetingen, in zulk een uitgebreidheid werden de metrische eigenschappen ingevoerd door middel van een kwadratische differentiaalvorm, zodat in het oneindig kleine de betrekkingen euklidisch waren. Waar Riemann, in zijn analyse, een complexe functie had gedefinieerd door haar lokale gedrag, zo bepaalde hij in deze verhandeling over de meetkunde het karakter van de ruimte op dezelfde manier. Zo kon Riemann niet alleen de verschillende vormen, die de meetkunde had aangenomen, als een eenheid overzien, zelfs de nog tamelijk onbekende en ongewaardeerde niet-euklidische meetkunde, doch hij kon ook een onbepaald aantal nieuwe ruimtevormen scheppen. Verscheidene van deze ruimtevormen hebben sedert Riemanns tijd een bruikbare plaats gevonden in de meetkunde of in de mathematische fysica en speciaal in Einsteins relativiteitstheorie. Deze verhandeling bevatte nauwelijks een enkele formule, ze was zuiver beschrijvend, hetgeen de bestudering ervan geenszins vergemakkelijkte. Later verschenen sommige der bijbehorende formules in het antwoord op

1 De een of andere kromme met de vrije hand beschreven (Institutiones Calculi Integralis iii § 301).

[p. 216]

een prijsvraag over het warmtetransport in vaste lichamen, uitgeschreven door de Académie in Parijs (1861). Wij vinden hier een schets van de transformatietheorie der kwadratische vormen en ze bevat tevens de uitdrukkingen die later bekend zijn geworden als de componenten van de krommingstensor.

De laatste verhandeling van Riemann die we willen vermelden bevat zijn onderzoek naar het aantal priemgetallen F(n) minder dan een gegeven geheel getal n (1859). Gauss had reeds aangegeven dat F(n) tot de logaritmische integraal ʃⁿ₂(log t)^-1 dt nadert. Riemann onderzocht Gauss' ontdekking met complexe getallen en kwam tot bepaalde conclusies door een hypothese op te stellen die sedert die tijd heel beroemd is geworden en door vele wiskundigen als een uitdaging is - en wordt - beschouwd. Deze hypothese houdt in dat de zgn. zètafunctie van Euler ζ(s) die bij Euler voorkomt voor s geheel positief als

ζ(s) = 1/1 ^s + 1/2 ^s + 1/3 ^s + ... + 1/n^s + ...,

nu als functie van complexe s = x + iy beschouwd alle niet-reële nulpunten op de lijn x = ½ heeft (de notatie ζ(s) is van Riemann). Deze hypothese is tot nu toe noch bewezen noch weerlegd, ondanks veel waardevol onderzoek.¹

1 R. Courant, Bernhard Riemann und die Mathematik der letzten hundert Jahre. (Die Naturwissenschaften 14 (1926) 813-818). Zie ook het uitvoerige artikel van H. Freudenthal, DSB xi (1975) 447-456, met literatuur.

14.

Men heeft vaak Riemanns opvatting van een complexe functie vergeleken met die van Weierstrass. Karl Weierstrass doceerde vele jaren als wiskundeleraar aan een Pruisisch gymnasium en werd in 1856 hoogleraar in de wiskunde aan de universiteit van Berlijn waar hij dertig jaar onderwijs gaf. Zijn steeds voorbeeldig voorbereide colleges genoten een steeds groter wordende beroemdheid; het is vooral door die colleges dat Weierstrass' ideeën diep in het tegenwoordige wiskundige bewustzijn zijn binnengedrongen.

Gedurende zijn gymnasiale periode schreef Weierstrass verscheidene verhandelingen over hyperelliptische integralen, functies van Abel, en algebraïsche differentiaalvergelijkingen. Zijn meest bekende bijdrage is zijn gebruik van de machtreeks als grondslag voor de leer der complexe functies. In zekere zin was dit

[p. 217]

een terugkeer tot de opvattingen van Lagrange, met het verschil dat Weierstrass in het complexe vak en met volkomen strengheid werkte. De waarden van de machtreeks binnen haar convergentiecirkel vormden het ‘functie-element’, waarbuiten dan, zo mogelijk, de functie over het vlak wordt uitgebreid door zgn. analytische voortzetting. In het bijzonder onderzocht Weierstrass gehele functies en functies door oneindige produkten gedefinieerd. Zijn functie ℘ (u) heeft naast de oudere functies sn u, en u en dn u van Jacobi een blijvende plaats in de leer der elliptische functies ingenomen.

De roem van Weierstrass is in de eerste plaats gebaseerd op zijn uiterst verzorgde redenering, op de ‘strengheid van Weierstrass’, niet alleen in zijn leer der reële en complexe functies, doch ook in zijn variatierekening. Hij verhelderde de begrippen van het minimum, van de functie, van de afgeleide, en bevrijdde op deze wijze de differentiaal- en integraalrekening van verscheidene overblijfsels van de oude vaagheid die nog uit de tijd van Newton en Leibniz dateerden. Hij was bij uitstek het wiskundige geweten, methodisch en logisch. Zo kwam hij ook op het begrip uniforme convergentie. Met hem begon de reductie van de beginselen der analyse tot rekenkundige begrippen die we de arithmetisering der wiskunde noemen.

‘Als heden in het volgen van bewijsredenen, die op het begrip irrationaal getal en limiet in het algemeen berusten, in de analyse volmaakte eensgezindheid en zekerheid bestaat, en in de meest ingewikkelde vragen die de theorie der differentiaal- en integraalrekening betreffen, toch overeenstemming over alle resultaten bestaat, ondanks de meest gedurfde en verschillende combinaties met gebruik van super-, juxta- en transpositie van limieten - dan is dit in principe een verdienste van de wetenschappelijke activiteit van Weierstrass.¹

1 D. Hilbert, Über das Unendliche. Mathem. Annalen 95 (1926) 161-190, Franse vertaling: Acta Mathematica 48 (1926) 91-122.

15.

Deze arithmetisering was een karaktertrek van de zogenaamde Berlijnse school, en in het bijzonder van Leopold Kronecker. Tot deze school behoorden wiskundigen als Kronecker, Kummer en Frobenius, die uitblonken in algebra en in de theorie van algebraische getallen. Wij kunnen in zekere zin tezamen met hen Dedekind en Cantor noemen. Ernst Kummer werd in 1855 als opvolger van Dirichlet naar Berlijn beroepen, waar hij tot 1883 doceerde; daarna gaf hij vrijwillig zijn wiskundig werk op, omdat hij voelde

[p. 218]

dat zijn scheppende kracht af zou nemen. Kummer ontwikkelde de differentiaalmeetkunde van de lijnencongruenties, die door Hamilton was begonnen, hetgeen hem o.a. bracht tot het vierdegraadsoppervlak met zestien knooppunten dat zijn naam draagt. Zijn beroemdheid heeft hij eveneens te danken aan de ‘ideale’ getallen in zijn theorie van de algebraïsche rationaliteitsgebieden (1846). Deze theorie dankt haar ontstaan ten dele aan Kummers pogingen het grote theorema van Fermat (xⁿ + yⁿ = zⁿ onmogelijk voor positief gehele x, y, z, n > 2) te bewijzen en ten dele aan Gauss' theorie der kwadraatresten, waarin hij in het gebied der complexe getallen het begrip priemgetallen had ingevoerd. Kummers ‘ideale’ getallen maakten het mogelijk eenduidige ontbinding van getallen in priemfactoren binnen algemenere rationaliteitsgebieden in te voeren. Met deze nieuwe begrippen kon men nu diep in de rekenkunde van de algebraïsche getallen doordringen, hetgeen tot ontdekkingen voerde die David Hilbert in 1897 voor de Deutsche Mathematische Gesellschaft op meesterlijke wijze heeft samengevat. De theorie van Richard Dedekind en Heinrich Weber, die de theorie der algebraïsche functies en die der algebraïsche getallen in bepaalde rationaliteitsgebieden op elkaar betrokken (1882), waren een voorbeeld van de vruchtbaarheid van Kummers ideeën in de arithmetisering van de wiskunde.

Leopold Kronecker, die op het gymnasium door zijn leraar Kummer de liefde voor de wiskunde was bijgebracht, vestigde zich na enige omzwervingen in 1855 te Berlijn, waar hij jarenlang zonder een formele leerstoel doceerde. Hij aanvaardde die eerst in 1883 toen zijn oude leermeester Kummer aftrad. Kroneckers voornaamste verhandelingen betreffen elliptische functies, ideaaltheorie en de aritmetica van kwadratische vormen; zijn gepubliceerde voordrachten over getallentheorie zijn zorgvuldige uitwerkingen van zijn eigen en van voorafgaande ontdekkingen en laten duidelijk zien hoe hij geloofde in de noodzakelijkheid de wiskunde te aritmetiseren. Deze overtuiging was een gevolg van zijn zoeken naar strenge bewijzen; en zo geloofde hij dat de wiskunde op het getal als grondslag moest worden opgebouwd, en het getal zelf weer op het natuurlijke getal. Zo moest het getal π niet, zoals gewoonlijk het geval was, meetkundig worden ingevoerd; het was beter met de reeks 1 - ⅓ + ⅕ - 1/7 + etc. te beginnen, dus met een betrekking van gehele getallen. Hetzelfde doel kon worden bereikt met bepaalde oneindige produkten voor π. Kroneckers streven alles wat wiskundig was op de getallenleer terug te voeren, wordt belicht door zijn bekende uitspraak tijdens een vergadering in Ber-

[p. 219]

lijn in 1886: ‘De gehele getallen zijn door de goede God gemaakt, al het andere is mensenwerk’.¹ Hij aanvaardde een definitie van een mathematisch begrip alleen als het in een eindig aantal stappen kon worden geverifieerd. Op die manier loste hij de moeilijkheid van het actueel oneindige op door te weigeren het te aanvaarden. Plato's leuze dat God altijd ‘geometriseert’ werd in Kroneckers school vervangen door de leuze dat God altijd ‘arithmetiseert’.

Kroneckers beschouwingen over het actueel oneindige stonden in scherp contrast tot die van Dedekind en vooral die van Cantor. Richard Dedekind, éénendertig jaar lang professor aan de Technische Hogeschool in Brunswijk, schiep een strenge theorie van het irrationale getal. In twee boekjes, Stetigkeit und Irrationalzahlen (1872) en Was sind und was sollen die Zahlen (1882) volbracht hij voor de moderne wiskunde met haar aritmetisering wat Eudoxos had gedaan voor de Griekse wiskunde met haar geometrisering. Er is, met alle verschil, een zekere overeenkomst tussen de ‘snede van Dedekind’, waarmee de moderne wiskunde (met uitzondering van de school van Kronecker) het irrationale getal postuleert en de antieke theorie van Eudoxos zoals we die uit het vijfde boek van Euklides' Elementen kennen. Cantor en Weierstrass gaven rekenkundige definities van irrationale getallen die enigszins van die van Dedekind verschilden, doch op hetzelfde beginsel berustten.

De grootste ketter in Kroneckers ogen was echter Georg Cantor. Cantor, die van 1869 tot 1905 in Halle doceerde, heeft zijn beroemdheid niet zozeer aan zijn theorie van het irrationale getal, maar aan zijn theorie der oneindige verzamelingen (‘Mengenlehre’) te danken. Met deze theorie ontsloot Cantor een geheel nieuw wiskundig gebied, dat, als eenmaal de grondbeginselen worden aanvaard, aan de hoogste eisen van strengheid voldoet. Cantors publikaties begonnen in 1870 en volgden elkaar regelmatig op; in 1883 verschenen zijn Grundlagen einer allgemeinen Mannigfaltigkeitslehre. In deze verhandeling schiep hij een theorie van transfiniete kardinaalgetallen die voortvloeide uit een systematische wiskundige behandeling van het actueel oneindige. Het laagste transfiniete getal, dat hij א (aleph) noemde, gaf hij aan een verzameling zoals die der gehele getallen, dus een zgn. aftelbare verzameling. Aan het continuüm kende hij een hoger transfiniet getal toe, omdat het onmogelijk is een een-eenduidige afbeelding van een aftelbare verzameling op de punten van het continuüm te con-

1 Die ganzen Zahlen hat der liebe Gott gemacht, alles Andere ist Menschenwerk.

[p. 220]

strueren. Zo was het mogelijk een arithmetica van transfiniete getallen te scheppen. Cantor definieerde ook transfiniete ordinaalgetallen, die samenhingen met de wijze waarop oneindige verzamelingen geordend zijn.

In deze ontdekkingen gelukte het Cantor een wiskundige grondslag te geven aan vele oude scholastieke speculaties over de natuur van het oneindige en hij was zich van dit resultaat wel bewust. Hij verdedigde Augustinus' volkomen aanvaarding van het actueel oneindige (in een theologische vorm)¹, maar moest zich zelf verdedigen tegen de oppositie van vele zijner collega's die weigerden het oneindige te aanvaarden behalve als een proces gesymboliseerd door het teken ∞. Cantors voornaamste tegenstander was Kronecker, die in hetzelfde proces van de arithmetisering der wiskunde een geheel tegenovergestelde richting vertegenwoordigde. Tenslotte gelukte het Cantor zijn inzichten door de meeste wiskundigen aanvaard te zien, vooral toen de enorme betekenis van de leer der verzamelingen voor de theorie der reële functies en de topologie werd beseft. Dit werd vooral duidelijk nadat H. Lebesgue in 1902 de theorie van Cantor verrijkt had met zijn maattheorie. Er bleven echter logische moeilijkheden in de theorie der transfiniete getallen die tot paradoxen aanleiding gaven, zoals die van Burali Forti en Bertrand Russell. Dit leidde weer tot scholen, wier opvattingen over de grondslagen der wiskunde scherpe verschillen vertoonden - en nog vertonen. De strijd in de twintigste eeuw tussen logistici, formalisten en intuïtionisten is een vervolg op de strijd tussen Cantor en Kronecker, maar op een nieuw niveau.²

1 Zie de voetnoot bij Augustinus, hoofdstuk v, p. 112.

2 Zie b.v. M. Black, The Nature of Mathematics (New York, 1934), ook E.N.S.I.E. Encyclopedie iv (Amsterdam 1949) 14-16.

16.

Deze merkwaardige ontwikkelingen in de algebra en analyse gingen samen met even merkwaardige ontwikkelingen in de meetkunde. Als uitgangspunt kunnen wij het onderwijs van Monge nemen, omdat deze zowel het ‘synthetische’ als het ‘algebraïsche’ element in de meetkunde had doen uitkomen. In het werk van zijn leerlingen zien wij een splitsing van beide methoden, die ieder een eigen weg gaan: de ‘synthetische’ methode voert naar de projectieve meetkunde, de ‘algebraïsche’ naar onze moderne analytische en algebraïsche meetkunde. De projectieve meetkunde begon als een zelfstandige wetenschap met Poncelets boek van 1822. Er waren prioriteitskibbelarijen, zoals zo vaak ontstaan als iets belangrijks

[p. 221]

wordt ontdekt: en hier was het Joseph Gergonne, professor in Montpellier, die als rivaal van Poncelet optrad. Gergonne publiceerde verscheidene belangrijke artikelen over onderwerpen uit de projectieve en analytische meetkunde, waarin hij o.a. gelijktijdig met Poncelet het begrip dualiteit ontwikkelde. Artikelen hierover verschenen in de Annales de mathématiques, het eerste tijdschrift dat geheel aan de wiskunde gewijd was en waarvan Gergonne redacteur was; het verscheen van 1810 tot 1831. Reeds in 1806 had Monges leerling Charles Julien Brianchon dit dualiteitsbeginsel toegepast op Pascals zeshoek, ingeschreven in een kegelsnede en op die manier de duale stelling over een omgeschreven zeshoek met zijn ‘punt van Brianchon’ verkregen. In 1836 werden de Annales voortgezet door Liouvilles Journal de mathématiques pures et appliquées, titel in navolging van die van Crelles Journal (dan van 1826 af was verschenen).

Voor Poncelets manier van denken is ook een ander beginsel karakteristiek, het beginsel der continuïteit. Dit beginsel, dat het hem mogelijk maakte uit de eigenschappen van de ene figuur die van een andere af te leiden, formuleerde hij als volgt:

Wanneer een figuur uit een andere figuur door een continue verandering kan worden voortgebracht, en even algemeen is als de eerste, dan kan een eigenschap die voor de eerste figuur bewezen is zonder meer naar de tweede worden overgebracht.

Dit was een beginsel dat wel met de grootste voorzichtigheid moest worden behandeld, want het liet aan nauwkeurige formulering veel te wensen over. Eerst met de hulpmiddelen van de moderne algebra heeft men het scherper kunnen omschrijven. Gehanteerd door Poncelet en zijn school leidde het tot belangwekkende, nieuwe en juiste resultaten, zelfs als het werd toegepast op veranderingen van het reële naar het imaginaire gebied. Zo werd Poncelet ertoe gebracht te verklaren dat alle cirkels in het vlak ‘twee imaginaire punten in het oneindige’ gemeen hadden, hetgeen ook de invoering betekende van de ‘lijn in het oneindige’ van het vlak. Hier, en op andere plaatsen, nam hij dus de gedachtengang weer op die Desargues in de zeventiende eeuw had geschetst, doch die niet meer verder was gevolgd. Wat de lijn in het oneindige betreft, G.H. Hardy heeft opgemerkt dat met dit begrip de projectieve meetkunde niet geaarzeld heeft het actueel oneindige te aanvaarden.¹ De analisten bleven in dit opzicht verdeeld.

1 G.H. Hardy, A Course of Pure Mathematics (Cambridge, 6e uitg. 1933), Appendix iv.

[p. 222]

Poncelets ideeën werden verder ontwikkeld door Duitse meet-kundigen. In 1826 verscheen de eerste publikatie van Steiner, in 1827 Der barycentrische Calcul van Möbius, in 1828 het eerste deel van Plückers Analytisch-geometrische Entwicklungen. In 1831 verscheen het tweede deel, in 1832 gevolgd door Steiners Systematische Entwicklung. Het laatste van deze Duitse pionierswerken op het gebied van deze meetkunde verscheen in 1847 met de axiomatische Geometrie der Lage van Von Staudt.

Wij vinden onder deze Duitse meetkundigen zowel vertegenwoordigers van de synthetische als de algebràïsche opvatting. De typische vertegenwoordiger van de synthetische (of ‘zuivere’) meetkundige school was Jakob Steiner, een Zwitserse boerenzoon, een ‘Hirtenknabe’, self-made, wiens geestdrift voor de meetkunde werd gewekt toen hij kennis maakte met de opvoedkundige ideeën van Pestalozzi. Hij besloot naar Heidelberg te gaan om te studeren en gaf later onderwijs in Berlijn, waar hij van 1834 tot aan zijn dood in 1863 een leerstoel aan de universiteit bezat. Steiner was een meetkundige door-en-door, hij verafschuwde het gebruik van algebra en analyse zozeer dat hij zelfs bezwaar had tegen figuren als hulp bij het zuiver meetkundig denken.¹ Dit, zo dacht hij, kon het best geschieden door geconcentreerd denken. Dit was zeker het geval met Steiner zelf, wiens denken onze meetkunde met een groot aantal mooie en soms ingewikkelde theorema's heeft verrijkt. Zo hebben wij aan hem de ontdekking van het zgn. Romeinse oppervlak (of oppervlak van Steiner) te danken, dat een tweevoudige oneindigheid van kegelsneden bevat. Hij publiceerde zijn stellingen vaak zonder bewijs, hetgeen zijn verzamelde werken tot een goudmijn heeft gemaakt voor meetkundigen op zoek naar vraagstukken die nog bewezen moeten worden.

Steiner bouwde de projectieve meetkunde streng systematisch op, van perspectiviteit tot projectiviteit en vandaar tot de kegelsneden. Daarnaast was hij ook in isoperimetrische vraagstukken geïnteresseerd, waarvan hij er een aantal op zijn eigen karakteristieke meetkundige manier oploste. Zijn bewijs van 1836, dat de cirkel van alle gesloten krommen met gegeven omtrek het grootste oppervlak heeft, werd geleverd door aan te tonen dat iedere figuur van dien aard die niet een cirkel is, kan worden veranderd in een andere figuur met dezelfde omtrek doch groter oppervlak. In zijn

1 Dit doet denken aan N.L.W.A. Gravelaar, wiskundeleraar in Deventer (1851-1913), van wie verteld werd dat hij geloofde dat men het best de meetkunde kon doceren in een donker vertrek.

[p. 223]

conclusie dat daarom de cirkel het maximum voorstelde, miste hij een schakel, namelijk het bewijs dat een maximum werkelijk bestaat. Dit heeft Dirichlet aan Steiner trachten duidelijk te maken, doch eerst Weierstrass heeft het strenge bewijs geleverd.¹

Steiner had nog een metriek nodig om de dubbelverhouding van vier punten op een rechte lijn of van vier lijnen door een punt in een vlak te definiëren. Dit was geen zuivere projectieve meetkunde. Deze tekortkoming werd door Christian von Staudt, vele jaren lang hoogleraar in Erlangen, verbeterd. In zijn Geometrie der Lage (1847) definieerde hij de Wurf Van vier punten op een rechte op zuiver projectieve wijze, en toonde dan aan dat deze Wurf met de dubbelverhouding geïdentificeerd kan worden. Hiervoor gebruikte hij de zgn. netconstructie van Möbius, die tot axiomatische beschouwingen leidt die in verband staan met de snede van Dedekind als men irrationale waarden van projectieve coördinaten wil invoeren. In 1857 liet Von Staudt zien hoe men op strenge wijze imaginaire elementen in de meetkunde kan invoeren als dubbelelementen van elliptische involuties.²

Op deze grondslagen, door Poncelet, Steiner en Von Staudt gelegd, werd in de volgende jaren een uitgebreide synthetische meetkunde opgebouwd, die dan in tekstboeken werd vastgelegd. Een der meest invloedrijke van deze boeken was de standaardtekst van K.T. Reye, de Geometrie der Lage (1868, 3e uitg. 1886-92). Er bestaan ook Nederlandse leerboeken.³

1 W. Blaschke, Kreis und Kugel (Leipzig 1916) 1-12.

2 H. Freudenthal, The Impact of Von Staudt's Foundations of Geometry, in For Dirk Struik (Reidel, 1974), 189-200.

3 Vele historische bijzonderheden over deze meetkundigen vindt men in H. de Vries, Historische Studiën, tussen 1923 en 1954 in het Nieuw Tijdschrift van Wiskunde en enige andere tijdschriften gepubliceerd. Zie N.T.v. Wisk (1953) 298-299. De meeste van deze studiën zijn ook in boekvorm uitgegeven (2 delen).

17.

Vertegenwoordigers van de algebraïsche richting in de meetkunde waren Möbius en Plücker in Duitsland, Chasles in Frankrijk en Cayley in Engeland. August Ferdinand Möbius, gedurende meer dan vijftig jaren waarnemer, later directeur van de sterrenwacht in Leipzig, was een veelzijdige geleerde. In zijn boek Der barycentrische Calcül (1827) was hij de eerste die homogene coördinaten invoerde. Wanneer in de hoekpunten van een vaste driehoek de massa's m₁, m₂, m₃ worden geplaatst, gaf Möbius aan het

[p. 224]

zwaartepunt (barycentrum) deze massa's de homogene coördinaten m₁ : m₂ : m₃. Deze coördinaten bleken dan zeer geschikt te zijn om niet alleen projectieve, doch ook affiene eigenschappen van het vlak af te leiden - het woord ‘affiniteit’ ontleende Möbius aan Euler. Zo werden homogene coördinaten in de loop der jaren het algemeen aanvaarde hulpmiddel voor de algebraïsche behandeling der projectieve meetkunde. Möbius, die evenals zijn tijdgenoot Von Staudt, een rustig en tamelijk geïsoleerd geleerdenleven leidde, kwam tot menige belangrijke ontdekking, zoals die van het nulsysteem in de leer der lijnencongruenties, die men in zijn boek over statica van 1837 vindt. De tegenwoordig zo bekende band van Möbius, een eerste voorbeeld van een eenzijdig (niet oriënteerbaar) oppervlak, herinnert ons aan het feit dat Möbius ook zijn aandeel heeft aan de grondlegging der topologie.

Julius Plücker, die jarenlang in Bonn doceerde, was niet alleen een meetkundige, doch ook een experimenteel fysicus. Hij deed een reeks ontdekkingen omtrent het magnetisme van kristallen, over elektriciteitsgeleiding in gassen (hij ontdekte de kathodestralen) en in de spectroscopie. In een aantal verhandelingen en boeken, speciaal de Neue Geometrie des Raumes (1868/'69) bouwde hij een analytische meetkunde op met behulp van vele nieuwe ideeën.

In het bijzonder demonstreerde Plücker de voordelen van een afgekorte notatie, waarin b.v. C₁ + λC₂ = 0 een bundel kegelsneden kan voorstellen die door de snijpunten van de kegelsneden C₁ = 0 en C₂ = 0 gaan. Zo leerde hij eigenschappen van de figuur uit de constructie van hun vergelijkingen af te lezen. In dit boek van 1868/'69 voerde Plücker homogene coördinaten als ‘projectieve’ coördinaten in met betrekking tot een fundamenteel viervlak en formuleerde ook het belangrijke beginsel dat de meetkunde niet noodzakelijk op het punt als primair element behoeft te worden opgebouwd, lijnen, vlakken, cirkels, bollen, enz. kunnen ook als zodanig in het vlak of in de ruimte en als de grondslag van bepaalde meetkunden worden ingevoerd. Deze vruchtbare gedachte wierp nieuw licht op de synthetische en op de algebraïsche meetkunde en schiep nieuwe vormen van dualiteit. De dimensie van een bepaalde meetkunde kon een willekeurig positief getal zijn, dat gelijk is aan het aantal parameters waarvan het primaire element afhangt. Plücker publiceerde ook een algemene theorie van algebraïsche krommen in het platte vlak, waarin hij de ‘relaties van Plücker’ tussen het aantal der verschillende singulariteiten afleidde (1834, 1839).

Michel Chasles, gedurende een lange tijd de leidende meetkun-

[p. 225]

dige in Frankrijk, was een leerling van de Ecole Polytechnique in de latere jaren van Monge. Hier werd hij in 1841 tot hoogleraar benoemd. In 1846 aanvaardde hij de speciaal voor hem ingestelde leerstoel in de hogere meetkunde aan de Sorbonne en gaf daar jarenlang onderwijs. Er is een zekere overeenkomst tussen het werk van Plücker en van Chasles, vooral in hun bedrevenheid om uit de vorm van de vergelijkingen een maximum aantal meetkundige stellingen te halen. Zo vindt men bij Chasles een handig manipuleren met isotrope lijnen (asymptoten van de cirkel) en oneindig verre cirkelpunten. Chasles nam van Poncelet het gebruik van zgn. ‘aftellende’ methoden over, en onder zijn behandeling ontwikkelden deze methoden zich tot een nieuw meetkundig gebied, de zgn. ‘aftellende’ meetkunde. Dit gebied werd later door Hermann Schubert in zijn Kalkül der abzählenden Geometrie (1879), gevolgd door H.G. Zeuthens Abzählende Methoden (1914), systematisch onderzocht. Beide boeken openbaren zowel de sterke als de zwakke punten van deze vorm van algebra in meetkundige taal. Haar aanvankelijk succes riep een tegenstroming in het leven, waaraan o.a. E. Study leiding gaf met zijn uitspraak: ‘Exactheid mag in de meetkunde niet eeuwig als iets bijkomstigs worden behandeld’.¹

Chasles had een grote belangstelling voor de geschiedenis van de wiskunde, en in het bijzonder van de meetkunde. Zijn gevoel voor het historische openbaart zich in zijn bekend Aperçu historique sur l'origine et le développement des méthodes en géométrie (1837), een der eerste belangrijke geschriften over de geschiedenis van de meetkunde. Dit nog zeer leesbare boek behandelt zowel de Griekse als de toen moderne meetkunde en is een goed voorbeeld van een geschiedenis der wiskunde geschreven door iemand die zelf een zelfstandig onderzoeker was. Deze liefde voor de geschiedenis maakte Chasles ook wel eens wat blind en zo is hij het slachtoffer geworden van een grappenmaker, die aan Chasles tussen 1861 en 1870 duizenden valse documenten verkocht, brieven van Galilei, Pascal en Newton tot brieven van Plato en zelfs van de apostelen toe.²

1 E. Study, Verhandl. des dritten Mathem. Kongresses, Heidelberg 1905, 388-395, zie ook B.L. van der Waerden, Dissertatie Leiden 1926.

2 J.A. Farrer, Literary forgeries (Londen, 1907) Chapter xii.

18.

Gedurende deze jaren, waarin in bijna koortsachtig tempo gehele nieuwe meetkundige gebieden werden ontsloten, bleef een an-

[p. 226]

der, nieuw en in haar consequenties nog veel meer revolutionair gebied verborgen in enkele obscure verhandelingen, die door de meeste leidende wiskundigen vrijwel geheel geïgnoreerd werden. De vraag, of het euklidische parallellenpostulaat een onafhankelijk axioma is of een stelling die uit andere, meer eenvoudig schijnende, axioma's kan worden afgeleid, had voor meer dan tweeduizend jaar de wiskundige wereld verontrust. Ptolemaios had in de Oudheid getracht, een antwoord te vinden, Omar Khayyam en Nasīr al-dīn in de Middeleeuwen, de Italiaan Girolamo Saccheri, de Zwitser Lambert en de Fransman Legendre in de achttiende eeuw.¹ Al deze geleerden hadden geprobeerd het axioma te bewijzen, wat niet gelukte, al vonden ze in de loop van hun onderzoek menig interessant resultaat. Gauss schijnt wel de eerste geweest te zijn, die aan de onafhankelijkheid van het parallellenaxioma geloofde en dus tot de conclusie kwam dat andere meetkunden, die op een ander axioma berusten, logisch mogelijk waren. Gauss maakte zijn gedachten over dit onderwerp niet publiek. De eersten die openlijk de autoriteiten van tweeduizend jaar wiskundig onderzoek durfden tegen te spreken en een niet-euklidische meetkunde construeerden² waren een Rus, Nikolai Iwanowitsch, Lobačevskiǐ en een Hongaar, Janos (Johan) Bolyai. Van hen heeft Lobačevskiǐ zijn ideeën het eerst gepubliceerd. Zijn eerste boek verscheen in 1829/'30, doch al reeds in 1826 had hij er over in Kazan, waar hij professor was, voordrachten gehouden. Het boek was in het Russisch geschreven, toen een taal die weinig mensen buiten het tsarenrijk lazen; doch ook van een latere uitgave in het Duits onder de naam Geometrische Untersuchungen zur Theorie der Parallellinien (1840) werd weinig notitie genomen, ofschoon Gauss belangstelling toonde. In de tussentijd had ook Bolyai zijn gedachten over dit onderwerp gepubliceerd.

1 F. Engel-P. Stäckel, Die Theorie der Parallellinien von Euklid bis auf Gauss (2 delen, Leipzig) 1895. Het is merkwaardig dat de Schotse wijsgeer Thomas Reid in 1764 een niet-euklidische meetkunde (van het elliptische type) ontwikkelde, waaraan verder niemand enige aandacht schonk, in: An inquiry into the human Mind. Reid, die tegenover Berkeley een realistische en ‘common sense’ filosofie vertegenwoordigde, polemiseerde tegen Berkeley's theorie van het gezichtsvermogen. Zie N. Daniels, Thomas Reid's Discovery of Non-Euclidean Geometry, Philosophy of Science 39 (1972) 219-234.

2 Behalve dan Thomas Reid, maar diens niet-euklidische meetkunde, die slechts enige bladzijden innam, was polemisch tegenover Berkeley maar niet tegenover Euklides.

[p. 227]

Janos (Johan) Bolyai was de zoon van een wiskundeleraar in een Hongaarse provinciestad. Deze leraar, Farkas (Wolfgang) Bolyai, had in Göttingen gestudeerd in dezelfde tijd als Gauss, en wisselde wel eens een brief met hem. Farkas besteedde veel tijd aan een poging het parallellenaxioma te bewijzen, doch kon tot geen bevredigende conclusie komen. Zijn zoon had deze hartstocht geërfd en begon ook naar een bewijs te zoeken, ondanks de waarschuwing van zijn vader:

Je moet dit evenzo verafschuwen als liederlijk verkeer; het kan je van al je vrije tijd, je gezondheid, je rust en je hele levensgeluk beroven. De pikdonkere duisternis van dit probleem kan wel duizend reuzen als Newton verslinden, het zal nooit licht op aarde geven (brief van 1820).

De zoon werd voor het leger opgeleid en verwierf zich een naam als een officier, handig met degen en viool. Maar hij begon ook in te zien dat het euklidische axioma werkelijk onafhankelijk van de andere axioma's was en ontdekte dat het mogelijk was een meetkunde op te stellen waarin door een gegeven punt in een vlak een oneindig aantal lijnen lopen die een gegeven lijn in dit vlak niet snijden. Dit was hetzelfde denkbeeld waarmee Gauss en Lobačevskiǐ hadden gespeeld. Bolyai schreef zijn ideeën op en had ze in 1832 gepubliceerd als een appendix bij een boek van zijn vader, dat de titel had: Appendix scientam spatii absolute veram exhibens.¹ De vader was ongerust over de onorthodoxe opinies van zijn zoon en schreef aan Gauss om raad. Toen het antwoord uit Göttingen binnenkwam, bevatte het een warme waardering voor het werk van de jongere Bolyai. Gauss voegde eraan toe, dat hij Bolyai niet kon prijzen daar dit zou betekenen dat hij zichzelf zou prijzen, aangezien de gedachten van de Appendix hem reeds jaren bekend waren geweest.

De jonge Janos was van deze lofbrief, die hem verhief tot een positie van een groot man van wetenschap, en tegelijk hem van zijn prioriteit beroofde, ten zeerste ontdaan. Zijn teleurstelling verdiepte zich, toen bleek dat men zich van zijn theorie maar heel weinig aantrok. Hij werd nog meer ontmoedigd toen hij Lobačevskiǐ's boek in de Duitse vertaling van 1840 te zien kreeg. Hij heeft geen wiskunde meer gepubliceerd.

De theorieën van Bolyai en van Lobačevskiǐ waren in beginsel gelijk, doch verschilden zeer in de wijze waarop zij werden uitge-

1 H.J.E. Beth, Inleiding tot de Niet-Euclidische Meetkunde op historischen grondslag (Groningen, 1929), ook E.J. Dijksterhuis, De Elementen van Euclides i (Groningen 1929) Hoofdstuk ii.

[p. 228]

werkt. Het blijft intussen interessant te zien hoe de nieuwe ideeën onafhankelijk van elkaar in Göttingen, Budapest en Kazan ontstonden, en dat ongeveer tegelijkertijd, na een periode van relatieve stilstand die tweeduizend jaar heeft geduurd. Ook is het interessant dat ze gedeeltelijk buiten de grenzen van de scheppende wiskundige wereld van die dagen hun oorsprong vonden. Het komt wel meer voor dat grote en nieuwe ideeën buiten en niet binnen de scholen worden geboren. Toch was er verband tussen die ontdekkers: Gauss was als student een vriend van de oudere Bolyai, en Lobačevskiǐ's leraar in Kazan was J.M. Bartels, een van de leraren van Gauss. En we moeten ook niet vergeten dat het probleem van het parallellenaxioma in Göttingen om zo te zeggen ‘in de lucht hing’, want professor A.G. Kästner, van 1756 tot zijn dood in 1800 professor in Göttingen, besteedde veel tijd en moeite aan dit postulaat.¹

Niet-euklidische meetkunde - de naam is van Gauss - bleef jarenlang een vrijwel onbekend gebied van wetenschap. De meeste wiskundigen trokken er zich niets van aan, en zij die onder de invloed van Kants filosofie stonden, weigerden haar in beginsel ernstig te nemen.² De eerste wiskundige van de eerste rang, die haar belang volledig begreep, was Riemann, in wiens algemene theorie van uitgebreidheden (1854) niet alleen de bestaande niet-euklidische meetkunde haar juiste plaats verwierf, maar ook ruimte overliet voor vele andere vormen van meetkunde, die men nu als meetkunde van Riemann samenvat. Volledige erkenning van deze meetkunden kwam eerst toen, na 1870, een jongere generatie Riemanns ideeën begon te begrijpen en uit te werken.

Er bestond nog een andere generalisatie van de klassieke meetkunde die ontstaan was in de jaren voor Riemann, doch eerst na zijn dood werd gewaardeerd. Dit was de meetkunde van meer dan drie dimensies. Ze kwam volledig uitgerust ter wereld in de Ausdehnungslehre (‘leer der uitbreiding’) van Hermann Grassmann, die in 1844 gepubliceerd werd. Grassmann was een leraar aan het gymnasium in Stettin en een man van buitengewone veelzijdigheid; hij schreef met grote scherpzinnigheid over de meest verschillende onderwerpen zoals elektrische stromen, kleuren, geluidsleer, linguïstiek, plantkunde en folklore. Zijn Sanskriets woordenboek over de Rigveda (1873-75) wordt nog gebruikt. De Ausdehnungslehre, waarvan een herziene en beter leesbare editie

1 Zie hierover o.m. G. Goe's artikel over Kästner in DSB vii (1973) 206.

2 En dat ofschoon Kant het werk van Reid kende.

[p. 229]

in 1862 uitkwam, was in strikt euklidische vorm geschreven; stelling na stelling werd afgeleid in logische volgorde. Hier vinden wij een meetkunde in een ruimte van n dimensies, eerst affien, later metrisch. Hierbij gebruikte Grassmann een invariante notatie, waarin wij nu vectoren en tensoren herkennen (zijn Lückenprodukte zijn tensoren), maar die voor zijn tijdgenoten vrijwel onleesbaar was. Een latere generatie nam gedeelten van Grassmanns breed opgezette theorie over, om een vectoranalyse voor affiene en metrische ruimten op te bouwen. Grassmann zelf gebruikte zijn theorie o.a. om het zgn. probleem van Pfaff aan te pakken, een probleem dat inzicht geeft in de structuur van lineaire differentiaalvormen.

Ofschoon de Engelse wiskundige Cayley in 1843 eveneens dit begrip van meerdimensionale ruimte invoerde, en dit in een veel minder afschrikwekkende vorm, bleef de meetkunde van deze ruimten een onderwerp dat met wantrouwen en ongeloof werd aangezien. Hier was het weer Riemanns verhandeling van 1854 die een beter begrijpen mogelijk maakte. Daar kwam bij dat Plücker, door erop te wijzen, dat men een meetkunde niet alleen op punten, maar ook op andere figuren als primaire elementen kan opbouwen, een nieuwe en gemakkelijk te aanvaarden interpretatie van meerdimensionale ruimten mogelijk maakte. Zo kon de meetkunde van rechte lijnen in de gewone ruimte van Euklides beschouwd worden als een vierdimensionale ruimte, omdat zulk een lijn van vier parameters afhangt. Felix Klein wees later op het voordeel verkregen door diezelfde meetkunde te interpreteren door de punten van een tweedegraadsoppervlak in een vijfdimensionale ruimte. Zulke ‘afbeeldingen’ van de ene meetkunde op een andere werden steeds meer onderzocht. Daarbij werd de overeenstemming in de begrippen van dimensie en vrijheidsgraad, reeds sinds Lagrange uit de mechanica bekend, meer en meer als bijna vanzelfsprekend erkend. Toch ging men eerst laat in de negentiende eeuw de meetkunde in ruimten van meer dan drie dimensies waarderen, voornamelijk om zijn nut in de interpretatie van algebraïsche vormen en van differentiaalvormen in meer dan drie veranderlijken. De Groninger hoogleraar P.H. Schoute (1846-1912) heeft de vierdimensionale meetkunde ook op ‘Euklidisch-Cartesiaanse’ wijze beoefend, waarbij hij speciale aandacht wijdde aan de regelmatige lichamen (de zgn. polytopen).¹

1 Zie hoofdstuk IX, sectie 8.

[p. 230]

19.

De namen Hamilton en Cayley getuigen van het feit dat rond 1840 en later Engels schrijvende wiskundigen ernstig met hun continentale collega's begonnen te concurreren. Tot diep in de negentiende eeuw werd, onder de invloed van de koloniale en Napoleontische oorlogen, door de meeste academici, en vooral de dons van Cambridge en Oxford, elke poging om continentale wiskunde te beoefenen beschouwd als een vergrijp tegen de door fluxies geheiligde naam van Sir Isaac Newton. Reeds Euler, in zijn Integraalrekening (1768) bezag de mogelijkheid van een compromis tussen beide richtingen met een zwaar hoofd. Het dilemma werd in 1812 door een aantal jonge wiskundigen in Cambridge doorbroken toen ze, in overleg met de oudere Robert Woodhouse, een ‘analytische club’ oprichtten om de differentiaalmethodes van de school van Leibniz te verbreiden. Leiders waren George Peacock, Charles Babbage en John Herschel. Zij trachtten, om met Babbage te spreken, ‘the principles of pure d-ism, as opposed to the dot-age of the university’¹ te propageren. Deze poging werd in het begin van de zijde van de oudere academici nogal bekritiseerd, maar deze kritiek werd beantwoord door acties als de publikatie van een Engelse vertaling van de Traité élémentaire du calcul differentiel et intégral van Lacroix, de Franse leerboekschrijver (1816). Zo werd de jongere generatie in het Verenigd Koninkrijk van een voor die tijd modern leerboek voorzien.

De eerste belangrijke bijdrage kwam echter niet van de groep in Cambridge, doch van enige wiskundigen die onafhankelijk van hen de continentale wiskunde hadden verwerkt. Wij denken hierbij allereerst aan Hamilton en Green. Zowel voor hen als voor hun tijdgenoot Nathaniel Bowditch in Boston (VS) was het boek dat zij speciaal bestudeerden de Mécanique céleste van Laplace, waarin het ‘d-isme’ de grootste triomfen had geboekt. George Green, een ‘self-made’ molenaarszoon uit Nottingham, was vooral in de nieuwe ontdekkingen op het gebied der elektriciteit geïnteresseerd. Dit was de tijd van de grote ontdekkingen van Oersted en Ampère, de tijd van het ontdekken van het elektromagnetisme. In die dagen (ca. 1825) bestond er haast geen wiskundige theorie om de elektrische verschijnselen te verklaren; Poisson had in 1812 slechts een begin gemaakt. Green las Laplace en - om zijn eigen woorden te gebruiken:

1 Woordenspel op de d-notatie van Leibniz en de punt (dot)notatie van Newton; dx/dt tegenover ẋ. Het woord ‘d-ism’ betekent zowel d-isme als Deisme, ‘dot-age’ zowel de periode van de dot als ‘seniliteit’. Vertaling: ‘de beginselen van het “deisme” tegen de “seniliteit” van de universiteit’.

[p. 231]

‘Gezien hoe wenselijk het was dat een universeel werkende macht als de elektriciteit zo ver mogelijk aan berekening zou worden onderworpen, en nadenkende over de voordelen die voortspruiten uit de oplossing van moeilijke problemen, zo men ervan wordt bevrijd iedere kracht die op de verscheidene lichamen in een willekeurig systeem werkt op zichzelf te onderzoeken en de aandacht alleen vestigt op diè bijzondere functie, van welke differentialen al deze krachten afhangen - zo werd ik ertoe geleid te proberen of het mogelijk zou zijn enige algemene betrekkingen te ontdekken tussen deze functie en de hoeveelheden elektriciteit in de lichamen die haar voortbrengen’.

Het resultaat van deze overwegingen was Greens Essay on the Application of Mathematical Analysis to Theories of Electricity and Magnetism (1828), de eerste poging om tot een wiskundige theorie van het elektromagnetisme te komen. Hiermee begon in Engeland de mathematische fysica, en tevens, naast Gauss' verhandeling van 1839, de potentiaaltheorie als een speciaal wiskundig gebied. Gauss wist, naar het schijnt, niets af van Greens werk, dat eerst beter bekend werd toen William Thomson (de latere Lord Kelvin) het in Crelles Journal van 1846 opnieuw publiceerde. Toch was de gedachtengang van Gauss en van Green zo verwant dat Green de term ‘potential function’ en Gauss met zijn ‘Potential’ bijna een zelfde term invoerden om een oplossing van de vergelijking van Laplace aan te geven. Twee verwante identiteiten, die lijn- en oppervlakte- en ruimte-integralen verbinden, worden de formules van Green en van Gauss genoemd. Het gebruik van ‘functies van Green’ in de oplossing van partiële differentiaalvergelijkingen is een herinnering aan de molenaarszoon die in zijn vrije tijd Laplace bestudeerde.

Green kon later zijn werk voortzetten aan Caius College, Cambridge, waar hij echter eerst in 1833, op veertigjarige leeftijd, kwam. Doch dit is niet de plaats om de verdere ontwikkeling der mathematische fysica in Engeland - of in welk ander land dan ook - te schetsen. Met deze ontwikkeling zijn de namen van Stokes, Rayleigh, Kelvin, Maxwell, Kirchhoff, Helmholtz, Gibbs, Boltzmann en van vele anderen verbonden. Deze fysici droegen zozeer bij tot de oplossing van vele, gewoonlijk lineaire, partiële differentiaalvergelijkingen, dat het soms scheen dat de mathematische fysica en de leer van zulke differentiaalvergelijkingen identiek waren. De mathematische fysica verrijkte de wiskunde evenwel ook in andere opzichten, zoals in haar bijdragen tot de waarschijnlijkheidsrekening en de theorie der complexe functies. Ook de meetkunde profiteerde van haar onderzoekingen. Wij vermel-

[p. 232]

den slechts James Clerk Maxwells Treatise on Electricity and Magnetism (2 delen, 1873) met haar systematische ontwikkeling van de elektromagnetische theorie gebaseerd op Faraday's experimenten. Ze bevat o.a. een mooie theorie der bolfuncties. Deze theorie van Maxwell werd op den duur algemeen aanvaard en leidde later tot de theorie van H.A. Lorentz over het elektron en tot de relativiteitstheorie van Albert Einstein en tot de vectoranalyse in de wiskunde.

20.

De zuivere wiskunde was in Engeland gedurende de negentiende eeuw voornamelijk algebra met toepassingen op de meetkunde. Wij denken hier in de eerste plaats aan Cayley, Sylvester en Salmon. Arthur Cayley begon als advocaat, doch aanvaardde in 1863 het nieuwe ‘Sadlerian professorship’ in de wiskunde aan de universiteit van Cambridge, waar hij dertig jaar lang doceerde. Toen hij in de jaren veertig in Londen nog advocaat was, ontmoette hij Sylvester, die toen actuaris was, en van die jaren dateert de gemeenschappelijke belangstelling van Cayley en Sylvester voor algebraïsche vormen - of ‘quantics’ zoals Cayley ze noemde. Uit de samenwerking van deze twee mannen ontwikkelde zich de algebraïsche invariantentheorie.

Deze theorie hing al verscheidene jaren in de lucht, in het bijzonder nadat men begonnen was de determinantentheorie verder te bestuderen. In hun eerste periode gingen Cayley en Sylvester reeds verder dan de leer der determinanten, zij trachtten stelselmatig een invariantentheorie van kwadratische en hogere algebraische vormen op te bouwen, een theorie met eigen notatie en compositieregels. Deze theorie werd later door Aronhold en Clebsch in Duitsland verder ontwikkeld en vormde het algebraïsche complement van Poncelets projectieve meetkunde. Cayley schreef vele verhandelingen, over eindige groepen, -algebraïsche krommen, determinanten, matrices en analytische meetkunde. Zijn negen verhandelingen over ‘quantics’ zijn vooral bekend gebleven door de Sixth Memoir on Quantics (1859), omdat in deze verhandeling werd aangetoond hoe men ten opzichte van een kegelsnede een projectieve metriek kan definiëren. Dit leidde tot een projectieve definitie van een euklidische metriek, waardoor het aan Cayley gelukte deze meetkunde een plaats aan te wijzen binnen de projectieve meetkunde - daarbij het historische proces omkerende, omdat de projectieve meetkunde uit de euklidische was afgeleid en eerst door Von Staudt een eigen plaats had gekregen. Cayley miste echter de betrekking tussen zijn projectieve metriek en de niet-eukli-

[p. 233]

dische meetkunden; deze werd een tiental jaren later door Felix Klein ontdekt.

James Joseph Sylvester was niet alleen een wiskundige, maar ook op zijn manier een dichter en in het algemeen een geestige kerel met zoveel fantasie dat zijn repertoire van nieuwe wiskundige termen met die van Leibniz wedijvert. Van 1855 tot 1869 doceerde hij aan de Militaire Academie in Woolwich. Hij was tweemaal in de Verenigde Staten, de eerste keer als professor aan de door Thomas Jefferson gestichte Universiteit van Virginia (1841-'42), de tweede keer als professor aan Johns Hopkins University in Baltimore (1877-'83). Gedurende deze tweede periode was hij een der eersten die aan een Amerikaanse school de moderne wiskunde doceerde; zijn invloed is blijvend geweest.

Twee van Sylvesters vele bijdragen tot de algebra zijn klassiek: zijn theorie der elementaire delers (1851, herontdekt door Weierstrass in 1868) en zijn traagheidswet der kwadratische vormen (1852, reeds bekend aan Jacobi en Riemann, doch toen niet gepubliceerd). Van de vele termen die Sylvester heeft ingevoerd zijn verscheidene blijvend bezit van de wiskundigen gebleven, wij denken b.v. aan de woorden invariant, covariant, contravariant, cogrediënt en syzygie. Er plachten over Sylvester nogal wat anekdoten de ronde te doen - gewoonlijk van de verstrooide-professorsoort.

De derde Engelse meetkundige en algebraïcus was George Salmon, die zijn lang leven doorbracht aan Hamiltons Alma Mater, Trinity College in Dublin, waar hij zowel wiskunde als godgeleerdheid doceerde. Zijn hoofdverdienste ligt in zijn nu nog wel bekende leerboeken, die uitmunten in helderheid en charme. Deze boeken hebben, ook door vertalingen, hele generaties in de geheimen van de analytische meetkunde en de invariantentheorie ingewijd. Zij zijn de Conic Sections (1848), Higher Plane Curves (1852), Modern Higher Algebra (1859) en Analytic Geometry of Three Dimensions (1862). Al deze boeken kunnen ook nu nog wel aan studenten in de analytische meetkunde worden aanbevolen, al doen ze misschien een beetje ouderwets aan.

21.

Twee onderwerpen, door Engelse wiskundigen in de algebra ingevoerd, verdienen onze speciale aandacht: Hamiltons quaternionen en Cliffords biquaternionen. Nadat Hamilton, de Astronomer Royal van Ierland, zijn werk over mechanica en optica had voltooid, keerde hij zich in 1835 tot de algebra. Zijn Theory of Algebraic Couples definieerde de algebra als de zuivere wetenschap

[p. 234]

van de tijd en bracht een strenge theorie van het complexe getal als een getallenpaar. Dit deed hij waarschijnlijk zonder van Gauss' theorie van bikwadraatresten te weten, waarin ook de complexe getallen streng waren ingevoerd, maar nu door punten in het complexe vak. Beide methoden worden nu algemeen aanvaard. Hamilton trachtte daarna in de algebra van drietallen en viertallen van getallen binnen te dringen. Zijn bewonderaars vertellen ons, dat hij een ingeving kreeg, toen hij op een zekere oktoberdag van 1843 langs een brug bij Dublin wandelde en het quaternion ontdekte.¹ Zijn onderzoekingen over quaternionen zijn in twee dikke boeken gepubliceerd, de Lectures on quaternions van 1853 en de Elements of Quaternions, in 1866 na zijn dood verschenen. Het best bekende gedeelte van de quaternionenleer is de vectortheorie die ook in de Ausdehnungslehre van Grassmann is besloten (de term ‘vector’ is van Hamilton). Het is vooral om deze reden, dat de algebraïsche werken van beide mannen nu vaak worden geciteerd. In de dagen van Hamilton echter, en lang daarna, waren de quaternionen zelf het onderwerp van overdreven bewondering. Sommige Engels-Schotse wiskundigen zagen er - om met Leibniz te spreken - een soort Arithmetica universalis in, en die opvatting kweekte weer een reactie, die o.a. in het dispuut tussen P.G. Tait en Oliver Heaviside aan het licht kwam. De theorie der hypercomplexe getallen, door Benjamin Peirce, Georg Frobenius, Eduard Study en anderen ontwikkeld, plaatste inmiddels de quaternionen op hun natuurlijke plaats als het eenvoudigste associatieve getallenstelsel van meer dan twee eenheden. De cultus van de quaternionen leidde in zijn bloeitijd zelfs tot een International Association for the Promoting of the Study of Quaternions and Allied Systems of Mathematics, dat verdween als slachtoffer van de Eerste Wereldoorlog. De gemoederen werden ook bewogen door de strijd tussen Hamiltonianen en Grassmannianen toen in de jaren tachtig jaren door het werk van Oliver Heaviside in Engeland en Josiah Willard Gibbs in Amerika, de vectoranalyse zich als een eigen wiskundig gebied be-

1 Deze brug heet nu Hamilton Bridge en draagt de inscriptie: ‘Here as he walked by on the 16th of October 1843 Sir William Rowan Hamilton in a flash of genius discovered the fundamental formula for quaternion multiplication i² = j² = k² = ijk = - 1 and cut it on a stone of the bridge’. (Toen op 16 Oktober 1843 Sir William Rowan Hamilton hier voorbij wandelde ontdekte hij door een geniale ingeving de grondformule voor de vermenigvuldiging van quaternionen i² = j² = k² = ijk = - 1 en kerfde die in een steen van de brug).

[p. 235]

gon te ontpoppen. De twist, die vooral tussen 1890 en de Eerste Wereldoorlog woedde, verliep, toen betere kennis van de groepentheorie en de lineaire algebra het mogelijk maakte aan elke methode haar eigen operatieterrein toe te wijzen.¹ Het gebrek aan internationale eenheid in de vectornotatie is als een soort litteken uit deze verwarring overgebleven.

William Kingdon Clifford, die in 1879 op drieëndertigjarige leeftijd overleed, was verbonden aan Trinity College in Cambridge en aan University College in Londen. Hij behoorde tot de eersten in Engeland die Riemann begrepen en met hem zijn kritische belangstelling in onze ruimteopvattingen deelden. Daarbij ontwikkelde Clifford een meetkunde van de beweging, en daarbij kwam hij tot zijn biquaternionen als generalisatie van de quaternionen (1873-'76). Deze biquaternionen zijn quaternionen, waarvan de coëfficiënten complexe getallen zijn van de vorm a + be, waarbij e² + 1, - 1 of 0 mag zijn, die voor e² = 0 voor de studie van euklidische, voor e² = ± 1 voor die van niet-euklidische bewegingen kunnen worden gebruikt. Cliffords Common Sense in the Exact sciences blijft nog steeds het lezen waard; men kan hierbij Cliffords gedachtenwereld met die van Felix Klein vergelijken. Dit komt ook uit in de benaming ‘ruimten van Clifford-Klein’ voor zekere gesloten euklidische uitgebreidheden in niet-euklidische ruimten. Zo Clifford langer had geleefd, hadden de ideeën van Riemann de Engelse wiskunde een generatie eerder kunnen bereiken dan het geval is geweest.

Tientallen jaren lang bleef de nadruk op de formele algebra karakteristiek voor de zuivere wiskunde in de Engelssprekende landen. Wij denken hierbij o.a. aan Benjamin Peirce, professor aan Harvard College in Massachusetts, een leerling van Nathaniel Bowditch, die Laplace had vertaald en met wie (en met Peirce) de scheppende wiskunde in de Verenigde Staten begint. Peirce, die ook verdienstelijk werk in de hemelmechanica heeft verricht, publiceerde in 1870 zijn Lineair Associative Algebra, dat een der eerste onderzoekingen was over hypercomplexe getallenstelsels. Deze formalistische trek in de Engelse wiskunde van die tijd komt ook

1 F. Klein, Vorlesungen über die Entwicklung der Mathematik im 19. Jahrhundert ii (Berlin, 1927) 27-52; J.A. Schouten, Grundlagen der Vektor- und Affinoranalysis (Leipzig, 1914), en de vele bijdragen van E. Cartan. Voor de geschiedenis van de vectoranalyse met het gekibbel tussen Tait en Heaviside zie M.J. Crowe, A History of Vector Analysis (Notre Dame Press 1967, Dover herdruk 1985).

[p. 236]

tot uitdrukking in het werk van George Peacock, die in 1830 het zgn. principe van de permanentie van equivalente vormen formuleerde (later scherper geformuleerd door Hermann Hankel in Leipzig¹), en van Augustus De Morgan, van 1828 tot 1866 professor in Londen. Zijn pogingen in de jaren '40, om tot een symbolische logica te komen leidde tot het fundamentele onderzoek van George Boole, van Queens College, Cork (Ierland). In zijn hoofdwerk The Laws of Thought (1854) toonde hij aan hoe de wetten van de formele logica, zoals die het eerst door Aristoteles waren opgesteld en later in eeuwenlange lessen en onderzoekingen aan de universiteiten verder zijn bestudeerd, aan een mathematische rekenwijze kunnen worden onderworpen. Boole schiep een symbolische taal voor een brede ontleding van logische processen. Met deze rekenwijze, verwant aan Leibniz' characteristica generalis, begon de herleiding van logica tot wiskunde en daarbij de vernieuwing van de axiomatiek. Hier was daarna het werk van Gottlob Frege, die professor in Jena was, van grote invloed. In zijn boek Die Grundlagen der Arithmetik (1884) gaf hij een logische afleiding van de grondbeginselen der rekenkunde. Deze onderzoekingen die tot verschillende richtingen in de vraag naar de verhouding van wiskunde en logica voerden, bereikten in de twintigste eeuw een voorlopig hoogtepunt in de driedelige Principia Mathematica van Bertrand Russell en A.N. Whitehead (1910-'13); zij hebben ook het werk van Hilbert over de grondslagen van de rekenkunde en het overwinnen van de paradoxen van het oneindige ten sterkste beïnvloed. In deze debatten kwam ook de oude strijdvraag omtrent de rol van het actueel oneindige, die met de namen Cantor en Kronecker is verbonden, in een nieuw licht te staan.²

1 H. Hankel, Theorie der complexen Zahlensysteme (Leipzig, 1867) gaf een nog steeds leesbare uiteenzetting van het werk van Grassmann zowel als van Hamilton. Zowel Hankel als De Morgan waren ook in de geschiedenis der wiskunde geïnteresseerd.

2 D. Hilbert-W. Ackermann, Grundzüge der theoretischen Logik, 4e Aufl. (Berlin 1959); M. Black, The Nature of Mathematics (New York-London 1934). Zie ook, behalve de eerder geciteerde geschiedenissen van E.W. Beth, en I.M. Bochenski, Formale Logik (Freiburg-München 1956). Bochenski (blz. 314) onderscheidt in de geschiedenis der formele logica vier perioden: 1) de voorgeschiedenis van Leibniz tot Boole, 2) de periode van Boole, tot aan de Operationskreis des Logikkalküls (1877) en de Vorlesungen über die Algebra der Logik (1890) van Ernst Schröder, 3) de periode van Frege, van Freges Begriffschrift van 1877 tot de Principia Mathematica (1910-'13) en 4) de jongste periode, na de Principia, waarin het werk van Hilbert en vele anderen valt.

[p. 237]

22.

Het werk van Cayley en Sylvester over de invariantentheorie vond in Duitsland grote belangstelling. Hier, onder leiding van Hesse, Aronhold, Clebsch en Gordon, werd deze theorie verder ontwikkeld met behulp van een speciale en handige notatie. Otto Hesse, die eerst in Koningsbergen en later in Heidelberg en München professor was, bewees evenals Plücker hoeveel nut men in de analytische meetkunde kan trekken van een verkorte wijze van schrijven; daarbij gebruikte hij graag homogene coördinaten en determinanten. Siegfried Heinrich Aronhold, die aan de Technische Hogeschool in Berlijn doceerde, publiceerde in 1858 een verhandeling, waarin hij met behulp van ‘ideale’ factoren (die met die van Kummer niets te maken hadden) zijn eigen symboliek voor de invariantentheorie ontwikkelde; en daar ongeveer terzelfder tijd Clebsch zulk een schrijfwijze ontwikkelde (1861), spreekt men vaak van de ‘symboliek van Clebsch en Aronhold’, die algemeen werd aanvaard voor het systematisch onderzoek van de invarianten en covarianten van algebraïsche vormen. Tegenwoordig zien wij in deze rekenwijze, evenals in de vectoren van Hamilton, de uitwendige produkten van Grassmann en de dyaden van Gibbs, bijzondere vormen van de tensoralgebra. Deze invariantentheorie werd later nog door Paul Gordan, professor in Erlangen, verrijkt met het bewijs dat tot iedere binaire vorm een eindig stelsel van rationale invarianten en covarianten behoort, en dat hierin alle andere rationale invarianten en covarianten op rationale manier kunnen worden uitgedrukt (1868-69). Deze zgn. eindigheidstelling van Gordan werd in 1890 door Hilbert op algebraïsche vormen in n veranderlijken uitgebreid.

Alfred Clebsch was hoogleraar in Karlsruhe, Giessen en Göttingen en stierf in 1872, nog geen veertig jaar oud. In zijn korte leven heeft hij heel wat mooie resultaten kunnen boeken. Hij publiceerde een werk over de elasticiteitsleer (1862), waarin hij van de ideeën van Lamé en De Saint Venant in Frankrijk uitging, en hij paste zijn invariantenleer toe op de projectieve meetkunde. Hij was ook een der eersten die Riemanns theorieën begreep en legde de grondslagen voor die tak der algebraïsche meetkunde waarin Riemanns functietheorie en zijn theorie van meervoudig samenhangende oppervlakken op reële algebraïsche krommen werden toegepast. Men vindt een breed opgezette schets van deze ideeën in de Theorie der Abelschen Funktionen van Clebsch en Gordan (1866). Clebsch was eveneens de stichter der Mathematische Annalen, dat meer dan een halve eeuw lang het leidende wiskundige tijdschrift was, en nog steeds van belang is. Zijn voordrachten

[p. 238]

over meetkunde, door F. Lindemann uitgegeven (‘Clebsch-Lindemann’) gaven een solide inleiding in de algebraïsche behandeling der projectieve meetkunde.

23.

Tegen 1870 was de wiskunde uitgegroeid tot een enorm en vrijwel onoverzichtelijk wetenschappelijk gebied, dat verdeeld was in een aantal gebieden waarin alleen specialisten de weg wisten. Zelfs grote wiskundigen als Hermite, Weierstrass, Cayley en Beltrami beheersten slechts enkele van deze vele deelgebieden. Deze specialisatie is steeds toegenomen en heeft tegenwoordig alarmerende proporties aangenomen. Maar ze heeft ook steeds tot een reactie geleid, en een aantal van de belangrijkste en mooiste resultaten van de wiskunde der laatste honderd jaren zijn juist het gevolg geweest van pogingen om tot een synthese van de verschillende wiskundegebieden te geraken.

In het eind van de achttiende en het begin van de negentiende eeuw stelden de grote boeken van Lagrange en Laplace zulk een synthese voor, en zij vormden weer het uitgangspunt voor verder werk van grote diepte. Tot de beginselen die in de negentiende eeuw tot eenheid van opvatting leidden, behoren de groepentheorie en Riemanns begrip functie en ruimte. Hun betekenis kan het best begrepen worden in het werk van Klein, Lie en Poincaré.

Felix Klein was Plückers assistent in Bonn gedurende de jaren '60 en hier leerde hij diens meetkunde. In 1870 bracht hij een bezoek aan Parijs, waar hij Sophus Lie, een Noor, ontmoette. Klein was toen tweeëntwintig, Lie zes jaar ouder en nog slechts kort in de wiskunde geïnteresseerd. Wij hebben reeds vermeld hoe in Parijs vooral Camille Jordan, van de Ecole Polytechnique, een grote indruk op hen maakte. Jordan had juist in 1870 zijn Traité des substitutions geschreven, waarin hij een uiteenzetting gaf van Galois' leer der substitutiegroepen. Klein en Lie begonnen de centrale positie te begrijpen die door de groepentheorie wordt ingenomen. Zij verdeelden het grote rijk der wiskunde min of meer in twee delen: Klein gaf gewoonlijk zijn aandacht aan discontinue, Lie aan continue groepen.

In 1872 kreeg Klein een leerstoel te Erlangen. In een artikel van dat jaar schetste hij, hoe het groepenbegrip dienstbaar kon worden gemaakt aan de classificatie van de verschillende wiskundige gebieden, vooral de meetkunde. Het artikel, dat bekend is geworden als het ‘Erlanger program’, verklaarde elke meetkunde als een theorie van de invarianten van een speciale transformatiegroep. Door de groep uit te breiden of te beperken kunnen wij van de ene

[p. 239]

meetkunde overgaan in de andere. De euklidische meetkunde is de leer van de invarianten van de groep der translaties, rotaties en spiegelingen, projectieve meetkunde die der projectieve groep. De classificatie van transformatiegroepen geeft ons de classificatie der meetkunden, de theorie der algebraïsche en differentiaal invarianten van iedere groep geeft ons de algebraïsche en analytische structuur van de bijbehorende meetkunde. Cayley's projectieve definitie van een metriek laat ons toe de metrische meetkunde als een vorm van projectieve meetkunde te zien. Zelfs de toen nog tamelijk onbekende topologie vond haar speciale plaats als de theorie van de invarianten van de groep der continue punttransformaties.

In het voorafgaande jaar had Klein een belangrijk voorbeeld gegeven van deze beschouwingswijze, door aan te tonen hoe de niet-euklidische meetkunde ook kan worden opgevat als projectieve meetkunde met een metriek van Cayley. De ontdekking van deze afbeelding bracht tenslotte nog steeds verwaarloosde theorieën van Bolyai en Lobačevskiǐ in het volle daglicht. Vele wiskundigen hadden nog steeds geloofd, dat ergens in die niet-euklidische meetkunde wel een logische fout zou zitten. Nu bleek dat zulke logische fouten, als ze bestonden, ook in de projectieve meetkunde moesten voorkomen, en dus ook in de euklidische, en dat was een ketterij die de meeste, zo niet alle, wiskundigen toch te ver ging. De niet-euklidische meetkunde van Bolyai en Lobačevskiǐ werd nu algemeen geaccepteerd als een hyperbolische meetkunde, terwijl een andere vorm van deze meetkunde, door Riemann alreeds aangegeven, als elliptische werd aangeduid. In deze meetkunde bestaan in het vlak alleen maar lijnen die elkaar snijden. Wij hebben reeds vermeld dat deze methode van Klein, waarbij een gebied van de wiskunde op een ander wordt afgebeeld, zeer vruchtbaar bleek te zijn, ze is o.a. door Hilbert in zijn axiomatiek van de meetkunde veel gebruikt.¹

De groepentheorie maakte een synthese mogelijk van vele ontdekkingen van Monge, Poncelet, Gauss, Cayley, Clebsch, Grassmann en Riemann. Riemanns ruimteleer, waaraan het Erlanger program menig idee ontleende, inspireerde niet alleen Klein doch ook Helmholtz en Lie. Hermann Helmholtz, bekend als fysicus en fysioloog, onderzocht in 1868 en 1884 Riemanns ruimtebegrip, gedeeltelijk omdat hij zocht naar een meetkundig beeld voor zijn

1 Zie o.a. H.J.E. Beth, Inleiding tot de niet-euklidische meetkunde op historischen grondslag (Groningen, 1932).

[p. 240]

kleurentheorie, en gedeeltelijk omdat hij de oorsprong van onze visuele ruimteopvatting zocht. Dit bracht hem tot een studie van het wezen van onze meetkundige axioma's en in het bijzonder van dat van Riemanns kwadratische metriek. Lie verscherpte Helmholtz' analyse omtrent het karakter van de kwadratische metriek door de transformatiegroepen te onderzoeken die daaraan ten grondslag liggen (1890). Dit ruimteprobleem van Lie en Helmholtz heeft de aandacht blijven trekken, niet alleen omdat het van belang bleek te zijn voor de relativiteitstheorie, doch ook voor de fysiologie’.¹

In zijn boekje Über Riemann's Theorie der algebraischen Funktionen (1882) gaf Klein een uiteenzetting van Riemanns begrip der complexe functie. Hier legde hij er de nadruk op, dat ook fysische beschouwingen tot subtiele wiskundige bespiegelingen kunnen leiden. In zijn Vorlesungen über das Ikosaeder (1884) maakte hij op verrassende wijze duidelijk hoe de toen moderne algebra vele nieuwe en merkwaardige eigenschappen van de welbekende Platonische lichamen aan het licht kon brengen. Hiertoe bestudeerde Klein de draaiingsgroepen der regelmatige lichamen en hun betrekkingen tot de groepen van algebraïsche vergelijkingen van Galois. In uitgebreide onderzoekingen, ondernomen met de medewerking van collega's en studenten, paste Klein de groepentheorie toe op lineaire differentiaalvergelijkingen, elliptische moduulfuncties, op functies van Abel en op automorfe functies, op deze laatste in een interessante en vriendschappelijke wedstrijd met Poincaré. Onder de inspirerende invloed van Klein werd Göttingen, waar hij in 1886 professor werd, met haar op Gauss, Dirichlet en Riemann teruggaande traditie, een Mekka voor wiskundig onderzoek en onderwijs, waar jongere en oudere wiskundigen van vele landen elkaar ontmoetten om de studie over gespecialiseerde vraagstukken ter hand te nemen als een bijdrage tot de wiskundige kennis als een geheel gezien. Kleins voordrachten waren steeds op dit geheel gericht, afschriften ervan circuleerden in verscheidene landen en vele wiskundigen hebben van Klein of uit zijn collegedictaten hun begrip van de wiskunde als een één en ondeelbaar totaalgebied verkregen, een gebied dat verder in de nevengebieden van natuur- en sterrenkunde haar vele vertakkingen heeft. Na de dood van Klein in 1925 zijn verscheidene dezer dictaten in boekvorm uitgegeven, o.a. zijn voordrachten over de geschiedenis van

1 H. Freudenthal, Neuere Fassungen des Riemann-Helmholtzschen Raumproblems. Math. Zeitschr. 63 (1956) 374-405.

[p. 241]

de wiskunde in de negentiende eeuw, die vele persoonlijke herinneringen bevatten.

In de tussentijd had Sophus Lie in Parijs de contacttransformaties ontdekt en daarbij de sleutel tot de dynamica van Hamilton als een speciaal gebied van de groepentheorie gevonden. Na zijn terugkeer in Noorwegen werd hij professor in Christiania (Oslo); van 1886 tot 1898 doceerde hij in Leipzig. Zijn hele leven was aan de studie der continue transformatiegroepen en hun invarianten gewijd, waarbij hij hun centrale positie in de meetkunde, in de mechanica, in de gewone en in de partiële differentiaalvergelijkingen met vele voorbeelden aantoonde. Het resultaat van dit levenswerk werd in een aantal standaardboeken neergelegd, die samengesteld werden met behulp van zijn leerlingen Georg Scheffers en Friedrich Engel: Transformationsgruppen (1888-'93), Differentialgleichungen (1891), Kontinuierliche Gruppen (1893) en Berührungstransformationen (1896). Lie's werk is sindsdien in het bijzonder door de Franse wiskundige Elie Cartan naar alle zijden uitgewerkt en verdiept.

24.

Gelijktijdig met de kolossale ontwikkeling der wiskunde in Duitsland heeft Frankrijks wiskunde het hoge niveau behouden waarop ze zich sinds de tijd van Viète en Descartes had bewogen. Het is niet on-interessant Franse en Duitse wiskundigen van die dagen met elkaar te vergelijken, b.v. Hermite met Weierstrass, Darboux met Klein, Hadamard met Hilbert, Paul Tannery met Moritz Cantor.¹

1 De laatste twee waren historici der wiskunde. De beoefening der geschiedenis der exacte wetenschappen, die in de achttiende eeuw in Montucla, in de helft van de negentiende eeuw in Chasles uitstekende vertegenwoordigers had gevonden, begon zich in de tweede helft tot een speciaalgebied te ontwikkelen. Hoogtepunten waren Moritz Cantors Vorlesungen über die Geschichte der Mathematik (4 delen, 1900-1908), de vele artikelen van Paul Tannery (later in zijn Mémoires verenigd), de uitgave van het tijdschrift ‘Bibliotheca mathematica’ (1884-1914) door de Zweed Gustav Eneström, en de uitgave van de verzamelde werken van grote wiskundigen van het verleden, als Euklides, Archimedes, Descartes, Fermat, Lagrange, Galilei en Huygens. De Huygens-uitgave door Nederlandse geleerden begon in 1888 en eindigde eerst met deel xxii in 1950. De leiding was eerst in handen van J. Bosscha, later van D.J. Korteweg, later van J.A. Vollgraff. Andere Nederlandse historici der wiskunde van die dagen waren de Leidse hoogleraar David Bierens de Haan (1822-95), ook bekend door zijn nog steeds nuttige integraaltafels (1858, 1864, 1867), en de Deventer leraar N.L.W.H. Gravelaar (1851-1913).

[p. 242]

In de jaren 1840-'60 was de leidende Franse wiskundige Joseph Liouville, professor aan het Collège de France in Parijs. Hij was een goed docent en organisator, vele jaren lang redacteur van het Journal de mathématiques pures et appliquées. Hij onderzocht de rekenkundige theorie van kwadratische vormen in twee en meer veranderlijken, doch het ‘theorema van Liouville’ in de statische mechanica laat hem weer van een geheel andere zijde kennen. Ook maakte hij het verschil tussen algebraïsche en transcendente getallen duidelijk en bewees in 1844 dat noch e noch e² wortels kunnen zijn van een vierkantsvergelijking met rationale coëfficiënten. Dit was een stap vooruit in de reeks van onderzoekingen over de natuur van e en π, die in 1761 tot Lamberts bewijs gevoerd hadden dat π irrationaal is, en later voerden tot het bewijs van Hermite (1873) dat e, en dat van F. Lindemann (1882) dat π transcendent is. Liouville en enige zijner medewerkers hielden zich ook bezig met de differentiaalmeetkunde van krommen en oppervlakken: zo zijn de formules van Serret-Frenet (1847) in de leer der ruimtekrommen in de kring om Liouville ontstaan.

Charles Hermite, professor aan de Sorbonne en aan de Ecole Polytechnique, werd na de dood van Cauchy in 1857 de leidende vertegenwoordiger van de analyse in Frankrijk. Evenals bij Liouville vindt men bij Hermite vele onderzoekingen in de traditie van Gauss en Jacobi, andere vertonen een zekere verwantschap met het werk van Riemann en Weierstrass. Elliptische functies, moduulfuncties, thètafuncties, getallen- en invariantentheorie - Hermite bewoog zich op al deze gebieden, zoals de namen ‘getallen van Hermite’, ‘vormen van Hermite’, ‘veeltermen van Hermite’ getuigen. Zijn vriendschap met de Hollandse wiskundige Thomas Jan Stieltjes, die in Delft gestudeerd had, en die door hem zijn bescheiden positie als rekenaar aan de Leidse sterrenwacht voor dat van een professoraat in Toulouse kon verwisselen (1889) was een grote aanmoediging voor de ontdekker van de Stieltjes-integraal en de toepassing van kettingbreuken op de theorie van momenten in de theoretische statistiek. De waardering was wederzijds: ‘Vous avez toujours raison et j'ai toujours tort’¹ schreef Hermite eens aan zijn vriend. De vierdelige briefwisseling tussen Hermite en Stieltjes, door het Wiskundig Genootschap te Amsterdam uitgege-

1 ‘U hebt altijd gelijk en ik heb altijd ongelijk’. De wiskundige Stieltjes was de zoon van Thomas Joannes Stieltjes, ingenieur van de Overijsselsche Kanaalmaatschappij en ontwerper van havenwerken in Feyenoord bij Rotterdam.

[p. 243]

ven, bevat een schat van interessant materiaal, voornamelijk over functies van een complexe veranderlijke. Door J.C. Kluyver, hoogleraar te Leiden, zijn de methoden van Hermite ook in Nederland beter bekend geworden.

In de verhandelingen en boeken van Gaston Darboux bleef de grote Franse meetkundige traditie gehandhaafd. Darboux was een meetkundige in de zin van Monge: bij hem ging een diep ruimtegevoel gepaard met de beheersing van de theorie der differentiaalvergelijkingen en van de analytische mechanica. Hij was professor aan het Collège de France en doceerde meer dan een halve eeuw. Nog steeds bekend is zijn elegant standaardwerk Leçons sur la théorie générale des surfaces (4 delen, 1887-'96), waarin hij de resultaten van een eeuw van onderzoek in de differentiaalmeetkunde van krommen en oppervlakte verwerkte. Darboux liet zien hoe deze differentiaalmeetkunde op de meest verschillende wijzen met de leer der gewone en partiële differentiaalvergelijkingen zowel als met de mechanica, verbonden kon worden. Met zijn administratieve en pedagogische bekwaamheid, zijn fijne meetkundige intuitie, zijn beheersing van de analytische techniek en zijn begrip van Riemanns ideeën, nam Darboux in Frankrijk een positie in die aan die van Klein in Duitsland doet herinneren.

Dit tweede deel van de negentiende eeuw was in Frankrijk de periode van de grote Franse leerboeken, waarin de resultaten van het analytisch onderzoek en zijn toepassingen in brede lijnen werden uiteengezet. De bekendste van deze leerboeken zijn de Cours d'analyse van Camille Jordan (3 dln, 1882-87) en de Traité d'analyse van Emile Picard (3 dln, 1891-96), waaraan we de Cours d'analyse mathématique van Edouard Goursat (2 dln, 1902-05) mogen toevoegen.

25.

De grootste Franse wiskundige van deze periode was Henri Poincaré, van 1881 tot aan zijn dood in 1912 professor aan de Sorbonne in Parijs. Geen wiskundige van zijn tijd beheerste zulk een breed gebied, en was in staat op zoveel gebieden de theoretische zowel als de toegepaste wiskunde te verrijken. Elk jaar placht hij college te geven over een verschillend gebied; deze colleges werden door studenten uitgegeven en bestrijken een geweldig terrein: potentiaaltheorie, licht, elektriciteit, warmtegeleiding, capillariteit, elektromagnetisme, hydrodynamica, hemelmechanica, thermodynamica, waarschijnlijkheidsrekening. Al deze voordrachten hadden hun eigen verdiensten, zij hebben ideeën verbreid die weer in het werk van anderen vrucht hebben gedragen of die nog vrucht

[p. 244]

kunnen dragen. Poincaré schreef bovendien een aantal populaire of half-populaire boeken die ertoe bij hebben gedragen in brede kringen begrip te wekken voor de kardinale vraagstukken der moderne wiskunde. Bekende titels zijn La Valeur de la Science (1905) en La Science et l'hypothèse (1906).¹ Daarnaast publiceerde Poincaré een aantal verhandelingen over de zgn. automorfe functies en functies van Fuchs, over differentiaalvergelijkingen en de topologie waartoe zij voeren, en de grondslagen der wiskunde. Hier legde hij de nadruk op de scheppende rol van de volledige inductie, het eerst door Pascal geformuleerd. Zo doorzocht hij met volmaakte beheersing van de mathematische techniek welhaast alle belangrijke gebieden van de theoretische en toegepaste wiskunde. Met Gauss en Riemann behoort hij tot de wiskundigen van de vorige eeuw die meer dan anderen latere generaties tot een inspiratie zijn geweest.

Misschien kan men de sleutel tot het werk van Poincaré vinden in zijn beschouwingen over de hemelmechanica, en in het bijzonder het drielichamenprobleem (Les méthodes nouvelles de Mécanique céleste, 3 dln, 1893). Hier ziet men zijn verwantschap met Laplace en het bewijs dat de eeuwenoude mechanische problemen die met de hemellichamen samenhangen, nog steeds de scheppende geest van de wiskundige konden inspireren. In verband met deze vraagstukken schonk Poincaré hernieuwde aandacht aan divergente reeksen, waarbij hij de theorie der asymptotische ontwikkelingen schiep, ontwikkelde hij de leer der integraalinvarianten, en bestudeerde de stabiliteit der planetenbanen en de vorm van de hemellichamen. Ook zijn fundamentele onderzoekingen over het gedrag van de integraalkrommen van differentiaalvergelijkingen, zowel bij singulariteiten als in hun globale ontwikkeling, houden met zijn werk over het gedrag der hemellichamen verband. Dit geldt zelfs voor zijn onderzoekingen in de waarschijnlijkheidsrekening, een ander gebied waarin hij Laplace' belangstelling deelde. Onze tegenwoordige theorieën over relativiteit, kosmogenie, waarschijnlijkheidsrekening en topologie zijn alle beïnvloed door de geest van Poincaré.

1 Lenin heeft het idealisme dat in Poincarés opvattingen over de verhouding van geest en natuur tot leven komt bestreden in zijn Empiriokriticisme en Materialisme (1908).

26.

Het Risorgimento, de nationale wedergeboorte van Italië, betekende ook de wedergeboorte van de Italiaanse wiskunde. Onder

[p. 245]

de wiskundigen die aan dit herstel hebben meegewerkt waren er verscheidenen die deel hadden genomen aan de strijd die hun land van de Oostenrijkers bevrijdde en tot eenheid bracht, later verbonden zij vaak politieke posities met de bezetting van hun leerstoelen. Riemanns invloed woog zwaar, en door Klein, Clebsch en Cayley verkregen de Italiaanse wiskundigen hun kennis van de meetkunde en de invariantentheorie. De elasticiteitsleer trok hen aan door haar verband met de meetkunde.

Onder deze stichters van de nieuwe Italiaanse school van wiskundigen vinden wij Brioschi, Cremona en Betti. In 1852 werd Francesco Brioschi professor in Pavia, en in 1862 organiseerde hij het technisch instituut in Milaan waar hij tot zijn dood in 1897 onderricht gaf. Hij was een der oprichters van de Annali di matematica pura et applicata (1858), dat in zijn naam de wens der redacteuren uitdrukte om voor Italië te doen wat Crelle voor Duitsland en Liouville voor Frankrijk hadden gedaan. In het gezelschap van Betti en Casorati bezocht Brioschi in 1858 de leidende Franse en Duitse wiskundigen. Vito Volterra, de invloedrijkste Italiaanse wiskundige van de volgende generatie, heeft later eens geschreven dat ‘het wetenschappelijk bestaan van Italië als een natie’ bij deze reis begon.¹ Brioschi was de Italiaanse vertegenwoordiger van de algebraïsche invariantentheorie in de geest van Cayley en Clebsch. Luigi Cremona, na 1873 directeur van de ingenieursschool te Rome, heeft zijn naam gegeven aan de birationale transformaties in het vlak en de ruimte, de zgn. Cremona-transformaties (1863-'65). Hij was ook een der eersten die de zgn. grafostatica ontwikkelde.

Eugenio Beltrami, een leerling van Brioschi, was hoogleraar aan de universiteiten van Bologna, Pisa, Pavia en Rome. Zijn voornaamste verhandelingen over de meetkunde verschenen tussen 1860 en 1870, toen hij met zijn differentiaalparameters de rekening met differentiaalinvarianten in de oppervlakkentheorie invoerde. Een andere bijdrage uit die periode was zijn onderzoeking van zgn. pseudosferische oppervlakken, oppervlakken met negatieve kromming van Gauss. Beltrami merkte op, dat men op zulke oppervlakken de niet-euklidische meetkunde van Bolyai kan afbeelden zo men als ‘lijnen’ de geodetische krommen van het oppervlak beschouwt. Dit was dus, evenals de projectieve interpretatie van Klein, een methode om te bewijzen dat elke inwendige tegenspraak in de niet-euklidische meetkunde zich ook als zodanig

1 V. Volterra, Bulletin American Mathem. Soc. 7 (1900) 60-62.

[p. 246]

in de euklidische ruimte zou openbaren. Deze verhandeling, die van 1868 dateert en dus aan die van Klein nog voorafgaat, gaf dus aan de niet-euklidische meetkunde om zo te zeggen haar eerste legitimatiebewijs.

Omstreeks 1870 waren de ideeën van Riemann meer en meer tot het gemeenschappelijke bezit van de jongere generatie van wiskundigen geworden. Zijn theorie der kwadratische differentiaalvormen werd door de twee Duitse mathematici E.B. Christoffel en R. Lipschitz uitgewerkt (1869-'70). In de verhandeling van de eerstgenoemde, een professor in Zürich, Berlijn en na 1871 professor te Straatsburg, vindt men de uit de relativiteitstheorie zo bekende ‘symbolen van Christoffel’. Lipschitz, hoogleraar te Bonn, is ook bekend door zijn ‘voorwaarden van Lipschitz’ in de leer der reële functies (Lehrbuch der Analysis, 1877-'80). Door de onderzoekingen van Christoffel en Lipschitz over differentiaalvormen en van Beltrami over differentiaalparameters werd Gregorio Ricci-Curbastro in Padua op de idee van de zgn. absolute differentiaalrekening gebracht (1884). Deze rekening was op een nieuwe invariante notatie gebaseerd, die in het eerste werk van Ricci op de transformatie van partiële differentiaalvergelijkingen werd toegepast; en ook toepasselijk bleek op de transformatietheorie van de kwadratische differentiaalvormen.

Uit deze absolute differentiaalrekening ontwikkelde zich, door het werk van Ricci en van enige zijner leerlingen, onder wie Tullio Levi-Civita, de methode die we met Einstein nu tensorrekening noemen. Met behulp van tensoren konden verscheidene invariante symbolismen vanuit één standpunt worden bezien, en zij hebben ook in de behandeling van algemene stellingen der elasticiteitstheorie, hydrodynamica en relativiteitstheorie hun waarde bewezen. De naam tensor voor deze symbolen is in de elasticiteitstheorie ontstaan (W. Voigt, omstreeks 1890).

De studie der lineaire differentiaalvormen, was reeds door Euler en Monge begonnen, en, als reeds gezegd, is de eerste algemene theorie met de naam Pfaff verbonden (J.F. Pfaff, professor in Helmstedt, bij wie Gauss promoveerde). Pfaffs artikel van 1815 verwierf door Jacobi in 1827 bekendheid. De vele onderzoekingen op dit gebied, o.a. door Grassmann en Frobenius, leidden in het eind der negentiende eeuw Elie Cartan tot die studies over Liegroepen en hun betekenis voor algebra en meetkunde, die juist heden ten dage de grote belangstelling der wiskundigen hebben verworven.

[p. 247]

27.

David Hilbert, sinds 1895 professor in Göttingen, hield in 1900 voor het tweede internationale congres van wiskundigen in Parijs een voordracht, waarin hij voor de nieuwe eeuw drieëntwintig gebieden aangaf waarop belangrijk werk kon worden verricht. Toen Hilbert deze voordracht hield, had hij reeds een naam verworven door zijn onderzoekingen op het gebied van algebraïsche getallen-lichamen en door zijn juist verschenen Grundlagen der Geometrie (1899), dat opnieuw de vraag naar een bevredigende axiomatiek der euklidische meetkunde aan de orde stelde (de 8e druk kwam in 1956, na Hilberts dood, uit). Het was in menig opzicht voorbereid door het pionierswerk van Moritz Pasch in Giessen, in het bijzonder door diens boek Vorlesungen über neuere Geometrie (1882), waarin Pasch op de grondslagen der meetkunde een axiomatische methode had aangewend, te vergelijken met die welke Frege in diezelfde tijd op de grondslagen der rekenkunde had toegepast. Hilbert gaf in zijn boek aan hoe de resultaten der Grieken in hun opbouw van de meetkunde verbeterd konden worden, en ook hoe zekere meetkunden eruit zien die op gewijzigde axioma's zijn gebouwd.¹

In zijn voordracht van 1900 trachtte Hilbert de geest van het wiskundig onderzoek van de afgelopen tientallen jaren te begrijpen en enige aanwijzingen te geven voor vruchtbare arbeid in de toekomst.² Een overzicht van enige der problemen die Hilbert aangaf, kan misschien ons inzicht in de betekenis van de wiskunde in de negentiende eeuw verhelderen. Daar ze de eerste schreden zijn van de wiskunde in de 20e eeuw, worden ze in het volgende hoofdstuk behandeld.³

Hilberts program bewees de levenskracht van de wiskunde aan

1 Een bespreking van dit boek van modern standpunt bij H. Freudenthal, Zur Geschichte der Grundlagen der Geometrie, Nieuw Archief v. Wisk. (4) 5 (1957) 105-142, ook Mathem.-Physik. Semesterberichte (Göttingen) 7 (1960) 2-25, 10 (1963) 114-117; O. Bottema, ib. 9 (1962) 164-168; M.M. Toepell, Über die Entstehung von D. Hilberts Grundlagen der Geometrie (Göttingen, 1986).

2 Göttingen Nachrichten (1901) 253-297.

3 Een discussie van de problemen door Hilbert voorgesteld en hun status na dertig jaar vindt men in E. Bieberbach, Über den Einfluss von Hilberts Pariser Vortrag über ‘Mathematische Probleme’ auf die Entwicklung der Mathematik in den letzten dreizig Jahren. Naturwissenschaften 18 (1936) 1101-1111. Sedert die tijd heeft men verdere vooruitgang kunnen boeken. Zie Die Hilbertschen Probleme door P.S. Aleksandrov, Ostwalds Klassiker 252 (Leipzig, 1971), uit het Russisch vertaald.

[p. 248]

het eind der negentiende eeuw en vormt een scherp contrast met het pessimisme dat we tegen het einde van de achttiende eeuw hebben waargenomen. Tegenwoordig zijn verscheidene problemen van Hilbert opgelost, andere wachten nog steeds op een bevredigende behandeling. De ontwikkeling der wiskunde in de jaren na 1900 heeft de verwachtingen die aan het einde van de negentiende eeuw zijn gekoesterd, niet bedrogen, en men kan wel zeggen dat de verwachtingen overtroffen zijn. Toch heeft zelfs Hilberts scherpe geest sommige der meest belangrijke en verrassende ontwikkelingen niet kunnen voorzien. De wiskunde der twintigste eeuw heeft haar eigen weg moeten vinden onder haar eigen voorwaarden.

Literatuur

De nog steeds beste geschiedenis der wiskunde in de negentiende eeuw is

F. Klein, Vorlesungen über die Entwicklung der Mathematik im 19. Jahrhundert (2 dln, Berlin, 1926/27). Men vindt ook vele gegevens in het boek van E.T. Bell, The Development of Mathematics (2e uitg. New York-London 1945), zowel als in sommige monografieën, in onze inleiding aangegeven. Een lijst van biografieën van leidende wiskundigen, ook van de negentiende eeuw, vindt men in:

G. Sarton, The Study of the History of Mathematics (Cambridge, Mass. 1936) blz. 70-98. Verder biografisch materiaal o.a. in DSB en in de verschillende jaargangen van Scripta Mathematica (New York, van 1932 tot heden). Van vele negentiende eeuwse wiskundigen zijn de verzamelde werken uitgegeven, die vaak ook een levensbeschrijving bevatten. Ook sommige tijdschriften, bijv. het Jahresbericht der deutschen Mathematikervereinigung, bevatten levensbeschrijvingen.

Van de in dit hoofdstuk vermelde wiskundigen zijn de verzamelde werken geheel of gedeeltelijk uitgegeven: Abel, Beltrami, Betti, Bolzano, Bolyai, Brioschi, G. Cantor, E. Cartan, Cauchy, Cayley, Clifford, Cremona, Dedekind, Dirichlet, Fourier, Fuchs, Galois, Gauss, Gibbs, Grassmann, Green, Hamilton, Hermite, Hilbert, Jacobi, Klein, Kronecker, Levi-Civita, Lie, Lobačevskiǐ, Möbius, Plücker, Poincaré, Ricci, Riemann, Ruffini, Steiner, Sylvester, Weierstrass.

Verder:

L. de Launay, Monge, Fondateur de l'Ecole Polytechnique (Pa-

[p. 249]

ris, 1934) R. Taton, Monge (Paris 1951). ook, korter: Elemente der Mathematik, Beiheft 49 (Basel 1950).

N. Nielsen, Geomètres français sous la Révolution (Copenhagen 1929).

F. Klein e.a. Materialen für eine wissenschaftliche Biographie von Gauss (8 dln, Leipzig 1911-20).

G.W. Dunnington, Carl Friedrich Gauss, Titan of Science (New York, 1955).

E. Worbs, Carl Friedrich Gauss, Ein Lebensbild (Leipzig, 1955). [C.F. Gauss] Gedenkband anläszlich des 100. Todestages, he rausg. von H. Reichardt (Leipzig, 1957). Bij diezelfde gelegenheid werd ook een Russisch gedenkboek uitgegeven. (Moskou, 1956).

S. Picard, Lobačevskiǐ, grand mathématicien russe. Conférence Palais de la Découverte D 47 (Paris, 1957).

Quaternion centenary celebration, Proc. Roy Irish Acad A 50 (1945) 69-98, bevat o.a. A.J. Mc Connell, The Dublin Mathematical School in the First Half of the Nineteenth Century.

De Scripta Mathematica Studies (New York, 1945) bevatten een aantal artikelen over William Rowan Hamilton.

F. Kötter, Die Entwicklung der synthetischen Geometrie von Monge bis auf von Staudt, Jahresber. Deutsche Mathem. Verein. 5 (1901) 1-486.

H. Burckhardt, Entwicklungen nach oscillierenden Funktionen. Jahresber. Deutsch. Math. Ver. 10 (1908).

M. Simon, Über die Entwicklung der Elementargeometrie im XIX. Jahrhundert (Leipzig, 1906).

V.F. Kagan, Lobačevskiǐ (Moskou, Leningrad, 1944, in het Russisch). [A.P. Norden, red] Honderd vijf en twintig jaren niet-euklidische meetkunde van Lobačevskiǐ (Moskou, Leningrad, 1952, in het Russisch).

D.J. Struik, Outline of a History of Differential Geometry, Isis 19 (1933) 92-120, 20 (1934) 161-191.

J.L. Coolidge, Six female mathematicians, Scripta mathematica 17 (1951) 20-31. Besproken worden Hypatia, M.G. Agnesi, E. du Chatelet, M. Sommerville, S. Germain en S. Kowalewskaja. Voortgezet door E.G. Kramer, ib. 23 (1957) 83-95.

Sonia Kowalewskaja, Her recollections of childhood, vertaald uit het Russisch door I.F. Hapgood (New York, 1895). In dit boek ook de biografie van A.C. Leffler uit het Zweeds vertaald, ook uitg. in Sammlung Reclam, Leipzig.

[p. 250]

Ter herinnering aan S.V. Kowalewskaja. Een verzameling van essays (Moskou, 1951, in het Russisch). Zie ook Istor. Mathem. Issled 7 (1954) 666-715 (Russisch).

A.H. Koblitz, A convergence of lives. Sofia Kovalevskaja, Scientist, Writer, Revolutionary (Birkhäuser, Boston etc., 1983). Een uitstekende levensbeschrijving.

L.P. Wheeler, Josiah Willard Gibbs (New Haven, 1951).

I. Kollros, Jakob Steiner, Elemente der Mathematik, Beiheft 7 (Basel, 1947).

G. Prasad, Some Great Mathematicians of the Nineteenth Century: Their lives and their Works (2 dln, Benares 1933/34). bevat biografieën van Gauss, Cauchy, Abel, Jacobi, Weierstrass, Riemann, (deel i) en Cayley, Hermite, Kronecker, Brioschi, Cremona, Darboux, G. Cantor, Mittag-Leffler, Klein en Poincaré (deel ii).

E. Winter, B. Bolzano und sein Kreis (Leipzig, 1933; Halle, 1949).

E. Kolman, Bernard Bolzano (Moskou, 1955, in het Russisch, ook in het Duits).

O. Ore, Niels Henrik Abel (Minneapolis 1957, in het Engels. Ook een uitgave in het Noors).

L. Infeld, Whom the Gods love (New York, 1948). een roman berustend op het leven van Galois; ook in een Duitse vertaling: Wen die Götter lieben (Wien 1954). Over Galois zie ook R. Taton, Revue Hist. Sci. appl. 1 (1947) 114-130, en

A. Dalmas, Evariste Galois, Révolutionnaire et Géomètre (Paris, 1958).

J. Hadamard, The Psychology of Invention in the Mathematical Field (Princeton, N.Y. 1945).

K.R. Biermann, Über die Förderung deutscher Mathematiker durch Alexander von Humboldt. Gedenkschrift zum 100. Wiederkehr seines Todestages (Berlin 1959) 83-159.

K.R. Biermann, J.P.G. Lejeune Dirichlet, Dokumente für sein Leben und Wirken, Abh. Deutsch. Akad. d. Wiss., Klasse für Mathem. 1959, No. 2.

L. Koenigsberger, C.G.J. Jacobi (Leipzig, 1904).

H. de Vries, Historische Studies (3 dln, Groningen 1918-40). 21 opstellen, meestal over meetkundigen, oorspronkelijk verschenen in ‘Christiaan Huygens’, ‘Euclides’ en het ‘Nieuw Tijdschrift voor Wiskunde’. Zij zijn door verdere studies gevolgd, no. 30 (het laatste) verscheen in het N.T.v.W 42 (1955).

Mathematics of the 19^th century: Mathematical Logic, Algebra, Theory of Numbers, Theory of Probability, uitg. door A.N.

[p. 251]

Kolmogorov en A.P. Juškevič (Moskou, 1978, in het Russisch).

E. Scholtz, Geschichte des Mannigfaltigkeitsbegriffs von Riemann bis Poincaré (Boston, 1980).

P. Dugac, Richard Dedekind et les fondements des Mathématiques (Paris, 1976).

I. Grattan-Guinness, The Development of the Foundation of Mathematics from Euler to Riemann (Cambridge, Mass., 1970).

J. Herivel, Joseph Fourier, the Man and the Physicist (Oxford, 1975). zie I. Grattan-Guinness, Annals of Science 32 (1975) 503-514.

J.W. Dauben, George Cantor, his Mathematics and Philosophy of the Infinite (Cambridge, Mass., 1979).

B.A. Rosenfeld, A History of Non-Euclidean Geometry (Springer, New York etc. 1988). Vertaling van de Russische uitgave, Moskou, 1975. Zie ook HM 6 (1979) 460-464.

P. en E. Morrison, Babbage's calculating Machine or Differential Engine (New York, 1965).

J.V. Grabiner, The Origins of Cauchy's rigorous Calculus (Cambridge, Mass., Londen, 1981).

C. Reid, Hilbert (New York, 1970).

M. Métivier, P. Costabel, P. Dugac, Siméon-Denis Poisson et la Science de son Temps (Paris, 1981).

G. Temple, Thirty Years of Mathematics. A personal Viewpoint (Springer, New York etc., 1981). Speciaal de periode 1850-1900.

H. Kennedy, Life and Works of G. Peano (Dordrecht, 1980).

U. Bottazzini, Il Diciannovesimo Secolo in Italia pp. 249-312 van D.J. Struik, Matematica, un Profilo Storico (Il Mulino, Bologna, 1981).

K. Marx, Matematičeskie Rukopisi (Moskou, 1968). Marx's wiskundige manuscripten in het oorspronkelijk Duits met Russische vertaling en commentaar. Zie hierover:

D.J. Struik, Marx and Mathematics, Science and Society 12 (1948) 181-196, zie ook A.P. Gokieli, De wiskundige handschriften van Karl Marx (Tiflis 1947, Russisch).

H.C. Kennedy, Karl Marx and the Foundations of the differential Calculus, HM 4 (1977) 303-18.

H. Mehrtens, H. Bos, I. Schneider, Social History of Nineteenth Century Mathematics (Birkhäuser, Boston etc., 1981).

H.J.M. Bos-H. Mehrtens, The Interactions of Mathematics and Society in History, HM 4 (1977) 7-30 met uitgebreide bibliografie.

[p. 252]

Over Nederlandse wiskundigen, behalve de reeds geciteerde geschriften van M. van Haaften en de artikelen van D. Bierens de Haan, zie het artikel van D.J. Struik in

A.J. Barnouw-B. Landheer, The contribution of Holland to the Sciences (New York, 1943). en dat van C.J. van der Corput in

K.F. Proost, J. Romein, Geestelijk Nederland 1920-1940 ii (1942) en dat van H.D. Kloosterman, op blz. 234-255, in Natuurwetenschappelijk onderzoek in Nederland (Amsterdam, 1942), zowel als biografieën in ‘Nieuw Archief voor Wiskunde’.