Wisconstighe gedachtenissen. Deel 4: van de weeghconst

⁺ Cortbegryp.

Dese Weeghdaet salvervaten de vvercklicke vinding der svvaerheyts middelplats, svvaerheyts middellini, ende svvaerheyts middelpunts: Voort de making des aldervolmaecksten vvaeghs, met verclaring van etlicke heur ghedaenten. Oock den aldervolmaecksten Onsel. Wijder, de ghedaenten der steerten daermen ghevvelt me doet: De ghedaenten der ghedreghen ghevvichten; Der Windassen; Der ghetrocken gevvichten; Ende de oneyndelicke crachten.

+ Argumentū.

[p. 91]

1 Voorstel.

Wesende ghegheven een lichaem van form soot valt: Sijn svvaerheyts middelplat, hanghende svvaerheyts middellini, ende svvaerheydts middelpunt vverckelick te vinden.

1 Voorbeelt.

Tghegheven. Laet A B een lichaem sijn van form soot valt.

Tbegheerde. Wy moeten sijn swaerheyts middelplat, hanghende swaerheyts middellini, ende swaerheyts middelpunt wercklick vinden.

Twerck.

Men sal t'lichaem hanghen ande coorde C D, treckende door t'opperste punt C, de rechte lini E F, hanghende uyt de selve lini twee fijne draen met haren ghewichtkens, als E G, F H, nevens het lichaem A B, ende t'plat vervaet tusschen



de linien G E, F H, t'welck by gedacht door t'lichaem lijt, is des lichaems swaerheyts middelplat. Maer om sijn uyterste sijden op t'lichaem te teeckenen, men mach de draen E F, G H, becrijden, die gespannen treckende, ende daer op teeckenende, gelijck de saghers haer boomen doen daer sy doorsaeght moeten sijn; Ick neme die linien te wesen I K, L M, teeckenende daer naer insgelijcx de linien L I, ende M K, t'plat L I K M, sal t'begheerde sijn.

Maer om nu de hangende swaerheyts middellini te vinden, men sal t'lichaem noch hangende an C, een weynich draeyen ende teeckenen een ander der ghelijcke swaerheyts middelplat, snyende t'voorgaende ick neem onder in N, ende boven in D, ende haer ghemeene sne D N sal de begheerde hanghende swaerheyts middellini sijn: Maer om t'swaerheyts middelpunt te vinden, men sal t'lichaem verhanghen inde d'weersde, ick neem by t'punt O, ende vinden aldaer oock des lichaems hanghende swaerheyts middellini als vooren, ick neem die

[p. 92]

te wesen O P, ende daer sy de lini D N snijt, als in Q, is t'begheerde swaerheyts middelpunt.

2 Voorbeelt.

Tghegheven. Laet A B een lichaem sijn van form soot valt.

Tbegheerde. Wy moeten sijn swaerheyts middelplat, hanghende swaerheyts middellini, ende swaerheyts middelpunt werckelick vinden.

Twerck.

Men sal t'lichaem A B legghen op eenighen scherpen cant als C D, dat vertreckende ter eender ende ander sijde, tot datmen sich bemercke de evestaltwichticheyt beyder sijden getroffen te hebben, t'welckick neem te wesen in E. daerom t'plat rechthouckich op den^⋆ sichteinder t'lichaem door E snyende, sal t'begheerde swaerheyts middelplat sijn. Ende een derghelijcke plat t'voorgaende plat doorsnyende, heur ghemeene sne sal



hanghende swaerheyts middellini sijn. Ende sodanighen derde plat snijt die hanghende swaerheyts middellini des lichaems swaerheyts middelpunt. Welcker bewijs uyt de voorgaende openbaer is. Tbeslvyt. Wesende dan gegheven een lichaem van form soot valt, wy hebben sijn swaerheyts middelplat, hangende swaerheyts middellini, ende swaerheyts middelpunt werckelick ghevonden, naer de begheerte.

⋆ Horizontem.

2 Voorstel.

Een aldervolmaeckste vvaegh te maken.

Twerck.

Men sal eerst int middel des balcx A B, wiens tongh ter behoirlicker plaets sy, teeckenen de lini C D onder t'middel der tongh, rechthouckich op de canten des balcx, ende vijlen ofte weeren van d'een ende d'ander sijde soo veel stof, tot dat den balck (ligghende met de lini C D op eenighen scherpen cant) over beyden sijden met even ermen evewichtich bevonden wort. Daer naer salmen trecken D E oock rechthouckich op de canten, ende legghen den balck op eenen scherpen stalen punt, genakende inde lini D E, souckende inde selve lini D E des balcx hangende swaerheyts middellini, te weten den balck ter eender ende ander sijde vertreckende (welverstaende dat den stalen punt altijt inde lini D E blijve) tot datmen bemerckt de evewichticheyt ghetroffen te sijne, t'welck ick neem te wesen in F; Daer na geteeckent een dergelijcke punt overd'ander sijde, de rechte lini door die twee punten sal de hangende swaerheyts middellini des balcx sijn, beteeckenende t'scherp vanden dweersas, so noem ick t'yserken daer op den balc int huysken rust. Daer naer soo de schalen an dien balck met haecken moeten hanghen, men sal de plaetsen der ghenaeckselen des balcx ende dier haecken als an A, B, alsoo stellen, dat sy ende t'scherp vanden dweersas in een rechte lini A F B commen te staen: verstaet wel t'voornoemde woort Genaeckselen, want wy spreken vande eyghen wesentlicke ghenaeckselen der haecken teghen de stof des balcx. Maer soo t'ghene daer mede de schalen anden balck hanghen yet

[p. 93]

anders waer dan haecken, men sal op haer dergelijcke naeckselen letten. T'wele ghedaen sijnde, ende t'huysken t'sijnder plaets ghevoucht wesende, soodanighen waegh met alle even ghewichten diemen in haer schalen soude meughen legghen, sal, soo lang den dweersas op haer scherpte rust, alle ghestalt houden diemen haer gheeft, door het 10 voorstel des 1 boucx vande beginselen der Weeghconst.

Maer dat alsulcken waegh de aldervolmaeckste sy, is openbaer door het 1 voorbeelt van het 12 voorstel des voornoemden 1 boucx, alwaer bethoont is, dat wesende E vastpunt, wat ghewicht men an D soude moeten hanghen, om den as in ghegheven ghestalt te houden, maer soo t'vastpunt aldaer had geweest N, te weten het swaerheyts middelpunt des gheghevens, daer en soude geen ghewicht soo cleen connen sijn,^* Wisconstelick sprekende, dat an Dghehanghen, die sijde niet en soude doen gantschelick neerdalen: T'selve is hier oock alsoo te verstaen, te weten dat tot d'een ofte d'ander deser evewichtigher deelen een seer cleen ghewichtgheleyt, die sijde sal stracx ten gronde sincken, daer sy van sommighe ander waghen nau verroeren en soude.

Maer soot den Waeghmakers te moeylick viel die plaets van t'scherp des dweersas, metgaders de ghenaeckselen der haecken ende des balcx, altijt so puntelick te treffen, sy meughen t'ghene gheseyt is houden als voor hun wit, dat so naer commende als sy willen oft connen; Ende so sy van t'volmaeckste yet souden begheeren te verschillen, meughen ghedachtich sijn t'naecksel der haecken ende des balcx liever te stellen een haerken beneden de rechte lini A B, dan daer boven, want daer boven ghestelt sijnde, alles keert omme door het 8 voorstel des 1 boucx, t'welck onbequaem is om te weghen; Ia t'ghene t'swaerste waer, soude altemet t'lichtste schijnen, voornamelick als den as door de langde des

* Mathematicè.

[p. 94]

balcx int begin des wegens niet evewijdich en waer vanden^* sichteinder, overmits alles an die zijde keert daert eerst begint.

Aengaende dat de ermen des balcx evelanck moeten wesen, dat is kennelick, want soo d'eene een honderste deel des erms langher waer als d'ander, dat soude een bedriechlicke waegh sijn, overmits t'ghene evewichtich schene, soude een ten hondert verschillen; ende waer d'een een vijventwintichste deel langher als d'ander, t'soude 4 ten hondert schillen, &c. Want ghelijck den langsten erm tot den cortsten, alsoo dit ghewicht tot dat, door het 1 voorstel des 1 boucx.

Merckt oock dat inde langste dunste ende lichtste balcken, t'grootste voordeel is om scherpelick te weghen. Want wesende twee evesware balcken maer d'een tweemael langher als d'ander, tis kennelick dat een once, aes oft wattet sy, ande langste tweemael meer ghewelts sal doen dan ande cortste door t'voornoemde eerste voorstel.

Tbeslvyt. Wy hebben dan een aldervolmaeckste waegh ghemaect na t'voornemen.

* Horizonte.

3 Voorstel.

Wesende ghegheven een vvaegh diens balck evevvijdich blijft vanden^⋆ sichteinder: T'ghevvicht te vinden dat in d'een schael gheleyt, den black in begheerde ghestalt houde.

T'ghebeurt dickmael dat d'een waegh veel steger gaet als d'ander, sonder datmen weet waer an het liecht, want t'scherp des dweersas is van d'een so bequaem als van d'ander, ende inde reste en openbaert hem niet ooghenschijnelicx daermen de reden door bemercken can: Daerom sullen wy d'oirsaeck beschrijven, bethoonende wat ghewicht men in d'een schael van soodanighen waegh sal moeten legghen op dat den balck blijve in begheerde ghestalt aldus.

Tghegheven. Laet de waegh A B C D sulck sijn, dat alles vry hangende, den balck soude eyntlick evewijdich vanden sichteinder rusten, ende E sy t'scherp vanden dweersas. Tbegheerde. Wy moeten inde schael D eenich gewicht legghen, sulcx dat den balck in die ghegheven ghestalt blijve.

⋆ Horizonte.

Twerck.

Men sal t'huysken ende de schalen met haren coorden ende haecken afdoen, vindende des balcx met de tong daer an swaerheyts middellini, evewijdich mettet scherp vanden dweersas E, door het 1 voorstel deses boucx, t'welck ick neem F te sijne, daer naer salmen trecken een lini tusschen de plaetsen der naeckselen des balcx ende der haecken vande schalen, welcke sy G H, wiens middel sy I: Daer naer salmen F I deelen, alsoo dat de stucken inde reden sijn van t'ghewicht des balcx met de tong, welcke sy 1 ℔, tot de schalen met haer coorden ende haecken, welcke ick neem te wegen oock 1 ℔, daerom gedeelt F I, int middel K, soo sal K t'punt sijn daer an de ghegheven waegh alle gestalt soude houden diemen haer geeft; Daer na getrockƽ de lini K G, ende de hangende door Eals E L, snyende K G in M; Ick seg dat een gewicht in sulckƽ reden tot 2 ℔ (te weten 1 ℔voor den balck, en̄ 1 ℔ voor de schalen, t'samen 2 ℔) als M K tot M G, t'begeerde sal sijn, t'welck geleyt inde schael D, de waegh in die stant sal houden. Ghe-

[p. 95]

nomen dan dat M K het vijventwintichste deel waer van M G, so sal het vijventwintichste deel van 2 ℔ de waegh in die gestalt houden, waer af t'bewijs openbaer is door het 12 voorstel des 1 boucx, maer wy sullender hier om meerder claerheyt, noch een weynich af segghen.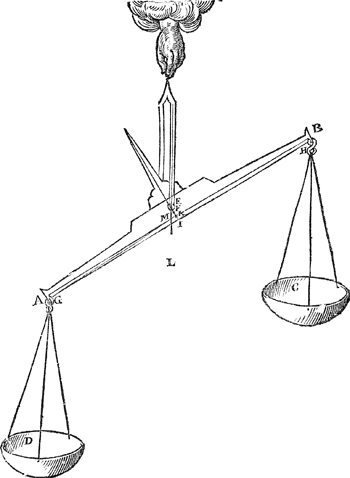

Tbewys.

Anghesien K swaerheyts middelpunt beteeckent des gheghevens, soo sal de^* hanghende door K, des selfden swaerheyts middellini wesen, ende de hangende door G, is swaerheyts middellini des toegheleyden inde schael D, daerom de lini K G, tusschen die twee swaerheyts middellinien, is der selver weeghconstighen balck; Maer sy is ghedeelt in M, also dat den erm M G, sulcken reden heeft tot den erm M K, als diens swaerheyt tot desens; De hanghende dan door M, is swaerheyts middellini ofte hanthaef des heels, ende vervolghens den balck blijft in die ghestalt, t'welck wy bewijsen moesten. Tbeslvyt. Wesende dan ghegeven een waegh, diens balck evewijdich blijft vanden sichteinder, wy hebben t'ghewicht ghevonden, dat in d'een schael gheleyt, den balck in begheerde ghestalt hout, na t'voornemen.

* Perpendiculatis.

[p. 96]

4 Voorstel.

Wesende ghegeven een balck, vvelcke met haer schalen evevvijdich blijft vandƽ^⋆ sichteinder, maer sonder schalen op t'scherp vanden dvveersas niet rusten en can: Te vinden hoe svvare schalen men daer an hanghen sal, op dat den balck alle ghestalt houde diemen haer gheeft.

T'ghebeurt sommighe balcken, dat sy sonder schalen op t'scherp van haren dweersas niet rusten en connen, maer wel de schalen daer an hanghende, welcker dinghen oirsaken wy door de daet versoucken moeten.

Tghegheven. Laet A B een balck wesen van gedaente deses voorstels, wiens dweersassens scherp sy C. Tbegheerde. Wy moeten an desen balck twee schalen vinden (daer by men verstaen sal schalen met haer coorden en haecken) van sulck ghewicht, dat sy den balck alle ghestalt doen houden diemen haer gheeft.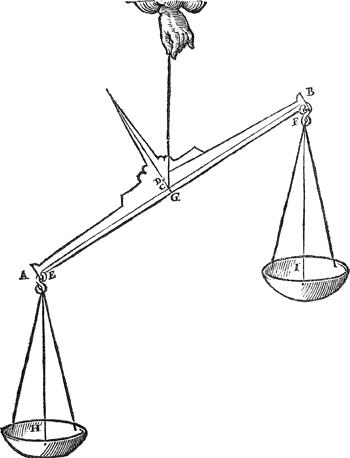

⋆ Horizonte.

Twerck.

Men sal vinden des balcx met de tong daer an swaerheyts middellini, evewijdich van t'scherp des dweersas C door het 1 voorstel deses boucx, welcke sy D,

[p. 97]

boven C, want in C noch onder C en salse niet vallen, overmits den balck op C, door t'ghestelde niet rusten en can, noch min onder C. Daer naer salmen trecken de lini E F tusschen de plaetsen der ghenaeckselen des balcx, ende de haecken der schalen, de selve sal nootsaeckelick vallen onder C, want vielse daer in, of daer boven, gheen schalen hoe swaer sy waren, en souden den black alle ghestalt connen doen houden diemen haer gave, ofte evewijdich doen blijven vanden sichteinder. Daer naer geteeckent G int middel van E F, men sal trecken de rechte lini D C G, ende ghelijck dan C D, tot C G, also moet t'ghewicht der begheerde schalen H I sijn, tot t'ghewicht des balcx; ick neme dat C D even sy an C G, t'ghewicht dan der schalen sal even moeten wesen an t'ghewicht des balcx, waer af t'bewijs^* Wisconstlick ghedaen is int 10 voorstel des 1 boucx, daer toe wy hier tot meerder claerheyt noch een weynich sullen segghen.

* Mathematicè.

Tbewys.

De^* hangende door D, is swaerheyts middellini des balcx ter eender sijden, ende de hanghende door G is swaerheyts middellini der schalen ter ander sijde; G D dan is weegconstighen balck: Maer gelijck den erm C D tot den erm C G, alsoo dese swaerheyt tot die door t'ghestelde, het hout dan op C alle ghestalt diemen hem gheeft, t'welck wy bewijsen moesten. Tbeslvyt. Wesende dan ghegheven een balck, welcke met haer schalen evewijdich blijft vanden sichteinder, maer sonder schalen op t'scherp vanden dweersas niet rusten en can; wy hebben ghevonden hoe sware schalen men daer an hanghen sal, op dat de balck alle ghestalt houde diemen haer gheeft, naer de begheerte.

* Perpendicularis.

Merckt.

Tisopenbaer, dat by aldien de schalen yet swaerder waren dan boven geseyt is, ofte dat in haer eenighe even swaerheden gheleyt wierden, soo en soude den balck dan niet alle ghestalt houden diemen hem gheeft, maer evewijdich blijven vanden sichteinder, daerom en sijn sulcke waghen niet de volmaeckste.

5 Voorstel.

Een aldervolmaecksten onsel te maken.

Twerck.

Men sal des lichamelicken balcx oppersten cant A B voorttrecken tot in C, ende laten inde lini B C de scherpten commen der twee dweersassen D, E, welverstaende dat de scherpte van D neerwaert strecke, ende van E opwaert; Daer naer salmen van het dick eynde des balcx naer B C, so veel afvijlen ofte weeren, tot dat alles int huysken F evestaltwichtich hanghe, ende dat boven dien de scherpte vanden dweersas D (t'huysken F geweert sijnde) swaerheyts middellini blijve des lichamelicken balcx A C. T'welck soo sijnde ende den selven balck int huysken F hanghende, sy sal daer in (so lang den dweersas D op haer scherpte rust) alle ghestalt houden diemen haer gheeft. Daer naer salmen sien van wat swaerheyt t'schuyfwicht G, ende den haeck H sullen sijn, diemen daer an begeert te hanghen; Ick neem G een pont, ende H een once, dat is t'sesthiende deel van G; Daerom salmen teeckenen I, also dat de lini tusschen Ien̄ t'scherp des dweersas D, even sy an t'sestiendedeel van D E, Daer naer salmen de langde D E (dat is de lini tusschen de scherpten der twee dweersassen) teeckenen van I

[p. 98]

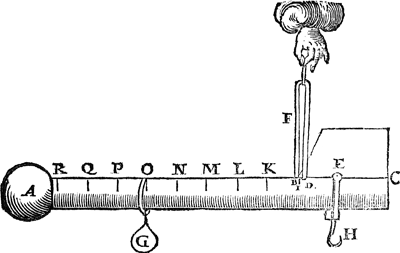naer A, so dickmael als sy daer in commen wil, t'welck ick neem te wesen in K, L, M, N, O, P, Q, R, daer naer machmen elcke langde als I K, K L, L M, &c. deelen in soo veel even deelen alst de plaets toelaet, als in tween, of in vieren, oft in achten, oft in sesthienen, &c. ende alles sal volmaeckt sijn.

Maer oft dit soo nau passen der dweerssassen den onselmaeckers te moeylick viel, sy meughent (ghelijck int voorgaende 2 voorstel vande waegh oock geseyt is) houden als voor hun wit, dat soo naer volghende als sy connen, ende t'scherp des dweersas D liever een haerken boven de lini A C laten commen, dan daer onder.

Wat de gebruyck belangt, als G an O hangt, ende anden haeck H een swaerheyt met de rest evestaltwichtich, die swaerhcyt sal vijf pont weghen, overmidts van I tot O vijf tecckenen staen. Maer soo elcke langde als I K, K L, L M, &c. ghedeelt waer in sesthienen, elck deel soude een once beteeckenen. By voorbeelt of G hinghe tusschen P en Q, an het, vijfthiende deel van P naer Q, de swaerheyt an H soude dan sijn van 6 ℔ 15 oncen, ende alsoo metten anderen. Nu overmits desen onsel (genomen t'schuyfwicht niet neerwaert en sliere als d'een sijde leeghst daelt) met alle evestaltwichtighe deelen die op beyde sijden hanghen, alle ghestalt hout diemen haer gheeft, soo ist (om de redenen die wy int voorgaende voorstel vanden aldervolmaecksten waegh gheseyt hebben) den aldervolmaecsten onsel. Aengaende t'bewijs, alles is openbaer door het 2 voorstel des eersten boucx. Tbeslvyt. Wy hebben dan een aldervolmaecksten onsel ghemaeckt naer de begheerte.

6 Voorstel.

De scheesvvaegh temaken.

Want de ghewichten niet altemael rechtneerwaert noch rechtopwaert en roeren, maer sijdeling, ende scheef; ghelijck voren verscheyden voorbeelden daer af beschreven sijn, ende hier na beschreven sullen worden, soo behouven dese een waegh van ander form dan de ghemeene, welcke wy tot onderscheyt van d'ander scheefwaeg noemen: Heur voornaemste eynde is om door oogenschijnelicke ervaring te sien, ondersoucken, ende verstaen, de waerheyt der voorstellen vande everedenheyt soodanigher ghewichten int eerste bouck

[p. 99]

^* Wisconstlick beschreven, op datmen hem also te vastelicker betrou in t'gene men inde Daet tot s'menschen voordering daer door uytrechten wil.

* Mathematicè.

Twerck.

Men sal maken een voet als A, met een reghel daer op tot verscheyden plaetsen door boort als B, daer naer een caterol als C, met een grouve rontom inden cant daer een draet in loopen mach, ende in sijn middel sy een as D, rustende met beyde haer eynden in een huysken, t'welck met het pinneken E, ghesteken mach worden inde gaetkens der reghel B, soo hooghe ofte leeghe alsmen wil, ende sal volmaeckt sijn. Maer t'voornaemste daermen op letten moet (op datmen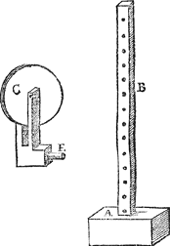



een scheefwaegh heb die scherpelick weghe) is, dat het caterol ende den as daer in al t'samen moeten ghedracyt sijn, ende t'selve caterol ende den as soo dun alsmen can, ende dat de ronden nerghens int huysken en ghenake, latende tusschen de eyndē des dweersas ende t'plat des caterols, eenighe dickte, wat dicker dan de eynden des as. Ick heb voor my daer toe doen draeyen een caterol van bosboom, wiens dickte niet meer en was dan als den rugghe van een dun mes, ende des rondts middellini van ontrent vijf duymen, ende den as (al met den anderen ghedraeyt) van yvoor, van de dickte als een cleermakers naelde, te weten soo dun alst den draeybanck lijden mocht.

7 Voorstel.

T'ondersoucken de ghedaenten der steerten daermen ghevvelt mede doet.

Siende de menschen datmen met langher steerten een merckelicker grooter ghewelt dede dan met de corter, sy hebben veel gemeene reetschappen tot heuren grooten dienste ende voordeele daer door ter daet ghebrocht: Maer want sulcx alleen gheschiede door ervaringhen, ende niet door grondelicke kennis der^* everedenheyt in heur bestaende, soo en sijn veel groote nieuwe wercken dickmael niet wel gheluckt, tot groote schade der Makers, ende verachtering des voornemens. Op datmē dan wete eermen begint, wat de steerten int volmaecte werck souden connen doen, wy sullen (boven de^* Wisconstighe voorstellen des eersten boucx alsulcx vervatende) eenighe daetlicke voorbeelden daer af beschrijven. Ten eersten, want eenighe persoonen wel van meyning sijn gheweest, datmen de schepen bequamelicker ende met minder schade over een dam soude meughen brenghen, deur t'behulp van lange steerten, dan door een windas, naer de ghemeene gebruyck, wy sullen t'selve nemen als voorbeelt om te sien wat daer uyt volghen soude in deser voughen.

* Propositionis.

* Mathematicè.

[p. 100]

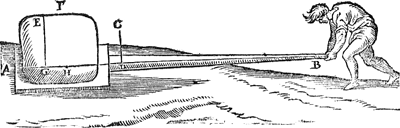
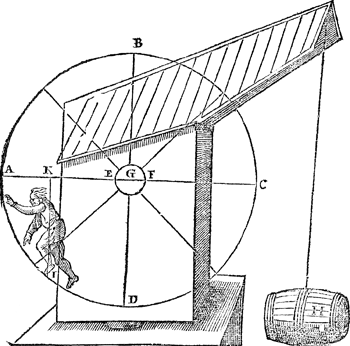
1 Voorbeelt.

Tghegheven. Lact A een dam wesen, ende B C een plat houten bereytsel daer het schip D weghende 24000 ℔ op rusten mach (hoe t'ghewicht eens schips met al datter in is int water ligghende, bekent can worden, sal int Waterwicht sijn plaets hebben) ende dat E middel van B C passe op t'middel des dams A, ende laet B F den eenen steert sijn, ende C G (even an B F) den anderen, ende t'schip D gheweert sijnde, soo is de sijde E F evewichtich tegen E G, ende om t'schip over den dam te crijghen, men soude trecken an F, ofte heffen an G, ofte an beyde t'samen. Ende laet H I des schips swaerheyts middellini wesen, ende F E sy sesvoudich tot E H: uyt het welcke men begheert te weten wat macht ofte ghewicht an F of G met het schip evestaltwichtich sal sijn.

Twerck.

Overmits F G is als balck eens waeghs, diens vastpunt E, ende schips swaerheyts middellini H I, ende dat F E sesvoudich is teghen E H, soo sal t'schip sesvoudich sijn teghen t'ghewicht dat an F hanghende met hem evestaltwichtich sy, maer t'schip weeght door t'ghestelde 24000 ℔; An F dan soude moeten hanghen 4000 ℔: Daerom sooder anhinghen 25 menschen elck weghende 160 ℔, die souden tegen t'schip evestaltwichtich sijn: Maer dit verstaet hem op de stant daert nu in is, want nemende K voor swaerheyts middelpunt des schips, ende het deel E G rijsende, soo sal an F min dan 4000 ℔ behouven. Om van t'welck met voorbeelt te spreken, Laet ons trecken de lini K L rechthouckich op t'plat E C, inder voughen dat als t'plat E C evewijdich sal sijn vanden sichteinder, soo sal K L des schips swaerheyts middellini sijn. Ick neem nu dat E F sevenvoudich sy teghen E L, daerom t'sevenste deel van 24000 ℔ als 3428 4/7 ℔, sal t'ghewicht sijn t'welck an F hanghende met de rest alsdan in die standt evestaltwichtich sal sijn.

Merckt.

Wy hebben hier een voorbeelt gestelt daermen hem in sulcken handel soude naer meughen rechten, maer tis te ghedencken dat E F sesvoudich genomen is teghen E H, t'welck wel eenen seer langhen steert soude moeten wesen ende sterck naer de gheleghentheyt. Ick achte dattet in groote schepen (int ansien van beter) gheen goet eynde en soude nemen; met cleyne schuytkens mochtet sijn bescheet hebben. Wel is waer, datmen an de eynden F G windassen soude meughen stellen, om soo veel volcx daer niet te behouven, maer wy sullen een beter manier beschrijven int volghende 10 voorstel, ons hier vernoughende

[p. 101]

met de rekening van soodanighen voorbeelt verclaert te hebben, watmen t'sijnen voordeele daer het te pas mochte commen, bequamelicxt sal meughen gebruycken.

2 Voorbeelt.

Wy hebben in t'eerste voorbeelt verclaert, de ghedaente der steerten die evelanck ende evewichtich sijn, wy sullen nu dit voorbeelt stellen van oneven steerten. Tghegheven. Laet A B C den eenen steert sijn, ende A B D den anderen, rustende met de lini A B op de cant E; Ende de lini D C snyende A B in F, sy den as des heels D A C B weghende 400 ℔, ende sijn swaerheyts middelpunt sy G, (tis wel waer datter swaerheyts middelplat rechthouckich op den as inde daet ghenouch soude doen, soo wel int volghende 3 ende 4 voorbeelt, als in dit, doch om eyghentlicker daer af te spreken, wy nemen het swaerheyts middelpunt) ende op het deel A B D light een swaerheyt H van 2000 ℔, diens swaerheyts middellini I K sy, te weten Kinden as C D; De vraegh is hoe sterck men an C sal moeten trecken, om H op te lichten.

Twerck.

Men sal vinden de swaerheyts middellini der swaerheyt H, ende des reetschaps D A C B al t'samen, aldus: Men sal K G deelen in Lalso dat G L sulcken reden hebbe tot L K, als 2000 ℔ tot 400 ℔, dat is als 5 tot 1, ende eenighe^* hangende door L sal des heels swaerheyts middellini sijn; Ic neem nu dat F C twaelfvoudich bevonden sy tegen F L, daerom seg ick F C 12, gheeft F L 1, wat 2400 ℔? (te weten de somme des swaerheyts ende reetschaps) comt 200 ℔, voor t'ghene



dat an C hanghende met de rest in die gheleghentheyt evestaltwichtich sal sijn, daerom een man weghende 200 ℔, ofte soo stijf treckende als 200 ℔ daer an hanghende trecken souden, sal met de reste evestaltwichtich sijn. Maer dit verstaet hem op de ghestalt daert nu in is, want nemende M voor swaerheyts middelpunt des ghewichts H, ende het deel A B D rijsende, soo sal an C min dan 200 ℔ behouven. Om t'welck opentlicker te verstaen, laet ons trecken de lini N O, door t'punt M rechthouckich op t'plat A B D, inder voughen dat als t'plat A B D evewydich sal sijn vanden^* sichteinder, soo sal N O swaerheyts middellini wesen der swaerheyt H, daerom ghedeelt O G in P, alsoo dat P G wederom vijfvoudich sy tot P O, te weten als 2000 ℔ tot 400 ℔, soo sal de hanghende door P alsdan swaerheyts middellini wesen des heels; Ick neem nu dat

* Perpendicularis.

* Horizonte.

[p. 102]

FC vijfthienvoudich sy teghen F P, daerom seg ick F C 15, gheeft F P 1, wat 2400 ℔? coemt 160 ℔, voor t' ghene dat an Changhende met de rest alsdan evestaltwichtich sal sijn.

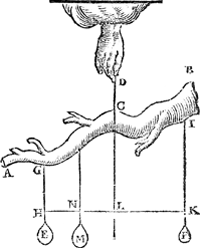
3 Voorbeelt.

Anghesien de wichtighe ghedaenten der lancien ofte dierghelijcke, op de schouder ghedraghen, ghelijck ghenouch sijn ande ghedaenten des voorgaende tweede voorbeelts, soo sullen wy daer af dit derde beschrijven.

Tghe gheven. Laet A een man sijn, hebbende op sijn schouder B, een lanci C D, weghende 12 ℔, wiens as sy C D, ende haer swaerheyts middelpunt sy E, ende van t' punt des naecksels der lanci ende sijn schouder, sy ghetrocken de lini B F, rechthouckich op den sichteinder, snyende den as D C in G; Ende sijn handt rechtneerwaert treckende comt an t'punt H inden as, ende G H sy dobbel an G E. Tbegheerde. De vraegh is wat gewelt de hant ande lanci doet.

Twerck.

Overmits de lini G H dobbel is an G E, so sal t' ghewicht an E, dat is der lanci, dobbel sijn an t'ghewicht an H, dat is t'gene de hant treckt; Maer de lanci weegt



12 ℔, de hant dan sal soo stijf trecken als 6 ℔ souden an H hanghende.

Maer so den man A waer een Snaphaen, met een ghesnapten haen I an K hanghende, weghende 3 ℔, ende alsoo dat K G drievoudich waer an G H, tis kennelick dat den buyt sijn handt van 9 ℔ meer verswaren, ende in alles 15 ℔ trecken soude.

Dit is ghenomen dat de hant recht neerwaert trecke, maer als sy scheef treckt, ghelijck dan rechtdaellini tot scheefdaellini, alsoo rechtdaelwicht tot scheefdaelwicht, door het 21 voorstel des 1 boucx der beginselen, waer wt alles bekent wort door het 22 voorstel des selfden boucx.

4 Voorbeelt.

Wy hebben tot hier de ghedaente verclaert alwaer twee steerten sijn, over clcke sijde des vastpunts een; Wy sullen nu een voorbeelt gheven vanden steert alleenelick over een sijde. Tghegheven. Laet A B een steert sijn, vast an t'eynde A, de rest verroerlick, weghende 400 ℔, diensas A B, ende swaerheyts middellini C D, ende de steert A B sy lanck 10 voeten, waer op een ghewicht E light van 1000 ℔, diens swaerheyts middellini F G. De vraegh is hoe sterck men an B sal moeten heffen om den steert met t'ghewicht E op te lichten.

[p. 103]

Twerck.

Men sal vinden de swaerheyts middellini des heels, deelende eenighen balck tusschen de middellinien F G en C D, als G D, in H, alsoo dat H G sulcken reden hebbe tot H D, als 400 ℔ des steerts, tot 1000 ℔ des ghewichts F, dat is als 2 tot 5: Ick neem nu dat A H sy 2 voeten, ende segh, A B 10 voeten, gheeft A H 2 voeten, wat 1400 ℔ voor t'geheele gewicht des steerts ende pacx? comt 280 ℔. Men sal dan an B soo grooten ghewelt moeten doen om met de reste evestaltwichtich te sijn, als oftmen 280 ℔ ophielde, waer af t'bewijs openbaer is door het 14 voorstel des 1 boucx der beginselen.

Maer soo den Wegher de voornoemde rekening wilde maken door naeckter kennis des gronts, hy mach sich selfs Weeghconstighe formen beschrijven, ghelijck den^* Meter om t'verstercken des ghedachts, hem^* Meetconstighe voorstelt, aldus: Ick treck de lini I K, beteeckenende den steert A B van 10 voeten, ende overmits A H twee voeten was, ende H swaerheyts middelpunt, ick teecken L, also dat I L beteecken 2 voeten van I K 10, hanghende M 1400 ℔ an L, treckende daer naer I N even an I K, ende houde I voor vastpunt, ick sie wat ghewicht an N sal moeten hanghen, op dattet met M evestaltwichtich sy: T'selve is door het 3 voorstel des 1 boucx openbaer, maer wy sullender tot meerder claerheyt noch dit af segghen: Overmits I L is als vijfden deel van I N, soo moet



an N (door t'voornoemde 3 voorstel des 1 boucx) t'vijfdendeel hanghen van M 1400 ℔, t'welck is voor O 280 ℔ evestaltwichtich teghen M; Maer O doet soo veel an N dalende, als t'selve ghewicht an K heffende, door het 13 voorstel des 1 boucx der beginselen (want I N is even an I K) daerom die an K heft sal moeten 280 ℔heffen om met M evestaltwichtich te sijn, en̄ vervolgens hy moet 280 ℔ lichten an B, om met de rest evestaltwichtich te wesen. Derghelijcke formen mach den Wegher in alle werckelicke voorbeelden sijn selven altijt voorstellen, welcke hier om cortheyt achterghelaten sijn. Tbeslvyt. Wy hebben dan ondersocht de ghedaenten der steerten daermen ghewelt mede doet, naer de begheerte.

* Geometra.

* Geometricas.

8 Voorstel.

Te ondersoucken de ghedaenten der gedregen svvaerheden.

Tghegheven. Laet A B een leere wesen, op t'een eynde swaerder als op t'ander soo sy ghemeenlick sijn, welcke ghedreghen moet worden van twee

[p. 104]

mannen, alsoo dat d'een soo veel ghewichtsdraghe als d'ander, dat is elck den helft, ende haer middellini C D, sal int draghen evewijdich vanden^* sichteinder blijven.

* Horizonte.

Twerck.

Men sal de leere op eenighen scherpen cant legghen, die vertreckende voorwaert ende achterwaert, tot datmen bemercke de evestaltwichticheyt getroffen te sijne, t'welck ick neem in E te wesen, ende soo sy dickwils moet verdreghen sijn van d'een plaets ten anderen, men mach an E een kerfken stellen; Laet daer naer ghetrocken worden de hangende E F, snyende C D in F, daer naer salmen teeckenen eenighe twee punten evewijt van E F, als G, H, ende die an G draecht sal even soo veel draghen als die an H.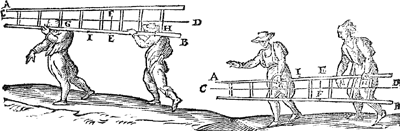

Maer soomen dien noch soo veel ghewichts wilde doen draghen als desen, men sal desens langde tusschen hem ende E F, dobbel maken an diens. Als H E dobbel sijnde an E I, die an I droughe soude noch soo veel ghewicht draghen als die an H. Ende alsoo salmen de reden des ghewichts vanden eenen tot den anderen, connen stellen naer de begheerte.

T'gene boven geseyt is vande leere sal hem also verstaen op yder lichaem, als by voorbeelt, de form hier onder, ghedenckende dat der ongheschicter lichamen linien door haer swaerheyts middelpunt lijdende als C D, gevonden worden door het 1 voorstel deses boucx, oock dat de hanghende linien door G en H, eveverre sijn vande linien E F.

[p. 105]

Wy hebben hier voorbeelden ghestelt alwaer de lini C D ghenomen is evewijdich vanden sichteinder, maer soo sy daer af onevewijdich waer, ende dat de selve mannen eenen berch ofte hooghde opsteghen, de reden vande gewichten soude veranderen, doch bekent blijven. Laet tot meerder claerheyt de voornoemde mannen een hooghde opgaen als hier onder, die an G vooren gaende d'ander achter.

Nu ghetrocken^* hanghende linien door de punten G, H, snyende C D in K en L, so en sal dan elck niet even veel draghen als in d'eerste ghestalt, want F K inde twee opperste formen is meerder dan F L, ende inde onderste formen minder: Ende ghelijck F K tot F L, alsoo t'ghewicht des draghers an H, tot het ghewicht des draghers an G. Alwaer oock blijckt dat als de vastpunten G, H, onder de lini C D sijn, soo draecht den voorsten minst, maer die vastpunten boven de lini C D wesende, soo draecht den voorsten meest. Tis oock kennelick dat de vastpunten G, H, inde lini C D sijnde, dat alsdan elck over al altijt sijn selfde gewicht sal dragen, so wel een berch opstigende, als langs den sichteinder: Van alle welcke de bewijsen openbaer sijn door de 14 15 16 17 18 27 28 voorstellen des 1 boucx. Maer want veler wercklieden gheleghentheyt niet en is die voorstellen te leeren, noch henlieden daer in te oeffenen, ende nochtans geerne wat ooghenschijnelicx saghen, waer door sijt gheloofden, die meughen nemen een rechten gheschickten, ofte crommen ongheschickten stock, soot valt, als A B,

* Perpendiculares.

[p. 106]

hem hanghende tot eenigher plaets



als C, an een coorde C D. Daer naer hanghende anden stock even gewichten als E, F, alsoo dat haer coorden G H, I K, eveverre sijn vande lini C D neerwaert ghetrocken, te weten dat H L even sy an L K, den stock sal haer eerste stant houden, t'selve sal sy oock doen soomen E weerde, ende datmen anhinghe t'ghewicht M, dobbel an F, ende alsoo dat L K oock dobbel sy an L N, ende soo met allen anderen, waer uyt sy de nootsaecklicheyt van t'ghene boven gheseyt is, lichtelick ghevoelen sullen. DE linien daer mede de mannen in



de voorgaende formen t'lichaem draghen, sijn rechthouckich op den sichteinder ghestelt, maer soo sy daer op scheefhouckich waren, als hier neven, sy sullen t'samen meerder ghewelt moeten doen, dan de eygen swaerheyt des lichaems is. Maer om te weten hoe veel yeghelick draecht, men sal trecken de^* hanghende linien I M, ende N O, segghende, ghelijck M I tot I G, alsoo diens rechtheswicht tot t'ghewicht dat den man an G treckt, wederom gelijck O N tot N H, alsoo diens rechthefwicht tot t'ghewicht dat den man an H treckt, door het 27 voorstel des 1 boucx der beginselen, ende yders macht wort bekent door het 22 voorstel des selvē boucx.

Wy souden meer verscheyden voorbeelden vande wichtige ghedaenten der ghedreghen lichamen meughen beschrijven, maer wy latent eensdeels om de cortheyt, ten anderen dat sy door t'voorgaende kennelick ghenouch schijnen.

* Perpendiculares.

9 Voorstel.

Te ondersoucken de ghedaenten der vvindassen, ende der ghetrocken svvaerheden.

Het treckendwicht ende ghetrocken wicht des windas, sijn^* everednich met de^* halfmiddellini des as, ende de halfmiddellini des radts, maer om alles oirdentlicker te beschrijven, wy sullender een^* Vertooch af maken soodanich.

* Proportionales.

* Semidiameter.

* Theorema.

[p. 107]

Vertooch.

VVesende een vvindas an diens as een ghevvicht hangt, evestaltvvichtich teghen t'ghevvicht an t'eynde des radts middellini die evevvijdich is vanden^* sichteinder: Ghelijck dan de halfmiddellini des radts, tot de half-middellini des rondts vanden as, alsoo t'ghevvicht anden as, tottet ghevvicht ant'radt.

Tghegheven. Laet A B C D E F G een windas sijn, diens as E F G, wiens rondts middellini E F, ende middelpunt H sy, ende I een ghewicht anden as hanghende, ende A B C D sy het radt, diens middellini evewijdich vanden sichteinder, sy A C, an wiens eynde A een ghewicht K hangt, evestaltwichtich teghen I, ende L sy t'onderste ghenaecksel des as teghen t'ghene daer sy op rust.

Tbegheerde. Wy moeten bewijsen dat ghelijck H A tot H F, alsoo I tot K.

* Horizonte.

Tbewys.

Laet ons t'radt A B C D ansien als voor balck eens waeghs, diens hanthaef L B, inder voughen dat de sijde des radts B D A, de ghewichten K, I, gheweert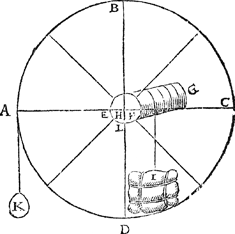



sijnde, evewichtich hangt teghen de sijde B D C. Laet ons nu nemen dattet ghewicht I hanghe an t'punt F (want het daer van de selve macht soude sijn, diet t'sijnder plaets is) ende K t'sijnder plaets an A. Dit so wesende, ghelijck den langsten erm H A, tot den cortsten H F, alsoo de swaerste swaerheyt I, tot de lichtste K, door het 1 voorstel des 1 boucx der beginselen. Daerom by aldien H A sesvoudich waer teghen H F, soo sal I sesvoudich wesen tegen K dat is, wegende I ses hondert pont, K salder hondert weghen, daerom een man treckende an A, soo stijf als hondert ponden neerdrucken, die soude teghen I 600 ℔ evestaltwichtich sijn, ende om I te doen rijsen soude (om t'ghenaecsel des as &c.) wat stijver moeten trecken dan 100 ℔ neerdrucken.

2 Voorbeelt.

De ghedaenten der cranen ende der ghelijcke raeyers daer menschen in gaen sijn door t'voorgaende oock openbaer. Laet tot voorbeelt A B C D een radt wesen, diens^* middellini A C, evewijdich sy vanden^* sichteinder, ende t'rondt des as ty E F, wiens middelpunt G, ende t'ghewicht anden as sy H, ende I sy een man in tradt evestaltwichtich tegen H, diens swaerheyts middellini rechthouckich op A C sy I K. Ende is kennelick dat ghelijck G K tot G F, alsoo t'gewicht

* Diameter.

* Horizonte.

[p. 108]

H tot het ghewicht des mans I, ghenomen dan dat G K viervoudich sy teghen G F, soo sal t'ghewicht H viervoudich sijn teghen t'ghewicht des mans, daerom soo den man woughe 150 ℔, soo sal H weghen 600 ℔. Oock en sal den man op die plaets de swaerheyt H niet connen opwinden, overmits hy aldaer maer evestaltwichtich teghen H en staet; Maer by aldien hy voortgaet naer A, soo sal H



rijsen, want de reden vande lini G K tot G F, soude dan grooter wesen dan sy nu is. Maer alsser meer menschen int radt gaen dan een, die naest A sijn doen t'meeste ghewelt, ende de reden van haer altsamen ende van yder int besonder tot t'ghewicht H, is openbaer door het 3 voorstel des 1 boucx.

3 Voorbeelt.

Dit heeft hem alsoo met de ghewichten die recht op ghetrocken worden, als packen ende vaten diemen door cranen uyt schepen windt, ende dier ghelijcke; Maer de ghewichten die scheef opwaert commen, als onder anderen de schepen diemen in Neerlant tot veel plaetsen over dammen windt, tis met de^* everedenheyt van dien wat anders ghestelt. Laet tot voorbeelt A een dam wesen, ende B een schuyt die daer over getrocken moet worden, ende C D het radt, wiens middellini evewijdich vanden^* sichteinder sy C D, ende daer in een man tegen de schuyt Bevestaltwichtich, wiens swaerheyts middellini F E, ende de coorde sy G H, ende des assens rondt sy I K, ende haer,^* middelpunt L: Laet oock ghetrocken sijn N M, rechthouckich op t'plat des dams, ende M inde coorde G H; Daer naer de^* hanghende O N; Laet nu L F sesvoudich sijn tot L K, ende N O drievoudich tot O M, ende den man weghen 150 ℔. Dit so sijnde ghelijck L F tot L K, alsoo t'ghewicht dat ande coorde H G recht neer soude hanghen, tot t'ghewicht des mans van 150 ℔, door t'voorgaende vertooch, maer L F is door t'ghestel de sesvoudich an L K, t'ghewicht dan dat ande coorde H G recht neer

* Propositione.

* Horizonte.

* Centrum.

* Perpendiculares.

[p. 109]

hinghe, soude sesvoudich sijn an 150 ℔, dat is 900 ℔; den man dan doet in t' radt soo veel ghewelts ande schuyt B, als ofter met de scheefwaegh 900 ℔ an hinghen. T'welck soo sijnde t'ghewicht der schuyt B, heeft sulcken reden tot die



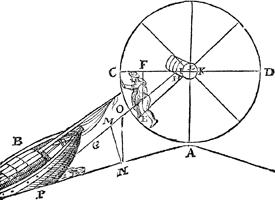900 ℔, als N O tot O M door het 20 voorstel des 1 boucx; Maer N O is drievoudich an O M door t'gestelde, de schuyt dan weegt driemael 900 ℔, dat is 2700 ℔, dat is achtienmael den man. T'welck hem soo verstaet wesende de schuyt in die ghestalt, maer als sy hoogher comt, soo sal de coorde G H steylder sijn (ten waer men die ande schuyt versette) ende vervolghens de lini als M O sal wat meerder reden hebben tot O N, dan sy nu doet, waer door oock het evestaltwicht teghen de schuyt alsdan meerder soude sijn dan 900 ℔; Daerom yemant willende een radt ende as van pas bouwen, niet te groot noch te cleen, mach sijn rekening maken naer de ghestalt daer in een der swaerste schuyten ofte schepen de meeste ghewelt behouft.

Tis oock te ghedencken dat den man E in t'radt de meeste ghewelt doet, als de coorde G H evewijdich is van t'plat des dams P N, door het 24 voorstel des 1 boucx der beginselen, want dan is H G rechthouckich op den as (op dat ickse soo noem) der schuyt, dat is op de lini door t'swaerheyts middelpunt der schuyt, ende rechthouckich op t'plat P N: Daerom hoe dat G H ende P N de evewijdicheyt naerder sijn, hoe lichter werck, ende hoe verder, hoe swaerder.

4 Voorbeelt.

uyt het voorgaende is oock kennelick, hoe veel ghewichts een peert in een waghen ghespannen, meer treckt een hooghde op stijghende, dan opt plat lant. Laet by voorbeelt A B t'plat sijn eens berghs, ende C D een waghen, wegende met datter op is al tsamen 2000 ℔, ende E F (inde plaets der strijnghen) sy de coorde, ende G sy t'peert, evestaltwichtich teghen den waghen. Laet oock getrocken sijn de^* hanghende H I, ende I K, rechthouckich op t'plat A B, ende laet I H viervoudich sijn tot H K, ende is kennelick door het 20 voorstel des 1 boucx der beginselen, dat ghelijck K H tot H I, alsoo t'ghewicht der scheefwaegh sooder een waer (in diens plaets nu t'peert is) tottet ghewicht des waghens, maer K H is t'vierendeel van H I door t'ghestelde; des scheefwaeghs wicht dan soude van 500 ℔ sijn, te weten t'vierendeel van t'ghewicht des waghens; Daerom t'gareel oft riem oft sulcx alst waer,

* Perpendicularis.

[p. 110]

druckt t'peert soo stijf voor den borst L, als een pack van 500 ℔ op sijn rugghe duwen soude, ende dat (welverstaende alst voortgaet) boven het duytsel dattet lijdt op t'plat lant treckende.

Tis oock openbaer door het 24 voorstel des 1 boucx, ende door t'ghene wy hier voren vande schuyt gheseyt hebben, dat als de strijngen evewydich sijn vande wech daer de waghen over vaert, dat de peerden dan de meesten ghewelt ande waghen doen, welverstaende op eenen harden gantsch effenen wech, maer op eenen oneffenen hobbelighen ende sandighen, so voorderet de strijnghen achter wat leegher te doen dan vooren. T'welck den Hollantschen voerlien door d'ervaring niet onbekent en is, diens wagens daer naer gemaeckt sijnde, doen de strijnghen, langs t'zeestrant varende, ende in derghelijcke even harde weghen, achter hoogher, dan inde oneven ende sandighe. Reden is dese, dat wesende de strijnghen evewijdich vanden sichteinder, soo en sijnse niet evewijdich met die oneven verhefselen, t'welck int overtrecken nootsaeckelick meerder last anbrengt, dan als de strijnghen achter leegher sijn, overmits sy dan de evewijdicheyt met die verhefselen naerder sijn. Inde sandighe daer de waghen diep insinckt, daer drucken de raeyers dieper ende moeylicker door t'sant, wesende de strijnghen evewijdich vanden sichteinder, dan als sy achter wat leegher sijn.

Merckt.

Yemant mocht ons nu twee saken voorworpen; Ten eersten, waerom wy hier boven gheseyt hebben: Ghelijck H K tot H I, alsoo t'ghewicht der scheefwaegh sooder een waer (in diens plaets nu t'peert is) tottet ghewicht des waghens; Achtende datmen niet en behoort te segghen tottet ghewicht des waghens, maer, tottet rechthefwicht van t'ghewicht des waghens.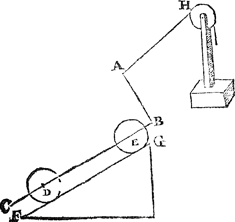

Ten tweeden waerom wy geen onderscheyt beschreven en hebben vande plaets der coorde E F, twijfelende dat de selve voortghetrocken ende lijdende door t'swaerheydts middelpunt des waghens, een ander ghewicht voor t'peert mocht veroirsaken, dan als sy daer boven of daer onder comt. Om op t'welck te verantwoordē, en̄^* Wisconstlic te bewijsen dat de bovēschreven everedenheyt volcom-

* Mathematice.

[p. 111]

men is: soo laet A B C een waghen sijn, al van wisconstighe linien ghemaeckt, wiens raeyers sijn D, E, ende den wech daer hy op rust sy F G, ende de coorde des toecomenden scheefhefwichts sy A H.

Laet ons nu op desen waghen legghen een pylaer I K als hier onder, alsoo dat H A voortghetrocken comme in des pylaers swaerheyts middelpunt L, ende laet het scheefhefwicht M teghen den pylaer evestaltwichtich sijn; Laet oock an L ghevoucht worden t'rechthefwicht N, met den pylaer evestaltwichtich: Laet ons oock trecken de^* hanghende B O, snyende A H in O, t'welck so sijnde, wy segghen door het 20 voorstel des 1 boucx, dat ghelijck A O tot O B,



alsoo M tot t'rechthefwicht N; Maer anghesien N ghevoucht is an t'swaerheyts middelpunt L, des pylaers I K, soo sal N evewichtich sijn met den pylaer door het 14 voorstel des 1 boucx; Daerom meughen wy segghen ghelijck A O tot O B, also M tot den pylaer, waer uyt d'eerste voorgheworpen saeck openbaer is als H A comt uyt het swaerheyts middelpunt L.

Maer om nu het tweede voorgheworpen te bewijsen, dat is de selve^* everedenheyt dus ooc te bestaen al en comt A H niet uyt het swaerheyts middelpunt L, soo laet ons den pylaer I K rechtopwaert uyt den waghen trecken, rustende op de hangende swaerheydts middellijn L P, als hier neven: Ende door de 3 Begheerte, sy en brengt op den waghen A B C, gheen meerder swaerheyt dan in d'eerste ghestalt, ende vervolghens Men heeft niet meer te trecken dan sy te vooren en dede: Maer H A voortghetrocken comt nu onder t'swaerheyts middelpunt L. Commende dan de voortghetrocken H A onder t'swaerheyts middelpunt L, soo treckt M t'selfde ghewicht dat sy track doen H A in t'swaerheyts middelpunt quam. T'selve salmen oock alsoo bethoonen

* Perpendicularem.

* Proportionē.

[p. 112]

commende de voortghetrocken lini H A boven t'swaerheyts middelpunt L, dat is treckende den pylaer I K rechtneerwaert onder den waghen. Uyt het welcke t'voornemen openbaer ende bewesen is.

10 Voorstel.

Ghedaenten en omstandigen der oneyndelicke crachten te verclaren.

De menschen maecken verscheyden reetschappen om cracht met te doen, waer in sy de ghewelt altijt connen vermeerderen sonder eynde, welcke wy daerom int ghemeen oneyndelicke crachten noemen. Om te verclaren de ghedaenten en omstandighen der selfde; Als wat doende ghewelt in sulcken voorghestelden tuych evestaltwichtich sal sijn teghen het vertreckelick ghewicht: Hoe langhe tijt datter sal behouven om t'selve een seker verheyt te beweghen, en dierghelijcke, daer toe sal ick een form teyckenen van eenvoudighe gedaente, doch sulcx dat icker mijn voorghenomen verclaring bequamelick me sal connen te kennen gheven, eerst wat geseyt hebbende van Archimedes oneyndelicke cracht, daer Plutarchus en ander af schrijven: Te weten dat Hiero Coninc van Sicilien dede bouwen een schip van uytnemender grootheyt, en constiger form, om te schencken an Ptolemeus Coninck van Egypten: T'welck doent volmaeckt was, de Burghers van Syracusa om sijn swaerheyt in zee niet crijghen en conden, maer doen Archimedes daer an ghestelt hadde sijn tuych diemen opt Griecx Charistion noemde, Hiero heeftet daer door selfs alleen metter hant vertrocken. Dese Charistion (nae de form die Iacques Besson daer af heeft laten uytgaen, ghevonden inde bouckas des Conincx van Vranckrijck) hadde assen met oneyndelicke schrouven: Een werck voorwaer weerdich sijn eewige ghedachtenis, en soudet hier beschrijven overmidts wy tot sulcke stof ghecommen sijn, ten waer ick in die plaets stelde de boveschreven oneyndelicke cracht, als connende daer me bequamelick verclaren, ghelijck gheseyt is, de ghemeene reghel der eyghenschappen vande oneyndelicke crachten, en dat boven dien dit mijns bedunckens tot sulcke daet bequamer is: Te weten stercker ghedueriger werck: Van minder cost: Door t'welckmen op eveveel tijts meer afveerdicht: En ghelijck de Charistion van oneyndelicke cracht. T'maecksel daer af is dusdanich.

Men sal nemen een boom ofte balck als A B, sterck ende groot naer de cracht dieder door gedaen moet sijn: Daer nae salmen maken een yser sterreken als C, ick neem dat sijn^* middellini van drie duymen sy, ende dattet ses tanden heb, ende in sijn middel stekende een yseren as C D, an d'eynden C D viercantich, ende tusschen beyden rondt, daer naer de sterre E, ick neem met 18 tanden, ende t'sterreken F met 6 tanden, daer in stekende een yseren as E F, even ende ghelijck met den as C D, te weten ande eynden viercantich, ende tusschen beyden ront: ende ghelijck E F is, soo salmen oock maken G H, ende I K, dat is G ende K elck met ses tanden, ende H ende I met 18 tanden. Maer want de bovenste sterren de meeste last sullen lijden, als hier naer blijcken sal, soo sullen sy stercker ende grooter sijn dan d'onderste, daer uyt oock volghen sal dat de assen evewijdich van malcanderen wesende, de sterre H sal connen ghenaken an F, ende niet an K, ende de sterre G an I, ende niet an E, t'welck soowesen moet.

Daer naer salmen maken de kruck L M N, wiens viercantich gat des viercantighen cokers L, passe op alle de viercantighe eynden der assen, als D, F, H, K,

* Diameter.

[p. 113]

ende L M sy lanck een voet, so gemeenlick sulcke langden in crucken van slijpsteenen ende dierghelijcke sijn, ende M N soo lanck als hier naer geseyt sal worden. Daer naer salmen inden boom A B vier gaten booren, van malcander in sulcker wijde als de vierassen staen, ghelijck de gaten O, P, Q, R, van achter door commende, daer de vier assen I K, G H, E F, C D in passen meugen, ende de langde der assen tusschen de sterren, sal even sijn ande dickte des booms, ende der assen vierhouckighe eynden an K, H, F, D, sullen al ontrent de drie ofte vier duymen buyten de sterren steken, Daer naer aftreckende de sterre I, men sal den as I K steken, int gat O, ende insgelijcx den as G H in t'gat P, ende E F in Q, ende C D in R, stellende



wederom elcke sterre van achter an heur as, alsoo dat de tanden der sterre F ande voorste sijde, meughen doen draeyen de sterre H, ende dat de tanden der sterre C ande achterste sijde, meughen doen draeyen de sterre E, ende dat de tanden van G, doen draeyen I, ende haer ghestalt voor volmaeckt Almachtich sal dan sijn als hier nevens.

Nu ghelijck wy t'voorbeelt hier ghegheven hebben van vier assen, soo machmender meer ofte min stellen: Ende de 18 tanden der groote sterren welcke drievoudich sijn tot de ses tanden der cleene sterren, die machmē in meerder ofte minder reden stellen, naer ghelegentheyt van t'ghene daermen t'Almachtich toe maeckt.

Van tghebrvyck ende ander Ancleving des almachtichs.

Maer om degebruyck deses Almachtichs te verclaren, wy sullen een voorbeelt gheven daer alle d'ander ghenouch door sullen bekent sijn, te weten

[p. 114]

van schepen daer mede over dammen of dijcken te trecken, want dat den cleynsten dienst niet en schijnt, die dese landen hier in gedaen mach worden, voornamelic Hollant. Laet A B t'bovenschreven Almachtich sijn, met de sterrē, K, H, F, over dees sijde des booms A B, ende de sterren I, G, E, C, over d'ander sijde, ende L M N sy de cruck, ende S den as, diens middellini van 1½ voet sy, commende door den boom met een yser sterre an t'eynde als T, wiens middelliniick neem te sijn van 2 voeten (sy moet ten minsten so veel langher sijn dan de middellini van t'rondt des as S, dat de sterre I den as S niet en gheraecke) ende te hebben 36 tanden, ende V sy den dam, wiens hoochde bovē t'onderste des scheeps vryelick



int water ligghende (dat is int ansien der^* hangende lini van t'sop des dams totet plat evewijdich vanden^* sichteinder door t'onderste des schips) sy vier voeten, ende X sy t'schip. Nu om t'selve over te winden, men sal draeyen ande kruck L M N, daerom sal d'hanthaef M N so lanck sijn, datter al de ghene diemender toe bruycken wil, over beyden sijden bequamelick an staen meughen.

* Perpendiculares.

* Horizonte.

Reden dieder is vande keeren des krvcx tot de keeren des as.

Want de kruck L M N driemael omdraeyt teghen F eenmael, soo sal sy 9 mael omdraeyen teghen H eenmael, ende 27 mael teghen Keenmael, ende 162 mael teghen T ofte den as S eenmael. Tisoock kennelick dat de kruck ghestelt an t'eynde des as F, sy sal 54 mael omdraeyen teghen Seenmael, ende gestelt an H sal 18 mael omdraeyen teghen S eenmael, ende ghestelt an K, sal ses mael omdraeyen teghen S eenmael, ende ghestelt an T, sal soo dickmael om-

[p. 115]

draeyen als S. Maer als yemant draeyt an een hoogher dan D, by ghelijcknis an K, op dat dan alle de onderste sterren niet snellick mede omdraeyen, t'welck onnoodighe swaerheyt soude aenbrenghen, soo salmen d'eerstvolghende der onderste, t'welck hier G soude wesen, op sijn as wat verschuyven, tot dat heur tanden buyten de tanden van I sijn, ende dan sullen alle d'onderste stil staen.

Reden vande cracht des draeyers ande crvck, tot het ghetrocken vvicht als t'schip X.

Wan't L M lanck een voet door t'ghestelde, achtvoudich is teghen de halve middellini vande sterre C, soo sal t'ghewicht veroirsaeckt uyt de sterre E op C, teghen sijn evestaltwichtighe swaerheyt ofte macht an M N, wesen als van 8 tot 1, ende om de selve reden door t'veroirsaekte van H op F, als van 24 tot 1, ende van I op G, als 72 tot 1, ende van T op K, als 216 tot 1: Maer t'rondt des as S is^* machtelick even an t'rondt T, (wy segghen machtelick, want^* daetlick, de middellini des rondts van S doet 1½ voet van T twee voeten door t'ghestelde, maer want de tanden van T, sesvoudich sijn an de tanden van K, daerom sal sijn middellini machtelick sesvoudich sijn teghen de middellini van K, doende 3 duymen, die van T dan 18 duymen, dat is 1½ voet, als de middellini des as S) t'ghewicht dan anden as S recht neerhanghende, sal sulcken reden hebben tot sijn evestaltwicht, ofte macht an M N, als van 216 tot 1. Wy souden oock connen vanden as S neerwaert de rekening maken ghelijck sy hier van onderen opwaert ghedaen is.

Wy connen t'voornoemde oock aldus verclaren: Anghesien M N 162 mael omdraeyt, tegen den as S eenmael, (als boven bewesen is) ende dat de middellini des radts beschreven door den keer van M N, sulcken reden heeft tot de middellini des rondts vanden as S, als 4 tot 3, (want L M is een voet, ende de^* half-middellini des rondts vanden as S is ¾ voets) soo sal de langde der omtrecken vande 162 ronden beschreven door de keeren van M N, sulcken reden hebben tot de langde vanden omtreck des rondts der as S, als 216 tot 1, de selfde reden sullen oock hebben de 216 halfmiddellinien van dat rondt, tot de eenighe halfmiddellini van dit rondt, Daerom oock, door het 1 voorstel des 1 boucx, sal t'ghewicht an die, sulcken reden hebben an t'ghewicht ofte de macht an dese, als van 216 tot 1 ghelijck vooren. Waer uyt volght dat wesende an M N een gheduerighe macht soo groot als 25 ℔ souden neertrecken, t'welck ick de macht schat van eē man, ende grooter als hy wil, (wel is waer dat een man ter noot onghelijck veel grooter macht doen can, maer wy nemen dit voorbeeltsche wijse) de selve macht sal evestaltwichtich sijn teghen 5400 ℔ (dat is 216 mael 25 ℔) recht neerhanghende anden as S: Ghenomen nu dat het schip X sesvoudich sy, teghen dat sijn evestaltwicht an den as S recht neerhanghende, soo sal t'schip X weghende 32400 (dat is 9 last ghewichts reeckenende 3600 ℔ voor t'last) evestaltwichtich sijn teghen t'ghewicht, ofte die gheduerighe macht van 25 ℔an M N.

* Potentiae.

* Actis.

* Semidiameter.

[p. 116]

Vande menichte der keeren des crvcx om tschip over den dam

te vvinden: Ende vanden tijt die de arbeyders behouven.

Maer wesende door t'ghestelde t'schip sesvoudich teghen t'ghewicht anden as Shanghende, soo sal de langde van t'sop des dams scheefneerwaert, oock sesvoudich sijn tegen de hoochde diet schip moet verheven worden, (door het 19 voorstel des 1 boucx) welcke door t'ghestelde is 4 voeten, de selve dan ses mael maeckt 24 voeten, voor de voornoemde langde; Laet ons nu nemen dat dese 24 voeten ghewonden moeten worden op den as S, om t'swaerheyts middelpunt des schips over t'middel des dams te crijghen; Soo wy dan als vooren, den omtreck van t'rondt des as stellen als drievoudich (die reden is in desen ghevalle naer ghenouch) teghen sijn middellini 1½ voet, sy sal 4½ voeten wesen, de selve sijn inde voornoemde 24 voeten 5½ mael, den as S dan, sal 5⅓ keeren moeten omdraeyen, maer elcke keer van die behouft 162 keeren van M N als vooren bewesen is, daer sullen dan in als behouven 864 keeren van M N.

Wy souden oock meughen aldus segghen: Elcken keer van M N vervoert 25 ℔ ses voeten verre, dat is, hanghende een ghewicht anden as S van 5400 ℔, elcken keer van M N doet soo veel, als oft het van dien telckemael 25 ℔ 6 voeten hoogh trocke, ende vervolghens als oftet sesmael 25 ℔, dats 150 ℔ des scheeps, trocke 6 voeten verre, daerom gedeelt 32400 ℔ door 150 ℔, comt 216, waer door t'schip met elcke 216 keeren van M N ses voeten voort commen sal, maer t'moet viermael 6 voeten commen, t'moet dan hebben viermael 216 keeren, dat is als vooren 864 keeren. Ofte andersins (anghesien t'schip in als 4 voeten hooch moet commen) men machaldus segghen, met eenen keer trecktmen 25 ℔ ses voeten hooch, met hoe veel keeren salmen 32400 ℔ trecken 4 voeten hooch?comt als vooren met 864 keeren.

Maer wy achten datter een man 1000 can doen op een vierendeel uyrs, ghenomen dan dat hem alles soo heb als gheseyt is, hy sal t'schip met datter in is t'samen 9 last weghende, alleen overwinden op min dan een vierendeel uyrs. Maer sooder drie mannen toe waren, sy meughen de cruck an F steken, ende sullent dan overtrecken op t'derdendeel van een vierendeel uyrs, dat is op 1/12 uyrs: Ende sooder neghen mannen toe waren, sy mochten de kruck an H steken, ende sullent in 1/36 uyrs overwinden. Men soude oock meughen anden anderen boom Y een Almachtich maken als an den boom A B, ende bedeelen de menschen op beyden sijden.

Merckt.

Wy hebben hier een voorbeelt ghestelt al of t'schip in t'overwinden voor den arbeyders altijt van eenvaerdigher swaerheyt waer, welcke nochtans merckelick verandert naer de form ende ghestalt van t'voorghesette, want swaerder gadet int laetste dan int begin, om de redenen die int 3 voorbeelt des 9 voorstels deses boucx van derghelijcke gheseyt sijn; Daerom salmen t'voorgaende achten als voorbeelt verclarende hoemen in yder voorghestelde ofte begheerde form sijn rekening maken sal.

Angaende de sterren die in t'Almachtich recht boven malcanderen ghestelt

[p. 117]

sijn, men soudese oock meughen neven den anderen voughen, ofte met paren, daert de gheleghentheyt hiessche.

Verclaring van t'ghene vooren belooft is.

Ick heb hier vooren int t'begin deses voorstels gheseyt dat dese oneyndelicke cracht mijns bedunckens soude sijn stercker werck; Ende van minder cost dan den Charistion; Ende door t'welckmen op corter tijt meer afveerdicht; Ende van oneyndelicke cracht.

Angaende de sterckte des wercx, ick achte die openbaer, (daer beneven een beter nemmermeer versmaende) want wat soudemen tot sulcken daet vromer wenschen, dan een stercke boom soo hy ghewassen is, wiens stof vaster in een hout dan eenich gheraemte van verscheyden stucken vergaert. De cleynen cost is oock kennelick.

Wat den corteren tijt belangt, die volght daer uyt, datmen de kruck mach steken an sulcken as der sterren alsmen wil, naer ghelegentheyt vande menichte der arbeydende menschen, ende het tetreckenwicht, te weten voor de lichter ghewichten de kruck hoogher, ende voor de swaerder leegher te steken, al soo datmen door eenen behoirlicken arbeyt, het tetreckenwicht hoe swaer het sy, altijt gaende hout sonder stil staen, t'welck inde Charistion noch ander windassen soo niet gheschien en can, want om een cleyne lichte schuyt, ghebruycktmen door windassen, t'ghene een veel grooter cracht vermach, t'welck den tijt langher doet an loopen. Maer is het te treckenwicht swaerder dan daer door bequamelick can gedaen worden, soo moetmen daer toe nemen groote menichte van menschen ofte peerden, welcke met grooten arbeyt altemet voortgaen, altemet stil staen, ende daer door den tijt verlanghen; Ia boven dien de schepen seer beschadighen, want een der grootste die over den Leytschen Dam getrocken worden van derthien oft veerthien last, behouft twintich menschen die inde raeyers gaen, welcke dickwils naer eenen stille stant al t'samen neerdalen, ende met eenen grooten gheweldigen hurt de schepen seer quetsen, t'welck door t'Almachtich niet gheschien en can, overmits t'schip altijt eenvaerdelick ende sachtkens voorcomt.

Maer om vande oneyndelicke cracht te segghen, het is te weten datmen met de kruck hier boven an D, so veel vermach alsmen soude met een windas diens radts middellini van 324 voeten waer, t'welck aldus betoocht wort: Laet wesen een radt diens middellini 324 voeten, ende sijn as sy S, wiens rondts middellini sy van 1½ voet, waer door de halfmiddellini des radts sulcken reden sal hebben tot de halfmiddellini des as, als 216 tot 1, daerom oock t'gewicht ofte de macht anden as, sal sulcken reden hebben tot sijn evestaltwicht an t'uyterste des radts, als 216 tot 1 door het 9 voorstel deses boucx, de selve reden isser oock van t'ghewicht an den as S, tot sijn evestaltwicht an M N, daerom soo wy gheseyt hebben wesende de kruck an D, men sal door haer anden as S so veel vermeughen, als door een radt diens middellini lanck waer 324 voeten. Maer de meeste diemen maeckt en schijnen de 30 voeten niet te bereycken, waer uyt opentlick blijckt hoe veel t'Almachtich meer vermach dan de windassen, wel is waer dat eenen gaende int radt eens windas, sijn ghewelt met minder arbeyt doet, maer ghemerckt de voorgaende omstaende, ten is niet het nutste. Doch soo yemant sulcken voordeel door den ganck in t'radt begheerde daert noodich viel, hy

[p. 118]

soude an eenighen as der assen D, F, H, K, T, meughen steken een schijfloop, inde plaets vande kruc, stellende tanden an t'uyterste van eenich radt eens windas, die in die schijfloop draeyen mochten, maer t'voordeel en soude dickmael de oncosten niet weerdich sijn.

Maer soo dees voornoemde reetschap niet gheweldich ghenouch bevonden wierde, om daer mede t'voornemen te volbrenghen, daer en is verloren cost, noch onnoodighen arbeyt ghedaen, want stellende alleenelick onder D noch een as als d'ander, drievoudighende de voorgaende 216, ende daer an de kruck stellende, 1 soude ande selve evestaltwichtich sijn teghen 648 anden as S, door welck middel men tot de begheerde ghewelt commensal.

Maer datmen alsoo maeckte een almachtich met 30 assen, wiens tanden van de grootste sterren thienvoudich waren teghen de tanden vande cleynste sterren, ende het deel des crucx als L M, even ande halfmiddellini der grootste sterre, ende t'rondt des as als S, even an t'rondt der cleenste sterre (t'welck alsoo wonderlicken grooten werck niet en waer) t'ghewicht an soodanighen as hanghende, soude sulcken reden hebben tot sijn evestaltwicht ande kruck, als 1000000000000000000000000000000 tot 1: Genomen dan dat den omtreck van t'ront der cleenste sterre waer 1 voet, soo soude den omtreck van t'radt eens windas (diens assens ronts omtreck oock een voet) om de selve cracht daermede te doen, moeten sijn van 1000000000000000000000000000000 voeten: Maer den omtreck van t'grootste rondt des eertrijcx (rekenende den^* trap op 480 stadien, ende elcke stadie op 125 Meetconstighe stappen, ende elcken Meetconstighen stap op 5 voeten) en is maer 108000000 voeten; Siet dan hoe menich hondert duysentmael grooter dan t'grootste rondt des eertbodems, dat het ront eens radts van een windas soude moeten wesen, om soo grooten ghewelt mede te doen als met sulcken slechten Almachtich. Laet ons nu ande kruck (stekende anden leeghsten as van soodanighen Almachtich) een kindeken stellen, wat meer macht daer an doende dan een hangende pont, t'selve soude op dē hoochsten as een ghewicht winden van 100000000000000000000000000000000 ℔, (maer ghedenckt dat dien hoochsten as op den eersten dach gheen heele keeren doen en soude) dat is een ghewicht swaerder dan vier duysentmael t'eertrijck met al datter in is, t'welck aldus bewesen wort: Den omtreck van t'grootste rondt des eertrijcx is van 108000000 voeten, als boven gheseyt is, daerom t'plat des selfden ronts is minder dan 1000000000000000 voeten, daerom ooc is t'vlac des werelts-cloots minder dan 4000000000000000 voeten, ende t'sestendeel der middellini is corter dan 6000000 voeten, daer mede vermenichvuldicht de voornoemde 4000000000000000, soo is t'eertrijck minder dan 24000000000000000000000 teerlijncksche voeten; Laet elcken voet 100 ℔ weghen (sy en is op veel na soo swaer niet) t'gheheele eertrijck dan is lichter als 240000000000000000000000000 ℔, t'selfde is meer dan vier duysent mael in 1000000000000000000000000000000 ℔ soo wy bethoonen wilden.

Wy segghen dan met reden dat dese reetschap machtelick van oneyndelicke cracht is: Daerom doen Archimedes seyde, soomen hem een vaste plaets leverde buyten t'eertrijck daer hy sijn Charistion mocht stellen, hy soude t'eertrijck uyt sijn plaets trecken, hoe vreemt het luyt, tis nochtans de reden lijckformich, want by aldien het soo niet en waer, de swaerste swaerheyt en soude niet sulcken reden hebben tot de lichtste, als den langsten erm tot den cortsten, t'welck door het 1 voorstel des 1 boucx onmeughelick is. Maer om by voorbeelt hier af te spreken; Ghenomen dat de Charistion ofte t'Almachtich op soodanighen plaets stonde, ende dat het certrijck woughe alsvooren gheseyt is

* Gradum.

[p. 119]

240000000000000000000000000 ℔, ende dat een man met yder keer der kruck 100 ℔ drie voeten hoogh trocke, ende op yder uyr 4000 keeren dede, ende dat gheduerende thien jaren lanck, rekenende t'jaer op 365 daghen, tis openbaer dat hy t'eertrijck op dien tijt het 10512/24000000000000000000 eens voets, dats bycans 1/2400000000000000 voets, uyt sijn plaets vertrecken soude, t'welck wel is waer een onsienlicke langde is, maer wy moesten de oneyndelicke cracht verclaren, die machtelick hier in bestaet.

Nu hoe alsulcke Almachtighen tot verscheyden wercken sullen meughen ghevoucht worden, als dat een schip in hem sal connen hebben een seer cleen reetschap van gheringhen cost, nochtans seer crachtich, hem dienende voor Craen om te laden ende ontladen: Om groote anckers op te winden: Voort om perssen te maken, als lakenperssen ende dierghelijcke, gheweldelicker druckende dan noyt perssen en dructen: Om in groote ghebouwen sware steenen op te trecken, ende meer ander daermen groote ghewelt behouft, van alle dese en gheven wy gheen besonder voorbeelden, overmits yder uyt het voorschreven Almachtich an sijn werck een derghelijcke, naer gheleghentheyt sal meughen vougen, beter dan wy segghen connen; Tis voor ons ghenouch sijn ghedaente alhier beschreven te hebben.

derde bovcx

EYNDE.