Wisconstighe gedachtenissen. Deel 1: van 't weereltschrift

Nv van satvrnvs stilstanden en deys inghen.

Van desen handel der stilstanden en deysingen sullen eerst beschreven worden drie^* vertoogen, dienende tot gront der werckstucken niet alleen van Saturnus, maer int ghemeen van al d'ander Dwaelders die stilstandt en deysing hebben, te weten Iupiter, Mars, Venus, en Mercurius.

* Theoremata.

Vertooch. 50 Voorstel.

De sijde eens rechtlinich driehoucx in tvveen gesneen⁺ sijnde, soo dattet een deel niet cleender en is dan de sijde hem gherakende: de reden des houcx het ander deel gerakende, totten houck het eerste deel gherakende, is cleender dan de reden van t'eerste deel tottet ander.

T'ghegheven. Laet A B C een rechtlinich driehouck sijn, diens sijde B C in tween ghesneen is an t'punt D, soo dattet een deel C D, niet cleender en is dan de sijde A C hem gherakende: Ick neem ten eersten dat C D even is an A C. T'begheerde. Wy moeten bewijsen dat de reden des houcx B het ander deel D B gherakende, totten houck B C A het eerste deel C D gherakende, cleender is dan de reden van t'eerste deel C D, tottet ander D B.

T'bereytsel. Laet ghetrocken worden D A, daer na A E, even en evewijdege met D C, daer na C E, en de selve voorwaert tot datse de voortgetrocken B A ontmoet in F. Voort sy op A als middelpunt beschreven de booch

+ Ptol. lib. 12. Cap. 1. Regi. lib. 12. prop. 3. Coper. lib. 5. prop. 35.

[p. 222]

C G, vallende G inde lini A F, en sal de selve booch C G nootsakelick strecken deur t'punt E, om dat A C en A E even sijn.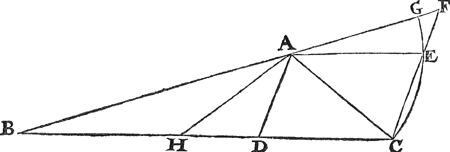

t'Bewys.

Gelijck het rontsdeel G A E, tottet rontsdeel E A C, alsoo het rontsdeel G A E, tottet rontsdeel E A C.

Maer dē driehouck E A C, is cleender dā het rontsdeel E A C, daerom

Het rontsdeel G A E, heeft totten driehouck E A C, grooter reden dan t'selve rontsdeel G A E, tottet rontsdeel E A C.

Maer den driehouck F A E, is grooter dan het rontsdeel G A E, daerom deur noch merckelicker oirsaeck

Den driehouck F A E, heeft totten driehouck E A C, grooter reden dan het rontsdeel G A E, tottet rontsdeel E A C.

Maer ghelijck den driehouck F A E, totten driehouck E A C, alsoo de lini F E, totte lini E C, daerom

De lini F E, heeft totte lini E C, grooter reden dan het rontsdeel G A E, tottet rontsdeel E A C.

Maer ghelijck het rontsdeel G A E, tottet rontsdeel E A C, alsoo den houck G A E, totten houck E A C, daerom

De lini F E, heeft totte lini E C, grooter reden dan den houck G A E, totten houck E A C.

Maer den houck B, is even an dē houck G A E, en den houck A C B, anden houck E A C, daerom

De lini F E heeft totte lini E C, grooter reden dan den houck B, totten houck A C B,

Maer ghelijck F E tot E C, alsoo C D tot D B (want ghelijck F E tot A D, alsoo E A tot D B, maer E C is even met A D, en C D met E A, waer deur als boven gheseyt is, gelijck F E tot E C, alsoo C D tot D B) daerom

De lini C D, heeft totte lini D B, grooter reden dan den houck B, totten houck A C B. Ende de laetste reden eerst ghestelt: Den houck B, heeft totten houck A C B, cleender reden dan de lini C D, tot D B.

Maer by aldien C D grooter ghestelt waer dan A C, ick neem van C tot H, soo sal uyt noch merckelicker oirsaeck den houck B, tottē houck A C B, cleender reden hebben dan C H tot H B. T'beslvyt. De sijde dan eens rechtlinich driehoucx in tween ghesneen sijnde, soo dattet een deel niet cleender en is dan de sijde heur gherakende: De reden des houcx hei ander deel gherakende, totten houck het eerste deel gherakende, is cleender dan de reden van t'eerste deel tottet ander, t'welck wy bewijsen moesten.

[p. 223]

Vertooch. 51 Voorstel.

Soo de reden des inronts middelpunts loop, tot des⁺ Dvvaelders inronts loop, grooter vvaer dan vande halfmiddellijn des inronts, totte lini tusschen des Eertcloots middelpunt en des inronts naeste punt: T'is onmeughelick den Dvvaelder te deysen.

T'ghegheven. Laet A B C een inront sijn diens middelpunt D, Eertcloots middelpunt E, verstepunt A, naestepunt C, deur t'welck ghetrocken is de lini A D C E: En de redē van des inronts middelpunts loop tot des Dwaelders inrontsloop, sy grooter dan de reden van D C halfmiddellijn des inronts, totte lini E C tusschen des Eertcloots middelpunt E en des intonts naestepunt C. T'begheerde. Wy moeten bewijsen onmeughelick te sijn den Dwaelder te deysen. T'bewys. Soot meughelick waer dat sal ten merckelicksten geschien by het naestepunt C: Latet ten eersten sijn an F, sulcx dat C F het cleenste booghsken sy, dat, soot meughelick waer, ghevoelick is, te weten van C tot F na t'vervolgh der trappen. Maer om te bewijsen dattet daer niet en ghebeurt, ick treck E F met E D, en segh aldus: Want des driehoucx F D E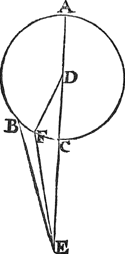



sijde D E in tween gesneen is an C, soo dattet een deel D C, niet cleender en is dan de sijde D F heur gerakenke, soo is de redē des houcx D E F, tottē houck E D F, cleender dan de reden vant eerste deel D C, tottet ander C E deur het 50 voorstel: Daerom de reden van des inronts middelpunts loop tot des Dwaelders schijnbaer inrontloop, is grooter dā des houcx D E F, totten houck E D F, waer uyt volght dat E D F gestelt sijnde voor Dwaelders inronts loop, dat den houck F E D cleender is dan na t'behooren, om de ware inronts middelpunts loop te beteyckenen: Daerom laet ons een grooter trecken als D E B, die dē warē houck beteyckē. Dit soo wesende, op dē tijt dat den Dwaelder int inront gheloopen heeft den booch C F, dats schijnbaerlick den houck F E D teghen t'vervolgh der trappen, soo heeft hem des inronts middelpunts loop op dien tijt voorwaert ghebrocht den houck D E B, t'welck meer voorwaert is dan F E D achterwaert, soo veel als dē houck B E F, daerom hy en heeft gheen deysing ghehadt.

En sghelijcx sal oock betoont worden wesende den Dwaelder ghestelt over d'ander sijde des naestepunts C. T'beslvyt. Soo dan de reden des inronts middelpunts loop, tot des Dwaelders inronts loop, grooter waer dan vande halfmiddellijn des inronts, totte lini tusschen des Eertcloots middelpunt en des inronts naestepunt: T'is onmeughelick den Dwaelder te deysen.

+ Ptol. lib. 12. cap. 1. Regi. lib. 12. prop. 4.

1 Vervolgh.

Vyt het verkeerde deses voorstels volght, dat als die reden cleender is, den Dwaelder deysing te connen hebbē: Maer sulcke reden in Saturnus loop cleender te wesen, blijckt aldus: Des inronts middelpunts loop is deur het 18 voor-

[p. 224]

stel des 1 boucx op een dach, van	2 ①. 0. 3.
Sijn loop int inront is op een dach deur het 19 voorstel des 1 boucx, van	57 ①. 7. 44.
Des inronts halfmiddellijn is deur het 47 voorstel deses 2 boucx, vā	1165.
De lini tusschen des Eertcloots middelpunt en des inronts naestepunt alst ten versten vanden Eertcloot is, doet deur het 46 voorstel deses 2 boucx	10064.
Daerom segghende 2 ① 0. 3 eerste in d'oirden, gheeft 57 ① 7.44 tweede in d'oirden, wat 1165 derde in d'oirden ?Comt	33264.

Sulcx dat dese vier ghetalen 2 ① o. 3. 57 ① 7.44. 1165. 33264 everedenich sijnde, dats d'eerste redē even mette tweede, soo moet d'eerste cleender wesen dan van 1165, tot 10064. Inder voughen dat, als gheseyt is, Saturnus deysing heeft wesende het inronts middelpunt an sijn wechs verstepunt. Maer want de lini 10064 de langste is dieder valt tusschen des Eertcloots middelpunt en des inronts naestepunt, waer deur sijn deysing daer ten cleensten is, soo blijckt met noch stercker reden dat hy oock deysing moet hebben wesende het inronts middelpunt tot ander plaetsen sijns wechs in ghedaente als boven.

2 Vervolgh.

Wy hebben hier vooren de reden van Saturnus inrontsloop tot des inronts middelpuntsloop, ghestelt van 57 ① 7.44, tot 2 ① 0. 3. Doch machmen in die plaets om lichticheyts wille van ander volgende rekeninghen nemen twee heele ghetalen inde selve reden, maer t'een van 10000: Om welcke te vinden ick segh, 57 ① 7. 44, gheven 2 ① 0. 3, wat 10000? Comt 350. Sulcx dat 10000 en 350, of in die plaets 1000 en 35 (die inde selve reden sijn) ons connen dienen in plaets der boveschreven 57 ① 7. 44, en 2 ① 0. 3.

Vertooch. 52 Voorstel.

Wesende ghetrocken een lini van des Eertcloots middelpunt⁺ deur het inront, soo dat den helft des deels dier lini binnen het inront, in sulcken reden sy tottet deel buyten het inront, als des inronts middelpuntsloop tot des Dvvaelders inronts loop: De sne dier lini int inront is des Dvvaelders stantpunt.

T'ghegheven. Laet A B C D het inront sijn diens middelpunt E, des Eertcloots middelpunt F, van t'welck deur E ghetrocken sy de lini F D E A, soo dat A is t'verstepunt, D t'naestepunt, en de reden van des inronts middelpunts loop tot des Dwaelders inronts loop, sy cleender dan de reden van E D inronts halfmiddellijn, totte lini D F tusschen des Eertcloots middelpunt en het naestepunt D, want anders waert onmeughelick den Dwaelder te deysen deur het 51 voorstel: Daer na sy getrocken de lini F B, sniende het inront in G en B, soo dat H G helft des deels G B binnen het inront, in sulcken reden sy tottet deel G F buyten het inront, als des inronts middelpunts loop, tot des Dwaelders inronts loop. T'begheerde. Wy moeten bewijsen dat de sne G dier lini int inront des Dwaelders stantpunt is.

+ Prol. lib. 12. cap. 1. Regi. lib. 12. prop. 5.

[p. 225]

Merckt.

Wy sullen dit bewijs in tween deelen, betoonende int eerste dat den Dwaelder van C tot G overal voortganck heeft, maer int tweede van G na D overal deysing, waer uyt besloten sal worden G des Dwaelders stantpunt te wesen.

Bereyt sel vant eerste deel des bevvijs.

Laet ghenomen worden een booch van C tot G, als Dwaelders inrontsloop na t'naestepunt toe, en getrocken sijn de rechte linien F C, F G, E G, E C, sulcx dat C E G is den houck van des Dwaelders inrontsloop, waer me wy hem bewijsen moeten van C tot G gheen deysing, maer overal voortganck te hebben.

Bevvijs van t'eerste deel.

Des driehoucx B C F sijde B F is an G in tween gesneen, soo dattet deel B G, niet cleender maer grooter is dan de sijde B C, daerom deur het 51 voorstel De reden des houcx B F C, totten houck F B C is cleender dan van B G tot G F.

Laet ons nu nemen des tweedē en vierden paels dobbel, t'welck soo sijnde, De reden des houcx B F C, tottet dobbel des houcx F B C, is cleender dan van B G, tottet dobbel van G F.

Laet ons nu nemen des derden en vierde paels helft, t'welck soo sijnde, De reden des houcx B F C, tottet dobbel des houcx F B C, is cleender dan dē helft van B G, totten helft des dobbels van G F, dats tot G F eenmael.

Maer den houck C E G opt middelpunt E, is het dobbel des houcx F B C op den omtreck: En H G dē helft van B G, daerom De reden des houcx B F C, totten houck C E G, is cleender dan van H G, tot G F.

Maer C E G is hier des Dwaelders inrontsloop deur t'bereytsel, daerom De redē des houcx B F C, tot des Dwaelders inrontsloop C E G, is cleender dā van H G tot G F.

Maer H G is deur t'gegeven in sulcken reden tot G F, als des inronts middelpuntsloop, tot des Dwaelders inrontsloop, daerom

Den houck B F C, is cleender dan des inronts middelpuntsloop op den voorghestelden tijt, daerom laet ons een meerder teyckenen, soo groot wesende als na t'behooren, welcke sy B F I: Dit soo wesende, te wijle den Dwaelder int in-

[p. 226]

ront loopt den booch C G, of den houck C E G, soo beschrijft hy uyt des Eertcloots middelpunt F ghesien van weghen den selven sijn inrontsloop schijnbaerlick den houck C F B, of C F G tegen t'vervolgh der trappen. Maer in dien tijt beschrijft het in ronts middelpunt een houck even an B F I, of G F I, na t'vervolgh der trappen, daerom den Dwaelder is van weghen des inronts middelpuntsloop schijnbaerlick meer voorwaert ghegaen, dan van weghen sijn inrontsloop achterwaert, soo veel als den houck C F I, welcke den Dwaelder schijnbaerlick ghevoordert is, daerom heeft hy inden gantschen booch van C tot G voortganck.

Maer om nu te bewijsen dat hy van G na t'naestepunt D toe altijt deyst, soo stellen wy tot dien eynde het

Bereytsel vant tvveede deel des bevvijs.

Laet genomen worden een booch van G tot K als Dwaelders inrontsloop na t'naestepunt toe, en getrocken sijn de rechte linien F K, E K, sulcx dat G E K is den houck des Dwaelders inronts loop, waer me wy hem bewijsen moeten van G tot K overal deysing te hebben.

Bevvijs vant tvveede deel.

Des driehoucx B K F sijde B F, is an G in tween ghesneen, soo dattet deel G F niet cleender maer grooter is dan de sijde K F, daerom deur het 51 voorstel

De reden deshoucx F B K, tottē houck B F K, is cleender dan van G F, tot B G. En deur verkeerde stelling,

De reden des houcx B F K, tottē houck F B K, is grooter dan van B G tot G F. Laet ons nu nemen des tweeden en vierden paels dobbel, t'welck soo sijnde,

De reden des houcx B F K, tottet dobbel des houcx F B K, is grooter dan B G, tottet dobbel van G F.

Laet ons nu nemen des derdē en vierde paels helft, t'welck soo sijnde, De reden des houcx B F K, tottet dobbel des houcx F B K, is grooter dan den helft van B G, totten helft des dobbels van G F, dats tot G F eenmael.

Maer den houck K E G opt middelpunt E, is het dobbel des houcx F B K op den omtreck, en H G den helft van B G, daerom

De reden des houcx B F K, tottē houck K E G, is grooter dan van H G tot G F.

Maer K E G is hier des Dwaelders inrontsloop deur t'bereytsel, daerō

De redē des houcx B F K, tot des Dwaelders inrontsloop K E G, is grooter dan van H G, tot G F.

Maer H G is deur t'ghegeven in sulcken reden tot G F, als des inronts middelpuntsloop, tot des Dwaelders inrontsloop, daerom

Den houck B F K, is grooter dan des inronts middelpuntsloop op den voorgestelden tijt. Daerom laet ons een minder teyckenen, soo cleen wesende als na t'behooren, welcke sy B F L. Dit soo wesende, te wijle dē Dwaelder int inront loopt den booch G K, of den houck G E K, soo beschrijft hy uyt des Fertcloots middelpunt F ghesien van weghen den selven sijn inrontsloop, schijnbaerlick den houck B F K, of G F K teghen t'vervolgh der trappen: Maer in dien tijt beschrijft het inronts middelpunt een houck even an L F B, of L F G, na t'vervolgh der trappen, daerom den Dwaelder is van weghen des inronts middelpuntsloop schijnbaerlick min voorwaert gegaen, dan van wegen sijn inrontsloop achterwaert, soo veel als den houck L F K, welcke den Dwaelder schijnbaerlick verachtert is, daerom heeft hy inden gantschen booch van G tot K dey-

[p. 227]

sing. T'beslvyt. Wesende dan getrocken een lini van des Eertcloots middelpunt deur het inront, soo dat den helft des deels dier lini binnen het inront, in sulckē reden sy tottet deel buyten t'inront, als des inronts middelpuntsloop, tot des Dwaelders inrontsloop, de sne dier lini int inront is des Dwaelders stantpunt, t'welck wy bewijsen moesten.

53 Voorstel.

Wesende ghegeven Saturnus inronts vvechlangde: Te vinden de lini van des Eertcloots middelpunt tot sijn stantpunt, in sulcke deelen alsser des inrontvvechs halfmiddellijn 10000 doet: Boven dien de schijnbaer booch van Saturnus stantpunt tot des inronts middelpunt en des stantpunts inrontlangde, deur vvisconstighe vverckingghegront op stelling eens vasten Eertcloots.

T'ghegheven. Laet A B Saturnus inronts wech sijn, diens middelpunt C, des Eertcloots middelpunt D, middellijn A D C B, verstepunt B, naestepunt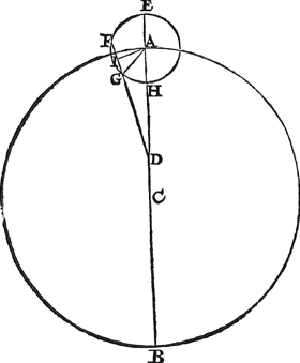



A: Het inront sy E F G H, met sijn middelpunt neem ick an des wechs naestepunt A, en des selven inronts naestepunt is H, het stantpunt G, van het welck tot des Eertcloots middelpunt D, ghetrocken is de rechte lini D G, daer na A G. T'begheerde. Wy moeten de lini D G vinden, in sulcke deelen alsser des inrontwechs halfmiddellijn A C 10000 doet: Daer na de schijnbaer booch van Saturnus stantpuut G, tot des inronts middelpunt A, dats den houck G D A, en des stantpunts G inrontlangde, dats de booch E F G of houc E A G.

[p. 228]

T'bereytsel. Laet D G voortghetrocken worden tot datse het inront snijt in F, en F G sy int middel ghedeelt an I.

t'Werck.

De lini D H van des Eertcloots middelpunt tot des inronts naestepunt, doet deur het 46 voorstel	7606.
Die ghemenichvuldicht deur E D 9936 (te weten D H 7606 eerste in d'oirden met H A, A E, elck 1165 deur het 47 voorstel) comt voor den rechthouck begrepen onder E D en H D	75573216.
Maer anden selven rechthouck is even den rechthouck begrepen^+ onder F D, G D, daerom sy doet oock	75573216.
Voort segh ick, ghelijck des inronts middelpunts loop, tot Saturnus inrontsloop, alsoo I G tot G D deur het 53 voorstel: Maer des inronts middelpuntsloop, is tot Saturnus inrontsloop, in sulcken reden als 35 tot 1000 deur het 2 vervolgh des 52 voorstels, daerom I G is tot G D in sulcken reden als 35 tot 1000; En tot I G 35, ghedaen andermael 35 voor I F als daer me even sijnde, en noch 1000 van D G, comt t'samen voor F D 1070: Inder voughen dat F D, in sulcken reden is tot G D, als 1070 tot 1000: Dit soo sijnde, en om nu te vinden de begheerde lini D G, ick stel my selven dit werckstuck voor: Te vinden twee ghetalen tot malcander inde redē van 1070 tot 1000, en also dat haer uytbreng doe 75573216 derde in d'oirden: Die twee ghetalen ghesocht ick neem deur de^* Stelreghel, worden bevonden het grootste 8993, en het cleenste voor begheerde D G in sulcke deelen alsser A C 10000 doet, van	8404.
Om nu de rest te vinden ick segh aldus: De driehouck A G D heeft drie bekende palen, te weten drie sijden, als D A 8771 deur het 46 voorstel, A G halfmiddellijn des inronts 1165 deur het 47 voorstel, en D G 8404 vierde in d'oirden: Hier me ghesocht de twee houcken G D A, D A G, worden bevonden deur het 8 voorstel der platte driehoucken, te weten den houck G D A voor begeerde schijnbaer booch van het stantpunt G tot des inronts middelpunt B, van	7 tr. 23.
En den houck D A G van 67 tr. 58 ①, welcke getrocken van 180 tr. blijft voor den houck E A G, dats oock de booch E F G, als begheerde inrontlangde des stantpunts G	112 tr. 2.

Waer af t'bewijs deur t'werck openbaer is. T'beslvyt. Wesende dan ghegheven Saturnus inronts wechlangde, wy hebben ghevonden de lini van des Eertcloots middelpunt tot sijn stantpunt in sulcke deelē alsser des inrontwechs halfmiddellijn 10000 doet, boven dien de schijnbaer booch van Saturnus stantpunt tot des inronts middelpunt, en de stantpunts inrontlangde, deur wisconstighe wercking ghegront op stelling eens vasten Eertcloots, na den eysch.

+ 3 b. 36 voor stel van Euc.

* Per Algebram.

1 Vervolgh.

Anghesien deur dit voorstel bekent is de schijnbaer booch van Saturnus stantpunt tot des inronts middelpunt, en des selfdē inronts middelpunts schijnbaer duysteraerlangde deur het vervolgh des 49 voorstels, soo is oock bekent des stantpunts schijnbaer duysteraerlangde.

[p. 229]

2 Vervolgh.

T'is kennelick datmen sal meughen maken een tafel der schijnbaer boghen van Saturnus stantpunten tot des inronts middelpunt, en der stantpuntens inrontlangden van trap tot trap, om daer deur t'begheerde met lichticheyt te crijghen.

1 Merck.

De saeck is inde boveschreven wercking ghenomen al of gheduerende de deysing den schijnbaer loop vant middelpunt des inronts altijt eenvaerdich evegroot waer, en al of het inronts naestepunt altijt op eē plaets bleef: T'welck soo wel sijn soude als de wech middelpuntich waer, maer nu uytmiddelpuntich wesende, en daerom den voorschreven schijnbaer loop vant middelpunt des inronts oneven, en des inronts naestepunt gheduerlick van plaets veranderende, soo moet dit int berekenen des deysboochs eenich verschil veroirsaken: Doch inde schriften der ouden Ptolemeus ter handt ghecommen, schijnt sulcx ghehouden als inde saeck gheen hinderlicke dwaling by te brenghen: Maer Regiomontanus int 9 voorstel des 12 boucx, beschrijft spiegelingsche wijse de ghedaente van sulck verschil. So ymant wilde ondersouckē hoe groot dat is, en oft weerdich waer int rekenen daer op acht te nemen, mochter int werck op lettē.

2 Merck.

Tot hier toe is wisconstelick beschreven d'oirsaeck en gedaente der deysing vande Dwaelders met inronden: Angaende de ghene die in uytmiddelpuntighe weghen loopen, als Son en Maen, t'is open bae ronmeugelick te sijn de selve deysing te crijghen, wat reden oock datmen stelt tusschen haer loop int inront en den loop des verstepunts, of der uytmiddelpunticheytlijn tot des wechs halfmiddellijn, want hoe na men den Eertcloot by den omtreck brengt, altijt isser voortganck, ja al waerser ingestelt noch en souder maer een stantpunt vallen sonder deysing, en dat opt punt des tijts, als des Dwaelders middelpunt waer ghecommen ant oochpunt des sienders, sulcx dattet soucken van soodanighe deysing onnoodich is.

3 Merck

Noch is te weten dat de ouden soo Ptolemeus schrijft, gagheslaghen hebben der Dwaelders en vaste sterren twee uyterste verschijninghen, als t'bgin mettet einde, te weten t'begin wanneermense eerst siet, na datse een tijt lanck hebben verborghen gheweest: Maer t'einde alsmense de laetste mael siet na datse een tijt lanck gheschenen hebben. En gheschiet dese uyterste verschijning om bekende oirsaken telckens in of ontrent den sichteinder. De rekeninghen der selve wierden by hun ghedaen om van te vooren te weten wanneer een ongesien Dwaelder of sterre weerom eerst sichtbaer wort, t'welck aldus toegaet: Men slaet eerst ga deur dadelicke ervaring eenighe daghen achter malcander, op wat dach datmē hem de laetstemael siet, ondersouckende hoe leegh op dien tijt de Son onder den sichteinder was (want leegher isse onder de cleender sterren dan onder de grooter, om dat de grooter t'savonts eer en smorghens later ghesien worden) dese leeghde ghevonden wesende, men besluyt daer uyt dat soo dickwils hy inden sichteinder is met derghelijcke leeghde der Son daer onder, dat hy in sijn uyterste verschijning sal sijn: Als by voorbeelt, Ptolemeus seght

[p. 230]

deur dadelicke ervaring bevonden te hebben, dat wesende de Son 11 tr. onder dē sichteinder, Saturnus t'elckens in sijn uyterste verschijning was. Dese booch van 11 tr. bekent wesende, en ghegheven sijnde de Eertcloots breede der plaets daer d'ervaring geschiet, mette Sonnens schijnbaer duysteraerlangde, t'is openbaer dat men deur rekeninghen ghegront op hemelclootsche werckstucken als die des 4 boucx des driehoucxhandels can seggen hoe groot dē schijnbaer duysteraers booch moet sijn vande Son tot Saturnus, om in sijn uyterste verschijning te wesen (welcke bogen om des duysteraers scheefheyts wille groote verandering crijghen) Sulcx dat de saeck hier me ghenouch verclaert schijnende, om tot allen plaetsen gaslaginghen te doen als boven, en daer op als gront dese uyterste verschijninghen te berekenen, soo achten wy onnoodich besonder voorstellen daer af te beschrijven.

Doch staet hier noch te ghedencken, dat om vande uyterste verschijninghen der Dwaelders by ghemeene reghel meerder sekerheyt te hebben, noodich soude sijn te letten op haer verheden vanden Eertcloot in d'een en d'ander uyterste verschijning, welcke, voornamelick in Mars, seer verscheyden sijn, en hun grijphoucken seer doen veranderen, waer deur sy oock in d'een uyterste verschijning verder vande Son moeten wesen als in d'ander, niet teghenstaende de houcken die den duysteraer op den sichteinder maeckt even waren.