Wisconstighe gedachtenissen. Deel 1: van 't weereltschrift

(1608)–Simon Stevin– rechtenstatus

Nv vande effening der daghen.

Tot hier toe de Sonloop aldus beschreven sijnde, daer rest noch te segghen vande effening der oneven of natuerlicke daghen, wiens ghedaente verclaert is deur de bepaling int begin des 2 onderscheyts deses 2 boucx, want hoewel haer grootste verschil inde Sonloop om haer traecheyts wille gheen hinderlicke dwaling en veroirsaeckt, nochtans t'selve niet gagheslaghen wesende, soude inde Maenloop die rasscher is merckelicker feyl connen by brenghen: Oock souden hierom ons rekeningen vanden anvang der duysteringhen somwijlen soo veel tijts connen ghemist sijn, t'welck na de rekeningen van Erasmus Reinholdus t'sijnder tijt, in rassche loop 7 tr. 36 ① bedraecht, doende in tijt 0 uyr 30 ① 24 ②. Maer het can deur verloop van des Sonwechs verstepunt tot eenighe ander tijden gebeuren, dat dit verschil in rassche loop sal bedragen over de 10 tr. doende ⅔ uyrs.

13 Voorstel.

Wesende ghegeven de Sonnens schijnbaer duysteraerlangde, haer vvechlangde te vinden deur vvisconstighe vvercking ghegront op stelling eens vasten Eertcloots.

T'gegeven. Laet A B C D dē duysteraer beteyckenē, diens middelpunt, dats den Eertcloot E, voort sy F G H I de Sonwech, diens middelpunt K, verstepunt

illustratie

F, t'welck sy onder A als schijnbaer verstepunt inden 94 tr. 35 ① deur het 1 voorbeelt des 7 voorstels: Boven diē is H het naestepunt onder het schijnbaer naestepunt C indē 274 tr. 35 ①: Voort wesende de ware Sō in haer wech an I, sy is schijnbaerlick in des duysteraers 30 tr. an L.

T'begeerde. Wy moeten haer wechlangde vinden, dats den booch F G H I.

t'Werck.

Anghesien A is schijnbaer verstepunt in des duysteraers 94 tr. 35 ①, en L inden 30 tr. soo doet L A, t'welck oock is voor den houck L E A, en sgelijcx voor dē houck I E K 64 tr. 35 ①: Dit soo sijnde de driehouck K E I heeft drie bekende palen, te weten K E I 64 tr. 35 ①, K I 10000, E K 323 deur het 1 voorbeelt des 7 voorstels. Hier me ghesocht den houck E K I, t'welck oock is voor den booch H I, wort bevondē deur het 5 voorstel der platte driehouckē van 113 tr. 45 ①: Daer toe vergaert het halfront E G H 180 tr. comt de begeerde wechlangde der Son, te weten den booch F G H I 293 tr. 45 ①. Waer af t'bewijs deur t'werck openbaer is. T'beslvyt. Wesende dan ghegeven de Sonnens schijnbaer duysteraerlangde, wy hebben haer wechlangde ghevonden deur wisconstige wercking ghegront op stelling eens vasten Eertcloots, na den eysch.

Merckt.

Alsmen aldus souckt de Sonnens wechlangde wanneerse schijnbaerlick is in des duysteraers begin, of inde lentsne, sy wort bevonden van 263 tr. 34 ①: Sulcx dat op desen tijt tot die plaets des Sonwechs de lentsne valt.

14 Voorstel.

Wesende ghegheven de Sonnens vvechlangde, te vinden haer schijnbaer duysteraerlangde deur vvisconstighe vvercking ghegront op stelling eens vasten Eertcloots.

T'ghegheven. Laet de form des 13 voorstels andermael de ghegeven sijn waer in de Son sy an I, sulcx dat haer wechlangde F G H I doet 293 tr. 45 ①, en L haer schijnbaer duysteraerlangde. T'begheerde. Wy moeten vinden de duysteraerlangde des punts L.

t'Werck.

Anghesien de booch F G H I doet deur t'gegeven 293 tr. 45 ①, soo treck ick daer af het halfront F G H 180 tr. blijft voor de booch H I dats oock voor den

houck E K I 113 tr. 45 ①: Dit soo sijnde de driehouck E K I heeft drie bekende palen, te weten E K I 113 tr. 45 ①, K I 10000, en E K 323 deur het 1 voorbeelt des 7 voorstels: Hier me ghesocht den houck K E I, t'welck oock is voor de booch, L A wort bevondē deur het 6 voorstel der platte driehoucken van 64 tr. 35 ①, welcke getrocken vande duysteraerlangde des schijnbaer naestepunts A, wesende inden 94 tr. 35 ①, blijft voor de begeerde duysteraerlangde des punts L 30 tr. Waer af t'bewijs deur t'werck openbaer is. T'beslvyt. Wesende dan gegeven de Sonnens wechlangde, wy hebben ghevonden haer schijnbaer duysteraerlangde deur wisconstighe wercking ghegront op stelling eens vasten Eertcloots, na den eysch

15 Voorstel.

Wesende ghegheven oneven natuerlicke daghen: Te vinden hoe veel sy doen in evendaghen deur vvisconstige vvercking ghegront op stelling eens vasten Eertcloots.

1 Voorbeelt met ghegheven oneven natuerlicke daghen, vandeGa naar margenoot* Sonnens inganck der lentsne beginnende.

T'ghegheven. Laet de oneven natuerlicke daghen vande lentsnees inganck beginnende sijn 30. T'begheerde. Wy moeten vinden hoe veel sy doen in evendaghen.

t'Werck.

Ick souck op soo veel even of middeldaghen alsser ghegeven oneven of natuerlicke daghen sijn, dats 30, de Sonnens loop in haer wech vande schijnbaer lentsne af beginnende, en bevinde die deur het 3 voorstel des 1 boucx van	29 tr. 34.
Om nu te vinden die plaetsens schijnbaer duysteraerlangde ick segh aldus: De schijnbaer lentsne is deur t'merck des 13 voorstels in des Sonwechs 263 tr. 34 ①: Daerom totte selve gedaen 29 tr. 34 ① eerste in d'oirden, comt des Sonwechs 293 tr. 8 ①, diens schijnbaer plaets inden duysteraer deur het 14 voorstel deses 2 boucx	29 tr. 24.
Des selfden evenaerlangde is deur het 2 werckstuck vant 4 bouck des Wereltschrifts (welverstaende dat des duysteraers afwijcking hier ghenomen is op 23 tr. 30)	27 tr. 20.
T'verschil tusschen het eerste en derde des oirdens	2 tr. 14.
Welcke (nemende 15 tr. te gheven 1 uyr) uyt brenghen	0 uyr 9 ①.
Merckt nu dat als het eerste in d'oirden even is ant derde in d'oirden, soo doen de ghegheven oneven natuerlicke daghen oock soo veel even.
Maer als het eerste meerder is, dan trecktmen het vijfde van de gegheven daghen.
Ende het eerste minder sijnde, soo vergaertmen het vijfde totte gegheven daghen.
Nu dan anghesien het eerste meerder is dan het derde, soo moeten wy, volghende de boveschreven reghel, het vijfde des oirdens

als 0 uyr 7 ①, trecken vande ghegheven 30 daghen, blijft voor t'begheerde

29 evedaghen 23 uyr 51 ①.

T'bereytsel. Laet A B C D E eē cloot wesen, diēs A D evenaer sy, E C dē duysteraer, F lentsne, B aspunt, G de Evedachson, sulcx dat F G doet 29 tr. 34 ①

illustratie

eerste in d'oirden, en H sy de Schijnbaerson doēde 27 tr. 20 ① tweede in d'oirdē, en deur H sy getrocken het middachront B I, sulcx dat F I sy de evenaerlangde van H doende 27 tr. 20 ① derde in d'oirden, en I G verschil tusschen F G, F I moet doē de 2 tr. 14 ① vierde in d'oirden.

T'bewys. Wesende de ware Son tē tijde haers ingancx der lentsne in haer wech recht onder F, de Schijnbaerson en Evedachson beyde in F, soo sijn dese drie Sonnen op de gegeven 30 dagen van daer gegaen elck haers weechs als volght: De ware Son van onder F in haer wech 29 tr. 34 ① eerste in d'oirden: En daerentusschen moet de Evedachson inden evenaer t'welck is van F tot G, oock soo veel gheloopen sijn, te weten 29 tr. 34 ①. En op dien selven tijt is de Schijnbaerson inden duysteraer gecommen an H, sulcx dat alsdan F H doen moet 29 tr. 24 ① tweede in d'oirden: Over dese H getrockē sijnde het middachront van B totten evenaer in I, soo doet F I 27 tr. 20 ① derde in d'oirden. By aldien nu de Schijnbaerson H, en de Evedachson G, beyde t'samen waren in een selve middachrondt, soo en souden haer daghen, te weten natuerlicke en even gheen verschil hebben: Maer van t' een middachront tottet ander is 2 tr. 14 ① vierde in d'oirden, want soo veel doet I G, en daerom verschillense soo veel als op dien tijt bedraecht de Sonnens rassche loop van Oosten na Westen, te weten 0 uyr 9 ① vijfde in d'oirdē. De reden waerom dese nu moesten ghetrocken sijn vande ghegheven 30 daghen, en niet toegedaen, is dusdanich: Anghesien de Evedachson G, diens daghens langde wy soucken met haer rassche loop ghecommen is van Oosten an D, na Westen tot G, en de Natuerlickedachson, anders gheseyt de Schijnbaerson H van Oosten na Westen tot H, 2 tr. 14 ① voorder, soo moeten wy die af trecken om de langde der begheerde evedaghen vande Evedachson te behouden: Maer sulcx is de ghedaente des wercx, daerom t'is goet.

Merckt.

Ghelijck hier boven ghevonden is watmen moet toedoen op 30 daghen na de Sonnens inganck der lentsne, alsoo is kennelick datmen can vinden wat-

men moet toedoen of af trecken op yder dach des jaers, waer deur openbaer is hoemen om t'begheerde met lichticheyt te vinden, can maken een tafel van dach tot dach, dienende voor seer langen tijt, te wetē tot dat des Sonwechs verstepunt soo verre mocht verloopen sijn, datter merckelick hinder uyt mocht volghen.

2 Voorbeelt met ghegheven oneven natuerlicke daghen na de Sonnens inganck der lentsne beginnende.

T'ghegheven. Laet de oneven natuerlicke daghen sijn 20, te weten vanden 30 na de lentsnees inganck totten 50. T'begheerde. Wy moeten vinden hoe veel die 20 oneven natuerlicke daghen doen in even daghen.

t'Werck.

Ick souck eerst hoe veel dat doen de 30 oneven natuerlicke daghen na de lentsnees inganck beginnende, wort bevonden deur het 1 voorbeelt	29 evedaghen 23 uyr 51 ①.
Daer na hoe veel dat doen de 50 oneven natuerlicke daghen na de lentsnees inganck beginnende, wort bevonden deur het boveschreven 1 voorbeelt	49 evedaghen 23 uyr 52 ①.
Daer af ghetrocken de 29 evedaghen 23 uyr 51 ① eerste in d'oirden, blijft voor t'begheerde	20 evedaghen 0 uyr 1 ①.

1 Vervolgh.

Men mach, die wil, de uyren welcke benevens heele gegeven dagen mochten ghegheven sijn, indeGa naar margenoot* daet wel achterlaten, om dat daer op int voornaemste gheen hinderlick verschil en valt.

2 Vervolgh.

Sooder te vinden waren de evendagen van een heel of meer heele jaren, t'is openbaer dat sulcx gheen rekening en soude behouven, om dat die even dagen even sijn met soo veel natuerlicke.

3 Vervolgh.

Sooder te vinden waer de even daghen van een of meer jaren, met noch eenighe natuerlicke dagen daer by, t' is ken nelick datmen t'selve jaer of jaren soude meughen verlaten, en alleenelick rekening maken vande daghen.

4 Vervolgh.

Sooder ghegheven waren natuerlicke daghen voor een lentsnees inganck beginnende, t'is kennelick datmen in plaets der ghegheven volghende lentsne verkiesen mach de voorgaende, tellende hoe veel daghen den ghegheven dach daer achter valt, en met die ghevonden daghen machmen de voorgaende regel volghen. Van alle welcke dinghen t'bewijs openbaer is.

T'beslvyt. Wesende dan ghegeven oneven natuerlicke dagen, wy hebben ghevonden hoe veel sy doen in evendaghen, deur wisconstighe wercking ghegront op stelling eens vasten Eertcloots, na den eysch.

16 Voorstel.

Wesende ghegheven evendaghen: Te vinden hoe veel sy doen in oneven natuerlicke, deur vvisconstighe vvercking ghegront op stelling eensvasten Eertcloots.

Merckt.

Men soude t'merck deses voorstels hebben connen verclaren, sonder daer af te maken een eyghentlick voorstel met al sijn leden, aldus: Men sal wercken mette ghegheven evendaghen ghelijck int 15 voorstel mette ghegheven oneven natuerlicke ghedaen wiert, uytghenomen datmen ghecommen sijnde ant vijfde des oirdens, in plaets van daer af te trecken hier vergaren sal: En in plaets van daer te vergaren hier sal af trecken, en daer me t'begheerde hebben.

Doch op dattet bewijs van dese diepsinnige stof te claerder, en de navolging int dadelick werck te lichter sy, soo beschrijf ick daer af dit volcommen voorstel, daer in soo groote gelijckheyt der woorden gebruyckende mettet 15 voorstel, alsser bequamelick vallē wil, om de redenē vā dies elders breeder verclaert.

1 Voorbeelt met ghegheven evendaghen vande Sonnens inganck der lentsne beginnende.

T'ghegeven. Laet de evendagen vande lentsnees inganck beginnende sijn 30. T'begheerde. Wy moeten vinden hoe veel sy doen in oneven natuerlicke daghen.

t'Werck.

Ick souck eerst de Sonnens middelloop vande ghegheven 30 evedaghen, en bevinde die deur het 3 voorstel des 1 boucx van	29 tr. 34.
Om nu op dien tijt te vinden de Sonnens schijnbaer duysteraerlangde ick segh aldus: De schijnbaer lentsne is deur t'merck des 13 voorstels in des Sonwechs 267 tr. 16 ①, daerom totte selve ghedaen 29 tr. 34 ① eerste in d'oirden (want soo veel heeft de Son op den ghegeven tijt oock gheloopen in haer wech) comt des Sonwechs 296 tr. 50 ①, diens schijnbaer plaets inden duysteraer deur het 14 voorstel deses 2 boucx	29 tr. 24.
Des selfden evenaerlangde is deur het 2 werckstuck vant 4 bouck des Wereltschrifts	27 tr. 20.
T'verschil tusschen het eerste en derde des oirdens is	2 tr. 14.
Welcke (nemende 15 tr. te gheven 1 uyr) uytbrenghen	0 uyr 9 ①.
Merckt nu dat als het eerste in d'oirden even is ant derde in d'oirden, soo doen de ghegheven even daghen oock soo veel oneven natuerlicke. Maer als het eerste meerder is, dan vergaertmen het vijfde tot de ghegheven daghen. En het eerste minder sijnde, soo trecktmen het vijfde vande gegheven daghen. Mu dan anghesien het eerste meerder is dant derde, soo moeten wy volghende de boveschreven reghel, het vijfde des oirdens als 0 uyr 9 ① vergaren totte ghegheven 30 evedaghen, en comt voor t'begheerde	30 oneven natuerlicke daghen 0 uyr 9 ①.

T'bewys. Laet de form des 15 voorstels van beteyckening sijn als daer int bereytsel gheseyt is, waer me ick andermael aldus segh: Wesende de ware Son ten tijde haers ingancx der lentsne in haer wech onder F, de Schijnbaerson en Evedachson beyde in F, soo sijn dese drie Sonnen op de ghegheven 30 evedaghen van daer voortghegaen elck haers wechs, als volght: De Evedachson van F tot G 29 tr. 34 ① eerste in d'oirden: En daerentusschē moet de ware Son van onder F in haer wech oock soo veel gheloopen sijn, te weten 29 tr. 34 ①: En op dien selven tijt is de Schijnbaerson inden duysteraer ghecommen an H, sulcx dat alsdan F H doen moet 29 tr. 24 ① tweede in d'oirden: Over dese H getrocken sijnde het middachront van B totten evenaer in I, soo doet F I 27 tr. 20 ① derde in d'oirden. By aldien nu de Schijnbaerson H, en de Evedachson G, beyde t'samen waren in een selve middachront, soo en souden haer daghen, te weten oneven natuerlicke en even gheen verschil hebben: Maer van t'een middachront tottet ander sijn 2 tr. 14 ① vierde in d'oirden, want soo veel doet I G, en daerom verschillense soo veel als op dien tijt bedraecht de Sonnens rasscheloop van Oosten na Westen, te weten o uyr 9 ① vijfde in d'oirden. De reden waerom dese nu moesten vergaert sijn totte ghegheven 30 evedaghen, en niet af ghetrocken, is dusdanich: Anghesien de Schijnbaerson diens daghens langde wy soucken, met haer rasscheloop ghecommen is vant Oosten na Westen tot H, en de Evedachson G vant Oostē D, na Westen tot G 2 tr. 14 ① min, soo moeten wy die toedoen, om de langde der begheerde oneven natuerlicke daghen te crijghen: Maer sulcx is de ghedaente des wercx, daerom t'is goet.

2 Voorbeelt met ghegheven evedaghen na de Sonnens inganck der lentsne beginnende.

T'ghegheven. Laet de evedaghen sijn 20, te weten vanden 30 na de lentsnees inganck totten 50. T'begheerde. Wy moetē vinden hoe veel die 20 evedaghen, doen in oneven natuerlicke.

t'Werck.

Ick souck eerst hoe veel dat doen de 30 evendaghen vande lentsnees inganck beginnende, wort bevonden deur het 1 voorbeelt	30 oneven natuerlicke o uyr 9 ①.
Daer na hoe veel dat doen de 50 evendaghen na de lentsnees inganck beginnende, wort bevonden deur het boveschreven 1 voorbeelt	50 oneven natuerlicke 0 uyr 12 ①.
Daer afgetrockē de 30 oneven natuerlicke dagen 0 uyr 9 ① eerste in d'oirdē, blijft voor t'begeerde	20 oneven natuerlicke dag, 0 uyr 3 ①.

1 Merck.

T'is openbaer dat de tafel daer int merck des 15 voorstels af gheseyt is oock soude dienen tot dese verkeering der evedaghen in oneven natuerlicke, soo wel als daer totte verkeering der oneven natuerlicke in even, sulcx dat daer af hier gheen besonder tafel en behouft.

T'is oock kennelick de vier vervolghen des selven 15 voorstels te meughen verstaen worden op dit.

2 Merck.

Daer valt noch effening der daghen van weghen de verscheyden middachronden daer verscheyden menschen onder woonen, want hoewel, by voor-

beelt den anvang van een Maenduystering over al daermense sien can op een selve tijt ghesien wort, soo noemt nochtans den eenen sulcken tijt met ander uyren als den anderen: Daerom wanneer ons ter handt comt eenighe gaslaging der hemelsche lichten op eenige seker uyr geschiet, tot een plaets in langde met d'onse verschillende, soo isser op onsenGa naar margenoot* sichteinder uyt soodanige oirsaeck effening des tijts noodich: Maer want elcke 15 tr. verschil der langde een uyr gheven, soo is daer me sulcke effening openbaer ghenouch, sulcx dat daer af hier gheen besonder voorstel en behouft beschreven te sijn.

T'beslvyt. Wesende dan ghegheven even daghen, wy hebben gevonden hoe veel sy doen in oneven natuerlicke, deur wisconstighe wercking ghegront op stelling eens vasten Eertcloots, na den eysch.

Vertooch. 17 Voorstel.

Wesende getrocken een booch vanden aspunt des evenaers totten duysteraer, sulcx dat haer houckmaet middeleveredenighe is tusschen rechthoucx houckmaet en vierendeelrontschils houckmaet der grootste afvvijcking des duysteraers: Sy geraeckt den duysteraer int punt diens evenaerlangde van haer overcommende duysteraers booch meest verschilt.

T'verschil tusschen natuerlicke en even daghen is int 15 en 16 voorstel deur ghetalen gevonden: Maer beneffens dat, soo is der menschen spiegheling voorder ghestreckt tottet meetconstich bewijs waer sulck verschil ten grootsten valt, eerst van weghen de afwijcking des duysteraers, daer na om des Sonwechs uytmiddelpunticheyts wille, en hier af is dit 17 voorstel mette volghende.

Merckt noch dat dese stof diepsinnich sijnde, in Ptolemeus boucken niet en staet, dan hebse genomen uyt Regiomontanus schriften gheseyt Epitomes in Almagestum, staende daer int 25 voorstel des 3 boucx, welcke die seght uyt dē Arabier Geber ghetrocken te hebben, doch ten schijnen gheen Arabische vonden, maer eer overblijfsels des wijsentijts, die ghelijck oock de schriften van Hypparchus en Ptolemeus t'haerder handt gerocht meugē sijn. Noch is te wetē dat Regiomontanus inden handel deser stof anwijsing doet tot seker schriften van Geber, die ick niet en weetgeopēbaert te wesen: Doch op dat dit werck van dies angaēde by sijn selven soude bestaen, ick heb t'gebrekende op mijn wijse vervult, en dat beschrevē op de cortste en bequaemste manier die my doē te voorē quam: Hoe wel ick daerentusschē achte te meugē sijn dat Geber corter wechgebruycte, of ymant anders nauwer daer op lettende corter wech soude connen vinden.

Om dan totte saeck te commen ick segh aldus: Alsmen na de leering des 2 wercksticx der Hemelclootsche werckstucken, maeckt een tafel der evenaerlangden des duysteraers, die ick tot meerder claerheyt hier onder stel, getrocken uyt Prutenicis tabulis aldaer genoemt Canon ascentionum rectarum, men siet dat de boghen des evenaers ontrent het begin van trap tot trap cleender sijn dan haer overcommende duysteraerlangden, welcke vermeerdering gheduert tot ontrent des duysteraers 46 tr. alwaerse tē hoochstē wesende, en t'verschil tusschē die twee bogen ten meestē van 2 tr. 28 ① 24 ② soo crijcht den evenaer daer na vermeerdering van trap tot trap, sulcx dat eintlick haer 90^en tr. effen overcomt metten 90^en des duysteraers.

Tafel van des dvysteraers evenaerlangden.

Duysteraer.	Evenaer.

tr.	tr.①.②.

1.	0.55.2.
2.	1.50.5.
3.	2.45.8.
4.	3.40.13.
5.	4.35.18.
6.	5.30.25.
7.	6.25.34.
8.	7.20.45.
9.	8.15.59.
10.	9.11.15.
11.	10.6.35.
12.	11.1.58.
13.	11.57.26.
14.	12.52.57.
15.	13.48.32.
16.	14.44.12.
17.	15.39.57.
18.	16.35.47.
19.	17.31.43.
20.	18.27.45.
21.	19.23.53.
22.	20.20.7.
23.	21.16.27.
24.	22.12.55.
25.	23.9.30.
26.	24.6.12.
27.	25.3.2.
28.	26.0.0.
29.	26.57.6.
30.	27.54.20.
31.	28.51.43.
32.	29.49.15.
33.	30.46.56.
34.	31.44.45.
35.	32.42.45.
36.	33.40.54.
37.	34.39.12.
38.	35.37.41.
39.	36.36.19.
40.	37.35.7.
41.	38.34.7.
42.	39.33.16.
43.	40.32.36.
44.	41.32.6.
45.	42.31.48.
46.	43.31.40.
47.	44.33.43.
48.	45.31.56.
49.	46.32.21.
50.	47.32.57.
51.	48.33.43.
52.	49.34.40.
53.	50.35.49.
54.	51.37.8.
55.	52.38.38.
56.	53.40.19.
57.	54.42.11.
58.	55.44.13.
59.	56.46.25.
60.	57.48.48.
61.	58.51.21.
62.	59.54.4.
63.	60.56.57.
64.	62.0.0.
65.	63.3.12.
66.	64.6.34.
67.	65.10.4.
68.	66.13.43.
69.	67.17.31.
70.	68.21.27.
71.	69.25.31.
72.	70.29.42.
73.	71.34.1.
74.	72.38.27.
75.	73.42.59.
76.	74.47.38.
77.	75.52.23.
78.	76.57.13.
79.	78.2.8.
80.	79.7.8.
81.	80.12.13.
82.	81.17.21.
83.	82.22.33.
84.	83.27.49.
85.	84.33.6.
86.	85.38.26.
87.	86.43.48.
88.	87.49.11.
89.	88.54.35.
90.	90.0.0.

Maer om nu in plaets van die onvolcommen wijse met ghetalen, te kennen deur dit meetconstichGa naar margenoot* vertooch waer dat voorschreven punt des grootsten verschils vallen moet, soo sullen wy daer toe commen.

T'ghegheven. Laet A B C D een cloot wesen, diens aspunt A, duysteraer D E B, evenaer D F B, lentsne E D F, grootste afwijcking E F, haer schilbooch A F, voort sy A G een booch vanden aspunt A totten duysteraer, sulcx dat haer houckmaet middeleveredenighe is, tusschen rechthoucx houck maet, als des vierendeelronts A F, ende houckmaet van A E schilbooch der grootste afwijcking, ende de selve A G sy voortgetrocken tot H inden evenaer, sulcx dat D H sy evenaerslangde des punts G. T'begheerde. Wy moeten bewijsen dat de booch A G, den duysteraer int punt G also geraeckt, dat sijn evenaers langde D H, van haer overcommende duysteraersbooch D G, daer meest ver-

schilt. T'bereytsel. Sooder int vierendeel des duysteraers D E een ander punt waer dan G, dat soude moeten vallen of tusschen D G, of tusschē G E: Laet die punten sijn I, K, ende deur de selve ghetrocken worden de boghen tot inden evenaer, als A I L, A K M, soo is D L evenaerslangde van D I, ende D M van D K, welcke D L van D I, ofte D M van D K, wy betoonen moeten min te verschillen, dan D H van D G: Tot welckē einde ick noch treck de booch G N, rechthouckich op A I, ende G O rechthouckich op K M, en̄ treck de selve G N voorwaert tot datse den evenaer in P ontmoet, welverstaende datmen deur t'ghedacht neemt P van achter op den cloot te commen, sghelijcx G O voorwaert tot datse den evenaer in Q ontmoet. T'bewys.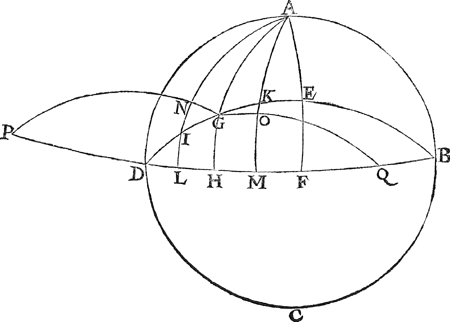

1 Lidt.

Anghesien N P, L P beyde rechthouckich sijn op N L deur t'bereytsel, soo doense elck een vierendeelrondts deur het 4 vervolgh des 1 voorstels vande clootsche driehoucken, daerom G H P is een driehouck wiens L H, N G sijn schilboghen der sijden P H, P G, sulcx dat G H P een clootsche driehouck is recht an H, wiens eyghenschap deur het 25 voorstel der clootsche driehoucken dusdanich is:

Ghelijck rechthoucx houckmaet,

Tot Schilboochs houckmaet van d'een rechthoucksijde P H, dats houckmaet van L H.

Alsoo schilboochs houckmaet van d'ander rechthoucksijde G H, dats Houckmaet van A G,

Tot schilboochs houckmaet der schoensche G P, dats houckmaet van G N.

Maer houckmaet van A H is rechthoucx houckmaet, daerom

Ghelijck houckmaet van	A H,
Tot houckmaet van	L H,
Alsoo houckmaet van	A G,
Tot houckmaet van	G N.

2 Lidt.

En deur overhandtsche reden,

Ghelijck houckmaet van	A H,
Tot houckmaet van	A G,
Alsoo houckmaet van	L H,
Tot houckmaet van	G N.

3 Lidt.

Maer houckmaet van A G is middeleveredenighe tusschen de houckmaten van A F en A E deur t'ghegheven, ofte (dattet selve is, om dat A H en A E elck een vierendeelronts doen) tusschen A H en A E, daerom

Ghelijck houckmaet van	A H,
Tot houckmaet van	A G,
Alsoo houckmaet van	A G,
Tot houckmaet van	A E.

4 Lidt.

Sulcx dat de twee laetste palen des 2 lidts, ende de twee laetste palē des 3 lidts, tot een selve een selve reden hebben, daerom sy oock met malcander everedenich sijn, dat is,

Ghelijck houckmaet van	L H,
Tot houckmaet van	G N,
Alsoo houckmaet van	A G,
Tot houckmaet van	A E.

5 Lidt.

Voort anghesien A G cleender is dan A I, soo segh ick,

De reden der houckmaet van	A G,
Totte houckmaet van	A E,
Is cleender dan de reden der houckmaet van	A I,
Totte houckmaet vande selve	A E.

6 Lidt.

Maer ghelijck houckmaet van A G, tot houckmaet van A E, alsoo houckmaet van L H, tot houckmaet van G N, deur het 4 lidt, daerom

De reden der houckmaet van	L H,
Tot houckmaet van	G N,
Is cleender dan de reden der houckmaet van	A I,
Tot houckmaet van	A E.

7 Lidt.

Ghenomen nu des driehoucx A I E sijde E I als grondt, ick segh deur het 24 voorstel der clootsche driehoucken, dat

Ghelijck houckmaet des rechterhoucx	A E I,
Tot houckmaet des slijn ckerhoucx	A I E,

Alsoo houckmaet der slijnckersijde	A I,
Tot houckmaet der rechtersijde	A E.

8 Lidt.

VVederom.

Ghenomen des driehoucx G N I sijde I N als grondt, ick segh deur het boveschreven 24 voorstel der clootsche driehoucken, dat

Ghelijck houckmaet des slijnckerhoucx	G N I,
Tot houckmaet des rechterhoucx	G I N,
Alsoo houckmaet der rechtersijde	G I,
Tot houckmaet der slijnckersijde	G N.

9 Lidt.

Maer den houck A E I des 7 lidts, is even metten houck G N I des 8 lidts, wantse beyde recht sijn: Oock is den houck A I E des 7 lidts, even anden houck G I N des 8 lidts, wanttet al een selven houck is, daerom de twee laetste palen des 7 lidts, ende de twee laetste palen des 8 lidts, sijn met evē palen everedenich, ende daerom oock met malcander everedenich, dat is,

Ghelijck houckmaet van	A I,
Tot houckmaet van	A E,
Alsoo houckmaet van	G I,
Tot houckmaet van	G N.

10 Lidt.

Nu dan de houckmaten van A I, A E, inde selve reden sijnde der houckmaten van G I, G N, deur het 9 lidt, soo volght daer uyt dat alle reden cleender als der houckmatē van A I, A E oock cleender is als der houckmatē van G I, G N. Maer reden der houckmaten van L H, G N, is cleender als reden der houckmaten van A I, A E, deur het 6 lidt: Daerom reden der houckmatē van L H, G N, is cleender als reden der houckmaten van G I, G N.

Ende deur verkeerde reden van dien:

Reden der houckmaten van G I, G N is grooter dan reden der houckmaten van L H, G N:

Daerom de houckmaet van G I, is grooter dan de houckmaet van L H.

11 Lidt.

Ende vervolgens alsoo dier houckmaten boghen elck cleender sijn dan een vierendeelrondts, soo moet de booch G I grooter sijn dan de booch L H.

12 Lidt.

Voort alsoo des driehoucx G H D rechthouck G H D, grooter is dan den scherphouck D G H, soo is deur het 15 voorstel der clootsche driehoucken des houcx G H D teghenoversijde G D, grooter dan des houcx D G H tegenoversijde D H.

13 Lidt.

Sghelijcx alsoo des driehoucx I L D rechthouck I L D, grooter is dan den

scherphouck D I L, soo is deur t'boveschreven 15 voorstel der clootsche driehoucken des houcx I L D teghenoversijde D I, grooter dan des houcx D I L teghenoversijde D L.

14 Lidt.

D I dan grooter sijnde als D L deur het 13 lidt, by aldien nu I G even waer an L H, soo soude t'verschil tusschen D G en D H, even sijn an t'verschil tusschen D I en D L: Maer I G is grooter dan L H deur het 11 lidt, daerom t'verschil van D G boven D H, is grooter dan t'verschil van D I boven D L,

Waer mede bewesen is het eerste deel dat wy int bereytsel voorghenomen hadden te betoonen.

DAer rest nu noch het ander deel te bewijsen, namelick datter verschil van D G boven D H oock grooter is dan t'verschil van D K boven D M: Tot desen einde segh ick aldus:

15 Lidt.

Anghesien O Q, M Q, beyde rechthouckich sijn op O M, deur t'bereytsel, sco doense elck een vierendeelronts deur het 4 vervolgh des 1 voorstels vande clootsche driehoucken, ende daerom G H Q is een driehouck, wiens M H, O G, sijn schilboghen der sijden Q H, Q G, sulcx dat G H Q een clootsche driehouck is recht an H, wiens eygenschap deur het 25 voorstel der clootsche driehoucken dusdanich is:

Ghelijck rechthoucx houckmaet,

Tot schilboochs houckmaet van d'een rechthoucxsijde Q H, dats houckmaet van M H,

Alsoo schilboochs houckmaet van d'ander rechthoucxsijde G H, dats houcmaet van A G,

Tot schilboochs houckmaet der schoensche G Q, dats houckmaet van G O, Maer houckmaet van A H is rechthoucx houckmaet, daerom

Ghelijck houckmaet van	A H,
Tot houckmaet van	M H,
Alsoo houckmaet van	A G,
Tot houckmaet van	G O.

16 Lidt.

Ende deur overhandtsche reden,

Ghelijck houckmaet van	A H,
Tot houckmaet van	A G,
Alsoo houckmaet van	M H,
Tot houckmaet van	G O.

17 Lidt.

Maer houckmaet van A G is middeleveredenighe tusschen de houckmaten van A F en A E, deur t'ghegheven, ofte (dattet selve is, om dat A H en A F elck een vierendeelronts doen) tusschen A H en A E, daerom

Ghelijck houckmaet van	A H,
Tot houckmaet van	A G,

Alsoo houckmaet van	A G,
Tot houckmaet van	A E.

18 Lidt.

Sulcx dat de twee laetste palen des 16 lidts, ende de twee laetste palen des 17 lidts, tot een selve een selve reden hebben, daerom sy oock met malcander everedenich sijn, dat is,

Ghelijck houckmaet van	M H,
Tot houckmaet van	G O,
Alsoo houckmaet van	A G,
Tot houckmaet van	A E.

19 Lidt.

Voort anghesien A G grooter is dan A K, soo segh ick

De reden der houckmaet van	A G,
Totte houckmaet van	A E,
Is grooter dan de reden der houckmaet van	A K,
Totte houckmaet vande selve	A E.

20 Lidt.

Maer ghelijck houckmaet van A G, tot houckmaet van A E, alsoo houckmaet van M H, tot houckmaet van G O, deur het 18 lidt, daerom

De reden der houckmaet van	M H,
Totte houckmaet van	G O,
Is grooter dan de reden der houckmaet van	A K,
Totte houckmaet van	A E.

21 Lidt.

Ghenomen nu des driehoucx A K E sijde E K als gront, ick segh deur het 24 voorstel der clootsche driehoucken, dat

Ghelijck houckmaet des rechterhoucx	A E K,
Tot houckmaet des slijnckerhoucx	A K E,
Alsoo houckmaet der slijncker sijde	A K,
Tot houckmaet der rechtersijde	A E.

22 Lidt.

Ghenomen des driehoucx G O K sijde K O als gront, ick segh deur het boveschreven 24 voorstel der clootsche driehoucken, dat

Ghelijck houckmaet des slijnckerhoucx	G O K,
Tot houckmaet des rechterhoucx	G K O,
Alsoo houckmaet der rechtersijde	G K,
Tot houckmaet det slijnckersijde	G O.

23 Lidt.

Maer den houck A E K des 21 lidts, is even mettē houck G O K des 22 lidts, wantse beyde recht sijn: Oock is den houck A K E des 21 lidts, even anden

houck G K O des 22 Lidts, deur het 6 vervolgh des 1 voorstels vande clootsche driehoucken, daerom de twee laetste palen des 21 lidts, ende de twee laetste palen des 22 lidts, sijn met even palen everedenich, ende daerom oock met malcander everedenich, dat is,

Ghelijck houckmaet van	A K,
Tot houckmaet van	A E.
Alsoo houckmaet van	G K,
Tot houckmaet van	G O.

24 Lidt.

Nu dan houckmaten van A K, A E, inde selve reden sijnde der houckmaten van G K, G O, deur het 23 lidt, soo volght daer uyt dat alle reden grooter als der houckmaten van A K, A E, oock grooter is als der houckmaten van G K, G O. Maer reden der houckmaten van M H, G O, is grooter als reden der houckmaten A K, A E, deur het 20 lidt: Daerom reden der houckmaten van M H, G O, is grooter als reden der houckmaten van G K, G O.

Waer deur oock de houckmaet van M H, grooter is dan de houckmaet van G K.

25 Lidt.

Ende vervolghens alsoo dier houckmaten bogen elck cleender dan een vierendeelrondts sijn, soo moet den booch M H grooter sijn dan den booch G K.

26 Lidt.

Voort alsoo des driehoucx K M D rechthouck K M D, grooter is dan den scherphouck D K M, soo is deur het 15 voorstel der clootsche driehoucken, des houcx K M D teghenoversijde K D, grooter dan des houcx D K M teghenoversijde D M.

27 Lidt.

D K dan grooter sijnde als D M deur het 26 lidt: By aldiē nu G K even waer an M H, soo soude t'verschil tusschen D G en D H even sijn an t'verschil tusschen D K en D M: Maer G K is cleender dan M H deur het 25 lidt: Daerom t'verschil van D G boven D H, is grooter dan t'verschil van D K boven D M.

Waer mede bewesen is het ander deel dat wy int bereytsel voorghenomen hadden te betoonen. T'beslvyt. Wesende dan ghetrocken een booch vanden aspunt des evenaers totten duysteraer, sulcx dat haer houckmaet middeleveredenighe is tusschen rechthoucx houckmaet ende schilboochs houckmaet der grootste afwijcking des duysteraers: Sy gheraeckt den duysteraer int punt, diens evenaerslangde van haer overcommende duysteraersbooch meest verschilt, t'welck wy bewijsen moesten.

18 Voorstel.

Den duysteraers booch die van haer overcommende evenaerslangde meest verschilt, bekent te maken.

T'ghegheven. Laet inde form des 17 voorstels D G de begeerde booch

wesen, alwaer d'ander linien van beteyckening sijn na t'inhoudt des selfden voorstels. T'begheerde. Wy moeten de selve D G bekent maken.

t'Werck.

Anghesien dat deur t'gestelde des 17 voorstels de houckmaet van A G, middeleveredenighe is tusschen rechthoucx houckmaet 10000000, en houckmaet van A E 9145680, als schilboochs houckmaet der grootste afwijcking E F, (de reden waerom wy hier al de letters des tafels nemen, en de rekening tot op ③ maken, sal int volghende merck des 19 voorstels gheseyt worden)

soo vinde ick t'middel everedenich getal tusschen 10000000 en̄ 9145680, t'welck bevonden wort van	9563304
Diens booch A G	73 tr. 0 ① 18 ② 4 ③
Welcke ghetrocken van A H	90 tr.
Blijft voor G H	16 tr. 59 ① 41 ② 56 ③
Daerom heeft den driehouck G H D nu drie bekende palen, te weten de sijde G H 16 tr. 59 ① 41 ② 56 ③, den houck G H D recht, ende dē houck G D H van 23 tr. 51 ① 20 ②, Hier mede gesocht de sijde G D, wort deur het 35 voorstel der clootsche driehouckē bevonden voor t'begheerde van	46 tr. 16 ① 43 ② 43 ③
Ende die daer toe noch begheerde haer overcommende evenaerslangde, dats den booch D H, salse bevinden deur t'selve voorstel van	43 tr. 43 ① 16 ② 44 ③

Waer af t'bewijs deur t'werck openbaer is, als gegront sijnde op het 17 voorstel. T'beslvyt. Wy hebben dan dē duysteraers booch die van haer overcommende evenaerslangde meest verschilt, bekent ghemaeckt, na den eysch.

Vertooch. 19 Voorstel.

Wesende tvvee even platte rechthoucken, elck begrepen onder een houckmaet ende haer Schilboochs houckmaet: Die tvvee rechthoucken hebben even sijden.

Merckt.

Want wy int volgende 20 voorstel betoonen willē, dat de duysteraers booch die van haer evenaerslangde meest verschilt, mette selve evenaerslangde een vierendeel rondts doet; Soo beschrijven wy eerst dit vertooch, als noodich tottet bewijs des selfden 20 voorstels, t'welck Regiomontanus oock verclaert in Epitome lib. 3. prop. 26. ghebruyckende daer toe bewijsinghen van Mileus elders beschreven, maer wy sullen ghelijck int 17 voorstel oock ghedaen is, t'bewijs hier by voughen.

T'ghegeven. Laet A B een rechthouck wesen, begrepen onder A C houckmaet des boochs C D, ende C B haer schilboochs houckmaet: Voort E F een rechthouck even an A B, begrepen onder E G houckmaet van G H, ende G F haer schilboochs houckmaet. T'begheerde. Wy moeten bewijsen dat de grootste sijde A C, even is ande grootste sijde E G, ende de cleynste sijde C B even ande cleinste sijde G F.

T'bereytsel. Laet ghetrocken worden I C, I G. T'bewys. Angheghesien A B, E F, twee even rechthoucken sijn deur t'ghegheven, soo moeten

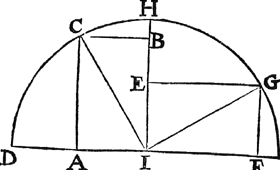haer helften C B I, I E G twee even driehoucken sijn, beyde rechthouckich an E en B, ende met twee even schoenschen C I, I G, want het sijn twee halfmiddellijnen eens selfdē rondts, daerom haer twee grootste recht houcxsijden A C, E G, moeten even sijn, alsoo oock moetē de cleynste C B, G F: Want waer, by voorbeelt gheseyt, de cleynste sijde C B cleynder dan G F, den rechthouck A B soude cleynder sijn als den rechthouck E F, t'welck tegen t'gestelde soude wesen. T'beslvyt. Wesende dā twee even platte rechthoucken elck begrepen onder een houckmaet ende haer schilboochs houckmaet, die twee recht houcken hebben even sijden, t'welck wy bewijsen moesten.

Vertooch. 20 Voorstel.

De duysteraers booch die van haer evenaerslangde meest verschilt: Maeckt mette selve evenaerslangde een vierendeel rondts.

Tghegheven. Laet inde form des 17 voorstels D G de duysteraers booch sijn die van haer evenaerslangde D H meest verschilt, voort sy de beteyckening van d'ander linien na t'inhoudt des selfden 17 voorstels.

T'begheerde. Wy moeten bewijsen dat de selve D G met D H t'samen een vierendeel rondts maken, Tbewys.

1 Lidt.

Gestelt des driehoucx D G H sijde H G als grondt, ick segh deur het 24 voorstel der clootsche driehoucken, dat

Ghelijck houckmaet des slijnckerhoucx	D H G,
Tot houckmaet des rechterhoucx	D G H,
Alsoo houckmaet der rechtersijde	D G,
Tot houckmaet der slijnckersijde	D H.

2 Lidt.

Daer na gestelt des driehoucx A E G sijde G E als grondt, ick segh deur t'boveschreven 24 voorstel der clootsche driehoucken, dat

Ghelijck houckmaet des rechterhoucx	A E G,
Tot houck maet des slijnckerhoucx	A G E,
Alsoo houckmaet der slijnckersijde	A G,
Tot houckmaet der rechtersijde	A E.

3 Lidt.

Maer den houck A E G des 2 lidts, is even anden houck D H G des 1 lidts, om datse beyde recht sijn: Ende den houck A G E des 2 lidts, is even anden

houck D G H des 1 lidts deur het 6 vervolgh des 1 voorstels vande clootsche driehoucken, daerom de twee laetste palen des 1 lidts, ende de twee laetste palen des 2 lidts, sijn tot even palen everedenich, ende daerom oock met malcander everedenich, dat is

Ghelijck houckmaet van	D G,
Tot houckmaet van	D H,
Alsoo houckmaet van	A G,
Tot houckmaet van	A E.

4 Lidt.

Voort, want de houckmaet van A G, middeleveredenighe is tusschen de houckmaten van A F en A E deur t'gegeven des 17 voorstels, soo segh ick dat

Ghelijck houckmaet van	A F,
Tot houckmaet van	A G,
Alsoo houckmaet van	A G,
Tot houckmaet van	A E.

5 Lidt.

Maer A H is even met A F, daerom

Ghelijck houckmaet van	A H,
Tot houckmaet van	A G,
Alsoo houckmaet van	A G,
Tot houckmaet van	A F.

6 Lidt.

Sulcx dat de twee eerste palē des 3 lidts, ende de twee eerste palen des 5 lidts, tot een selve reden everedenich sijn, ende daerom oock met malcander everedenich, dat is

Ghelijck houckmaet van	D G,
Tot houckmaet van	D H,
Alsoo houckmaet van	A H,
Tot houckmaet van	A G.

7 Lidt.

Ghestelt daer na A E als grondt, ick segh deur het 24 voorstel der clootsche driehoucken, dat

Ghelijck houckmaet des rechterhoucx	G A E,
Tot houckmaet des slijnckerhoucx	G E A,
Alsoo houckmaet der slijnckersijde.	G E,
Tot houckmaet der rechtersijde	A G.

8 Lidt.

Maer houckmaet van H F, is houckmaet des houcx G A E deur de 2 bepaling der clootsche driehoucken; Ende houckmaet A H, is even ande houckmaet des rechthoucx G E A, daerom

Ghelijck houckmaet van	H F,
Tot houckmaet van	A H,

Alsoo houckmaet van	G E,
Tot houckmaet van	A G.

9 Lidt.

Ende deur overhandtsche reden,

Ghelijck houckmaet van	H F,
Tot houckmaet van	G E,
Alsoo houckmaet van	A H,
Tot houckmaet van	A G.

10 Lidt.

Sulcx dat de twee eerste palen vant 6 lidt, en̄ de twee eerste palen vant 9 lidt, met een selve reden everedenich sijn, ende daerom oock met malcander everedenich, dat is,

Ghelijck houckmaet van	D G,
Tot houckmaet van	D H,
Alsoo houckmaet van	H F,
Tot houckmaet van	G E

11 Lidt.

Dit soo sijnde, den rechthouck begrepen onder de twee uyterste palen vant 10 lidt, te weten de houckmaten van D G, G E, is even anden rechthouck begrepen onder de twee middelste palen, te weten de houckmaten van D H, D F. T'welck wesende twee even platte rechthoucken, elck begrepen onder een houckmaet ende haer schilboochs houckmaet, soo hebbē die twee rechthoucken twee even sijden deur het 19 voorstel, dat is, de cleenste sijde G E even mette cleenste sijde D H.

12 Lidt.

Maer D G met G E doen een vierendeel rondts, daerom D G met D H (die even is an G E deur het 11 lidt) doen t'samen oock een vierendeel rondts.

T'beslvyt. De duysteraers booch dan die van haer evenaerslangde meest verschilt, maeckt mette selve evenaerslangde een vierendeel rondts, het welck wy bewijsen moesten.

Merckt.

Anghesien datmen de duysteraers booch die van haer evenaerslangde meest verschilt, nauwer ende eyghentlicker souckt danse deur de tafels ghemeenlick beschreven worden, waer in verscheyden werckingen op een selve booch somwijlen 1 ① of 2 ① van malcander connen verschillen, waer uyt oock niet na genouch ghesien en wort dat de duysteraers booch die van haer evenaerslangde meest verschilt, mette selve evenaerslangde een vierendeel rondts maeckt: Soo heeft sijne Vorstelicke Ghenade die rekening des 18 voorstels tot op ③ berekent, en̄ daer mede degetalē der houckmatēen̄ bogē alsinsten naestē genomē: Waer mede gevondēwiert des duysteraers booch D G	46 tr. 16.43.43.
Ende voor de evenaersbooch D H	43 tr. 43.16.44.
Maken t'samen	90 tr. 0.0.27.

Sulcx dat dit besluyt deur ghetalen maer 27 ③ en schilt, vant warachtich wisconstich bewijs.

21 Voorstel.

Te vinden het meeste verschil, datterinde natuerlicke dagen veroirsaeckt vvort, alleenelick deur de uytmiddelpunticheyt des Sonvvechs deur vvisconstighe vvercking ghegront op stelling eens vasten Eertcloots.

T'ghegheven. Laet A B C D de Sonwech sijn, diens middelpunt E, verstepunt A, naestepunt C, ende F G H I den duysteraer, diens middelpunt K, schijnbaer verstepunt F, schijnbaer naestepunt H, ende de lini deur t'punt K rechthouckich op F H, sy I G, sniende de Sonwech inde punten D en B, deur welcke ghetrocken sijn tot inden duysteraer de linien E B L, E D M.

t'Werck.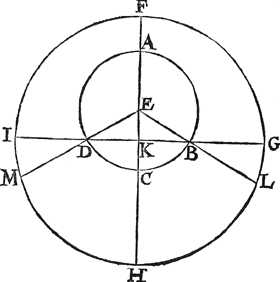

Hier is voorgestelt te moeten vinden t'meeste verschil datter veroirsaeckt wort inde natuerlicke daghen, alleenelick deur de uytmiddelpunticheyt: Waermen mede verstaen sal, dat by malcander vergaert wesende al de natuerlicke daghen des natuerlick jaers, die om de voorschreven uytmiddelpunticheyt alleen, grooter sijn dan middeldaghen: Ende die verleken by al de natuerlicke daghen des natuerlick jaers die cleender sijn dan middeldaghen, datmen moet vinden wat verschil de selve daghen aldus meer hebben, danse souden alsser geen uytmiddelpunticheyt noch afwijcking en waer: Tot desen einde segh ick, dat by aldien de Son waer ter plaets van A, soo soude den siender soo wel uyt E (van daermen de middeldagen siet) als uyt K (voor wien de natuerlicke dagen verschijnen) de Son schijnbaerlick sien in F: Maer de Son van A gecommen wesende tot D, sy soude uyt E schijnbaerlick ghesien worden in M, ende uyt K schijn baerlick in I: Daerom by aldien I waer in eenich middachsrondt, M soude (om dat de rassche loop gaet van M over I na F) so veel daer voor sijn, als bedraecht de booch I M, welcke doet 2 tr. 23 ①, uyt oirsaeck dattet is den booch des houcx I D M, even anden houck

E D K, welcke wesende de grootste voorofachtring deur het

4 voorstel, sy doet deur t'vervolgh des selfden als boven	2 tr. 23.
Sulcx dat soo veel tijts de Son mette rassche loop deurbrengt op de selve 2 tr. 23 ①, Soo veel sijn de natuerlicke daghen vande Sonloop A D corter dan middeldaghen. Ende om derghelijc-

ke redenen sijn de natuerlicke dagen vande Sonloop B A oock corter dan middeldaghen	2 tr. 23.
Comt tsamen dat de natuerlicke daghen vande Sonloop B A D corter sijn dan middeldaghen	4 tr. 46.
Ende vervolghens nadien al de natuerlicke daghen des jaers, even sijn met derghelijcke menichte van middeldaghen, soo moeten al de natuerlicke daghen van de rest des rondts, dat is des Sonloops D C B, soo veel langer sijn dan dergelijcke menichte van middeldaghen als d'ander corter, te weten	4 tr. 46.
Maer vande booch B A D corter wesende 4 tr. 46 ①, ende van D C B soo veel langher, soo moetet verschil der selve twee boghen wesen het dobbel van dien, te weten	9 tr. 32.
Welcke om dat 15 tr. een uyr gheven, doen voor t'begheerde	0 uyr 38 ①

Fnde soo veel sijn, om de uytmiddelpunticheyts wil, de natuerlicke dagen des boochs M F L verleken by de natuerlicke daghen des boochs M H L, cleender danse sijn souden alsser gheen uytmiddelpunticheyt noch afwijcking en waer. Daer af t'bewijs deur t'werck openbaer is, T'beslvyt. Wy hebben dan ghevonden t'meeste verschil datter inde natuerlicke daghen veroirsaeckt wort alleenelick deur de uytmiddelpunticheyt des Sonwechs, deur wisconstige wercking ghegront op stelling eens vasten Eertcloots, na den eysch.

22 Voorstel.

Te vinden het meeste verschil datter inde natuerlicke dagen veroirsaecktvvort, alleenelick deur de afvvijcking des duysteraers deur vvisconstighe vvercking ghegront op stelling eens vasten Eertcloots,

T'gegeven. Laet A B C D E een cloot sijn, diens aspunt is A, evenaer E C, duysteraer D B, lentsne F, duysteraersbooch F G 46 tr. 17 ①, die over d'eē sijde der lentsne F van haer evenaerslangde F H, doende deur het 18 voorstel 43 tr. 43 ①, meest verschilt, te weten 2 tr. 34 ①: Voort sy F I de duysteraers booch, die over d'ander sijde der lentsne F van haer evenaerslangde F K meest verschilt.

t'Werck.

De boghen daer in de natuerlicke daghen corter bevonden worden dan middeldaghen, sijn I G, doende deur het 18 voorstel tweemael 46 tr. 17 ①,

dats 92 tr. 34 ①, met noch een derghelijcke ende even booch over d'ander sijde des cloots, deur de herftsne streckende, maken t'samen	185 tr. 8.
De bogen daer in de natuerlicke dagē langer bevondē worden dan middeldagen, sijn G B, I D, doende elck 43 tr. 43 ① deur het 18

voorstel, t'samē 87 tr. 26 ①, met noch twee dergelijcke en̄ even boghen over d'ander sijde des cloots, maken t'samen	174 tr. 52.
Die ghetrocken vande boveschreven 185 tr. 8 ①, blijft	10 tr. 16.
Welcke (om dat 15 tr. een uyr gheven) doen voor tbegheerde	0 uyr 41 ①.

Ende soo veel sijn om de afwijckingens wil de natuerlicke dagen des boochs I G, met dergelijcke over d'ander sijde des cloots, verleken by de natuerlicke dagen der twee bogen G B, I D, met dergelijcke twee bogen over d'ander sijde des cloots, cleender danse sijn souden alsser geen afwijcking en waer. Van t'welck het bewijs deur t'werck openbaer is. T'beslvyt. Wy hebben dan gevonden het meeste verschil datter inde natuerlicke daghen veroirsaect wort alleenelick deur de afwijcking des duysteraers, deur wisconstighe wercking gegront op stelling eens vasten Eertcloots, na den eysch.

margenoot*: Ab introitu Solis in vernalem sectionem.

margenoot*: Prazi.

margenoot*: Horizontem.

margenoot*: Theoremate.

Vorige Volgende