Wisconstighe gedachtenissen. Deel 1: van 't weereltschrift

(1608)–Simon Stevin– rechtenstatus



[pagina 354]
Nv de werckstvcken. 1 Werckstvck. Wesende bekent de duy steraerlangde eens gheghevenGa naar margenoot+ punts inden duysteraer sijn evenaerbreede te vinden. Tghegheven. Laet A B C D E een middachsront sijn diens aspunt A is, ende B D den duysteraer, C E den evenaer, F lentsne, F B, F C elck 90 tr. G een punt inden duysteraer diens langde is de booch F G van 30 tr. B C 23 tr. 51 ① 20. ②. Tbegheerde. wy moeten vinden hoe groot de booch G H is.
Twerck. Anghesien F G doet 30 tr. ende A H middachront is op den evenaer C E, soo is den houck G H F recht, ende doende B C 23 tr. 51 ① 20 ② soo is den houck B F C dats G F H oock soo veel, daerom G H F is een rechthouckich driehouck met twee bekende houcken ende de schoensche, waer af ghesocht de rechthoucksijde G H, deur het 34 voorstel der clootsche driehoucken wort bevonden voor t'begheerde van 11 tr. 39 ① 59 ②. 21 ③. Beslvyt. Wesende dan bekent de duysteraerlangde eens ghegheven punts inden duysteraer, wy hebben sijn evenaerbreede ghevonden na den eysch.
Vervolgh. Hier uyt is kennelick hoemen sal maken de tafel der Sonnes evenaerbreeden van trap tot trap, die Ptolemeus tot dese plaets vervought.
2. Werckstvck.Ga naar margenoot+ Wesende bekent de duysteraerlangde eens ghegheven punts inden duysteraer: SijnGa naar margenoot⋆ evenaerlangde te vinde. Tghegheven. Laet inde form des 1 werckstucx G t'punt inden duysteraer sijn, diens duysteraerlangde dats vande lentsne F tot G doet 30 tr. Tbegheerde. Wy moeten des punts G evenaerlangde vinden, dat is de booch F H.
Twerck. Om de redenen verhaelt int werck des 1 werckstucx, soo is G H F een rechthouckighe driehouck met drie bekende palen, te weten G H F recht, G F H 23 tr. 51 ① 20 ②, ende G F 30 tr. waer af ghesocht de rechthoucksijde F H deur het 34 voorstel der clootsche driehoucken, wort bevonden voor t'begheerde van 27 tr. 50 ① 6 ②. Tbeslvyt. Wesende dan bekent de duysteraerlangde eens ghegheven punts inden duysteraer, wy hebben sijn evenaerlangde ghevonden na den eysch.

[pagina 355]
Vervolgh. Hier uyt is kenelick hoemen maken sal deGa naar margenoot* tafel der duysteraers evenaerlande die Ptolemeus tot dese plaets vervought.
3 Werckstvck.Ga naar margenoot+ Wesende bekent den langsten dach: Te vinden den booch desGa naar margenoot⋆ sichteinders begrepen tusschen den evenaer ende duysteraer. Tghegheven. Laet A B C D een middachront sijn, A C de twee aspunten, D B den evenaer, E F den sichtein der snyende den 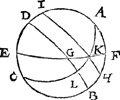evenaer D B in G, voort is H I een evewijdich rondt metten evenaer deur des duysteraers 90 tr. snyende E F in K, sulcx dat G K den ghegheven booch des sichteinders is, begrepen tusschen den evenaer B D, ende den duysteraer H I: Den grootsten dach doet 14½ uyren, diens helft voor den booch D L 108 tr. 45 ①. Tbegheerde. Wy moeten den booch G K vinden.
Twerck. Anghesien D L doet 108 tr. 45 ①, soo treck ick daer af D G 90 tr. blijft voor G L 18 tr. 45 ①: Ende K L alsGa naar margenoot* grootste evenaerbreede der Son doet 23 tr. 51 ① 20 ②, ende den houck K L G is recht. Sulcx dat K L G een driehouck is met drie bekende palen, te weten twee sijden een rechthouck begrijpende. Hier me ghesocht de derde sijde K G, wort bevonden deur het 33 voorstel der clootsche driehoucken van 30 tr. Tbeslvyt. Wesende dan bekent den langsten dach, wy hebben den booch des sichteinders ghevonden begrepen tusschen den evenaer ende duysteraer.
Vervolgh. Den booch G K wort oock ghenoemtGa naar margenoot* breede des opgancx der Son, waer deur kennelick is datmen van yder punt des duysteraers sal connen vinden de breede des opgancx, want ghevonden deur het 1 werckstuck van desen sijn evenaerbreede kleender dan K L, ende gheweten sijnde de langde van dien dach, men gaet daer me voort ghelijck mette selve K L. Door t'welck openbaer is hoemen daer af tafelen mach maken dienende tot alle trappen des duysteraers. Tis oock kennelick hoemen deur de grootste breede des opgancx G K, vinden can den langsten dach, want alsdan sullen bekent sijn des rechthouckighen driehoucx K L G twee houcken L, G, mette schoensche K G, daerom mette selve ghesocht de sijde L G deur het 34 voorstel der clootsche driehoucken, ende die vergaert tot G D 90 tr. men heeft L D, van welcke yder 15 tr. een uyr doen. Ende deur ghelijcke redenen sietmen hoe dat deur de bekende D L en G K, ghevonden can worden de Sonnens evenaerbreede als L K.

[pagina 356]
4 Werckstvck. Wesende bekent den langsten dach: DeGa naar margenoot⋆ verheffing des aspunts te vinden. Tghegheven. Laet het ghegheven des 3 werckstucx andermael t'ghegheven sijn.
Twerck. Anghesien des rechthouckighen driehoucx K L G sijde L G doet ghelijck daer gheseyt is 18 tr. 45 ①, K L 23 tr. 51 ① 20 ②, ende den houck K L G recht, soo ist een rechthouckighe driehouck met twee bekende sijden den rechthouck begrijpende: Hier me ghesocht den houck K G L, die oock is den houck F G B, wort bevonden deur het 1 voorbeelt des 33 voorstels der clootsche driehoucken van 53 tr. 59 ①: Maer F B is de grootheyt des houcx F G B, daerom F B doet 53 tr. 59 ①, de selve ghetrocken van A B 90 tr. blijft voor des aspunts A verheffing A F 36 tr. 1 ①. Tbeslvyt. Wesende dan bekent den langsten dach, wy hebben de verheffing des aspunts ghevonden na den eysch.
Vervolgh. Tis openbaer hoemen deur de bekende verheffing des aspunts A F, ende de Sonnens grootste evenaerbreede K L, sal vinden de breetheyt der sonnens opganck G K, ende ander dierghelijcke. Het 4, 5 ende 6 Hooftstick van Almagestus handelen vande grootheyt der middaechsche schaeuwen welcke sake ande middelbaer ervaernen der wisconsten bekent ghenouch sijnde hebben die Hooftsticken overghesleghen ende an dit 7 begost.
5 Werckstvgk.Ga naar margenoot+ wesende ghegheven de verheffing des aspunts, mette duysteraer boochGa naar margenoot⋆ tusschen de lentsne en sichteinder: Te vinden den evenaerbooch tusschen de lentsne en sichteinder. Tghegheven. Laet A B C D een middachront sijn, D B den sichteinder, 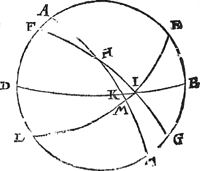B E 36 tr. verheffing desGa naar margenoot* aspunts, A C evenaer, F G duysteraer, H lentsne, H I 30 tr. voor den duysteraerbooch tusschen de lentsne en sichteinder, ende H K den evenaer booch tusschen de lentsne en sichteinder. Tbegheerde. Wy moeten vinden hoe lanck die H K is. Tbereytsel. Laet ghetrocken worden een rondt E L deur t'punt I snyende A C in M.
Twerck. Den driehouck H M I heeft drie bekende palen, te weten den houck H M I recht,
[pagina 357]
M H I 23 tr. 51 ① 20 ②, ende deschoensche H I 30 tr. Hier mede ghesocht de rechthoucksijde H M, wort bevonden deur het 32 voorstel der clootschedriehoucken van 27 tr. 50 ①: Ick souck daer na deur het 1 werckstuck van desen de booch M I evenaerbreede des punts I vanden evenaer A C, ende bevinde die van 11 tr. 40 ①: Voort van t'vierendeel ronts E C ghetrocken E B 36 tr. blijft B C 54 tr. voor grootheyt des houcx B K C, dats voor den houck I K M des driehoucx K M I, diens houck M recht is. Sulcx dat K M I nu een driehouck is met drie bekende palen, te weten M I, I K M, K M I recht hier mede gesocht de rechthoucksijde K M deur het 35 voorstel der clootsche driehoucken, wort bevondē van 8 tr. 38 ①, die getrocken van H M hier boven bevonden te doen 27 tr. 50 ① blijft voor de begheerde H K 19 tr. 12 ①. Tbeslvyt. wesende dan ghegheven de verheffing des aspunts, mette duysteraerbooch tusschen de lentsne en sichteinder: Wy hebben gevonden den evenaerbooch tusschen de lentsne en sich teinder, na den eysch.
Vervolgh. Ten eersten ist openbaer hoe dat deur de bekende E B en H K, ghevonden sal worden H I. Ten tweeden hoemen deur de bekende H K en H I, vinden sal des aspunts E verheffing E B. Ten derden hoemen deur eenighe bekende palen der boveschreven manieren, den langsten dach sal vinden, want tot M K 8 tr. 38 ①, vergaert K A 90 tr. maken tsamen 98 tr. 38 ①, diens dobbel 197 tr. 16 ① is een booch van 13 uyren 9 ①. Ten vierden soo canmen weten tot wat uyr een voorghestelt punt des duysteraers daer de Son schijnbaerlick in is, inden sichteinder comt, want K M 8 tr. 38 ① gebrocht tot uyren, doen o uyren 35 ①, ende soo veel smorghens voor ses uyren dats ten 5 uyren 25 ①, sal den 30 tr. des duysteraers als punt I inden sichteinder commen. Ten vijfden is kennelick hoemen vande voorschreven manieren tafels sal connen maken, dienende voor verscheyden sichteinders, ghelijck Ptolemeus tot dese plaets ghedaen heeft. Het 8 ende 9 Hooftstuck van Almagestus niet in hebbende t'ghene wy voornemen hier te beschrijven, sullen die overslaen, ende an het 10 commen.
6 Werckstvck Wesende ghegheven deGa naar margenoot⋆ duysteraerbooch tusschen de lentsne ende middachront: Te vinden den houck begrepen tusschen den selven duysteraer ende middachront. Tghegheven. Laet A B C D een middachrondt sijn, A C den duysteraer, D B den evenaer, E lentsne, A E booch des duysteraers 30 tr. Tbegheerde. Wy moeten den houck E A B vinden.
Twerck. Want A D E een rechthouckich driehouck is met drie bekende palen, als A D E recht, A E D 23 tr. 51 ① 20 ②, ende A E 30 tr. soo vinde ick daer me deur het 36 voorstel der clootsche driehoucken den houck D A E van 69 tr. 3 ①, die ghetrocken van 180 tr. blijft voor den begeerden houck E A B 110 tr. 57 ①.
[pagina 358]
Tbeslvyt. Wesende dan ghegheven de duysteraerbooch tusschen de lentsne ende middachront, wy hebben gevonden den houck begrepen tusschen den selven duysteraer ende middachront, na den eysch.
7 Werckstvck Wesende ghegheven de duysteraerbooch tusschen de lentsne ende denGa naar margenoot⋆ sichteinder, mette verheffing des evenaers: Te vinden den houck begrepen tusschen de selve duysteraer ende sichteinder. Tghegheven. Laet A B C D een middachront sijn diens sichteinder E F, duysteraer A C, snyende E F in G, ende D B sy evenaer, snyende A C in H als lentsne, ende E F in I, en G H doe 30 tr. ende sijn verheffing boven den sichteinder sy E D 54 tr. Tbegheerde. Wy moeten den houck A G E vinden.
Twerck. Anghesien H G I een driehouck is met drie bekende palen, als G H 30 tr. G H I 23 tr. 51 ① 20 ②, H I G 126 tr. (want DI, E I doen elck 90 tr. ende den booch E D 54 tr. diens halfrondts vervulling 126 tr. waer deur den houck D I F, dats oock H I G, 126 tr. doet) soo vinde ick daer mede deur het 41 voorstel der clootsche driehoucken den houck H G I, t'welck oock is den begeerden houck A G E van 32 tr. 10 ①. Tbeslvyt. Wesende dan ghegheven de duysteraerbooch tusschen de lentsne ende den sichteinder, mette verheffing des evenaers, wy hebben gevonden houck begrepen tusschen de selve duysteraer ende sichteinder, na den eysch.
8 Werckstvck.Ga naar margenoot+ Wesende bekent de verheffing desGa naar margenoot* aspunts, mette schijnbaerplaets der Son inden duysteraer, ende de uyr des daechs: Te vinden de hooghde der Son boven den Sichteinder: Oock denGa naar margenoot⋆ houck des topboochs ende duysteraers. Tghegheven. Laet A B C D een middachront sijn, D B den sichteinder, E den Noortschen aspunt, verheven boven B 36 tr. F den Zuytschen aspunt, A C den evenaer snyende D B in G, ende H I den duysteraer snyende D B in K, voort is L herftsne, M de Son, diens schijnbaer duysteraerlangde sy 90 tr. Ende is, neem ick, voor middach te elfuyren, te weten de Son een uyr vant middachrondt, 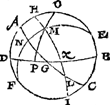dat is, ghetrocken van d'een aspunt E, tot d'ander F, de booch E M F, sy snijt den evenaer A C in N, alsoo dat A N een uyr doet, dats 15 tr. Voort soo valter van het top O door M de topbooch O P. Tbegheerde. Wy moeten vinden de booch M P, verheffing der Son boven den sichteinder: Oock den houck H M O, ghemaeckt vanden topbooch M O, ende den duysteraer M H.

[pagina 359]
Twerck. O M E is een driehouck met drie bekende palen, want O E schilbooch van E B 36 tr. doet 54 tr. Ende M E schilbooch van 23 tr. 51 ① 20 ②, doet 66 tr. 8 ① 40 ②, ende den houck O E M 15 tr. (want A E, N E elck 90 tr. doende, soo is A N 15 tr. de grootheyt des houcx A E N van 15 tr. maer A E N, of O E M is al een selve houck, waer deur ghelijck gheseyt is den houck O E M 15 tr. doet) Daerom van desen driehouck O E M, ghesocht deur het 40 voorstel der clootsche driehoucken de sijde O M, wort bevonden van 17 tr. 46 ①, die ghetrocken van O P 90 tr. blijft voor de begheerde M P 72 tr. 14 ①. Ende vanden selven driehouck O E M, ghesocht den houck O M E, wort bevonden van 43 tr. 21 ①, die getrocken van H M E doende in dit voorbeelt 90 tr. blijft voor den begheerden houck H M O 46 tr. 39 ①. Tbeslvyt. Wesende dan bekent de verheffing des aspunts, mette schijnbaerplaets der Son inden duysteraer, ende de uyr des daechs, wy hebben gevonden de hooghde der Son bovē den Sichteinder: Oock den houck des topboochs ende duysteraers na den eysch.
Vervolgh. Ten eersten sooder bekent waer verheffing des aspunts, mette schijnbaerplaets des Sons inden duysteraer, ende haer verheffing bovē den sichteinder: Tis openbaer hoemen de uyr des daechs sal vinden, want alsdan sullen inden driehouck O M E, bekent sijn de drie palē O E, M E, O M, daer mede gevonden den houck O E M deur het 43 voorstel der clootsche driehoucken, de trappen des selfden sijn oock voor den booch A N, welcke tot uyren gebrocht men weet dattet soo verre vanden middach is. Tē tweedē sooder bekent waer verheffing des aspunts, uyr des daechs, en̄ hoogde der Son boven den sichteinder: Tis openbaer hoemen de schijnbaerplaets der Son in den duysteraer sal vindē, want alsdan sullen indē driehouck O M E, bekent sijn de drie palen O E, O M, O E M, daer me ghevonden desijde E M deur het 40 voorstel der clootsche driehoucken, ende dieghetrocken van E N 90 tr. de rest is voor M N afwijcking der Son vandē evenaer, welcke bekent sijnde, soo heeft de driehouck M L N drie bekende palen, te wetē den houck M N L recht, dē houck M L N 23 tr. 51 ① 20 ②, en de sijde M N: Hier me ghesocht de sijde L M, wort ghevonden deur het 35 voorstel der clootsche driehoucken, voor t' begheerde. Ten derden sooder bekent waer plaets der Son inden duysteraer, de uyr des daechs, ende hooghde der Son: Tis openbaer hoemen de verheffing des aspunts vinden sal, want alsdan sullen inden driehouck O M E, bekent sijn de drie palen O M, M E, O E M, daer mede ghevonden de sijde O E deur het 40 voorstel der clootsche driehoucken, ende die ghetrocken van O B 90 tr. de rest is voor E B begeerde verheffing des aspunts. Ten 4 soomen wilde weten wat trap des evenaers int middachrontis, men vergaert A N tot N L, ende men comt tottet begheerde. S'gelijcx om te weten wat trap des duysteraers int middachront is, men vindt de sijde H L deur des driehoucx H A L drie bekende palē A L, H A recht, A L H herfthouck, ende men comt tottet begheerde. De trap des evenaers inden sichteinder ter plaets van G, is oock bekent, want vande bekende A tot G sijn 90 tr. S'ghelijcx can oock bekent worden den trap des duysteraers K inden sichteinder D B deur het 5 werckstuck van desen. Ten 5 soo is kennelick hoemen vinden sal de lanckheyt desGa naar margenoot* dagheraets op een ghegheven dach, ende verheffing des aspunts: Want ghestelt hetGa naar margenoot* teghenoverpunt der Son soo hooch boven den sichteinder, als de Son self int begin oft
[pagina 360]
eynde des dagheraets daer onder is, t'welck gemeenlick genomen wort op 18 tr. ende ghevonden hoe veel tijts of trappen dat punt van den sichteinder is, men heeft t'begheerde.
Merckt. Alsoot sijn Vorstelicke Ghenade dochte de natuerlicke oirden te vereysschen, dat benevens het vinden van hooghde der Son deur bekende uyr des daechs, oock ter contrarie behoort te commen het vinden vant uyr des daechs, door de bekende hoochde der Son: Van t' welck by Ptolemeus, noch sijn uytlegghers namelick Regiomontanus, Copernicus, ende Oswaldus, niet vermaent sijnde, wy hebben een manier van wercking vercoren alsvoren bestaende int nemen der bekende palens schilboghen, door wiens herneming yder pael der vier soo opentlick deur d'ander drie bekent wort, dat wy niet noodich en achteden daer af besonder werckstucken te maken, maer in die plaets de boveschreven vervolghen te setten ghelijckmen siet.
9 Werckstvck. Wesende bekent eens sterrens duysteraerlangde en breede: Te vinden haer evenaerlangde en breede. Tghegheven. Laet A B C D een rondt sijn, streckende door beyde de aspunten, als E des evenaers D B, ende F des duysteraers A C, ende G sijde lentsne: Voort isser ghetrocken de booch van F tot H inden duysteraer, in welcke booch F H, staet, neem ick, een sterre I, sulcx dat de booch H I is haer duysteraerbreede van 12 tr. ende G H haer duysteraerlangde van 30 tr. Tbegheerde. Wy moeten vinden des sterrens I evenaerlangde en breede. Tbereytsel. Ick treck van E door t'punt I tot inden evenaer de booch E K, daer na E G, sulcx dat I K is evenaerbreede der sterre I, ende G K haer evenaerlangde, welcke twee boghen ghevonden sijnde, men sal t'begheerde hebben.
Twerck. De driehouck E F I heeft drie bekende palen, F E 23 tr 51 ① 20 ②, F I 78 tr. schilbooch van I H 12 tr. Voort den houck E F I 60 tr. als schilhouck van G F H 30 tr. Daer me ghesocht deur het 40 voorstel der clootsche driehoucken de sijde E I, wort bevonden van 67 tr. 10 ①, die ghetrocken van E K 90 tr. blijft voor de begheerde evenaerbreede I K 22 tr. 50 ①. Daer na ghesocht den houck F E I, wort bevonden van 113 tr. 13 ①, daer af ghetrocken den rechthouck F E 90 tr. blijft voor den houck G E K 23 tr. 13 ①, t'welck oock is voor de begheerde langde G K. Tbeslvyt. Wesende dan bekent een sterrens duysteraerlangde en breede, wy hebben ghevonden haer evenaerlangde en breede, na den eysch.
Merckt. Copernicus heeft int 4 Hooftstuck sijns 2 boucx een ander wijse van wercking ghedaen als de voorgaende: Ende noch een ander manier heeft daer in sijn Vorstelicke Ghenade ghemerckt van deser ghedaente: Ghetrocken sijnde de booch G I, soo is I H G een rechthouckich driehouck met drie be-
[pagina 361]
kende palen, als I H 12 tr. H G 30 tr. ende den houck I H G recht: Daer mede gesocht de schoensche I G, bevantse door het 33 voorstel der clootsche driehouckē van 32 tr. 6 ①, ende den houck I G H van 23 tr. 2 ①, de selve vergaert totten houck H G K 23 tr. 51 ① 20 ②, maken tsamē voor den houck I G K 46 tr. 53 ① 20 ②. Sulcx dat I K G een rechthouckich driehouck is met drie bekende palen, te weten I G 32 tr. 6 ①, I G K 46 tr. 53 ① 20 ②, en̄ den houck I K G recht: Hier mede ghesocht de sijde I K deur het 34 voorstel der clootsche driehoucken, wort bevonden voor de begheerde evenaerbreede van 22 tr. 50 ①: Ende de sijde G K voor de begheerde evenaerlangde van 23 tr. 12 ① als boven. Doch wy stellen int boveschreven werckstuck alsulcke wercking, om de voorverhaelde ghemeene reghel te volghen deur een driehouck die ghemaeckt wort uyt schilboghen der bekende palen.
10 Werckstvck. Wesende bekent een sterrens duysteraers en evenaerbreede: Te vinden haer duysteraers langde. Dit werckstuck wort deur Copernicus lib. 3 cap. 2 ende ander, afgheveerdicht deur gemeene sneen van t'vlack des middachronts ende vlacken van ander ronden daer op rechthouckich. Maer om hier breeder te verclaren de wercking der clootsche driehoucken ende voornamelick de gemeene reghel vant nemen der schilboghen vande bekende palen, soo stellen wy hier dit voorbeelt. Tghegheven. Laet A B C D een rondt sijn, streckende door beyde de aspunten als E des evenaers D B, ende F des duysteraers A C, ende G sy de herftsne, H een sterre, ick neem deGa naar margenoot* Maechts are, waer deur streckt de booch van F tot I inden duysteraer, sulcx dat H I is de duysteraer breede der sterre doende 2 tr: Voort comter vanden evenaers aspunt E deur t'punt H tot inden evenaer de booch E K: Sulcx dat H K sy haer evenaers breede doende, ghelijck die Copernicus stelt, 8 tr. 40 ①. Tbegheerde. Wy moeten de booch vande herftsne G tot I vinden, welcke bekent wesende soo is oock de begheerde langde openbaer. Tbereytsel. Laet ghetrocken worden de booch F G.
Twerck. Anghesien H I doet 2 tr. haer schilbooch H F doet 88 tr. voort doende K H 8 tr. 40 ①, haer schilbooch H E doet 81 tr. 21 ①, ende F E even ande duysteraers afwijcking vanden evenaer, die doet ghelijckse Copernicus ghestelt heeft 23 tr. 28 ① 30 ②: Sulcx dat H F E een driehouck is met drie bekende sijden: Hier mede ghesocht den houck H F E wort bevonden deur het 43 voorstel der clootsche driehoucken van 72 tr. 37 ①, die ghetrocken vanden rechthouck G F E 90 tr. blijft voor den houck G F I 17 tr 23 ①: daer Copernicus voor stelt 17 tr. 21 ①, daer toe vergaert 180 tr. voor het halfront vande lentsne totte herftsne G, comt voor begheerde langde 197 tr. 23 ①. Beslvyt. Wesende dan bekent een sterrens duysteraer breede ende haer evenaerbreede, wy hebben haer duysteraerlangde ghevonden na den eysch.
1 Vervolgh. Tis kennelick dat soomen wilde weten de sterrens evenaerlangde, datmen soude moeten vinden des driehoucx H F E houck H E F, ende daer af getrocken den rechthouck G E F 90 tr. de rest soude t' begheerde sijn.

[pagina 362]
De na beschreven drie vervolghen sijn deur sijne Vorstelicke Ghenade verdocht. 2 Vervolgh. Tis openbaer dat soomen door de sterrens bekende duysteraerlangde en evenaerlangde, wilde weten haer duysteraerbreede ende evenaerbreede, datmen alsdan vanden rechthouck G F E, soude moeten trecken den houck G F I, wiens grootheyt de ghegheven duysteraerlangde G I is, ende sal daer mede des driehoucx H E F houck H F E bekent sijn: Daer na totten rechthouck F E G, vergaert den houck G E K, wiens grootheyt de ghegheven evenaerlangde G K is, ende sal daer mede des voorschreven driehoucx H E F ander houck H E F oock bekent sijn, daer toe noch de bekende sijde F E tusschen beyde de aspunten, soo heeft den driehouck H E F drie bekende palen, daer mede ghesocht deur het 42 voorstel der clootsche driehoucken ten eersten de sijde F H, ende die ghetrocken van F I 90 tr. de rest is voor H I begheerde duysteraerbreede der sterre. Ten tweeden ghevonden de sijde E H, ende die ghetrocken van E K, de rest is voor H K begheerde evenaerbreede der sterre.
3 Vervolgh. Tis openbaer dat soomen deur de sterrens bekende duysteraerlangde, en evenaerbreede, wilde weten haer duysteraerbreede, en evenaerlangde, datmen alsdan vanden rechthouck G F E, soude moetentrecken den houck G F I, wiens grootheyt de ghegheven duysteraerlangde GI is, ende sal daer mede des driehoucx H E F houck H F E bekent sijn: Daer na ghetrocken de gegeven bekende evenaerlangde H K van K E, blijft de sijde H E bekent, daer toe noch de bekende sijde F E tusschen beyde de aspunten, soo heeft de driehouck H E F drie bekende palen, daer mede ghesocht deur het 40 voorstel der clootsche driehoucken ten eersten de sijde F H, ende die ghetrocken van F I 90 tr. de rest is voor H I begeerde eyghen breede der sterre: Ten tweeden ghevonden den houck H E F, en̄ daer af ghetrocken G E F 90 tr. de rest is voor den houck G E K, wiens grootheyt de begheerde evenaerlangde G K is.
4 Vervolgh. Tis openbaer dat soomen door de sterrens bekende eyghen breede en evenaerlangde, wilde weten haer eyghen langde ende evenaerbreede, dat alsdan totten bekenden houck G E K (want haer grootheyt is de bekende evenaerlangde G K) vergaert den rechthouck G E F, soo is des driehoucx H E F houck H E F bekent, alsoo oock is H F schilbooch der bekende eyghen breede H I: En ten derden de sijde F E tusschen beyde de aspunten: Sulcx dat de driehouck H E F drie bekende palen heeft, daer mede ghevonden den houck H F E, ende die ghetrocken van G F E 90 tr. de rest is voor den houck G F I, wiens grootheyt de begeerde eyghen langde G I is. Ten tweeden ghevonden de sijde H E, ende die getrocken van E K 90 tr. de rest is voor de begheerde evenaerbreede H K.
11 Werckstvck. Wesende ghegheven tvveer sterren breede en langde: Te vinden hoe verre die van malcander staen. Tghegheven. Laet A B C D een hemelcloot sijn, diens duysteraer D B, wiens lentsne D, ende aspunt A, voort sy E een sterre diens breede G E
[pagina 363]
30 tr. ende langde D G 40 tr. Ende F een ander sterre diens breede H F 50 tr. ende langde D H 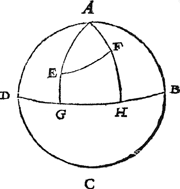110 tr. Tbegheerde. Wy moeten vinden hoe verre die twee sterren E, F van malcander staen, te weten de grootheyt des boochs E F. Tbereytsel. Laet G E, H F beyde voort ghetrocken worden tot inden aspunt A.
Twerck. Anghesien G E, H F, doen 30 tr. en 50 tr. haer schilboghen E A, F A doen 60 tr. en 40 tr. Voort ghetrocken D G 40 tr. van D H 110 tr. blijft G H 70 tr. voor grootheyt des houcx G A H, ofte E A F des driehoucx E A F: Sulcx dat E A F een driehouck is met drie bekende palen, te weten twee sijden E A, F A den bekenden houck A begrijpende: Daer mede ghesocht de sijde E F deur het 40 voorstel der clootsche driehoucken, wort bevonden voor t'begheerde van 51 tr. 1 ①. Beslvyt. Wesende dan gegheven twee sterren breede en langde, wy hebben ghevonden hoe verre die van malcander staen na den eysch.
1 Vervolgh. Sooder bekent waer hoe verre de twee boveschreven sterren E, F van malcander sijn met haer breede alleen: Tis kennelick dattet verschil haerder langden als G H openbaer can worden, want alsdan sullen des driehoncx A E F drie sijden bekent sijn, daer mede ghevonden den houck A deur het 43 voorstel der clootsche driehoucken men heeft t'begh eerde, want de grootheyt des selfden is voor de begheerde G H.
2 Vervolgh. Sooder bekent waer de breede van dien sterre als neem ick van E, ende den booch van d'een tot d'ander als E F, mettet verschil haerder langden G H: Tis openbaer dat de breede van d'ander sterre ghevonden can worden, want alsdan sal den driehouck A E F drie bekende palenhebben, als twee sijden A E, E F, metten houck E A F, daer mede ghevonden de sijde A F deur het 39 voorstel der clootsche driehoucken men heeft t'begheerde.
3 Vervolgh. Sooder ghegheven waer drie of meer sterrens langde en breede, tis openbaer datmen yder booch van d'een tot d'ander sal vinden, met d'ander ghedaenten lijckformich an die des 1 ende 2 vervolghs.
12 Werckstvck. Wesende ghegheven tvvee paer sterren van bekende breede en langde, staende in tvvee verscheyden grootste ronden, ende noch een vijfde sterre inde gemeene sne dier tvvee ronden: Te vinden hoe verre die vijfde sterre van een der vier is.
[pagina 364]
Tghegheven. Laet A B en C D twee paersterren sijn van bekende langde en breede, staende in twee verscheyden grootste ronden, ende noch een vijfde sterre E in de gemeene sne der twee ronden. Tbegheerde. Wy moeten vinden hoe verre die sterre E van D is.
Twerck. De booch A D met B D wort bekent deurt 11 werckstuck van desen, en B D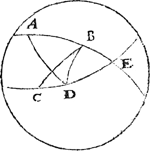 deurt ghegheven, sulcx dat den driehouck A B D drie bekende sijden heeft, daer mede ghevonden den houck A B D deur het 43 voorstel der clootsche driehoucken, ende die ghetrocken van 180 tr. blijft den houck E B D bekent: Ende sgelijcx sal oock bekent worden den houck E D B, sulcx dat den Driehouck B D E drie bekende palen sal hebben, daer mede ghevonden de sijde D E deur het 42 voorstel der clootsche driehoucken men sal tottet begheerde commen. Sulcke voorbeelden connen te pas commen alsmen inden hemel drie sterren ghelijck A B E op een rechte reghel sier passen, ende sghelijcx oock de drie sterren C D E, want alsdan is de sterre E in tweer ronden ghemeene sne, ende can de booch tusschen haer ende een van d'ander sterren gevonden wordē alsboven.
13 Werckstvck. De uyr des daechs deur een sterre te vinden. Tghegheven. Laet A B C D een middachront sijn, A C den duysteraer, D B den evenaer, E de Lentsne, F een sterre diens duysteraerbreede F G, duysteraerlangde E G. Tbegheerde. Wy moeten daer mede de uyr des daechs vinden.
Twerck. Ick vinde deur het 9 werckstuck van desen de sterrens evenaerbreede F H, en̄ evenaerlangde E H.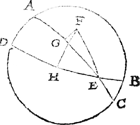 Twelck soo sijnde F H E is een rechthouckich driehouck met twee bekende sijden F H, E H, ende den houck F H E recht, daer mede vinde ick deur het 33 voorstel der clootsche driehoucken dē houck F E H, ende de sijde F E. Dit soo wesende ick ansie F E als duysteraer, diens houck F E H, ende F als Son, vinde daer me de uyr des daechs deur het 8 voorstel van desen. Maer want het waer uyr soo veel vrougher is dan dit, als de evenaerlangde der Son grooter is dan de evenaerlangde deser sterre, soo treck ick de evenaerlangde der sterre, altijt vande evenaerlangde der Son (welcke soose kleēder waer, ick doeder na de ghemeene ghebruyck 360 tr. toe) de rest der trappen wijst my an de menichte der uyren die ick vande ghevonden uyren der sterre aftrecken moet. Tbeslvyt. Wy hebben dan de uyr des daechs deur een sterre ghevonden, na den eysch. DES VIERDEN BOVCX EYNDE.	margenoot+ 13 Hooftstuck des 1 boucx Almagestus. margenoot+ 14 Hooftstuck des 1 boucx Almagestus. margenoot⋆ In venire ascensiones in sphaera recta. margenoot* Tabula ascensionum in sphaera recta. margenoot+ 2 Hooftstuck des 2 boucx Almagestus. margenoot⋆ Arcus horizontis inter aquatorem & eclipticā. margenoot* Maxima declinatio Solis. margenoot* Latitudo ortus. margenoot⋆ 2 Hooftstuck des 2 boucx Almagestus. Elevationem poli. margenoot+ 7 Hooftstuck des 2 boucx Almagestus. margenoot⋆ Inter sectionem vernalem & horizontem. margenoot* Poli. margenoot⋆ 10 Hooftstuck des 2 boucx Almagestus. Arcus eclipticae, inter sectionem vernalem & meridianum. margenoot⋆ 11 Hooftstuck des 2 boucx Almagestus. Horizontem. margenoot+ 12 Hooftstuck des 2 boucx Almagestus. margenoot* Poli. margenoot⋆ Angulus arcus verticalis & eclipticae. margenoot* Crepusculi. margenoot* Oppositum punctum. margenoot* Spica Virginis.