Dialectike ofte bewysconst
(1585)–Simon Stevin–
[pagina 89]
| |
Eerst vande verkeering der verkeerder bewysreden.MerkctEEr wy commen tot de wercking, soo dienen verstaen de Regulen vande verkeeringhe der propositien als volght. | |
Ie. Reghel. A Verkeert in I.Als,
A. Alle Mensche is een Dier.
Welck verkeert,
I. Eenich Dier dan is een Mensche. | |
IIe. Reghel. E. Verkeert in E.Als,
E. Gheen Mensche en is Steen,
Welck verkeert.
E. Gheen Steen dan is Mensche. | |
IIIe Reghel. E Verkeert in O.Als,
E. Gheen Mensche en is Steen.
Welck verkeert.
O. Eenich Steen dan is geen Mensch. | |
IIIIe Reghel. I. Verkeert in I. | |
[pagina 90]
| |
Als,
I. Eenighe keten is Govdt.
Welck verkeert.
I. Eenich Govdt dan is keten. | |
Ve. Reghel. Onscheydelicke Ontkenninghe, verkeert volcomentlick.Als,
Pieter en is Ian niet.
Welck verkeert.
Ian dan en is Pieter niet.
DE, O, en wort niet verkeert, By exempel Eenich Ghedierte en is gheen Mensche, Ende verkeert, Eenich Mensche dan en is gheen Ghedierte, dat is valsch. Het is wel waer, datter sommige Verkeeringen in O, warachtich geschieden, als, Eenighen Rinck en is gheen Goudt, ende wederom, Eenich Goudt en is gheen Rinck: Desghelijcx oock verkeert A, altemael wel in A, als, Alle Swaerste Metael is Goudt, ende wederom, Alle Goudt is Swaerste Metael, maer dese sijn byghevalle warachtich, niet uyt de cracht der Verkeeringhe, anghesien het niet in allen en is als d'ander.
Dit verstaen sijnde laet ons nemen voor ghegheven Verkeerde Bewijsreden, die wy in Rechte willen verkeeren, dese: E. Geen Metael en is Houdt, | |
[pagina 91]
| |
Werckinghe.OM door de Verkeeringhe te bethoonen, dit nootsaeckelick vervolgh te wesen, soo sien ick door de ghesteltheyt des Middeltermijns, dat de Bewijsreden is, vanden aert der Eerster Soorten, ende overmidts d'eerste Propositie is E, ende de tweede A, soo ist nootsaeckelick die te sijne vanden aert der tweeder Manieren, diens Rechte Bewijsreden aldus is: E. Gheen Metael en is Houdt, Nu dan door dit Besluyt gheen Coper Houdt wesende, soo en sal door de voorgaende tweede Reghel der Verkeeringhe, gheen Houdt Coper sijn: T'eerste Besluyt is dan warachtich, want Tgene datter volght uyt het vervolgh eender wettelicker argumenteringhe, moet oock volghen uyt het voorgaende der selver: Dat is in dit exempel te segghen: Onse ghegheven Besluyt volght (door de tweede Reghel deser propositien) uyt dit laetste Besluyt, volghende uyt een wettelicke argumenteringhe, daerom oock volght onse ghegheven Besluyt, uyt de selve wettelicke argumenteringe. S'ghelijcx sal den voortganck sijn in allen Bewijsredenen van deser gedaente, want wesende vanden aert der tweeder Soorten, soo salmen met haer ghelijcke Maniere der selver Soorten, te werck gaen als boven. Maer soo wy gheseyt hebben onder de 42. definitie, daer sijn by Aristoteles beschreven noch twee Verkeerde Bewijsredenen, vanden aert der | |
[pagina 92]
| |
Eerster Soorten, die door gheen Besluyts Verkeering als de voorgaende, ghebrocht en connen worden tot d'Eerste Soorte, de reden is, dat sy besluyten in O, welcke als vooren gheseyt is, niet verkeert en wort: Omme dan te verkeeren soodanighen Bewijsreden, By exempel dese: A. Alle Mensche is een Dier, Men sal d'eerste ende tweede Propositie verkeeren (wat verkeeringhe dit moet wesen, is kennelick uyt hare letteren, ende de voorgaende Reghelen, te weten A in I, ende E in E, t'welck wy hier eenmael voor al segghen) verstellende deerste ende tweede Propositie in malcanders plaetse aldus: E. Gheen Menscheen is een Peert, Twelck is een Bewijsreden, der vierder Manieren vande eerste Soorte, daer uyt wy besluyten (omme de redenen als int eerste exempel verclaert sijn) t'voorgaende Besluyt goedt te wesen. Ende op de selve manier salt oock toegaen, in dander Bewijsreden die sulck is: I. Eenich Dieris een Peert, Want verkeerende d'eerste ende tweede Propositie, ende haer verstellende in malcanders plaetse, als boven ghedaen is, sal oock een Bewijsreden | |
[pagina 93]
| |
sijn der vierder Manieren vande Eerste Soorte, aldus: E. Gheen Dier en is Steen, Voort canmen oock de drie eerste Soorten in malcanderen verkeeren, twelck ghebruyckelicxt is, der tweeder ende derder, te doen inde eerste, daer af wy van elck int besonder segghen sullen aldus. E A E, der tweeder Soorten, wort verkeert in E A E, der eerster, verkeerende d'eerste Propositie. A E E, der tweeder Soorten, wort verkeert in E A E der eerster, verkeerende de tweede Propositie, ende het Besluyt, oock verstellende d'eerste ende tweede Propositie in malcanders plaetse. E I O, der tweeder Soorten, wort verkeert in E I O der eerster, verkeerende d'eerste Propositie. A O O, der tweeder Soorten, en can aldus tot d'eerste niet verkeert worden, de reden is dese: Tot alle veranderinghen der Soorten, moet d'eerste tweede ofte derde Propositie verkeert worden, maer gheen van allen en is daer toe bequaem, want d'eerste Propositie wort verkeert in I, die met de tweede ofte t'Besluyt O, maect twee besondere Propositien gheen Onscheydelicke wesende, uyt de welcke gheen Wettelicke Bewijsreden Ghemaect en can worden door de vijfde anteyckening der 40. definitien. Maer datmen de tweede Propositie, ofte t'Besluyt O, soude meenen | |
[pagina 94]
| |
te verkeeren, om by de eerste te voughen, dat is oock onmueghelick, overmidts in O, gheen verkeeringhe en gheschiedt als boven geseyt is; A O O dan en can aldus niet verkeert worden, maer wel door het Onmueghelicke der 5. propositien. A A I, der derder Soorten, wort verkeert in A I I, der eerster, verkeerende de tweede Propositie. E A O, der derder Soorten, in E I O, der eerster, verkeerende de tweede Propositie. I A I, der derder Soorten, in A I I, der eerster, verkeerende d'eerste Propositie, ende Besluyt, oock verstellende d'eerste ende tweede Propositie, in malcanders plaetse. A I I, der derder Soorten, in A I I, der eerster, verkeerende de tweede Propositie. O A O, der derder Soorten, en wort in d'eerste niet verkeert, om de redenen die boven van A O O, gheseyt sijn, alleenlick, can verkeert worden door t'Onmueghelick der voorgaender 5. Propositien. E I O, der derder Soorten, in E I O, der eerster, verkeerende de tweede Propositie. Van alle welcke wy souden mueghen exempelen gheven, maer sy sijn door de voorgaende openbaer. Angaende de Verkeeringhe der Bewijsreden, diens eerste Propositie staet inde plaetse der tweeder, ofte voor diens Besluyts generale beteyckeninghe, ghenomen is besondere: De veranderinghe der selver tot Rechte, is kennelick ghenouch | |
[pagina 95]
| |
uyt d'exempelen van dien der 42. definitien, daerom sullen wy voortgaen, met de verkeering van d'ander Cromme Bewijsredenen. | |
Vande verkeering der overvloedigher bewysreden.Laet ons nemen voor Ghegeven Overvloedighe Bewijsreden, die wy verkeeren willen, dese: Pieter is een Leyenaer, | |
Werckinghe.DE Overvloedighe Bewijsreden, wort in soo vele Rechte verkeert, alsser Propositien sijn, tusschen d'Eerste ende t'Besluyt, die hier twee sijn, diens Werckinghe aldus toegaet: De ghedaente der twee eerster Propositien, bethoont die te wesen der eerster Soorten, staende d'eerste Propositie, inde plaetse der tweeder, daerom die recht ghestelt, metgaders hare Besluyt, soo salder uyt commen d'eerste Bewijsreden soodanich: A. Alle Leyenaer is een Hollander Daer naer de tweede Bewijsreden aldus: A. Alle Hollander is een Duytsch (door de derde ghegheven propositie) | |
[pagina 96]
| |
Inder voughen dat wy hier wettelick besluyten, door twee Rechte Bewijsredenen, t'ghene door een Cromme (als Overvloedighe) besloten was: Ende inder selver vougen soudemen voortvaren, sooder meer dan twee Propositien waren, tusschen de gegheven Eerste ende t'Besluyt. | |
Vande verkeering der bewysreden met voorwaerde.Laet de ghegheven Bewijsreden met Voorwaerde dese sijn: Soo het Dach is, de Sonne is boven het Horizon, | |
Werkinghe.GHelyck inde Onvolmaecte Bewijsreden, altijt een Propositie inde memorie blijft, welcke ghestelt by dander twee, die volmaect: Alsoo blijft in dese Bewijsreden altijt inde memorie, niet een Propositie, maer een Termijn, twelck oirdentlick daer by ghevoucht, bethoont de selve eenighe specie der rechter Bewijsredenen te wesen: Als in onse ghegheven ghebreect het derde Termijn, Nu, t'welck daer by ghestelt, maect een Rechte Bewijsreden der eerster Soorten aldus: A. Soo het is Dach, soo is de Sonne boven het Horizon. Tsy andermael de ghegheven Bewijsreden dese: | |
[pagina 97]
| |
Ten is gheen Dach ende Nacht, Waer by ghevoucht het derde Termijn, Nu, sal aldus wettelick volmaect sijn: E. Als het is Dach, ten is gheen Nacht, Laet wederom de Ghegheven Bewijsreden dese sijn: Het is Dach ofte Nacht, Alwaer d'eerste Propositie soo veel te segghen is, als; Als het is Dach, ten is gheen Nacht, waer duer de Rechte Bewijsreden van dien is als de voorgaende. | |
Vande verkeering der beweghender bewysreden.Het sy een ghegheven Beweghende Bewijsreden, diemen begheert te verkeeren, aldus: Dit Vier is Heet, dat Vier is Heet, ende alsoo met yeghelick ander Vier, | |
Werkinghe.Uyt het ghegheven Besluyt blijct, dat de begheerde Rechte Bewijsreden, sal moeten sijn van d'eerste Maniere der eerster Soorten, want | |
[pagina 98]
| |
gheen ander en besluyt in A, daerom stelle ick alle t'ghene datter door t'Besluyt bekent is (als inde 3. propositie oock ghedaen is) aldus: A. Alle . . . . . is Heet, Soo datter nu niet en ghebreect, dan inde twee ydel plaetsen, te vinden het Middeltermijn, twelck altijt ghetrocken sal worden, uyt d'eerste ghegheven Propositie, in deser voughen: A. Alle dat dit Vier ofte dat Vier is, ende soo met yeghelick ander Vier, is Heet, | |
Vande verkeering der bewysreden van dobbelbesluyt.Laet de ghegheven Bewijsreden dese sijn: V Dienaer is rechtveerdich, ofte onrechtveerdich, | |
Werkinghe.Ghelyck dese Cromme Bewijsreden bestaet uyt twee Besluyten, alsoo machse ver- | |
[pagina 99]
| |
keert worden in twee Rechte Bewijsredenen, aldus: I. Soo u Dienaer rechtveerdich is ghy beschuldicht hem t'Onrecht, O. Ghy en Hovdt gheen onrechtveerdich Dienaer, Het is wel waer dat d'eerste Bewijsreden so wel aldus clincken soude: A. Alle Rechtveerdighe wort t'onrecht beschuldicht, Maer overmidts dit gheen forme der Rechter vande vierde Soorte en is, soo hebben wy d'eerste alsoo ghestelt om den Reghel te volghen. | |
Vande verkeering der onvolmaecter bevvysreden.Het sy een Onvolmaecte ghegheven Bewijsreden als dese: Alle Leyenaer is Hollander, | |
[pagina 100]
| |
Werkinghe.HEt blijct an het Middeltermijn Hollander, dat de Rechte Bewijsreden des gheghevens, mach sijn der eerster, ofte tweeder Soorten, ende naer de selve volmaect, soo sal d'eerste aldus sijn: E. Gheen Hollander en is Brabander, Naer de tweede Soorte soodanich: E. Gheen Brabander en is Hollander,
Somwijlen ghebreecter de tweede Propositie, als inde 47. definitie gheseyt is, waer af de Werckinghe ghelijck sal sijn, ande voorgaende. Wy hebben dan alle ghegheven Cromme Bewijsreden, verkeert in een Rechte; naar het voornemen. | |
Merckt.NAdemael int voorgaende ghenouch bethoont schijnt, het Maecken, Verkeeren, ende de Eyghenschappen der Bewijsredenen sullen dat, soo veel dies belangt, daer by laten blijven. Maer wy moeten ten laetsten noch een weynich segghen, vande Valscheyt des Besluyts; Ende vande Oirden die int argumenteren ghehouden dient. Het is dan te weten dat alle Bewijsreden yet Valsch besluytende, heeft ghebreck, ofte inde Forme, ofte inde Materie, ofte in beyde t'samen. T'gebreck der Forme can den Dialecticien | |
[pagina 101]
| |
in allen questien altijt mercken, uyt dies dat int voorgaende opentlick daer af verclaert is. Maer t'ghebreck der Materien, en leertmen door de Dialectike niet bekennen; Alsoo der ghelijcken met velen anderen Consten ghemeen is. By exempel, yemandt seght, I. pondt peper is weert 4. ℔. daerom sijn 100. ponden peper weert 20. ℔. Voorwaer den Arithmeticien can segghen, dat de Forme der rekeninghe goedt is, al en hadde hy gheen verstandt van peper; Maer so hy betoonde datter ghebreck inde Materie ware, als het peper beseeut, ende door wentelinghe in d'asschen (naer de ghebruyck) hem weder een bedriechlick coluer ghegheven te sijne, ende naer martganck soo veel niet weert te wesen; dat en weet hy niet uyt de Arithmetike maer duer wat anders: Alsoo oock hier. By exempel, yemandt argumenteert aldus: 22. tot 7. is een bekende Reden, Den Dialecticien can segghen, dat de Forme der argumenteringhe goedt is, al en hadde hy gheen verstandt van het Rondt, want hy siet die te wesen vande eerste Maniere der eerster Soorten. Maer soo hy bethoonde datter ghebreck inde Materie ware, te weten, de tweede Propositie valsch te sijne, dat en weet hy niet uyt de Dialectike, maer uyt de Geometrie ende Arithmetike. Wederom yemandt segghende, I. pondt peper gheldende I. , de 100. ponden peper sijn weert 20. ℔: Daer op sal den Arithmeticien connen segghen, dat die 100. ponden peper misschien 20. ℔. mueghen weert sijn, maer dat sulcx niet en volght uyt die voorgaende reden. Alsoo oock yemant aldus argumenterende: , de 100. ponden peper sijn weert 20. ℔: Daer op sal den Arithmeticien connen segghen, dat die 100. ponden peper misschien 20. ℔. mueghen weert sijn, maer dat sulcx niet en volght uyt die voorgaende reden. Alsoo oock yemant aldus argumenterende:
Alle | |
[pagina 102]
| |
Alle Overhoucksche dan des Viercants tot sijn Sijde is Onmetelick. Twelck sommighe ghenouch ervaren persoonen, dickmael souden ansien voor nootsaeckelick vervolch; Maer den Dialecticien (ia al waren hem des Viercants eyghenschappen teenemael onbekent) sal bewijsen dat sulck Besluyt, soodanich het is, niet en volght uyt de cracht der voorgaender, ghevende een opentlick derghelijcke valsch exempel, aldus: Alle Govdt is Metael, Ofte dat andersins weerlegghende, door eenighe der Anteyckeninghen, int eynde der 40e. definitie beschreven. Inder voughen dat (soo boven gheseyt is) het ghebreck der Formen, altijt door de Dialectike bekendt is, maer niet der Materien, Welcker wetenschap thaerder plaetse moet ghehaelt sijn.
Wijder is te anmercken, als voor Generale Reghel, datmen int argumenteren nummermeer en moet ontkennen des Bewijsredens Besluyt, maer altijt tghene datmen in d'eerste ofte tweede Propositie acht de oirsake te wesen van sijne valscheyt: Om van het welcke door ghelijckenisse te spreecken; Ick neme dat de vraghe sy, Wat 16 ℔ te betalen binnen Een Iaer, weert sullen sijn binnen twee Iaren, rekenende Simpelen Intrest teghen den penninck 16 tsiaers. T'welck een questie is, van wiens Besluyt sommighe ervaren Arithmeticienen hier in Hollandt nu ter tijt niet over een en commen, tot welcx ondersouck sy te meer beweecht sijn, dat het niet en is een questie van enckele Woorden, maer oock der Saecken, overmidts den eenen de rekeninghen (die daghelijcx te voren commen) aldus maect, den anderen alsoo, t'welck op groote sommen, dickmael strect tot merckelicke schade van desen ofte dien. | |
[pagina 103]
| |
15 1/17 ℔ ghereedt, sijn weert binnen twee iaren 16 16/17 ℔. Nu, hy die van meeninghe is, dit Besluyt valsch te sijne, en moet het selfde Besluyt niet ontkennen, maer t'gene hy acht de oirsaecke der valscheyt van dien te wesen, t'welck (anghesien de Forme goedt is, te weten in A A A) nootsaeckelick soude moeten sijn inde Materie der voorgaender Propositien. VVant alsoo canmen oirdentlick, ende cortelick, commen tot de kennisse der waerheyt. VVy hebben van dese questie ons goet dincken inde Arithmetike (nu onder de parsse sijnde) beschreven. Angaende de questien door vele woorden verclaert, ende met cierlicke Redenen toeghemaect, ghelijck dickmael sijn heymelicke ofte openbare uytspraecken, ofte gheschriften, om een Gemeente tot dit ofte dat te beweghen; Om sich te ontschuldighen; Om sijn ghevoelen goedt te maecken, &c. Die (questien segh ick) sal den Dialecticien blooten van alle haer toerustinghen, als bedriechlicke cieraet, ende verduysterende veelheydt, niet Arithmetelick tellende de menichte der woorden; maer Dialectikelick weghende de cracht der eenvoudige argumenten. T'welck in alles alsoo recht vervolght,sal hem altijt brenghen ter rechter kennissen van sijn recht voornemen. |


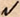 2. tot I. is Onmetelick,
2. tot I. is Onmetelick,