|
| |
| |
| |
III Het begin van de stellaire sterrekunde. William Herschel en zijn opvolgers.
Gedurende de geheele ontwikkeling der sterrekunde tot aan het einde van de achttiende eeuw werd er nauwelijks eenige aandacht aan de vaste sterren geschonken. De opvatting van de ouden dat de vaste sterren vastzaten aan een bol en dus alle dezelfde afstand van ons hadden, werd slechts langzamerhand overwonnen. Kepler nog spreekt over de vaste sterren als waren zij begrensd in een laag tusschen twee bollen en zegt er niet veel meer van.
De eerste werkelijke afstandsbepaling van een ster is die van Sirius door Huygens. Het licht heeft twee eenvoudige eigenschappen die als grondslag voor de afstandsbepaling kunnen dienst doen: de rechtlijnige voortplanting, die
| |
| |
de grondslag is van de trigonometrische methode der paralaxbepaling, en de vermindering van intensiteit omgekeerd evenredig met het kwadraat van de afstand. De trigonometrische methode is de meer fundamenteele; wij nemen pas onze toevlucht tot het tweede alternatief voor afstanden die te groot zijn voor het eerste. Zoo is het altijd geweest, maar tot bijna het midden van de negentiende eeuw waren alle afstanden te groot voor de directe trigonometrische methode. Het was door Tycho beproefd; Kepler had er Galilei op gewezen, de juiste waarnemingen aangegeven en de dagen, waarop ze gedaan moesten worden, genoemd. De voornaamste prikkel echter voor het doen van deze waarnemingen was niet de afstanden der sterren te bepalen maar om in de paralactische beweging een bewijs voor het stelsel van Copernicus te vinden. De afstand, zooals zij uit de lichtintensiteit werd bepaald, zou er natuurlijk practisch onafhankelijk van zijn, welk planetenstelsel het ware was.
Huygens vergeleek het licht van Sirius met een klein gedeelte van de zonneschijf, dat door een diaphragma uitgesneden en door een
| |
| |
kleine bol van glas gereflecteerd werd. In de vooronderstelling, dat de ware lichtkracht van Sirius dezelfde is als die van de zon, vond hij de afstand 28000 maal zoo groot als die van de zon, en maakte hij daaruit de gevolgtrekking dat de paralax te klein was om gemeten te kunnen worden. Dezelfde conclusie trok hij hij uit het feit dat de sterren Mizar en Alcor geen beweging ten opzichte van elkaar met een jaarlijksche periode vertoonden. Hij loopt hier dus meer dan een eeuw vooruit op Herschel's voorstel relatieve paralaxen te bepalen uit de verplaatsing van heldere sterren ten opzichte van zwakke sterren, die aan den hemel dicht bij elkander staan. Waarbij hij dan, evenals Herschel deed, vooronderstelt dat de werkelijke lichtkracht dezelfde is. Het is bekend dat Herschel, toen hij deze methode in verschillende gevallen werkelijk probeerde, geen paralaxen vond, maar de ontdekking der dubbelsterren deed. Had Huygens geweten, wat wij nu weten, nl. dat de lichtuitstraling van Sirius ongeveer vijf en twintig maal grooter is dan die van de zon, dan zou zijn afstand slechts vier maal te klein zijn uitgevallen inplaats van twintig maal.
| |
| |
William Herschel is de eerste geweest die de overtuiging had, dat de vaste sterren een stelsel van een zekere structuur vormden, die het plan opvatte deze structuur om haarzelfs wille te bestudeeren en dit onderzoek op werkelijke waarnemingen baseerde.
Kepler en Huygens hadden de meening uitgesproken dat de zon een ster was, en de sterren zonnen, omringd door planetenstelsels.
Kant en Lambert hadden beiden - uitgaande van zeer verschillende principes en langs verschillende lijnen hun redenering opbouwend - wereldsystemen samengesteld die volkomen speculatief waren. Het eenige feit aangaande de bouw van het sterrenstelsel, dat zeker bekend was, vóór Herschel zijn werk begon, was, dat de melkweg bestond uit een menigte van sterren. Dit was door Galilei ontdekt.
Afzonderlijke aandacht moet echter aan Herschel's oudere tijdgenoot John Michell geschonken worden, die (in 1767) eenige opmerkelijke opvattingen over sterrehoopen publiceerde, en over de eigen beweging, die hij meende dat gedeeltelijk de afspiegeling van de beweging van de zon moest zijn.
| |
| |
Hij wees er op dat de seculaire paralax in de loop der tijden een middel kon zijn om de afstand te bepalen. De directe meting der paralaxen, zegt hij, zal de constructie van betere verrekijkers moeten afwachten, waarmede men een twintigste boogsecunde kan meten, wat hij geen hopelooze opgave voor de toekomst acht.
Herschel wijst er op dat wij uit de directe waarneming slechts twee coördinaten der sterren kennen; de derde, de ‘diepte’ zooals hij hem noemt, is onbekend.
De sterren zijn zeer verschillend in helderheid. Is dit alleen te wijten aan hun verschillende afstanden, of verschillen zij ook in werkelijke helderheid, in ‘lichtkracht’, zooals wij dit nu noemen met een woord door Kapteyn ingevoerd?
De verdeeling van de sterren over de hemel is ook zeer ongelijkmatig. Is hun werkelijke verdeeling in de drie-dimensionale ruimte regelmatig en homogeen of niet? Wij hebben dus is werkelijkheid twee onbekenden: de lichtkracht en de dichtheid. Pas Kapteyn pakte dit probleem in zijn geheele omvang aan. Herschel begon slechts. Hij maakte de veronderstel-
| |
| |
ling dat de lichtkracht van alle sterren dezelfde is, en dat de dichtheid constant is. Het is duidelijk dat deze beide veronderstellingen elkaar tegenspreken, d.w.z. niet a priori: er zou een heelal kunnen bestaan waarin aan beide onderstellingen voldaan was, maar dat zou er geheel anders uitzien dan het onze.
In Herschel's eerste mededeeling ‘Over de paralax der vaste sterren’ (1781) gaat hij expliciet uit van de twee volgende
Algemeene hypothesen
|
| 1. | De sterren worden verondersteld ongeveer van de grootte van de zon te zijn. |
| 2. | Het verschil in hun schijnbare grootte wordt verondersteld het gevolg te zijn van hun verschillende afstanden, zoodat een ster van de tweede, derde, of vierde grootte twee, drie of viermaal zoo ver weg staat als een van de eerste groote. |
Wat de eerste hypothese betreft merk ik op, dat uit verschillende plaatsen blijkt dat Herschel aanneemt dat de oppervlaktehelderheden van de zon en de sterren gelijk zijn; ‘grootte’ slaat hier dus op de werkelijke afmetingen.
Wat de tweede hypothese betreft zegt Herschel zelf in een noot dat dit neerkomt op een
| |
| |
definitie van de grootteklasse. De schaal der magnitudines volgens welke de schijnbare helderheid der sterren gemeten wordt, is uit traditie ontleend aan de Grieksche astronomen. Het verband tusschen de conventioneele schaal en de werkelijke intensiteitsverhouding zou met behulp van photometrische methoden gevonden moeten worden. Herschel doet geen poging hiertoe, maar stelt in de plaats daarvan zijn definitie. Aangezien hij de wet van het omgekeerd evenredig zijn met de tweede macht van de afstand accepteert en gebruikt, wordt hierdoor de grootte gedefinieerd als omgekeerd evenredig te zijn met de vierkantswortel uit de intensiteit. Sir John Herschel bevestigt dit, dank zij een photometrisch onderzoek aan de Kaap, en vindt de formule i = 1/(m+0.414).2 De logarithmische schaal, die wij nu gebruiken, is natuurlijk pas veel later aangenomen. Herschel beschouwt deze wet, m = Δ, blijkbaar als bijna vanzelf sprekend, en hij heeft er gedurende zijn geheele leven consequent aan vastgehouden. Zelfs keerde hij haar om en sprak hij bv. van een ster van de magnitude 1342, waarmede hij een ster op een afstand van 1342 maal de ge-
| |
| |
middelde afstand van een ster van de eerste grootte bedoelde. In de genoemde noot brengt hij de mogelijkheid van absorptie in de ruimte onder de aandacht, die, zooals hij zegt, hem gesuggereerd is door het feit dat hij ‘in 't algemeen de zeer zwakke telescopische sterren rood, of roodachtig gekleurd heeft gevonden’. Indien er absorptie is, dan zou natuurlijk de afstand veel kleiner zijn dan het getal dat de magnitudo aangeeft. Maar deze noot is de eenige plaats in zijn werken waar de absorptie genoemd wordt. Hij houdt er in zijn verdere afleidingen geen rekening mede.
Herschel's groote werk zijn zijn sterpeilingen, die hij begon zoodra de 6-meter telescoop (brandpuntsafstand 6 meter, opening 47.5 cm.) voltooid was, in 1784. Als eerste resultaat van zijn nauwkeurige navorsching van de hemelen komt hij tot de conclusie dat de meeste der zoogenaamde nevels opgelost zijn in sterren, en hij vermoedt dat zij met grootere telescopen alle op die manier op te lossen zullen zijn. De melkweg - het melkwegstelsel zouden wij zeggen - is zoo een ontzaglijke ‘sterrelaag’. Zijn opvatting wordt duidelijk gemaakt door een figuur, die duidelijk de zwij-
| |
| |
gend gemaakte onderstelling van een gelijkmatige verdeeling, d.i. van een constante dichtheid, laat zien, waarop zijn eerste theorie berust.
In de tweede publicatie begint hij met zijn ideeën aangaande verschillende stadia in de ontwikkeling der nevels mede te deelen: alle nevels worden nog steeds ondersteld uit sterren te bestaan. Dan komt zijn conclusie: ‘Wij bewonen de planeet behoorend bij een ster, die lid is van een samengestelde nevel van de derde klasse’. Een ‘samengestelde nevel van de derde klasse’ is in zijn nomenclatuur een stelsel, dat bolvormige sterrehoopen, onregelmatige clusters, en sterren in ‘rissen en kronkelingen enz.’ gerangschikt bevat. Zijn gedetailleerde structuur is er dus niet een van uniforme dichtheid. Toch gaat Herschel door, de hypothese van de uniforme dichtheid consequent toe te passen, maar men krijgt de indruk dat hij deze zelfs in die tijd beschouwde als niet meer dan een eerste benadering. Hoe dit zij, hij gaat verder: ‘ik zal nu in het volgende aan toonen dat het kolossale sterrestelsel, dat wij bewonen, deze uitgestrekte sterrelaag en haar secundaire zijtak, bestaande uit vele
| |
| |
millioenen sterren, in alle waarschijnlijkheid, een vrijstaande nevel is’, d.i. in Herschel's vocabulaire, een geïsoleerd systeem, overal omringd door leege ruimte.
Indien de dichtheid constant is, dan is de afstand waarop het systeem zich uitstrekt in een bepaalde richting direct evenredig met de derdemachtswortel uit het aantal sterren in die richting gezien, aangenomen dat wij tot de grens ervan zien kunnen. Herschel stelt het zoo:
Probleem: De lengte van de straal in de gezichtslijn te bepalen, als ondersteld wordt dat de sterren zoo goed als gelijkmatig verspreid zijn, en haar aantal in een gezichtsveld van bekende diameter in hoekmaat gegeven is.
Dit hangt natuurlijk af van de rangschikking, of de sterren ondersteld worden in de hoekpunten van een kubus te liggen of van een tetraëder, of in andere mogelijke regelmatige verdeeling. Hij neemt als plausibele verdeeling die in de hoekpunten van kubussen aan. Dan is de oplossing van het probleem eenvoudig. De ‘Table of Star-Gages’ bevat het resultaat van 683 peilingen. De aantallen sterren varieeren van 0.5 tot 588. Ieder getal is het gemiddelde van verscheidene velden in de omgeving,
| |
| |
dikwijls tien. Het is opmerkelijk dat vele van de zeer ster-arme velden in de melkweg liggen; zoo ligt bijv. het armste veld van alle, met 0.5 sterren (het gemiddelde van 10 velden), in de Schorpioen. Herschel noemt het ‘een opening in de hemel’. Uit deze aantallen leidt hij dan de afstanden af volgens de regel die uit zijn oplossing van het bovengenoemde probleem volgt. Zoo is hij in staat een model van het stelsel te construeeren. In zijn ges-
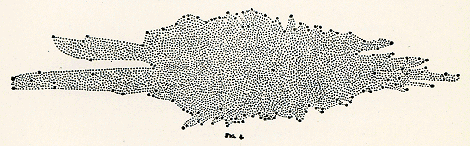
Figuur 3
Doorsnede door het melkwegstelsel volgens de eerste theorie van Sir William Herschel (1785).
chrift geeft hij alleen een doorsnede in een vlak loodrecht op het centrale vlak van de melkweg. Deze doorsnede, die berust op 129 peilingen en bij benadering ligt in een groote cirkel door de sterrebeelden Aquila, Coma, Canis Major, Cetus (galactische lengten 191 o en 11 o), is hier in figuur 3 gereproduceerd.
| |
| |
Men ziet dat de hypothese van de gelijkmatige dichtheid een tamelijk onregelmatige omtrek geeft. De kortste afstand van de zon tot de grens is 75 eenheden naar Coma (de bovenkant van de figuur) en 83 eenheden in tegengestelde richting, naar Cetus. De langste stralen naar links, in Aquila, zijn 420 en 497 eenheden respectievelijk, tegen 352 eenheden in de richting van de Groote Hond. De eenheid is de afstand van Sirius, of twee parsec. Herschel gaat dan verder de gronden aan te voeren waarop hij zijn meening, dat hij werkelijk de grenzen van het stelsel bereikt heeft, baseert.
Want het is waar dat het niet veel waarde zou hebben zeer gedecideerd te verzekeren dat wij ons op een eiland bevonden, tenzij wij onszelve werkelijk overal door de oceaan begrensd hadden gezien.
Maar, zegt Herschel, indien daar nog meer sterren achter waren, te zwak om afzonderlijk in de telescoop waar te nemen, dan zouden de peilingen een melkachtige onoplosbare nevelachtigheid als achtergrond geven, en dit doen zij nergens:
Zoodat het uit deze overwegingen wederom zeer waarschijnlijk lijkt, dat de telescoop, die ik nu gebruik, daar zij een dergelijke nevelachtigheid in de
| |
| |
melkweg niet vertoont, alreede verre buiten de grenzen van het stelsel reikt.
Ons stelsel is dus, concludeert hij, ‘een zeer uitgestrekte, vertakte, samengestelde opeenhooping van vele millioenen sterren’. Het aantal sterren dat het volgens Herschel's gegevens zou bevatten bedraagt 75 tot 100 millioen, maar Herschel zelve geeft geen nauwkeuriger opgave dan ‘vele millioenen’.
Dit is dan het stelsel van 1785.
Aan het einde van zijn publicatie noemt hij vele andere nevels op die, volgens zijn meening, ook galactische stelsels zijn. De dichtst bijzijnde en grootste van deze is de Andromedanevel. Haar afstand wordt op twee duizend maal de afstand van Sirius geschat, d.i. op 4000 parsec of 13000 lichtjaar. Combineeren wij deze geschatte afstand met Herschel's schatting van de schijnbare diameter, ‘meer dan anderhalve graad’, dan vinden wij voor de ware doorsnede 50 tot 60 Herschel-eenheden, of 100 tot 120 parsec, terwijl de doorsnede van ons eigen stelsel volgens Herschel's teekeningen, ongeveer 850 eenheden, dus 1700 parsec is.
De grondslag, waarop Herschel's eerste the-
| |
| |
orie (1785) berust, is zijn overtuiging, dat alle nevels in sterren oplosbaar zijn. Zijn voortgezette waarnemingen deden hem echter inzien, dat dit niet het geval is. In een publicatie uit 1791 maakt hij onderscheid tusschen oplosbare nevels of clusters en ‘melkachtige nevelvlekken’, waarvan hij aanneemt dat zij bestaan uit ‘een lichtgevend fluïdum van een ons geheel onbekende aard’. Hij wijdt dan uit over verschillende hypothesen aangaande de aard van dit ‘lichtgevende fluïdum’: ‘Mogen wij het vergelijken met de flikkeringen van het electrische fluïdum in het noorderlicht?’ Deze onderstelling wijst hij af, evenals de hypothese dat het van dezelfde aard als het zodiakale licht zou zijn, aangezien dit te zwak is om op eenige afstand nog zichtbaar te zijn, en hij waagt ten slotte een poging door te onderstellen dat het uit lichtpartikeltjes bestaat, die onder verschillende invloeden van hun rechte weg door de ruimte zijn afgeweken, waartoe ook de aantrekking tengevolge van de gravitatiekracht van sterren en sterrestelsels behoort. ‘Echter’, zoo besluit hij:
Wij zullen niet de nadruk op een dergelijke gissing leggen, daar de midelen om deze te verifieeren ontbre-
| |
| |
ken: ook is het voor ons niet van eenig direct belang de oorsprong van deze lichtgevende materie te kennen. Laat het voldoende zijn, dat haar bestaan bewezen is door de nevelvlekken.
De groote 12-meter telescoop (met opening van 1.20m.) werd tegen het einde van 1789 voltooid, en hoewel zij zeer onhandig in het gebruik was, en er slechts zeer weinige nachten goed genoeg voor waren, heeft zij zeer zeker Herschel grootelijks geholpen tot klaardere inzichten te komen. Zelfs één goede nacht met deze kijker zou voldoende geweest zijn de evolutie in zijn denkbeelden te weeg te brengen, die ten slotte zijn tweede theorie over het melkwegstelsel tot resultaat gehad heeft. Behalve het bestaan van onoplosbare nevelvlekken, bracht het feit, dat hij met de groote kijker meer sterren in hetzelfde veld zag dan met de 6-meter telescoop, hem er toe zijn opvatting dat hij de grenzen van het heelal bereikt had te laten varen: ‘De 6-meter telescoop kon de diepte van de melkweg niet peilen’. De 12-meter kijker kan het evenmin; er blijft altijd een achtergrond.
Daarom mogen wij concludeeren, dat wanneer onze peilingen de melkweg niet langer in sterren kunnen
| |
| |
oplossen, dit niet 't geval is omdat haar wezen tweeslachtig is maar omdat zij onpeilbaar is.
‘Tweeslachtig’ beteekent bij Herschel: sa mengesteld uit sterren en nevelachtige materie door elkaar.
Bovendien was hij er langzamerhand toe gekomen in te zien, dat een gelijkmatige dichtheid zelfs niet als benadering te gebruiken is: hij had in het melkwegstelsel het ‘groepeeringsvermogen’ ontdekt; de sterren hebben de neiging zich in groepen te vereenigen, en hij gelooft dat de melkweg uiteindelijk geheel zal worden opgelost in afzonderlijke groepen en clusters. Het melkwegstelsel is als gevolg van de onderlinge aantrekking der sterren ‘onderworpen aan een groepeeringsstreven ........ en moet ten slotte in afzonderlijke gedeelten uiteenvallen, en ophouden een laag van overal verstrooide sterren te zijn’.
Hij geeft hiermede de uniforme dichtheid als leidend principe op, en gebruikt in de plaats daarvan de uniforme lichtkracht.
De sterren, tenminste zij die onsystematisch verdeeld schijnen te zijn, hebben waarschijnlijk alle een bepaalde grootte.
Hoe zwakker sterren wij daarom in een be-
| |
| |
paalde richting zien, hoe verder wij in de ruimte kijken. Wanneer men dan de grootte omgekeerd evenredig aan de vierkantswortel uit de intensiteit stelt, volgens zijn definitie van grootteklasse, dan kan men de grootte van de zwakste sterren theoretisch uit het vermogen van de kijker afleiden. Of beter nog, men geeft het gebruik van grootte-klassen heelemaal op en werkt met de afstanden alleen. Om deze te bepalen berekent hij wat hij noemt het ‘doordringingsvermogen’ van zijn kijkers. Het lichtverlies door absorptie en reflectie in het oculair wordt zorgvuldig bepaald en behoorlijk in rekening gebracht. De opening van de pupil van ons oog wordt op 5 mm. geschat. Het doordringingsvermogen van het bloote oog, dat in deze publicatie, in tegenstelling met wat hij gewoonlijk doet, ondersteld wordt tot de zevende grootte te reiken, wordt als eenheid genomen. Voor het doordringingsvermogen van de 6-meter kijker, in de vorm van Newton gebruikt, wordt dan 61.2 eenheden gevonden, bij recht doorzicht is het 75; voor dat van de 7.5-meter kijker wordt 95.85 en voor dat van de 12-meter kijker 191.69 eenheden gevonden. Later (in 1817) drukte hij de eenheid uit in de gemiddelde
| |
| |
afstand van de sterren van de eerste grootte. Toen hij de aantallen sterren van verschillende magnitudo tot aan de zevende grootte onderling vergeleek, bevond hij dat de wet, dat de magnitudo gelijk aan de afstand zou zijn, niet juist was. Na werkelijke photometrische vergelijking (door de helderheid met behulp van diafragmas gelijk te maken) vond hij voor verschillende sterren van de zesde grootte, die nu weer als de grensmagnitudo voor het bloote oog wordt genomen, een helderheid tusschen (1/10)2 en (1/15)2 van die van een ster van de eerste grootte. Hij neemt dan als gemiddelde voor de ‘zichtbaarheidsstraal’ van het bloote oog het getal 12 aan, waarbij de eenheid, zooals reeds gezegd werd, de gemiddelde afstand van een ster van de eerste grootte is. De zichtbaarheidsstraal van de 6-meterkijker wordt dan 75×12=900 eenheden, en die van de 12-meter 2300. Zelfs op die afstand was de grens van het stelsel niet bereikt. De ‘Slot-opmerkingen’ van zijn publicatie, gedateerd Slough, bij Windsor, 10 Mei 1817 kan men opvatten als een weergave van zijn laatste beschouwingen over de ‘bouw der hemelen’, het onderzoek waaraan hij zijn
| |
| |
beste krachten gewijd heeft. Zij luiden als volgt:
Slot-opmerkingen.
Wat over de uitgestrektheid en de samenstelling van de melkweg in verschillende van mijn geschriften over de bouw van de hemelen gezegd is, waar de waarnemingen, waarop deze poging berust, bijgevoegd waren om een zuiverder idee te geven van de diepte in de ruimte, zal wel bijna alle objectieve kennis, die wij ooit over deze schitterende verzameling sterren kunnen verkrijgen, omvatten. Het zou verre buiten het bestek

Figuur 4
William Herschel's diagram ter illustratie van zijn tweede theorie (1817).
van dit geschrift vallen in te gaan op de vraag, wat de hemel in de twee vergelijkenderwijze leege ruimten, die aan beide kanten de melkweg begrenzen, bevat, op de ligging van de bolvormige sterrehoopen, van
| |
| |
de planetaire nevels en van de uitgestrekte nevelvlekken.
Afgezien van het feit dat hij de planetaire nevels en de uitgestrekte nevelvlekken, waarmede hij de onregelmatige nevels als die in Orion bedoelt, bij de extra-galactische objecten rekent, kon dit bijna vijftien jaar inplaats van honderdvijftien jaar geleden geschreven zijn. Een kleine figuur is daar bijgevoegd, hier in figuur 4 gereproduceerd. De overeenkomst met het diagram van Shapley uit 1918 (zie vijfde hoofdstuk figuur 6) is zeer opvallend.
De diameter van de cirkel, die een doorsnede is van een bol die alle met het bloote oog zichtbare sterren bevat, bedraagt 24 eenheden, of wanneer wij één van Herschel's eenheden als twee parsec aannemen, - voor de paralax van een ster van de eerste grootte heeft Herschel gedurende zijn geheele leven 0″.5 aangenomen, - 48 parsec. De dikte van de melkweglaag is 2 × 39 eenheden = 156 parsec. Deze afmetingen, die Herschel en zijn tijdgenooten kolosaal groot voorkwamen, lijken ons zeer matig.
Herschel's eerste theorie leidde tot een af-
| |
| |
gerond systeem; zijn latere waarnemingen en deducties maakten deze conclusies waardeloos, en hij begon - op de leeftijd van ongeveer 60 jaar - zijn vroegere inzichten te herzien, en zijn wereldstelsel volgens geheel nieuwe richtlijnen op te bouwen. In zijn groote geschrift van 1785 zegt hij reeds dat hij zijn tegenwoordige resultaten als voorloopig beschouwt en vatbaar voor verandering op grond van verdere waarnemingen.
Ik zal daarom wachten tot de waarnemingen, waarmede ik op het oogenblik al bezig ben, mij zullen voorzien van materiaal noodig voor de navorsching van een zoo nieuw onderwerp. En al zullen de pogingen van mijn persoon alleen er niet in slagen een werk te voltooien dat de gezamelijke krachten van alle sterrekundigen schijnt op te eischen, toch is het misschien niet te gewaagd te hopen, dat wij, wanneer wij onszelf met al onze macht wijden aan de verbetering der verrekijkers, die volgens mij nog in hun beginstadium zijn, en wanneer wij deze met onverdroten ijver op de bestudeering van de hemel richten, na verloop van tijd eenige zwakke kennis zullen verkrijgen van, en misschien in staat zullen zijn een gedeeltelijke uitbeelding te verkrijgen van de inwendige bouw van het heelal.
En hij karakteriseert zijn methode met de volgende woorden:
| |
| |
Maar laat mij er eerst op wijzen, dat wij, als wij hopen eenige steenen bij te dragen tot een zoo delicaat onderzoek, twee tegengestelde uitersten moeten vermijden, waarvan ik haast niet zeggen kan welke de gevaarlijkste is. Indien wij ons overgeven aan een al te levendige verbeelding en werelden van onszelf gaan bouwen moeten wij ons niet verbazen wanneer wij ons verre verwijderen van de paden van waarheid en natuur; maar zij zullen verdwijnen evenals de vortices van Cartesius, die weldra werden opgegeven toen betere theorieën voorgesteld werden. Aan de andere kant, als wij waarneming op waarneming stapelen, zonder een poging te doen hieruit niet alleen een zekere conclusie te trekken, maar ook niet gissenderwijze ons een inzicht trachten te verwerven, dan zondigen wij wederom tegen het uiteindelijke doel, waarvoor toch de waarnemingen alleen behooren te worden gedaan. Ik zal mijn uiterste best doen de juiste middenweg te houden; maar zoo ik er vanaf moet wijken, dan kan ik slechts wenschen niet in de laatste fout te vervallen.
De publicatie van 1811, gedateerd Slough, 26 Mei begint:
Kennis van de bouw van het heelal is altijd het laatste doel van mijn waarnemingen geweest, en nu ik mij vele jaren lang heb bezig gehouden om met mijn 12-meter, 6-meter en groote 3-meter kijker, van wege hun groot ruimte-doordringend vermogen, de belangrijkste objecten, die ik binnen het bereik van mijn kijkers ontdekt had, zoowel als die welke daarvóór al gepubliceerd waren in de Connoïssance des Temps, vóór 1784 [d.i. Messier's catalogus], nog eens te herzien, vind ik dat men deze objecten, wanneer men ze op een bepaalde regelmatige
| |
| |
wijze rangschikt, in een nieuw licht kan zien, en, als ik mij niet vergis, zal een nader onderzoek daarvan tot consequenties leiden die een onderzoekende geest niet onverschillig kunnen laten.
Wanneer men de opmerking zou maken, dat ik in deze nieuwe rangschikking niet geheel in overeenstemming blijf met wat ik reeds in vroegere publicaties over de aard van sommige objecten, die onder mijn aandacht gevallen zijn, gezegd heb, dan moet ik openhartig bekennen, dat bij het voortzetten van mijn onderzoekingen van de hemel, mijn meening over de rangschikking van de sterren en hun magnitudines, en van eenige andere bijzonderheden langzamerhand een verandering heeft ondergaan; en inderdaad, wanneer wij bedenken hoe nieuw het onderwerp is, kunnen wij niet verbaasd zijn dat vele dingen die vroeger als vaststaand werden aangenomen, bij nader onderzoek blijken anders te zijn dan in het algemeen, maar zonder grond ondersteld werd.
In een vroegere publicatie zeide hij eens:
Het is somtijds zeer nuttig in de natuurphilosophie te twijfelen aan dingen die algemeen als vaststaand wordt aangenomen.
Hij had de geestkracht niet alleen aan algemeen aanvaarde opvattingen te twijfelen, maar ook aan zijn eigen vroegere conclusies.
In het begin van dit hoofdstuk is er op gewezen dat men twee onbekenden moet bepalen om de bouw van het sterrestelsel te kennen:
| |
| |
de lichtkrachtwet en de dichtheidswet. Herschel zag geen kans deze beide onbekenden te bepalen. Hij baseerde zijn onderzoekingen op onderstellingen dienaangaande, en koos natuurlijk de eenvoudigste veronderstelling, nl. dat de lichtkracht en de dichtheid constant waren. De conclusies, die hij uit zijn waarnemingen trok met behulp van deze twee onderstellingen waren met elkander in tegenspraak en hij was gedwongen te bekennen dat hij het probleem niet had opgelost. Desondanks is er geen enkel astronoom, noch vóór hem, noch na hem geweest, die zooveel voor de uiteindelijke oplossing van het probleem gedaan heeft als William Herschel.
Zijn zoon, Sir John Herschel, zette zijn vaders waarnemingen voort en breidde ze speciaal uit over het zuidelijk halfrond. Hij bracht echter de oplossing van het groote probleem niet verder.
De volgende, die het algemeene probleem weder opvatte, was F.G.W. Struve, de stichter van de Pulkowa sterrewacht. Hij ook moest een onderstelling maken ten aanzien van de dichtheidsverdeeling: hij neemt aan dat deze
| |
| |
alleen een functie is van de verticaal gemeten afstand z van het melkwegvlak, d.i. hij onderstelt voorloopig een volkomen symmetrie ten-opzichte van het melkwegvlak, en in alle richtingen, en verder neemt hij, zooals Herschel in zijn laatste theorie doet, aan, dat het stelsel zich oneindig ver uitstrekt in een richting evenwijdig aan dit vlak. Het eenige verschil met Herschel is dat hij de dichtheid doet afnemen met z inplaats van haar als constant aan te nemen. Uit deze onderstelling en de waarnemingsgegevens verkregen uit W. Herschel's peilingen (de waarnemingen van John Herschel aan de zuidelijke hemel waren nog niet gepubliceerd) leidt hij dan een dichtheidsverdeeling af, d.w.z. berekent hij empirisch de coëfficienten van een zekere algebraïsche formule, die de dichtheid als een functie van z moet voorstellen. De formule is nogal ingewikkeld en ziet er niet erg overtuigend uit. Wat het werk van Struve speciaal karakteriseert is, dat hij zeer opzettelijk alle details, die Herschel zoo zeer fascineerden, buiten beschouwing laat. Het eenige wat hij zoekt te vinden zijn de groote lijnen, d.w.z. hij zoekt een ‘typeerend’ beeld (volgens de uitdrukking van Seeliger) en
| |
| |
laat het invullen der details over aan latere tijden. De discussie van het materiaal is zeer zorgvuldig en een voorbeeld van degelijke wetenschappelijke kritiek.
Nadat hij de dichtheidswet uit Herschel's peilingen heeft afgeleid gaat hij verder en bepaalt dezelfde wet voor de sterren, in Argelander's Uranometria en in Bessel's zones. Van de laatste mag men niet veronderstellen dat ze volledig zijn. Daarom leidt hij ‘aanvullingsfactoren’ af door met de Uranometria en met Piazzi's zones te vergelijken. De dichtheidswet is op deze wijze afgeleid uit Bessel's sterren van de zevende grootte en uit die van de achtste grootte. Om nu de eenheden van afstand in de drie gevallen onderling te vergelijken worden deze omgekeerd evenredig met de vierkantswortel uit de aantallen met galactische breedte = nul aangenomen. Hij berekent dan als contrôle de dichtheid op twee lineaire afstanden van het melkwegvlak uit de verschillende wetten, en vindt een bevredigende overeenstemming.
Zijn volgende stap is, uit zijn dichtheidswet te berekenen, hoe groot de straal is van de bol die alle sterren tot een bepaalde grootte-
| |
| |
klasse omvat. De straal van de bol die alle sterren van Argelander tot de zesde grootte bevat wordt als eenheid genomen. Dan is de straal van de bol die Argelander's sterren van de eerste grootte bevat 0.142, van de tweede grootte 0.241 enz. Voor Bessel's sterren van de negende grootte is de straal 4.25, en voor Herschel's sterren, de zwakste, die nog met de 6-meter kijker te zien zijn, is de straal 25.67. Deze zijn dan alle nog uitgedrukt in een willekeurige eenheid. Maar in Struve's tijd bestonden er reeds eenige parallax-bepalingen. Deze waren door Peters bediscussieerd en Struve neemt uit dit onderzoek de gemiddelde parallax van een ster van de tweede grootte aan als p = + 0″.116 ± 0″.014, wat overeenkomt met een afstand van 28 lichtjaar. Dit getal gebruikt hij om de relatieve afstanden om te zetten in absolute. Op deze manier wordt voor de afstand van de zwakste sterren door Herschel gezien 3541 lichtjaar gevonden.
Struve gaat nu verder deze getallen te bediscussieeren. Inplaats van ze direct met waarnemingen met het bloote oog te vergelijken, en de opening van de oogpupil op 5 mm. aan te nemen, zooals Herschel had gedaan, constru-
| |
| |
eerde Struve een kleine telescoop, die hij zijn ‘Herschelsche modulus’ noemde, met dezelfde opening (0.211 duim), en driemaal vergrootend. Met deze modulus zag hij 183 sterren op hetzelfde oppervlak waarop Argelander's Uranometria, waarvan de opzet was dat zij alle sterren die voor het bloote oog zichtbaar waren zou bevatten, er 100 had. Het doordringingsvermogen van Herschel's telescoop was 61.2, maar dit heeft betrekking op een opening van 5 mm. - dus op de ‘modulus’ - als eenheid. Aangezien de modulus 1.83 maal meer sterren geeft dan het aantal sterren van dezelfde grootte uit Argelander's catalogus, moet dit getal met de vierkantswortel uit 1.83 vermenigvuldigd worden, wat het tot 74.8 maakt, of practisch driemaal de afstand in de tabel gegeven en afgeleid uit de dichtheidswet.
Struve vindt op deze manier een contradictie. Dit is niet te verwonderen, want bij zijn berekening van de afstand neemt hij stilzwijgend aan, zooals ook Herschel deed, dat de lichtkracht een constante is en ook dat de dichtheid langs het melkwegvlak constant is. Struve echter verklaart deze contradictie niet uit deze oorzaken, maar uit absorptie in de
| |
| |
ruimte. Hij vindt op die wijze een absorptie van ongeveer 1% van het licht per eenheid van afstand, d.i. de afstand van een ster van de eerste grootte.
Het is duidelijk dat de schijnbare contradictie, die Struve verklaart door extinctie, evengoed op andere wijze verklaard kan worden. John Herschel had het idee geopperd dat de sterren in de melkweg, die hij evenals Kepler, als een ring beschouwt, in werkelijkheid zwakker waren dan die in onze omgeving. Het is duidelijk, dat de tegenspraak ook opgelost kan worden, indien wij een afneming van de dichtheid met de afstand aannemen, zooals Kapteyn later deed. De volledige behandeling van het probleem, waarbij zoowel de dichtheid als de lichtkracht als onbekenden worden beschouwd, die uit de waarnemingen bepaald moeten worden, is eerst door Kapteyn opgelost. Deze oplossing, die wij in het volgende hoofdstuk zullen bespreken, was niet mogelijk voordat vertrouwbaarder gegevens over de afstanden der sterren evenals over hun aantallen en grootteklassen beschikbaar waren.
|
|