Nederlandsche helden der wetenschap
(1946)–T.P. Sevensma–Levensschetsen van negen Nobelprijswinnaars. Hoogtepunten van wetenschappelijken arbeid in Nederland
[pagina 125]
| |
door Dr. G.C. Gerrits
| |
Het levenswerk van Van der Waals.De levensarbeid van Van der Waals kan worden samengevat in drie werken van fundamenteel belang: de toestandsvergelijking, de wet der overeenstemmende toestanden en de theorie der binaire mengsels. Naast deze baanbrekende onderzoekingen mogen hier nog als belangrijke werken genoemd worden: de theorie der capillariteit en die der ternaire mengsels. | |
Wet van Boyle-Gay Lussac.Door den Engelschen natuurkundige Boyle was in 1662 gevonden, dat, wanneer een gas in een ruimte bij een bepaalde temperatuur | |
[pagina 126]
| |
samengeperst wordt, de spanning van het gas evenveel malen zoo groot wordt, als het volume wordt verkleind. Het product van de spanning en het volume van een zekere gewichtshoeveelheid gas blijft, mits de temperatuur niet verandert, bij die samendrukking dus even groot. Deze eigenschap wordt de wet van Boyle genoemd. Uitdrukkelijk moet daarbij verondersteld worden, dat het gas tijdens de proefneming niet verwarmd of afgekoeld wordt, dat dus de temperatuur dezelfde blijft. De wiskundige uitdrukking voor deze wet van Boyle is p × v = C; hierin stelt p de spanning van het gas voor en v het volume, en het product van die beide blijft constant (C). Door den Franschen natuurkundige Gay Lussac werden in 1802 onderzoekingen verricht, waarbij werd nagegaan, hoe het volume van een hoeveelheid gas verandert, wanneer de temperatuur ervan gewijzigd wordt. Hij kwam tot de conclusie, dat alle gassen bij dezelfde temperatuursverhooging dezelfde regelmatige uitzetting vertoonen, een resultaat, dat met de wet van Gay Lussac aangeduid wordt. Wordt nu tijdens de samenpersing van een hoeveelheid gas in een ruimte behalve het volume ook de temperatuur gewijzigd, dan is niet meer het product van spanning en volume steeds hetzelfde, maar het product van spanning en volume, gedeeld door de absolute temperatuur (of het aantal graden Kelvin) blijft dan tijdens de volume- en temperatuursverandering even groot. Dit wordt uitgedrukt door: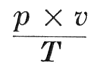 = constant (R). Hierin is T de absolute temperatuur, d.i. het aantal graden boven het absolute nulpunt (het aantal graden Kelvin); het absolute nulpunt ligt 273 graden beneden het smeltpunt van ijs. Deze eigenschap nu, die verkregen is uit een combinatie van de wet van Boyle en de wet van Gay Lussac, wordt de wet van Boyle-Gay Lussac genoemd. Ze vindt haar wiskundige uitdrukking in 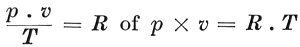 | |
Verzadigde en onverzadigde damp.Wanneer men in een ledige ruimte een zekere hoeveelheid vloeistof, bijv. water, brengt, dan verdampt een gedeelte van dit water | |
[pagina 127]
| |
 Van der Waals 1837-1923.
| |
[pagina 128]
| |
 Herinneringspenning.
 Van der Waals ten tijde van de verdediging van zijn dissertatie.
| |
[pagina 129]
| |
en daarboven ontstaat waterdamp, die dan een bepaalden druk uitoefent. Bij standvastige temperatuur is deze druk onafhankelijk van de hoeveelheid vloeistof, die zich in de ruimte bevindt, dus de druk is ook standvastig. Wordt de ruimte grooter gemaakt, dan blijft de druk van den damp even groot, tenminste zoolang er nog vloeistof in de ruimte aanwezig is. Bij het vergrooten van de ruimte gaat er alleen vloeistof in damp over, zoodat de hoeveelheid vloeistof kleiner en de hoeveelheid damp grooter wordt. De eigenschappen van den damp en die van de vloeistof veranderen daarbij niet. Dezen damp noemt men verzadigd of ook zegt men wel, dat de dampruimte ‘verzadigd’ is en de standvastige spanning van den damp noemt men de ‘maximumspanning van den damp’ of zijn ‘verzadigingsdruk’. Nu kan men met het vergrooten van de ruimte zoo ver gaan, dat alle vloeistof juist in damp is overgegaan; ook dan bevat de ruimte nog verzadigden damp. Maar wanneer men dan de ruimte nog iets grooter maakt, dan wordt de spanning van den damp kleiner en spreekt men van ‘onverzadigden damp’. Wordt de ruimte, waarin zich de onverzadigde damp bevindt, grooter, dan wordt de spanning van den damp zooveel maal zoo klein, als het volume vergroot is, m.a.w. de onverzadigde damp volgt de wet van Boyle. En wanneer de onverzadigde damp van een vloeistof, b.v. waterdamp, in een betrekkelijk groote ruimte wordt samengeperst, wordt de spanning aanvankelijk zooveel malen zoo groot als het volume kleiner wordt, m.a.w. de onverzadigde damp volgt aanvankelijk ook de wet van Boyle: het product van het volume en de spanning blijft even groot. Bij voortgezette samenpersing komt er dan evenwel weer het oogenblik, waarop de damp zijn grootste spanning, zijn maximumspanning of verzadigingsdruk bereikt; van af dat oogenblik vangt de verdichting tot vloeistof aan. De damp is dan weer ‘verzadigd’. En wanneer de verzadigde toestand bereikt is, volgt de damp de wet van Boyle niet meer: bij het kleiner worden van het volume condenseert steeds meer damp tot vloeistof, terwijl de spanning, de maximumspanning of de verzadigingsdruk, steeds even groot blijft. Dat ook een gas zich juist zoo gedraagt en daarom beschouwd moet worden als de damp van een vloeistof, die bijzonder vluchtig | |
[pagina 130]
| |
is, zoodat deze stof bij de kamertemperatuur in den gastoestand voorkomt, werd het eerst door Faraday aangetoond (in 1823). Door het gas onder grooten druk te brengen en tegelijkertijd af te koelen, gelukte het Faraday een groot aantal gassen vloeibaar te maken. Evenwel bleven nog een zestal gassen over, die Faraday niet in vloeibaren toestand kon brengen, hoe groot de druk ook was, die er op uitgeoefend werd; deze gassen werden daarom de permanente gassen genoemd. | |
Kritische temperatuur.In 1869 werd nu door den Schotschen natuurkundige Andrews ontdekt, toen hij koolzuur bij verschillende temperaturen aan een samendrukking onderwierp, dat er een temperatuur bestond, - deze werd sedert de ‘kritische temperatuur’ van het gas genoemd - waarboven het gas bij samenpersing in den gasvormigen toestand bleef; van een samenpersing tot den verzadigden toestand was boven de kritische temperatuur geen sprake, dus ook niet van een verdichting tot vloeistof. Het lag voor de hand, dat deze kritische temperatuur bij de permanente gassen zeer laag zou liggen, zoodat Faraday bij de samenpersing steeds daarboven gebleven was, waardoor hij dus deze gassen bij de samenpersing niet in den vloeibaren toestand zag overgaan. Inderdaad bleek dit later ook het geval te zijn. De minst lage kritische temperatuur heeft nog de zuurstof; deze bleek later 154 graden Kelvin te bedragen, d.i. 119 graden lager dan het vriespunt van water, een temperatuur, die door Faraday geenszins bereikt werd. | |
Wet van Van der Waals.Vanwaar deze kritische temperatuur? Bestaat er voor alle stoffen zoo'n kritische temperatuur? Hoe komt het, dat beneden deze bepaalde temperatuur vloeistof en damp naast elkaar in een ruimte bestaan kunnen en boven die temperatuur alleen de dampvormige toestand mogelijk is? In 1873 verscheen de dissertatie van Van der Waals: ‘Over de continuïteit van den gas- en vloeistoftoestand’, waarin naast een beantwoording van deze vragen nog vele andere eigenschappen, die omtrent den gas- en vloeistoftoestand der stof bekend waren, op geniale wijze verklaard werden. | |
[pagina 131]
| |
Enkele jaren te voren waren de Duitsche natuurkundige Clausius en de Engelsche natuurkundige Maxwell bijna gelijktijdig van de veronderstelling uitgegaan, dat de moleculen van de gassen zich met groote snelheid volgens rechte lijnen bewegen, totdat zij tegen elkaar of tegen den wand van de ruimte, waarin het gas besloten is, terugbotsen. Hieruit kon het bestaan van de spanning van een gas onmiddellijk verklaard worden: de tegen den wand botsende moleculen oefenen hierop een druk uit. Daar deze spanning in een afgesloten ruimte steeds even groot blijft, werd aan de genoemde hypothese nog deze toegevoegd, dat de moleculen volkomen veerkrachtig zijn, zoodat bij de botsing wel de richting, maar niet de grootte der snelheid gewijzigd wordt; daardoor kon dan de spanning van een gas in een afgesloten ruimte voortdurend even groot blijven. Door deze hypothesen konden direct eenige eenvoudige eigenschappen der gassen gemakkelijk verklaard worden, b.v. de vermenging van twee gassen in een ruimte. Maar ook werd met behulp van de hypothesen door Clausius in een verhandeling ‘Over de soort van beweging, die wij warmte noemen’, in de onderstelling, dat het volume van een molecule zoo klein is, dat dit wel verwaarloosd kon worden, de wet van Boyle afgeleid. ‘Deze verhandeling,’ zegt Van der Waals in de inleiding tot zijn dissertatie, ‘was voor mij een openbaring, maar tegelijkertijd kwam bij mij de gedachteGa naar voetnoot*) op: als een gas in uiterst verdunden toestand - waar het volume zoo groot is, dat dat der moleculen verwaarloosd kan worden - uit kleine, zich bewegende lichaampjes bestaat, dan spreekt het toch vanzelf, dat dit ook het geval is, wanneer men het volume kleiner maakt. Ja, dan moet dit ook nog het geval zijn, bij de uiterste verdichting en ook bij de zoogenaamde vloeistoffen, die toch slechts als verdichte gassen beschouwd moeten worden bij lage temperatuur. En zoo had ik het denkbeeld ontvangen, dat er geen wezenlijk verschil bestaat tusschen den gasvormigen en den vloeibaren toestand der materie, - dat de omstandigheden, die naast de beweging der moleculen in het spel zijn om den druk te bepalen wel quantitatief verschillend moesten worden aangenomen bij veranderde | |
[pagina 132]
| |
dichtheid en wellicht bij veranderde temperatuur, maar dat het toch dezelfde omstandigheden moesten zijn, die over het geheele gebied werking uitoefenen. En daarmede was de gedachte der continuïteit bij mij gevestigd.’
Van der Waals ging dan van de gedachte uit, dat al zouden de afmetingen der moleculen wel gering zijn, zoodat deze bij een verdunden toestand van het gas, - wanneer zich dus een kleine hoeveelheid gas in een groote ruimte bevindt, - wel verwaarloosd zouden kunnen worden, dit toch geenszins het geval mocht zijn, wanneer het gas verdicht werd, dus in een kleine ruimte werd samengeperst. Het probleem, dat gesteld werd, was nu dit: In een bepaald volume bewegen zich een gegeven aantal moleculen met een zekere snelheid. Hoe groot is de druk, dien zij bij hun beweging op den wand van de ruimte uitoefenen? M.a.w. hoe groot is de kracht, die de wand per vierkanten centimeter naar binnen moet uitoefenen, opdat het volume niet grooter wordt? Daniel Bernoulli bracht in het midden van de achttiende eeuw dit vraagstuk het eerst aan de orde. Het bleef langen tijd rusten, totdat ongeveer honderd jaar later Clausius en Krönig het vraagstuk weer opnamen en daarmee den grondslag legden voor de ‘kinetische gastheorie’. Zij namen aan: de moleculen hebben geen uitgebreidheid en zij trekken elkaar niet aan. Zij botsen dus nooit tegen elkaar en bewegen zich van den eenen wand naar den anderen. Met deze twee vereenvoudigingen is het niet zoo heel moeilijk het vraagstuk op te lossen. De druk op den wand van de ruimte, waarin de moleculen zich bewegen, wordt dan gevonden en uitgedrukt in de grootheden, die op den aard, de beweging der moleculen en hun aantal betrekking hebben. Nu is bij een gas in verdunden toestand, - wanneer dus een kleine hoeveelheid gas zich in een groote ruimte bevindt, - de uitgebreidheid der moleculen in verhouding tot de grootte der ruimte zoo gering, dat in dit geval de uitgebreidheid der moleculen verwaarloosd kan worden. En ook de onderlinge aantrekking der moleculen is bij een hoeveelheid gas in verdunden toestand te verwaarloozen. Het is daarom begrijpelijk, dat de verkregen uitkomst getoetst kon worden voor verdunde gassen. En inderdaad zijn uit die uit- | |
[pagina 133]
| |
 Laplace 1749-1827.
 Regnault 1810-1878.
 Joule 1818-1889.
 Lord Kelvin 1824-1907.
| |
[pagina 134]
| |

Kamerlingh Onnes en Van der Waals bij den heliumliquefactor (in 1908).
| |
[pagina 135]
| |
komst de wetten van Boyle en Gay Lussac af te leiden, wetten, die voor gassen in verdunden toestand gelden. De wiskundige uitdrukking voor den druk van de bewegende moleculen op den wand van de ruimte, waarin zij zich bevinden, kan dan ook in dezen vorm gebracht worden:
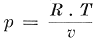 een vorm, die overeenkomt met de wiskundige uitdrukking voor de wet van Boyle-Gay Lussac. een vorm, die overeenkomt met de wiskundige uitdrukking voor de wet van Boyle-Gay Lussac.
Maar, - wanneer men niet te doen heeft met een ‘verdund gas’? Wanneer het gas samengeperst, dus verdicht wordt, wanneer het vloeistof wordt, hoe is het dan met deze aannamen? In dat geval is er natuurlijk geen sprake van, dat de uitgebreidheid der moleculen over het hoofd kan worden gezien; en ook de onderlinge aantrekking der moleculen kan niet verwaarloosd worden. Het vraagstuk dat dan opgelost moet worden, is buitengewoon moeilijk en dit vraagstuk is door Van der Waals in zijn dissertatie tot oplossing gebracht. Van der Waals' beschouwingen in populairen vorm weer te geven, op welke wijze hij tot den druk van de bewegende moleculen tegen den wand van de ruimte komt, wanneer de beide boven genoemde vereenvoudigende aannamen vervallen, is niet doenlijk. Over het resultaat, waartoe Van der Waals kwam, zal hier iets worden medegedeeld. Wanneer met de uitgebreidheid der moleculen rekening gehouden wordt, zou men mogen verwachten, dat het volume, dat voor de beweging der moleculen in aanmerking komt, eenvoudig het totale volume van de ruimte zou zijn, verminderd met het gezamenlijke volume der moleculen; de ruimte, door de moleculen zelf ingenomen, is dan aan de beweging onttrokken. Deze onderstelling werd evenwel niet bevestigd. Uit de ingewikkelde wiskundige beschouwingen bleek, dat de gezochte correctie verkregen wordt door het totale volume te verminderen met de grootheid, die door Van der Waals door b wordt voorgesteld en die ongeveer 4 maal het gezamenlijk volume der moleculen bedraagt. Clausius en Maxwell hebben destijds wel verschillende bezwaren tegen deze berekeningen aangevoerd; zij kwamen tot andere conclusies. Deze zijn evenwel weerlegd en bovendien bleken Korteweg en Lorentz later langs geheel andere wegen tot dezelfde uitkomst te komen als Van der Waals. Wel gaf Van der Waals reeds in zijn dissertatie in bedenking, dat | |
[pagina 136]
| |
de factor 4 niet standvastig zou zijn, hetgeen later ook inderdaad het geval bleek te zijn.
Behalve het feit, dat de moleculen zelf ook ruimte innemen, bracht Van der Waals ook de onderlinge aantrekking der moleculen in rekening. Deze moleculaire aantrekking is op zeer kleine afstanden slechts merkbaar en van beteekenis. Zagen we een stuk metaal door en voegen we de stukken tegen elkaar, dan zullen die stukken zich niet aan elkaar hechten, daar de moleculen niet dicht genoeg bij elkaar komen. Worden de stukken tegen elkaar geklemd, dan is het aan elkaar gehecht zijn, dat soms te voorschijn treedt, een gevolg van het verdrijven van de lucht tusschen de twee stukken, zoodat ze door de buitenlucht tegen elkaar gedrukt worden. Wordt de lucht buiten de stukken weggenomen of verdund, dan vallen ze ook van elkaar.  Denken wij ons nu een hoeveelheid vloeistof in een ledige ruimte. Boven de vloeistof zal verzadigde damp ontstaan van een zekere spanning (afhankelijk van de temperatuur). Wij kunnen ons nu afvragen, of dit verschijnsel niet in strijd is met de hypothese, dat de moleculen zich bewegen? Waarom verdeelen de moleculen, die toch een zeer groote snelheid bezitten, zich niet over de geheele ruimte gelijkmatig? Waardoor zijn ze in de vloeistof opgehoopt en in de dampruimte daarboven betrekkelijk schaarsch? Dit feit maakte vroeger, dat men een principieel verschil aannam tusschen den vloeibaren en den gasvormigen (of dampvormigen) toestand. Laplace (1749-1827) had evenwel reeds de oplossing van deze vraag gegeven bij de verklaring van de capillaire verschijnselen. Hij voerde het begrip attractiespheer in en verstond daaronder de bolvormige ruimte om een molecuul, waarbinnen het op andere moleculen een aantrekkende werking kan uitoefenen. Deze attractiesfeer kan men geen grooteren straal toeschrijven dan honderdduizendsten van een millimeter. Uit deze beschouwing volgde, dat een molecuul midden in de vloeistof zich gedraagt, alsof er geen attractie van uitgaat of er op uitgeoefend wordt en dat de moleculen aan de grens van de vloeistof, | |
[pagina 137]
| |
die de zoogenaamde grenslaag vormen (ter dikte van den straal der attractiesfeer) naar binnen in de vloeistof worden gedrukt. In het geval van zooeven, waar een zekere hoeveelheid vloeistof een ledige ruimte gedeeltelijk vult, is het deze moleculaire druk, die de moleculen tegenhoudt en hen belet uit de vloeistof- in de dampruimte over te gaan. De grenslaag gedraagt zich voor de moleculen als de wanden van een vat, waarin ze zijn opgesloten. En daar slechts een enorme uitwendige druk hetzelfde kan bereiken en de moleculaire druk de rol van dezen uitwendigen druk overneemt, moet de moleculaire druk buitengewoon groot zijn. Ook aan de grens van een gas, dus bij den wand van de ruimte, waarin het gas besloten is, ontstaat zoo een moleculaire kracht naar binnen. Deze moleculaire druk, die voorgesteld wordt door K, moet te zamen met de spanning p van het gas, dus met de kracht, die de wand van de ruimte, waarin het gas besloten is, per vierkanten centimeter naar binnen uitoefent, evenwicht maken met den druk, dien de botsende moleculen naar buiten uitoefenen. In de vergelijking p × v = R . T moet nu p vervangen worden door p + K (waardoor de onderlinge attractie der moleculen in rekening is gebracht) en v door v - b (waardoor met de uitgebreidheid der moleculen rekening is gehouden). De vergelijking gaat dan over in: (P + K) (v - b) = R . T. Bovendien werd door Van der Waals aangetoond, dat de kracht K door a/v2 vervangen kan worden, waarin a een constante grootheid is, die evenals b van den aard van het gas afhangt en v het volume van de ruimte, waarin het gas besloten is. De beide omstandigheden, door Van der Waals in aanmerking genomen, voerden hem dan tot deze vergelijking: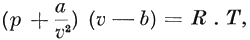 die de ‘toestandsvergelijking’ genoemd wordt. Deze bewonderenswaardige vergelijking drukt de ‘wet van Van der Waals’ uit. Met p, v en T worden de druk, het volume en de temperatuur van het gas aangegeven, terwijl R, evenals a en b, een constant getal is. De betrekking tusschen den druk p en het volume v bij een bêpaalde temperatuur kan in een grafiek worden weergegeven. Deze grafiek draagt den naam van ‘isothermische lijn’ of ‘isotherm’. | |
[pagina 138]
| |
De beschouwing omtrent het verloop der isothermen vormt een integreerend deel van de dissertatie van Van der Waals. En de betrekking tusschen den druk p, het volume v en de temperatuur T van een gas of vloeistof in een ruimte wordt weergegeven door een oppervlak; op de keerzijde van de medaille is dit oppervlak weergegeven (zie de afbeelding der medaille). De toestandsvergelijking in de magistrale dissertatie van Van der Waals tot uitdrukking gebracht, gaf niet alleen een verklaring van de reeds lang bekende afwijkingen, welke de gassen van de wetten van Boyle, Gay Lussac en Dalton vertoonen, maar loste ook alle vraagstukken omtrent het vloeibaar worden van gassen op eenvoudige wijze op. Zij vormde een luisterrijke samenvatting van vele op zich zelf staande eigenschappen.
Uit de toestandsvergelijking volgde onmiddellijk het bestaan eener kritische temperatuur en werd het verschijnsel er door verklaard, dat een gas, boven deze temperatuur verwarmd, door samenpersing niet tot vloeistof verdicht kan worden. Van der Waals zegt hiervan in zijn proefschrift (blz. 85): ‘Ik vlei mij dit tot nu toe raadselachtige feit door het voorgaande te hebben verklaard; tenminste als men verklaring van een verschijnsel mag noemen het aantoonen, dat het een gevolg is van een algemeen heerschende natuurwet.’ Maar bovendien konden door de toestandsvergelijking de afwijkingen van de wet van Boyle verklaard worden, welke de gassen volgens de nauwkeurige onderzoekingen van Regnault bij sterke samenpersing vertoonen en die zoozeer de aandacht der natuurkundigen getrokken hadden. Door middel van de toestandsvergelijking kon Van der Waals de grootte van a en b voor koolzuur berekenen en met behulp daarvan de kritische temperatuur van koolzuur. De uitkomst van deze berekening gaf een goede overeenstemming met de proeven van Andrews. Zoo werd ook b.v. de kritische temperatuur van lucht uit de toestandsvergelijking bepaald. Van der Waals vond hiervoor -158°, een temperatuur, die destijds niet bereikt kon worden. Toen deze temperatuur veel later verwezenlijkt werd, bleek ze van de berekende niet ver af te liggen. | |
[pagina 139]
| |
De toestandsvergelijking opende ook nog de gelegenheid tot het bepalen van de afmetingen der moleculen en van hun aantal in één kubieken centimeter. Op deze wijze vond Van der Waals voor de middellijn van een waterstofmolecule 2 tienmillioensten millimeter en voor de massa van een waterstofmolecule 2 kwadrillioensten gram. Tenslotte kon nog de grootte van de kracht K, die Laplace in zijn theorie der capillariteit had ingevoerd, bepaald worden. Deze kracht stelt den moleculairen druk bij een vloeistof, die door een plat vlak begrensd is, per vierkanten centimeter voor. Bij de theoretische beschouwingen van Laplace valt ze uit de eindvergelijkingen steeds weg. De wensch de grootte van deze kracht te leeren kennen, was het, zooals Van der Waals ons in de voorrede van zijn proefschrift meedeelt, welke hem tot het inzicht omtrent de continuïteit tusschen den gas- en vloeistoftoestand bracht. Door Laplace was reeds een vermoeden geopperd, dat hem tot een uitkomst voor de grootte van K leidde, een uitkomst evenwel, die hij zelf onwaarschijnlijk moest noemen. Hij vindt dan, dat de grootheid K gelijk te stellen zou zijn aan het gewicht van een zuil water, die een hoogte zou hebben van 10.000 maal den afstand van de aarde tot de zon. Inderdaad bleek later, dat deze schatting zeer vele malen te groot was. De uitkomst, waartoe Van der Waals bij verschillende stoffen komt, is vrij wat beter in overeenstemming met wat latere, op nieuwere gegevens gebaseerde onderzoekingen ons deden kennen. Maar vooral opmerkelijk is, dat Van der Waals voor het eerst deze grootheid wist te benaderen.
Van der Waals eindigt zijn proefschrift aldus: ‘Mochten mijn onderzoekingen iets bijdragen tot het spoediger aanbreken van dien schoonen tijd, dien W. Thomson in 1871 in zijn rede voor de British Association aldus aankondigde: Wij zijn niet zonder hoop, dat het absoluut gewicht der atomen te eeniger dage zal gevonden worden, niet alleen het betrekkelijk gewicht der verschillende atomen, - maar het aantal, dat in een bepaald gedeelte van een stof aanwezig is; dat de vorm en de bewegingen en de afstanden, waarop zij van elkaar liggen, bekend zullen zijn; dat de bewegingen, waardoor zij warmte, electriciteit en licht voortbrengen, door meetkundige diagrammen zullen kunnen worden opgehelderd. | |
[pagina 140]
| |
Dan zal de beweging der planeten en de muziek der sferen voor een poos vergeten worden in de bewondering voor het fijn en kunstig weefsel, dat door de banen dier onzichtbare atomen wordt gevormd.’
De dissertatie van Van der Waals werd, wat tot de hooge zeldzaamheden behoort, alom als een meesterstuk erkend en kort na het verschijnen reeds wijdde de grootmeester der natuurwetenschap, de Engelsche natuurkundige Maxwell, aan het werk van Van der Waals een artikel in het tijdschrift ‘Nature’, waarin hij voorspelde, ‘dat ongetwijfeld de naam van Van der Waals spoedig tot de allereersten in de moleculaire wetenschap zal behooren’. Maxwell merkt daarbij op: ‘Dit werk heeft zeker de aandacht van meer dan één onderzoeker gevestigd op het bestudeeren van de Nederlandsche taal, waarin het geschreven is.’ En de Duitsche natuurkundige Voigt drukte later zijn bewondering uit door te zeggen: ‘Der Wendepunkt zu dem Aufsteigen der Niederlände zu einer Grossmacht im Gebiete der Physik bezeichnet das Jahr 1873 durch das Erscheinen der genialen Dissertation von Van der Waals.’ Het is niet te verwonderen, dat dit proefschrift later in het Duitsch, Fransch en Engelsch vertaald werd. | |
De wet der overeenstemmende toestanden.Scheen de oplossing van het probleem, waardoor Van der Waals tot de continuïteit van den gas- en vloeistoftoestand gekomen was, betrekkelijk eenvoudig, in nog sterkere mate schijnt dit het geval te zijn met de ontdekking, die in 1880 door hem in een vergadering van de Koninklijke. Akademie van Wetenschappen te Amsterdam werd uitgesproken en in de Verslagen daarvan gepubliceerd werd en die hij de ‘wet der overeenstemmende toestanden’ genoemd heeft. En toch is Van der Waals eerst na langdurigen, moeitevollen arbeid tot deze wet gekomen, na vele vergeefsche pogingen om de moeilijkheden, die zich ophoopten, te overwinnen. Men bedenke daarbij, dat het wetenschappelijk standpunt van dien tijd zoodanig was, dat men het als een uitgemaakte zaak beschouwde, dat voor iedere stof een eigen wet zou gelden. De constanten a en b, voor iedere stof verschillend van waarde, voerden licht tot dat denkbeeld. | |
[pagina 141]
| |
Tenslotte is evenwel de wijze, waarop Van der Waals tot de wet der overeenstemmende toestanden gekomen is, hoogst eenvoudig. De wet luidt: Wanneer men den druk van een gas meet en daarbij zijn kritischen druk als eenheid gebruikt, het volume evenzoo in het kritische volume uitdrukt en de temperatuur in de kritische temperatuur en deze aldus in de toestandsvergelijking substitueert, ontstaat een vergelijking, waaruit de a en b, de grootheden, die den aard der stof bepalen, weggevallen zijn, zoodat deze wet voor alle stoffen dezelfde is. De wet kan ook aldus omschreven worden: Als men alle stoffen beschouwt bij temperaturen, die evenveel malen haar kritische temperatuur zijn, en ze brengt in volumes, die een gelijk aantal malen haar kritisch volume zijn, dan zijn de drukkingen een gelijk aantal malen haar kritische drukking. Of ook aldus: Als de temperatuur, het volume en de druk voorgesteld worden in kritische maat, dan volgen alle stoffen eenzelfde wet.
Aan elke stof worden dus eigen maten toegekend. De temperatuur van een stof, uitgedrukt in de kritische temperatuur, werd door Van der Waals de ‘gereduceerde temperatuur’ genoemd, het volume, uitgedrukt in het kritische volume, het ‘gereduceerde volume’ en de druk, uitgedrukt in den kritischen druk, de ‘gereduceerde druk’. Het aannemen der kritische temperatuur als eenheid had de meeste bezwaren. Iedereen is er toch van overtuigd, dat gelijke temperatuur in de natuur van veel beteekenis is. Wanneer twee lichamen met elkaar in aanraking worden gebracht, zullen zij in evenwicht zijn en elkaar geen warmte meedeelen, wanneer hun temperaturen gelijk zijn. Maar hier blijkt nu de gereduceerde temperatuur ook van groote beteekenis te zijn. ‘Zoo,’ zegt Van der Waals in een verhandeling, die later in de ‘Deutsche Revue’ verscheen, heeft ook het begrip ‘gelijke hoogte’ een groote beteekenis. Maar daarnaast kan toch ook het begrip ‘evenredige hoogte’ van groote beteekenis zijn. Als wij alleen begrip hadden kunnen vormen van gelijke hoogte, bijv. als onze oogen alleen in horizontale richting hadden kunnen | |
[pagina 142]
| |
zien, zouden wij nauwelijks allen, die ons omringen, hebben kunnen erkennen als behoorende tot het menschelijk geslacht. Dan zouden alleen verschillen ons hebben getroffen. Bij den een hadden wij den mond, bij den ander de kin waargenomen. Eerst nu ons oog het vermogen heeft om naar boven en naar beneden te zien en nu wij de hoogte van den eenen mensch hebben leeren verdeelen in gelijke deelen, kunnen wij op correspondeerende hoogten bij den ander de overeenkomstige eigenschappen ontdekken en zijn wij in staat geworden om over de vroegere verschillen heen de overeenkomst op te merken. Stellen wij, als wij de overeenkomst in het gedrag der verschillende lichamen willen opmerken, voor hoogte in de plaats ‘temperatuur’, dan moet het bedrag der kritische temperatuur de maat zijn. Nu is er een reeks van stoffen, n.l. vele bekende organische stoffen, waarvoor de kritische temperatuur ligt tusschen 200° à 300° boven het smeltpunt van ijs en waarvoor ze dus in absolute maat niet ver van 500° verwijderd is. Deze kunnen dan vergeleken worden met personen van gemiddelde hoogte. Deze kennen wij bij de gewone temperatuur als vloeistoffen en die vertoonen dan ook veel overeenkomst, zelfs zonder dat wij het begrip van gereduceerde temperatuur toepassen. Maar er zijn ook stoffen, die wij met dwergen en andere, die wij met reuzen moeten vergelijken. Waterstof is dan al bijzonder klein en helium is nog veel kleiner. Wij kunnen het beeld, dat wij gekozen hebben om de wet der overeenstemmende toestanden toe te lichten, nog verder uitwerken. De verschillende personen verschillen niet alleen in lengte, maar ook in breedte. Het kan voorkomen, dat de langere minder breed is en omgekeerd. Toch is dit geen beletsel om ze als behoorende tot hetzelfde menschelijk geslacht te beschouwen. Vergelijken wij ze dan met elkander, dan moeten wij de eene figuur uit de andere afgeleid denken door de hoogte naar zekere maatstaf te vergrooten of te verkleinen en voor de breedte een andere schaal te kiezen. Doen wij dit voor lengte en breedte beiden, dan kunnen wij overeenkomstige punten bepalen. Wij zouden zelfs nog verder kunnen gaan en de derde afmeting in onze beschouwing kunnen opnemen. Wij zullen echter ons voorbeeld niet verder uitwerken. Wij zouden natuurlijk gevaar loopen op verschillen te moeten wijzen. Onder anderen bestaat er reeds dit verschil. Voor de menschelijke figuur | |
[pagina 143]
| |
hebben wij de geheele lengte, de geheele breedte en de geheele dikte als maat aangenomen. Voor het opmerken van overeenstemming bij de verschillende stoffen, moeten wij de temperatuurmaat, de volumemaat en de maat der drukking ontleenen aan deze grootheden in een bepaalden karakteristieken toestand, n.l. den kritischen toestand. Vatten wij samen, wat uit het gekozen voorbeeld volgt, dan kunnen wij zeggen: Door de ontdekking van de wet der overeenstemmende toestanden is het genus ‘stof’ opgemerkt. Van der Waals voerde dus de gereduceerde grootheden in, den gereduceerden druk h = 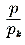 (pk is de kritische druk), het gereduceerde volume n = (pk is de kritische druk), het gereduceerde volume n =
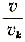 (vk is het kritisch volume, het volume dus bij den kritischen toestand) en m = (vk is het kritisch volume, het volume dus bij den kritischen toestand) en m =
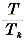 (Tk is de kritische temperatuur). (Tk is de kritische temperatuur).
Dus p = h × pk; v = n × v en T = m × Tk. De substitutie daarvan in de toestandsvergelijking doet de constanten a, b en R wegvallen. Zoo werd dan een algemeene vergelijking voor alle stoffen verkregen. Deze vergelijking luidt: 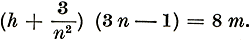 Deze vergelijking, voor alle stoffen dezelfde, zegt ons, dat alle stoffen volgens eenzelfde plan gebouwd zijn, maar volgens verschillende maten. Ze geeft de wet der overeenstemmende toestanden weer.
Wanneer men dus twee verschillende stoffen, bijv. zuurstof en waterstof beschouwt onder drukken, die een gelijk aantal malen hun kritische druk zijn en bij temperaturen, die een gelijk aantal malen hun kritische temperaturen zijn, dan zullen de volumes van die beide stoffen een gelijk aantal malen hun kritische volumes bedragen. Van die stoffen zegt men, dat ze in overeenstemmende toestanden verkeeren. In 1908, toen in de aula der Amsterdamsche Universiteit aan Van der Waals en Kamerlingh Onnes de gouden medaille van het aloude Genootschap ter bevordering der Natuur-, Genees- | |
[pagina 144]
| |
en Heelkunde werd aangeboden, de hoogste onderscheiding, waarover het Genootschap beschikt, heeft Van der Waals zijn wet der overeenstemmende toestanden aldus omschreven: ‘Alle stoffen vormen een enkel geslacht (genus). Vergelijkt men bijv. hoogte met temperatuur, breedte met druk en dikte met volume, dan kan men dus zeggen, dat alle stoffen copieën van elkaar zijn. Heeft de eene stof een merkwaardig punt, dan moet dit dus ook bij elke andere voorkomen.’ | |
Gebied der laagste temperaturen.Terwijl de verschijnselen in quantitatief opzicht niet geheel aan de toestandsvergelijking beantwoorden, bleek de wet der overeenstemmende toestanden met veel grooter benadering bevestigd te worden. Van onschatbare waarde was zij bij het in vloeibaren toestand brengen van de gassen waterstof en helium, welke zoo lang aan alle pogingen weerstand boden. Dat het ten slotte gelukt is, aan Dewar te Londen in 1898 de waterstof vloeibaar te maken en aan Kamerlingh Onnes te Leiden in 1908 het helium, is te danken aan de theoretische beschouwingen van Van der Waals. Daardoor ook is het mogelijk geweest het zoo belangrijke gebied der laagste temperaturen te ontsluiten, dat nieuw inzicht bracht in den bouw der stof en een nieuwen tak aan de industrie, de koeltechniek, heeft toegevoegd. Groote waardeering had Kamerlingh Onnes dan ook voor de theoretische beschouwingen van Van der Waals. ‘Zijn theorieën,’ zoo schreef hij in 1910, ‘zijn de onmisbare gidsen geweest bij een groot deel van het werk in het Leidsche laboratorium. Aan ieder, die het werk van dit laboratorium nagaat, zal het in het oog vallen, dat de denkbeelden van Van der Waals er steeds beschouwd zijn als een tooverstaf om experimenteel werk te wekken, en dat het cryogeen laboratorium te Leiden zich onder den invloed van zijn theorieën heeft ontwikkeld.’ | |
Het Boyle-punt en het Joule-punt.Zooals reeds werd opgemerkt, is door Regnault in een zeer nauwkeurig onderzoek nagegaan of de verschillende gassen, zooals lucht, stikstof, koolzuur, zuurstof, waterstof volkomen juist de wet | |
[pagina 145]
| |
van Boyle volgen, m.a.w. of het product van het volume en de spanning bij de samenpersing precies even groot bleef. De resultaten, waartoe hij kwam, vatte hij aldus samen: alle gassen zijn meer samendrukbaar dan de wet van Boyle aangeeft, met uitzondering van waterstof, dat minder samendrukbaar is. Of anders uitgedrukt: bij de samenpersing wordt het product van het volume en de spanning bij alle gassen kleiner, met uitzondering van waterstof, waarbij het product grooter wordt. Regnault zegt dan ook eenigszins ironisch, dat, indien de wet van Boyle het criterium moet zijn, waarnaar men het volkomen of niet volkomen zijn van gassen moet beoordeelen, waterstof als ‘un gaz plus que parfait’ moet worden beschouwd. In elk geval meende men hieruit te moeten besluiten, dat waterstof geheel verschillende eigenschappen bezit en dus apart zou staan. Nog bij een ander verschijnsel scheen waterstof een uitzondering te vormen. De Engelsche natuurkundigen Joule en Kelvin verrichtten onderzoekingen, waarbij zij verschillende gassen uit een ruimte, waarin hoogere druk heerschte, langzaam door een poreuzen wand lieten gaan in een andere ruimte, waarin de druk laag gehouden werd. Of ook zij lieten de verschillende gassen zich in een luchtledige ruimte uitzetten (zij pasten vrije expansie toe). Zij namen toen waar, dat alle gassen zich daarbij afkoelden met uitzondering van waterstof, dat verwarmd werd. Het zou evenwel onjuist zijn uit deze verschijnselen te besluiten, dat waterstof zich anders gedraagt dan de overige gassen. De wet van de overeenstemmende toestanden schrijft toch voor, dat alle stoffen zich gelijksoortig gedragen. Uit de onderzoekingen van Van der Waals bleek nu, dat een verdund gas nauwkeurig de wet van Boyle volgt, wanneer de temperatuur ervan 27/8 maal zijn kritische temperatuur is, gemeten van af het absolute nulpunt. Deze temperatuur wordt het ‘Boyle-punt’ genoemd. Is de temperatuur lager dan het Boyle-punt, dan is het gas meer samendrukbaar dan de wet van Boyle aangeeft of m.a.w. dan wordt het product van het volume en de spanning kleiner. Bij een temperatuur hooger dan het Boyle-punt is het gas minder samendrukbaar dan de wet van Boyle aangeeft of wordt het product van spanning en volume grooter. De uitkomsten van de onderzoekingen van Regnault toonden dus | |
[pagina 146]
| |
alleen aan, dat de temperatuur bij de proefnemingen met waterstof hooger was geweest dan 27/8 maal de kritische temperatuur van waterstof, terwijl bij de overige gassen de temperatuur van het onderzoek beneden 27/8 maal de kritische temperatuur van het gas gelegen was. Waterstof nam dus niet een uitzonderlijke plaats in. De wet van de overeenstemmende toestanden had dit duidelijk aan het licht gebracht. Ook de afwijking van waterstof bij de proeven van Joule en Kelvin bleek slechts een schijnbare te zijn. Of een stof bij vrije expansie zal afkoelen of zich zal verwarmen, is eveneens afhankelijk van de temperatuur, waarop het gas eerst gebracht is, alvorens men het laat uitzetten. De temperatuur, waarbij het gas bij vrije expansie nóch afkoeling nóch verwarming vertoont, - het Joule-punt genoemd, - bleek bij de berekening 27/4 maal zoo hoog te liggen als de kritische temperatuur, gemeten van af het absolute nulpunt. Wanneer nu het gas bij zijn vrije expansie een temperatuur heeft beneden het Joule-punt, dan zal het afkoelen; is zijn temperatuur er boven gelegen, dan zal het zich verwarmen. Uit het feit, dat waterstof bij de proeven van Joule en Kelvin eenige verwarming vertoonde, had men dus moeten besluiten, dat de kritische temperatuur van waterstof zoo laag was gelegen, dat men nog boven 27/4 maal die kritische temperatuur die proeven verrichtte. Inderdaad bleek dit later het geval te zijn. En bij de overige gassen waren de proeven toevallig steeds bij temperaturen beneden het Joule-punt uitgevoerd. Waterstof nam dus ook ten opzichte van deze proeven geen uitzonderlijke plaats in. Het bleek dus in wezen geenszins te verschillen van de andere onderzochte gassen. Het schijnbaar bijzondere gedrag van waterstof werd door de wet van de overeenstemmende toestanden in een eenvoudig licht geplaatst. Zoo zijn er nog tal van andere verschijnselen, die door deze wet een eenvoudige verklaring vinden. En het was nu ook duidelijk, dat men, om waterstof vloeibaar te maken, was aangewezen op de afkoeling, welke door vrije expansie beneden het Joule-punt verkregen kan worden. De sterkste afkoeling toch, die men om waterstof teweeg kon brengen, door snel verdampende vloeibare lucht, deed de temperatuur nog niet beneden | |
[pagina 147]
| |
de kritische temperatuur van de waterstof dalen. Tot de vrije expansie beneden het Joule-punt moest de Engelsche natuurkundige Dewar dus zijn toevlucht nemen, om de waterstof vloeibaar te maken. Maar dit Joule-punt moest eerst met behulp van de wet der overeenstemmende toestanden berekend worden. Van hoe groot belang deze wet beschouwd werd, daarvan getuigen de woorden, door Dewar in een rede voor de British Association uitgesproken: ‘Het is waarschijnlijk niet te boud gesproken als ik zeg, dat wij tot het kringproces van Carnot zouden moeten teruggaan, als wij iets wilden noemen, dat een even belangrijke bron voor onze kennis vormt als de wet van de overeenstemmende toestanden.’ Hetzelfde geval als bij waterstof, deed zich ook voor bij het vloeibaar maken van helium door Kamerlingh Onnes. Ook hier moest weer vrije expansie toegepast worden bij een temperatuur beneden het Joule-punt, ja zelfs, om genoegzame afkoeling te verkrijgen, zoodat de temperatuur beneden de kritische temperatuur van het helium zou kunnen dalen, beneden het Boyle-punt. Door bij zoo laag mogelijke temperaturen metingen omtrent volume en druk te doen, werd dit Boyle-punt met behulp van de toestandsvergelijking berekend en daarna de kritische temperatuur van helium op 5 à 6 graden boven het absolute nulpunt geschat, een schatting, die bij de latere proeven weer bevestigd werd. Steunende op de wet der overeenstemmende toestanden werd de hoeveelheid helium berekend, die voorradig moest zijn, de temperatuur, waartoe het helium met behulp van vloeibare waterstof moest worden afgekoeld, opdat het bij vrije expansie beneden de kritische temperatuur zou worden afgekoeld en de drukking, waartoe het zou moeten worden samengeperst. Dat, op deze berekeningen steunend, het helium inderdaad op den gedenkwaardigen 10den Juli 1908 door Kamerlingh Onnes in vloeibaren toestand verkregen werd, was, behalve aan het genie van Kamerling Onnes, die zoovele experimenteele moeilijkheden wist te overwinnen, te danken aan de theoretische leiding, die Van der Waals daarbij gegeven had. In de voordracht, door Kamerlingh Onnes gehouden naar aanleiding van den hem verleenden Nobelprijs zegt hij dan ook: ‘Recht gelukkig was ik, vloeibaar helium te kunnen toonen aan | |
[pagina 148]
| |
mijn hooggeachten vriend Van der Waals, wiens theorie bij het vloeibaar maken van dit gas tot het einde toe de gids gebleven was.’ En dat dit ook weer bij de latere proeven van Kamerlingh Onnes het geval was, waarbij een temperatuur bereikt werd, slechts 0,82 graad verschillend van het absolute nulpunt, hiervan getuigde de rede, door Kamerlingh Onnes in October 1922 voor de Faraday-Society te Londen gehouden, waarin wederom op de wet der overeenstemmende toestanden gewezen werd als de gids, die bij deze proeven leiding verleend had. | |
Geldigheid van de wet der overeenstemmende toestanden.Welke eigenschappen bij gereduceerde temperatuur en in gereduceerd volume overeenstemmend zijn, kan aldus worden samengevat: alle eigenschappen, die van den graad van opeenhooping van de moleculen afhangen; niet de eigenschappen, die afhankelijk zijn van de chemische samenstelling der moleculen. Als nu de wet der overeenstemmende toestanden volkomen streng geldt, dan behoeven wij slechts één enkele stof proefondervindelijk te bestudeeren. Kent men dan voor een andere stof de kritische grootheden, dan zouden zonder verder onderzoek van die andere stof ook de eigenschappen ervan bekend zijn. Belangrijk is nu nog de vraag, in hoeverre door experimenteel onderzoek de geldigheid van de wet der overeenstemmende toestanden bevestigd werd. Van der Waals deelt in de verhandeling, waarin de wet werd neergelegd, mede, dat ze aan het toen voorhanden zijnde materiaal werd getoetst en dat de overeenstemming met de feiten der ervaring van dien aard was, dat hij zich gerechtigd achtte tot de uitspraak, dat als de numerieke juistheid niet volkomen was, de regels, waartoe zij voerde, toch een hoogen graad van benadering bezaten. Zoo werd, aether als standaardstof aannemende, berekend de dampspanning, de uitzettingscoëfficient, de samendrukbaarheidscoëfficient, de densiteit, de capillariteitsconstante van tal van andere stoffen. Deze berekende waarden werden vergeleken met die, welke rechtstreeks door het experiment waren bepaald. In zulke gevallen kan men natuurlijk nooit volkomen overeenstemming vinden, want ook de getallenwaarden, welke rechtstreeks bepaald zijn, zijn met een waarnemingsfout behept, maar de verschillen waren betrekkelijk gering. | |
[pagina 149]
| |
Sedert is door verschillende natuurkundigen, hetzij langs theoretischen of langs proefondervindelijken weg, de juistheid van de wet nagegaan en in overeenstemming met de experimenteel gevonden uitkomsten bevonden. Wel bleken er, wat heel begrijpelijk is, kleine afwijkingen te bestaan. Van der Waals zegt hiervan: ‘Reeds het beeld, dat wij gebezigd hebben, om de beteekenis der wet te verduidelijken, n.l. de menschelijke figuur, had ons op een dergelijke uitkomst kunnen voorbereiden. De overeenstemming gaat toch niet zoo ver, dat wij den eenen mensch als een volkomen juiste copie van den ander mogen beschouwen. En een schilder, die een portret heeft te maken, of een beeldhouwer, die een beeld heeft te ontwerpen, volstaat toch niet met een vaststaand type volgens behoorlijke maten te vergrooten of te verkleinen. Er blijven fijne, individueele verschillen over, die ons in staat stellen, den eenen mensch van den ander te onderscheiden, zelfs zonder dat wij op de grootte of de breedte letten. Evenzoo merken wij bij nauwkeurig onderzoek individueele verschillen op bij de planten, die tot eenzelfde soort behooren en wordt zelfs een statistische wet vervuld bij het aantal gevallen, waarin een bepaalde afwijking voorkomt van een gemiddeld type. Maar dat neemt niet weg, dat het samenbrengen van alle menschen tot één zelfde menschelijk geslacht zijn hooge beteekenis heeft. Naast den schilder staat toch de wijsgeer, de staatsman, ja, staan wij allen, als wij niet schilderen, in de duizenden omstandigheden van het dagelijksch verkeer. Zoo zal de natuurkundige, dien ik bij den schilder zou willen vergelijken, en die zich tot taak heeft gesteld om met de hoogste nauwkeurigheid de waarde van zekere grootheden bij een bepaalde stof te bepalen, misschien kunnen meenen, dat de wet geen nut voor hem heeft. Maar naast hem staat, dien ik bij den wijsgeer onder de physici zou willen vergelijken en die erkent, dat hij door het begrip “overeenstemmende toestanden” eenheid en harmonie in den gang opmerkt, waar anders willekeur en verwarring zou schijnen te heerschen, en die juist door de grootere of kleinere afwijkingen er toe gebracht wordt om te gaan nadenken over de oorzaak dier afwijkingen. Zeker, het bijeenbrengen van nauwkeurig feitenmateriaal is ook in de natuurkunde van groot belang. Maar wat zou het ons baten, | |
[pagina 150]
| |
al hadden wij het meest uitgebreide feitenmateriaal bijeengebracht, zoodat het grootste museum het nauwelijks zou kunnen bevatten, als wij niet tegelijkertijd in staat zijn de eenheid in die verscheidenheid op te merken. Voor hem, die gelooft, dat ook de stoffelijke wereld niet moet beschouwd worden als het spel van het toeval, maar dat zij volgens eenvoudige wetten is ingericht en werkt en die het aan onze onkunde toeschrijft, wanneer wij dien eenvoud niet inzien, is het een feit van verreikende beteekenis, als hij door een beginsel van zóó vèrstrekkenden omvang zich een, al ware het dan ook gebrekkig inzicht in die eenvoudige inrichting vormen kan. En als hij het nog gebrekkige van het verkregen inzicht erkent, zal hij met nieuwen ernst er naar streven om dat inzicht te verbeteren en te verscherpen.’ | |
Theorie der binaire mengsels.Tien jaren na de wet der overeenstemmende toestanden, in 1890, verscheen in de ‘Archives Néerlandaises’ de eerste verhandeling over ‘de theorie der binaire mengsels’, de derde groote ontdekking van Van der Waals. Van der Waals behandelt hierin de verschijnselen, die zich voordoen, wanneer in een afgesloten ruimte twee stoffen gebracht zijn, bijv. aether en aceton, waarvan de hoeveelheden in verschillende verhoudingen vermengd zijn. Het is gemakkelijk in te zien, dat, waar de verschijnselen, die bij één enkele stof optreden, alleen door meesterlijke grepen geïnterpreteerd kunnen worden, dit in nog sterkere mate het geval moet zijn bij de verklaring van de meer gecompliceerde verschijnselen, welke zich bij de vermenging van twee stoffen voordoen. Zoo zal in het algemeen de damp een andere samenstelling hebben dan de vloeistof, waarmee hij in dezelfde ruimte besloten is, daar het bestanddeel, dat gemakkelijker verdampt, in de ‘dampphase’ in grooter hoeveelheid aanwezig zal zijn dan de stof, die minder gemakkelijk verdampt. Ook kan het voorkomen, dat de beide vloeistoffen zich niet geheel met elkaar vermengen, zooals bijv. bij water en aether het geval is. Dan treden drie ‘phasen’ op: twee vloeistoffen in van elkaar gescheiden lagen, n.l. water met een hoeveelheid aether vermengd en aether, vermengd met een hoeveelheid water en bovendien een mengsel van waterdamp en aetherdamp. | |
[pagina 151]
| |
 Titelblad van de dissertatie van Van der Waals.
| |
[pagina 152]
| |
 Boyle 1626-1691.
 Gay Lussac 1778-1850.
 Clausius 1822-1888.
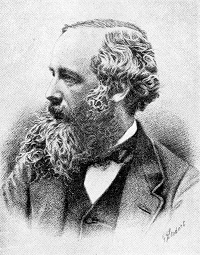 Maxwell 1831-1879.
| |
[pagina 153]
| |
Bevindt één enkele stof zich in de afgesloten ruimte en zijn dan vloeistof en damp met elkaar in evenwicht, dan treden de vragen naar voren: Hoe groot is de druk in deze ruimte bij een bepaalde temperatuur? En welke dichtheid heeft de vloeistof en welke de damp? Maar bij een mengsel komen daar nog andere vragen bij: Hoe is de vloeistof en hoe de damp samengesteld? Hoe wordt de samenstelling der beide ‘phasen’ gewijzigd, als men de temperatuur of den druk verandert? En wanneer drie phasen aanwezig zijn: welke zijn dan de drie samenstellingen? Hoe worden deze met den druk en de temperatuur gewijzigd? Kunnen de beide vloeistoffen, die zich eerst niet volkomen met elkaar vermengden, door verandering van druk of temperatuur daartoe gebracht worden? Ook de ‘kritische verschijnselen’ zijn veel gecompliceerder bij een mengsel van twee stoffen dan bij één enkele stof het geval is. In de nabijheid van de kritische temperatuur kunnen zich toch eigenaardigheden voordoen van geheel anderen aard dan die, welke bij één stof optreden. In dit labyrinth van verschijnselen heeft Van der Waals nu den weg gewezen. Als grondslag voor zijn beschouwingen heeft hij de toestandsvergelijking gebruikt, waarin nu a en b afhankelijk zijn van den aard der moleculen, waaruit het mengsel bestaat en van de verhouding tusschen de aantallen moleculen der beide stoffen. Door deze toestandsvergelijking in verband te brengen met de tweede hoofdwet der mechanische warmtetheorie, - in een vorm, waarin de Amerikaansche natuur- en scheikundige Willard Gibbs dien het eerst gebracht had, - slaagde Van der Waals er in met behulp van geniale grepen de moeilijkheden te overwinnen en een theorie op te bouwen, waardoor een schifting van de verscheidenheid van verschijnselen mogelijk was. Een voorname rol speelt in deze theorie een oppervlak, waarvan de vorm met de temperatuur verandert en dat de uitkomsten der ingewikkelde mathematische berekenigen in beeld brengt. Dit oppervlak heeft Van der Waals ter eere van Gibbs, die de grootheid, welke door dit oppervlak wordt voorgesteld met de Grieksche letter Ψ aangaf, het Ψ-vlak genoemd. En uit den vorm van dit oppervlak konden nu de waargenomen verschijnselen verklaard en nieuwe bijzonderheden voorspeld worden. Tal van onderzoekingen zijn onder leiding van Van der Waals | |
[pagina 154]
| |
en van Kamerlingh Onnes aan het Amsterdamsche en het Leidsche Natuurkundig Laboratorium verricht ter toetsing van deze ‘theorie der binaire mengsels’. De eerste, die zich hiermee bezig hield en de verschijnselen op meesterlijke wijze naging, was Kuenen (in 1892), die later hoogleeraar te Leiden was. In het bijzonder werden door hem de kritische verschijnselen bestudeerd, waarbij hij eigenaardigheden waarnam, die geheel uit de theorie voorspeld konden worden. In 1900 heeft Van der Waals zijn talrijke verhandelingen over de mengsels van twee stoffen, - waaraan later evenwel nog verscheidene werden toegevoegd, - vereenigd in een werk, dat als tweede deel van ‘de continuïteit van den gas- en vloeistoftoestand’ in het Duitsch te Leipzig in het licht verscheen. Later, na zijn aftreden als hoogleeraar, werden zijn colleges over dit onderwerp in het ‘Lehrbuch der Thermodynamik’ door Kohnstamm verzameld en gepubliceerd. | |
Theorie der capillariteit.Behalve deze baanbrekende onderzoekingen, zoo magistraal behandeld, verschenen in de Verslagen van de Koninklijke Akademie van Wetenschappen te Amsterdam nog een groot aantal verhandelingen, wel niet van zoo fundamenteelen aard, maar die toch van zijn schitterend vernuft getuigen. Van deze mogen hier nog worden vermeld: de thermodynamische theorie der capillariteit, de theorie der ternaire mengsels en de onderzoekingen van de latere jaren, welke ten doel hadden de toestandsvergelijking van één enkele stof nog beter aan de experimenteele resultaten te doen aansluiten. In de theorie der capillariteit, die in haar grondvorm in 1893 verscheen, - later werd ze verder ontwikkeld, - ging Van der Waals uit van een geleidelijke, zij het zeer snelle, dichtheidsverandering in de oppervlaktelaag van de vloeistof, bij den overgang van de vloeistof tot den damp, een opvatting, welke verschilde van die van Gibbs, die bij de verklaring van de capillaire verschijnselen een plotselingen overgang van de dichtheid der vloeistof tot die van den damp had aangenomen. En tevens nam Van der Waals in tegenstelling met Laplace, die reeds veel vroeger een theorie betreffende deze verschijnselen had opgesteld, aan, dat de moleculen der stof in voortdurende snelle beweging verkeeren. | |
[pagina 155]
| |
Experimenteele onderzoekingen, betrekking hebbende op verschijnselen in de nabijheid van de kritische temperatuur, waaromtrent beide theorieën met elkaar in strijd waren, beslisten ten gunste van de opvattingen van Van der Waals. De eertijds zoo beroemde theorie van Laplace was daarmee vervallen. | |
Theorie der ternaire mengsels.Kan omtrent de verschijnselen, welke zich bij de vermenging van twee stoffen voordoen, geen inzicht verkregen worden zonder de wiskundige voorstellingen en berekeningen, die Van der Waals in zijn theorie der binaire mengsels ontwikkelde, in nog sterkere mate is dit het geval bij de verschijnselen, die optreden bij de ternaire mengsels, de vermenging van drie stoffen in een ruimte. In 1902 verschenen hierover verhandelingen in de Verslagen van de Akademie van Wetenschappen. Een paar jaren vroeger had de Duitsche natuurkundige Wilhelm Ostwald, die gedurende vele jaren het bestaan van moleculen en atomen ontkende en een verklaring der natuurverschijnselen met behulp van de moleculair-hypothese uit den booze achtte, getracht door theoretische beschouwingen tot een overzicht te komen van de verschillende gevallen, die zich bij mengsels van drie stoffen kunnen voordoen. De resultaten, waartoe Ostwald kwam, waren in vele opzichten niet in overeenstemming met die van Van der Waals. Hoewel het aantal onderzoekingen betreffende dit onderwerp niet zo groot is, is toch duidelijk gebleken, dat Ostwalds beschouwingen niet steekhoudend waren. | |
Steun aan physisch-chemische onderzoekingen.Hier moge ook nog vermeld worden, de hulp en steun, die Van der Waals in den aanvang aan de physisch-chemische onderzoekingen van Bakhuis Roozeboom verleend heeft. ‘Van der Waals heeft daarmee,’ aldus merkte prof. Smits later op, ‘voor de chemie zulk een uiterst belangrijken arbeid geleverd, dat wij hem zeer zeker ook een “chemicus” kunnen noemen. Van der Waals had het juiste gevoel voor en den juisten kijk op de chemie. Het was bewonderenswaardig, hoe hij onmiddellijk het probleem doorzag, niet alleen van den theoretischen, maar, en dit was wel zeer opmerkelijk, ook van den experimenteelen kant.’ | |
[pagina 156]
| |
Schijnassociatie.Werd door de toestandsvergelijking voor één enkele stof kwalitatief van de verschijnselen, die zich kunnen voordoen, op bewonderenswaardige wijze rekenschap gegeven, een betere kwantitatieve overeenstemming trachtte Van der Waals nog in latere jaren te bereiken door de b uit de toestandsvergelijking niet als een constante te beschouwen, maar haar van het volume, dat de stof inneemt, afhankelijk te stellen. Van der Waals neemt daartoe aan, dat een associatie van moleculen tot grootere complexen kan plaats grijpen, welke door hem, om dit verschijnsel te onderscheiden van de associatie, die haar oorsprong in chemische oorzaken heeft, ‘schijnassociatie’ genoemd wordt. Hoe daardoor bij verandering van het volume de waarde van b gewijzigd wordt, is een onderwerp, waarmee Van der Waals zich nog na zijn aftreden als hoogleeraar herhaaldelijk heeft bezig gehouden. | |
Intuïtief gevoel bij de oplossing van problemen.Wat bij het bestudeeren van het werk van Van der Waals wel het meest bewondering afdwingt, is de groote moed, waarmee een uiterst moeilijk en gecompliceerd probleem wordt aangevat en het fijne intuïtief gevoel, dat telkens weer uit den gang der oplossing spreekt. Schijnbaar eenvoudig verloopt de oplossing. Het probleem is meestal van dien aard, dat, wanneer het in een wiskundig kleed gestoken is, de wiskunde te kort schiet om tot een oplossing te leiden. Maar dan komt het intuïtief gevoel Van der Waals te hulp. Hij weet uit het doolhof van wiskundige formules en vergelijkingen, die ter beschikking staan, juist die ter hulp te roepen, die het vraagstuk, hoewel nog niet oplosbaar, toch nader tot zijn oplossing brengen. Hij voelt, welke grootheden door andere vervangen moeten worden om hiertoe te geraken. Veelal geschiedt dit niet zuiver wiskundig, maar worden benaderingen ingevoerd en grootheden verwaarloosd, waarvan hij vermoedt, dat dit aan de waarde van de oplossing geen afbreuk zal doen, - een vermoeden, dat later, wanneer het vraagstuk zijn eindoplossing bereikt heeft, bevestigd wordt. Maar al verloopt de oplossing der grootsche problemen ook schijn- | |
[pagina 157]
| |
 Kuenen 1866-1922.
 Afbeelding van den gedenksteen in het Natuurkundig Laboratorium te Amsterdam.
| |
[pagina 159]
| |
baar eenvoudig, de inspiraties, die tot het gelukkige einddoel voerden, zijn ongetwijfeld door dagen van inspannenden arbeid voorafgegaan. Van der Waals zelf verhaalt ons hiervan, waar hij spreekt over de wijziging, die de b uit de toestandsvergelijking voor één enkele stof met het oog op betere aansluiting aan de experimenteele onderzoekingen moet ondergaan, een onderwerp, dat herhaaldelijk door hem ter hand genomen is. In 1896 gaf van der Waals voor het eerst een beschouwing over de oorzaak van het verkleinen van b bij vermindering van het volume. Vijftien jaren later zegt hij: ‘steeds weer vraag ik mij zelf af, of er een betere weg bestaat. Eigenlijk vervolgt mij deze vraag voortdurend; ik raak haar niet kwijt; zij vervolgt mij zelfs tot in mijn droomen.’ | |
Vaste geloof in de realiteit der moleculen.Bij al zijn onderzoekingen is Van der Waals geleid door het vaste geloof in de realiteit der moleculen. In de jaren, waarin deze onderzoekingen begonnen, werd de moleculair-hypothese nog veelal als een werk-hypothese beschouwd, die nieuwe gezichtspunten opende, van waaruit nieuwe beschouwingen mogelijk werden; of deze hypothese de werkelijkheid ook weergaf, werd in het midden gelaten of betwijfeld. Reeds in 1873, in zijn proefschrift, had Van der Waals, - zooals al boven werd opgemerkt, - het aantal moleculen in een kubieken centimeter berekend, hun afmetingen en gemiddelde afstanden, de snelheid van hun beweging. Van der Waals beschouwde hun bestaan dan ook allerminst als een hersenschim, zelfs vatte hij ze nooit op, zooals veelal geschiedde, als punten, vanwaar krachtwerkingen uitgaan. Hij beschouwde ze als de eigenlijke lichamen, zoodat hetgeen in het dagelijksch leven lichaam genoemd wordt, als een aggregaat van lichamen en ledige ruimten moest opgevat worden en beter met den naam ‘schijnlichaam’ moest worden aangeduid. Hoe verdroot het hem, toen nog veel later Wilhelm Ostwald van uit Leipzig een campagne tegen de moleculaire opvattingen ondernam en in zijn ‘Landhaus Energie’ een werk schreef, waardoor hij de energetische natuurbeschouwing ingang trachtte te doen vinden. Niet slechts in Duitschland, ook in Frankrijk vond deze beschouwing aanhangers. Hoe sterk was Van der Waals er van overtuigd, dat | |
[pagina 160]
| |
zonder het in aanmerking nemen van den moleculairen toestand der stof een verdere ontwikkeling der natuurwetenschap onmogelijk zou zijn. Het gebeurde in dien tijd op het college wel, dat Van der Waals den studenten, zijn leerlingen, vroeg, hoe zij over de moleculaire hypothese dachten. En tot hen, die niet zoo rotsvast overtuigd bleken te zijn van de realiteit der moleculen, zei hij met kracht en overtuiging: ‘Gij zult nooit iets op moleculair gebied presteeren.’ Maar even later voegde hij er dan vergoelijkend aan toe: ‘Dit is niet zoo heel erg; ge kunt toch op ander gebied wel iets bereiken.’ Hoe genoot Van der Waals later, toen in zijn laboratorium de ‘Brownsche beweging’, de beweging van kleine deeltjes onder invloed van de tegen hen botsende, onzichtbare moleculen, zoodanig geprojecteerd werd, dat ze met het bloote oog was waar te nemen en toen door den Franschen natuurkundige Perrin uit berekeningen geconcludeerd werd, dat deze bewegingen geheel in overeenstemming waren met de eischen, die de moleculair-theorie stelde. Een twijfelen aan het werkelijk bestaan der moleculen was toen niet meer mogelijk en Ostwald verklaarde zich daardoor dan ook overwonnen. ‘Hierdoor’ schreef Ostwald, ‘is de atomistische hypothese tot den rang van een wetenschappelijk gegrondveste theorie verheven’, een wijze van zich gewonnen geven, die begrijpelijkerwijze de sympathie van Van der Waals niet wekken kon. In 1911, op ruim 72-jarigen leeftijd, kon Van der Waals toen schrijven: ‘Ik geloof niet te veel te zeggen, wanneer ik constateer, dat het werkelijk bestaan der moleculen algemeen door de physici wordt aangenomen. En velen van hen, die zich het meest er tegen verzet hebben, zijn - en daartoe mag mijn theorie hebben bijgedragen - ten slotte bekeerd. En juist dit is, naar ik geloof, een stap vooruit. Met groote vreugde zie ik een gansche schaar van jongere Hollandsche physici en chemici de bezieling tot hun werk vinden in moleculair-theoretische beschouwingen en onderzoekingen.’ | |
Van der Waals als docent.Muntte Van der Waals als geleerde uit, zoodat zijn naam onafscheidelijk verbonden zal zijn aan de ontwikkeling van de natuurwetenschap in de tweede helft der negentiende eeuw, als docent had hij zijns gelijke niet. | |
[pagina 161]
| |
Het best kwam dit misschien nog uit op het ‘groote’ college, waar Van der Waals voor de studeerenden in de wis- en natuurkunde en in de medicijnen, - een schare van 100 tot 150 toehoorders, - in twee jaren tijds de hoofdtrekken der experimenteele natuurkunde behandelde. Hoe wist hij die menigte te beheerschen, ze te dwingen met intensieve aandacht het onderwerp te volgen, dat met groote helderheid en met vuur werd voorgedragen. Reeds in het eerste college-uur na de groote vacantie maakte Van der Waals op zijn hoorders een indruk, die hun zou bijblijven en hun deed gevoelen, dat bij dezen hoogleeraar de studie ernstig moest worden opgevat. Al begon Van der Waals vroeg na de vacantie, de collegezaal was tot in de bovenste rijen banken gevuld; de vacantiestemming was veelal nog merkbaar aan het rumoer en het geschreeuw der wachtenden. Bij het binnentreden van den hoogleeraar, gevolgd door zijn assistent, breekt een geweldig applaus en getrappel los, dat onder invloed van den op den katheder staande rustige persoonlijkheid snel verzwakt en in een ‘hoorbare’ stilte vangt Van der Waals zijn college aan. Met grooten ernst werden de colleges gegeven en met ernst ook gevolgd. Helder en scherp werden de onderwerpen, ook die, welke voor de ‘eerste-jaars-studenten’ groote moeilijkheden inhielden, behandeld, waarbij overzichtelijke, demonstratieve proeven, door den assistent genomen, - Van der Waals zelf experimenteerde niet, - de verschijnselen toelichtten. Diezelfde helderheid kenmerkte ook de voordrachten over de moeilijke onderwerpen der theoretische natuurkunde, welke alleen voor de physici en chemici behandeld werden. Hier was het aantal toehoorders slechts gering, in den eersten tijd van zijn hoogleeraarschap slechts een drietal, later iets meer. Nu kwam een andere zijde van zijn begaafdheid als docent meer naar voren: het zich snel indenken in de moeilijkheden, die door zijn toehoorders werden opgeworpen en door zijn volkomen beheersching der stof met groote helderheid werden opgeheven. Hier liet Van der Waals zijn toehoorders voortdurend op zijn vragen respondeeren, zoodat zij den indruk kregen, dat zij te zamen met den hoogleeraar de oplossing van het probleem ontwikkelden. Somtijds bracht Van der Waals het onderwerp ter sprake, waarmee hij zich den laatsten tijd had bezig gehouden of waarover hij zoo juist in de Akademie | |
[pagina 162]
| |
van Wetenschappen een voordracht gehouden had. Of ook liet hij zich wel leiden door de een of andere vraag, die opgeworpen werd, waardoor bij de oplossing van het probleem een zijweg werd ingeslagen. Daardoor waren zijn voordrachten wel minder afgerond van vorm, maar de toehoorders kregen nu den indruk, dat zij de eerste ontwikkeling van het probleem meemaakten, waardoor de belangstelling in het onderwerp in hooge mate verlevendigd werd. | |
Van der Waals als examinator.Het is begrijpelijk, dat iemand, die zich zoo geheel aan de wetenschap en zijn colleges gaf, bij tentamens en examens hooge eischen stelde en dikwijls zeer scherp in zijn critiek kon zijn. Veel kennis werd door Van der Waals niet op prijs gesteld. Wat hij bij de tentamens verlangde, was, dat men inzicht verkregen had in de bestudeerde problemen. Die mate van inzicht werd door hem doorpeild, het deficit aangevoeld, de kennis en het inzicht op de juiste waarde geschat. Een langdurig onderzoek had deze scherpzinnige geest niet noodig om tot een juist oordeel te komen. | |
Levensbijzonderheden.Van der Waals was een self-made man. Geboren den 23sten November 1837 te Leiden, werd hij, na lager onderwijs genoten te hebben, onderwijzer en behaalde daarna verscheidene akten middelbaar onderwijs in de wis- en natuurkunde. In 1864, op 26-jarigen leeftijd, werd hij tot leeraar aan de hoogere burgerschool te Deventer benoemd en twee jaren later te 's-Gravenhage eerst tot leeraar en daarna tot directeur der hoogere burgerschool. Toen zag hij zich, na dispensatie te hebben verkregen van het examen in Latijn en Grieksch, in de mogelijkheid gesteld academische examens af te leggen en zoo kon hij op 14 Juni 1873 te Leiden tot doctor in de wis- en natuurkunde promoveeren op de dissertatie, die hem met één slag tot een der grootste natuurkundigen stempelde: ‘Over de continuïteit van den gas- en vloeistoftoestand’. Toen in 1876 de nieuwe Hooger-Onderwijswet tot stand gekomen was, werd het volgend jaar het Amsterdamsche Atheneum Illustre tot Universiteit verheven en was Van der Waals de eerste hoogleeraar in de physica, die aan deze universiteit verbonden werd. | |
[pagina 163]
| |
Gedurende vele jaren is hij met Van 't Hoff en Hugo de Vries de roem der Amsterdamsche universiteit geweest. Hij is Amsterdam trouw gebleven, ook toen hij van elders vereerende aanbiedingen ontving. Langen tijd doceerde Van der Waals alleen de geheele physica, de experimenteele physica voor de medici en de filosofen en de mathematische physica in haar geheelen omvang voor de physici en de chemici, terwijl hem bovendien de leiding bij de practische oefeningen was toevertrouwd. Ondanks deze zware en moeilijke taak, het groote aantal examens, dat hij had af te nemen en vele andere bezigheden in het belang van wetenschap of onderwijs, heeft Van der Waals in dezen tijd zijn belangrijke werken het licht doen zien. Zijn taak aan de universiteit werd eerst in 1897, toen hij den 60-jarigen leeftijd bijna bereikt had, gedeeltelijk overgenomen door Sissingh en Zeeman, nadat die reeds enkele jaren te voren eenigszins verlicht was. Van 1897 tot 1908 doceerde Van der Waals nog de geheele mathematische physca en gaf hij herhaaldelijk leiding bij de bewerking van proefschriften. Van 1875 af was hij lid van de Koninklijke Akademie van Wetenschappen, van 1896 tot 1912, toen hij door Zeeman werd opgevolgd, secretaris van de wis- en natuurkundige afdeeling. Tal van jaren is hij de ziel dier afdeeling geweest. Bijna het geheele levenswerk van Van der Waals heeft het licht gezien in de publicaties van de Koninklijke Akademie van Wetenschappen. Het secretariaat werd met de uiterste nauwgezetheid door hem vervuld en hoe afkeerig hij ook van nieuwigheden was, op zijn initiatief werden de oude Verslagen en Mededeelingen door een meer modern zittingsverslag vervangen en werd een Engelsche vertaling daarvan ingevoerd, wat de beteekenis van de wis- en natuurkundige afdeeling der Akademie belangrijk verhoogde. Toen in 1898 herdacht werd, dat 25 jaren vroeger zijn beroemde dissertatie verschenen was, brachten zijn vereerders, oud-leerlingen en leerlingen als een hulde, het meest in overeenstemming met zijn eenvoudigen en bescheiden aard, het ‘Van der Waals-fonds’ bijeen, waaruit buitengewone uitgaven bestreden zouden kunnen worden ten behoeve van experimenteele onderzoekingen, welke in verband | |
[pagina 164]
| |
met de theoretische beschouwingen van Van der Waals verricht zouden worden. En bij zijn aftreden als hoogleeraar in 1908 werd in de groote collegezaal van het Natuurkundig laboratorium, waar Van der Waals gedurende zoovele jaren den jongeren bij hun studie leiding gegeven had, als hulde aan den voortreffelijken geleerde en docent een gedenksteen aangebracht, waarop zijn belangrijkste werken met de jaartallen, waarin zij gepubliceerd zijn, gegrift staan. Talrijke hooge wetenschappelijke onderscheidingen zijn hem ten deel gevallen. Tot de twaalf grootste geleerden buiten Frankrijk, die de ‘Académie des Sciences’ te Parijs als ‘associé étranger’ aan zich verbonden had, behoorde Van der Waals. In de jaren van zijn emeritaat valt de groote onderscheiding, welke hem van de zijde van het buitenland in 1910 ten deel viel, toen hem de Nobelprijs verleend werd, een erkenning van de verdienste van zijn levenswerk, dat reeds van den beginne af, - dit werd boven reeds opgemerkt, - de aandacht, ook van de buitenlandsche wetenschappelijke wereld, in sterke mate getrokken had. Van der Waals was een geloovig Christen; over dit geloof sprak hij evenwel nooit in het openbaar. Natuurwetenschap beoefenen was voor hem in gehoorzaamheid opnemen van een taak, die strekt om in de kennis van Gods schepping Hem te verheerlijken. Op 8 Maart 1923 is Van der Waals overleden. Als hoogleeraar in de theoretische natuurkunde werd hij opgevolgd door zijn zoon J.D. van der Waals Jr., als hoogleeraar in de thermodynamica door Kohnstamm, die tot zijn beste leerlingen behoorden. | |
Herdenking, een eeuw na de geboorte van Van der Waals.Toen het op 23 November 1937 een eeuw geleden was, dat Johannes Diderik van der Waals te Leiden geboren werd, werd als een buitengewone hulde aan zijn nagedachtenis te Amsterdam in het naar hem genoemde Van der Waals-Laboratorium een internationaal natuurkundig congres gehouden, onder voorzitterschap van Zeeman. In zijn openingswoord merkte Zeeman op: ‘In Van der Waals bewonderen wij het groote verstand, den onvermoeiden geest, de onvergankelijke trouw aan het doel, dat hem voor oogen stond; de perioden van wonderbaarlijken arbeid, afwisselend met tijdperken van niet minder wonderlijke rust.’ | |
[pagina 165]
| |
Op dit congres, dat zich in hoofdzaak bezig hield met de vraag naar de eigenlijke oorzaak van de moleculaire aantrekking, kwamen Nederlandsche, Fransche, Engelsche, Duitsche, Amerikaansche, Italiaansche, Zwitsersche geleerden samen en hielden er hun voordrachten. Het congres werd gesloten met een plechtige herdenkingszitting, waarin Debye, - ook een Nederlandsche Nobelprijswinnaar, - toen hoogleeraar te Berlijn, de herdenkingsrede uitsprak. ‘Met bewondering,’ zoo besloot Debye zijn rede, - ‘staan wij heden, honderd jaar na Van der Waals' geboorte tegenover den geleerde, wiens naam in de wetenschap leeft en die door hen, die hem het naast stonden, beschreven wordt als: de man met dat stoere, onbuigbare karakter, dat trouwe, fijn besnaarde hart en dat vrome, diepdeemoedige gemoed.’  Handschrift van Van der Waals.
|
|

