De natuurkunde van 't vrije veld. Deel III

Rust en beweging

[p. 110]

Stromend water.⁺

Vurige vlammen, watervallen, zeegolven, met hun rusteloze bewegelijkheid, hebben voor den mens een voor de hand liggende, duidelijke gelijkenis met bedrijvigheid en leven, ditmaal in de onbewerktuigde natuur. En daar ons oog zich bij voorkeur tot het levende aangetrokken voelt, is hier stellig de oorzaak gelegen van de merkwaardige, onbeschrijfelijke bekoring, welke deze eenvoudige natuurverschijnselen veroorzaken, en waardoor zij het oog onvergelijkelijk veel langer boeien dan een nog zo bekoorlijk en verheven tafereel, als dit onbewegelijk blijft.
J.J. Oppel, Pogg. Ann. 99, 540, 1856.

+ Voor veel der in dit hoofdstuk behandelde onderwerpen, zie b.v. H. Bouasse, Houle, rides, seiches et marées (Paris, 1924). - Vaughan Cornish, Waves of the Sea (London, 1910). - Vaughan Cornish, Ocean Waves and other geophysical Phenomena (London, 1934). - H. Thorade, Probleme der Wasserwellen (Hamburg, 1931). - Handbuch der Experimentalphysik, Bd. 4 (Leipzig 1930-32).

70. Indrukken bij een fontein.¹⁾

‘Kom, laat ons hier op de bank onder de bloeiende linden uitrusten. De heerlijke geur, de koele schaduw, de hoge fontein vlak vóór ons: alles nodigt er ons toe uit. Als ik de machtige, bijna armdikke straal beschouw die wel zes man hoog opstijgt, krijg ik de indruk dat hier een geheimzinnige kracht in 't spel is, die het water noodzaakt trots zijn gewicht op te stijgen. De aanblik van iets ongewoons wekt in ons steeds een verborgen verwondering, ook al kennen we de oorzaak zodra wij er nader over denken.

Wat gewoonlijk het eerst onze aandacht trekt, is de toenemende dikte van de opstijgende straal. Die ontstaat, doordat de waterdeeltjes voortdurend snelheid verliezen terwijl ze stijgen; en dat de stroom een des te breder baan nodig heeft naarmate hij langzamer beweegt, wil dezelfde watermassa per tijdseenheid door elke doorsnede gaan. Die toenemende dikte, die als 't ware van binnen uit komende groei, boeien onze fantasie en wekken de voorstelling van een inwendig leven.

1) Verkort naar H.C. Oersted, Der Springbrunnen (Ges. Schr. 1, 39; omstreeks 1840).

[p. 111]

Velen zouden het geluid weg willen hebben van de ruisende druppels die het watervlak treffen; maar wie zich aan de natuurindruk in zijn geheel overgeeft, zal deze mening niet delen. Moesten de druppels geruisloos vallen, dan zouden ze in ons een gevoel van onbehagen wakker roepen, ongeveer als een lichaam zonder schaduw het zou doen.

Ik ben overtuigd dat de tuinkunstenaar deze bank met overleg juist hier heeft geplaatst. Als men zo dicht bij een fontein staat, dat men het plassen van het water te sterk hoort, dat men haar niet goed kan overzien, dat zij niet een aangenaam geheel met de omgeving maakt: dan is het alsof men een schilderij bij verkeerde belichting en in een storende omgeving zou zien.

Het komt mij vóór dat het licht dat van het neervallende water komt, zekere eigenaardigheden vertoont, en niet gelijkt op het schitteren van heldere glazen parels, noch op dat van een rustig wateroppervlak; het vertoont een merkwaardige fonkeling. Dit is te wijten aan de onophoudelijke beweging der druppels, maar ook aan twee andere omstandigheden: de voortdurende vormveranderingen van elke druppel tengevolge van de capillaire trillingen; en het feit dat er zowel zeer grote druppels zijn, als zeer kleine tussen de andere in.

Ik heb veel fonteinen gezien welke een heel ander karakter hadden dan deze hier, en die niet dezelfde stempel droegen van rust in de beweging. De zeer kleine maakten natuurlijk slechts een geringe indruk, zoals alle onbetekende dingen; ik kan mij zelfs voorstellen dat een al te onbeduidend fonteintje als een mislukte poging spot kan opwekken. Dan zijn er fonteinen die door een grote kracht gedreven worden in verhouding tot hun massa, zodat ze in veel kleine druppels verstoven worden; ze dragen dus een veel sterkere stempel van leven en beweging; ze bruisen en schuimen, en overweldigen ons als het ware met hun kracht, zodat ze mij goed schijnen te passen voor grote, volkrijke steden en zeer druk bezochte tuinen. Daarentegen schijnt deze dikkere en langzamer straal meer geschikt voor een rustiger omgeving. De grootste fontein die ik ooit gezien heb was (geloof ik) 181 voet hoog, en slechts zo dik als een gemiddeld ontwikkeld mensenlichaam; ze maakte geen geringe indruk, maar die indruk was van een andere soort: sterker en grootser, een schouwspel meer verheven dan harmonisch-bevredigend. De inwendige harmonie was niet bedorven, maar de indruk ervan werd verdrongen door het gevoel van kracht en grootsheid.’

[p. 112]

71. Het balletje op de fontein.¹⁾

In kermistenten, in oude tuinen ziet men soms een heel licht balletje van kurk of celluloid, dat op en neer danst op de straal van een fontein. Men kan zich voorstellen dat de kracht van

Fig. 56. Het draaiende balletje op de fontein.

de straal ruim voldoende is om het gewicht van het balletje op te heffen; maar geheel onbegrijpelijk lijkt het, dat het nooit opzij uitwijkt en van de straal af valt. De straal treft het balletje zelfs niet aan de onderkant, maar gewoonlijk een 45^o daar vandaan. Klaarblijkelijk is dit een soort even wichtstoestand waar het omheen schommelt; wipt het per ongeluk iets te ver, dan valt het, maar zó dat het meestal nog wel in de straal terugkeert. Men beweert soms dat de waterstraal het balletje zwevende houdt doordat hij de omgevende lucht met zich meezuigt; maar het is een feit dat het verschijnsel zich net zo goed in 't luchtledige afspeelt.

We komen tot de juiste verkaring door op te merken dat het balletje voortdurend om zijn as tolt, blijkbaar door de schuine stoot van het water (fig. 56). Een gedeelte van de straal hecht zich aan het balletje door adhesie, wordt meegenomen door de snelle wenteling, en spat er slechts aan de achterkant af; hij oefent een vertikale opwaartse kracht uit in het punt A, maar ook een reactiekracht in de punten B, waar hij door de middelpuntvliedende kracht het balletje loslaat en wegspat. Die reactiekracht helpt het balletje zwevende houden, en zij is het die het telkens terug in de straal drijft. Ze blijft zelfs nog even werken als het balletje al niet meer aan de straal raakt, want er ligt dan toch nog een waterlaagje op dat nog moet wegspatten, en dat gedurende een breukdeel van een sekunde nog een merkbare reactiekracht levert. - Dat onze verklaring wel de juiste is, blijkt uit een eenvoudige proef: zodra men het balletje met een weinig vet inwrijft, valt het neer en kan niet meer zweven; de adhesie van het water is nu vervallen.

Naar gelang van de kracht van de straal kan het balletje op

1) O. Reynolds, Mem. lit. philos. Soc. Manchester 4, 1869-70; Papers, 1, 1. - W. Baker, Science, 64, 161, 1926. - Het volledigst in E. Hagenbach, Ann. Phys. 159, 497, 1876.

[p. 113]

twee verschillende manieren zweven (fig. 57). a) Bij een zwakke straal blijft het in het gladde gedeelte van de straal; het zweeft afwisselend rechts, dan links, dan weer rechts enz. van de straal. De verklaring is, dat het nog om zijn as tolt op het ogenblik dat het over de evenwichtsstand heen schiet, zodat de kracht die nu in omgekeerde richting moest werken slechts in actie komt als het balletje al een vrij grote uitwijking gekregen heeft. Op deze

Fig. 57. Twee bewegingsvormen van het balletje op de fontein.

wijze wordt het heen en weer schommelen voortdurend onderhouden. b) Bij een sterkere straal stijgt het balletje tot in het gedeelte van de straal dat uit afzonderlijke druppels bestaat; de straal treft het verder van zijn onderste punt dan bij de vorige toestand, blijkbaar omdat de reactiekracht nu geringer zou zijn, als er niet een groter componente van benuttigd werd. Het balletje tolt snel om een horizontale as, maar draait daarenboven om de straal als vertikale as, nu eens rechtsom, dan linksom, volgens dat het toevallig een schuine stoot van het water krijgt.

Soms gelukt het door openen of sluiten van de kraan van de ene toestand naar de andere over te gaan zonder dat het balletje valt.

72. Profiel van een rivierbedding.

Ik moet bekennen dat ik jaren lang haast niets geweten heb van de vorm der bedding van de kanalen en rivieren in mijn omgeving. Toch is het zo eenvoudig om de diepgang te bepalen en het profiel van de doorsnede. We doen dit van op een brug of van uit een roeibootje; in dit laatste geval spannen we eerst een touw van oever tot oever, en bevestigen daaraan merktekens om de 5 m. Nu peilen we achtereenvolgens op verschillende afstanden van de oever; kleine diepten meten we met een peilstok, een willekeurige lat waarop we een ruwe schaalverdeling hebben getekend; grotere diepten met een touw waaraan een flink gewicht hangt. Het dwarsprofiel kan nu op verkleinde schaal getekend worden.

[p. 114]

De grootste diepgang vinden we in onze gewesten bij het Noordzeekanaal (14 m).

Lees dagelijks de waterstand van een rivier af op een der peilschalen die men bij bruggen en elders aangebracht vindt. Maak een grafische voorstelling! Hoe valt het peil als er een lange periode van droogte optreedt?

73. De stroomsnelheid van een rivier met de vlottermethode.

Men kan de stroomsnelheid schatten uit de snelheid van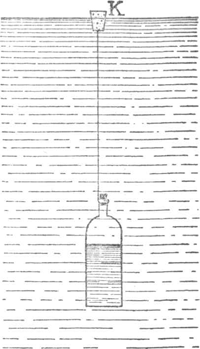

Fig. 58. Vlotter voor de bepaling der stroomsnelheid van een rivier.

takjes, enz. die op het oppervlak drijven. Weldra zal men echter bemerken dat daarbij grote vergissingen kunnen ontstaan, omdat de wind te veel invloed heeft. Daarenboven zou men op die manier nooit de snelheid op verschillende diepten kunnen bepalen.

De volgende werkwijze is eenvoudig en nauwkeurig. Neem een flesje van 50 of 100 cm³, vul het gedeeltelijk met water en zet er een kurk op. Beproef eerst de hoeveelheid water zó te regelen dat het flesje in het water zweeft: dat mislukt, het flesje zinkt of stijgt altijd! Bevestig echter aan de hals een dunne ijzerdraad, en daaraan weer een kurkje K (fig. 58); nu is het gemakkelijk het flesje zó te vullen dat dit kurkje net even boven het oppervlak komt: het evenwicht is nu stabiel (waarom?). - Laat het flesje ergens midden in een rivier los: statig drijft onze vlotter met de stroom mee. Zijn snelheid is die van de laag waarin zich het flesje bevindt, want de weerstand van het kurkje tegen wind of stroom is te verwaarlozen.

Bepaal op die wijze de snelheid op verschillende afstanden van de oevers en op verschillende diepten. Is er geen brug, dan doet u het best een touw van oever tot oever te spannen, zoals uitgelegd is in § 72; een helper staat in een roeiboot bij het touw, een andere 50 m stroomafwaarts. De waarnemer die de tijd bepaalt loopt langs de oever met de drijver mee. Als u genoeg metingen heeft kunt u een doorsnee der rivier op schaal tekenen, en daarin krommen van gelijke stroomsnelheid trekken (fig. 59). De snelheid is in 't algemeen het grootst in het midden van de

[p. 115]

rivier¹⁾; misschien is zij nog iets groter op 10 tot 30 cm diepte dan aan het eigenlijke oppervlak. Hiermee zou samenhangen dat

Fig. 59. Doorsnede van een rivierbedding; gestippeld: de lijnen van constante stroomsnelheid.

drijvende voorwerpen die tot een geringe diepte in het water dompelen, de gemiddelde snelheid aannemen van al de lagen waarin zij zich bevinden, en dus sneller stroomafwaarts bewegen dan het water aan de oppervlakte. De lijn van grootste stroomsnelheid heet de stroomdraad of verhangdraad. Nabij de bodem en langs de oevers is de snelheid geringer door de wrijving tegen de vaste wanden; die invloed neemt geleidelijk naar het midden der rivier af. Bepaal eens de gemiddelde snelheid voor alle punten die vertikaal onder elkaar liggen met de staaf van Cabeo: een eenvoudige houten lat, aan het ondereind omwikkeld met ijzerdraad of bezwaard met lood zó dat zij stabiel vertikaal drijft;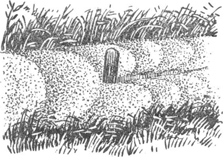

Fig. 60. Eendekroos op een langzaam stromend beekje.

het bezwarende gewicht is van de orde van de helft van het gewicht van de lat. Deze moet voldoende lang zijn om tot niet ver van de bodem in te zinken, veiligheidshalve echter 50 cm er van afblijven. Merk op hoe de staaf als ze drijft schuin voorover helt, en aldus laat zien dat de snelheid boven groter is dan beneden.

Dat de stroomsnelheid in 't midden groter is dan aan de randen, is dikwijls zonder enige meting mooi waar te nemen aan het eendenkroos dat op een sloot drijft; of aan afgevallen wilgeblaadjes die zich in bogen rangschikken. De invloed van een paal is bijzonder duidelijk (fig. 60).

Als er in een beek groenwieren voorkomen, die aan rietstengels en andere ondergedompelde voorwerpen hangen, kan men zien hoe ze als evenveel windvaantjes overal de stromingsrichtingen aanwijzen: 't lijkt wel een kaart van de zeestromingen! Vooral waar de stroom zich splitst is het beeld zeer fraai.

Langs de straatweg die over de Wageningse berg loopt, liggen

1) Bij een bocht, meer aan de buitenkant.

[p. 116]

lange, open rioleringen. Het was merkwaardig om de felle waterstroom na te gaan die zich daarin gevormd had na een zware regenbui. Vooreerst zag men hoe van beide zijwanden een stelsel schuine strepen uitging, dat we nog verder zullen beschrijven (§ 89, fig. 85). Maar daarenboven kon men opmerken hoe schuimbellen, die zich gevormd hadden, precies in de middendraad bewogen, keurig op een rijtje, over de gehele lengte van het kanaal. Blijkbaar was daar de stroming het sterkst, en werden de bellen vanzelf daar naartoe gezogen.

74. De buis van Pitot.

Het is een eenvoudige glazen buis, rechthoekig omgebogen en aan een uiteinde lichtelijk vernauwd. Ze wordt in de rivier gehouden

Fig. 61. Het bepalen der stroomsnelheid met de buis van Pitot.

op de wijze die fig. 61 aangeeft. Het aankomende water stijgt door zijn vaart een eindje h in de glazen buis, net zo lang tot de kinetische energie van het stromende water geheel is overgegaan in potentiële energie van de vloeistofzuil(vergelijkmet een opwaarts geworpen steen!) De evenwichtsvoorwaarde is dus: ½mv² = mgh, of v = √2gh.

De aflezing van het hoogteverschil h, tot hetwelk het water gestegen is boven het normale peil, kan vrij goed met behulp van een spiegeltje geschieden, dat half in het water dompelt, onder een helling van 45^o. Iets gemakkelijker werken we, wanneer we de Pitot-buis met een eindje gummislang verbinden aan een omgebogen glazen buisje, dat als manometer dient: in de U-vormige bocht brengen we een weinig water, en we zien hoe dit vloeistofzuiltje zich verplaatst zodra de Pitot-buis in het water wordt gehouden. Drie gummiringetjes worden over de glazen buis geschoven; het eerste (A) dient om nauwkeurig aan te geven hoe diep we de buis in het stromende water dompelen, zodat dit

[p. 117]

steeds op dezelfde wijze geschiedt; het tweede (B) geeft het peil in de manometer aan, als de Pitot-buis in rustend water wordt gehouden; het derde (C) geeft het peil aan, als men de buis in de stromende vloeistof tegen de stroom in keert. Men vindt voortdurende kleine wisselingen in de stijghoogte, tengevolge van het onregelmatige stromen der rivier; het is zaak, de ringetjes B en C zo goed mogelijk op het gemiddelde peil in te stellen.

De meting der stroomsnelheid met ons eenvoudige toestelletje is zeer vlug uit te voeren, maar zij wordt slechts voldoende nauwkeurig bij snelheden van tenminste 50 cm/sec; h is dan 12 mm. Vergelijk uw meetresultaat met dat, uit de vlottermethode verkregen.

Op deze wijze bepaalde Pitot in 1723 de snelheid van de Seine onder de Pont Royal te Parijs. De Pitot-buis is nog steeds een der meestgebruikte instrumenten voor de bestudering van vloeistof- of gasstromen. De juiste bepaling van de ongestoorde, statische druk is één der grote moeilijkheden die men daarbij te overwinnen heeft.

75. Waterafvoer van een rivier.¹⁾

1. Om te schatten hoeveel water per sekunde door een rivier vervoerd wordt, is het voldoende de snelheid even onder het oppervlak op enkele punten van de bedding te bepalen, en daarvan het gemiddelde V₀ te nemen; men kiest de punten nooit te dicht bij de oevers. De gemiddelde snelheid over de gehele doorsnede der rivier is dan volgens de ervaring ongeveer: V = 0,86 V₀. Vermenigvuldigt men die snelheid met het oppervlak van de doorsnede, dan vindt men de hoeveelheid water die per sekunde voorbijstroomt; men drukt die altijd uit in m³ per sekunde.

Nog eenvoudiger is het, alleen de maximale snelheid te bepalen die even onder het oppervlak optreedt; in een recht stuk der rivier treft men die natuurlijk in het midden aan. De verhouding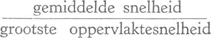



hangt af van de aard der bedding, en bedraagt volgens de ervaring:

0,51	grint met gras en riet;	0,74	leem en zand;
0,69	grint;	0,81	hout, beton.

In de praktijk neme men voor ons land 0,7.

Tenslotte kan men de gemiddelde diepte H van de rivier door peiling bepalen, en dan de snelheid meten op een diepte

1) B.J. Kerkhof, Practische Hydrometrie (Amsterdam, Ahrend).

[p. 118]

0,62 H: de snelheid die men daar aantreft is de gemiddelde snelheid V van de rivier.

2. Andere empirische formules geven schattingen van de gemiddelde snelheid en dus van het watertransport zonder dat rechtstreekse metingen nodig zijn. Een der meest bekende luidt:
V = c√RJ.

Hierin betekenen:
J = het verhang van de rivier, af te lezen van een stafkaart met hoogtelijnen: men deelt het hoogteverschil tussen twee punten door hun afstand, langs de rivier gemeten. Zo bedraagt het verhang van de Rijn:

Emmerik - Nijmegen	12,0 cm/km	Bommel - Gorkum	8,6
Nijmegen - Bommel	10,8	Gorkum - Moerdijk	5,0

Men ziet dat het in 't algemeen afneemt, naarmate men de monding nadert.

;

deze ‘natte omtrek’ is de omtrek van het deel der beddingdoorsnede waar water aan grond raakt. Bij ondiepe wateren is R ongeveer gelijk aan de gemiddelde diepte.

c, een empirische constante, is een maat voor de gladheid der wanden; zij bedraagt:

voor rivieren tussen stenen muren	80
voor kanalen	51
voor rivieren tussen aarden oevers	40
voor rivieren met veel klei	30.

Deze waarden gelden slechts als R gerekend wordt in meters, V in meters per sekunde; J is natuurlijk een onbenoemde breuk (bv. meters per meter).

Andere formules gelden alleen voor natuurlijke wateren:

V = 44R^⅔J^½.	{ V = 31HJ^½ ... H < 1,50 m
V = 25(1 + 0,5√R)√RJ	{ V = 34H^¾J^½... 1,50 m < H < 6 m
	Hierin is H de gemiddelde diepte van de bedding.

Bepaal volgens die verschillende formules en methoden het watertransport van een rivier en vergelijk de uitkomsten onderling!
Zoek een punt waar twee rivieren samenvloeien; bepaal het watertransport van elk, en zie of het watertransport van het geheel gelijk is aan de som van dat der twee delen (Continuïteitsbeginsel der hydrodynamica!)
Men zou kunnen beproeven de snelheid van het water in een rivier te

[p. 119]

vergelijken met de snelheid die het onder een brug heeft, waar de doorsnede van de bedding geringer is. Het is de vraag of de onregelmatige wervelingen het verkrijgen van goede uitkomsten niet zullen bemoeilijken.
Onderzoek hoe het watertransport afhangt van de hoogte van de waterspiegel. Als het peil stijgt blijft het verhang hetzelfde, maar de wrijving tegen de wanden neemt af.

3. Sommige rivieren zijn afgedamd; het waterpeil stijgt dan, tot er evenveel over de stuw stroomt als wat de rivier aanvoert. Stel b de breedte der rivier, h de afstand van de vloeistofspiegel benedenwaarts gemeten (fig. 53). Volgens de wet van Torricelli is op een diepte h de uitstroomsnelheid √2gh; door een strook op deze diepte, dh hoog en b breed, gaat er per sekunde b√2gh dh; door de gehele doorsnede van totale diepte h gaat er b√2gh dh = ⅔hb√2gh. Ongelukkig moet er alweer een empirische correctiefaktor bij, voor wervelvorming enz., zoals dat zo dikwijls in de leer der

Fig. 62. Profiel van een rivier bij een stuw.

stromende vloeistoffen het geval is! Die faktor is ongeveer 0,60 voor een stuw ‘met vrije straal’ (§ 76). Tenslotte wordt dus het watertransport:
0,40 bh √2gh.

De hoogte h van de waterspiegel boven de stuw is dus een rechtstreekse aanwijzing voor het watertransport.

Zoek in uw streek een afgedamde rivier en vergelijk de uitkomst dezer methode met de vorige! Bij een grote stuw vrage men de hoogte h aan den wachter. Grote stuwen komen voor te Borgharen, Linne, Roermond, Belfeld, Sambeek, Grave, Lith.

76. Uitstromingsvormen bij een stuw.¹⁾

De hoogte van de opgestuwde waterspiegel boven de dam noemen we h; die hangt af van het watertransport (§ 75). Het verschil van hoogte der waterspiegels vóór en na de dam noemen we V; dit hangt enerzijds af van het watertransport, anderzijds van het verval en de weerstand stroomafwaarts. Stel nog D de hoogte van de dam.

De volgende schone verscheidenheid van uitstromingsvormen kan nu voorkomen (fig. 63).

1) Enz. d. mathem. Wiss. IV.

[p. 120]

Fig. 63. Uitstromingsvormen bij een stuw.

[p. 121]

77. Rivier of stortbeek.

Deze onderscheiding is geen kwestie van letterkundige smaak, maar heeft een scherpe wetenschappelijke betekenis! Bij een rivier is het verval van de bodem kleiner dan g / c²; bij een stortbeek is het verval groter dan g / c².

De grootheid c is onze constante voor de gladheid der wanden,

Rig. 64. Verschil tussen de stuwingsvormen bij een rivier en bij een stortbeek.

die 30 tot 80 bedraagt (§ 75). Het ‘kritische verval’ is dus van de orde 0,4%.

Echte stortbeken hebben we in ons land niet veel, maar na een zware regenbui kunnen wij er zien ontstaan, waar de regen afgevoerd wordt door de tramrails, door de greppels van hellende straten. Bij watermolens, bij fabrieken vinden we soms open waterleidingen met een flinke helling.

Om uit te maken of men met een rivier of met een stortbeek

[p. 122]

te maken heeft, is het al voldoende een plank dwars op de stroom in het water te houden; ze mag niet àl te kort zijn, anders zouden de wervels aan de uiteinden de waarneming hinderen. Al naarmate we die plank slechts een weinig in het water dompelen, of dieper, of ze helemaal onder water houden, ontstaan typisch verschillende stuwingsvormen, afgebeeld in fig. 64.

Waarvandaan komt nu dat merkwaardige verschil, waarom is g / c² juist die kritische grens? Wel als het verval van de grond



is, is de stroomsnelhied (volgens § 75):



; en voor niet te diep water is R niet zeer verschillend van de diepte H. Zodat het erom gaat of de snelheid van het water kleiner of groter is dan √gH. Maar dit is juist de snelheid van de snelste golf die in een rivier van diepte H kan ontstaan (§§ 91, 100). Ons kritisch verval is dus eenvoudig hierdoor bepaald: bij een rivier lopen de golven sneller dan het water; bij een stortbeek, langzamer. Daarom kan de plank geen echte golven vormen in een stortbeek: zij verwekt slechts een ‘enkelvoudige golf’ (§ 100).

78. Het ontstaan van waterwervels.

Een snelvlietende beek in de Veluwe. Zomerzon schijnt door het klare ondiepe water op de heldere zandbodem. Alle stromingen

Fig. 65. Beweging van twee waterwerveltjes om elkaar.

tekenen zich prachtig op de bodem af als lichte of donkere patronen, blijkbaar doordat ze kleine verhevenheden of uithollingen van het wateroppervlak veroorzaken. Voortdurend vormen zich werveltjes, ieder daarvan geeft een donker schaduwvlekje van enkele centimeters middellijn, omgeven door een lichte ring¹⁾. Vele heel zwakke werveltjes worden aldus zichtbaar, waarvan men anders niets gemerkt zou hebben. Men kan mooi zien hoe verrassend lang ze blijven bestaan, en hoe ze om elkaar draaien volgens de wetten der hydrodynamica (fig. 65).

Dompelt men een plankje in de beek, loodrecht op de stroomrichting, dan ziet men op het schaduwbeeld hoe zich daarachter een dubbele wervel vormt; beide verenigen zich in het midden tot een ‘terugstroom’, die het plankje van achteren’ treft (fig. 66).

1) Vgl. Science, 72. 478, 1930.

[p. 123]

Belangrijk is ook het beeld dat ontstaat als men het plankje schuin op de stroomrichting houdt (fig. 66). De aankomende stroom splitst zich asymmetrisch, het verdelingspunt ligt altijd

Fig. 66. Wervels achter een plankje.

dichter naar de voorste rand toe. Achter die vóórrand vormt zich een grote wervel, die stationair blijft ten opzichte van

Fig. 67. Wervelweg volgens von Kármàn.

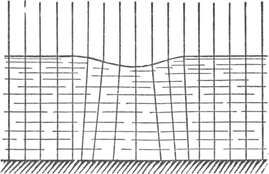Fig. 68. Breking van het licht door een waterwerveltje.

het plankje; meer naar achteren toe, aan de lijzijde, ontstaan er kleine werveltjes, telkens loslatend en wegdrijvend, terwijl nieuwe ervoor in de plaats komen. De terugstroom treft nu het plankje even ver van de achterrand als het verdelingspunt aan de

[p. 124]

loefzijde verwijderd was van de vóórrand. - Dit stroomlijnenbeeld geeft een prachtig model van de vloeistofbeweging om een gierpont; het is ook het beeld dat we leerden kennen toen we de windstroming om het zeil van een zeilboot onderzochten (§ 65).

Achter een potlood dat ik vertikaal in het water houd, ontstaan de wervels afwisselend aan de linker- en aan de rechterzijde, telkens loslatend en door nieuwgevormde vervangen, samen een beroemde stromingsfiguur vormend: de wervelweg van Von Kármàn (fig. 67) (vgl. II, § 51).

Het tot stand komen van het schaduwbeeld der wervels is gemakkelijk te verklaren uit de breking der lichtstralen aan het wateroppervlak (fig. 68). Waar het oppervlak hol is, wordt de lichtbundel uitgespreid en vormt zich schaduw; waar het bol is, worden de stralen verzameld en zien we een grotere helderheid.

Op andere plaatsen kan men de waterwerveltjes beter in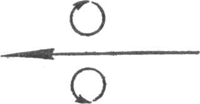

Fig. 69. Vorming van waterwervels aan de beide kanten van een roeispaan.

teruggekaatst licht waarnemen, als men bijvoorbeeld op die plaats de grenslijn weerspiegeld kan zien tussen een donker gebouw, een brug, een boomkruin, en de heldere hemel. De kleine uithollingen van het oppervlak boven elk werveltje tekenen zich dan helder af tegen donkere grond, of omgekeerd. Overal waar een rivier plotseling vernauwt of waar een bruggehoofd vooruitsteekt kan men ze zien ontstaan. Achter een uitstekend takje van een waterplant vormt zich ook alweer een wervelweg.

Merk bij het roeien op, hoe elke roeispaan telkens bij een riemslag twee werveltjes in het water maakt, die tegengesteld draaien, en die soms in hun centrum een verscheidene centimeters diepe uitholling van het wateroppervlak vertonen (fig. 69).

Op grote schaal vormt zich een wervel achter elk der kribben van onze rivieren (fig. 70).

De waterwervels die we hebben waargenomen leren ons een geheel andere bewegingswijze van het water kennen dan die welke we gewoonlijk aan een stromende vloeistof toeschrijven. Hoe meer men de beweging der vloeistoffen bestudeert, hoe meer men doordrongen wordt van het fundamentele verschil tussen:

a) de laminaire stroming, waarbij de vloeistofdeeltjes zich

[p. 125]

ogenschijnlijk alle evenwijdig aan dezelfde richting bewegen (al is het niet uitgesloten, dat er een ‘mikroskopische’ werveling plaats vindt);

b) de turbulente stroming, waarbij duidelijk zichtbare onregelmatige wervelingen optreden.

Fig. 70. Vorming van grote wervels achter de kribben ener rivier.

Osborn Reynolds, die het grote belang van dit onderscheid het eerst in het licht stelde, heeft theoretisch aangetoond dat elke vloeistof die enige viskositeit bezit stabiel laminair zou stromen, als de invloed van de wanden er niet was. Die zijn het die wervels doen ontstaan, en die de stroming in een turbulente omzetten¹⁾.

In wervelend water is de weerstand van een schip altijd groter dan wanneer de waterdeeltjes in evenwijdige banen stromen. Elk zeiler weet, hoeveel moeilijker hij vooruitkomt in het kielzog van een tegenstrever, niet alleen omdat die hem de wind uit de zeilen neemt, maar ook omdat de waterweerstand groter is geworden. Met ruim 50% kan de weerstand door deze oorzaak toenemen.

1) Reynolds steunde daarbij op een merkwaardige waarneming in 't vrije veld; vgl. Philos. Trans. 1883; Papers, 2, 58. - Proc. R. Inst. 35, 84, 1885.

79. Draaiingszin van de waterwervels in een rivier.²⁾

Er is een heel merkwaardige theorie betreffende de draaiingszin van de waterwervels die in snelstromende rivieren ontstaan. De grote meerderheid daarvan zou tegengesteld aan het uurwerk draaien, net zoals de barometrische depressies! En dit zou zelfs voor 90% der wervels het geval zijn! Men neemt voor de statistiek liefst de goed gevormde wervels, en telt die niet mee welke veroorzaakt zijn door brugpijlers, grote rotsblokken enz.; u voelt dat er hier een groot gevaar schuilt, en dat de waarnemer moeilijk zal kunnen vermijden een partijdige keuze te doen,

De oorzaak van die voorkeursrichting zou men moeten zoeken in de aswenteling der aarde: het is welbekend dat deze aanleiding

2) J. Brunhes, C.R. 138, 915, 1904.

[p. 126]

geeft tot de versnelling van Coriolis, waardoor bewegende lichamen op het noordelijk halfrond naar rechts afwijken; uit

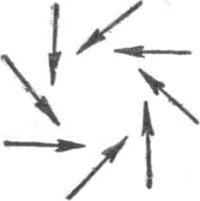Fig. 71. Het ontstaan van wervels door de versnelling van Coriolis.

fig. 71 kan men zien dat de waterdeeltjes die naar het drukminimum van de wervel toestromen aldus een wervelende beweging krijgen. Het zou dus voldoende zijn een blik te werpen op een snelvlietende rivier, een bergstroom bijvoorbeeld, om een proefondervindelijk bewijs van de draaiing der aarde te verkrijgen!

Jammer genoeg leert een kleine berekening, dat de krachten van Coriolis zeer gering zijn, en het schijnt wel zeker dat zij in het beschouwde geval geen praktische betekenis hebben. Vermoedelijk is het schijnbare overheersen van een bepaalde draaiingsrichting niets anders dan zelfbedrog; men zou eens kunnen nagaan, of de draaiingsrichting omgekeerd wordt gevonden in het zuidelijk halfrond.

80. Vloeistofweerstand. Stroomlijnvorm.

Wanneer men een lichaam door het water sleept, voelt men een weerstand, die ten dele ontstaat door wrijving van het water tegen het lichaamsoppervlak, ten dele door de golven die zich achter het gesleepte lichaam uitbreiden. Men zou kunnen menen, dat althans deze laatste weerstand bepaald wordt door de doorsnede van het lichaam, dwars op de voortbewegingsrichting.

Fig. 72. Luchtweerstand van verschillend gevormde lichamen met gelijke dwarse doorsnede.

Niets is minder waar! Voor 6 omwentelingslichamen van gelijk dwarsoppervlak, in fig. 72 voorgesteld, lopen de weerstanden uiteen van 8 tot 126!

Onder deze vormen is de stroomlijnvorm verreweg de gunstigste: het is een soort visvorm, die met het dikste uiteinde stroomopwaarts gericht moet worden. Het gaat er dus niet om, dat de aankomende waterstroomstralen geleidelijk opengebogen worden; veel belangrijker is, dat de wervelvorming aan de achterzijde zoveel mogelijk vermeden wordt. - Een enkele maal

[p. 127]

vertoont de natuur zelf ons het model van een dergelijk stroomlijnenlichaam. Het komt vóór, dat een ijsschots blijft vastzitten aan de bodem van een rivier, en dat ze langzamerhand door het voorbijstromende water bijgelikt en gefatsoeneerd wordt, tot ze de vorm van kleinste weerstand heeft bereikt: men krijgt dan prachtige visvormen. - Of een zandbank wordt op dergelijke wijze door de stroming vervormd. - Of een hoop zand of sneeuw, om een heggetje verzameld, eindigt met de visvorm aan te nemen (§ 120). - De vissen zelf, de kikkervisjes, de walvissen en tal van andere waterdieren vertonen de stroomlijnvorm, als prachtige aanpassing aan het leven in het water.

81. Ebbe en vloed.¹⁾

Het water van de zee, tweemaal daags rijzend en tweemaal daags terugwijkend, vertoont ons een groots en indrukwekkend schouwspel. Het leven aan het strand is voor een goed gedeelte door de wisseling van eb en vloed bepaald, en vanzelf komt de wens bij ons op, die waterbeweging nauwkeuriger te onderzoeken. Het is mogelijk dat dit het best zal gelukken van op een pier; of in een haven, waar de golfslag uitgedempt is en

Fig. 73. Het bepalen lan het peil der zee, voor het onderzoek van ebbe en vloed.

men allicht bij een brug of bij een sluis peilschalen zal aantreffen. Maar te Zandvoort, waar ik gelegenheid had enkele eenvoudige waarnemingen uit te voeren, was ik niet in zulke bijzonder gunstige omstandigheden; en vermoedelijk zal dit evenmin het geval zijn voor de meeste lezers, die dus wellicht willen horen hoe men zich gewoon aan 't strand behelpen kan (fig. 73).

1) Zie het aardige maar verouderde populaire boek: Time and Tide, door R.S. Ball (London 1889). - F. Hopper, Hdb. d. Experimentalphysik, XXV, 687, 1931. - H. Thorade, Ebbe und Flut (Hamburg, 1941).

[p. 128]

Hoe rustiger de zee, hoe beter. We verschaffen ons een stokje van 1-2 m lengte (gordijnrol), en zetten daar grove, duidelijke strepen op, met afstanden van 10 cm; de 5 cm-streepjes worden lichter aangegeven. Nu maken we gebruik van de rijen paaltjes, die aan de meeste badplaatsen het strand in verschillende stukken onderverdelen¹⁾. We kiezen het laatste paaltje dat met zijn voet nog aanhoudend in het water staat, op een punt dus waar

Fig. 74. Ebbe en vloed, met eenvoudige hulpmiddelen waargenomen te Zandvoort.

het waterlaagje zeer ondiep is. De top van dit paaltje zal nu het vaste peil zijn, ten opzichte waarvan wij telkens de stand van het water aflezen. Zet uw stok naast het paaltje, druk hem in het natte zand tot hij vast staat, en tot een gehele decimeterstreep zich bij de top van het paaltje bevindt. Het aflezen van het peil van het water is niet gemakkelijk, omdat elke golf het doet stijgen als ze aankomt en doet dalen als ze terugvloeit. Kies het ogenblik waarop de stroming omkeert; als u dit voor enkele achtereenvolgende golven doet, zult u merken dat zelfs bij niet zeer rustige zee het gemiddelde peil verrassend standvastig is (bedenk daarenboven dat een fout van 5 cm nog niet veel hindert!).

Dergelijke metingen doen we nu ongeveer om het kwartier

1) In geval die mochten ontbreken, werkt men op de wijze, aangegeven in § 83.

[p. 129]

of om het halve uur. Weldra bemerken we dat het peil verandert; wellicht daalt het, straks is het misschien al zoveel lager, dat we ons paaltje niet meer gebruiken kunnen en naar een ander moeten overgaan. Maar het is heel gemakkelijk de toppen der paaltjes op elkaar te betrekken, door te mikken op de kim en het hoogteverschil af te lezen; dat gaat heel scherp! (Zie fig. 73). Zo krijgen we dus telkens enige metingen aan elk paaltje, tellen er een vast getal bij of trekken het af om te herleiden op het éne paaltje dat wij als vast peil hadden uitgekozen, en maken een grafische voorstelling van het geheel. Het is zaak, tenminste 12 uur vol te houden, en niet op te zien tegen het telkens uittrekken van schoenen en kousen, noch tegen de belangstelling der overige badgasten, die u wel voor een ambtenaar van de Waterstaat zullen houden!

De kromme lijn die we verkrijgen is buitengewoon belangwekkend (fig. 74). Nu pas krijgen we inzicht in de ware peilverandering van de zeespiegel, terwijl we anders voortdurend misleid werden door de golvende zandbanken en zwinnen van het strand. - Het verschil in peil tussen hoog water en laag water heet het tijverschil; in het door ons gemeten geval bedroeg het 1,55 m, wat aardig uitkomt met fig. 76 b. Verwar deze benamingen niet met eb en vloed, die betrekking hebben op het dalen of op het stijgen van de waterspiegel!

Vervolgens zien we, dat de kromme sterk afwijkt van een sinuslijn. Laag water valt niet midden tussen twee maxima; het water daalt gedurende ongeveer 9 uur, en stijgt in slechts 3 uur! Vandaar het spannende ‘opkomen van de vloed’, als de

Fig. 75. De dubbele vloedgolf welke de Maan op Aarde doet ontstaan (de hoogte van de golf is sterk overdreven).

zandkastelen met heldenmoed verdedigd worden tegen de aanstormende golven. Merk ook op dat het water geruime tijd in zijn laagste stand blijft vóór het merkbaar gaat wassen, terwijl hoog water slechts even bereikt wordt. - Dit verloop van het getij verschilt van de ene kustplaats tot de andere.

Tenslotte geeft onze kromme ons de gelegenheid, nader in te gaan op de oorzaak der getijbeweging. - Men leert in de

[p. 130]

sterrekunde hoe de getijden in hoofdzaak ontstaan tengevolge van de aantrekkingskracht van de Maan (fig. 75). Maan en Aarde draaien om hun gemeenschappelijk zwaartepunt; voor het centrum der Aarde (B) heffen aantrekkingskracht en middelpuntvliedende kracht elkaar net op. Het water bij A echter bevindt zich dichter bij de Maan en wordt sterker aangetrokken dan het punt B; het water bij C bevindt zich verder van de Maan en wordt zwakker aangetrokken, zodat daar de middelpuntvliedende kracht overheerst. Er ontstaat aldus een dubbele vloedgolf, en in een bepaald punt van de Aarde moet men in één etmaal tweemaal vloed en tweemaal ebbe waarnemen. Men zou verwachten hoog water te zien op het ogenblik dat de Maan zoveel mogelijk ‘boven ons hoofd’ staat, dus in het Zuiden; of (onzichtbaar) ‘onder onze voeten’, in het Noorden. Dit is het geval:

	bij nieuwe Maan, om 12^h of 24^h;
7 dagen ↕		↕ 6 uur
	bij eerste kwartier, om 18^h of 6^h;
7 dagen ↕		↕ 6 uur
	bij volle Maan, om 24^h of 12^h;
7 dagen ↕		↕ 6 uur
	bij laatste kwartier om 6^h of 18^h.

Laten wij nu eens door eigen ervaring nagaan of het uitkomt! De kromme welke wij hebben waargenomen (fig. 74) heeft betrekking op 23 Augustus 1936. Een willekeurige almanak leert ons, dat de Maan op 25 Augustus, 6^h voormiddag, de schijngestalte van het eerste kwartier vertoonde; zij moest zich dus op 23 Augustus ongeveer om 16^h 45^m in het Zuiden bevinden, dit is te 17^h 45^m zomertijd. Dit komt helemaal niet uit met de getijkromme! Hoog water is in werkelijkheid pas om 19^h 30^m ingetreden.

Deze waarneming is geen uitzondering, zij is integendeel de regel. Het hoog water komt in 't algemeen verscheiden uren nadat de Maan in 't Zuiden (of in 't Noorden) stond! Deze vertraging t.o.v. de Maan heet het maanvloedinterval; en het maanvloedinterval omstreeks volle of nieuwe Maan is de haventijd der betreffende kustplaats. Ieder die een tijdje aan 't strand verblijft moest zijn haventijd kennen, want daarmee kan men al aardig benaderd de ogenblikken van hoog en laag water voorspellen. Als we deze bepalingen op verschillende dagen uitvoeren, vinden we dat het tijdsverschil niet altijd nauwkeurig gelijk is aan de haventijd, maar soms iets korter, soms iets langer; gemiddeld is er dus een correctie aan te brengen. -

[p. 131]

Bovenste regel: ogenblik waarop de Maan in 't Zuiden staat (van middag of middernacht gerekend). Onderste regel: de aan te brengen correctie.

0	1	2	3	4	5	6	7	8	9	10	11	12 uur
+32	+17	0	-17	-32	-43	-46	-33	0	+33	+46	+43	+32 min

Deze correctie heet: de halfmaandelijkse ongelijkheid; zij is te

Fig. 76a. De haventijden langs de Nederlandse kust.

wijten aan de Zon, die evenals de Maan getijden veroorzaakt.

Te Zandvoort is de haventijd ongeveer 2^h 40^m. Op 23 Augustus ging de Maan te 16^h 45^m door het Zuiden; het moest dus vloed zijn te 16^h45^m + 2^h40^m - 0^h43^m = 18^h 40^m (of 19^h40^m zomertijd). Dit klopt nu heel aardig met de waarneming.

Krachtiger dan anders moesten de getijden zijn bij volle en nieuwe Maan, als de werking der Zon die van de Maan komt

[p. 132]

versterken; in werkelijkheid zijn ze dat een paar etmalen later: het is dan springvloed. De nieuwe eigenaardige vertraging die hier optreedt noemt men de ouderdom van het getij. Bij springtij is het tijverschil te Westkapelle 0,50 m groter dan gewoonlijk, elders 0,30 m.

Wat is nu de verklaring voor die vertragingen? Men zou kunnen denken aan de invloed van de Zon. Inderdaad is deze

Fig. 76b. Het gemiddelde tijverschil langs de Nederlandse kust, in meters.

zeer merkbaar; maar de eigenlijke oorzaak is dit niet, want bij volle en nieuwe Maan kan de Zon alleen de werking van de Maan verzwakken of versterken, maar niet van richting doen veranderen; en hetzelfde geldt ook bij eerste en laatste kwartier. - Op de juiste verklaring komt men, als men weet dat de haventijd van kustplaats tot kustplaats verandert. In Zeeland is het 1 uur, bij IJmuiden 3 uur, bij Texel al 7 uur (fig. 76a)! De schommeling van eb en vloed geschiedt dus wel overal in

[p. 133]

de periode die de Maan haar opdringt, maar phase en amplitude worden door de eigentrillingen der oceanen bepaald: waar

Fig. 76c. De getijgolven in de Noordzee, naar R. von Sterneck. De cijfers geven de tijdsverschillen in uren aan.

een oceaanbekken de geschikte afmetingen heeft om met de getijschommelingen mee te trillen, ontwikkelt zich de eb- en vloedbeweging het sterkst. De Noordzee is een binnenzee, die

[p. 134]

geen ‘eigen’ getijden heeft, ze krijgt echter door haar noordelijke verbinding met de Atlantische Oceaan een getijstuwing, die telkens op ingewikkelde wijze in het Noordzeebekken rondloopt (fig. 76c).

Het zal hieruit duidelijk zijn, dat het geheel theoretisch vooruitberekenen van de bijzonderheden die we bij de getijverschijnselen waarnemen, slechts in de eenvoudigste gevallen mogelijk is. Uit lange reeksen getijwaarnemingen kan men echter bepaalde constanten afleiden, met behulp waarvan voor de komende jaren zeer nauwkeurige getijtafels te berekenen zijn.

82. Zeebeer.

In zeldzame gevallen ontstaat ook in onze zeeën soms een plotselinge stijging of daling van het water, buiten alle getijregelmaat om. Zo is het in 1924 voorgekomen dat de zee aan onze kust ineens over 1,60 m in 10 minuten steeg, en dan weer snel over 1 m daalde!¹⁾

Het is mogelijk dat zulke verschijnselen, die aan andere kusten veelvuldiger voorkomen, aan hozen of onweders toe te schrijven zijn, soms ook aan aardbevingen.

Merk op, of de evenwichtsstoring met een stijging of met een zuiging begint. In het tweede geval blijft het daar niet bij, doch volgen er altijd nog verscheidene golvingen: want een enkelvoudige golfverheffing kan zich onveranderd voortplanten, een golfdal echter vervormt zich (§ 100).

1) P.M. van Riel, De Zee, 989, 1924.

83. De beweging van het grondwater.

Een verblijf aan 't strand is een goede gelegenheid om te onderzoeken hoe het zeewater door het zand dringt, en op die wijze een voorbeeld te hebben van de stroming van grondwater.

Spit een kuil in het vochtige zand, op enkele meters van de lijn tot waar de verste uitlopers van de golven op dit ogenblik komen. Zodra een zekere diepte bereikt is, begint er water onder in de kuil te komen. Druk in het zand van de bodem een stokje, waarop hele en halve decimeters met dikke strepen aangegeven zijn (fig. 77). U ziet dat het water in de kuil langzaam stijgt en tenslotte een grens bereikt.

Klaarblijkelijk stond het water in het naburige zand tot op deze hoogte; door het wegnemen van het zand van de kuil is tegelijk

[p. 135]

het water tussen de zandkorrels weggehaald: er ontstaat een stroming om het drukverschil te vereffenen, maar die gaat langzaam, omdat het water door de nauwe tussenruimten tussen de zandkorrels moet dringen.

Maak daarnaast snel een tweede kuil, tenminste even diep, en verbind hem met de eerste: het peil van het water zakt eerst, maar weldra herstelt het

Fig. 77. Een kuil, in het strand gegraven, vult zich met grondwater.

zich. Gooi enige scheppen aarde in het water: het peil stijgt eerst boven het normale, maar zijgt dan langzaam weg tot dit laatste weer bereikt is. Zou het water in zulk een kuil de getijbeweging meemaken die de zee ons vertoont? - Op een dag dat de zee nogal rustig is, graven we een flinke kuil, een meter of twee landwaarts van de hoogwatergrens. Liefst beginnen we ongeveer één uur voor het ogenblik van hoog water, en we graven, tot er een of twee decimeters water in de kuil staan. We zetten naast de kuil een plankje, waarvan de bovenrand A ons zal dienen als willekeurig maar vast peil (fig. 78). We bukken ons tot we die bovenrand op de horizon zien, en lezen op een duimstok van 1 meter af,

Fig. 78. Het meten der beweging van het grondwater gedurende eb en vloed.

op welke diepte BC het water in de kuil zich onder ons vast peil bevindt. Om de hoogte van het peil der zee af te lezen, nemen we een lange stok DE, insgelijks in decimeters en halve decimeters verdeeld, en duwen hem in 't natte zand, waar de laatste uitlopers der golven nog komen. Het is meestal gemakkelijk hem zover te duwen tot een gehele deelstreep precies op de hoogte van 't vaste peil staat. De meting bestaat nu in het geregeld aflezen van de afstanden BC en DE; het zal nodig

[p. 136]

zijn, af en toe de stok DE te verzetten, maar met behulp van het vaste peil A en de kim zijn de verschillende standen van de maatstok altijd op elkaar te betrekken.

In fig. 79 ziet men een dergelijke reeks waarnemingen grafisch voorgesteld. Beschouwen wij vooreerst het peil der zee: we zien hoe het opkomende water zijn hoogste stand bereikt, en daarna begint te dalen; de stijging is steil, de daling veel langzamer (vgl. § 81). Nu het water in de kuil! Dit vertoont ook een snelle stijging en een langzame daling; maar aanzienlijk vertraagd ten opzichte van het getij der zee: het ogenblik van

Fig. 79. De vloed, met eenvoudige hulpmiddelen gemeten: a) voor de zee, b) voor het grondwater.

hoogwater bijvoorbeeld is een vol uur verschoven. Daarenboven is de amplitude van de schommeling geringer; de hoogste stand blijft 18 cm beneden die van de zee.

We hebben geen waarnemingen omstreeks het ogenblik van de laagste stand, maar als we schatten dat het water op dat ogenblik 12 cm boven het laagste peil der zee staat, zou het tijverschil in de kuil 1,25 m bedragen tegen 1,55 m in zee (vgl. § 81). De vertraging en de demping der getijbeweging in het zand zijn natuurlijk te verklaren door de wrijving die het water in de capillaire ruimten tussen de zandkorrels ondervindt; zijn stroming wordt daardoor in hoge mate belemmerd. Zo komt het, dat water in de kuil nu eens hoger, dan weer lager staat dan het peil van de zee. - Merk op dat bij hoog water, als het zeewater bijna tot de rand van de kuil spoelt, het water daar nog wel 25 cm beneden zeepeil staat.

Verenig u met andere waarnemers; graaft een reeks kuilen op verschillende afstanden van de hoogwatergrens en leest gedurende een zo lang mogelijke tijd het peil van het water op die verschillende punten af.
Vergelijk met II, § 67.

[p. 137]

87. De plemyrameter.¹⁾

Dit is een eenvoudig maar uiterst gevoelig toestel, bestemd om kleine veranderingen in het peil van een meer of van een rivier te bestuderen. Het is uitgevonden door Forel, een geboren natuuronderzoeker van 't vrije veld; en het was hem een waardevol hulpmiddel bij zijn onderzoekingen over de eigentrillingen van meren.

Een waskom van 25 cm middellijn wordt op een geschikte, lage plaats van de oever ingegraven, tot de bodem enkele cm onder het peil van het water staat (fig. 80). Met een gummislang, die men eerst geheel met water vult en die dan als hevel dient,

Fig. 80. Onderzoek naar kleine schommelingen in het waterpeil met de plemyrameter van Forel.

verbindt men de waskom met het meer; elke peilverandering heeft nu ten gevolge, dat er water door de gummislang naar of van de waskom stroomt. Om die stromingen goed te kunnen waarnemen, verdelen we de gummislang in tweeën, en schakelen er een glazen buis in van ongeveer 30 cm lengte en 1 cm middellijn. In die buis komt een index, bestaande uit een bolletje was, waarin enkele zandkorrels gekneed zijn die hem bezwaren, tot hij bijna precies zweeft (zorgvuldig regelen!); twee koperdraadjes, spiraalsgewijs gewonden en aan beide uiteinden in de buis geschoven, beletten dat de index te ver meegesleept wordt. Zodra nu het peil verandert en het water in de buis gaat stromen, beweegt de index naar het ene of het andere uiteinde, en blijft daar zitten zolang de stroming duurt. Het toestelletje is buitengewoon gevoelig, hoogteverschillen van 1 mm worden al duidelijk aangewezen.

Met de plemyrameter kan men ‘vibraties’ aantonen in vrijwel elke vijver of waterplas. Een grote steen of een plank, die men er in werpt, een boot die in de verte nadert veroorzaken lange,

1) πλημνϱα = vloed. - Forel, Le Léman (1895), blz. 89.

[p. 138]

onzichtbare golven, die een aantal malen heen en weer lopen en die met vaste tijdsruimten terugkeren (enkele sekunden tot enkele minuten). Dikwijls vindt men eigentrillingen van de vijver als geheel of van bepaalde bochten, welke trillingen dan bijzonder versterkt worden. Het zijn dezelfde verschijnselen welke bij de grote meren als ‘seiches’ bekend zijn.¹⁾

1) Een ander eenvoudig toestelletje is beschreven door A. Endrös, Pet. Mitt. 50, 294, 1904. Vgl. ook Pet. Mitt. 58, 257, 1912.

85. Oefeningen in het waarnemen van watergolven.²⁾

Er zijn twee wijzen om naar snelbewegend water te kijken.

1. Vooreerst kan men strak in dezelfde richting blijven kijken. Men bemerkt dan dat een steen, die boven het water van de beek uitsteekt, omringd is door een mooi golvenpatroon, hetwelk volmaakt in rust blijft; overigens schijnt het oppervlak vrijwel glad. Dergelijke beelden krijgt men ook door te fotograferen.

2. Men kan echter ook het oog met het water mee bewegen; enige oefening is daartoe nodig: men volge bijvoorbeeld een blaadje met de blik, of sluite half de ogen. Nu komen allerlei golven te voorschijn die met het water meelopen, het schijnbaar gladde oppervlak blijkt vol oneffenheden en strukturen te zitten. Prachtig kan men deze kunst beoefenen als het regent en men aan de oever van een vijver of singel staat. In alle richtingen lopen rimpels over het oppervlak. Door de blik langzaam en gelijkmatig over het water te laten glijden, ziet men alle golfjes die in een bepaalde richting bewegen als één groot front vooruitschuiven, terwijl de andere golfjes onzichtbaar of zeer onduidelijk worden. Beweegt men zijn blik in een andere richting, dan ziet men ook daar een golffront.

De oefening der ogen die men met zulke waarnemingen verwerft is van grote waarde voor de bestudering van staande en lopende golven bij beken, watervallen, brandingverschijnselen enz. Vaughan Cornish, die een groot stuk van zijn leven aan die onderzoekingen heeft besteed, beweert dat hij sommige golfverschijnselen slechts kan onderscheiden als hij zich eerst weer opnieuw maandenlang in het waarnemen heeft getraind!

Fotografeer allerlei golfverschijnselen! Lichtsterk objektief; belichtingstijd nooit meer dan 1/20 sec.

2) Over watergolven: Scott Russell, Rep. Brit. Assoc. 1844. - Vaughan Cornish, Geogr. Journ. 1903. - Zie ook de algemene litteratuur, aangegeven op blz. 109.

[p. 139]

86. Een steen valt in het water.

Neem eerst een vrij grote steen van een centimeter of vijf, en gooi hem in het water. Wat er precies gebeurt op het ogenblik van de plons is moeilijk uit te maken; feitelijk heeft de steen een holte in het wateroppervlak gemaakt, die holte sluit zich aan de bovenkant en men hoort een geluid (II, § 50), het water heeft een duw gekregen naar alle kanten en is dan weer teruggeschommeld. Maar nu wachten we. Enkele fijne rimpels dempen na een paar sekunden uit; en daar ontstaan de welbekende kringen, verrassend lang nadat de steen gevallen is; 5 sekunden, 10 sekunden na die tijd pas hebben ze zich goed ontwikkeld. Er komen er steeds meer, hoe langer we wachten, maar tegelijk worden ze vlakker tot we ze tenslotte niet meer kunnen zien. Duidelijk merken we op dat de voorste golven de grootste golflengte hebben, de achterste de kleinste (1 of 2 cm). Als ik al die golfjes bij mekaar kon optellen, zou ik voor het ogenblik waarop ik de proef begon, weer de oorspronkelijke stuwing van het water krijgen, die de steen veroorzaakt heeft. Al die golven van verschillende golflengten zijn nu uit elkaar gehaald, doordat de grote golven sneller lopen dan de kleine, en dus op een gegeven ogenblik verder gekomen zijn. Het water werkt als een echte spektroskoop, die wit licht in zijn samenstellende kleuren ontleedt!

Herhaal nu de proef met een klein licht dingetje: een stuk van een grasje, een korreltje, een ineengefrommeld bolletje papier, en kijk onmiddellijk naar wat er gebeurt. Ook nu ontwikkelen zich kringen, maar de voorste golfjes zijn ditmaal heel fijne rimpelingen, terwijl de laatste toenemend breder zijn, tot een golflengte van 1 of 2 cm. Dus net andersom als bij de grote golven!

Bij toenemende golflengte lopen de watergolven dus eerst langzamer, bij een golflengte van een paar cm is de snelheid het geringst, en de grotere golven lopen weer toenemend snel.

Door slechts een geringe evenwichtsverstoring teweeg te brengen, hebben we de vorming van lange golven vermeden, die bij de eerste proef de even snel lopende rimpeltjes overdekten; en door snel na het inwerpen te kijken, hebben we vermeden dat de kleine rimpels al uitgedempt zouden zijn.

Dat golven van verschillende golflengte verschillend snel lopen, is een der merkwaardigste eigenschappen waardoor watergolven zich onderscheiden van geluid- of lichtgolven in het luchtledige. (Zodra echter het licht of het geluid zich voortplanten door

[p. 140]

stoffen ‘met dispersie’, ontstaat er ook verschil van voortplantingssnelheid: in water loopt bijvoorbeeld het licht van een violet lichtsignaal langzamer dan dat van een rood). Het gevolg daarvan is, dat een mengsel van watergolven van allerlei golflengten weldra door het voortlopen uiteengerekt wordt, vervormd.

Van een groepje golven is de groepsnelheid soms veel kleiner dan de individuele golfsnelheden. Om dit waar te nemen heeft u slechts de proef met de grote steen te herhalen, en nu op één bepaald golfje te letten. Volg het scherp met de ogen: het loopt veel sneller dan de groep; het is eerst een der achterste golfjes, komt vooruit en wordt groter, bereikt ten slotte de voorste rangen van de groep en sterft daar uit. Deze waarneming is niet heel gemakkelijk en lukt maar als men de proef verscheiden malen herhaalt.

87. Voortplantingssnelheid, golflengte, trillingsgetal.

We zitten aan de oever van een stille vijver, en vermaken ons met een plankje. We houden het loodrecht, terwijl zijn smalle kant het water raakt, en tikken dan snel met de andere hand, zodat het plankje telkens in en uit het water wipt. De golfjes lopen langzaam voort over het wateroppervlak; we zien ze vooral prachtig als het water ondiep is, en de zon onder ieder golfje een lichtribbel over de boden laat lopen.

Eigenlijk is het vanzelfsprekend dat de afstand V die de golfjes per sekunde afleggen gelijk is aan de golflengte λ maal het aantal golven per sekunde n:
V = nλ
Toch willen we 't nog door een schatting bevestigen. We beproeven nauwkeurig 4 maal in de sekunde te tikken. Een ander waarnemer schat de lengte van de golfjes, liefst door vergelijking met een duimstok, een takje van bekende lengte, enz.; hij schat de golflengte op λ = 8 cm. Tenslotte vat hij een bepaald golfje scherp in 't oog, wijst het aan met een stok en volgt het: de weg die de stok in 5 sekunden aflegt is 150 cm, zodat V = 30 cm/sec, wat niet slecht klopt met het produkt 8 × 4 = 32.

U zult wel merken dat het rechtstreeks bepalen van V moeilijker en onnauwkeuriger is dan het berekenen uit nλ.

[p. 141]

88. Voortplantingssnelheid van watergolven.

Toen we de golven bekeken om het punt waar een steen in het water gevallen was, kwamen we tot volgend besluit (§ 86): ‘bij toenemende golflengte lopen de watergolven eerst langzamer; bij een golflengte van een paar centimeter is de snelheid het geringst, de grotere golven lopen weer toenemend snel.’

William Thomson heeft daar een verklaring voor gegeven.¹⁾ De watergolven worden door twee onderscheidene krachten in beweging gehouden, de gravitatie en de oppervlaktespanning. Bij lange golven werkt vooral de eerste: het water van de golfberg heeft de neiging in het golfdal te vallen; bij korte golven werkt vooral de tweede, want als de rimpelingen heel klein worden verzet zich het oppervlak tegen de sterke krommingen, die het plaatselijk uitrekken. In het tussengeval spelen beide krachten een rol. Hiervan uitgaande vond Thomson, dat de voortplantingssnelheid in een vloeistof van dichtheid s door volgende formule beschreven wordt: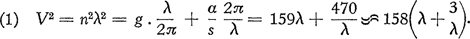

De eerste term van deze formule slaat op de gravitatie, hij overweegt sterk zodra λ > 10 cm. De tweede term heeft betrekking op de oppervlaktespanning a, waarvan wij de waarde hebben ingevuld; hij overweegt voor λ < 0,5 cm. Men ziet dat er voor λ = 3/λ een minimum-snelheid optreedt van ongeveer 23 cm/sec bij een golflengte λ = √3 = 1,7 cm en een trillingsgetal n = 14. Het gehele verloop van V is uit fig. 81 af te lezen.

Om die theorie aan de werkelijkheid te toetsen nemen we weer het eenvoudige plankje, dat we periodiek in het water dompelden om golfjes te maken. We tikken er eerst zo snel mogelijk op, daarna langzamer. Volg de golfjes met de ogen: het is opvallend hoeveel sneller ze lopen naarmate ze groter worden! Versnel het tempo weer waarin u tikt: de golfjes worden weer kleiner en trager. Klaarblijkelijk zijn dit gravitatiegolven.

We veranderen het trillingsgetal n binnen zo wijd mogelijke grenzen. Zes, zelfs zeven maal in de sekunde kunnen we nog vrij regelmatig tikken; dan gaan we geleidelijk over tot steeds langzamer bewegingen. Om mooie golven te krijgen, moet de afstand waarover we op en neer gaan geschikt gekozen worden;

1) Phil. Mag. 42, 368, 1871. - Vgl. ook Matthiesen, Ann. Phys. 38, 118, 1889; Berl. Ber. 772, 1889.

[p. 142]

beproef hem wat groter of wat kleiner te maken; voor een trillingsgetal in de buurt van 1 trilling per sekunde gebruiken we met voordeel de brede vlakke zijde van de plank. - Telkens bepalen we zo goed mogelijk λ, en berekenen V door het produkt nλ op te maken. Zet de waargenomen punten in fig. 81 uit, en zie of ze ongeveer op de theoretische lijn vallen! Ik denk dat u verrast zult zijn over de goede overeenstemming! - Alleen moet ik nog even opmerken dat de formule van Thomson slechts geldt zolang het water tenminste één, liever twee golflengten diep is, en dat u de plaats waar u uw proeven neemt wel in overeenstemming met die eis dient te kiezen.

De heel korte golfjes kunnen we op deze wijze niet bestuderen, omdat we het plankje niet snel genoeg aan het trillen kunnen brengen. Toch zijn die juist zó belangwekkend! Om ze te zien te krijgen, houden we een plankje, een tak, een potlood, een zakmes in een snelvlietende beek; of laten eenvoudig een touwtje, met een gewicht bezwaard, in het water hangen. Om het touw vormt zich een allersierlijkst golvenpatroon, dat volmaakt stilstaat terwijl het water stroomt. Heeft u wel eens bedacht hoe buitengewoon merkwaardig dat eigenlijk is? De golfjes van het patroon hebben dus ten opzichte van het water een voortplantingssnelheid die nauwkeurig gelijk en tegengesteld is aan de stroomsnelheid van het water; automatisch worden juist golfjes van een dusdanige golflengte gevormd dat aan die voorwaarde voldaan is. Er moet dus een vast verband bestaan tussen de golflengte der stationaire ribbels en de snelheid van het water: het verband dat gegeven is door de formule van Thomson. Het is nu duidelijk wat we te doen hebben om de heel kleine rimpels te bestuderen: de golflengte van de stationaire rimpels om een afhangend touw schatten, en tegelijk de snelheid van het water afleiden uit de beweging van drijvende voorwerpen. Nog iets gemakkelijker kunnen we 't ons maken door een rustig vijvertje of kanaaltje op te zoeken, en ons touw zelf te bewegen ten opzichte van het rustende water: we kunnen dan proeven nemen met allerlei snelheden V naar keuze. Het mooist gaat dat als we ons in een boot bevinden, waarvan de snelheid vanzelf geleidelijk afneemt; maar het is ook al voldoende als we eenvoudig langs de oever lopen, en het touw met uitgestrekte hand vasthouden.

We beginnen met ons touw betrekkelijk snel door het water te bewegen, en het golfpatroon aandachtig te bekijken. Het is opvallend dat de golfjes vóór het touw zeer kort zijn, die achter het touw veel langer. Blijkbaar zijn er twee soorten golfjes die

[p. 143]

zich met dezelfde snelheid kunnen voortplanten. Zie maar naar figuur 81: dat klopt inderdaad met de theorie! De korte golfjes vóór het touw zijn de capillaire rimpels, die achter het touw zijn de gravitatiegolven. De twee golflengten λ₁, λ₂, die wij op het oog vrij goed kunnen schatten, zijn de twee wortels van vergelijking (1), die men zich naar λ opgelost kan denken! - Op de schuine golfjes die op schone wijze naar rechts en links wegbuigen, willen we voorlopig niet teveel letten.

Verminder nu de snelheid van het touw: de twee soorten golven schelen niet meer zoveel,

Fig. 81. De snelheid van watergolven als funktie van de golflengte.

de capillaire golven zijn langer geworden, de gravitatiegolven korter. Dit komt precies overeen met de overgang van de lijn AA naar BB in fig. 81. Merk tevens op dat de zijdelingse golfjes, die het patroon rechts en links begrenzen, nu meer zijn gaan uiteenwijken, en een veel grotere hoek met de symmetrielijn vormen dan eerst.

Bij nog kleinere snelheid worden tenslotte de twee soorten golven even lang, terwijl de zijdelingse golfjes zich geheel en al loodrecht op de bewegingsrichting instellen. Dit komt overeen met het samenvallen der twee snijpunten in C in fig. 81, en met het optreden van twee gelijke wortels in vergelijking (1) op blz. 141. We hebben thans de kleinste snelheid bereikt die watergolven kunnen krijgen: 23 cm/sec, bij λ = 1,7 cm.

Bij een snelheid beneden 23 cm/sec vormen zich geen golven meer om het bewegende touw. Als men af en toe soms een kringetje ziet, is het wanneer het touw toevallig een rukje gekregen heeft.

Schat λ₁ en λ₂ bij allerlei snelheden V; behelp u met duimstok en horloge! Vul de kurve aan die u aan het construeren waart en vergelijk met de theoretische: ook thans is de overeenstemming in het algemeen uitmuntend.

Bemerk hoe het golvenpatroon terug te vinden is bij elk voorwerp dat door het water beweegt; capillaire golfjes ziet men ook mooi aan de voorsteven van een boot die met een snelheid van bijvoorbeeld 50 cm/sec voortbeweegt.
Van de waterrimpels die zich vóór het bewegende touw vormen, hebben

[p. 144]

de een of twee eerste iets groter golflengte dan de andere: blijkbaar wordt het water een weinig meegevoerd door het bewegende voorwerp.¹⁾
Soms zijn er een groot aantal van die rimpels, even later zijn er maar twee of drie meer te zien, en dan onverwacht spreiden ze zich weer uit; deze veranderingen schijnen samen te hangen met geringe verontreinigingen van het oppervlak. Men zou verwachten dat de voortplantingssnelheid van de kleine rimpels op een verontreinigde sloot merkbaar kleiner is dan op zuiver water; kijk eens of u daar iets van vindt!
Bekijk aandachtig de rimpeling die ontstaat als u een touw (met er aan hangend gewicht) of een plankje langzaam door rustig water beweegt. Giet nu enkele druppels terpentijn of ether op het wateroppervlak: de rimpeling is verdwenen²⁾! Verklaring: door terpentijn of ether wordt de oppervlaktespanning sterk verminderd.

Er is nog een opmerking die betrekking heeft op onze proef

Fig. 82. Golfsnelheid en groepsnelheid bij watergolven.

met het schietlood dat we door het water bewogen, en die te belangrijk is om ze niet te vermelden³⁾. Hoe komt het toch, dat we de capillaire rimpels alleen vóór het touw zien, de gravitatiegolven er achter? Dat is alweer een gevolg van het verschil tussen golfsnelheid en groepsnelheid, een verschil dat ontstaat zodra golven van verschillende golflengte verschillende snelheden hebben, - zodra er dispersie is, dus. Een groep bestaat altijd uit componenten van allerlei golflengten; hebben die verschillende snelheden, dan zullen ze zich meer en meer van elkaar verwijderen en het profiel van de groep zal niet tegelijk met hen meegenomen worden. Men bewijst dat



Voor capillaire golven is zij dus groter dan V, en wel gelijk aan 3/2V. Voor gravitatiegolven is zij kleiner, en wel in diep water gelijk aan V/2, in ondiep water gelijk aan V. Zo komt het dat het patroon der capillaire golven altijd het touw vooruit loopt, en dat der gravitatiegolven achteraan komt! - Voor de golven

1) L. Matthiesen, Ann. Phys. 38, 126, 1889. - Scott Russell, t.a.pl. blz. 377-378.

2) J. Langton, Nat. 5, 241, 1872.

3) O. Reynolds, Nat. 16, 343, 1877.

[p. 145]

die zich met minimumsnelheid voortplanten, is dV/dλ = 0, dus groepsnelheid en golfsnelheid zijn gelijk.

In de grafische voorstelling van V als functie van λ is dit onmiddellijk aanschouwelijk te maken (fig. 82): voor golven overeenkomend met het punt P is de golfsnelheid OM, de groepsnelheid ON is kleiner (NP is de raaklijn in P). Voor een punt Q is de golfsnelheid ook OM, maar de groepsnelheid OR is ditmaal groter.

89. De bepaling der minimum-snelheid.

William Thomson vertelt¹⁾:

‘Ongeveer drie weken later bevond ik mij bij windstilte in het zeegat van Mull (Schotland), en had ik een uitstekende gelegenheid om met de hulp van Professor Helmholtz en mijn broeder uit Belfast enigszins nauwkeurig de minimum-snelheid uit waarnemingen te bepalen. Op een afstand van twee of drie voet buiten boord hingen we een hengelsnoer uit, zo dat dit het water trof op een punt dat niet merkbaar door de beweging van het vaartuig gestoord was. Onze snelheid bepaalden we door stukjes papier in zee te gooien, die eerst nat gemaakt waren, en de ogenblikken na te gaan waarop ze door twee evenwijdige vlakken gingen, op 912 cm van elkaar, vastgelegd ten opzichte van het vaartuig door merktekens op het dek en het slamdek. Door aandachtig te kijken naar het patroon van rimpels en golven dat de rimpels vóór met de golven achter verbond, had ik opgemerkt dat daarin ook een stel evenwijdige golven voorkwam dat schuin naar elke zijde liep,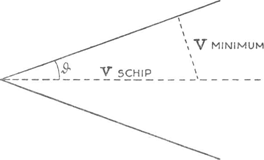

Fig. 83. Het bepalen der minimum-snelheid van watergolven, uit het golvenpatroon om een hengelsnoer.

en waaraan men duidelijk kon zien dat het golven waren van de kritische golflengte en van minimum-snelheid (fig. 83). De componente der snelheid van het hengelsnoer loodrecht op het golffront dezer golven was dus de ware minimum-snelheid. Om die te meten had men slechts de hoek te bepalen tussen de twee evenwijdige groepen golfbergen en golfdalen aan beide zijden van het zog

1) Nat. 5, 1, 1871.

[p. 146]

van het hengelsnoer, en tegelijk de snelheid waarmee het snoer zich door het water verplaatste. De hoek werd gemeten door de benen van een soort houten passer zo goed mogelijk op het oog evenwijdig aan de twee stelsels golfribbels in te stellen; de hoek waaronder de passer geopend moest worden was de gezochte hoek. Door hem op papier te leggen, twee rechte lijnen langs zijn benen te trekken, en een eenvoudige meetkundige constructie uit te voeren met een geschikte maatstaf, aangepast aan de snelheid van het schip, werd de gevraagde minimumsnelheid gemakkelijk gevonden. Van zes dergelijke waarnemingen werden er twee als onbetrouwbaar verworpen. Hier volgen de uitkomsten der vier andere:

snelheid van 't bewegende lichaam	minimum golfsnelheid
51 cm/sec	23,0 cm/sec
38	23,8
26	23,2
24	22,9
	_____
	Gemiddeld 23,22

De uiterst geringe afwijking van deze uitkomst ten opzichte van de theoretische schatting (23 cm/sec) was natuurlijk slechts een toeval, maar bewees toch dat de oppervlakte-spanning van zeewater bij de (niet opgetekende) temperatuur der waarneming niet zeer verschillend kan zijn van die welke ik uit Gay Lussac's waarnemingen aan zuiver water had afgeleid.’

Deze waarnemingen zijn gemakkelijk te herhalen, ook wanneer men niet over een boot beschikt en gewoon langs de oever loopt. Men berekent bij verschillende waarden van de snelheid V het produkt V sin ϑ, dat constant hoort te zijn, en gelijk aan de minimum-snelheid.

Maak een golvenpatroon door een potlood door 't water te bewegen, en trek dan plotseling het potlood uit het water. De ribbels worden dan zwakker gebogen, meer evenwijdig, en bewegen voort met de grenssnelheid van 23 cm/sec.¹⁾

Scott Russell heeft zeer zorgvuldig de eerste stadia van de golfvorming in de buurt van de grenssnelheid onderzocht, door op te letten hoe het vloeistofoppervlak nabij het bewegende touw het licht terugkaatst. Als het touw in rust is, vormt de vloeistof capillair een heuveltje dat zich ongeveer tot 2 cm van het touw uitstrekt; zodra men het touw beweegt wordt dit heuveltje asymmetrisch; bij 20 cm/sec heeft het zich in twee

1) Scott Russell, Rep. Brit. Ass., York 1844.

[p. 147]

verdeeld, en weldra vormt zich het eerste capillaire golfje (fig. 84).

De minimum-snelheid in zeer ondiep water (< 1 cm) schijnt nog niet gemeten te zijn. Volgens de theorie is ze kleiner dan in diep water, en de golfjes zijn langer.¹⁾

Elke steen, elke kleine hindernis die in snel stromend water

Fig. 84. Golvenpatroon om een hengelsnoer bij snelheden in de buurt van de minimum-snelheid (naar Scott Russell).

Fig. 85. Schuine golfjes in een hellende tramrail na een regenbui.

hangt, is omringd door een stationair golvenpatroon, waarvan de twee uiterste schuine strepen het meest kenmerkende zijn. Let ook op het water dat na een regenbui langs de tramrails vloeit, als de straat een weinig helt (fig. 85): op een aantal plaatsen lopen schuine strepen dwars over het waterstroompje, alle onder eenzelfde hoek ten opzichte van de wanden; blijkbaar gaan ze uit van bepaalde korreltjes en oneffenheidjes, waaraan zich ook golfjespatronen met lijnen van minimumsnelheid vormen. In die verschillende gevallen is de snelheid van het stromende water steeds onmiddellijk te schatten uit

1) H. Jeffreys, Proc. R. Soc. 110, 241, 1926.

90. Golfjes op water dat met een ijskorst bedekt is.

Op een wintermorgen was de singel aan beide oevers omzoomd met een zeer dun laagje ijs, terwijl het gehele middengedeelte ijsvrij was. Wierp men nu een steen in het ijsvrije water, dicht bij de ijszoom, dan zag men de gewone, zich kringvormig uitbreidende golfjes ontstaan; maar: 1. de korte, capillaire golfjes breidden zich helemaal niet uit in de ijslaag, blijkbaar omdat de grenslaag hier niet meer vloeibaar was, en er dus geen

[p. 148]

oppervlaktespanning meer overbleef; 2. de grotere gravitatiegolven liepen op de merkwaardigste wijze vrijwel ongestoord

Fig. 86. De voortplantingssnelheid van watergolven is groter, als het water met een zeer dun ijslaagje bedekt is.

door, maar men kreeg de indruk dat de kringen zich vervormden in het met ijs bedekte gedeelte, en wel schenen zij zich daar sneller voort te planten (fig. 86). De veerkracht van het elastisch doorbuigende ijsplaatje hielp hier de zwaartekracht dus nog beter dan de oppervlaktespanning het anders doet. Naderhand bleek mij dat de theorie van deze golven al gegeven is.¹⁾ Als e = de dikte van het ijslaagje, E = zijn elasticiteitsmodulus, komt er ongeveer: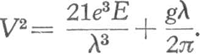

E is van de orde 10¹². Het ijslaagje moet slechts een of twee tienden van een millimeter dik geweest zijn.

Dit verschijnsel is een goed model voor de wijze waarop lichtgolven gebroken worden bij overgang van de ene middenstof naar de andere.

1) Greenhill, Americ. Journ. of Math. 9. - Basset, Hydrodynamics, II, blz. 180.

91. Golven in ondiep water.

Aan het strand merken we op hoe al de schuimende golfkammen evenwijdig aan de strandlijn gericht zijn, terwijl toch de golfkammen in de verte, in volle zee, alle mogelijke richtingen hebben. Alleen wanneer sterke wind van opzij waait, bijna langs de kust, is een kleine afwijking van de evenwijdigheid waar te nemen.

Iets dergelijks ziet men aan een meertje: de golven die door de wind naar de oever gedreven worden, richten zich meer en meer evenwijdig eraan, het golffront kromt zich, tot het tenslotte vrijwel geheel de vorm van de strandlijn overgenomen heeft. Hoe kan toch de golf dat ‘voorgevoel’ krijgen van de vorm van de kust?

Deze verschijnselen zijn eenvoudig een gevolg van het feit, dat de snelheid der gravitatiegolven kleiner wordt naarmate

[p. 149]

de diepte van het water afneemt; deze invloed begint merkbaar te worden, wanneer de diepte van de orde der golflengte wordt of kleiner. Zolang het golffront schuin op de kust staat, planten zich de verst verwijderde delen voort in het diepste water, dus het snelst, en halen de andere in; geleidelijk zwaait het golffront om, tot alle delen ervan in even diep water lopen. Dikwijls kan men dit omzwaaien mooi waarnemen van op een hoog standpunt, bijvoorbeeld van op de pier te Scheveningen. Aan het strand kan een opmerkzaam waarnemer ondiepe plaatsen in zee uit de

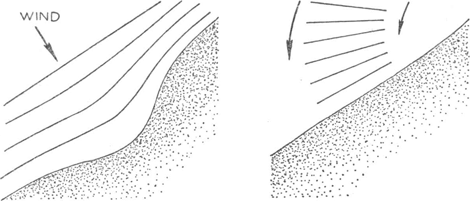Fig. 87. Bij nadering van de kust zwaaien de golffronten om, tot ze evenwijdig aan de kustlijn lopen.

verte herkennen, doordat de golfkammen daar enigszins achterblijven en zich krommen.

Een zeer opvallende waarneming over dit onderwerp kan men doen na een flinke regenbui. Overal langs de weg liggen er plassen, overal druipen de regendruppels nog van de bomen. Ons oog valt op de kringen die zich om zo'n druppel vormen als hij in de waterplas valt, en we merken op dat die ‘kringen’ helemaal geen cirkels zijn! Ze zijn onregelmatig vervormd, hier een afplatting, daar een uitstulping. We moeten aandachtig kijken, want het gaat snel, maar de afwijkingen zijn toch onmiskenbaar. Blijkbaar is de diepte van de waterplas van de ene plaats tot de andere zeer verschillend, en wordt de snelheid der golven daardoor beïnvloed.

Is dit de juiste verklaring, dan zouden capillaire golfjes wèl zuivere cirkels moeten vormen. Let maar op plassen die niet onder de bomen liggen en waarin slechts af en toe een heel klein druppeltje valt, dat fijne rimpelingen opwekt. Inderdaad zijn deze kringen helemaal gaaf!

[p. 150]

De volledige formule voor de voortplantingssnelheid der golven ziet er zo uit:

Voor grote diepte H is de tangens hyperbolicus = 1 en krijgen we de formule (1) der ‘oppervlaktegolven’ (§ 88); voor kleine diepte wordt hij gelijk aan 2πH/λ, en hebben we formule der ‘lange golven’: V² = gH (bij verwaarlozing der capillariteit).

92. Hoe watergolven door de inwerking van de wind ontstaan en groeien.

In de natuur ontstaan de watergolven meestal doordat de wind over het wateroppervlak strijkt; zodra hij een zekere snelheid bereikt, begint zich het oppervlak te rimpelen. De bepaling van deze kritische snelheid en van de golflengte der eerstgevormde golfjes is van groot belang om uit te maken of we de invloed van de wind op het water wel bevredigend theoretisch kunnen beschrijven. Toch is er na de waarneming van Scott Russell in 1844 slechts één- of tweemaal een onderzoek naar ingesteld!

Beproef enige bepalingen uit te voeren aan een groot vrij wateroppervlak. Bepaal de windsterkte op verschillende hoogten boven het water, op het ogenblik dat de eerste rimpelingen ontstaan (§ 159); schat de golflengte der golfjes door vergelijking met een duimstok. - H. Jeffreys¹⁾ vindt dat de eerste rimpels optreden bij een wind van 1,15 m/sec, en geeft voor hun golflengte 7 cm op: het zijn dus van den beginne af reeds kleine gravitatiegolfjes. Volgens de verouderde theorie van Helmholtz - Wien, die alleen rekening houdt met de wrijving van de wind over het wateroppervlak, zou de vorming integendeel moeten beginnen met capillaire rimpels, maar slechts bij een windsnelheid van tenminste 6,50 m/sec! De eerste golfjes hebben zeer lange kammen, wel 5 maal hun golflengte en meer. Ze planten zich niet voort over aanzienlijke afstanden, omdat ze (als alle korte golven) sterk gedempt zijn door de taaiheid van het water: een plek die toevallig tegen de wind beschermd is vertoont dan ook geen golfjes.²⁾

1) Proc. R. Soc. 107, 189, 1925.

2) Vaughan Cornish beschrijft de vorming der eerste golfjes enigszins anders: eerst zouden golfjes met korte kammen ontstaan, die na 10 tot 30 sekunden in lange kammen overgaan. Scott Russell en Apstein geven nog weer andere beschrijvingen. Moeilijkheden onstaan, doordat men niet nauwkeurig weet hoe groot de windsterkte vlak bij de waterspiegel is, en dat de wind altijd min of meer onregelmatig, buiig blaast.

[p. 151]

Van de verschillende theoriën die de invloed van de wind op het water beschrijven, is die van Jeffreys¹⁾ de enige welke met de moderne waarnemingen klopt. Zij houdt rekening met de wervelingen die in de wind ontstaan als hij over de golven strijkt, en maakt er gebruik van dat hij een grotere druk uitoefent tegen de voorzijde dan tegen de achterzijde van de golf (fig. 88). Waar de druk het grootst is, beweegt zich het oppervlak benedenwaarts; in de luwte, waar de druk het kleinst is, wordt het water opwaarts gezogen. Op die wijze wordt de golf vooruit gestuwd, althans zolang als ze nog de windsnelheid niet bereikt heeft. Een aantal verschijnselen betreffende watergolven worden

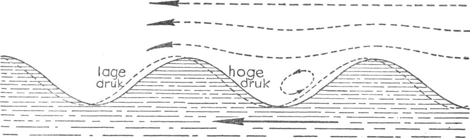Fig. 88. Het onderhouden der golfbeweging door de wind. Voluit getrokken: het oppervlak op een bepaald ogenblik; gestippeld: het oppervlak even later.

aldus verklaarbaar, maar er blijven toch ook nog moeilijkheden bestaan.

Een studie op zichzelf is weer het onstaan der eerste golfjes op zeer ondiepe plassen, minder dan 1 cm diep. Merk op hoe die plassen nog ongestoord zijn, terwijl de wind al sterk genoeg is om merkbare golfjes te vormen op diep water! Wordt de wind veel sterker, dan vertonen zich het eerst golfjes van slechts 2 à 3 cm golflengte (ongeveer 4 maal de diepte van de waterplas); hun kammen zijn zeer lang ten opzichte van hun golflengte, evenals dit het geval was voor de golfjes die zich in diep water vormden. Grotere golven kan de wind op zulke ondiepe plassen niet doen ontstaan, omdat deze al te sterk in hun ontwikkeling worden belemmerd door de taaiheid van het water.²⁾

De verdere groei en ontwikkeling van de golven geschiedt niet alleen wanneer de windsterkte geleidelijk toeneemt, maar

1) Samengevat in Vaughan Cornish, Ocean Waves, blz. 125.

2) H. Jeffreys, Proc. R. Soc. 110, 241, 1926.

[p. 152]

ook wanneer de windsterkte dezelfde blijft: hoe langer een golfje aan de inwerking van de wind blootgesteld is, hoe meer het groeit.

Op een ietwat winderige dag volgen we de golven die zich op een kleine vijver vormen welke vrij aan de wind blootgesteld is. We beginnen aan de windzijde van de vijver, waar de golven ontstaan, en nu gaan we verder en verder met de wind en de golfjes mee. We zien dan dat de golflengte en de hoogte der golfjes geleidelijk toenemen. en dat hun kammen steeds rechter en langer worden. Hetzelfde opvallende verschijnsel is aan elk kanaal te zien dat voldoende vrij ligt en min of meer in de windrichting loopt. Alleen helemaal aan het einde, aan de lijzijde van de vijver of het kanaal, verdwijnen de golfjes bijna geheel, omdat de wind daar allerlei verontreinigingen bijeengeblazen heeft en het oppervlak met een vetlaagje bedekt is.

Het is de moeite waard bij snel opkomende storm de golfjes waar te nemen aan de lijzijde van een meer, daar waar hun baan eindigt: ze worden geleidelijk groter, en bereiken hun grenswaarde misschien pas na een uur. En dit aangroeien is niet zozeer een gevolg van toenemende windsterkte, maar veeleer toe te schrijven aan het feit dat de eerst aankomende golfjes slechts een korte, de volgende een toenemend langere baan onder invloed van de wind hebben afgelegd. De grenswaarde wordt bereikt, als golfjes die helemaal aan de overkant ontstaan zijn de tijd hebben gehad ons te bereiken.

Op een dergelijke wijze nu is het, dat de golven der zee ontstaan. Waarom zijn er tenslotte grote golven op de zee en niet op een vijver? Dat is noch door de sterkere wind, noch door de grotere diepte te verkaren, maar eenvoudig omdat het wateroppervlak zo uitgestrekt is, en dat de golven tijd moeten hebben om door de inwerking van de wind te groeien. Vandaar ook dat ze bij storm slechts na geruime tijd hun grootste afmeting bereiken, en dat die eindwaarde des te groter is naarmate de wind meer vrije ruimte heeft gehad: de hoogste golven die men op de Noordzee heeft waargenomen zijn groter dan op de Zwarte Zee; nog groter zijn ze in de Atlantische Oceaan, en het grootst van al in de Stille Oceaan.

Bestudeer bij verschillende weersomstandigheden de golfjes op een snelstromende rivier. Als bijvoorbeeld een felle wind tegen de stroming in blaast, kunnen de golfjes zo groot worden dat ze vrijwel even snel lopen als de stroming, maar in tegengestelde richting. Men kan dan het merkwaardige schouwspel gadeslaaan van bijna onbewegelijke golfpatronen, waaronderdoor de rivier stromend gedacht moet worden.

[p. t.o. 152]

PLAAT I.
Zeeën en zware deining in de Atlantische Oceaan (§ 93). Naar Vaughan Cornish, Waves of the Sea, bl. 51.

[p. t.o. 153]

PLAAT II.
Branding, enkelvoudige golven en schuimrand aan een vlakke kust (§§ 97, 100). Naar Vaughan Cornish, Waves of the Sea, blz. 167.

[p. 153]

93. Zeeën en deining.¹⁾ - (Plaat I).

Het bewegende water van de watervallen of van het golven der zee maakt op ons een indruk als muziek. De aanstormende golven met hun rhythmisch zich herhalende beweging, die toch onophoudelijk weer wisselt, scheppen een vreemd gevoel van behagelijke rust zonder verveling, en roepen het beeld op van een machtig maar geordend en schoon, harmonisch leven.
H.v. Helmholtz, Tonempfindungen, 1863, blz. 388.

De verdere ontwikkeling der watergolven onder de invloed van de wind is vooral goed na te gaan bij de golven der zee. De echte zeegolven zijn niet de schuimende baren van de branding, maar die welke we van op het strand in de verte zien, en alleen van op een schip behoorlijk kunnen waarnemen.

Stellen wij ons voor dat de golven bij opkomende wind ontstaan en gegroeid zijn, en laten wij aannemen dat de wind aanhoudend blijft waaien. Capillaire rimpels vindt men nog alleen in de golfdalen of op de hellingen die naar de wind gekeerd zijn; langzamerhand verdwijnen de rimpels en de korte golfjes: a) omdat de grote golven hen tegen de wind beschermen en ze dus niet groeien; b) omdat de taaiheid van het water hen sterker dempt dan de grotere golven; c) omdat het plassen en spatten der grote golven hen verstoort. Tenslotte is het resultaat, dat men een aantal kortkammige zeeën krijgt, gesuperponeerd op een deining met lange kammen en grote golflengte: het typische beeld der bewogen zee. De zeeën zijn golven die voor onze ogen door de wind worden voortgedreven; de deining bestaat uit golven die elders door de wind gevormd zijn, en die zich over grote afstanden hebben voortgeplant tot buiten het windgebied.

De zeeën hebben volstrekt geen sinusvormig profiel meer, ze hebben een zwak gekromd golfdal maar een bijna hoekige golfberg; bij toenemende wind wordt de top een stompe hoek, bij nog sterkere wind krijgt hij een kuif van schuim. De vóór- en de achterkant der zeeën zijn niet symmetrisch. De kammen zijn kort, en hun onderlinge afstanden zijn gemiddeld ongeveer dezelfde in de windrichting als loodrecht daarop. De theorie van deze golfvormen met grote amplitude is nog zeer onvoldoende ontwikkeld; Stokes heeft aangetoond dat hun voortplantingssnelheid toeneemt naarmate ze hoger worden, en wel

1) Graf von Larisch Moennich, Sturmsee und Brandung (Bielefeld en Leipzig, 1925).

[p. 154]

bedraagt die toeneming 20% voor zeeën die schuim beginnen te vertonen. - Al lang geleden heeft Helmholtz berekend¹⁾ dat in 't algemeen de golflengte evenredig moet zijn met het kwadraat der windsnelheid, en het aantal golven dat bijvoorbeeld per minuut voorbijgaat omgekeerd evenredig met de windsnelheid. Op kaap Antibes, aan de Riviera, doet hij eenvoudige waarnemingen met een zakanemometer om de windsnelheid te bepalen, terwijl hij telkens het aantal golven per minuut telt (dit laatste vindt hij zeer moeilijk, hij schat de fout op tenminste 10%). Hij vindt in het algemeen dat bij toenemende wind het aantal golven per minuut afneemt, maar een streng verband is zoek, omdat de golven dikwijls afkomstig zijn uit naburige gebieden waar een andere windsterkte heerst. Een andere complicatie ontstaat ook, doordat wind van gegeven sterkte des te langer en hoger golven verwekt, naarmate hij langer waait. En tenslotte doet de wind tegelijk golven van verschillende golflengten ontstaan, die elk met hun eigen snelheid lopen. Om al die verschillende redenen is er weinig waarde te hechten aan waarnemingen in de trant van die van Helmholtz. Ook de theorie is niet houdbaar gebleken; ze leidt bijvoorbeeld tot het resultaat, dat de golven des te ronder vormen moesten hebben naarmate de wind sterker is!?

De deining bestaat uit lange kammen, niet hoog, maar met een grote golflengte. Ze vertonen geen schuimende toppen, maar zacht afgeronde vormen; hun vóór- en achterzijde zijn symmetrisch. In de verschillende oceanen heeft de deining niet dezelfde gemiddelde periode: 5,8 sec in de Atlantische Oceaan (ook aan de Nederlandse kust), 7,6 sec in de Indische Oceaan, 8,2 sec in de Grote Oceaan, en in 't algemeen des te langer naarmate de uitgestrektheid groter is en de wind een langere vrije baan heeft. Hoezeer die periode ook moge wisselen volgens het weer, toch onderscheidt de zeeman duidelijk dat zijn schip zich anders gedraagt in de ene dan in de andere zee. Aan de grootse, statige beweging van de oceaandeining merkt de reiziger dat hij het Kanaal verlaten heeft en in de Atlantiek gekomen is. Door haar grote golflengte heeft de deining ook een grote voortplantingssnelheid en geringe demping; dagen en dagen kunnen deze golven reizen zonder merkbaar zwakker te worden, en zo komen zij tot in streken waar er helemaal geen sterke wind heeft geheerst.

1) Wiss. Abh. Band 3. Verder ontwikkeld door W. Wien.

[p. 155]

‘Geen schouwspel is geheimzinniger voor den nieuweling, dan als de golven een voor een komen aanrollen over het windstille wateroppervlak, zich van de zeeën alleen onderscheidend door zachtere helling en afgeronde vormen en kammen.’
(A. Supan, Physische Erdkunde, blz. 290. Leipzig 1907).

De lange en zuchtende deining ....
(Ruskin, The seven Lamps of Architecture, VIII, 222).

De zeeën gaan altijd langzamer dan de wind; hoe langer hij blaast, hoe meer hun snelheid tot de windsnelheid nadert zonder ze ooit te overschrijden. Daarentegen kan men dikwijls opmerken dat de deining sneller beweegt dan de wind: men moet daar echter bij bedenken dat er veel sneller winden waaien in het stormgebied van waar de deining afkomstig is, en dat ze de snelheid die ze bij haar oorsprong had blijft behouden, zelfs als ze in gebieden van betrekkelijke windstilte komt. Geen deining is sneller dan de wind die haar vormde.

De onderscheiding tussen deining en zeeën is zeer fundamenteel, en ieder waarnemer moet leren de richting van elk van de twee afzonderlijk te bepalen. De richting waarin het schuim van de golftoppen wegstuift is die van de plaatselijke wind en van de zeeën, en verschilt dikwijls aanzienlijk van de richting waarin de deining zich voortbeweegt. Maar dat wil niet zeggen dat zeeën en deining geen invloed uitoefenen op elkaar! De snelheid der zeeën nadert veel meer tot de windsnelheid wanneer de deining in dezelfde richting golft, dan als ze in tegengestelde zin of dwars loopt; in het eerste geval worden de golven ook opvallend regelmatiger en hoger dan in het tweede, waarin de zee een veel verwarder tafereel vertoont. Ook wordt de richting van de brekende golfkammen gewijzigd wanneer de deining dwars op de windrichting aankomt: de schuimlijnen liggen dan tussen de normaal op de windrichting en de normaal op de voortplantingsrichting der deining in. In zulke gevallen is het onjuist om als windrichting te beschouwen de richting waarin de zeeën breken (wat zeelui wel eens doen); men moet trachten zuiver waar te nemen in welke richting de zeeën zich voortbewegen.

Maak gebruik van een zeereis om op twee achtereenvolgende dagen de voortplantingsrichting van de deining zo nauwkeurig mogelijk te bepalen, liefst op middagtijd, wanneer het bestek wordt opgemaakt en de positie van het schip bepaald wordt. Teken op de kaart beide waarnemingspunten, met de daarbij-

[p. 156]

behorende richtingen: deze twee lijnen snijden elkaar in een punt, dat klaarblijkelijk het stormgebied aangeeft van waar de deining is uitgegaan. Men vindt dikwijls, dat de deining afstanden van 1000-3000 km heeft afgelegd. Om de tijd te berekenen die ze daarover heeft gedaan, moet de periode van de deining gemeten zijn (§ 94) en hieruit de snelheid der deiningsgolven berekend (§ 94); de deining is echter een groep golven, waarin telkens de voorste uitsterven en de achterste aangroeien: de individuele golven die we waarnemen zijn al lang niet meer de oorspronkelijke, de groep echter heeft zich als geheel voortbewogen met een snelheid die de helft is van de golfsnelheid (§ 88).

94. Metingen aan zeegolven.

Om zich een juist denkbeeld te vormen van de grootte der zeegolven, moet men ze liefst van een voldoende hoogte bekijken, bijvoorbeeld van de kommandobrug van een groot schip, anders onderschat men hun afmetingen. Wat we meten is altijd de deining, niet de onregelmatige zeeën. Goed opletten en nooit twee golven die niet goed gescheiden zijn als een geheel beschouwen!

Beschouw eerst de golflengte. Neem het ogenblik waar waarop een golf de voorsteven van het schip bereikt, en schat op welk punt van het schip de vorige golf dan al aangekomen was; de afstand tot dit merkpunt kan men daarna gemakkelijk meten. - Of men viert een hout aan een touw van de achtersteven uit, zóver dat het hout boven op de ene golf drijft als de achtersteven van het schip al op de volgende is. Deze twee methoden zijn het betrouwbaarst als het schip stil ligt, anders verstoort dit de golven door zijn beweging; als men niet loodrecht op de golven meet, moet men een cosinus in rekening brengen. - Een derde methode bestaat daarin dat men trillingstijd en snelheid bepaalt (zoals verder aangegeven) en bedenkt dat λ = VT; men krijgt uitkomsten welke met die van vorige werkwijzen overeenstemmen, als er zorgvuldig gewerkt is.

De trillingstijd meten we als de tijd die een golf nodig heeft om van de voorsteven tot het merkpunt te lopen, of van de achtersteven tot het hout dat men gevierd heeft; anders nog: het is de tijdsruimte tussen het ogenblik waarop een golf de voorsteven bereikt, en dat waarop de volgende golf aankomt. Als het schip varende is, moet gecorrigeerd worden voor zijn snelheid ten opzichte van het water. - Een betere bepalingswijze is de volgende¹⁾: let op één bepaalde schuimvlek, hoe

1) Vaughan Cornish, Quart. Journ. 52, 145.

[p. 157]

die op en neer gaat door de zwalping van het water, en bepaal hoeveel sekunden er verlopen tussen twee hoogtemaxima. Er is aangetoond dat de wind het schuim aan het oppervlak geen groter snelheid meedeelt dan 16 cm/sec, hetgeen te verwaarlozen is. Door het gemiddelde te nemen van 10 dergelijke bepalingen - en met enige oefening! - verkrijgt u zeer nauwkeurig de trillingstijd T. Het oog onderscheidt weldra duidelijk de zeeën van de deining, en kan zowel van de ene als van de andere golving de periode bepalen zonder in de war te komen.

De snelheid wordt gevonden door de tijd te bepalen die een golf nodig heeft om van de vóór- tot de achtersteven te lopen. Men corrigeert weer voor de snelheid en de richting van het schip.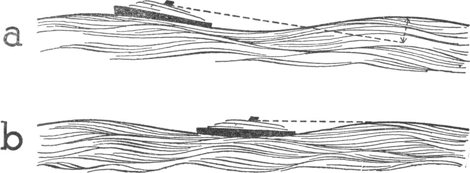

Fig. 89. a) Onjuiste, b) juiste bepaling van de hoogte der zeegolven.

De hoogte wordt dikwijls door den onervarene overschat, o.a. omdat hij geen rekening houdt met de helling van zijn schip (fig. 89). Een zuivere bepaling verkrijgt men door na te gaan van welk dek men moet kijken, midscheeps staande, om de top der golf aan de gezichteinder te zien raken, op het ogenblik dat het schip zich in een golfdal bevindt; meet de hoogte van uw oog boven de waterspiegel, of vraag de hoogte van uw waarnemingsdek aan een der officieren. Is het schip groter dan de golflengte der deining, dan geeft deze methode iets te geringe waarden.

Men heeft ook wel eens de aneroide barometer gebruikt¹⁾: de luchtdruk verandert 1 mm voor 10 m hoogteverschil (vgl. § 141); men ziet de naald kleine schommelingen maken naarmate het schip op en neer gaat.

Het is belangwekkend, bij zulke metingen ook telkens de windsterkte te schatten.

1) Abercromby, Phil. Mag. 25, 263, 1888.

[p. 158]

Tussen snelheid en golflengte kan men theoretisch een belangrijke betrekking afleiden:

welke gelden moet voor golven die niet rechtstreeks onder invloed van de wind staan (deining), en in water dat zeer diep is ten opzichte van de golflengte¹⁾. Thomson's algemene formule (1) § 88 gaat daarin over, wanneer de golven zo lang zijn dat men de capillariteit verwaarlozen kan. Deze formule (3) voor ‘oppervlaktegolven’ is wonderbaarlijk goed in overeenstemming met de ervaring gebleken, eigenlijk beter dan de meeste andere wetten die men voor watergolven uit de theorie afleidt.

Als men in die formule de vereiste numerieke waarden invult, en overal meters en sekunden als eenheden neemt, krijgt men de volgende betrekkingen, die voor het praktische gebruik geschikt zijn.

V = 1,25√λ = 1,56T

λ = 0,64V^2 = 1,56T^2

T = 0,80√λ = 0,64V

T	λ	V
0,5 sec	0,4 m	0,8 m/sec
1	1,6	1,6
2	6,2	3,1
3	14	4,7
4	25	6,2
5	39	7,8

De betrekking (3) volgde reeds uit de oudste theorie der watergolven, die van Gerstner. Deze theorie laat ons echter hopeloos in de steek als het er op aankomt de vorm der golven te beschrijven. Volgens haar zou bij zeer grote windsterkte de hoogte der golven moeten naderen tot λ/π, en zouden de toppen vlijmscherp moeten worden.

In werkelijkheid vinden we de hoogte veel geringer t.o.v. de lengte, en de toppen veel stomper. Om aan deze en nog andere bezwaren tegemoet te komen, heeft Stokes een betere theorie der watergolven ontwikkeld, volgens dewelke de hoogte moet

1) Eenvoudige afleidingen in: Zs. phys. chem. Unterricht 43, 11, 1930. - Müller-Pouillet 5, 336.

[p. 159]

naderen tot λ/7 en de tophoek tot 120^o, hetgeen al in de goede richting gaat.

De waargenomen verhouding hoogte: lengte is gemiddeld 1:13 voor de golven van een vijvertje zowel als voor zeegolven tot een golflengte van 100 m. Daarboven neemt de verhouding af tot 1:26 voor de allerlangste golven.

De grootste golven welke men op de verschillende zeeën heeft waargenomen hadden volgende hoogten¹⁾:

Baltische Zee	3,50 m
Kanaal	5-6 m
Zuidelijke Noordzee	4 m
Noordelijke Noordzee	6 m (λ = 45 m)
Middellandse Zee	6,7 m (λ = 100 m)
Noordelijke Atlantische Oceaan	8 m
Indische Oceaan	10 m
Grote Oceaan	12 m.

Deze laatste waren de hoogste die ooit goed en volledig waargenomen zijn; hun andere afmetingen waren: λ = 400 m, V = 24 m/sec, T = 15 sec. Men ziet duidelijk hoe de golven het hoogst worden in de meest uitgestrekte oceanen (vgl. § 92). Sedertdien zijn berichten ontvangen wier zorgvuldige discussie ertoe brengt, 25 m te beschouwen als de grootste hoogte, ooit aan zeegolven waargenomen.

In de praktijk rekent men soms:

hoogte der golf in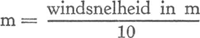



, maar dit regeltje geeft niet meer dan een ruwe schatting.

‘Als men vele jaren op zee heeft geleefd, heeft men misschien één- of tweemaal werkelijk hoge golven gezien.’
(Fitzroy)

1) A. Supan, Physische Erdkunde, Leipzig 1907. - Oudere literatuur in: Mém. soc. sc. nat. Cherbourg, 17, 265, 1873, waar zelfs golven van 13 m hoogte genoemd worden, met λ = 800 m.

95. Groepen van zeegolven.

De oude Romeinen dachten dat de zware golven altijd in groepen van 10 komen. Plato en de huidige zeelui beweren dat het er drie zijn (τϱιϰυμια), en sommige waarnemingen

[p. 160]

schijnen dit te bevestigen¹⁾. Anderen spreken weer van groepjes van 5 of van 7. Het lijkt echter niet onmogelijk, dat we hier eenvoudig te maken hebben met zwevingen tussen de eigen trillingstijd van het schip en die van de golven! Daarnaast is rekening te houden met de onbewuste neiging van ieder mens, om in een onregelmatige volgorde toch steeds regelmaat te zoeken.

Enigszins verschillend hiervan zijn de groepen deiningsgolven die Von Krümmel beschrijft²⁾: meestal 4-8 golven in 13-15 sec, ongeveer 10 minuten betrekkelijke rust, daarna weer een groep golven, enz.

De woelende golven, die de brede deining van de zee in eeuwige onrust verdelen .... zij rijzen niet overal, maar hier en daar, soms drie of vier samen, in wilde massa's, grillig en woest.
J. Ruskin, Modern Painters, III, 572.

1) Vaughan Cornish, Meteor. Mag. 1901, 56.

2) v. Richthofen Festschr. (Berlin 1893), 235.

96. Beweging der waterdeeltjes in een golf.

Gooi van het uiteinde van de pier een plankje in zee. De golven rollen voorbij, maar het plankje blijft vrijwel ter plaatse;

Fig. 90. Beweging der waterdeeltjes in een golf.

men zegt: de golf is dus een zich voortplantende bewegingsvorm, niet een zich voortbewegende materie (vgl. geluid). Treffend is de proef bijvoorbeeld bij ebbende zee: het plankje drijft zeewaarts, terwijl toch de golven strandwaarts bewegen.

Kijk echter nauwkeuriger: op een golfberg beweegt het plankje in dezelfde zin als de golven, in een golfdal tegengesteld. De waterdeeltjes in een golf gaan dus niet alleen op en neer, maar ook heen en weer.

Deze zelfde beweging vindt men ook onder het oppervlak, zij het ook met kleinere amplitude. Werp een natte bol papier in zee: hij zinkt langzaam, men ziet hem bij elke golf heen en weer gaan. De (overigens verouderde) theorie van Gerstner beschrijft deze bewegingen zeer aanschouwelijk: elk vertikaal vloeistofdraadje schommelt heen en weer aan zijn boveneind, terwijl het ondereind vast blijft; elk deeltje beschrijft een cirkel (fig. 90). Als echter de diepte geringer wordt en van dezelfde orde als de golflengte, verandert het karakter der beweging, doordat vertikale stromingen nabij de

[p. t.o. 160]

PLAAT III.
Overstortende brandingsgolf (§ 97).
Naar D.W. Johnson, Shore Processes, bl. 17.

[p. t.o. 161]

PLAAT IV.
Scheepsgolven op het meer van Thun: dwarse golven en zijgolven (§ 99).
Naar Vaughan Cornish, Waves of the Sea, blz. 351.

[p. 161]

bodem onmogelijk zijn. De banen der waterdeeltjes aan het oppervlak gelijken nu meer op ellipsen, met de lange as horizontaal; nabij de bodem bewegen ze volgens horizontale lijntjes heen en weer. Bij zeer lange golven schuiven de vloeistofdraden vrijwel evenwijdig aan zichzelf heen en weer, zoals men dat ook bij de vloedgolf waarneemt. - Volgens de veel volmaakter theorie van Stokes schommelen de deeltjes niet alleen ter plaatse, maar is de golfbeweging begeleid door een algemene stroming met de golven mee, die vooral dicht onder het oppervlak van belang moet zijn.

97. De branding. - (Plaat II en plaat III).

‘Gezien van de kust, is het krullen der brandingsgolven enigszins eentonig en eenvormig; ze schijnen elkaar op te volgen en op elkaar te gelijken, langzaam strandwaarts te bewegen, en in steeds dezelfde lijnen en vormen uiteen te vallen. Maar op een boot, al is het maar 20 meter van de kust, krijgen we een geheel andere indruk. Elke golf om ons heen lijkt groots, elk is weer anders dan de andere; en nu dat we ze van de rugzijde zien, vertoont ook ieder hunner de machtige, gestrekte, wisselende langgebogen lijnen die tegelijk snelheid en kracht uitdrukken. De brandingsgolven die een voor een naderen en breken, schijnen ons evenveel inviduen, die hun rol vervullen, vergaan, en door anderen opgevolgd worden. Maar als we begrijpen dat het geen opeenvolging van watermassa's is, maar hetzelfde water dat aanhoudend oprijst, uiteenspat, terugwijkt, en opnieuw vooruitrolt, in nieuwe vormen en met nieuwe woede, dan is het dat de geest der verstoring tot ons spreekt en dat we de kracht van zijn onvermoeibare razernij gevoelen’.¹⁾

Bekijk de golven dicht bij het strand. Ze onderscheiden zich van de golven op hoge zee:

a.	door hun richting evenwijdig aan de kust;
b.	door hun kortere golflengte;
c.	door hun asymmetrische vorm: de voorzijde is veel steiler dan de achterzijde;
d.	de hoogte neemt langzaam toe, en wel omgekeerd evenredig met de 4e machtswortel van de diepte;
e.	de golven in volle zee zijn gemiddeld even lang als breed,

1) Ruskin, Modern Painters, III, 562.

[p. 162]

	bij het strand daarentegen hebben zich kammen gevormd die vele malen langer dan breed zijn;
f.	de brandingsgolven gaan tenslotte overstorten, en gaan over in een vooruitschuivende waterplaat: een ‘enkelvoudige golf’.

Deze typische wijzigingen moeten niet toegeschreven worden aan ‘wrijving’ van de golven tegen de bodem; integendeel, de branding ontstaat juist in weerwil van de wrijving, als gevolg van de snel afnemende diepte en de vertraging welke de golf daardoor ondergaat. Wanneer de diepte H van de orde van de golflengte wordt, geldt (§ 91):



; de invloed van de bodem is dus slechts in zeer ondiep water merkbaar, want voor H = λ/2 is de uitdrukking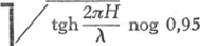



¹⁾.

De verklaring van a. is al hoger gegeven (§ 91); voor b. volgt ze onmiddellijk uit de beschouwing van twee opeenvolgende golven, waarvan die het langzaamst loopt welke het dichtst bij de kust is; c. ontstaat doordat de golfberg (waar 't water dieper is) het in snelheid wint van het golfdal (ondieper water); d. is nodig, wil de energie van de aankomende golven bewaard blijven, ook al neemt hun diepte af; e. moet aldus verklaard worden, dat er een keuze plaats grijpt onder alle golven en golfkammen die in hoge zee naast elkaar voorkomen: de korte kammen breken al zodra het water een weinig ondiep wordt, de lange kammen breken later en zijn de enige die dicht bij het strand nog overblijven. Men zou een ogenblik kunnen onderstellen, dat van een lange en een korte kam, die in diep water even hoog zijn, de lange kam in ondiep water het hoogste wordt en daardoor meer opvalt; maar dat is niet zo: beide groeien in dezelfde mate²⁾.

Volgens Scott Russell begint het overstorten, zodra de diepte a gelijk wordt aan de hoogte h der golf (fig. 91). Anderen zijn het daar niet mee eens en geven a = ⅖h, a = ⅗h, zelfs a = 2h; of ze beweren dat h gelijk moet zijn aan de diepte die het water hebben zou, indien de golven bedaard waren. Doe eigen waarnemingen als u in zee gaat baden! Weldra zal u de invloed van de wind blijken: bij zeewind zijn er verscheidene rijen brekende golven en hun schuimlijnen tekenen zich reeds ver van de kust af; bij landwind breken de golven slechts als ze vlak bij de kust

1) Metingen ter controle van deze formule in haar algemene vorm schijnen nog niet geschied te zijn.

2) H. Jeffreys, Phil. Mag. 48, 44, 1924.

[p. 163]

zijn en hun kuif al goed gevormd is, met luid geraas overstortend.¹⁾ Van groot belang is ook de helling van het strand, of eventuele terrassenvorming van de zeebodem; waarschijnlijk is aldus te verklaren dat men branding in het Kanaal heeft waargenomen bij 200 m diepte (Airy), en tussen de Faroër en de Shetlands bij 300 tot 500 m diepte (Tizard)! Langs een groot gedeelte van ons strand ziet men van op de dijk of van uit een vliegtuig hoe de branding een viertal blanke schuimlijnen veroorzaakt,

Fig. 91. Kritische verhouding a/h waarbij het overstorten van een golf begint.

die evenwijdig aan de kust lopen. Dit is natuurlijk toe te schrijven aan de achtereenvolgende rijen zandbanken die onze kust omzomen.

Let op een overstortende golf. Het overstorten begint in één punt van de golfkam en plant zich van daar over de gehele kam voort. - (Plaat III).

En langs haar groene rug loopt onbestendig schuim
- Een witheid - langzaam tegenstribbelend voort.

Keats, Endymion, II, 350.

‘Er is in de brandingsgolven een onverzoenbaar mengsel van wildheid en vormenstrengheid. Hun hol oppervlak is aangegeven door evenwijdige lijnen, als die van het gladde wateroppervlak bij een molenstuw, en het vertoont wonderlijk ingewikkelde overgangen van weerspiegeld en doorgelaten licht, terwijl zijn kromming toch noodzakelijk van wiskundige zuiverheid en precisie is; maar aan de top van deze ronding, waar de golf omknikt, is er een plotselinge slapheid en meegeven, het water zwaait en springt langs de graatlijn als een ketting die geschud wordt, en de beweging loopt van het ene naar het ander deel als langs het lichaam ener slang. Dan gaat de wind op die uiterste rand inwerken, en in plaats van hem zijn eigen, natuurlijke baan te laten volgen, houdt hij hem zwevend, en drijft hem terug, of schraapt hem af en drijft hem in zijn geheel voort. Zodat het schuim aan de top een voortdurende overgang is tussen vormen die door hun eigen massa worden voortgestuwd; en vormen die weggeblazen en weggevoerd worden, waarvan het gewicht overwonnen is’.²⁾

1) Vaughan Cornish, Waves of the Sea, hoofdstuk II.

2) Ruskin, Modern Painters, III, 561.

[p. 164]

Merk op hoe het fijne zand in wolkjes onder de overstortende golfkam opwervelt! Als de golf bijna tot stilstand gekomen is, ziet men hoe het water aan de achterzijde al begint terug te vloeien terwijl de kop nog vooruit loopt. Het water dat zijn snelheid verloren heeft, stroomt terug langs de bodem en veroorzaakt een zeewaartse ‘zuiging’, die meestal de voornaamste faktor is waardoor de nieuw aanstormende golven geremd worden.

98. Golvengeklots.

Waar de golfslag tegen een dijk aankomt of tegen de muur van een kade, worden de golven teruggekaatst, en ziet men de heengaande met de terugkerende golf interfereren. Soms versterken ze elkaar, andere malen verzwakken ze elkaar: de ‘lopende golf’ gaat in een ‘staande golf’ over; de amplitude zou in het gunstigste geval twee maal zo groot als die van de lopende golf kunnen worden.

In werkelijkheid is het verschijnsel veel onregelmatiger. De golven komen niet met constante snelheid en golflengte aanlopen; daarenboven wordt het water bij de kade in 't algemeen ondieper, wat al op zichzelf een toenemen der amplitude veroorzaakt en het breken van de golven, die op dat ogenblik met verhoogd geweld vooruitschieten. Zo kan men de geweldige hoogte begrijpen tot dewelke de zee kan opstormen tegen klippen en havenhoofden.

Men rekent in de praktijk dat golven van h meter hoogte bij het breken een drukking uitoefenen van 50 h² kg/m². Het is de moeite waard na een storm te zoeken naar de uitwerkingen van dat golvengeweld en de uitgeoefende kracht te schatten. Krachten van 5000 kg/m² komen zeker voor.

99. Scheepsgolven.¹⁾ - (Plaat IV).

Van alle mooie vormen van watergolven zijn de scheepsgolven wellicht de allermooiste, als men de schoonheid van zulke mooie dingen vergelijken kan.
W. Thomson, t.a.p.

De scheepsgolven bestaan uit twee groepen: de zijgolven AU₁, AU₂, AV₁, AV₂,,,,,; en de dwarse golven V₁U₁, V₂U₂,,,,, (fig. 92a). Even duidelijk als men de eerste soort ziet, even moeilijk ontdekt men de tweede. Het geheim bestaat eenvoudig daarin, dat men op een brug moet gaan staan of althans zoveel mogelijk in de lengterichting van het vaarwater kijken; we

1) W. Thomson, On Ship Waves (Popular Lectures, 1887). - Phil. Mag. 11, 1, 1906 = Papers, 4, 394.

[p. 165]

zien nml. alle golven beter wanneer we loodrecht op hun kammen kijken. Het is een wondermooi schouwspel, een snelvarend schip te zien aankomen van op de brug over een breed, rustig water (Amstelbrug te Amsterdam!), gevolgd door een statige trein van tientallen dwarsgolven.

Het eenvoudigste stelsel scheepsgolven ziet men als men een houten bal over een breed wateroppervlak voorttrekt, of als een eend snel aan 't zwemmen is (een zwaan is al te groot om een zuiver golvenpatroon te geven!). Ook dan bemerkt men zijgolven en dwarsgolven (⊥ op de kammen kijken!). De spitse uiteinden U₁, U₂, ..., V₁, V₂, ..., liggen op de rechte lijnen AB, AC, die in overeenstemming met de theorie een hoek van 19^o½ met de bewegingsrichting

Fig. 92. Schematisch patroon van de scheepsgolven achter één storingspunt. a) Waaierpatroon de zijgolven, tengevolge van de afhankelijkheid der voortplantingssnelheid van de golflengte. b.) Vereenvoudigd patroon voor het (denkbeeldige) geval dat de oortplantingssnelheid niet van de golflengte zou afhangen; dit wordt benaderd als de snelheid van de boot groter is dan √gH.

vormen; die uiteinden komen overeen met de typische ‘stoombootgolven’ waarop men de roeibootjes angstig op en neer ziet schommelen. Volgens de theorie zouden ze ‘oneindig hoog’ zijn, maar de taaiheid van het water vereffent het gehele patroon enigszins en rondt het af; als schepen zulke golven maken, kan men nog aan het schuim de ‘would be infinities’ (Thomson) herkennen. Tracht op te merken dat de zijgolf en de daarbijbehorende dwarsgolf niet in dezelfde phase zijn. - Indien de voortplantingssnelheid van watergolven niet afhing van de golflengte, zouden de slanke gebogen lijnen van de zijgolven zich herleiden tot twee rechten (fig. 92b); de scheepsgolven zouden er dan uitzien zoals de drukgolven in de lucht om een vliegende kogel, die men dikwijls gefotografeerd heeft.

[p. 166]

De vergelijking der scheepsgolven kan in de volgende eenvoudige vorm neergeschreven worden:



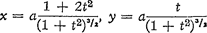. De richting waarin het schip beweegt is die van de x-as. Geef een vaste waarde aan a, en laat t alle mogelijke waarden aannemen: x en y doorlopen de kromme lijm AU₂V₂A; enz. De hoek van 19^o½ is bg sin ⅓.

Bij een schip werken vóór- en achtersteven als twee storingsmiddelpunten, een drukpunt en een zuigpunt, die elk een dergelijk patroon als fig. 92a veroorzaken. Daardoor is het geheel niet altijd eenvoudig te overzien: het verschil tussen zij- en dwarsgolven is duidelijk genoeg, eigenlijk veel mooier dan bij de bol die over het water beweegt; maar men onderscheidt niet altijd goed welke van ieder der twee stevens uitgaan. De achtersteven verstoort dikwijls de golven die hij maakt, doordat hij teveel wervels vormt; men ziet dan vooral het golvenstelsel van de voorsteven. Heeft het schip een zuiverder visvorm, dan zijn er minder wervels, en de twee stelsels golven kunnen op bepaalde wijze invloed op elkaar uitoefenen, al naar de lengte van het schip en de snelheid waarmee het vaart; de weerstand die het schip ondervindt hangt in belangrijke mate van deze interferenties af. Kenmerkend voor een schip is ook de vorm van de voorste zijgolf, wáár zij tegen de voorsteven opspringt, hoe zij breekt, en dit zowel bij langzame als bij snelle voortbeweging van het schip. De golven aan de achtersteven moeten zich beginnen te vormen iets vóór het punt, waar het evenwijdige middenschip begint te versmallen.

In een kanaal stoort de terugkaatsing der golven door de oevers altijd heel erg. Maar in een rustig water met wijd oppervlak kan men soms fraaie interferentieverschijnselen zien, dikwijls het best als men van op een hoogte naar beneden kijkt:

a.	tussen de zijgolven van vóór- en achtersteven;
b.	tussen de zijgolven van een sleepboot en die van het gesleepte schip;
c.	tussen de zijgolven van twee schepen die elkaar in tegenovergestelde richting voorbijvaren.
d.	In een bepaald geval heeft men opgemerkt, dat elk der zijgolven, als zij brak, in een reeks evenwijdige schuimbanden uiteenviel; men kon tot 6 van die banden waarnemen^1).

Let op een schip dat zich in een kanaal statig in beweging zet. Naarmate het verder vaart, ontwikkelt zich achter het schip een trein van plechtige golven, die langer en langer wordt. In een diep kanaal loopt het einde van de golftrein met de halve

1) Nat. 128. 838, 1931.

[p. 167]

snelheid van het schip, de golftrein wordt dus voortdurend langer en langer. Elke golf echter loopt met de volle snelheid van het schip, de waarnemer in het schip ziet die bepaalde golf altijd op dezelfde plaats, maar in het geheel van de groep komt ze meer en meer vooruit. Er is hier dus weer een verschil tussen golfsnelheid en groepsnelheid (§§ 86, 88).

De golflengte der scheepsgolven is bepaald door een eenvoudige voorwaarde: ze moeten juist zó lang zijn, dat ze gelijke tred met het schip houden. De dwarse golven moeten dus dezelfde snelheid V als het schip hebben; de zijgolven die een hoek α met de richting van het schip vormen, hebben een kleiner snelheid: als het schip een afstand V aflegt, komen zij vooruit over V sin α (vergelijk § 89). Aangezien nu de golflengte van gravitatiegolven in diep water evenredig is met het kwadraat hunner snelheid, moeten de golflengten der zijgolven kleiner zijn dan die van de dwarsgolven in de verhouding sin²α, en moeten alle scheepsgolven evenredig met het kwadraat van de snelheid van het schip groeien. Mocht een dwarsgolf bijvoorbeeld er ooit over denken om zich een iets kortere golflengte te permitteren, dan zou ze langzamer dan het schip bewegen en er zich van verwijderen, zodat weer vanzelf de golflengte zou toenemen en dus ook de snelheid. Zo stellen alle golven zich automatisch op de snelheid van het schip in.

Uit de golflengte λ der dwarsgolven krijgt men het eenvoudigst een indruk van de snelheid van het schip. Volgens formule (3) is immers



(als alles in m en m/sec wordt uitgedrukt). - Vgl. § 60.

Waarvoor wordt de arbeid van een varend schip gebruikt? Vooreerst is het water geen ‘ideale vloeistof’, maar een vloeistof met een zekere inwendige wrijving, een zekere taaiheid, zoals alle vloeistoffen trouwens die we kennen; het gevolg is: 1) een zekere wrijving van het water langs de kanten van het schip, die ongeveer 50% van de arbeid verbruikt; 2) de vorming van wervels in het zog van het schip, waarvoor men 10% rekent. 3) Daarnaast echter heeft het schip nog een weerstand te overwinnen die er net zo goed zou zijn als het water werkelijk een ideale vloeistof was, en die de overige 40% van de arbeid verbruikt: er is nml. arbeid nodig voor het vormen en voortdurend vergroten van de golftrein die het schip achter zich aan sleept. De inwendige wrijving speelt hier tenslotte toch weer een rol, want zij maakt dat de golftrein in werkelijkheid niet oneindig

[p. 168]

lang wordt, maar dat de golven langzamerhand gedempt worden. Het eindresultaat is natuurlijk altijd hetzelfde: dat de arbeid van het varende schip tenslotte dient .... om het water van het kanaal of van de zee een weinig warmer te maken!

De energie van watergolven is evenredig met het kwadraat hunner hoogte. Naarmate dus een schip sneller vaart en hoger golven opwekt, neemt de weerstand snel toe: eerst met het kwadraat van de snelheid, weldra met een hogere macht. Als echter het water niet zéér diep is, komt er op een gegeven ogenblik een wijziging in de weerstandswet, welke hierna uiteengezet zal worden.

In ondiep water nemen de scheepsgolven een gewijzigde vorm aan; de hoek van 19^o28' neemt toe naarmate het schip sneller vaart, en het patroon verandert geleidelijk in een enkelvoudige golf.¹⁾ Wanneer een motorboot evenwijdig aan de kust vaart, worden de dwarse golven hoger aan de kant waar de diepte het geringst is.²⁾

‘Als ik, na dit wellicht vrij droge wetenschappelijke betoog, u nog een enkel woord kan zeggen dat ieder van u ertoe brengt zijn ogen te gebruiken bij het kijken naar schepen, boten, eenden en eendjes, met verschillende snelheden over het water bewegend, en deze mooie golfverschijnselen waar te nemen, dan denk ik dat u iets voor de rest van uw leven zult gewonnen hebben, ook al mocht u zich niets meer herinneren van mijn lezing.’
(W. Thomson, On Ship-Waves, slot)

1) T.H. Havelock. Proc. R. Soc. 81, 398, 1908.

2) E.T. Hanson, Proc. R. Soc. 111, 518, 1926.

100. De enkelvoudige golf³⁾ (Wanderwelle, solitary wave, onde solitaire). - (Plaat II).

Eeuwen lang heeft men gedacht dat golven altijd in lange reeksen moesten voorkomen. Pas in 1837 bemerkte Scott Russell toevallig, op een wandeling, een geheel andere soort vloeistofbeweging: een enkelvoudige waterverheffing die zich met grote snelheid voortbewoog. Een enkelvoudige golfberg kan zich over grote afstanden ongestoord uitbreiden, een enkelvoudig golfdal verandert daarentegen weldra van vorm en is onbestendig.

Bij onze waarnemingen over de snelheid van watergolven in ondiep water en over de branding, hebben we gezien dat de golven steeds langzamer gaan lopen indien de diepte H van het water geringer wordt dan de golflengte (§ 97). Voor zeer

3) Een populaire uiteenzetting door Weinstein in: Naturwiss. 21, 383, 1929.

[p. 169]

ondiep water, of zeer lange golven (wat op hetzelfde neerkomt) is de grootst bereikbare snelheid (§ 91):

(4) V = √gH;

deze grenssnelheid is voor alle golflengten dezelfde.¹⁾

Maar wat gebeurt er dan, als we toch een voorwerp met groter snelheid dan die grens door het water trekken? In water van 0,20 m diepte ligt de grenssnelheid bij 1,14 m/sec, dus bij een gemakkelijk bereikbare snelheid. Beweeg een stok zo snel mogelijk door ondiep water: er vormen zich geen dwarsgolven meer, het zog achter de stok is glad en effen, alleen de zijgolven zijn er, en ze krullen hoog op aan beide kanten van het bewegende ‘vaartuig’. Metingen hebben bewezen dat de kracht nodig voor het voortbewegen van schepen ineens kleiner wordt als men de grenssnelheid overschrijdt: want dan moet er geen arbeid meer geleverd worden om een golvenpatroon achter het schip te vormen. Het schip wordt half uit het water getild en vaart op de top der enkelvoudige golf. Deze ontdekking werd eigenlijk gedaan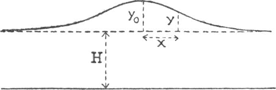

Fig. 93. Profiel der enkelvoudige golf.

door een paard, het paard van de trekschuit tussen Aberdeen en Glasgow, dat toevallig op hol ging, en zijn werk veel gemakkelijker bij die grotere snelheid bleek te verrichten! De vorm der enkelvoudige golf wordt gegeven door de vergelijking

Haar snelheid is √g(H + y_o).

De golf breekt wanneer y_o > 0,78 H.

Verder moeten we enkelvoudige golven overal zoeken waar zeer ondiep water een grote snelheid krijgt; zodra V > √gH gaat zich het water in enkelvoudige golven rangschikken. Als de baren aan het strand breken, gaat elke baar over in een vlakke plaat water, waarvan een schuimende rand over het strand loopt (Plaat II). Soms ziet men twee dezer golven over elkaar schuiven of elkaar kruisen. Als de stoep geschrobd wordt en het water der waterleiding daarover stroomt, verdeelt het zich in dergelijke enkelvoudige golven, terwijl toch de toevoer door de kraan

1) Eenvoudige afleiding in Müller-Pouillet, V, 340.

[p. 170]

voortdurend even snel is. Men ziet het verschijnsel al, wanneer een emmer water over de vlakke straatstenen wordt uitgegoten. De snelheid van een dergelijk ‘trapje’ in het wateroppervlak, op de grens tussen een laag van grotere dikte H₁ en een laag van geringe dikte H₂, wordt gegeven door de uitdrukking:

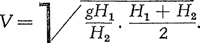Schat de waarde die men moet verwachten voor de platen water waarin de branding der zee zich oplost, en vergelijk met de door uzelf gemeten snelheid.

Een oppervlakkige gelijkenis met het varen op de top der enkelvoudige golf zou men kunnen zoeken in het planeren van zeil- en motorboten¹⁾. De echte ‘glijboten’ hebben een platte bodem en een achterschip van geringe diepgang; bij voldoende snelheid stellen ze zich met de vóórsteven schuin omhoog, en worden door de geweldige druk van het hun tegemoetstromende water bijna uit de vloeistof opgelicht, zodat de weerstand zeer verminderd wordt. Het water glijdt grotendeels onder het schip door, een kleiner gedeelte van de stroom buigt om en spuit van onder de vóórsteven schuin opwaarts naar voren. Reeds uit deze laatste trek ziet men welk een typische bewegingsvorm het planeren is; ook bemerke men, dat planeren des te gemakkelijker tot stand komt naarmate het vaarwater dieper is, terwijl een enkelvoudige golf zich op diep water niet eens vormen kan. Het planeren en het varen op de top der enkelvoudige golf zijn dus twee principiëel verschillende bewegingsvormen.

1) H. Wagner, Proc. Intern. Congress of Appl. Mech. 4, 126, 1934.

101. Stromend water dat in een reeks van enkelvoudige golven beweegt.²⁾ - (Plaat V).

Het mooist zien wij deze merkwaardige verschijnselen bij sterk hellende goten of kanalen, die dikwijls door technische bedrijven voor waterafvoer gebruikt worden en waarin een ondiepe waterlaag stroomt. In het eerste gedeelte is de waterstroom geheel gelijkmatig, een bewijs dat de toevoer ononderbroken is (centrifugaalpomp b.v.). Maar nadat het water voldoende snelheid gekregen heeft, verdeelt het zich ‘vanzelf’ in een aantal trappen: elk daarvan is een enkelvoudige golf, zeer vlak aan de achterzijde, steil aan de vóórzijde, naar dewelke zij zich beweegt. Die eigenaardige golfvorm ontstaat, doordat in dit ondiepe water de snelheid van de golfberg reeds zeer merkbaar groter is dan die van het golfdal: de golf wordt dus steeds steiler. De eigenlijke schuimende golfberg is ongeveer 7 maal zo breed als het water diep is.

Werp een snippertje papier op het water: de golf haalt het

2) Nat. 30, 1883. - Ph. Forchheimer, Sitz. Akad. Wien, 112, 1697, 1903. - Vaughan Cornish, Waves of the Sea, hoofdstuk III.

[p. 171]

in, zij beweegt dus sneller dan de stroom; noem V de snelheid van de golf. - Daar waar een dergelijke trappengolf uitstroomt ziet men bij elke golfberg die aankomt hoe het water ineens overvloediger en met groter sprongwijdte in een gulp uit de monding der pijp komt: blijkbaar heeft het een grotere snelheid bij de golfberg dan bij het golfdal.

Wij noemen de stroomsnelheden van het water in de golfberg V₁, in het golfdal V₂. Laten we een ogenblik in gedachte aan de gehele waterstroom een snelheid V geven in tegengestelde richting van de stroming: de golven staan nu voor ons stil, maar het water stroomt langzaam stroomopwaarts, met snelheid V-V₁ in de golfberg, V-V₂ in het golfdal. Door elke doorsnede moet er evenveel water stromen; als dus H₁ de diepte is in de golfberg, H₂ in het golfdal, moet

(1) H₁(V-V₁) = H₂(V-V₂).

Beschouw nu weer het stromende water zoals het is. Volgens § 75 mogen we schrijven: V₁ = c√H₁J, V₂ = c√H₂J. Door invullen in (1) komt er:



= voortplantingssnelheid van de golven (t.o.v. den rustenden waarnemer).

Beproef die formule aan de ervaring te toetsen! Haal c uit de tabel § 75, meet zo goed mogelijk H₁ en H₂ met een latje, schat het verhang J en bereken V. - De orde van grootte komt wel goed uit, maar een werkelijke overeenstemming kan men niet verwachten, omdat c voor zulk ondiep water niet de normale waarde heeft. Misschien kunt u c bepalen uit het eerste gedeelte van de helling, waar het water zich nog niet in golven heeft verdeeld.

De verschillende golfkammen hebben niet precies dezelfde snelheid, want in de hoogste is het water het diepst en de golfsnelheid het grootst: zij halen de kleinere in en versmelten ermee. Vandaar ook dat de afstanden tussen de golven zeer ongelijk zijn (volmaakt anders dan bij de gewone golfbeweging!). Aan lange leidingen kan men het aantal golven per minuut op verschillende punten van de helling bepalen, en ook de schommelingen in golflengte.

Meer dan eens ziet men het water uit lange pijpen in onregelmatige gulpen uitstromen; het is dan niet mogelijk binnen in de buis te kijken, maar als werkelijk de toevoer regelmatig is, en de buis slechts met een ondiep laagje water bedekt, kunnen we veilig aannemen dat zich hier ook een trap van enkelvoudige golven gevormd heeft.

Veel watervallen zijn om dezelfde reden pulserend. Houd uw hand in het vallende water: u voelt de opeenvolgende stoten. Kijk naar de weerspiegeling van het licht aan het oppervlak

[p. 172]

van het vallende water: u ziet er golfjes over lopen. Dikwijls hoort men ook een pulserend geruis. Bij Gasselternijeveen, waar de weg naar Gasselte de Hunse kruist, kan men zulk een watervalletje waarnemen, dat ongeveer 6 maal in de sekunde pulseert.

102. Demping van zeegolven door olie.

Een beroemd volksgeloof, dat men al vermeld vindt in Plinius, en dat tenslotte gebleken is in hoofdzaak juist en wetenschappelijk verklaarbaar te zijn!

Benjamin Franklin vertelt¹⁾:

‘Ik geloof, dat het in de laatste tijd al te zeer mode is geworden, de kennis van de oude volkeren te onderschatten. Ook zijn de intellectuelen teveel geneigd de wetenschap van den gewonen man te kleineren. Het glad maken van golven met olie is een voorbeeld van beide.

.... In 1757 bevond ik mij op zee met een vloot van 96 zeilen, met bestemming voor Louisbourg; ik merkte op dat het vaarwater achter twee der schepen merkwaardig effen was, terwijl het achter al de andere door de frisse wind gerimpeld werd. Getroffen door dit verschil, wees ik het tenslotte aan den kapitein, en vroeg hem de verklaring ervan. “De koks, zei hij, zullen wel juist hun vettig water door de spuigaten uitgegoten hebben, en dit heeft de zijkanten van de schepen een weinig vet gemaakt;” en hij gaf mij dit antwoord op ietwat achteloze wijze, alsof hij mij iets vertelde dat iedereen overigens wel wist. Ik geloofde in 't eerst niet veel van zijn verklaring, ook al kon ik geen andere bedenken. Maar, mij herinnerend wat ik vroeger bij Plinius had gelezen, besloot ik enige proeven te nemen over de invloed van olie op het water, zodra ik gelegenheid daartoe zou hebben.

.... Tenslotte, toen ik mij eens te Clapham bevond, waar er in het park een grote vijver is, en het water daarvan sterk door de wind golfde, haalde ik een flesje van een oliestel, en goot een weinig daarvan op het water. Ik zag hoe de olie zich met verrassende snelheid over het wateroppervlak uitspreidde; maar het deed de golven niet bedaren; want ik had het eerst aan de lijzijde van de vijver gegoten, waar de golven het grootst waren²⁾, en de wind dreef mijn olie naar de kant terug. Ik begaf mij toen aan de windzijde, waar de golven zich vormden; en daar veroorzaakte de olie (alhoewel ik niet meer dan een theelepeltje er van gebruikte) een onmiddellijke kalmte over een

1) Philos. Trans. 64, 447, 1774.

2) Vgl. § 92.

[p. t.o. 172]

PLAAT V.
Reeks van enkelvoudige golven in een ondiep, sterk hellend waterkanaal (§ 101).
Het water stroomt ons tegemoet; diepte ca. 7 cm, helling tenminste 7%.
Naar Vaughan Cornish, Waves of the Sea, blz. 303.

[p. t.o. 173]

PLAAT VI. Voortplanting van watergolven. a. Spiegelproef van Fresnel. - b. Buiging door een smalle spleet. - c. Buiging door een schermpje. - d. Verstrooiing van evenwijdige golven door een resonator. - e. Terugkaatsing van evenwijdige golven door een vlakke spiegel. - f. Een holle spiegel vereenigt evenwijdige golven in zijn brandpunt. - Vgl. § 110.
Naar L. Heck. Jahrb. f. drahtl. Telegraphie, 34, 121, 1929.

[p. 173]

oppervlak dat eerst verscheidene vierkante meters besloeg en zich dan verbazend uitbreidde, zodat het tenslotte de lijzijde bereikte, en dat gehele gedeelte van de vijver, wellicht een halve morgen groot¹⁾, zo glad als een spiegel maakte.

Voortaan zorgde ik ervoor, telkens als ik buiten ging wandelen, een weinig olie mee te nemen in de bovenste holle geleding van mijn bamboe wandelstok, om daarmee de proef te herhalen als er gelegenheid zou zijn; en ik vond dat zij onveranderlijk slaagde.’

Franklin kwam ook op de gedachte, een papiertje in de vorm van een komma met olie te drenken, en het op het water te werpen. De komma gaat aan het draaien als de olie snel van de punt wegstroomt en zich uitbreidt. - Deze proef lukt niet in een schotel water, een groot oppervlak is onontbeerlijk; want zodra het zich uitbreidend olieoppervlak het gehele water overdekt, houdt de uitstroming op.

Een poging om de golven van de branding te stillen mislukte in hoofdzaak, alhoewel de schuimvorming door de olie ophield.

Franklin verzamelde een groot aantal berichten over de werking van olie op de zeegolven. Plinius de Oude vermeldt dat de zeelui er gebruik van maakten, en ook na die tijd vindt men dergelijke vermeldingen telkens weer, nu hier, dan daar. Duikers gebruiken een weinig olie om het oppervlak effen te maken en er beter doorheen te kunnen zien. Bijna altijd is het kielzog der schepen gladder dan de zee daarnaast, hetgeen te wijten is aan de kleine hoeveelheden olie welke stoom- of motorschepen voortdurend in het water brengen; schepen die pas geteerd zijn hebben een effener vaarwater dan andere. De vissers weten dat plaatsen waar zich scholen vissen ophouden, aan het gladdere wateroppervlak kenbaar zijn: hetzij omdat de vissen een weinig van een olieachtige stof in 't water brengen; of omdat ze bij voorkeur gebieden opzoeken waar veel drijvende zeediertjes en mikroskopische plantjes voorkomen (het plankton), en die daardoor met een vettig oppervlaktelaagje bedekt zijn.

Nog voortdurend komt het voor dat schepen door het gebruik van olie van de ondergang gered worden.²⁾ Men hangt een zak buitenboord, waarin kleine gaatjes geprikt zijn, zodat de olie er langzaam uitstroomt. Een liter olie per uur is voldoende om de zee om een varend schip te doen bedaren.

Men kan gemakkelijk zelf proeven nemen in de aard van die van Franklin, zodra er eens een stormachtige dag komt. U zult

1) 1 morgen = 4000 m² ongeveer.

2) Zie bv. Ann. Hydr. 24, 136, 1896.

[p. 174]

dan merken dat de oliehuid wel de capillaire rimpels en het schuim doet verdwijnen, maar niet de gravitatiegolven. Het is dan ook een sprookje dat olie de zee geheel vlak zou maken: ze verhindert de vorming der zeeën en hun overstorten, maar grote, gladde deiningsgolven blijven op en neer gaan. Als u experimenteert bij het baden in zee, kunt u waarnemen dat de olie evenmin invloed heeft op de brandingsgolven; hier immers wordt het overstorten niet veroorzaakt door de werking van de wind op het oppervlak, maar door het ondieper worden van de zee.

De werking van de olie schijnt aan twee effekten te wijten¹⁾. 1) De oliehuid oefent een zeer merkbare weerstand uit tegen samendrukking; de werking van de wind, die anders van plaats tot plaats verschilt door de grote grilligheid der luchtstroming, wordt daardoor gelijkmatiger over het oppervlak verdeeld, meer vereffend. - 2) De oliehuid dempt door haar taaiheidsweerstand alle rimpels die zich zouden hebben kunnen vormen. Het belang dat deze tweede factor heeft zal nog overtuigend blijken bij de waarneming der rimpels, door regendruppels veroorzaakt (§ 104).

Taaie oliesoorten zoals raapolie werken het best. Paraffineolie en petroleum werken vrij slecht, tenzij wanneer men ze met ⅓ tot ¼ raapolie mengt. De gunstiger eigenschappen van vetoliën zijn terug te brengen tot het feit, dat hun molekulen polair zijn en zich loodrecht op het oppervlak instellen. Zeepwater, gemaakt door 2 tot 10% groene zeep in regenwater op te lossen, werkt tenminste zo goed als olie, want de zeepmolekulen zijn ook polair; voor onze proeven is echter een bezwaar, dat de laag helemaal niet zichtbaar is, en haar aanwezigheid dus alleen door de demping der golfjes bemerkbaar wordt, terwijl de oliehuidjes althans heel zwak de weerspiegeling van het oppervlak wijzigen. Terpentijn is zeer bruikbaar voor proefjes in een vijver, daar het door zijn mooie interferentiekleuren goed zichtbaar is, en daarenboven na enige tijd verdampt, zodat men opnieuw in dezelfde vijver kan experimenteren.

Met een eenvoudige proef van die aard bepaalde Forel de dikte van het oliehuidje: 20 cm³ olie deden de rimpelingen van het water verdwijnen over een gebied van 4000 m²; de laag was dus 5.10^-7 cm dik. Dit is de grootte van slechts twee molekulen olie, de laag is inderdaad twee molekulen dik. - Zo kan dus de afmeting der molekulen door een waarneming in 't vrije veld gevonden worden.

1) Adams, The Physics and Chemistry of Surfaces, p. 91 (Oxford, 1930).

[p. 175]

103. Demping van zeegolven door andere oorzaken.

Men beweert dat zeewier, afval, zaagsel, schoorsteenroet of zelfs eenvoudig schuim, de golven gladder maken. Het lijkt zeer waarschijnlijk dat in die verschillende gevallen kleine hoeveelheden olieachtige of harsachtige stoffen op het water gebracht worden; de aanwezigheid van schuim wijst al op het voorkomen van oppervlaktelaagjes. Maar wat te zeggen van de verhalen van zeelui over de bedarende werking van hagel, ijsnaalden, regen of natte mist (volgens Larisch)? In het geval van de regen acht Reynolds een verklaring mogelijk: elke druppel veroorzaakt een wervelring en mengt waterlagen van verschillende snelheid door elkaar¹⁾. Iets dergelijks kan men zich ook voor de hagelkorrels voorstellen. Maar voor ijsnaalden en mistdruppeltjes is die verklaring nauwelijks houdbaar. Sommigen beweren dat het voldoende is als de taaiheid der oppervlaktelaag gewijzigd wordt; anderen denken aan temperatuurverschillen, waardoor oppervlakjes van verschillende capillariteitsconstante naast elkaar voorkomen.

Goede waarnemingen hierover zijn nog zeer nodig.

1) Nat. 11, 279, 1875.

104. Gerimpelde en effen gebieden op onze binnenwateren²⁾ - (Vgl. deel I, Plaat XV).

Een vijver, een kanaal, vertonen haast altijd gedeelten die met rimpels overdekt zijn, naast andere die er geheel glad uitzien. Klaarblijkelijk is het de wind die de rimpelingen teweegbrengt, maar waarom hier wel en daar niet? We bemerken weldra dat men de rimpels alleen goed ziet aan de grens van de lichte en donkere partijen die het water weerspiegelt, omdat dan het gerimpeld oppervlak voorwerpen van andere helderheid terugkaatst dan het gerimpelde; om de verdeling der rimpels te beoordelen moeten we dus achtereenvolgens van verschillende standpunten kijken.

Het blijkt ons nu, dat het water nabij de oever van waar de wind waait bijna altijd gerimpeld is, de kant naar waar hij waait is effen. Merkwaardig is de scherpe grenslijn tussen beide gebieden, die vooral bij een regenbui verrassend duidelijk zichtbaar is. Het effen gedeelte is de strook naar dewelke de wind alle verontreinigingen

2) Halbfass, Beiträge z. Geophys. 13, 306, 1914. - Halbfass, Grundzüge einer vergleichenden Seeenkunde (Berlin 1923), blz. 147. - De bezwaren van dezen schrijver tegen de theorie der oliehuidjes zijn thans niet meer vol te houden.

[p. 176]

van het wateroppervlak heeft geblazen; dorre bladeren, grasjes, afval drijven daar, maar worden niet gewoon naar de kant bij elkaar gedreven: men kan duidelijk zien dat ze niet vrij bewegelijk zijn, maar verbonden door een onzichtbaar vlies dat hun bewegingen belemmert. Zo komen wij er vanzelf toe, te onderstellen dat de effen gedeelten door een uiterst dun vetlaagje bedekt zijn, waar de capillaire rimpels door gedempt worden. Aan de rimpels kan men zien hoe de uitbreiding van het vetlaagje verandert; een voorbijvarende boot, een schaar watervogels verstoren de regelmaat der grenslijn. Op grote plassen kan men soms duidelijk opmerken dat het oliehuidje zich juist bij de uitmonding van een riool vormt, in het kielzog van een schip, om het lijk van een vis. Weldra leert men uit de rimpelingen beoordelen of het water van een rivier min of meer verontreinigd is; het bewegelijke oppervlak der beek met al zijn tintelingen maakt een geheel andere indruk dan de stroperige, effen kanalen in de nabijheid van fabrieken en achterbuurten.

Het is niet alleen de wind die het oliehuidje met zich meevoert. Overal waar de stroming nabij het oppervlak vertraagd wordt, bijvoorbeeld door een stuw, door een in het water dompelende balk, wordt het capillaire huidje tegengehouden; dikwijls is zijn grens net zichtbaar, alsof er een fijne draad op het water dreef. Als het beekje zeer ondiep is en de bodem uit blank zand bestaat, kan men in de zonneschijn de schaduw van deze grenslijn bespeuren.¹⁾

De olielaagjes waarover het gaat zijn stellig dunner dan 0,2μ (= 0,0002 mm), anders moesten ze interferentiekleuren vertonen. Feitelijk komen allerlei dikten voor, van 0,001 μ tot 0,1 μ. Het schijnt dat olie zich alleen tot zulke uiterst dunne huidjes uitbreidt, wanneer ze niet volmaakt zuiver is, doch kleine hoeveelheden hars of vrij vetzuur bevat (vgl. I, § 160).

Op de effen gebieden kan men stelselmatig waarnemingen doen betreffende de invloed der verontreinigingen²⁾:

bij lichte wind rimpelt een verontreinigd wateroppervlak niet; bij sterkere wind vertoont het alleen golfjes die vloeiend afgerond zijn in plaats van een scherpe top te hebben;

bij regen vormt elke druppel er kleiner en minder talrijke kringen dan in het schone water; dit laatste siddert van duizend trillingen die in alle richtingen dooreenlopen, terwijl het geoliede oppervlak eenvoudig om elk druppeltje een beperkt

1) Nat. 137, 777 en 1073, 1936; 138, 466, 1936.

2) Ritter, Ann. Soc. météor. France, 43, 1895. - Naturwiss. 5, 137, 1917.

[p. 177]

ringenstelseltje vertoont; deze waarneming bewijst afdoende dat het ontbreken van fijne rimpeltjes in de oliegebieden niet te wijten is aan een ‘minder vat hebben’ van de wind, maar dat het door de sterkere demping te verklaren is;

bij buien geeft elke grote druppel in het geoliede gebied een bel, die verscheidene sekunden bestaat, terwijl in het schone gebied de druppel onmiddellijk in kleine druppeltjes uiteenspat; hetzelfde merkt men bij het roeien, als de riemen water doen opspatten;

een heel klein stukje kamfer (een paar mm groot), dat men op een verontreinigd oppervlak laat vallen, beweegt weinig, terwijl het op een schoon oppervlak de grilligste bewegingen uitvoert;

een druppel benzine spreidt zich slechter uit op een vuil dan op een schoon oppervlak;

talkpoeder of lycopodiumpoeder kunnen over een schoon oppervlak voortgeblazen worden (ze worden er niet door bevochtigd); in een verontreinigd oppervlak blijven ze plakken en zweven er niet over heen;

een goed gereinigd glazen staafje, niet met de vingers aangeraakt, wordt in het water gedompeld en er dan voorzichtig uit omhoog getrokken; als de stofjes op het omgevende wateroppervlak naar de staaf toe drijven, is er een oliehuidje; bij een schoon oppervlak bemerkt men een zwakke beweging van het staafje af;

als men een hete metalen knop boven het oppervlak houdt, vormt zich daaronder een stofvrije plek.

Verschillende dezer kenmerken vormen in de praktijk niet zulk een scherp kriterium: er zijn allerlei overgangen. De twee laatste waarnemingen gelukken alleen op een zeer zuiver oppervlak.

Naast de aanwezigheid van oliehuidjes zijn er nog sommige andere oorzaken van rimpeling van het wateroppervlak bekend, die in uitzonderlijke gevallen een rol kunnen spelen.

a.	Soms delen de stoom- of motorboten aan het oppervlak een reeks kleine trillingen mee die het oppervlak rimpelen; dat is de nog onvoldoend bekende ‘trepidatie’. Ik heb soms het water om een stilliggende boot, waarvan de motor evenwel werkte, aan alle kanten met een patroon van kleine ribbels bedekt gezien, die tussen de boot en de kade prachtige interferenties en staande golven vertoonden.
b.	Soms ziet men hoe de zee gerimpeld is op de plaats van de schaduw ener alleendrijvende wolk; rechtstreekse meting

[p. 178]

	toont aan dat het oppervlak daar snel afkoelt, en dit zou de dichtheid of de oppervlaktespanning voldoende veranderen opdat rimpelingen aan de grens van dit gewijzigde gebied tegengehouden zouden worden.^1)
c.	Gladde gebieden zouden kunnen ontstaan daar waar er een opstijgende stroming is.^2) Het water dat van beneden komt neemt nog geen deel aan de golfbeweging, en eer deze zich eraan meedeelt is het al door nieuw aankomend water vervangen. Uit de theoriën van Bjerknes over de diskontinuïteitsoppervlakken zou dan begrijpelijk zijn waarom die gebieden meestal een lange, smalle vorm hebben.

1) J. Thomson, Phil. Mag. 24, 247, 1862. - Halbfass, Naturwiss. 5, 496, 1917.

2) Ann. Hydr. 44, 227, 345, 1916.

105. Druppels.

Bekijk aandachtig de dauwdruppeltjes op een grashalm. Ze bevochtigen hem niet, omdat hij met een dun waslaagje bedekt is. De druppeltjes zijn des te mooier bolrond naarmate ze kleiner zijn, omdat de werking van de zwaartekracht dan geen rol meer speelt vergeleken met de oppervlakte-spanning. Ook op klaver, een Robiniablaadje en andere planten zijn de dauwdruppeltjes prachtig. Veel waterplanten worden niet bevochtigd door water dat er toevallig op spat; zo ziet men al van verre de zilveren pareltjes schitteren op het Rood Kroos (= Azolla), dat men in Holland en Utrecht op veel sloten aantreft.

Een struikje in de regen kan verrukkelijk mooi zijn, bijvoorbeeld meidoorn in de winter. Aan elke scherpe hoek hangt een parel van water, fonkelend in het licht. Bekijk ook de regendruppels aan de naalden van een denneboom.

Een spinnewebdraad die zich met dauw bedekt in de herfstmorgen, is niet bekleed met een gelijkmatig dun waterhuidje, maar met een parelsnoer van druppeltjes. Dat komt, omdat een dunne watercylinder labiel wordt onder de werking der oppervlaktespanning als zijn lengte groter is dan zijn omtrek. - Nog mooier kan men dit zien bij een gewoon, niet-bedauwd spinneweb van het rondgewerkte soort, liefst van een volwassen spin³⁾; knip een gaatje in een stuk karton en smeer daaromheen een weinig gom: u kunt nu gemakkelijk een of twee van de buitenste concentrische draden van het web vastgeplakt krijgen, zo dat ze over het gaatje lopen en met een flinke loupe bekeken kunnen

3) C.V. Boys, Soap Bubbles (London 1907), blz. 84.

[p. 179]

worden (fig. 94). Men ziet nu de draad bedekt met talloze druppeltjes van misschien 0,03 mm dik en op 0,06 mm afstand van elkaar. Er zijn er meer dan 250·000 over het gehele net! Zij ontstaan doordat de spin een draad maakt van snelstollende zijde, en daar omheen een lijmachtige vloeistof afscheidt, die eerst een cylinder vormt, en dan in een reeks bolletjes overgaat. Uit de hoger genoemde stabiliteitsvoorwaarde vindt men gemakkelijk dat de bolletjes op een afstand van



maal hun eigen straal van elkaar verwijderd moeten zijn, dus, gemeten van centrum tot centrum, op ongeveer 2 maal hun middellijn. Dat komt niet

Fig. 94. Druppeltjes langs de draad van een spinneweb.

slecht uit. Als u goed kijkt kunt u zelfs zien dat er midden tussen twee grote druppeltjes meestal nog een heel kleintje zit, precies zoals de theorie der minimum-oppervlakken het vereist! Men kan het verschijnsel volkomen nabootsen, door een zeer dunne kwartsdraad even in castorolie te dompelen; het is dus wel zeker dat het niet de spin is die de theorie der minimum-oppervlakken heeft bestudeerd!

Het is zelfs voldoende, een weinig speeksel tussen duim en wijsvinger tot een draadje uit te trekken: onder het vergrootglas ziet men dan duidelijk dat er een centrale, dunne draad is, bezet met afwisselend grote en kleine druppeltjes.

106. Rollende waterdruppels.¹⁾

Bij een heftige regenbui ziet men soms, op een vijver, waterdruppeltjes die enkele sekunden over het oppervlak van het water rollen, zweven om zo te zeggen, en die dan pas verdwijnen. Neen, het zijn geen luchtbellen! ze zijn kleiner en schitteren op een bijzondere manier. Men ziet ze ook bij de voorsteven van een snelvarende motorboot, als hij het water doet opspatten in zijn vaart.

Osborn Reynolds zegt, dat men die rollende droppels niet krijgt als men eenvoudig eens met een stok in het water plonst; hij geeft de raad een plaats uit te zoeken waar het oppervlak schoon lijkt, en daar herhaaldelijk en telkens opnieuw in het water te roeren en te plassen. Ir. P. Schut merkte onafhankelijk het verschijnsel op bij het baden in zee: men moet hard op het

1) O. Reynolds, Proc. Manch. Lit. Philos. Soc. 21, 39, 1881. - Papers, 1, 413.

[p. 180]

water slaan, alsof men iemand nat wil spatten. Reynolds verklaart de proef door te zeggen dat het oppervlak volmaakt vrij van vethuidjes moet zijn; het plonsen dient eenvoudig om het oppervlak te scheuren en vers water uit de diepte aan te voeren; en hij denkt dit aan te tonen, door het oppervlak eerst met zwavelbloem te bestuiven, die zich aan het onzichtbare huidje vasthecht: de rollende druppels verschijnen juist daar waar het bestoven oppervlak door helder water verdrongen is, en ze verdwijnen waar het ‘oude’ oppervlak weer begint. - In het licht van moderne onderzoekingen schijnt een andere verklaring echter waarschijnlijker. We weten nu dat een oliehuidje eer gunstig dan ongunstig is voor de vorming van rollende druppels; maar wat hindert zijn de stofjes, de stofjes op het water en zelfs de stofjes in de lucht. Door het plassen krijgt men een schoon, stofvrij oppervlak en verwijdert men zelfs de stofjes uit de onderste luchtlaag; op het gezwavelde oppervlak ontbreken de rollende druppels, omdat daar behalve de oorspronkelijke stofjes ook het fijne zwavelpoeder hun vorming belemmert.

107. Schuim.

Waar zich schuim op het water vormt dat niet onmiddellijk verdwijnt, kunnen we wel zeker zijn dat er bepaalde organische verontreinigingen in het water voorkomen, die het oppervlak als een huidje bedekken. Het zijn vooral de saponinen die dit doen (zo genoemd naar zeep = sapo, die in hoge mate dezelfde eigenschap bezit); ze worden gevormd door een aantal waterplanten en zeewieren. Hun molekulen zijn zeer langwerpig, en hebben aan het éne eind een grote affiniteit voor water, zodat ze zich loodrecht op het wateroppervlak stellen als korenaren op een akker.

Waar er zand gestort wordt in een sloot, ziet men grote hoeveelheden van een bruinachtig. schuim bovendrijven. Waaruit bestaat dat?

Als er na een storm grote hoeveelheden schuim op de zee voorkomen, kunt u er gemakkelijk een emmertje mee vullen en kijken hoe het er na een uur uitziet: een gedeelte van het schuim is overgegaan in een vuile, bruine vloeistof, waarin men soms met een mikroskoopje infusoriën ziet rondzwemmen.

‘Gewoonlijk blijft zeeschuim slechts even nadat het gevormd is bestaan, het gaat over in een witte laag en verdwijnt. Maar het schuim van een aanhoudende storm is geheel verschillend; het is “geslagen schuim”, dik, blijvend, en heel vies over een

[p. 181]

vuilgekleurde zee, vooral door zijn eigenschap om over de toppen der golven te blijven hangen en zich in klodders te verenigen, die door de wind voortgedreven worden.’

‘Na een felle storm van enkele dagen is het water niet alleen tot gewoon schuim geslagen, maar tot een massa zich ophopende “gist”, die in touwen en festoenen hangt van golf tot golf, en bij hun overstorten en breken als een draperie afhangt; het wordt door de wind meegenomen, niet in vervliegend stof, maar als geheel, in gewrongen, afhangende, gewonden massa's, die de lucht als met witte en dichte sneeuw vervullen, en waarvan de vlokken elk een voet of twee lang zijn.’¹⁾

1) Ruskin, Modern Painters, III, 569.

108. Donkere vlekken op asfaltwegen.²⁾

Op onze asfaltwegen ziet men dikwijls langwerpige vlekken; vers zijn ze donker, na een dag of twee worden ze bleker en verdwijnen tenslotte³⁾. Soms zijn er uitgerekte ringen bij, andere malen ringen met knobbels (fig. 95). Altijd zijn de vlekken verlengd

Fig. 95. Donkere olievlekken op asfaltwegen.

in de richting van de weg en van het verkeer. Sommige zijn maar een paar centimeter lang, men heeft er echter ook van 35 cm gezien. De vormen wisselen van plaats tot plaats en van dag tot dag.

Het lijkt waarschijnlijk dat we hier te maken hebben met oliedruppels die van automobielen weggespat zijn; zijn het dezelfde druppels die op natte wegen de prachtige gekleurde ringen vormen? Ontstaan dan de ring- en knobbelvormen bij het opdrogen, ofwel bij het uitwalsen van een druppel door een automobielwiel?

2) Quant, de Natuur, 51, 115, 1931.

3) Quant geeft op: vers, glinsterend blauw; later donkerder.

109. Slechte bevochtiging; flotatie.

Bij regenbuien vormen zich evengoed plassen op het droge zand der duinen als op gewone grond. Alleen het zand dat vlak bij het oppervlak ligt wordt bevochtigd en vult zich met water; reeds op 3 tot 8 cm diepte vindt men het gewone, kurkdroge en luchthoudende zand. Na enige tijd echter ontstaat de bevochtiging, en de hele plas loopt in enkele sekunden leeg.

[p. 182]

Men kan de ‘afvoerbuizen’ uitgraven en volgen, te midden van de droog gebleven laag.¹⁾

Goed door de zon gedroogd zand kan aan de oppervlakte van een rivier blijven drijven en meegenomen worden door de stroom, terwijl toch iedere korrel soortelijk veel zwaarder dan water is; de korrels kunnen vrij grof zijn, zelfs kleine steentjes van 2 mm middellijn komen voor! Roert men, dan zinkt het zand onmiddellijk. Het verschijnsel is zeldzaam, het wordt ook waargenomen aan meren met zandige oevers, wanneer een zachte wind van de oever naar het meer waait; het stuivende zand vormt vlekken van enkele centimeters middellijn, die echter al op enkele meters van de oever zinken, omdat de korrels nat geworden zijn. - Men kan het verschijnsel nabootsen in 't laboratorium en maakt er gebruik van in de techniek (‘flotatie’)²⁾.

1) J.W. van Dieren, Organogene Dünenbildung, blz. 92 (Diss. Amsterdam, 1934).

2) Nat. 4, 19, 1871. - Amer. Journ. of Sc. 40, 476, 1890. - Science, 63 en 64, 1926.

110. De watergolven als model van de algemene golftheorie. - (Plaat VI).

De vergelijking van watergolven met geluid en licht is inzoverre niet geheel goed, dat de interferentie van watergolven niet uit het eenvoudig optellen van de amplituden te berekenen is. Tussen twee interfererende watergolven is er altijd wisselwerking.
Bij de proeven hinderen de golven die door de oever teruggekaatst worden. Dit bezwaar is echter niet groot, wanneer de oever zacht glooiend oploopt: de golven worden daar dan gedempt.

1.	Uitzending van golven door een resonator. - Dompel een bal periodiek in het water: er ontstaat een stelsel concentrische golven.
2.	Interferentie. - Werp gelijktijdig twee stenen in 't water. Twee stelsels cirkelgolven breiden zich uit. Ieder van beide gaat zijn gang dwars door het andere, alsof dat stelsel er niet was; waar de golfjes elkaar doorkruisen ziet men ze interfereren: twee golfbergen of -dalen versterken elkaar, een golfberg en een golfdal verzwakken elkaar.
3.	Spiegelproef van Fresnel. - Bevestig twee balkjes aan een dwarsplankje van 50 cm lengte, gebruik dat als handvat om de twee balkjes gelijktijdig rhytmisch in het water te dompelen en eruit te trekken. Er ontstaan twee golvenstelsels die samen

[p. 183]

	interfereren zoals bij de spiegelproef van Fresnel met monochromatisch licht. Variëer de trillingstijd en de amplitude tot het patroon zo mooi mogelijk is. Met enige aandacht kan men zien hoe de knopen en buiken op hyperbolen liggen, waarvan de twee trillende balkjes de brandpunten zijn. - Terugkaatsing door de oever is bij deze proef zeer hinderlijk.
4.	Spiegelproef van Lloyd. - Kies ditmaal met opzet een steil afvallende oever, b.v. de vertikale muur van een kade. Laat een balkje op en neer trillen in het water, op 1 m afstand van de oever. De golven die ontstaan interfereren met de teruggekaatste, en hyperbolen worden zichtbaar zoals bij de vorige proef.
5.	Beginsel van Huygens. - Een plankje, dat met enkele grote spijkers bezet is op de wijze van een hark, wordt in het water gedompeld. Elke spijker geeft een golfkringetje, al deze kringen samen vormen een rechte golf die aan de uiteinden halfcirkelvormig om het plankje loopt.
	Een stok die in het water geworpen wordt vormt een dergelijk golvenstelsel, dat men zich ontstaan kan denken uit de samenwerking der elementaire golfjes van al zijn punten.
6.	Een gebogen staaf of tak geeft kringgolven, waarvan het middelpunt overeenkomt met het krommingsmiddelpunt der staaf. Aan de holle zijde worden de golfkammen steeds korter, en dus hoger; aan de bolle zijde steeds langer, dus lager (want de energie verdeelt zich over een groter watermassa).
7.	Evenwijdige golffronten. - Prachtige evenwijdige golffronten ontstaan als een touw min of meer waterpas in of uit het water gaat. Of als een lange plank in het water staat, met haar korte zijde vertikaal, en men haar een weinig heen en weer schommelt.
8.	Buiging aan een schermrand. - Laat evenwijdige golven tegen een plank aankomen, die evenwijdig aan de golfkammen staat. Achter de plank ontstaat een ‘schaduw’; maar: a) de golven buigen enigszins om de rand en komen binnen de geometrische schaduw, zij het ook verzwakt; b) buiten de geometrische schaduw voegt zich de invallende golf bij een zwakkere golf welke door de schermrand verstrooid wordt, zodat daar interferenties ontstaan.
	Aan golfjes zoals de wind ze verwekt kan men dikwijls verschijnselen waarnemen die oppervlakkig op buiging gelijken, maar die eigenlijk geheel anders op te vatten zijn. Wanneer we bijvoorbeeld zien hoe golven zich om een eilandje uitbreiden, ook aan de lijzijde, die in de windschaduw ligt, moeten we bedenken dat de door de wind gevormde golfjes geen lange even-

[p. 184]

	wijdige kammen hebben, maar dat ze te denken zijn als de superpositie van een aantal golfbewegingen, die allerlei kleine hoeken met de windrichting vormen. Het eilandje onderschept sommige van die golvenstelsels, maar hun divergentie is zo groot, dat er, ook afgezien van de echte buiging, altijd nog golven langs een groot deel van de kustlijn kunnen lopen.
9.	Buiging door een spleet. - Een plank met een poortvormige opening wordt in het water gedompeld, en men laat er evenwijdige golven op invallen. Aan de achterzijde ziet men hoe ze uit de opening te voorschijn komen en zich als cirkelvormige golven uitbreiden, wanneer de opening veel kleiner is dan hun golflengte. Als de opening ongeveer even groot is als de golflengte, beginnen de golven sterker te worden in de rechtdoorgaande richting. Bij een opening van 3 maal de golflengte is er al een duidelijke stralenbundel te zien die door de spleet gaat, maar de randen der golfjes zijn nog onscherp en gekromd. Bij een spleet van 10 maal de golflengte is de stralenbundel al vrij goed begrensd.
	Bij deze proeven kan men evengoed een puntvormige trillingsbron nemen, die concentrische golven uitzendt (‘buigingsverschijnselen volgens Fresnel’). Het is ook leuk, bij éénzelfde opening de golven eerst langzaam, dan sneller op elkaar te laten volgen, en na te gaan hoe het buigingsbeeld verandert naarmate de golflengte kleiner wordt.
	Dergelijke buigingsverschijnselen aan watergolven kan men dikwijls zonder enige voorbereiding waarnemen, bijvoorbeeld waar een smalle sloot in een breed kanaal uitmondt, en de wind in de richting van de sloot blaast en golfjes maakt. Of aan halfgeopende sluisdeuren. Of in een haven, waar de grote zeegolven binnendringen door de opening tussen de golfbrekers, en de hele haven vullen met beweging, terwijl de kleine kabbelingen dat niet doen.
10.	Buiging door een klein scherm.^1) - Bij wijze van tegenhanger onderzoeken we de buiging van evenwijdige golven door een plank. Als de plank meer dan 10 maal de golflengte lang is, werpt ze een duidelijke schaduw. Bij een plank van 3 maal de golflengte beginnen de golven al sterk in de geometrische schaduw door te dringen. Bij een plankje dat niet breder is dan de golflengte is de schaduw bijna weg. Een hindernis die veel kleiner is dan de golflengte geeft secundaire kringvormige golven: verstrooiing.

1) Zs. math. naturwiss. Unterricht, 60, 398, 1929.

[p. 185]

11.	Verstrooiing. - Het is winderig weer en op de singel hebben zich kleine golfjes gevormd. In evenwijdige rijen komen ze aan. Daar dobbert een stukje hout, en nu ziet men erg mooi hoe zich daaromheen kringgolfjes uitbreiden. De verstrooiing is gering, omdat het stukje hout drijft, en dus even zwaar is als het verplaatste water; er is slechts verstrooiing, omdat het zwaartepunt van het hout en van het verplaatste water niet overeenstemmen, en de kracht der aankomende golven dus anders op het hout werkt^1). Kijk hoe het gaat! Bij elke golving wordt het hout iets vroeger opgeheven dan het water, of valt het iets sneller terug; het is dus alsof de golf het hout geheel meenam, maar er daarenboven een ‘schijnkracht’ was, die het periodiek op en neer beweegt, ten opzichte van het water, in Fig. 96. Terugkaatsing van watergolven bij verschillende invalshoeken. hetzelfde tempo als de golven, maar in een andere phase. De uitgezonden kringgolven interfereeren met de rechtstreeks doorgaande golffronten en verzwakken ze; de energie die ze aan deze golven onttrokken hebben wordt naar alle zijden uitgezonden.
	Dit is nu precies wat met het licht gebeurt als het door een heel fijn stofdeeltje wordt verstrooid. Onze evenwijdig invallende watergolven zijn ‘gepolariseerd’, hun trillingen geschieden alleen op en neer; vandaar dat het buigende deeltje ook slechts in dezelfde richting gepolariseerde trillingen uitzendt (vgl. I, § 185).
12.	Terugkaatsing. - Laat evenwijdige golven schuin invallen op de oeverrand of op een vaste plank. Ze worden teruggekaatst, men ziet hoe de hoek van inval gelijk is aan de hoek van terugkaatsing (fig. 96). Volg aandachtig hoe de terugkaatsing gebeurt: de punten van het golffront die het eerst de oever bereiken geven het eerst een nieuwe teruggekaatste elementairgolf; al de elementairgolfjes samen vormen het nieuwe golffront.

1) De verstrooiing zou sterker zijn als het houtje met een veer aan de bodem verbonden was. Vgl. Physica, 9, 96, 1929.

[p. 186]

	Het proces is goed te volgen als men de golven laat terugkaatsen tegen de rij spijkers van proef 5.
	Voor kleine invalshoeken, dus als het golffront een geringe hoek met de ‘spiegel’ maakt, is het treffend hoe de hoogte der golven nauwelijks door de terugkaatsing verandert. Bij 45^o wordt de teruggekaatste golf echter zwakker; bij 60^o is dit nog opvallender. Daarboven is er geen eigenlijke terugkaatsing meer, men ziet alleen het uiteinde der golf krommen tot ze loodrecht op de wand staat en zeer hoog worden (doordat de teruggekaatste golf zich op de invallende superponeert).^1) Hier blijkt wel dat de terugkaatsing van een watergolf verschilt van die ener lichtgolf, en dat het niet een zo banaal verschijnsel is als u wellicht hadt gedacht!
13.	Virtueel beeld in een spiegel. - Werp een grote steen in het water bij een steile oever, en volg de zich uitbreidende kringen. Zodra ze de oever bereiken worden ze teruggekaatst (let precies op hoe dit gebeurt!); het denkbeeldige middenpunt der teruggekaatste golven ligt even ver achter de wand als het middenpunt van de oorspronkelijke golven ervóór.
	Een schip vaart door een kanaal, gevolgd door zijn sierlijk patroon van watergolven. Aan beide kanten worden ze door de oever teruggekaatst; het is alsof er beiderzijds een ‘spiegelschip’ voer, op een kanaalbreedte rechts en links van het echte schip. Heeft men zich eenmaal in die opvatting ingedacht, dan ziet men de twee spiegelbeelden elk met hun golfpatroon bijna lichamelijk voor zich.
14.	Holle spiegel. - Laat evenwijdige golven invallen op een plank die in de vorm van een cirkelboog gekromd is. De teruggekaatste golven zijn cirkels die zich samentrekken naar een ‘brandpunt’.
15.	Brandpunt. - Kringgolven die men in het brandpunt van een holle wand opwekt, geven bij terugkaatsing een evenwijdig golffront.
16.	Bolle spiegel. - Evenwijdige golven of kringgolven worden teruggekaatst tegen de bolle zijde van een plank of tegen de romp van een klein schip. De teruggekaatste kringgolven breiden zich uit als kwamen ze van een punt achter de bolle wand.
17.	Lens. - De breking van watergolven kan men onderzoeken door de golven in ondiep water te laten komen, waar ze langzamer lopen. Een plank die enkele millimeters onder het wateroppervlak bevestigd is, kan aldus de rol van een ‘lens’

1) Scott Russell, t.a.p.

[p. 187]

	vervullen en bijvoorbeeld cirkelgolven evenwijdig maken. Verander de afstand van de trillingsbron tot de lens.
18.	Beginsel van Doppler^1) - In een snelvlietend maar effen riviertje kan men mooi het verschijnsel van Doppler laten zien, door aan de kant voorzichtig golfjes teweeg te brengen. In een bepaald geval richtte de natuur zelf zulk een proef in, doordat er uit een pijpleiding voortdurend druppels vielen die mooie kringen maakten. Men ziet de kringen stelselmatig vervormd (fig. 97), in de ééne richting liggen de kammetjes veel dichter bij elkaar dan in de andere. Soms is het beeld ietwat gewijzigd, namelijk wanneer de stroming vlak bij de oever gering Fig. 97. Verschijnsel van Doppler aan watergolven. - Links: de snelheid van de stroming is dezelfde voor het gehele wateroppervlak; rechts: de stroomsnelheid neemt toe naarmate men zich verder van de oever verwijdert. is en meer naar het midden der rivier toeneemt; dit is dan tevens een model van de wijze waarop de geluidstralen in de dampkring gekromd worden door de wind (II, § 14 en 16).
	Waar een riviertje versnellingen en wervelingen vertoont, bijvoorbeeld onder een brug, worden de kringen sterk vervormd op onregelmatige wijze.
19.	Stralingsdruk.^2) - Gooi een plankje in het water, en beproef het naar de oever terug te bewegen door stenen vlak erachter in het water te gooien. Dat lukt! Wel is een golfbeweging iets geheel anders dan vervoer van materie; voortbewegende golfjes veroorzaken nog geen stroming (§ 96). Maar zij oefenen stralingsdruk uit, omdat het plankje hen ten dele terugkaatst en ten dele absorbeert. Met een stukje van een net zou de proef niet slagen.

1) O. Reynolds, Proc. R. Soc. 22, 531, 1874.

2) Physica, 3, 129, 1923.