De natuurkunde van 't vrije veld. Deel I

Licht en kleur in het landschap

[p. 30]

De breking van het licht.

23. Breking van het licht bij overgang van lucht in water.

De vaarboom waarmee de schipper zijn schuit voortduwt lijkt gebroken daar waar hij door het wateroppervlak gaat; dit beeld ontstaat, doordat de lichtstralen geknikt worden als ze

Fig. 28. De breking der lichtstralen veroorzaakt een schijnbare knik van de vaarboom.

van lucht naar water overgaan (of omgekeerd). Merk echter op dat ‘de gebroken stok’ daarom nog geen beeld geeft van de gebroken lichtstraal! Deze laatste is juist in omgekeerde zin geknikt; het verband blijkt uit fig. 28.

Schat de afstand van een voorwerp dat zich onder water bevindt en beproef het snel te grijpen: meestal komt u bedrogen uit, want door de breking van de lichtstralen schijnt het voorwerp opgeheven (vgl. fig. 29). Het ligt dieper dan u dacht. Toch is het verschijnsel niet zo eenvoudig, dat de breking van het licht het voorwerp als 't ware vervangt door een hoger gelegen beeld: als u voorbij een heldere sloot wandelt of fietst, ziet u de waterplanten in de diepte een eigenaardige plaatsverandering vertonen: het verplaatste beeld verschuift telkens en wordt des te meer opgelicht naarmate u schuiner kijkt. (plaat IVb)¹⁾

De schaduw van de drijvende bladeren van de waterlelie op de bodem van een heldere plas ziet er merkwaardig ingesneden uit alsof het die was van een palmblad.²⁾ Verklaring: aan de rand is het blad een weinig opgekruld, daar staat het water capillair tegen op, en de lichtstralen breken in het aldus gevormde pris-

1) F.A. Forel, Le Léman (Lausanne 1895), II, 456.

2) Kerner von Marilaun, Pflanzenleben.

[p. t.o. 30]

PLAAT III.
Het gerimpelde oppervlak van de gracht weerkaatst het zonlicht in een grillig netwerk van lijnen tegen 't gewelf van een oude brug.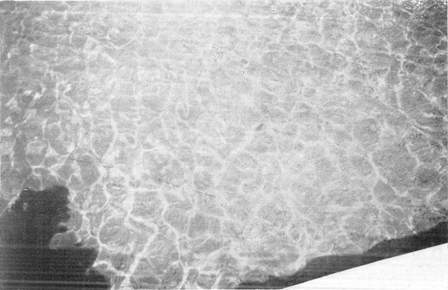

Zonlicht, gebroken door zacht golvend en ondiep water, wordt op de bodem tot lichtlijnen verenigd.

[p. 31]

matje: ze worden in onregelmatige vegen binnen het schaduwgebied geworpen.

Op de bodem van een ondiepe vijver of dicht bij de oever van een riviertje werpt de zon vrolijke lichtslierten door het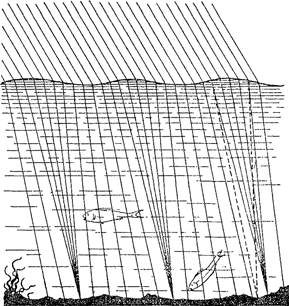

Fig. 30. Zonnestralen dringen in het water, en worden door de breking der golfjes tot lichtlijnen verzameld. De (gestippelde) blauwe stralen worden sterker gebroken

heldere water: de welvingen der golfjes werken als lenzen, en verenigen de lichtstralen in brandlijnen, die zachtjes met de golven mee voortlopen (fig. 29).¹⁾ We hebben al een dergelijk lichtverschijnsel in teruggekaatst licht leren kennen (§ 8), en vinden nu de tegenhanger bij de breking. - Wanneer de stralen schuin invallen, zijn de lichtlijnen met kleuren omzoomd: blauwachtig naar de zon toe, roodachtig van de zon af. Dit komt, omdat de blauwe stralen sterker gebroken worden dan de rode: het verschijnsel der kleurschifting (= dispersie). (Vgl. plaat IIIb).

Werp een wit keitje in diep, helder water en stel u op enige afstand om het te bekijken; het schijnt aan de bovenzij blauw en aan de onderzij rood gekleurd.²⁾ Ook dit is een gevolg van de kleurschifting.

1) F.A. Forel, Le Léman, II, 454. Deze verschijnselen zijn nog mooier waar te nemen met behulp van een waterkijker (§ 209).

2) L. Boltzmann, Populäre Schriften, 59.

24. Breking door hobbelige ruiten.

Als u in oude treinwagens door de raampjes kijkt, ziet u dikwijls dat er bepaalde stroken van de ruiten zijn die de beelden geheel vervormen. Schijnt de zon door zulk een ruit op een blad

[p. 32]

papier, dan ziet men bij dezelfde plaatsen heldere of donkere vegen zich op het papier aftekenen; houd het papier wat verder achteruit: zulk een veeg trekt zich samen tot een tamelijk scherpe lichtlijn.

Blijkbaar is de ruit geen planparallele plaat maar vertoont ze dunnere en dikkere delen; deze werken als onregelmatige lenzen: ze spreiden de lichtstralen uit of verenigen ze, geven grillige brandlijnen (vgl. § 23).

25. Dubbele beelden, teruggekaatst door spiegelglas.

Kijk naar een verre lantaarn of naar het beeld van de maan, teruggekaatst in de spiegelruiten van een huis langs de weg.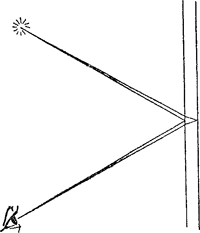

Fig. 31. Een zuivere planparallele spiegelruit geeft dubbele beelden, maar deze liggen uiterst dicht bij elkaar.

U ziet twee beelden, het ene verplaatst zich op onregelmatige wijze ten opzichte van het andere naarmate de weerspiegeling op het ene of op het andere gedeelte van de ruit gebeurt¹⁾. - Nog niet zo lang geleden heeft een ‘wijsgeer’ betoogd,²⁾ dat men hier een geval had van ‘werkingen zonder oorzaak’!! Laten wij natuurkundigen eens kijken of we hier geen oorzaak kunnen ontdekken.

We merken op dat de mooie gepolijste platen van zwart glas, die bij deftige firma's naast de deur prijken, geen dubbele beelden geven. Het is dus duidelijk dat bij een spiegelruit het éne beeld teruggekaatst is door het voorvlak, en dat het tweede gevormd is door stralen die door het glas zijn gegaan, tegen het achtervlak teruggekaatst, en dan weer door het glas ons oog hebben bereikt. Bij zwart glas wordt die tweede soort stralen opgeslorpt.

De breking doet een der stralen een weinig afwijken van zijn richting (fig. 31). Kan dit de oorzaak der dubbele beelden zijn? - Neen. Want a) dan zouden ze niet op verschillende delen van dezelfde ruit de ene maal veel dichter tot elkaar naderen dan

1) Ztschr. f.d. phys. chem. Unterricht, 4, 86, 1891; 37, 90, 1924.

2) E. Barthel, Arch. f. system. Philos. 19, 355, 1913.

[p. 33]

de andere maal; b) ze zouden niet veel verder uiteen liggen dan de dikte van 't glas, wat nauwelijks waar te nemen zou zijn; c) de verplaatsing zou nul zijn voor zeer kleine en zeer grote invalshoeken (met een maximum nabij 50^o, zoals men berekenen kan), terwijl wij ook bij loodrechte inval dubbelbeelden waarnemen; d) voor een oneindig verre lichtbron, zoals de maan, zou de afstand der dubbelbeelden altijd nul zijn.

Besluit: een planparallele glazen plaat kan zulke dubbelbeelden niet geven. Deze zullen echter wel ontstaan indien de ruit hier en daar een weinig wigvormig is, doordat de oppervlakken zwak golven. Eer we echter vrede hebben met die verklaring, moeten we berekenen hoe groot de hoek tussen vóóren achtervlak moet zijn, om de waargenomen afstand der dubbelbeelden te verklaren; want het is onwaarschijnlijk dat bij goed spiegelglas de afwijkingen van de evenwijdigheid groot zouden zijn.

Denk eerst de twee vlakken evenwijdig, en volg één straal die zich splitst: de twee teruggekaatste stralen zijn evenwijdig gebleven en alleen een weinig

Fig. 32. Het ontstaan der dubbele spiegelbeelden bij een ruit die niet overal even dik is.

verschoven. Laat nu het voorvlak AB hellen onder een hoekje γ (fig. 32). De straal I draait dan over een hoek 2γ. Om de weg van de straal II te volgen, denken wij ons CD als een spiegel, die van AB een spiegelbeeld in A'B' geeft, en van de straal II een spiegelbeeld II'. Nu zien we dat de lichtstraal LII' door een prismatje ABB'A' gegaan is, met een kleine brekende hoek 2γ; men leert in de geometrische optica dat zulk een prismatje een hoekafwijking (n - 1) 2γ aan de lichtstraal geeft, wanneer de invalshoek niet te groot is. De totale hoek tussen I en II is dus 2γ + (n - 1) 2γ = = 2nγ; voor glas is n = 1,52, dus wordt de hoek ongeveer 3γ.
In fig. 33 ziet men welke gevolgen dit heeft als een waarnemer O naar de lichtbron L kijkt, die zeer verwijderd is: de twee stralen I en II, die praktisch evenwijdig van de verre lichtbron aankomen, verenigen zich in het oog van den waarnemer onder een hoek 3γ¹⁾.

Besluit: schat de hoekafstand tussen de spiegelbeelden, de hoek van de twee glasoppervlakken is daar het derde gedeelte van.

De schatting van die hoek kan b.v. gebeuren door de afstand

1) Voor een ander bewijs, zie § 26.

[p. 34]

a der spiegelbeelden op het glas te bepalen, te delen door de

Fig. 33. Hoe men uit de hoekafstand γ der twee spiegelbeelden de wigvormigheid ener spiegelruit nauwkeurig bepalen kan.

afstand R van oog tot ruit, en te vermenigvuldigen met cos i. Men vindt bij gewoon spiegelglas hoeken van een paar duizendste radiaal¹⁾ = enkele boogminuten. Op 10 cm afstand verloopt de dikte van de ruit dus bv. 0,2 mm. Dat is zo weinig, dat we 't niet zouden merken zonder nauwkeurige diktemetingen aan de spiegelruit uit te voeren; toen men ging meten vond men die schatting inderdaad bevestigd.

Is het niet prachtig dat we dergelijke uiterst kleine fouten van het glas zonder enig hulpmiddel, al wandelend, nauwkeurig kunnen bepalen? En daarenboven is ons nu gebleken dat onze verklaring van de dubbele beelden wel juist is. Als we voor een verschijnsel in de natuur geen oorzaak weten aan te wijzen, dan ligt dat aan onze onwetendheid!

Algemener en nauwkeuriger formule: de hoekafstand der twee beelden is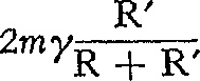



, waarin R' = afstand lichtbron - glas, R = afstand oog - glas, en 2m de volgende waarden heeft:

invalshoek i	=	0^o	20^o	40^o	60^o	80^o	90^o
2m	=	3,0	3,4	3,6	5,0	13,3	∞

Aan gewoon vensterglas kan men de meervoudige beelden niet goed onderzoeken, omdat ze op de vreselijkste wijze door het hobbelig oppervlak vervormd worden: de methode is te gevoelig.

1) Voor het begrip radiaal, vgl. § 1.

26. Meervoudige beelden, gegeven door spiegelglas in doorvallend licht.²⁾

Kijk 's avonds in schuine richting door een goede ruit van tram, auto of autobus naar een lantaren in de verte of naar de maan. U ziet verscheidene beelden op ongeveer gelijke afstanden van elkaar, het eerste sterk, de volgende steeds zwakker; hoe

2) H.M. Reese, J.O.S.A. 21, 282, 1931.

[p. t.o. 34]

PLAAT IV.
Zwevingen tussen de planken aan de vóór- en aan de achterzijde ener loods.

De man die de schuit voortduwt ziet de vaarboom ‘gebroken’ en de bodem van het riviertje ‘opgeheven’.

[p. 35]

schuiner u door de ruit kijkt, hoe groter hun afstanden worden en hoe minder ze in lichtsterkte ten opzichte van elkaar schelen.

Het is duidelijk dat dergelijke verschijnselen ontstaan door herhaalde terugkaatsingen tegen voor- en achterwand van de

Fig. 34. Het helderste der meervoudige spiegelbeelden ligt altijd aan dezelfde zijde van de waarnemer.

ruit. Het verschijnsel gelijkt eigenlijk zeer op dat der dubbel teruggekaatste beelden; we hebben weer dezelfde redenen om zeker te zijn dat de voor- en de achterkant niet evenwijdig zijn, en zelfs nog een reden meer: bij een planparallele ruit zou het helderste beeld altijd naar de kant moeten liggen die het verst van ons oog verwijderd is, onverschillig of we door de ruit kijken in de richting O of O'; de waarneming leert daarentegen dat het helderste beeld altijd aan dezelfde zijde ligt (altijd links of altijd rechts), zolang men door één bepaald punt van de ruit kijkt (fig. 34). Maar in dezelfde ruit kan men gedeelten vinden waar het helderste beeld het meest rechtse is, en andere waar het helderste beeld aan de linkerzijde ligt: in het eerste geval hebben we een wigvormig gebied getroffen waarvan de dikste zijde naar ons oog toe gekeerd is; in het tweede geval ligt de dikste zijde van ons oog af. Laten wij de hoekafstand der beelden berekenen volgens een ietwat andere

Fig. 35. Meervoudige beelden in doorvallend licht.

methode dan in § 25. Men ziet fig. 35) dat de stralen L₁, L₂, L₃, op het achtervlak invallen onder hoeken r + γ, r + 3γ, r + 5γ, .... Nu is sin α₁ = n sin (r + γ), of, daar γ een kleine hoek is,



Aangezien de aangroeiing van α gering is, mogen we de differentiaalformule d (sin α) = cos α. dα toepassen, zodat a₁ - a₂ =

Een dergelijke redenering zouden we met behulp van fig. 32 ook voor de herhaaldelijk teruggekaatste beelden kunnen houden. De scheiding der opeenvolgende beelden is precies even

[p. 36]

groot bij de waarneming in teruggekaatst als in doorvallend licht; de faktor vóór γ is inderdaad dezelfde die wij in § 25 door 2m hebben voorgesteld, en waarvan de waarde daar aangegeven is.

27. Waterdruppels als lenzen.

De regendruppels tegen de ruiten van een treincoupé geven heel kleine beeldjes, net als een sterk lensje; maar natuurlijk zijn die beeldjes vervormd, aangezien de druppel allesbehalve zuiver lensvormig is. Ze staan onderste boven; en terwijl het landschap buiten in tegengestelde richting van de trein schijnt voorbij te schuiven, ziet men de beeldjes in dezelfde richting als de trein bewegen.

Het beeld van een paal is boven veel breder dan onder: de lens verkleint de beelden des te meer naarmate ze een kleiner brandpuntafstand heeft, dus een sterker kromming. Aan de bovenzijde is onze druppel inderdaad veel vlakker dan aan de onderzijde.

28. Flonkeringen van het licht in dauwdruppels en rijpkristallen.

Wie kent niet de kleurige schitteringen van het licht in dauwdruppels? Merk op hoe rustig en fel ze schijnen aan de stevige, korte halmen van het grasveld, terwijl ze op de wuivende hoge grassen fonkelen als sterren.

Laten we een bedauwde grashalm van nabij bekijken. Pluk hem niet, raak hem niet aan! De kleine bolronde druppeltjes bevochtigen hem niet, zij liggen er capillair op, maar met een luchtlaagje tussen druppel en halm. Dat het bedauwde gras er zo grijs uitziet, komt door de terugkaatsing der lichtstralen tegen al die druppeltjes, zowel inwendig als uitwendig; een groot gedeelte der stralen bereikt dus niet eens het blad (vgl. § 168). Grote afgeplatte druppels glinsteren zilverachtig mooi onder nogal grote hoeken, omdat de stralen dan totaal teruggekaatst worden tegen de achterwand.

Kiezen wij een grote druppel en bekijken hem met één oog, dan verschijnen kleuren zodra we vanuit een voldoende grote hoek met de invalsrichting waarnemen; eerst verschijnt blauw, dan groen, dan het vooral duidelijke geel, oranje,

[p. 37]

rood. Dit is natuurlijk wat we bij elke regenboog op grote schaal zien (§ 119).

Dergelijke schitteringen en kleuren vertonen ook de kristallen van rijp en verse sneeuw.

Vgl. § 129 en 154.

Vraag aan Professor Clifton u te verklaren waarom een dauwdrop de tint van een groen blad of blauwe bloem tempert tot een zacht grijs, en zich als een lichtgevende schemering op het gras of op zuring vertoont; en waarom diezelfde druppel de kracht van alle warme kleuren versterkt, zodat u onmogelijk kunt beoordelen hoe de kleur is van een anjelier of van een roos tot u ze bedauwd ziet.

Ruskin, The Art of England, 33, 386.

Rijp van goud .... zie de dauw op een koolblad, of, nog beter, op een grijs korstmos in de vroege zonneschijn.

Ruskin, Arrows of the Chase, 34, 536.

Wanneer deze rijp van de takken stoof, schitterde hij in een rijkdom van kleuren in de zonnestralen.

M. Sjolochow, De Stille Don, blz. 273.