De natuurkunde van 't vrije veld. Deel I

Licht en kleur in het landschap

[p. 7]

De terugkaatsing van het licht.

5. De wet der terugkaatsing.

Zoek een plaats waar u de maan weerspiegeld ziet in een zeer rustig wateroppervlak. Vergelijk de hoek van de maan boven de gezichteinder, en de hoek van het weerspiegelde beeld onder de gezichteinder: binnen

Fig. 5. Zonlicht, teruggekaatst door een inspringend raam.

de waarnemingsfouten zijn beide gelijk. - Als de maan niet hoog staat, kunt u bv. uw wandelstok met gestrekte arm vertikaal vóór u houden, zodat u de punt tegenover de maanschijf ziet, terwijl uw duim de gezichteinder bedekt; draai dan de wandelstok onderste boven om uw arm als as, en kijk of de punt nu aan het spiegelbeeld der maan raakt.

Dergelijke metingen, met de kijker aan scherpe sterrebeeldjes uitgevoerd, geven de nauwkeurigste toetsing der terugkaatsingswet.

Een inspringend raam wordt door een niet te hoge zon schuin beschenen (fig. 5). De richting van de invallende bundel ziet men aan de schaduw AB; het teruggekaatste licht valt als een heldere lichtvlek in de richting BC. Men ziet nu dat die twee richtingen symmetrisch zijn ten opzichte van de normaal BN, dus dat ∠ ABN = ∠ CBN. Dit is niet hetzelfde als de terugkaatsingswet, maar 't volgt eruit. Bewijs dit!

Waarom weerspiegelen de ruiten der huizen alleen de op- of ondergaande zon?

[p. 8]

6. Terugkaatsing tegen draden.

Een bundel telegraafdraden blinkt in de zon; loopt men evenwijdig aan de draden, dan verplaatst zich de lichtvlek met dezelfde snelheid als de waarnemer. 's Avonds zien we evenzo hoe het

Fig. 6. Fantasieën van een nachtelijken wandelaar: de weerspiegeling van de straatlantaren tegen telegraafdraden.

licht van een straatlantaarn een verlichte lijn geeft op de trolleydraad van de tram. Waardoor wordt de juiste plaats van die reflexen bepaald? Construeer in gedachte het ellipsoide, dat als brandpunten ons oog en de lichtbron heeft en dat raakt aan de draad (fig. 5). Het raakpunt is dan de verlichte vlek; want het is een bekende eigenschap der ellipsoïde dat in elk punt de voerstralen gelijke hoeken maken met het raakvlak.

7. Verschillen tussen voorwerp en spiegelbeeld.

Menigeen denkt dat het spiegelbeeld van een landschap in een kalm watervlak er net zo uitziet als het landschap zelf, onderste boven gekeerd. Niets is minder waar! - Let maar 's avonds op, hoe sommige groepen straatlantarens weerspiegeld worden (fig. 7a). - Het spiegelbeeld van de dijk, die naar het water toe helt, schijnt verkort, en verdwijnt zelfs als we hoog genoeg boven het wateroppervlak staan (fig. 7b). - De top van een steen die in 't water ligt ziet u nooit teruggekaatst in het spiegelbeeld.

[p. 9]

Al zulke effekten zijn vanzelfsprekend als men bedenkt dat het spiegelbeeld wel identiek is met het landschap zelf, maar er perspektivisch anders uitziet omdat het verschoven is. Wij zien het zó, alsof we 't landschap zelf bekeken van een punt onder de waterspiegel, spiegelbeeld van ons oog.

Er schijnt echter nog iets anders te

Fig. 7a.

zijn! De spiegelbeelden van bomen en struiken in kleine vijvers en in de plassen langs de weg vertonen soms een zuiverheid, een scherpte, een warmte van kleur, groter lijkend dan die van het gespiegelde voorwerp zelf. Wolken zien we nooit zo mooi als teruggekaatst in een spiegel. Een straat, weerspiegeld in een winkelruit met een donker gordijn als achtergrond, had een verrassende scherpte.¹⁾ De oorzaak van deze verschillen is meer psychologisch dan physisch. Men heeft ze gezocht in het feit, dat het weerspiegelde

Fig. 7b. Een voorwerp kan er anders uitzien dan zijn spiegelbeeld.

tafereel altijd aangevoeld wordt als een schilderij dat in één vlak ligt (physisch liggen de spiegelbeelden natuurlijk net zo goed in allerlei vlakken als het voorwerp zelf). Anderen zeggen, dat de omlijsting ons onzeker maakt omtrent de positie van het ding in de ruimte, hetgeen sterkere relief-indrukken doet ontstaan.²⁾ Belangrijker nog schijnt mij, dat het oog beschermd blijft tegen overtollige verblinding door het grote, heldere veld van de hemel om het waargenomen tafereel: een effekt dus van dezelfde

1) H.R. Mill, Geogr. Journ. 56, 526, 1926. - Vaughan Cornish, ibid. blz. 518.

2) J.O.S.A. 10, 141, 1925.

[p. 10]

aard als het kijken door een buis. De geringere helderheid van het spiegelbeeld is ook op zichzelf al gunstig voor het bekijken van de hemel en de wolken, die anders iets te fel zijn voor ons oog.

Ik ging eens langs de oevers van de Aisne, ten prooi aan een onuitsprekelijk lijden, dat geen bepaalde reden had en juist daardoor ongeneselijk scheen. Het beeld van een brug, teruggekaatst in het water, heeft mij opeens het zelfvertrouwen teruggegeven en het kennen van de vreugde. En toch was dit slechts een weerspiegeling; maar geloof nooit wie u zeggen zou dat het slechts een weerspiegeling was.

G. Duhamel, La Possession du Monde, blz. 206.

8. Speelse weerspiegelingen. (Plaat III).

Een huizenrij werpt een donkere schaduwstrook over de straat; maar temidden daarvan zijn er hier en daar onverwachte lichtvlekken

Fig. 8. Ook in de donkerste arbeidersbuurt valt hier en daar een plekje zonneschijn.

(fig. 8). Hoe komt het licht daar? - Houd uw hand vóór de lichtvlek, en besluit uit de plaats van de schaduw uit welke richting de stralen invallen: het blijkt dat ze teruggekaatst zijn door de ramen van huizen aan de overzij.

Op dergelijke wijze ziet men lichtvlekken glinsteren op het oppervlak van een kanaal dat zelf in de schaduw ligt. De huizen aan de overkant werpen het licht terug.

Aan de oever van 't water staat een rij huizen waarvan de gevels geheel in de schaduw zijn; toch lopen er lichtspelingen over: een lichtschijn met daarin regelmatige, min of meer evenwijdige strepen die voortbewegen. 't Zijn terugkaatsingen van de watergolven (fig. 9). Het gedeelte AB van de golving werkt als holle spiegel en geeft een brandlijntje in L, een gedeelte BC van de golf is veel minder

[p. 11]

gekromd en verenigt de stralen op veel groter afstand. Zo is er voor elke afstand

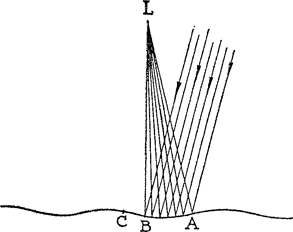Fig. 9. Vorming van lichte lijnen door weerspiegeling op zacht golvend water.

van de muur altijd een deel van het wateroppervlak dat een scherpe lichtlijn geeft; de andere delen geven dan de algemene lichtschijn.

Dergelijke lichtspelingen ziet men ook langs kaden en tegen 't gewelf van overkapte bruggen. We hebben hier eigenlijk een model van het fonkelen der sterren (vgl. § 40).

9. Schieten op een spiegelbeeld.

Bij Salzburg is er een meer, de Königsee, door hoge bergen omsloten en daardoor zeer rustig. Men houdt er schietwedstrijden, waarbij de schutter op het spiegelbeeld van de schijf in 't water mikt, en de kogel tegen het oppervlak ‘terugkaatst’ en het doel treft. De trefzekerheid schijnt tenminste even groot als bij een rechtstreeks schot. - Wie doet dit hier eens na?

Het eigenaardige is, dat de kogel niet aan de oppervlakte zelf teruggekaatst wordt, maar in het water dringt. Volgens een hydrodynamische stelling zijn de vloeistofstromingen dan zó, dat de bewegende kogel door het wateroppervlak ‘aangetrokken’ wordt; hij nadert er meer en meer toe, en treedt tenslotte onder dezelfde hoek uit als waaronder hij in het water gedrongen was. Door schermen op te hangen die onder water dompelen, heeft men de baan van de kogel kunnen volgen.¹⁾

1) Ramsauer, Ann. d. Phys. 84, 730, 1927.

10. De heliotroop van Gauss.²⁾

Kaats zonlicht terug met een spiegeltje; vlakbij heeft de lichtvlek de vorm van de spiegel zelf, verder afwordt ze minder scherp,

2) 2) A. Gruber: Heliograph (Verzameling ‘Spiel und Arbeit’, No. 29; Ravensburg).

[p. 12]

nog verder wordt ze rond, en op grote afstand is het een echt zonnebeeldje geworden. Als u dan een deel van het spiegeltje afschermt, blijft de lichtvlek rond maar wordt lichtzwakker. Meer dan 50 m ver zult u die lichtvlek wel niet kunnen volgen; een waarnemer echter die zich daar bevindt ziet het spiegeltje nog fel schitteren in de zon.

Zet het spiegeltje in een statief of klem het vast tussen stenen, ergens op een plek met vrij uitzicht, en wel zo dat de teruggekaatste zonnestraal goed waterpas loopt. Ga nu achteruit, zo ver als u het licht nog zien kunt. Het kost enige moeite in de bundel te blijven; gelukkig wordt zijn doorsnede breder naarmate men verder komt: dat merkt u als u zich dwars op de bundel verplaatst, en bepaalt binnen welke grenzen u hem nog ziet; op 100 m afstand is hij al 1 m breed. Verder moet bedacht worden dat de zon zich aan het uitspansel verplaatst; het is daarom best de proef rond middagtijd uit te voeren, dan blijft de teruggekaatste bundel althans in het horizontale vlak zonder dat veel bijregelen nodig is.

Het is verbazend, zo ver als zulk een lichtpuntje nog zichtbaar blijft! Gauss heeft op die wijze bij graadmetingen zeer scherpe lichtbronnen gemaakt, die met de kijkers der meetinstrumenten tot op afstanden van 100 km waargenomen konden worden. Zulk een heliotroop heeft bijzondere viseerinrichtingen om de lichtstraal precies te kunnen richten naar een willekeurig punt. Door afschermen en weer doorlaten van het licht kunt u Morsetekens seinen.

11. Weerspiegeling in een tuinbol.

De bolle spiegels waarvan men ons op school vertelt zijn altijd klein en weinig gekromd; zij komen overeen met het stukje AB van de tuinbol dat vlak naar ons toe gekeerd is, en waarin we ons eigen spiegelbeeld zien.

Maar de tuinbol als geheel is veel interessanter! Het merkwaardige van het ding is, dat we hier de gehele oppervlakte van de hemelsfeer (juister: hemel + aarde) samengedrongen zien in een beperkt kringetje: de tuinbol werkt als een optisch toestel met ideaal grote openingshoek! Natuurlijk kan dit slechts doordat de beelden vervormd worden; ze worden samengedrukt in de richting van de straal, en wel des te meer naarmate ze dichter bij de omtrek van de tuinbol liggen (fig. 10). Onderstel eenvoudig-heidshalve dat zowel het voorwerp als de waarnemer vrij ver van de tuinbol verwijderd zijn (ver t.o.v. de straal R); dan zal een

[p. 13]

voorwerp op hoekafstand α van de lijn CO afgebeeld worden op een afstand γ = R. sin α/2 van het midden van de bol. Men ziet dat γ → R voor α → 180^o, en dat dus inderdaad de hele ruimte op de bol wordt afgebeeld. Verloren wordt alleen het kleine stukje dat precies achter de

Fig. 10. Hoe een kleine tuinbol het heelal weerspiegelt.

tuinbol ligt, en dat des te kleiner wordt naarmate we verder van de bol staan.

Helmholtz heeft eens gezegd dat een landschap, door een tuinbol vervormd, weer normaal zou bevonden worden als de meetstaaf waarmee men het tafereel uitmeet volgens dezelfde wet vervormd was. Deze uitspraak is nauw verwant aan de beginselen der relativiteitstheorie.

De tuinbol kan voor alleraardigste waarnemingen gebruikt worden op 't gebied der meteorologische optica, juist omdat hij zulk een goed overzicht geeft van een geheel stuk van de hemel.¹⁾ Als men zich op een afstand van een paar meter plaatst, en wel zó dat men het spiegelbeeld van de zon met zijn hoofd bedekt, ziet men met bijzondere duidelijkheid (vgl. nog verder):

a. kringen, kransen, iriserende wolken, de ring van Bishop, de schemeringskleuren;

b. de bundels van Haidinger en de polarisatie van het hemellicht. Door de verkleining van het beeld worden de langzaam verlopende tinten omgezet in veel sterkere gradiënten, zodat de verschillen van helderheid en kleur meer in het oog vallen. In de glimmende oppervlakte van mijn fietsbel heb ik meer dan eens heel ijle wolkjes gevonden, die ik bij rechtstreeks waarnemen niet opgemerkt had.

1) A. Hoffmann, das Wetter, 34, 133, 1917.

12. Oneffenheden van een wateroppervlak.

Een effen plas in een duinpan; windstil weer. Hier en daar steekt een grashalm of een bies uit het water op, en nu is het leuk om te zien hoe elk halmpje omringd is door een schitteringetje van zonlicht, daar waar het uit het water komt: het kleine water-

[p. 14]

bergje, dat capillair om zo'n halm zit, wordt aldus van verre zichtbaar. Als een deel van de waterplas een donkere duinhelling weerspiegelt, een ander de heldere lucht, ziet men nabij de grenslijn hoe al de kleine waterbergjes oplichten of donker afsteken, al naar de richting waarin men kijkt.

Op dezelfde wijze kunnen we waterwerveltjes opsporen, overal waar een rivier noemenswaarde stroming vertoont. In ieder werveltje is de druk iets kleiner en het oppervlak lichtelijk uitgehold; orde van grootte der uitholling: 4 cm middellijn en een paar mm diep. Nabij een grens tussen licht en donker ziet men zelfs de zwakste werveltjes met grote duidelijkheid. Het is een heel gevoelige ‘slierenmethode’, toegepast in de vrije natuur.

Het heeft geregend. In de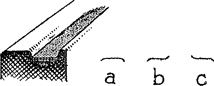

Fig. 11. Regen in een tramspoor vormt een gekromde spiegel.

tramsporen staat water, en nu zien we een dwarse horizontale lijn daarin teruggekaatst, bv. de ophangdraad van de trolleykabel. Kijken we in het vertikale vlak van de rail, dan zien we het teruggekaatste beeld symmetrisch vervormd (fig. 11a): een duidelijk bewijs dat het wateroppervlak gekromd staat en een capillaire meniskus vormt. Stellen we ons links van de rail, dan vervormt zich het beeld zoals in fig. 11b; rechts, zoals in fig. 11c. Overweeg eens waarom het spiegelbeeld juist deze vorm aanneemt.

De beelden, gegeven door een gebogen wateroppervlak, kunt u prachtig bestuderen van op een stoomboot, omdat u altijd in dezelfde stand en richting naar de golven kijkt die met hem meelopen. Bemerk vooral hoe de spiegelbeelden al vervormd worden door de eerste golving die de boeg teweegbrengt.¹⁾ De beelden zijn sterk samengedrukt; ze zijn rechtopstaand of omgekeerd, naarmate u naar een bol of naar een hol gedeelte van het oppervlak kijkt.

1) F.A. Forel, le Léman, II (Lausanne, 1895).

13. Vensterglas en spiegelglas.

Aan de weerspiegeling in de ruiten van de huizen kan men onmiddellijk zien of ze uit spiegelglas of uit vensterglas gemaakt zijn: in het eerste geval zijn de beelden vrij zuiver; in het andere geval zo onregelmatig, dat de hobbels in de ruit rechtstreeks te voorschijn komen.

Het is opvallend hoe verschillend de rijke buurten en de be-

[p. 15]

scheidener straten van een stad er ook van dit standpunt uitzien! Midden in een deftige rij met spiegelglas onderscheiden we één enkel huis met vensterglas. Aan twee spiegelglasruiten die naast elkaar zitten, merken we dat ze niet nauwkeurig in 't zelfde vlak liggen, want de spiegelbeelden van een daklijn zijn iets verschoven ten opzichte van elkaar. Elders zien we hoe een goede spiegelruit een ongelukkig hoekje heeft, of hoe een andere in haar geheel zwak gebogen is.

14. Onregelmatige terugkaatsing op een zacht gerimpeld oppervlak.¹⁾

Voor mij zijn de lange lichtstrepen der weerspiegelde lantarens onafscheidelijk verbonden met de rustige stemming van de avond. Ik zie de maan die zich spiegelt in zee, en er een brede stroom van licht over laat vloeien. Of ik denk aan de huizen en torentjes van het oude Brugge, weerspiegeld in de stille reien: iedere lichte vlek, iedere kleur uitgerekt tot een vertikaal lijntje, en al die lijntjes, soms langer, soms korter, wemelend van lichtwisselingen en onvatbare glansen ....

Als we de maan of een lantaren 's avonds zien weerspiegelen in zacht bewogen water, dicht bij ons, bemerken we hoe eigenlijk ieder golfje een afzonderlijk lichtbeeld geeft. Het geheel van alle verlichte golfjes is gemiddeld een langwerpige vlek, met haar langste as in het vertikale vlak oog-lichtbron. Dit uitrekken van een lichtpunt tot een zuil, die naar ons oog gericht is, terwijl de golfjes toch geheel onregelmatig zijn, en in alle richtingen even veelvuldig voorkomen, is het fundamentele verschijnsel dat we verklaren moeten. Aan het uiteinde dat naar ons toe gekeerd is, zien we goed hoe de lichtzuil soms langer, soms korter wordt, naar gelang van de golving van het water. Aan het uiteinde dat het verst van ons af is, vloeien daarentegen de lichtvlekjes meer tot een gemiddelde ineen.

Eigenlijk zou men dus de gemiddelde verdeling der lichtsterkte over zulk een zuil als kansvraagstuk moeten opvatten en bereke-

1) Zie vooral: J. Piccard, Arch. sc. phys. et nat. 21, 481, 1889. - Verder: J. Spooner, Correspondance Astronomique, 1 Mei 1822, blz. 331. - G. Galle, Ann. d. Phys. 49, 255, 1840. - C. Schoute, H. en D. 7, 1, 1909. - A. Wigand en E. Everling, Verh. d.d. phys. Ges. 15, 237 en 1117, 1913; Phys. Zs. 14, 1156, 1913; Met. Zs. 31, 150, 1914. - E.O. Hulburt, J.O.S.A. 24, 35, 1934. - W. Shoulejkin, Nat. 114, 498, 1924. - K. Stuchtey, Ann. d. Phys. 59, 33, 1919. - Deze verschillende schrijvers kenden geen van allen hun voorgangers!

[p. 16]

nen. Dit is nooit behoorlijk gebeurd. We maken het ons dus maar gemakkelijk door aan te nemen, dat de hellingen der golfjes niet groter worden dan een bepaalde hoek α, en vragen alleen naar de grenzen der lichtzuil die zich aldus vormt. Of, anders uitgedrukt: als er op elke plaats een groot aantal kleine golfjes zijn, alle hellend over een hoek α, maar naar al de verschillende windstreken, wat is dan de meetkundige plaats van de golfjes die zullen oplichten? Ook aldus gesteld wordt het vraagstuk nog ingewikkeld genoeg!

1. Het eenvoudigste geval: h = h'; waarnemer en lichtbron bevinden

Fig 12. Berekening van de lange as ener weerspiegelde lichtzuil.

zich even hoog boven het water. (fig. 12). Een horizontaal vlakje werpt licht in het oog van den waarnemer W, wanneer het zich precies halverwege bevindt, bij M, de plaats der regelmatige terugkaatsing. Een vlakje dat onder een hoek α helt moet een eind uit het midden geschoven worden,

Fig. 13.

wil het voor den waarnemer weer licht geven. Hoe ver?

Bij verschuiving in het vertikale vlak door oog en lichtbron is die vraag gemakkelijk te te antwoorden. Noem N de gunstige stand als het vlakje in de éne zin helt, N' als het in de andere zin helt. Om symmetrieredenen is MN = MN'. Let nu op de hoeken:

β + α = γ + δ

β - α = ϵ = δ

Dus is γ = α + β - (β - α) = 2α.

[p. 17]

Dit is een belangrijk resultaat! De hoek waaronder we de langste as van de lichtzuil zien, is tevens de hoek tussen de twee grootste hellingen van de golfjes (fig. 13).

Laten wij nu ons golfoppervlakje verschuiven in het vlak door M, loodrecht op de verbindingslijn oog-lichtbron, en noemen we P, P' de punten waar de gunstige terugkaatsing bereikt is (fig. 14). Klaarblijkelijk is MP = MP' = h tg α. De lichtzuil is dus breed: 2h tg α, en we zien die korte as onder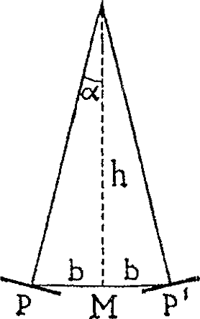

Fig. 14. Berekening van de korte as ener weerspiegelde lichtzuil.

een hoek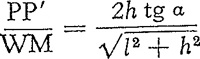



. De verhouding der schijnbare assen van de lichtzuil is dus: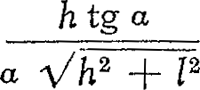



, of ongeveer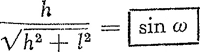



wanneer de lichtzuil niet te groot is. Kijken we dus van een heuvel op het water neer, dan is de lichtzuil weinig langwerpig (ω groot, sin ω bijna¹⁾. Hoe schuiner we over 't water kijken, hoe langwerpiger de zuil. Bij rakelingse blikrichting is ze oneindig lang en smal.

We moeten dus altijd onderscheiden tussen ‘de primaire ovaal’, een kromme die men op het rimpelende water getekend kan denken, de grens der lichtzuil aangevend; en tussen ‘de sekundaire ovaal’, die uit de vorige ontstaat door projektie op het vlak loodrecht op onze blikrichting. Van de primaire ovaal kan men wel de assen eenvoudig berekenen, maar de hele figuur is een kromme van de 6e graad, symmetrisch t.o.v.M. De sekundaire ovaal wordt een weinig asymmetrisch, de grootste breedte ligt eigenlijk iets meer naar ons toe dan het punt M waar we de dwarse as berekenden. Vooral kijkend onder een kleine hoek met het oppervlak is die asymmetrie merkbaar.

2. Het algemene geval: h ≠ h' (fig. 15).

Door dergelijke redeneringen als daareven toont men de twee fundamentele eigenschappen aan:

1)

[p. 18]

De verdere berekening bewijst dat de lichtzuil ongeveer elliptisch van omtrek blijft, maar de resultaten zijn ingewikkeld en onoverzichtelijk. Praktisch heeft het hoogteverschil tussen h en h' alleen invloed op de afmetingen der lichtzuil, niet op haar verhoudingen; bij benadering is natuurlijk



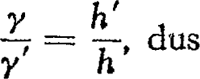, dus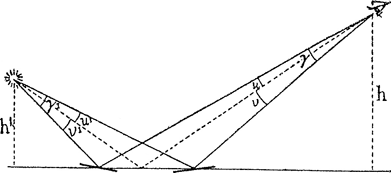

Fig. 15. Waarneming van een lichtzuil wanneer wij ons op een andere hoogte dan de lichtbron bevinden.

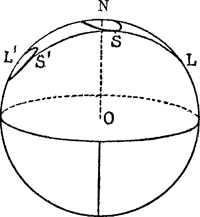
3. Bijzonder geval: h' = ∞. Dit geldt voor de zon, de maan en zeer hoge lantarens.

De formules worden nu: γ = 4α; PP' = 2h tg 2α (zoals men bewijst). Wij zien dus de assen der ovaal onder hoeken van ongeveer 4α en 4α sin ω. De verhouding van de schijnbare lengte en breedte der lichtzuil is dus sin ω, precies dezelfde als bij het geval 1, maar alle afmetingen zijn tweemaal groter.

De volgende redenering geeft zonder berekening een overzicht van de lichtverdeling bij deze weerspiegelingen (fig. 16). Denk u de spiegelende oppervlakjes op heel kleine schaal, vlak bij het centrum van een grote bol; de normaal op het ongestoorde wateroppervlak eindigt in N, de normalen op de hellende golfvlakjes eindigen dus in een cirkeltje op hoekafstand α van N; de oneindig ver verwijderde lichtbron wordt voorgesteld door een punt L op de bol. Om nu te vinden hoe bijvoorbeeld het oppervlakje met normaal OS de stralen weerspiegelt, is het voldoende de grote cirkel LS te trekken, en hem te verlengen tot S', zo dat SS' = SL. Men ziet aldus onmiddellijk, dat de door alle golfjes teruggekaatste stralen een kegel vormen met zeer langwerpige doorsnede, des te langwerpiger naarmate we schuiner op het wateroppervlak kijken. Het is ook gemakkelijk in te zien, dat de kegel der blikrichtingen, van het oog van den waarnemer naar de grenzen der lichtzuil, geheel en al dezelfde vorm heeft.

[p. 19]

Vergelijk de lichtzuil van de maan met die van een lantaren die u ongeveer in dezelfde richting weerspiegeld ziet. In het algemeen worden de lichtzuilen groter naarmate

Fig. 16. Het ontstaan van lichtzuilen, toegelicht door een konstruktie op de bol.

de lichtbron verder verwijderd is. Voorwerpen die zich vlak bij het water bevinden geven een bijna puntvormig, niet uitgerekt beeld.

Vergelijk de lichtzuilen die u onder verschillende hoeken met het wateroppervlak waarneemt.

Bepaal de hoek 2α uit de lengte der lichtzuilen (in hoekmaat) bij allerlei windsterkten.

Bemerk hoe de lichtzuilen prachtig lang, regelmatig, mooi vertikaal worden als het regent: de golfjes zijn wel klein, maar hebben sterke hellingen.

Het is ook de moeite waard, de vormen der lichtweerspiegeling na te gaan op elk

Fig. 17. a. Lichtzuil op zacht golvend water. b. Weerspiegeling van lichtreclames in de Amstel.

der afzonderlijke golfjes. Ieder golfje geeft een in horizontale richting uitgerekt lichtvlekje, des te meer tot een lijntje naderend naarmate de zon lager staat; en al die lijntjes samen vormen de vertikale zuil (fig. 17).

Eigenaardig is het verschijnen van gesloten kronkels (fig. 17), die men ziet als de lichtbron vrij hoog staat en een groot oppervlak heeft (b.v. lichtreclames met neonbuizen).

Er is nog een perspektivische bijzonderheid aan deze lichtzuilen verbonden. Elke lichtzuil ligt altijd in het vertikale vlak door mijn oog en de lichtbron (uitzonderingen, zie § 15). Wanneer ik een tekening of een schilderij maak, projekteer ik alles op een vlak dat vertikaal voor mij staat, en dus moeten alle lichtzuilen vertikaal

[p. 20]

lopen, ook al zijn ze buiten het midden van het tafereel. - Op een schilderij van Claudes in de Uffizi zit de zon nabij de zijkant van het doek, en heeft de schilder een lichtzuil weergegeven die van de zon schuin naar het midden van het voorplan toeloopt. Dit echter is fout!¹⁾

Richt een fototoestel op de zee, verlicht door de zon, en bekijk op het matglas de verdeling van het licht dat door de golven weerspiegeld wordt; daaruit zijn de hellingen der golven en eventuele voorkeursrichtingen af te leiden, de gehele toestand van het wateroppervlak is met één blik te overzien en kan fotografisch vastgelegd worden.²⁾

1) Ruskin, Modern Painters, III, 511.

2) W. Shoulejkin, t.a.p.

15. Terugkaatsing in een gerimpeld wateroppervlak met voorkeursrichting.

Dikwijls vertonen de lichtzuilen een duidelijke asymmetrie: zodra men schuin ten opzichte van de richting van het kanaal

Fig. 18. Een verwonderlijk gezicht: de lichtzuil ligt niet in het vertikale vlak door oog en lichtbron!

kijkt, liggen ze niet meer in het vertikale vlak door de lichtbron en het oog van den waarnemer, hun richting nadert dan meer tot de richting van het kanaal zelf (fig. 18). Kijkt men schuin over het kanaal naar de andere kant, dan wijken ze weer af van de vertikaal, ditmaal echter naar de andere zijde hellend: dus weer naderend tot de kanaalrichting.

Toch is onze theorie niet fout, want als het regent bij windstil weder zijn de zuilen zuiver vertikaal, in welke richting men ook kijkt. De oorzaak der afwijkingen is de wind, die de golfjes bij voorkeur dwars op de kanaalrichting rimpelt, zodat we niet meer van het beeld der ideaal onregelmatige golvingen mogen uitgaan. Ten bewijze dienen de volgende waarnemingen:

a.	in een zeer brede rivier is de afwijking veel minder stelselmatig, de golfjes hebben daar geen duidelijke voorkeursrichting loodrecht op de oevers;

[p. 21]

b.

is het water met een ijslaagje bedekt, dan schijnt dit veel kleine hobbeltjes te hebben en geeft een duidelijke lichtzuil: maar die is vertikaal;

c.

op een geasfalteerde straatweg, die vochtig is na een regenbui, zijn dezelfde afwijkingen waar te nemen als op een kanaal bij wind, zowel aan de terugkaatsing van straatlantarens als aan die van Fig. 19. Het ontstaan van scheve lichtzuilen als er een voorkeursrichting van de golfjes is. auto- en fietslampen. En inderdaad: in de asfaltlaag komen er hobbels door 't verkeer (hun ontstaan is op zichzelf een belangwekkend verschijnsel!). Als we het oppervlak van de weg bekijken, kunnen we de hobbels rechtstreeks zien, en opmerken dat het echte golven zijn, met hun kammen loodrecht op de richting van de weg.

De uitvoerige behandeling van dit verschijnsel is nog niet gegeven. Maar in hoofdtrekken kunnen we 't wel overzien met behulp van onze projektie op de bol, althans voor het geval ener oneindig ver verwijderde lichtbron (fig. 19). Wanneer de normalen over de vlakjes verdeeld zijn zoals voorgesteld door de kromme lijn die N omgeeft, zullen de gespiegelde stralen gericht zijn naar de onderscheidene punten van de kromme lijn om L'; de as der zuil ligt dus niet meer in het vlak LNL', maar wijkt schuin af.

16. Weerspiegeling in zeer grote gerimpelde wateroppervlakken.¹⁾

Bij weerspiegeling in de zacht golvende zee treedt een verschijnsel op dat we noemen zullen: de verschuiving der spiegelbeelden naar de gezichteinder (fig. 20). De grens AB tussen wolk en blauwe lucht ligt in de weerspiegeling A'B' heel veel dichter bij de horizon dan aan de hemel. De eerste 25^o of 35^o van de hemel boven de gezichteinder komen eigenlijk nauwelijks te voorschijn in de weerspiegeling! Natuurlijk zijn alle beelden onregelmatig vervormd, maar het effekt is toch zeer duidelijk, en zo opvallend, dat het de gehele lichtverdeling over de zee beheerst. Zo komt het ook dat men bomen aan de kust, duinen enz. nooit weerspiegeld ziet: ze zijn niet hoog genoeg. Ook schepen zijn ternauwernood ooit in de onregelmatige terugkaatsing terug te vinden, want de

1) E.O. Hulburt, J.O.S.A. 24, 35, 1934.

[p. 22]

donkere vlek die ze moesten geven wordt door dit effekt tot vlak bij het schip teruggedrongen.

De weerspiegeling van de zon in de golven is een verblindend

Fig. 20. Weerspiegeling op zee: het spiegelbeeld van de wolk is naar de kim toe ‘verschoven’.

Fig. 21. Zonlicht op de zee.

[p. 23]

heldere vlek, die bij laagstaande zon min of meer driehoekvormig is, en dus ook de verschuiving naar de gezichteinder vertoont (fig. 21).

De verklaring van deze verschijnselen is gemakkelijk te geven: op grote afstand van ons zien wij van de golven alleen de naar ons toe gekeerde hellingen;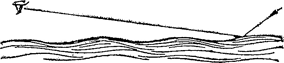

Fig. 22. Verklaring van de verschoven spiegelbeelden. De lichtstraal valt steil in maar wordt vrij vlak weerspiegeld.

het is dus alsof wij alle voorwerpen van de hemel weerspiegeld zagen in een naar ons toe hellende spiegel (fig. 22). Dit geeft vanzelf de verschuiving der spiegelbeelden naar de gezichteinder. Uit de verdwijning der eerste 30^o in de weerspiegeling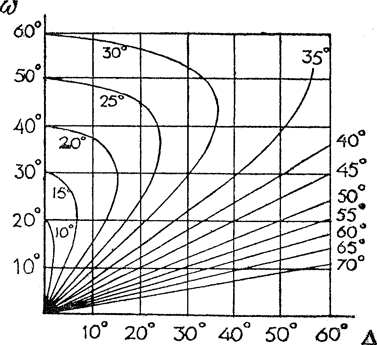

Bij elke waargenomen waarde van ω en Δ past een punt; beoordeel de ligging daarvan t.o.v. de kurven, die ieder met een zekere waarde van α overeenkomen.
(Naar E.O. Hulburt, J.O.S.A., 24, 35, 1934.)

volgt, dat de golven gemiddeld hellingen van ongeveer 15^o in elke richting vertonen (bij niet uitgesproken rustige noch erg stormachtige zee).

[p. 24]

Waarom kwam dit effekt niet te voorschijn bij onze theorie in § 14? Omdat we niet het geval hebben beschouwd, waarin ω < 2α, dus waarin we zeer schuin langs het wateroppervlak kijken; dit geval, waarin onze berekeningen niet meer opgaan, komt telkens voor als het wateroppervlak maar zeer uitgestrekt is, en inzonderheid bij de zee. Hoe kalmer het wateroppervlak, hoe schuiner men hiervoor kijken moet.

Of aan deze voorwaarde voldaan is, bemerkt men onmiddellijk bij het gadeslaan van de zonbeschenen zee: de lichtzuil bereikt dan de gezichteinder. We kunnen nu de hellingen der golfjes niet meer uit de lengte der lichtzuil meten, maar gebruiken een ander middel: worden de golfjes steiler, dan bedekt zich

Fig. 23. Kan ik aan het spiegelbeeld der opgaande zon in een uiterst rustige zee de kromming der Aarde waarnemen?

een toenemend breder stuk van de gezichteinder met fonkelend licht. Meet deze hoek Δ, de breedte dus van de zuil aan de horizon; meet ook de zonshoogte ω, en bepaal nu hieruit de helling α der golven met behulp van de grafische voorstelling blz. 23; ofwel met de formule van Spooner, vereenvoudigd voor zonshoogten beneden 15^o: α = Δ / 2ω. (Vgl. plaat I)

De opgaande en ondergaande zon vertonen in zeer kalme zee een bijna lijnvormig spiegelbeeld, dat met de vurige zonneschijf zelf ineenvloeit en een soort Ω vormt (fig. 23). Bij zeer uitzonderlijk effen zee heeft men wel eens het elliptische spiegelbeeld gezien toen de zon al wel 1^o boven de gezichteinder was; meestal krijgt men echter al heel gauw de overgang tot de reeds beschreven driehoekige lichtvlek. In dergelijke gevallen begint de kromming van het aardoppervlak ook al een rol te spelen; als er helemaal geen golfjes waren overgebleven, zou men kunnen zeggen dat men hier de rondheid van de Aarde rechtstreeks voor zijn ogen ziet! Echter is in het gunstigste tot nu toe onderzochte geval de

[p. t.o. 24]

PLAAT I.
De zon wordt door de zee weerspiegeld en vormt lichtzuilen, des te breder naarmate ze hoger staat en de zee sterker golft. Bemerk dat de verre kust geen spiegelbeeld heeft.
Naar E.O. Hulburt, J.O.S.A., 24, 35, 1934.

[p. 25]

waargenomen verschuiving naar de gezichteinder nog altijd wel dubbel zo groot als de kromming der Aarde kan doen verwachten.¹⁾

1) A. Ricco, V. Cerulli, A. Venturi, in Mem. Spett. Ital. 17, 203, 1888; 18, 23, 45 en 57, 1889. - Vgl. ook Spooner, t.a.p. blz. 337.

17. Zichtbaarheid van zeer zwakke golvingen.

Heel zwakke golvingen ziet men veel beter als men loodrecht op de golfkammen kijkt dan wanneer men evenwijdig eraan waarneemt. Voor een kanaal moet men dus in 't algemeen evenwijdig aan de kanaalrichting kijken om te zien hoe de wind het water rimpelt. Vandaar ook, dat de prachtige dwarsgolven achter een schip alleen van op een brug waargenomen worden, maar van op de oever praktisch onzichtbaar zijn! De reden is precies dezelfde als die waarom het beeld van een lantaren tot een lichtzuil wordt uitgerekt. Kijkt men loodrecht op de golfjes, dan ziet men om zo te zeggen de lange as der lichtzuil; kijkt men evenwijdig er aan, dan ontstaat de korte as. Het komt altijd daarop neer, dat een golfje meer ‘uitwerkt’ in een vlak loodrecht op zijn kamrichting dan in die richting zelf.

18. Lichtzuilen in een vuil wateroppervlak.

Bij een geheel effen, spiegelglad wateroppervlak, zien we toch dikwijls lichtzuilen om de spiegelbeelden der straatlantarens 's avonds. Deze lichtpluimen vertonen niet de wemelende wisselingen der lichtzuilen op de golfjes, ze staan volkomen rustig en onbewegelijk. Ze ontstaan overal waar het wateroppervlak niet geheel schoon is: blijkbaar vormen de stofjes op het water even zovele heel kleine hobbeltjes in het oppervlak, die optisch net als golfjes werken. Men zou dan verwachten, deze lichtzuilen des te slanker te zien worden naarmate men schuiner op het oppervlak kijkt; - dit komt inderdaad uit.

Bij min of meer loodrechte inval ziet men de lichtzuilen bijna niet; bij rakelingse inval zijn ze zeer opvallend, en vormen een gevoelig criterium voor de schoonheid van een wateroppervlak. Het intensiteitsverschil is zo sprekend, dat hier iets bijzonders in 't spel moet zijn. Die stofjes zijn zo klein, dat men al van verstrooien van het licht moet spreken; en nu zullen we zien dat de verstrooiing door zulke stofjes verreweg het sterkst is in de buurt van de richting van de invallende lichtbundel. Vandaar stellig dat de lichtverstrooiing en de hele lichtzuil sterker en sterker worden, naarmate men schuiner kijkt.

[p. 26]

19. Lichtzuilen op sneeuw.

Soms is de sneeuw bedekt met een laag mooie vlakke plaatjes en sterretjes, alle min of meer in horizontale stand. Zoekt men bij lage zon haar spiegelbeeld in de sneeuwlaag, dan ziet men een

Fig. 24. Regendruppels tekenen vurige vonkjes om het spiegelbeeld van een straatlantaren.

mooie lichtzuil, die toe te schrijven is aan kleine onregelmatige afwijkingen van de sneeuwplaatjes ten opzichte van het horizontale vlak. De zon moet laag staan, omdat de lichtzuil zich dan samentrekt in de dwarsrichting en duidelijker te voorschijn komt.

De vorming van die lichtzuilen is nog treffender in de avond, als de straatlantarens branden en als ieder licht zich spiegelt in de verse sneeuw.

20. Lichtzuilen op straatwegen.

Dezelfde lichtzuilen die we op golvend water zien, komen ook te voorschijn op onze straatwegen, het mooist wanneer het geregend heeft en alles glimt van de nattigheid; men ziet ze prachtig op ons moderne asfalt, maar ook op de ouderwetse straatkeien, zelfs op grintwegen. Ook zonder regen spiegelen onze wegen meestal zo goed, dat er wel altijd lichtzuilen ontstaan, mits men schuin genoeg kijkt (verder van de normaal en meer naar de gezichteinder toe). Vgl. § 15.

21. Lichtreflexen bij regen.

Bekijk het spiegelbeeld van een straatlantaren in een waterplas, 's avonds, bij regen. Het is omringd door een aantal lichtvonkjes, die overal ontstaan waar er net een regendruppel valt, en die er

[p. 27]

alle uitzien als lichtlijntjes die van het spiegelbeeld uitstralen. (fig. 24). Forel merkte een dergelijk verschijnsel op, als hij door een donker glas naar het zonsbeeld keek, weerspiegeld in rustig water waar hier en daar luchtbelletjes uit opstegen.¹⁾

Fig. 25. Hoe de vonkjes om het spiegelbeeld ontstaan.

De verklaring is eenvoudig. Elke druppel maakt een stelsel concentrische golfjes, en de reflexen tegen de zijkanten daarvan moeten altijd liggen op de verbindingslijn van het centrum der golven met het spiegelbeeld der lichtbron (fig. 25). Dit is bv.

Fig. 26. Hoe de lichtkringen in boomkruinen ontstaan.

ineens in te zien als lichtbron L en oog O even hoog boven het wateroppervlak zijn, en het druppeltje D even ver van beide neervalt: de punten D₁ en D₂ liggen dan op de lijn MD; als een golfje zich kringvormig om D uitbreidt, beschrijft de lichtreflex een stuk van de lijn DM, en dit zo snel, dat we een lichtlijntje menen waar te nemen. Even klaarblijkelijk is de stelling,

1) Le Léman, II, 507.

[p. 28]

wanneer de regendruppel in het vlak OML valt, hetzij vóór, hetzij achter M.

Het verschijnsel is na te bootsen als men een lamp gespiegeld ziet in een glazen plaat, en dan over die plaat een voorwerp verschuift dat concentrisch geribbeld is (deksel van suikerpot, op de draaibank geschuurd plaatje enz.).

Beproef het bewijs algemeen te leveren.

22. Lichtkringen in boomkruinen.¹⁾

Als een bladerloze boom vlak voor een lantaren staat, ziet men 's avonds hoe de takken en twijgen het licht hier en daar weerspiegelen; die lichtglansen zijn eigenlijk kortere of langere lichtlijntjes; en al die lijntjes zijn in concentrische cirkels om de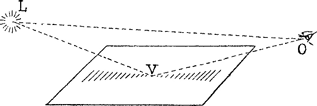

Fig. 27. Vergelijk de lichtkringen in boomkruinen met de lichtzuilen op golvend water.

lichtbron gerangschikt! (Plaat II) Men ziet het verschijnsel het best, als men zelf in de schaduw van de boomstam staat en als de lantaren dicht bij de boom hangt. Maar ook met zonlicht is het waar te nemen, bijvoorbeeld als de takken vochtig zijn van de regen, of als zich het fijne lijnenspel van glimmende berketwijgjes tegen een donkere achtergrond aftekent; de zon zelf moet liefst door een muur of dak afgedekt zijn, zodat ze ons niet verblinden kan.

Verklaring (fig. 26). - Beschouw een vlakje V dat het licht van de lantaren naar ons oog weerspiegelt. Alle takjes in dit vlak zullen wij zien glimmen. Maar de takjes zoals AB zien wij sterk perspektivisch verkort, de takjes CD in hun volle lengte. Waar takjes van allerlei richtingen even veelvuldig voorkomen, zullen wij dus in hoofdzaak lichtlijnen zien loodrecht op het vlak OLV. Een dergelijke stelling geldt ook voor andere vlakjes zoals V', die wij boven, rechts of links van de lichtbron zien:

1) Fokker, Physica, 2, 238, 1922.

[p. t.o. 28]

PLAAT IIa. Kijkt men 's nachts dwars door een boomkruin naar een brandende lantaren, dan ziet men de glimmende takken als kringen om de lichtbron.
PLAAT IIb. Dezelfde boom en de lantaren bij dag. De glimmende kringen komen één voor één met bepaalde takken overeen.
Naar opnamen van Dr. Ir. A.J. Staring, Wageningen.

[p. 29]

wij krijgen aldus de indruk van concentrische cirkels. - Men ziet gemakkelijk dat de voorkeur in de richting des te sterker uitgesproken wordt naarmate onze blik een kleinere hoek met de lijn OL vormt, en dat die voorkeur nog iets sterker zal zijn voor een oneindig verre lichtbron zoals de zon, dan voor een lantaren die dichtbij ons staat.

Vergelijk dit geval met de lichtzuilen op golvend water (fig. 27)! We moeten ons nu als 't ware denken, dat boomtakjes niet overal in de ruimte voorkomen, doch slechts in één vlak (= het wateroppervlak). De enige lijntjes die in dit vlak liggen en toch bij benadering deel uitmaken van concentrische cirkels om OL, zijn ieder loodrecht op het vlak OVL gericht, maar vormen samen een zuil in dit vlak. Dit is geheel analoog aan de watergolfjes.

Een dergelijk verschijnsel kan men nog waarnemen als men de laagstaande zon in een korenveld ziet schijnen. Of bij mistig weer, als de spinnewebben bedauwd zijn met kleine druppeltjes, en men door zulk een spinneweb naar een brandende straatlantaren kijkt. Of aan de krasjes op de ruiten van een treinraampje (vgl. 159). In al deze gevallen glimmen in hoofdzaak de lijntjes loodrecht op het invalsvlak van het licht, en krijgt men de indruk van concentrische cirkels om de lichtbron.