Logo DBNL
Oeuvres complètes. Tome XXII. Supplément à la correspondance. Varia. Biographie. Catalogue de vente (1950)

Oeuvres complètes. Tome XXII. Supplément à la correspondance. Varia. Biographie. Catalogue de vente

(1950)–Christiaan Huygens–rechtenstatus Auteursrecht onbekend

Vorige Volgende

Huygens en Hollande 1681-1695.

§ I. À la Haye et à Hofwijck de septembre 1681 à juin 1689.

À La Haye Christiaan s'installa comme toujours dans la maison paternelle. Il y fut doublement le bienvenu puisque le vieillard, depuis quelque temps, l'habitait seul, sans il est vrai être désoeuvré: il conservait toujours le titre de conseiller1) ou plutôt de président du conseil du stadhouder Willem III ce qui n'était pas une sinécure. En 1679 il avait publié son grand poème autobiographique ‘De vita propria’ dont nous avons cité plus haut2) un passage - pas le seul, comme on le conçoit - se rapportant à Christiaan. Nous n'en extrayons ici que cinq vers où il dit avoir dû se tourner vers Aristote dans sa jeunesse puisque Descartes n'avait pas encore fait briller sa nouvelle lumière.

Philosophia Physica

 
Jamque per abstrusas rerum caelique solique
 
Ducebar causas: quas ut de fonte Stagirae
 
Purius haurirem, (nondum Cartesius auctor
 
Luce nova fucum vero detraxerat) alter
 
Ecce labor sudorque, novum maris aequor arandum.

A. Loosjes traduit, fort librement:

 
Nu werd ik omgevoerd, als met een snelle vlugt,
 
Door al de paden heen van water, aarde en lucht,
 
Om met mijn zwak vernuft en jeugdig brein te dringen
 
Tot in het heiligdom en oorzaak aller dingen.
 
Nog had Cartesius vernuft en schranderheid
 
Het nevelheir niet door zijn licht uit één verspreid:
 
Tot Aristoteles moest ik me, als bron, begeven.

Il ne faut pas exagérer la portée de ce bref hommage rendu à Descartes; mais c'est un hommage tout-à-fait spontané, donc bien réel3).

Il était seul, disons-nous, puisque son fils aîné et sa famille avaient, à son grand regret, quitté la maison en juin 16804) pour s'installer ailleurs5). Il eût bien voulu que Christiaan fût venu lui tenir compagnie pour quelque temps déjà en cette année.

Qu'il s'intéressait toujours aux travaux de son fils, cela ressort des lettres sur les couronnes et parhélies qu'il recevait en avril et mai 1681 de Scandinavie par l'intermédiaire de Rumpf à Paris où Christiaan, malade, séjournait encore en ces mois6).

 

Dès que Huygens fut rentré dans sa ville natale, il s'adressa à l'habile van Ceulen7) pour la construction du planétaire projeté. Nous ignorons si cet artisan put saire usage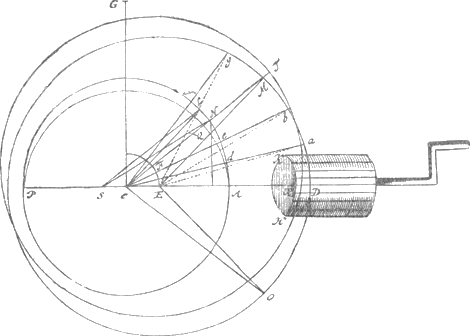

illustratie
[Figure 146 du T. XXI].


de ce qui avait déjà été construit à Paris. Au mois d'août 1682 Huygens annonce l'achèvement à Colbert8). La ‘Descriptio Automati planetarii’ (T. XXI) - publiée en 1703 dans les ‘Opuscula postuma’ - date de beaucoup plus tard. On peut consulter en outre la figure vis-à-vis de la p. 525 du T. XVIII et celle vis-à-vis de la p. 181 du T. XXI. Les planètes étaient mises en mouvement, et le sont encore aujourd'hui, par une horloge. Dans la ‘Descriptio’ (T. XXI) la figure que nous avons appelée Fig. 1469) fait défaut; elle sert pour ‘expliquer de quelle manière les justes inégalités des mouvements résultent des révolutions de nos roues’; la voici.

Un assez grand nombre de planétaires avaient été construits antérieurement, dont le plus ancien, celui d'Archimède, est brièvement mentionné par Huygens en 168210) et de nouveau dans la ‘Descriptio’11), plus longuement dans une autre Pièce de date incertaine12). Il emprunte des données sur d'autres constructions à l'‘Almagestum novum’ de Riccioli. On y voit e.a. que Kepler n'approuvait guère qu'un astronome perdît son temps à construire des planétaires10). Tel n'était pas l'avis de tous les contemporains de Huygens. Roemer, notamment, s'y appliquait; et il put, à Paris, profiter des talents de l'horloger Thuret. Nous avons mentionné plus haut13) son projet présenté à l'Académie pendant l'absence de Huygens; et la Pièce de Huygens ‘Avantages de ma machine par dessus celle de Mr. Roemer14)’ indique qu'en s'appliquant à son tour à ce sujet il entra délibéremment en concurrence avec l'astronome danois.

Nous avons dit ailleurs15) que Roemer, de même que Cassini, était tychonien et avait par conséquent donné la place centrale à la terre; tandis que Huygens, ayant l'ambition de collaborer au triomphe définitif du système de Copernic (où il s'agit toujours du système de Copernic simple, comparez la p. 511 qui précède), avait adopté ce système vrai encore assez généralement méconnu dans les écoles16). ‘Il est important de faire voir’, dira-t-il en 168617), ‘qu'en s'arrestant uniquement au systeme veritable la chose n'a rien d'embarassant, mais qu'elle est aisée et naturelle’.

Notre observation sur le planétaire de Roemer était-elle exacte? Nous l'avons corrigée ailleurs18) en disant que dans la figure du planétaire telle qu'on la voit dans le Journal des Sçavans de 1682, ce n'est pourtant pas la terre qui occupe la place centrale. Il est vrai que, puisqu'elle y est figurée, dirait-on, comme le corps le plus important, on peut se demander si ce n'est pas seulement pour la facilité de la construction que le soleil est mis au milieu.

La question de savoir si Roemer était tychonien convaincu ou non n'est pas simple: Huygens ne parle que d'un seul planétaire de lui à Paris, mais il y en eut plusieurs19) et de plus Roemer en construisit encore en Danemark après avoir définitivement quitté Paris dans la même année que Huygens. Dans le T. XVIII20) nous avons cité Horrebow disant dans sa ‘Basis astronomiae’ que la machine planétaire de Roemer (lisez: une de ses machines planétaires) était mue à la main et qu'elle représentait le mouvement du soleil et des planètes suivant le système géocentrique de Brahé.

Nous avons fait voir dans le T. XXI21) que l'étude, encore à Paris, de Huygens des vues de Kepler, de Boulliau, de Seth Ward, et de Mercator, sur les orbites planétaires, ainsi que sa connaissance de celles de Rembrantsz. van Nierop, le conduisirent à adopter pour le mouvement de ses planètes dans des orbites circulaires excentriques des formules indiquant nettement, pour chacune d'elles, la variation périodique de sa vitesse. Ces formules lui semblaient, non sans bonnes raisons, si exactes que de pareils mouvements pourraient même être admis comme véritables: la différence avec ce qui serait observé au ciel dans l'hypothèse d'une exactitude absolue des lois de Kepler était minime. Sans que ses planètes parcourussent des ellipses il put donc écrire à Colbert que leur marche était fort précise ‘tant pour le moyen mouvement que pour l'inegalitè qui demande qu'elles aillent plus lentement a mesure qu'elles se trouvent plus eloignées du soleil, en quoy j'ay representè l'hypothese de Kepler’. Il ne suffisait pas, bien entendu, d'avoir calculé ces mouvements, il avait fallu imaginer en outre le mécanisme qui pouvait les faire exécuter par les planètes. Sur le calcul des nombres des dents des roues etc. on peut consulter les différentes Pièces du T. XXI.

 

Les lettres du frère Constantyn - souvent absent de la Haye, et séjournant alors à Dieren en sa qualité de secrétaire du stadhouder - dont la première est datée le

2 février 1682, et les réponses de Christiaan, font voir que les deux frères travaillaient ensemble, comme jadis, à la taille de lentilles. De 168222) date la petite Pièce avec figure23) sur la ‘methode excellente et eprouvée pour donner la forme spherique parfaite aux formes de leton qui servent au travail des verres des telescopes’.

Les Pièces sur les passages de Mercure devant le soleil font voir24) que Huygens ainsi que les autres astronomes, s'intéressaient surtout à la position exacte des noeuds de l'orbite de la planète; il s'agit ici d'une discussion des résultats obtenus par divers observateurs. Une considération de 1682 sur les dimensions du système solaire25) a été gravée sur la plaque de devant du planétaire.

 

Pour le frère Lodewijk, Huygens fit construire un niveau à lunette ‘plus simplement, à meilleur marchè, et moins suject a estre esbranslè par le vent26)’.

Une longue Pièce sur les équations solides date également de 168227). Huygens a apparemment fait ses calculs pour son propre plaisir, non pas dans le but de les publier.

 

La même remarque s'applique à un calcul de probabilité de 1683 achevé en 168828).

 

En 1682 commencèrent les mauvaises attaques de l'abbé Catelan29), dénigrateur de l'‘Horologium oscillatorium’, auquel Huygens ne répondit alors que brièvement. Puisque nous avons énuméré et discuté les Pièces subséquentes tant de Catelan que

de Jacques Bernoulli, du marquis de l'Hospital et de Huygens lui-même (années 1684 et 1690) dans le chapitre ‘De Hugeniana centri oscillationis determinatione controversia ulterior30)’ du T. XVIII, nous croyons faire le mieux de nous en tenir à cet aperçu, où il est d'ailleurs aussi fait mention à la fin de l'article de Jacques Bernoulli de 1703 et de celui de 1727 de son frère Jean. Huygens, comme précédemment, considère comme parfaitement légitime de se baser sur le principe de l'impossibilité du mouvement, ou plutôt du moteur, perpétuel31). En particulier: le centre de gravité d'un système ne peut s'élever de lui-même au dessus d'un plan horizontal32).

 

Huygens eût voulu retourner à Paris déjà en cette année, croyant qu'on l'attendait. Mais ne recevant aucun encouragement, il demanda à Colbert la permission de rester encore trois ou quatre mois en Hollande, ce qui lui fut accordé33). Après l'expiration de ce délai il prolongea néanmoins son séjour à la Haye: ‘c'estoit - écrit-il34) - pour avancer l'invention des longitudes par le moyen de mes horloges en estant requis par la Compagnie des Indes Orientales’ (voyez sur ce sujet les p. 509-510 du T. XVIII). Colbert étant décédé le 6 septembre 1683, il crut devoir s'adresser de suite à son successeur35) le Tellier, marquis de Louvois, auquel il parla également dans sa lettre du planétaire ‘dont je me souviens d'avoir eu l'honneur de vous entretenir’. Il ajouta qu'il attendait les ordres du marquis. Le ton de la réponse de Louvois, que nous ne possédons pas, ne satisfit ni Christiaan ni surtout son père36). Et en effet, les démarches ultérieures - résumées par Brugmans dans son livre déjà plusieurs fois cité - ne conduisirent pas au but. Nous nous abstenons ici de nous étendre sur une chose qui ne nuisit nullement à l'activité de Huygens. Celui-ci écrira e.a. en 168537): ‘ce procedè des François a mon égard est assez barbare, et je ne scaurois l'imputer qu'a la maxime qu'ils ont de n'emploier personne qui soit de la Religion ou bien aux brigues de quelques envieux’. Nous devons cependant avouer que, si nous avions

été à la place de Louvois, nous aurions aussi pris en considération - ce qu'il a pu faire - que tant le père que le frère Constantyn étaient attachés au service du prince d'Orange, adversaire de Louis XIV; fallait-il donc rester en relations assez étroites avec cette famille? Le père Constantyn ne l'entendait pas ainsi; selon lui - comparez la p. 660 qui précède - une certaine solidarité des classes dirigeantes pouvait subsister malgré les guerres et les différends, de religion ou autres. L'impolitesse de Louvois qui n'accordait pas même à son fils ‘un congè un peu honneste’38) le choquait.

Il est vrai que ce n'aurait pu être qu'un congé relatif. Car tout en ne recevant plus de pension Huygens restait membre de Académie des Sciences39).

Louvois n'a pas soufflé mot sur la proposition d'acheter pour 620 écus le planétaire de Huygens. Ceux de Roemer avaient déjà été suffisament coûteux40). Il était d'avis que l'Académie devait surtout rechercher l'utile.

 

Le père Constantyn proposa à Christiaan d'entrer en sa place au conseil de Son Altesse, mais le fils refusa. Nous ne l'apprenons que plus tard, en 168941), alors que Christiaan, vu la lourdeur des impôts, sollicite une place vacante dans le conseil, laquelle le stadhouder, depuis 1688 roi d'Angleterre, ne lui accorda cependant pas, se disant persuadé qu'il avait des idées plus hautes que de s'attarder avec les administrateurs42). Le roi avait raison. Quoique la fortune des Huygens ne fût plus aussi grande qu'autrefois43) Christiaan, toujours célibataire, pouvait fort bien vivre sans charge. D'autant plus qu'il recevait depuis 168644) une prébende de la part du prince45).

Un de nos Avertissements du T. XVIII46) traite de l'‘application pratique aux horloges de différents mouvements vibratoires plus ou moins isochrones’ depuis 1675 jusqu'à 1694. L'application de décembre 1683 des vibrations de torsion (‘pendulum cylindricum trichordon’), le premier projet, de 1683 ou 1684, du ‘balancier marin parfait’ et l'application du pendule triangulaire à une horloge marine47) construite vers 1685 - p. 527-543 du T. XVIII - appartiennent à la période qui nous occupe. Huygens travailla avec van Ceulen au moins jusqu'en 1685. À noter48) la généralisation intuitive (datant d'ailleurs déjà de 1675) du tautochronisme des vibrations: ce tautochronisme, démontré dans le cas d'un mouvement linéaire accompli sous l'influence d'une force proportionnelle à l'écart linéaire, subsiste selon lui - et nous savons qu'il avait raison - lorsqu'il s'agit d'une oscillation autour d'un axe due à des forces dont le moment par rapport à l'axe est proportionnel à l'écart angulaire. Le rapport de Huygens sur la détermination des longitudes par ses horloges dans l'expédition de 1686-1687 au Cap de Bonne Espérance se trouve dans le T. IX49). Nous avons pu conclure dans le T. XVIII50) que s'il était en général impossible d'obtenir avec les horloges des longitudes exactes il serait cependant exagéré de dire que la valeur de quelques chiffres fut absolument nulle.

Ce n'est pas là un fort grand éloge, mais on conçoit qu'après cette réussite partielle la Compagnie des Indes Orientales désirait recommencer l'expérience.

 

Il y eut d'ailleurs, dans le voyage de retour du Cap à l'île de Texel, un résultat remarquable: la marche des horloges avait été suffisamment exacte pour démontrer à la satissaction de Huygens la diminution de la pesanteur due à la rotation journalière de la terre51). Malgré son instruction52) le pilote Helder n'avait malheureusement pas mesuré au Cap la longueur du pendule à secondes, ce qui eût pu confirmer l'observation de Richer de 1673 à la Guyane; mais il était désormais passablement évident que cette observation aurait été confirmée. C'est d'ailleurs ce que Huygens jugeait suffisamment probable déjà vers la fin de 1686 pour en conclure que la force centrifuge, due à la rotation de la terre, lui donne une forme sphéroïdale, légèrement aplatie, conformément à ce qu'on constate dans le cas de la planète Jupiter où cet aplatissement est plus prononcé à cause de la plus grande rapidité de sa rotation53). Voyez sur son doute antérieur la p. 620 qui précède.

Depuis 1684 une des occupations principales de Huygens furent les calculs et la rédaction de chapitres de dioptrique. Nous avons pu dire dans le T. XIII54) que les dates des différentes parties de ce que nous avons appelé la ‘Pars tertia’ sont souvent difficiles à déterminer, mais qu'en général les parties qui traitent des télescopes55) ont été rédigées ou révisées vers 1685. Nous remarquons que la table qui occupe la p. 353 existait en 1667; nous l'avons citée plus haut (p. 631). Quelques considérations sur les télescopes et microscopes56) - quoique de ces derniers, après avoir quitté Paris, il se soit occupé surtout plus tard - datent des premiers mois de 1684. Et nous avons cru devoir donner la date 1683 à une campanine conservée sur l'objectif duquel Huygens a écrit avec un diamant ‘Chr. Hugenius f.’57). Les considérations des p. XCII-CIV de l'Avertissement du T. XIII se rapportent surtout aux pièces de Huygens sur les télescopes; il est vrai que les p. C-CIV traitent de la diffraction de la lumière dans les télescopes et les microscopes. Ce savant Avertissement explique et amplifie les considérations de Huygens sans suivre exactement l'ordre historique. C'est ainsi que les pages précédentes XC-XCII traitent des ‘considérations et calculs de Huygens sur la distorsion des images’ qui datent de 1690-169258). Quant à l'‘aperçu général’ de cet Avertissement, il ne consacre qu'un seul alinéa59) aux recherches de 1684-1685 sur les télescopes lequel indique clairement leur portée principale: ‘Enfin, en 1684, Huygens reprend les recherches sur les règles concernant l'ouverture de l'objectif et le grossissement des lunettes en se basant cette fois sur la théorie des couleurs de Newton. En avril 168560) on trouve dans la correspondance la première mention des nouvelles règles auxquelles il est parvenu et qui diffèrent, en effet, entièrement des précédentes. Et c'est probablement en cette même année que fut écrite la préface “De Telescopiis” et presque tout ce que nous avons rassemblé dans la partie de la “Pars Tertia: De telescopiis et microscopiis” qui traite des télescopes’.

 

Il convient toutefois d'ajouter que la règle: ‘Aperturarum diametri in subdupla ratione foci distantiarum’ date déjà du commencement de 1684. La recherche de

cette règle constitue ce que nous avons appelé un peu plus haut ‘les premières considérations (de ce temps) sur les télescopes et microscopes’. Elle est mentionnée antérieurement à 1685, savoir vers la fin de l'‘Astroscopia compendiaria’ publiée en 1684, sous la forme: ‘subdupla aperturarum ad longitudines ratio’ (proportionnalité des ouvertures aux racines carrées des longueurs). Et comme Huygens avait conçu déjà en novembre 1683 la manière d'observer dont traite l'‘Astroscopia’, il ne semble nullement improbable que ce soit précisément son désir de tirer le meilleur parti de son invention qui lui a fait reprendre ses recherches sur la dioptrique. Comparez le premier alinéa de la p. 9 du T. XV.

La lunette sans tuyau, nous le disons dans l'Avertissement à l'‘Astroscopia compendiaria’61), existait déjà, mais le mode d'opérer de Huygens était nouveau.

Nous avons mentionné à la p. 604, comme nous l'avons fait aussi dans le T. XXI61), qu'en 1663 Huygens assista - ce fut à Issy, chez Thévenot - à des observations avec une lunette sans tuyau construite suivant l'idée d'Auzout. On a vu62) Auzout, rentré à Paris peu avant le départ de Huygens, y observer une comète; il s'intéressait donc encore toujours aux observations. En 1683, de passage à la Haye, il y avait visité Huygens63) avant que celui-ci se résolut à reprendre l'ancienne idée d'observer sans tuyau.

La publication de l'‘Astroscopia’ et l'expédition à diverses personnes à Paris (e.a. en mai à l'Académie des Sciences) furent pour Huygens un motif de correspondre avec Cassini. Le père Constantyn avait déjà écrit à Paris le 9 mars que son fils observait sans tuyau et recommandé cette méthode (sans la décrire) aux parîsiens possesseurs des lentilles de Campani64). On peut disputer sur la question de savoir si Cassmi, qui observa sans tuyau le 21 mars, a connu cette lettre65). L'année suivante, d'après l'‘Histoire de l'Académie Royale des Sciences’66), ‘Cassini fit un support pour loger l'objectif et lui laisser la liberté de tourner en tous sens..etc...la méchanique étoit d'ailleurs à peu près la même que celle que Mr. Huygens avoit employée’. Auzout n'avait pas approuvé cette mécanique67).

Déjà le 21 mars, grâce aux lentilles italiennes, Cassini découvrit un quatrième et un cinquième satellite de Saturne lesquels Huygens n'a jamais pu voir. Au début de l'‘Astroscopia’ Huygens rend hommage aux ‘organa Italica, ab egregiis artificibus

elaborata’, supérieurs à ce qu'il possédait lui-même. Il était déjà heureux de pouvoir voir en 1684, avec la lunette aérienne, trois satellites68).

On trouvera dans le T. XV, p. 130-160, toutes les observations faites à la Haye de 1682 à 1686. Consultez-y aussi les p. 8, 17-19, 31-33, 35-38, 41, 43-46 et 49. Le 22 mai 1684 (p. 147) il fut fait usage pour la première fois de la lunette aérienne. La comète de Halley fut observée en septembre 1682, les autres observations se rapportent à la lune et à différentes planètes. Des canaux ou fossés furent remarqués dans la lune (p. 155-158), des bandes etc. dans Jupiter, dans Mars des taches. Ces dernières observations ont pu être utilisées beaucoup plus tard pour la détermination exacte de la période de rotation de cette planète69). Huygens note souvent les noms des spectateurs présents, parmi lesquels parfois son père. Le mât était dressé dans le jardin de la maison paternelle70).

Malgré le fait qu'il ne disposait pas de l'excellent verre italien, Christiaan voulut - ou plutôt tant lui que son frère Constantyn voulurent - rendre au moins la forme des lentilles aussi parfaite qu'ils en étaient capables. Il semble71) que les ‘Mémoires sur la taille de lentilles pour lunettes à longue vue’, ou plutôt ‘Memorien aengaende het slijpen van glasen tot verrekijckers’ - car la Pièce ne fut écrite qu'en néerlandais72) - furent déjà partiellement rédigés dans la première moitié de 1682. Ils furent achevés par Christiaan trois ans plus tard. En août 1685 le frère Constantyn est en train de les copier73). Des petites additions ont été imprimées par nous en italiques74). C'est ainsi, pour en donner un exemple, qu'il est écrit en marge dans une Pièce de 1686 sur la taille d'une lentille: ‘Nous nous servions encore en ce moment [pour polir] de vert-de-gris au lieu de vitriol qui est infiniment meilleur’75). L'alinéa des Mémoires: ‘Depuis que nous avons pris du vitriol au lieu de vert-de-gris ce que nous disons du chauffage de l'écuelle n'est plus nécessaire etc.’76) date donc de plus tard. On voit que les frères amélioraient constamment leurs procédés77). Leur nouvelle

machine pour le polissage de 1683-168578) a déjà été mentionnée à la p. 12 qui précède79). Ce n'était plus un appareil dans le genre de ceux de 1665 et des années suivantes80).

A. Heller dans sa ‘Geschichte der Physik von Aristoteles bis auf die neueste Zeit’ de 1882 (T. II, p. 180) fait connaître l'existence, à Namur, de trois lentilles qui n'ont pas été mentionnées dans notre T. XV: elles portent respectivement les inscriptions: ‘C. Huygens 15. Mai 1685’; ‘C. Huygens 12. Juni 1685’; ‘Chr. Hugenius ao 1685, 24 Juli’.

Dans des remarques ajoutées à sa copie de 1685 le frère Constantyn mentionne encore, outre des lentilles déjà connues, un verre de Christiaan du 5 janvier 1686 et deux de lui-même: l'un de 120 pieds du 16 décembre 1685, l'autre de 42 pieds du 31 mars 1687. De ce dernier il dit avoir taillé l'un des deux côtés dans l'écuelle de Spinosa81).

 

En 1684 Huygens s'occupa probablement aussi de musicologie, puisque nous avons pu établir82) que ses citations de Théocrite de la f. 1 du Portefeuille ‘Musica’ datent de cette année. Il s'en était occupé en 1681 d'après le témoignage du compositeur van Blankenburg, organiste de l'église wallonne à la Haye, qui le connaissait fort bien83). Il est fort possible qu'il s'en soit occupé constamment. Il est plusieurs fois question dans les pages du T. XX de l'édition de 1682 des ‘Harmonika’ de Ptolémée; à la p. 96 nous avons signalé un passage probablement antérieur à cette édition. La Pièce ‘Tons de ma flute’84) est de 1686.

 

En 1685 ou 1686 Huygens vit dans le traité d'algèbre de Wallis (de 1685) des approximations de ce que nous appelons maintenant le nombre π déduites par Newton de certains développements en séries lesquels ce dernier compare avec les résultats obtenus en 1654 par Huygens85). Wallis y parle aussi du développement en une fraction continue, d'après Brouncker, de sa célèbre formule (celle de W.) pour 4/π, ce

qui donne lieu à Huygens de calculer la fraction continue qui représente le nombre π lui-même86). Cette formule de Wallis avait été obtenue jadis par une induction (‘induction incomplète’, dit-on parfois) que Huygens avait condamnée autrefois87) et qu'en cette occasion il condamne de nouveau. Quant aux fractions continues il s'en était déjà servi dès 1680 pour le calcul du nombre de dents des roues du planétaire. Il s'en trouvait d'ailleurs dans l'‘Arithmetica infinitorum’ de Wallis de 165688).

 

Il a été question plus haut89) de la détermination de la parallaxe des étoiles laquelle Hooke s'imaginait avoir mesurée, ce qu'on n'avait pas pu confirmer à Paris. Constatant l'impossibilité de cette mesure, Huygens se proposa de déterminer la distance d'une grande étoile fixe, supposée (pour le besoin de la cause) égale au soleil, ‘en prenant une petite parcelle du soleil par un trou a mettre un cheveu et s'en eloignant jusqu'a cela paroisse comme une des plus grandes fixes’. C'est ce qu'il dit dans un de ses manuscrits, de 1686, qu'il intitule ‘Pensees meslees’90). Ailleurs dans la même Pièce91) il observe qu'on ne réussirait pas à faire - au bout du tube fermé par lequel on regarde - un trou assez petit pour cet effet, ni aussi, si ce trou était fait, de le mesurer. Il faut donc d'abord prendre la lune au lieu du soleil, et puis mesurer ‘la quantieme [partie] fait la lune du soleil [pour l'éclairage]’. Un calcul numérique correspondant à cette expérience a été écrit en marge au § 15. Il est donc fort possible que ce calcul, et l'expérience, datent de plus tard.

 

Les ‘Pensees meslees’ traitent tant du planétaire que de l'univers réel dont il représente une petite partie. Huygens sait - il aurait pu citer Cléanthe, Aristarque et Plutarque - que le ‘systeme veritable’ des planètes de Copernic ‘perfectionnè d'avantage par Kepler’ a été ‘commencè par quelques anciens philosophes’92).

Apparemment il songe à publier un traité astronomique.

Il cherche le mouvement des comètes de leur embrasement comme aux fusées93).

Croyant toujours aux tourbillons unilatéraux cartésiens - qu'il n'avait remplacés par des tourbillons multilatéraux que pour la pesanteur auprès des corps célestes - il polémise contre ‘la fausse conclusion de Kepler qui veut que le soleil meuve [les planètes]’, ainsi que contre d'autres idées du même astronome94): pour Kepler le soleil était le centre de l'univers, il y avait autour de lui un grand vide, les étoiles se trouvaient toutes sur une même sphère. C'est ainsi que le vrai et le faux sont entremêlés chez les plus grands penseurs.

Il polémise aussi contre le système de Tycho Brahé95), contre la contiguïté des tourbillons de Descartes96) etc. Il ne peut admettre avec le cinquième livre de Lucrèce97) que le hasard ait produit le monde - comparez la p. 634 qui précède - ni avec Aristote que le soleil, la terre et ses habitants etc. n'auraient eu aucun commencement. Les planètes, pense-t-il, sont habitées98). Il peut y en avoir au delà de Saturne99). Nous avons affaire en somme à une première ébauche du ‘Cosmotheoros’ de 1694-1695. C'est peut-être le désir d'une conciliation partielle entre la conception géocentrique, ou d'autres conceptions anciennes, et la conception nouvelle du monde qui le conduit à écrire: ‘Vereri videntur ne veritas veritati contraria inveniatur, vel ne facta Dei dictis non consentiant100)’, sans qu'il puisse ne pas voir que l'effort de ceux qui voudraient sauvegarder à la fois des conceptions du monde de diverses époques est parfois aussi pénible que respectable.

 

Vers le même temps, en septembre 1686, Huygens fut visité par N. Fatio de Duillier, jeune savant suisse, qui avait étudié l'astronomie pratique chez Cassini à Paris et venait en Hollande, non seulement pour faire sa connaissance, mais aussi pour publier sa ‘Lettre à M. Cassini, touchant une lumière extraordinaire qui parut dans le ciel etc.’ (la lumière zodiacale) dans le premier tome, de cette année, de la ‘Blbliothèque universelle et historique’, revue d'Amsterdam. De la Hire, qui dans la suite fut un fidèle correspondant de Huygens - c'est surtout par ses lettres que Huygens resta en relations avec l'Académie - lui en avait écrit101). Fatio s'intéressait aussi

à d'autres phénomènes météorologiques: il donna à Huygens des ‘Observations touchant la figure des parcelles de neige’102). Huygens lui permit d'inscrire dans son Manuscrit F une ingénieuse petite Pièce de son invention sur l'engrenage de deux roues103), sujet auquel s'intéressaient tant Huygens que de la Hire. Il en résulta une véritable amitié.

Lorsque Fatio visita Huygens de nouveau, en mars 1687, celui-ci avait reçu - en octobre 1686 - un livre de Tschirnhaus intitulé ‘Medicina corporis, seu de sanitate conservanda’ qui venait de paraître à Amsterdam et peu après un deuxième (de 1687): ‘Medicina mentis, sive tentamen genuinae Logicae’. Dans ce dernier se trouvait l'énoncé, mais non pas la démonstration d'un théorème sur la façon de mener des tangentes à une certaine espèce de courbes. Huygens doutait de sa vérité, comme il le dit dans sa lettre à Tschirnhaus du 10 mars. Fatio, avec qui il en causa quelques jours après, en avait reconnu la fausseté. Nous l'avons dit aussi aux p. 483-484 du T. XX, en renvoyant dans une note à une publication de Fatio dans le no. d'avril de la ‘Bibliothèque universelle et historique’104). On peut consulter sur la collaboration de Fatio et de Huygens sur ce sujet ce que Fatio en a écrit en 1689105). Huygens continua les calculs; il s'agit de tangentes à des courbes exprimées en coördonnées bipolaires, tripolaires, etc.106).

 

Ce fut en ce temps, savoir le 26 mars 1687, que son père décéda. Si le vieillard avait vécu jusqu'à la fin de 1688 il eût vu son jeune maître, le stadhouder, roi d'Angleterre107).

Bientôt Huygens quitta la maison du Plein pour loger quatre mois chez son frère et s'établir ensuite à Hofwijck108) à Voorburg où, étant seul à dîner et à souper, il dira que cela lui fait un peu de peine109).

Le départ du frère Constantyn pour l'Angleterre en 1688 mit définitivement fin au travail conjoint des frères110) sur la taille des lentilles, dont d'ailleurs Christiaan avait dû s'abstenir depuis quelque temps pour cause de santé.

Nous observons encore que le père Constantyn légua à Christiaan ses compositions musicales manuscrites dont plus tard nous n'apprenons plus rien.

 

Revenons aux années 1686-1687. Les ‘Pensees meslees’ font déjà voir chez Huygens une tendance à ne pas se borner dans ses écrits à ce qui relève d'expériences, d'observations ou de mathématique. Le père Constantyn, indigné - la lettre l'a ‘fait rire’ - de voir que Louvois avait adressé une épître à Christiaan en l'appelant ‘mathematicien’, disait avec hauteur: ‘Je ne croyois pas avoir des gens de mestier parmi mes enfans...Il semble le prendre pour un des Ingenieurs de ses fortifications111)’. Et en effet Christiaan ne se bornait pas à exercer une profession. Sous ce rapport il était encore plus libre en Hollande qu'à Paris. Il fait preuve de son esprit ouvert en écrivant vers la fin de 1686 - ou peut-être dans un des premiers mois de 1687 - la Pièce qu'on a pu lire dans les ‘Varia’ du présent Tome112) ‘Ad Wetstenij dissertationem de linguae graecae pronuntiatione, contra Henninium’. On voit dans notre première note à cette Pièce que Huygens est d'accord avec Henninius dont il connaissait déjà avant 1684 le manuscrit (publié en cette année) où ce savant défend son opinion que les mots grecs ne doivent pas être prononcés suivant les accents.

L'argument de Huygens c'est que, si l'on prononce d'après les accents, il en résulte dans les vers une ‘absurdissima modulatio’. Vers la fin de la Pièce il propose même de rejeter entièrement les accents.

L'on constate ailleurs que désormais il suivait cette maxime. On trouve encore des accents dans quelques mots grecs antérieurement écrits113), on n'en trouve plus dans les citations de Théocrite de 1684114). Ce n'est pas par négligence que Huygens les omet, ou faute de les connaître, c'est par principe.

Vers la fin de la Pièce115) il fait des remarques étymologiques qui se prêtent à des discussions.

 

D'un tout autre genre est la Pièce, de 1686 ou 1687, se rattachant à la discussion de 1669 sur la cause de la pesanteur que Huygens envoya à Paris en juin 1687116)

avec d'autres Pièces qu'on se proposait d'imprimer117). Nous n'en avons publié que quatre pages puisque c'est, pour la plus grande partie, la même Pièce qui parut en 1690 à la Haye sous le titre: ‘Discours de la pesanteur’. Huygens y traite des tourbillons multilatéraux118) - ‘matière fluide...ayant [son] mouvement vers tous les costez’ -. Vers la fin de la quatrième page il parle de ce qu'il croit avoir été établi par l'expérience, savoir qu'un corps pesant ‘au fonds d'un puits, ou de quelque mine profonde’ ne perd rien de sa pesanteur. Comparez ce qu'il disait en 1666 admettre sur l'invariabilité de la pesanteur lorsqu'on s'élève à une hauteur de 3000 pieds119). Bientôt nous le verrons admettre par une extrapolation hardie que la pesanteur dans la terre est tout-à-fait indépendante de la profondeur.

 

La ‘Dernière manière pour expliquer les effets de l'aimant’ que Huygens se proposait d'envoyer à du Hamel - mais nous ne voyons pas qu'il l'ait fait - doit dater de la première moitié de 1687 au plus tard puisque nous y rencontrons la sentence prénewtonienne: ‘l'on sçait que les planetes sont portées dans un tourbillon autour du soleil, et les satellites des planetes au tour d'eux dans des tourbillons particuliers’120). Parlant de la matière etherée121) qui par sa pression ‘doit contribuer plus a tenir les parties du fer unies que celles des autres corps dans lesquels elle a partout des passages libres’122), Huygens entend la ‘matiere etherée qui sert a la propagation de la lumiere et qui passe facilement a travers le verre et toute sorte d'autres corps’123).

L'éther peut-il donc passer facilement à travers toute sorte de corps et néanmoins être la cause de leur cohésion? Malebranche lui aussi s'était montré d'avis en 1675, après bien des hésitations, que la cohésion ne peut être comprise autrement que par l'effet d'une pression extérieure124).

Nous ne pouvons dire exactement de quelle année date la détermination expérimentale de la fréquence des vibrations correspondant à un certain ton que nous avons rapportée au T. XIX125).

 

La visite de Fatio avait ranimé le zèle de Huygens pour la mathématique. La lecture des ‘Acta Eruditorum’ de Leipzig, où écrivaient Leibniz et Jacques Bernoulli126) - Leibniz y avait publié en 1684 sa célèbre ‘Nova methodus pro maximis et minimis, itemque tangentibus’ de lecture difficile et que Huygens n'avait pas tâché d'assimiler - agissait dans le même sens. En 1687 nous y trouvons une Pièce de Huygens, dans la livraison d'octobre. C'est la solution du problème, proposé par Leibniz en septembre, de la courbe de descente uniforme127).

En ce même mois d'octobre il reçut de Fatio de Duillier, d'Angleterre - après avoir déjà reçu une courte lettre de lui de fin juin128) - la longue lettre à laquelle il a été plusieurs fois fait allusion dans des Tomes antérieurs mais que l'on ne connaissait pas encore. C'est la ‘Epistola Fatij’ dont Huygens parle à la p. 514 du T. XX129). Elle est publiée pour la première fois dans le présent Tome, p. 126-151. Comme le dit l'en-tête, nous l'avons reçue de Mons. O. Spiess, de Bâle, bien connu par ses publications sur les mathématiciens suisses. Elle se rapporte au problème inverse des tangentes: Fatio avait trouvé une méthode, pour les courbes algébriques, d'établir leur équation ‘lorsque la propriété des tangentes est donnée’, c.à.d. lorsque ce que nous appelons la tangente trigonométrique de l'angle que fait avec l'axe des x la tangente à la courbe cherchée est donnée en fonction des deux coördonnées x et y. On peut dire plus simplement: lorsque la soustangente est donnée en fonction de x et y.

 

Toutefois, Huygens ne s'occupa pas encore en ce moment de cette méthode. C'est qu'il venait de recevoir un livre fort important et nullement aisé à lire: Fatio en parle au début de sa longue lettre: ‘Je ne voulus pas differer de vous envoier le livre de

Monsr. Newton, que vous aurez sans doute reçu depuis longtemps’. Les célèbres ‘Philosophiae naturalis principia mathematica’ avaient vu le jour au mois de juillet; Huygens a sans doute eu le livre en sa possession dès le mois d'août.

La lecture des ‘Principia’ le conduisit en novembre et décembre 1687 à faire des calculs sur l'aplatissement de la terre en vertu de sa rotation. Comme il avait déjà écrit une page sur ce problème, il est fort naturel que les considérations de Newton sur la forme de la terre attirèrent en premier lieu son attention. Nous l'avons dit dans notre Avertissement à ces ‘Considérations ultérieures sur la forme de la terre’130). Dans le § 1 le calcul du rapport des axes de la terre est basé sur la thèse - énoncée dans la page mentionnée - que la surface doit être perpendiculaire à la résultante de la force centrifuge et de la pesanteur dirigée vers le centre. Dans les paragraphes suivants Huygens adopte la méthode des canaux de Newton. Admettant une pesanteur constante dans toute la terre, il trouve suivant l'une et l'autre méthode la fraction 1/578 pour l'aplatissement131). Il y joint quelques calculs sur la variation de la longueur du pendule à secondes.

 

En 1688 Huygens écrivit pour la Compagnie des Indes orientales le rapport détaillé dont il a été question plus haut. Nous le supposons aussi absorbé dans l'étude des ‘Principia’. Nous avons déjà mentionné132) un calcul de probabilité. Dans les ‘Varia’ on voit une petite Pièce sur le redressement d'une tour à Rotterdam133). Vers la fin de l'année nous trouvons ausfi plusieurs pages sur la spartostatique, et la rupture d'une poutre134).

 

Nous saisissons cette occasion pour dire que depuis 1686 le frère Lodewijk habitait Rotterdam, ayant maintenant la charge de député à vie de la ville de Gorinchem au collège de l'Amirauté de la Meuse.

 

Vers la fin de l'année Huygens vérifia le calcul de Newton sur la gravité de la lune égale à la force centrifuge qui correspond à son mouvement. Nous le voyons bien convaincu de la diminution de la gravité en raison inverse du carré des distances, que ce soit celle auprès de la terre ou bien celle qui retient les planètes dans leurs orbites

autour du soleil, et il comprend et approuve aussi les théorèmes de Newton faisant voir qu'en vertu de cette propriété de la gravité les planètes doivent décrire des ellipses et qu'elle explique de plus les deux autres lois de Kepler. Il calcule, après Newton, la gravité à la surface de Jupiter ou d'une autre planète, ou du soleil, non sans y ajouter un calcul sur la rapidité que la circulation de la matière subtile, causant, pense-t-il toujours, cette gravité, doit avoir à la surface du soleil135).

Le 14 décembre 1688 il ajoute à ses considérations de 1680-1681 sur les orbites planétaires: ‘Hasce omnes difficultates abstulit Clar. vir Neutonus simul cum vorticibus Cartesianis; docuitque planetas retineri in orbitis suis gravitatione versus solem. Et excentricos necessarie fieri figurae Ellipticae’136).

Et en 1689 à ses Pièces de 1681 sur les comètes la remarque: ‘Je suis maintenant presque du sentiment de Mr. Newton qui veut que les Cometes tournent en des Ellipses fort oblongues autour du Soleil, qui fait l'un des foiers. Cela devient probable apres qu'il a ostè les tourbillons de des Cartes, qui d'ailleurs ne s'accommodaient point avec plusieurs phenomenes des mouvements planetaires’137).

Des observations sur quelques autres passages des ‘Principia’ ont été rapportées dans notre T. XXI138), lesquelles l'amènent aussi à faire de nouveau quelques calculs sur le mouvement avec résistance d'un corps punctiforme. On constate dans les mêmes pages la peine que se donnait l'intelligent Fatio pour comprendre lui aussi le chefd'oeuvre d'un savant pour qui il avait tant d'admiration.

 

Il y avait cependant dans la conception newtonienne du monde une idée que Huygens ne pouvait adopter. Le premier Scholium des ‘Principia’ dit: ‘Spatium absolutum, natura sua absque relatione ad externum quodvis semper manet similare & immobile’139). Or Huygens, on l'a vu plus haut140), était depuis longtemps convaincu de la non-existence du mouvement absolu. La plupart des petites Pièces sur la relativité se trouvent sur des feuilles séparées et ne sont pas datées, mais il y en a une

de 1688 dans le Manuscrit F141). C'est peut-être la première de toutes. Il ne parle pas seulement du mouvement progressif mais aussi de la rotation des corps. Dans la rotation, dit-il, les parties des corps ont un mouvement relatif les unes par rapport aux autres. Ce mouvement peut être appelé un mouvement vr ai car ‘corpora quae mutuo respectu moventur ea vere moventur’. Dans une autre Pièce142) il cite expressément Newton parmi plusieurs auteurs qui estiment à tort ‘verum quendam motum esse qui relativo opponatur’. Néanmoins il nous paraît être resté en doute sur cette question comme cela ressort de sa sentence143): ‘Non est mathematicè difficilis materia, sed physicè aut hyperphysicè144)’.


Vorige Volgende

Over dit hoofdstuk/artikel

plaatsen